二端口网络参数求法
电路分析基础二端口网络的VCR及参数

1 I1
U1
1
I2 2
N
U2
2
——二端口网络的A参数(传输参数)方程
矩阵形式:
UI&&11
A11 A21
A12 A22
U&I&22
A
U&I&22
A
A11 A21
A12
A22
——A参数矩阵
X
4. A参数及A参数方程
I&1 0
端口11的' 开路转移阻抗
数
Z 22
U&2 I&2
I&1 0
端口22的' 开路策动点阻抗
X
例题1 求如图所示二端口网络的Z参数。
解:22' 端口开路:
1 I1
R2
I2 2
Z11
U&1 I&1
I&2 0
U1
R1 R3
U2
1
2
R1
/
/( R2
R3 )
R1(R2 R3 ) R1 R2 R3
U1 0
0 U2
U1 0
0
U&1 0
返回
X
3.H参数及H参数方程
1 I1
I2 2
U&1 H11I&1 H12U&2 I&2 H21I&1 H22U&2
I1
二端口网络的参数

元素为阻抗,
单位是 。
与Y参数方程相同, Z11、Z12、Z21、Z22取决于电路结
构及参数。根据Z参数方程及I1 、I2,可求得 U1 、U 2 。
确定Z参数:
UU12
ZZ1211II11ZZ1222II22
在1-1' 端输入I1 ,将2-2'端开路,即 I2 0 代入上式 有
U1
Z11I1
有
A
U1 U 2
I2 0
称为输出端开路时传输电压比
C
I1 U 2
I2 0
称为输出端开路时转移导纳(S)
UI11CAUU22DB
( (
II22))
2、在输出端短路,即U 2 0 时
有
B
U1 I2
U2 0
称为输出端短路时转移阻抗()
对于图所示的一端口网络来说
Z
U I
或者
Y
I U
U Z I (以电流 I 为已知量)
或者 I YU (以电压U 为已知量)
一、Y 参数及方程(短路导纳参数)
已知 U1、U 2 ,求 I1 、I2 。 由替代定理可将 U1 、U 2 所在支路用理想电压源代替。
•
1 I1
•
I2 2
•
U1
N
•
U2
1′
确定Y参数:
II12 YY1211UU11YY1222UU24
在1-1' 端加 U1,将2-2' 端短路,即 U 2 0 代入上式
I1 Y11U1
Y11
I1 U1
U 2 0
称为输出端短路时的输入导纳(S)
I2 Y21U1
Y21
I2 U1
U 2 0
【推荐】电路原理基础:第二章 二端口网络的方程和参数
D
i1 i2
u2 0, 10
四、H参数方程: 已知i1和 u2求u1和 i2
u1 H11i1 H12u2 i2 H 21i1 H 22u2
1 i1
u1
1' i1
i2 2
N
u2
i2 2'
u1
i2
H11 H 21
H12 H 22
i1 u2
T
0.5 0.75S
0.6
0.5
将其变换为其它参数方程,则可求得其他参数,
注意变换时有些参数可能不存在。
12
六、二端口网络参数的互易性(reciprocal)
若网络中只含有R、 L、 C、 M 等线性元件而不 含有受控源,则网络参数就具有如下性质:
(1) R12 R21 (3) T AD - BC 1
注意与四端子网络(four terminal network)的区别。
无独立源的二端口电阻网络
1
第一节 二端口网络的方程和参数
i1
1
u1
1'
i1
i2
2
N
u2
2'
i2
二端口的外特性决定于网络的本身与外部所接
电路无关,用端口电压、电流(共四个量)间的关 系反映,共六种情况。
2
一、R参数方程:
i1
u1
i2
Rl
u2
R
Rl Rl
Rl
Rl
但G不存在
电路原理13.1.4二端口网络及其参数方程 - 二端口网络及其参数方程2
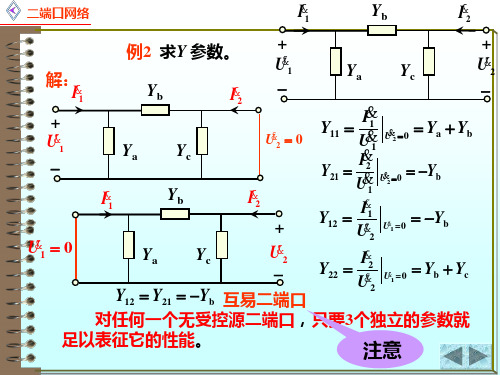
II&&12
Y
UU&&12
Y 1
II&&12
UU&&12
对称二端口 Z11 Z22 (Z12 Z21 )
Z11
Z
21
Z12 Z22
Y11 Y21
Y12 1
Y22
1 ΔY
Y22 Y21
Y12
Y11
若矩阵 Z 与 Y 非奇异
Y Z 1 Z Y 1
二端口网络
+ U1
解一: I1 1
+ U1
2 I2
+
2
U2
2
+ 2 U2
UI11
T11 T21
T12
T22
U2 I2
I1 1
+ U1
2 I2 2
T11
U1 U2
1 2 I2 0 2 1.5
T21
I1 U2
I2 =0 0.5S
T12
U1 I2
U2 =0
I1[1 + (2//2)] 4Ω 0.5I1
Yb
Y22
I&2 U&2
U&1 =0 Yb Yc
对任何一个无受控源二端口,只要3个独立的参数就
足以表征它的性能。
注意
二端口网络
Y
Y11 Y21
Y12
Y22
若Y12 Y21,称为互易二端口。 进一步,若Y11 Y22 ,则称为对称二端口。
I&1
Yb
I&2
+ U&1
Ya
Yc
+ U&2
二端口网络z参数求解技巧

二端口网络z参数求解技巧二端口网络是指由两个端口组成的网络,其中一个端口为输入端口,另一个端口为输出端口。
在分析和设计二端口网络时,我们常常使用参数化方法,其中最常见的是使用z参数。
z参数是指输入端口和输出端口之间的电压和电流之间的关系。
在二端口网络中,输入端口的电流I1和电压V1以及输出端口的电流I2和电压V2之间存在以下关系:```V1 = Z11 * I1 + Z12 * I2V2 = Z21 * I1 + Z22 * I2```其中,Z11、Z12、Z21和Z22是参数矩阵,代表了电路元件的特性。
我们可以利用这些参数来分析和计算二端口网络的性能。
接下来,我将介绍一些求解二端口网络z参数的技巧。
1. 网络简化:首先,我们要对二端口网络进行简化,即将网络中的电路元件替换为等效电路,以便更方便地分析。
我们可以使用电路分析方法,如电压分压法、电流分流法等,将网络简化为电阻、电容和电感等基本元件的串并联组合。
2. 确定输入和输出量:在分析二端口网络时,我们需要确定输入和输出量。
输入和输出量可以是电流和电压之间的关系,也可以是功率和电阻之间的关系。
通过确定输入和输出量,我们可以更准确地描述和计算二端口网络的特性。
3. 确定参数值:在求解z参数时,我们需要确定参数矩阵Z11、Z12、Z21和Z22的具体值。
参数值可以通过实验或仿真等方式获取。
如果我们已经知道了电路元件的数值,我们可以直接使用电路分析方法求解参数值。
如果我们只知道电路的结构和拓扑关系,我们可以使用矩阵分析方法求解参数值。
4. 参数矩阵运算:一旦确定了参数值,我们就可以进行参数矩阵的运算。
参数矩阵的运算包括矩阵加法、矩阵减法、矩阵乘法和矩阵逆运算等。
通过参数矩阵的运算,我们可以得到输入端口和输出端口之间的关系。
5. 分析和计算:最后,我们可以利用参数矩阵进行分析和计算。
例如,如果我们已知输入端口的电流和电压,我们可以使用参数矩阵得到输出端口的电流和电压。
二端口网络参数的计算
科技信息
U, +3 U
z =
高校 理科 研 究
f3
Z =y- 7 l = 4
I z
1 I
7
Y参数矩 阵为 Y :
【。 『1 一 4
叶
8
【丁 丁 J 一
}、数样求。 。H 同可出 T参
4 通 过 测 量 计 算 参 数 、
由此可见 , 两种计算方法所得结果相同。 而写方程求参数方法更简
科技信息
高校 理科 研 究
端 口 网 络 蚕数 晌 计 算
重庆三峡 学院物理 与 电子 工程 学院 宋金 燕
[ 摘 要] 本文介 绍 了几种二端 口网络参数的计算方法。利 用二端 口网络 参数 的定义直接计算 ; 利用建立电路的结点电压方程 、 网孔 电流方程的方法计 算; 通过测量计算。 [ 关键词 ] 端 口网络 二端 口网络参数 参数 的计算方法 二
u to 2 J-  ̄
c l:. 一 。 : 05 6 2L 0
u Io 2I= .
由第 二组测量 结果: f3L 。,f1L 0 , 05 5 A O=0 0 i . 3。 i . 1 。, V _5 A =2 0
U2 O =
由于 Y参数方程是 以端 口电压为 自变量 ,为列写结点电压方程将 电路 改画如下 。由图可见电路有两个独立结点 , 结点电压方程为 : 其
根 据 Y参 数 的定 义 :
=
缶
h r 七一 b
+
(+ 寺 z- 寺)一 i - - 寺o( 寺 it + j i + :一 :s
单。
如有 一二端 口网络 ,当端 口 2开路 时 . I10o4 0 t i 2 cs u 5 cs0 0V,, 5o = = (0 0一 5) U= 0 cs 0 0+ 5) 当端 口 2 40 t4  ̄ A, 210 o( 0 t1 ̄ 4 V; 短路 时,1 3 cs0 0V, U’ 0o40 t = i= .cs40 t3 。 i_ .5o(0 0+ 5 。 则 描 述 该 二 端 口网 络 特 。 1 o(00+ 0) 2 O2 cs 0 t10) ’ 5 A, l 4 A。
三、二端口网络的T方程和T参数(精)

三、 二端口网络的T 方程和T 参数在上述内容中我们已经介绍了Y 参数和Z 参数的求法,Y 参数和Z 参数都可用来描述一个二端口网络的端口外特性。
但在许多工程实际问题中,往往还要求知道一个端口的电流、电压与另一个端口的电流、电压之间的直接关系。
若把Y 参数方程:22212122121111U Y U Y I U Y U Y I +=+=的第二式化为2212212211I Y U Y Y U +-= 代入Y 参数方程第一式中,整理可得:221112212211121)(I Y Y U Y Y Y Y I +-= 把以上两式写成下列形式⎪⎩⎪⎨⎧-=-=221221I D U C I I B U A U式中 ⎪⎪⎩⎪⎪⎨⎧-=-=-=-=2111212211212121221Y Y D Y Y Y Y C Y B Y Y AA 、B 、C 、D 称为二端口网络的一般参数、传输参数、T 参数或A 参数。
它们的具体含义可用下式说明:0221==I U U A A 是输出端开路时,输入电压与输出电压的比值;0221=-=I I U B B 是输出端短路时,输入端对输出端的转移阻抗;0221==I U I C C 是输出端开路时,输入端对输出端的转移导纳;0221==U I I D D 是输出端短路时,输入电流与输出电流的比值。
可见,A 是一个量纲为一的量纲;B 的量纲为Ω;C 的量纲为s ;D 也是量纲为一的量。
对于无源线性二端口网络A 、B 、C 、D 只有3个是独立的,因为Y 11=Y 22,故A =D 。
所以T 参数方程为:其中 ⎥⎦⎤⎢⎣⎡=D C B A T ,称为T 参数矩阵。
AD BC 可逆时,-=1AD BC A D =对称时满足:-=1,【例】 求例1中电路的T 参数【解】:方法一:根据定义求解(略)方法二:根据KCL 直接列方程求解(略)方法三:根据T 参数与Y 参数或Z 参数的转换公式(可在表6-1中查到)求⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-∆---=2111212121221Y Y Y Y Y Y Y T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∆=1222212121111Z Z Z Z Z Z Z T 其中 2112221122211211Y Y Y Y Y Y Y Y Y -==∆2112221122211211Z Z Z Z Z Z Z Z Z -==∆因为已知例1的 s Y ⎥⎦⎤⎢⎣⎡--=4.02.02.04.0 12.004.016.0=-=∆Y所以 ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=26.0522.04.02.012.02.012.04.0T⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡2211D I U C B A I U【例 】:已知...1111122...2211222(1)(2)U Z I Z I U Z I Z I =+=+ ,求T 参数。
14.2 二端口网络的方程和参数
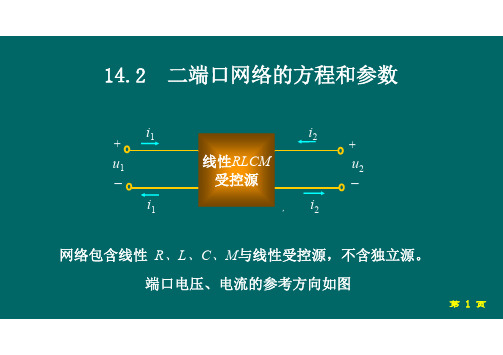
Z
Za Zb
Zb
Zb
Zb
Zc
第 20 页
例题 求二端口Z、Y 参数
I1 R1 j M R2 I2
+
U1
jL1
*
*
jL2
+ U 2
–
U1 R1 jL1 I1 jMI2
U2 jMI1 R2 jL2 I2
Z
R1 jL1
jM
jM
R2
j L2
R2 jL2
Y Z 1
Z I2 0
b
解法1
U1 Z11I1 Z12 I2 U 2 Z21I1 Z22I2
Z12
U1 I2
Z I10
b
Z22
U 2 I2
I10 Zb Zc
第 18 页
解法2
I1 Za
+
U1
Zc Zb
I2
+
U2
列KVL方程:
U1 ZaI1 Zb I1 I2 Za Zb I1 ZbI2
第2页
I1 I1 I1 Y11U1 Y12U2
I2
I2
I2
Y21U1
Y22U 2
I1 Y11U1 Y12U 2
I2
Y21U1
Y22U 2
I1
I2
Y11 Y21
Y12 U1
Y22
U
2
注意 Y参数的值由网络内部元件参数及连接关系决定。
第3页
② Y参数的物理意义
Y11
=
u1
i1
n 0
0
1
u2
i2
n
n 0
T 0
1
n
第 27 页
