二端口网络的传输参数、混合参数方程
演示文稿二端口网络参数和方程

二端口网络参数和方程
13.1 二端口网络及其参数方程
一、一端口网络和二端口网络的概念
1. 一端口网络
I
+
U
Z
-
(Y)
表征一端口网络电特性的独立 参数:输入阻抗Z或输入导纳Y。 且 Z = Y -1 。
i1 +
u1
i1
–
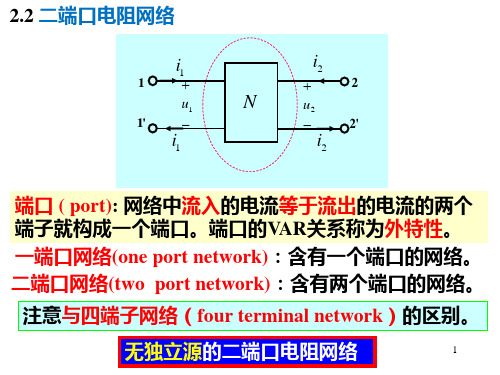
端口的概念:
端口由一对端子构成,且满足如下 条件:从一个端子流入的电流等于 从另一个端子流出的电流。此称为 端口条件。
i2 +
u2 – i2
4. 二端口与四端网络的区别:
二端口的两个端口必须 满足端口条件,四端网 络却没有上述限制。
i1
i2
i1
i2
二端口
i1
i2
i1
i2
具有公共端的二端口
i2 i1
i3 i4
四端网络
二端口的两个端口间若有外部连接,则会破坏原二端口的 端口条件。
1
i1
i 3
R
4 i2 2
u1
i1
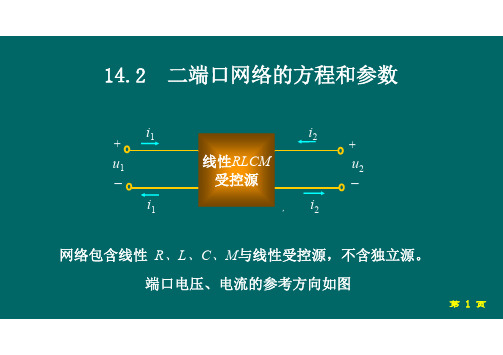
2.四端网络 在工程实际中,研究信号及能量的传输和信 号变换时,经常碰到如下形式的电路。称为 四端网络。
线性RLCM 受控源
四端网络
例1
R
C
C
滤波器 n:1
变压器
三极管 传输线
3. 二端口(two-port)
如果四端网络的两对端子同时满足端口条件, 则称为二端口网络。
+
i1
u1 –
i1
线性RLCM 受控源
整理可得
I1 = (Y1 Y2 )U1 - Y2U2 I2 = -Y2U1 (Y2 Y3 )U2
【推荐】电路原理基础:第二章 二端口网络的方程和参数
D
i1 i2
u2 0, 10
四、H参数方程: 已知i1和 u2求u1和 i2
u1 H11i1 H12u2 i2 H 21i1 H 22u2
1 i1
u1
1' i1
i2 2
N
u2
i2 2'
u1
i2
H11 H 21
H12 H 22
i1 u2
T
0.5 0.75S
0.6
0.5
将其变换为其它参数方程,则可求得其他参数,
注意变换时有些参数可能不存在。
12
六、二端口网络参数的互易性(reciprocal)
若网络中只含有R、 L、 C、 M 等线性元件而不 含有受控源,则网络参数就具有如下性质:
(1) R12 R21 (3) T AD - BC 1
注意与四端子网络(four terminal network)的区别。
无独立源的二端口电阻网络
1
第一节 二端口网络的方程和参数
i1
1
u1
1'
i1
i2
2
N
u2
2'
i2
二端口的外特性决定于网络的本身与外部所接
电路无关,用端口电压、电流(共四个量)间的关 系反映,共六种情况。
2
一、R参数方程:
i1
u1
i2
Rl
u2
R
Rl Rl
Rl
Rl
但G不存在
二端口网络参数和方程和等效电路相关知识讲解培训

(1) H 参数
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
矩阵形式:
UI21
H11
H
21
H12 H 22
UI12
(2) H 参数的计算与测定
H11
U 1 I1
U 2 0
H21
I2 I1
U 2 0
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
Y21
I2 U 1
U 2 0 Yb Y12
Ya Yb Y11 即:Yb Y12 Y21
Yb Yc Y22
解之得
Ya Y11 Y12 Yb Y12 Yc Y22 Y12
注意: (1) 等效只对两个端口的电压,电流关系成立。对端 口间电压则不一定成立。
(2) 适用于互易网络。
I2
Y12U1 Y22U 2
Y21 Y12
U 1
I2
其中
I1 I'2
Y11U 1 Y12U 1
Y12U 2 Y22U 2
相当于一互易二端口,
可求出其等效电路(型):
(计算见前例)
•
I1
+
•
U1
Yb
Ya
Yc
I2
+
•
U2
而I2 I2 Y21 Y12 U1相 当 于 在 端 口2并 入 一 受 控 源.
C
I1 U 2
I2 0
D
I1 I2
U 2 0
U1 AU 2 BI2
I1
CU 2
DI2
(3) 互易二端口 Y12 Y21
T 参数满足: AD BC 1
二端网络参数分析

二端网络参数分析二端网络(Two-port network)是指具有输入端和输出端的电气网络系统。
它是信号传输和处理的基础,广泛应用于通信、电子、电力等领域。
为了评估二端网络的性能和特性,人们引入了网络参数进行分析。
本文将介绍二端网络的四种主要参数:传输参数、散射参数、混合参数和链路参数,并分别解释它们的含义和应用。
1. 传输参数传输参数(Transmission parameters),又称为T参数,描述了输入和输出之间的传输关系。
它是输入电压与输出电流之比和输入电流与输出电压之比的比值。
通常用矩阵形式表示:T = [T11 T12; T21 T22]其中,T11和T22分别表示输入电压与相应输出电流之比,T12和T21表示输入电流与相应输出电压之比。
传输参数广泛应用于线性电路分析和设计领域,可以用来计算电压传输函数和电流传输函数,从而评估二端网络的增益和频率响应。
2. 散射参数散射参数(Scattering parameters),简称S参数,是描述电路中信号的反射和传播特性的重要参数。
它用于描述输入和输出之间的散射关系,即输入到输出的信号在电路中的散射情况。
散射参数也可以用矩阵形式表示:S = [S11 S12; S21 S22]其中,S11表示输入端口的反射系数,S22表示输出端口的反射系数,S12表示从输出端口到输入端口的传输系数,S21表示从输入端口到输出端口的传输系数。
散射参数可以用来计算功率增益、频率响应和信号的反射损耗,是无源二端网络分析中的重要工具。
3. 混合参数混合参数(Hybrid parameters),也称H参数或h参数,用于描绘二端网络中输入和输出端之间多种电路元件的相互作用情况。
它是电压和电流之间的线性关系,由下列方程组来描述:V1 = h11 * I1 + h12 * V2I2 = h21 * I1 + h22 * V2其中,h11和h22表示输入输出之间的电流传输关系,h12和h21表示输入和输出之间的电压传输关系。
14.2 二端口网络的方程和参数
Z
Za Zb
Zb
Zb
Zb
Zc
第 20 页
例题 求二端口Z、Y 参数
I1 R1 j M R2 I2
+
U1
jL1
*
*
jL2
+ U 2
–
U1 R1 jL1 I1 jMI2
U2 jMI1 R2 jL2 I2
Z
R1 jL1
jM
jM
R2
j L2
R2 jL2
Y Z 1
Z I2 0
b
解法1
U1 Z11I1 Z12 I2 U 2 Z21I1 Z22I2
Z12
U1 I2
Z I10
b
Z22
U 2 I2
I10 Zb Zc
第 18 页
解法2
I1 Za
+
U1
Zc Zb
I2
+
U2
列KVL方程:
U1 ZaI1 Zb I1 I2 Za Zb I1 ZbI2
第2页
I1 I1 I1 Y11U1 Y12U2
I2
I2
I2
Y21U1
Y22U 2
I1 Y11U1 Y12U 2
I2
Y21U1
Y22U 2
I1
I2
Y11 Y21
Y12 U1
Y22
U
2
注意 Y参数的值由网络内部元件参数及连接关系决定。
第3页
② Y参数的物理意义
Y11
=
u1
i1
n 0
0
1
u2
i2
n
n 0
T 0
1
n
第 27 页
四、二端口网络的H方程和H参数(精)

四、 二端口网络的H 方程和H 参数除去上述的3套方程和参数,还有一套常用的参数方程称为混合参数或H 参数。
即:...1111122...2211222U H I H U I H I H U =+=+在晶体管电路中,H 参数得到了广泛的应用。
其具体定义为:21111==U I UH H 11是输出端短路时,输入端的入端阻抗,在晶体管电路中称为晶体管的输入电阻;012112==I U UH H 12是输入端开路时,输入端电压与输出端电压之比,在晶体管电路中称为晶体管的内部反馈系数或电压传输比;21221==U I IH H 21是输出端短路时,输出端电流与输入端电流之比,在晶体管电路中称为晶体管的电流放大倍数或电流增益;12222==I U IH H 22是输入端开路时,输出端的入端导纳,在晶体管电流中称为晶体管的输出电导。
用矩阵形式表示为;⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡212221121121U I H H H H I U其中,H 称为H 参数矩阵⎥⎦⎤⎢⎣⎡=22211211H H H H H H 参数的求解方法也可分为3种,用定义直接求,用KCL 定理转换方程求解,在已知其他3种参数的前提下,用转换公式直接求(见表6-1)。
例如:在已知Y 参数下11211222112211212111121211111Y Y Y Y Y H Y Y H Y Y H Y H -==-==可见对于无源线性二端网络,H 参数中只有3个是独立的。
H 21=-H 12。
对于对称的二端口,由于Y 11=Y 22或Z 11=Z 22,则有121122211=-H H H H【例】 如例4所示电路图,求H 参数 【解】: 方法一:172644021111jU I U H -=== 1727012112jI U U H +=== 1741021221jU I I H +-=== 174012222jI U I H -=== 方法二:列写端口KVL 方程方法三:利用转换公式在已知Z 参数情况下求H 参数⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-∆=2222212212221Z Z Z Z Z ZZ H 已知⎥⎦⎤⎢⎣⎡++-=j j j j Z 422 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-+++-=17417411727172644414424410j j j j j jj j j jj H 【例】: 求如图6-1-7所示二端口的H 和T 参数。
《电路基础》第30讲 二端口电路及其方程和参数

组不同的方程来描述二端口电路的端口伏安特性。
8
(一)Z参数(流控型)和方程(VCR)
如果选端口电流 I1和I2
为自变量,U1和U2
为应变量。根据替代
I
S1
定理,端口电流 I1和I2
I
1
+
U
-1
N
可用相应的电流源替
代。如图所示。
I
2
+
U
-2
I
S2
根据叠加定理可得
二端口电路的 Z方程
U1 z11I1 z12I2 U2 z21I1 z22I2
9
z11、z
、z
12
21和z22为Z参数
U1 z11I1 z12I2
物理含义如下:
U2 z21I1 z22I2
z11
U1 I1
I2 0
出口开路时输入阻抗
z21
U2 I1
I2 0
出口开路时正向转移阻抗
z12
U1 I2
I1 0
入口开路时反向转移阻抗
z22
U2 I2
I1 0
入口开路时输出阻抗
Z参数称为“开路阻抗参数”。
U2
y11 y21
I2
(4
)
(3)(4)式组成A方程,即:
UI11
a11 a21
a12 a22
U2I2
18
例 : 求所示电路的A参数
I1
n:1
解: U1 nU2
+
U1
I1
1 n
I2
即
UI11
n 0
0 1
n
UI22
I2
+
U2
电路理论基础(哈尔滨工业大学陈希有第3版)14

2 阻抗参数方程 二端口的阻抗参数方程或Z参数方程
& & & U1 = Z11I1 + Z12 I 2 & & & U = Z I +Z I
2 21 1
22 2
矩阵形式:
& & U1 Z11 Z12 I1 & = & Z21 Z22 I2 U2
& I 2 =0
& U1 Z12 = & I2
Z22
& I1 =0
& U2 = & I2
& I1 =0
例题
& 1 I1
14.2
I&3
30Ω
40Ω
30Ω
I&2 2
& U2
2'
求左图所示二端口的阻抗参数矩阵。
& U1
1'
& I1
20Ω
& I2
解
& & 求Z 参数宜列回路电流方程 宜列回路电流方程。用电压源 U 和 U2 宜列回路电流方程 分别置换端口1和端口2的外接电路。
相量形式:
& & U = ZI
Z11 Z12 Z = Z21 Z22
二端口阻抗参数 矩阵或Z 参数矩 阵
•互易条件: Z12 = Z21
•对称条件: Z12 = Z21 和 Z11 = Z22
例:如图1所示二端口互感:
+ & U −
jωM
1
& I1 * jωL1
& * I2
jωL2
& I1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
放大小信号时的交流微变等效电路
U1 H11I1 H12U2 rbeI1
I2
H 21I1
H 22U 2
I1
1 rce
U2
忽 略
H
H11 H 21
H12 H 22
rbe
0
1
rce
P66 [例7-7]
解:求 H参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
P66 [例7-7]续 解:再求 T 参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
U1 2U 2
,
I1
I2 2
I1
I1
U1 3
即
I1
I2 2
2U 2 3
先列出 T 参数方程的结构,再具体化
U1 AU2 B( I2) 2U2 2U2 0
I1
CU2
D(
I
)=
2
U1 3
I1
2 3
电流 放大倍数
转移电导
转移电阻
二 端 口 网 络 参 数 方 程 小 结
二端口网络参数方程小结
互易二端口网络不含受控源,从互易网络应满足的 条件可知,四个参数中只有三个是独立的。
第7章 二端口网络的概念
7.1 二端口网络的端口条件及导纳参数、阻 抗参数方程
7.2 二端口网络的传输参数、混合参数方程 7.3 互易二端口网络的等效电路与级联
二端口网络的导纳参数、阻抗参数是基本参数, 而传输参数、混合参数是工程中的应用参数。
7.2.1 二端口网络的传输参数方程
U1
AU 2
B(
I
)
2
A
C、D的定义为:
•
U1
•
22′端口开路时
U2
•
I2 =0
的转移电压比。
•
C
I1
•
)
U2
•
I 2 =0
22′端口开路时 的转移导纳(S)
•
B
U1
•
I • 2 U 2 =0
22′端口短路时
的转移阻抗( )
•
D
I1
•
I • 2 U 2=0
22′端口短路时 的转移电流比
22′开路 22′短路
P66 [例7-4]
B(
I
)
2
I1
CU2
D(
I
)
2
U1
U2
Z(
I
)
2
I1 I2
T
1 0
Z
1
与该图结构相同的二端口 网络,其T参数均与此式一致。
——该式可作公式用
22′开路 22′短路
P66 [例7-5]
解 按T参数的定义计算:
U1
AU2
B(
I
)
2
I1
CU2
D(
I
)
2
I2 0、同时U2 U1
•
A
U
•
1
1
U2
I
)
2
I1
CU2
D(
I
)
2
传输参数方程 的矩阵形式
UI11
A C
B D
UI22
T
UI22
该方程以 U2、 I2 为自变量, U1、I1 为因变量,反映 了22′端口的电压、电流对11′端口电压、电流的控制能力, 即反映了二端口间的传输特性。
U1
AU2
B(
I
)
2
T参数A、B、
I1
CU2
D(
U1 H11I1 H12U2 I2 H21I1 H22U2
H参数 H11、H12、H21、H22 的定义为
H11
U1 I1
U2 0
22′端口短路时
的输入阻抗( )
I H I ) 21
2
U2 0 1
22′端口短路时 的转移电流比
H12
U1 U2
I1 0
H 22
I2 U2
I1 0
11′端口开路时 的转移电压比
11′端口开路时 的输入导纳(S)
比较并分析以下两个参数是否相等?
•
A
U1
•
U2
•
I 2 =0
条件是:I2 0
H12
U1 2
I1 0
条件是:I1 0
条件不 一致,因 此两者不 相等。
其他参数也有类似情况,条件不同,参数值不相等。
P66 [例7-6]
电子线路中的晶体三极管,它起电流 放大作用,有三个电极:
U1 2U 2
,
I1
I2 2
I1
I1
U1 3
即
先列出H参数方程的结构,再具体化
I1
I1
U1 3
U H I H U 2U H12 H21
1
11 1
12 2
2
0 2U2
I2 H21I1 H22U2
2(
I1
U1 3
)
2I1
4 3
U
2
0 2
H
2
4 3
S
该图不含受控源,是互易网络,
互易网络的H参数 : H12 H21
解 按T参数的定义计算:
U1
AU2
B(
I
)
2
I1
CU2
D(
I
)
2
I2 0、同时I1 0,则U2 U1
•
A
U1
•
1
U2
•
I 2 =0
•
C
I1
•
0
U2
•
I 2 =0
U2 0 , I2 I1
•
B
U1
•
Z
I • 2 U 2 =0
•
D
I1
•
1
I • 2 U 2 =0
P66 [例7-4]续
U1
AU2
——该式可作公式用
7.2.2 二端口网络的混合参数方程
U1 H11I1 H12U2 I2 H21I1 H22U2
混合参数方程 的矩阵形式
UI21
H11
H
21
H12 H 22
UI12
H
UI12
该方程自变量中有电压也有电流, 有11′端口的量也有22′端口的量, 是混合控制型。
U
2
1 2
(I2 )
2 0
T
2 3
S
1
2
该图不含受控源,是互易网络,
互易网络的 T 参数 : AD BC 1
P66
解 题目所给H参数与频率无关,可见是电阻
[例7-8] 性网络。该参数方程用直流电流、电压值表示。
解 方 程
I1
1 14
A
U1
68 7
V
I2
4A 35
U2
20 7
V
U2 20 / 7 20 5 U1 68 / 7 68 17
内容简介
本教材理论推导从简,计算思路交待详细,概念述 明来龙去脉,增加例题数量和难度档次,章节分 “重计 算”及“重概念”两类区别对待,编排讲究逐步引深的 递进关系,联系工程实际,训练动手能力,尽力为后续 课程铺垫。借助类比及对偶手法,语言朴实简练,图文 印刷结合紧密,便于自学与记忆,便于节省理论教学时 数。适用于应用型本科及高职高专电力类、自动化类、 机电类、电器类、仪器仪表类、电子类及测控技术类专 业。
电压 放大倍数
U1 16I1 3U2 I2 2I1 0.01U2 U1 4I1 10 U2 25I2
I2 4 / 35 414 8
I1 1/14
35 5
I1 1/14 1 7 1 S U1 68 / 7 6814 136
U2 20 / 7 2035 25 I2 4 / 35 7 4
•
I 2 =0
•
C
I1
•
Y
U2
•
I 2 =0
U2 U1=0, I2 I1
•
B
U1
•
0
I • 2 U 2 =0
•
D
I1
•
1
I • 2 U 2 =0
P66 [例7-5]续
U1
AU2
B(
I
)
2
I1
CU2
D(
I
)
2
U1 U2 I1 YU2 (I2 )
T
1 Y
0 1
与该图结构相同的二端口 网络,其T参数均与此式一致。
