13二端口网络参数和方程
合集下载
演示文稿二端口网络参数和方程

演示文稿二端口网络参数和方 程
二端口网络参数和方程
13.1 二端口网络及其参数方程
一、一端口网络和二端口网络的概念
1. 一端口网络
I
+
U
Z
-
(Y)
表征一端口网络电特性的独立 参数:输入阻抗Z或输入导纳Y。 且 Z = Y -1 。
i1 +
u1
i1
–
端口的概念:
端口由一对端子构成,且满足如下 条件:从一个端子流入的电流等于 从另一个端子流出的电流。此称为 端口条件。
i2 +
u2 – i2
4. 二端口与四端网络的区别:
二端口的两个端口必须 满足端口条件,四端网 络却没有上述限制。
i1
i2
i1
i2
二端口
i1
i2
i1
i2
具有公共端的二端口
i2 i1
i3 i4
四端网络
二端口的两个端口间若有外部连接,则会破坏原二端口的 端口条件。
1
i1
i 3
R
4 i2 2
u1
i1
2.四端网络 在工程实际中,研究信号及能量的传输和信 号变换时,经常碰到如下形式的电路。称为 四端网络。
线性RLCM 受控源
四端网络
例1
R
C
C
滤波器 n:1
变压器
三极管 传输线
3. 二端口(two-port)
如果四端网络的两对端子同时满足端口条件, 则称为二端口网络。
+
i1
u1 –
i1
线性RLCM 受控源
整理可得
I1 = (Y1 Y2 )U1 - Y2U2 I2 = -Y2U1 (Y2 Y3 )U2
二端口网络参数和方程
13.1 二端口网络及其参数方程
一、一端口网络和二端口网络的概念
1. 一端口网络
I
+
U
Z
-
(Y)
表征一端口网络电特性的独立 参数:输入阻抗Z或输入导纳Y。 且 Z = Y -1 。
i1 +
u1
i1
–
端口的概念:
端口由一对端子构成,且满足如下 条件:从一个端子流入的电流等于 从另一个端子流出的电流。此称为 端口条件。
i2 +
u2 – i2
4. 二端口与四端网络的区别:
二端口的两个端口必须 满足端口条件,四端网 络却没有上述限制。
i1
i2
i1
i2
二端口
i1
i2
i1
i2
具有公共端的二端口
i2 i1
i3 i4
四端网络
二端口的两个端口间若有外部连接,则会破坏原二端口的 端口条件。
1
i1
i 3
R
4 i2 2
u1
i1
2.四端网络 在工程实际中,研究信号及能量的传输和信 号变换时,经常碰到如下形式的电路。称为 四端网络。
线性RLCM 受控源
四端网络
例1
R
C
C
滤波器 n:1
变压器
三极管 传输线
3. 二端口(two-port)
如果四端网络的两对端子同时满足端口条件, 则称为二端口网络。
+
i1
u1 –
i1
线性RLCM 受控源
整理可得
I1 = (Y1 Y2 )U1 - Y2U2 I2 = -Y2U1 (Y2 Y3 )U2
二端口网络的参数

元素为阻抗,
单位是 。
与Y参数方程相同, Z11、Z12、Z21、Z22取决于电路结
构及参数。根据Z参数方程及I1 、I2,可求得 U1 、U 2 。
确定Z参数:
UU12
ZZ1211II11ZZ1222II22
在1-1' 端输入I1 ,将2-2'端开路,即 I2 0 代入上式 有
U1
Z11I1
有
A
U1 U 2
I2 0
称为输出端开路时传输电压比
C
I1 U 2
I2 0
称为输出端开路时转移导纳(S)
UI11CAUU22DB
( (
II22))
2、在输出端短路,即U 2 0 时
有
B
U1 I2
U2 0
称为输出端短路时转移阻抗()
对于图所示的一端口网络来说
Z
U I
或者
Y
I U
U Z I (以电流 I 为已知量)
或者 I YU (以电压U 为已知量)
一、Y 参数及方程(短路导纳参数)
已知 U1、U 2 ,求 I1 、I2 。 由替代定理可将 U1 、U 2 所在支路用理想电压源代替。
•
1 I1
•
I2 2
•
U1
N
•
U2
1′
确定Y参数:
II12 YY1211UU11YY1222UU24
在1-1' 端加 U1,将2-2' 端短路,即 U 2 0 代入上式
I1 Y11U1
Y11
I1 U1
U 2 0
称为输出端短路时的输入导纳(S)
I2 Y21U1
Y21
I2 U1
U 2 0
【推荐】电路原理基础:第二章 二端口网络的方程和参数
D
i1 i2
u2 0, 10
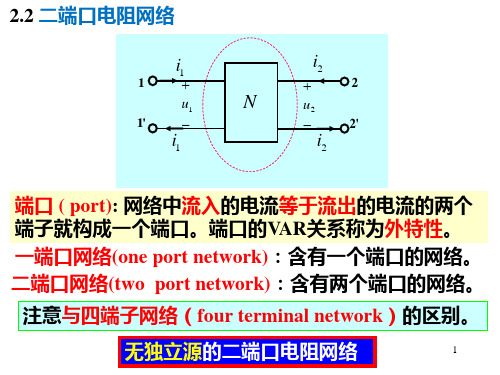
四、H参数方程: 已知i1和 u2求u1和 i2
u1 H11i1 H12u2 i2 H 21i1 H 22u2
1 i1
u1
1' i1
i2 2
N
u2
i2 2'
u1
i2
H11 H 21
H12 H 22
i1 u2
T
0.5 0.75S
0.6
0.5
将其变换为其它参数方程,则可求得其他参数,
注意变换时有些参数可能不存在。
12
六、二端口网络参数的互易性(reciprocal)
若网络中只含有R、 L、 C、 M 等线性元件而不 含有受控源,则网络参数就具有如下性质:
(1) R12 R21 (3) T AD - BC 1
注意与四端子网络(four terminal network)的区别。
无独立源的二端口电阻网络
1
第一节 二端口网络的方程和参数
i1
1
u1
1'
i1
i2
2
N
u2
2'
i2
二端口的外特性决定于网络的本身与外部所接
电路无关,用端口电压、电流(共四个量)间的关 系反映,共六种情况。
2
一、R参数方程:
i1
u1
i2
Rl
u2
R
Rl Rl
Rl
Rl
但G不存在
双口网络的方程和参数

双口网络的方程和参数
1.1双口网络的阻抗矩阵
若已知端口电流İ1和İ2,可以应用替代定理将两个端口电流 都看作是外施的电流源,这样就可以根据叠加定理,1和2 分别为各个电流源单独作用时所产生的电压之和,即
V1 Z11I1 Z12I2 V2 Z21I1 Z22I2
(13.1)
式中Z11、Z12、Z21、Z22称为双口网络的Z参数,由于这些 参数表明了电流对电压的关系,具有阻抗特性,因此又称 为阻抗参数。这些参数可以实际测量获得,也可按照下面 式子计算得到
2006-1-1
!
2
端口2开路时,端口1的驱动阻抗:
Z11
V1 I1
端口2开路时,端口1对端口2的转移阻抗:Z
I2 0
21
V2 I1
I2 0
端口1开路时,端口2对端口1的转移阻抗:Z12
V1 I2
I1 0
端口1开路时,端口2的驱动阻抗: Z22 VI22 I10
2006-1-1
!
3
• 可以看出,这些参数都是由一个端口开路时测得 的,因此又称为开路阻抗参数。根据式(13.1)所示, 可进一步得到其矩阵形式
7
解 假设正弦激励的角频率为ω,作出相量模型图,同时将受控电流
源转化为受控电压源如图13.8(b)所示。若假想左右两端加上电压
分别为1和2的电压源,并以网孔为回路,应用回路法,列写回路
方程为
V1
(R
j
1
C
)I1
RI2
j C
I
V2 RI1 2RI2
再根据主控量与回路电流的关系有İ = İ1 + İ2,则整理上述方程为
所以得到
0.1 j0.2 0.1
Y
1.1双口网络的阻抗矩阵
若已知端口电流İ1和İ2,可以应用替代定理将两个端口电流 都看作是外施的电流源,这样就可以根据叠加定理,1和2 分别为各个电流源单独作用时所产生的电压之和,即
V1 Z11I1 Z12I2 V2 Z21I1 Z22I2
(13.1)
式中Z11、Z12、Z21、Z22称为双口网络的Z参数,由于这些 参数表明了电流对电压的关系,具有阻抗特性,因此又称 为阻抗参数。这些参数可以实际测量获得,也可按照下面 式子计算得到
2006-1-1
!
2
端口2开路时,端口1的驱动阻抗:
Z11
V1 I1
端口2开路时,端口1对端口2的转移阻抗:Z
I2 0
21
V2 I1
I2 0
端口1开路时,端口2对端口1的转移阻抗:Z12
V1 I2
I1 0
端口1开路时,端口2的驱动阻抗: Z22 VI22 I10
2006-1-1
!
3
• 可以看出,这些参数都是由一个端口开路时测得 的,因此又称为开路阻抗参数。根据式(13.1)所示, 可进一步得到其矩阵形式
7
解 假设正弦激励的角频率为ω,作出相量模型图,同时将受控电流
源转化为受控电压源如图13.8(b)所示。若假想左右两端加上电压
分别为1和2的电压源,并以网孔为回路,应用回路法,列写回路
方程为
V1
(R
j
1
C
)I1
RI2
j C
I
V2 RI1 2RI2
再根据主控量与回路电流的关系有İ = İ1 + İ2,则整理上述方程为
所以得到
0.1 j0.2 0.1
Y
二端口网络参数和方程和等效电路相关知识讲解培训

(1) H 参数
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
矩阵形式:
UI21
H11
H
21
H12 H 22
UI12
(2) H 参数的计算与测定
H11
U 1 I1
U 2 0
H21
I2 I1
U 2 0
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
Y21
I2 U 1
U 2 0 Yb Y12
Ya Yb Y11 即:Yb Y12 Y21
Yb Yc Y22
解之得
Ya Y11 Y12 Yb Y12 Yc Y22 Y12
注意: (1) 等效只对两个端口的电压,电流关系成立。对端 口间电压则不一定成立。
(2) 适用于互易网络。
I2
Y12U1 Y22U 2
Y21 Y12
U 1
I2
其中
I1 I'2
Y11U 1 Y12U 1
Y12U 2 Y22U 2
相当于一互易二端口,
可求出其等效电路(型):
(计算见前例)
•
I1
+
•
U1
Yb
Ya
Yc
I2
+
•
U2
而I2 I2 Y21 Y12 U1相 当 于 在 端 口2并 入 一 受 控 源.
C
I1 U 2
I2 0
D
I1 I2
U 2 0
U1 AU 2 BI2
I1
CU 2
DI2
(3) 互易二端口 Y12 Y21
T 参数满足: AD BC 1
二端口网络的网络参数-文档资料

阻抗参数[Z]
u1
U1 Z e1
, i1
I1
Z e1
u2
U2 Ze2
, i2
I2
Ze2
代入整理可得 [u] [z][i]
其中,
z
z11 / ze1
z12 / ze1ze2
z21 / ze1ze2 z22 / பைடு நூலகம்e2
1、2 导纳参数[Y]
在上述双端口网络中, 以U1、U2为自变量, I1、I2 为因变量, 则可得另一组方程:
U 2
I
2
其中,[A]称为转移矩阵,方阵中各参数的物理意义 如下:
A11
U1 U2
|I2 0
A12
U1 I2
|U2 0
表示T2开路时电压的转移参数 表示T2短路时转移阻抗
转移参数[A]
A21
I1 U2
|I2 0
表示T2
A22
I1 I2
|U2 0
表示T2短路时电流的转移参数
若将网络各端口电压、电流对自身特性阻抗归一
对于如下图所示的两个网络的级联:
U1
I1
A1
U2
I
2
U2
I
2
A2
U3
I3
转移参数[A]
+ I1
I2
I3 +
+
U1
[A1]
U2
[A2]
U3
-
-
-
双端口网络的级联
转移参数[A]
则有
U1
I1
A1
A2
U3
I3
令 A A1A2
则对于n个双端口网络级联 A A1A2 An
散射参数[S]
电路原理13.1.4二端口网络及其参数方程 - 二端口网络及其参数方程2
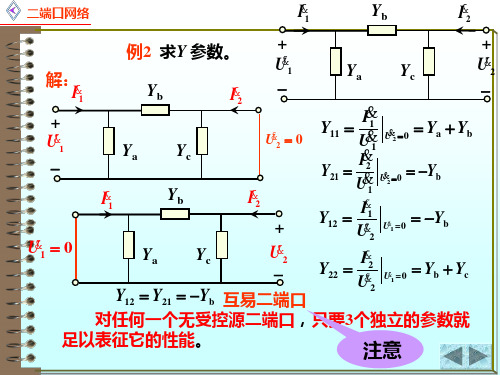
II&&12
Y
UU&&12
Y 1
II&&12
UU&&12
对称二端口 Z11 Z22 (Z12 Z21 )
Z11
Z
21
Z12 Z22
Y11 Y21
Y12 1
Y22
1 ΔY
Y22 Y21
Y12
Y11
若矩阵 Z 与 Y 非奇异
Y Z 1 Z Y 1
二端口网络
+ U1
解一: I1 1
+ U1
2 I2
+
2
U2
2
+ 2 U2
UI11
T11 T21
T12
T22
U2 I2
I1 1
+ U1
2 I2 2
T11
U1 U2
1 2 I2 0 2 1.5
T21
I1 U2
I2 =0 0.5S
T12
U1 I2
U2 =0
I1[1 + (2//2)] 4Ω 0.5I1
Yb
Y22
I&2 U&2
U&1 =0 Yb Yc
对任何一个无受控源二端口,只要3个独立的参数就
足以表征它的性能。
注意
二端口网络
Y
Y11 Y21
Y12
Y22
若Y12 Y21,称为互易二端口。 进一步,若Y11 Y22 ,则称为对称二端口。
I&1
Yb
I&2
+ U&1
Ya
Yc
+ U&2
二端口网络的传输参数、混合参数方程

b —基极; c—集电极;e—发射极。
放大小信号时的交流微变等效电路
U1 H11I1 H12U2 rbeI1
I2
H 21I1
H 22U 2
I1
1 rce
U2
忽 略
H
H11 H 21
H12 H 22
rbe
0
1
rce
P66 [例7-7]
解:求 H参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
P66 [例7-7]续 解:再求 T 参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
U1 2U 2
,
I1
I2 2
I1
I1
U1 3
即
I1
I2 2
2U 2 3
先列出 T 参数方程的结构,再具体化
U1 AU2 B( I2) 2U2 2U2 0
I1
CU2
D(
I
)=
2
U1 3
I1
2 3
电流 放大倍数
转移电导
转移电阻
二 端 口 网 络 参 数 方 程 小 结
二端口网络参数方程小结
互易二端口网络不含受控源,从互易网络应满足的 条件可知,四个参数中只有三个是独立的。
第7章 二端口网络的概念
7.1 二端口网络的端口条件及导纳参数、阻 抗参数方程
7.2 二端口网络的传输参数、混合参数方程 7.3 互易二端口网络的等效电路与级联
二端口网络的导纳参数、阻抗参数是基本参数, 而传输参数、混合参数是工程中的应用参数。
7.2.1 二端口网络的传输参数方程
U1
AU 2
B(
I
)
2
A
C、D的定义为:
放大小信号时的交流微变等效电路
U1 H11I1 H12U2 rbeI1
I2
H 21I1
H 22U 2
I1
1 rce
U2
忽 略
H
H11 H 21
H12 H 22
rbe
0
1
rce
P66 [例7-7]
解:求 H参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
P66 [例7-7]续 解:再求 T 参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
U1 2U 2
,
I1
I2 2
I1
I1
U1 3
即
I1
I2 2
2U 2 3
先列出 T 参数方程的结构,再具体化
U1 AU2 B( I2) 2U2 2U2 0
I1
CU2
D(
I
)=
2
U1 3
I1
2 3
电流 放大倍数
转移电导
转移电阻
二 端 口 网 络 参 数 方 程 小 结
二端口网络参数方程小结
互易二端口网络不含受控源,从互易网络应满足的 条件可知,四个参数中只有三个是独立的。
第7章 二端口网络的概念
7.1 二端口网络的端口条件及导纳参数、阻 抗参数方程
7.2 二端口网络的传输参数、混合参数方程 7.3 互易二端口网络的等效电路与级联
二端口网络的导纳参数、阻抗参数是基本参数, 而传输参数、混合参数是工程中的应用参数。
7.2.1 二端口网络的传输参数方程
U1
AU 2
B(
I
)
2
A
C、D的定义为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二端口网络
其矩阵形式为
Z11 U 1 = U 2 Z 21
Z11 Z= Z 21 Z12 Z 22
Z12 I 1 Z 22 I2
称为Z 参数矩阵
Z 参数的实验测定
U Z11 = 1 I 1 U Z 21 = 2 I
2 2 1 3 2
2
整理可得
= (Y Y )U -Y U I 1 1 2 1 2 2 = -Y U (Y Y )U I
2 2 1 2 3
2
二端口网络
I 1
U 1
+
I 2
线性 网络 2
-
1
+ U 2 -
如果线性网络内部不含独立源,且有 l 个独立回路, 则可列写l个回路电流方程:
Z12 = Z 21 Z11 = Z 22 ( Z12 = Z 21 )
若矩阵 Z 与 Y 非奇异
Y = Z -1
Z = Y -1
二端口网络
即
Z11 Z12 1 Y22 -Y12 Z Z = ΔY -Y Y 21 22 21 11
I 1
+ U Za Zb Zc -
I 2
2 4 2
+ U 1 -
+ U 2 -
互易二端口
Y12 = Y12
等效电路
16 Z1-1 U = 0 = 2 (5 // 10) = 2 3 16 Z 2- 2 U = 0 = 10 //[10 (5 // 2)] = 1 3
故
1 3 Y11 = = S Z1-1 16 1 3 Y22 = = S Z 2-2 16
I 2
I 1
I 2
=0 U 1
I Y11 = 1 U = 0 = Ya Yb 2 U 1 =0 U 2 I Y21 = 2 U = 0 = -Yb U1 2 I Y12 = 1 U = 0 = - Yb + U 1
2
U 2 -
I Y22 = 2 U 2
- Yb Yb
非互易二端口网络(网络内部有受控源)有四个独立参数。
二端口网络
三、Z参数和方程 + U 1 -
I 1
线性 无源
I 2
U 2 -
=Y U I 1 11 1 Y12U 2 由Y 参数方程 I 2 = Y21U 1 Y22U 2
i1
i2
i1 二端口 i2 i1
i2
i1
i2
i1
i2
i3 i4 四端网络
具有公共端的二端口
二端口网络
二端口的两个端口间若有外部连接,则会破坏原二端口的 端口条件。 u1 1 i1 3 3
i
i1
R i2
4 4
i2
2
1
i1
i2
2
u2 -
1-1’ 2-2’是二端口
3-3’ 4-4’不是二端口,是四端网络
R
I 2
U 1 U 2来自整理得- = j ( L L 2 M ) I j ( L M ) I = j8 I j4 I U 1 1 2 1 2 2 1 2 = j ( L M ) I ( j L R) I = j4 I (3 j3) I U 2 2 1 2 2 1 2
若网络内部无受控源(满足互易定理),则导纳矩阵Y对称
12 = 21 Y12 = Y21
互易二端口网络四个参数中只有三个是独立的。 Yb I I 1 2 例2 求Y 参数。 + + U U 1 2 Ya Yc -
二端口网络
解:
+ U 1 -
I 1
Ya
Yb Yc Yb Ya Yc
-
=Y U I 1 a 1 Yb (U1 - U 2 )
= Y (U -U ) - gU I 2 b 2 1 1
则
= (Y Y )U -Y U I 1 a b 1 b 2
= (- g - Y )U Y U I 2 b 1 b 2
注意
Ya Yb Y= - g - Yb
对称二端口只有2个参数是独立的。 对称二端口是指两个端口电气特性上对称。电路结构 左右对称的,端口电气特性对称;电路结构不对称的二端 口,其电气特性也可能是对称的。这样的二端口也是对称 二端口。
二端口网络
例3 I1 2 + U 1 5
10 10
I 2
2 I 1
+ U 2 -
I 1
+ U1 线性 无源
I 2
I Y12 = 1 U 2 I Y22 = 2 U
=0 1 U 2
转移导纳
=0 U 1
I 1
线性 无源
I 2
自导纳
=0 2 U 1
+ U 2 -
Y参数是在一个端口短路情况下通过计算或测试求得的, 所以又称为短路导纳参数。
Z I Z11 I 1 12 2 Z1 l I l = U 1 Z I Z I =U Z 21 I 1 22 2 2l l 2 Z I Z I = 0 解得 Z I
31 1 32 2 3l l
Z I Zl1 I 1 l 2 2 Z ll I1 = 0
rI 1
例5
+
I 2
+ U
-
1
2
-
=Z I Z (I I ) = ( Z Z )I Z I U 1 a 1 b 1 2 a b 1 b 2
= rI +Z I U 2 1 c 2 + Zb ( I1 + I 2 ) = (r + Zb ) I1 + ( Zb + Zc )I 2
= 11 U 21 U I 1 1 2 = 12 U 22 U I 2 1 2
二端口网络
分别用Y11、Y12、 Y21、 Y22表示这些系数,上式可写为:
=Y U I 1 11 1 Y12U 2 =Y U I 2 21 1 Y22U 2
= j L I U 1 1 1 j M ( I1 I 2 ) j L2 ( I1 I 2 ) j MI1 =RI j L ( I I ) j MI U 2 2 2 1 2 1
二端口网络
I 1
L1 M L2
开路输入阻抗
=0 I 2
开路转移阻抗
=0 1 I 2
二端口网络
U Z12 = 1 I 2 U Z 22 = 2 I
开路转移阻抗
=0 I 1
开路输入阻抗
=0 2 I 1
Z参数是在一个端口开路情况下通过计算或测试求得
的,所以Z参数又称开路阻抗参数。 互易二端口 对称二端口
表征一端口网络电特性的独立 参数:输入阻抗Z或输入导纳Y。 且 Z = Y -1 。 端口的概念: 端口由一对端子构成,且满足如下 条件:从一个端子流入的电流等于 从另一个端子流出的电流。此称为 端口条件。
+ u1 –
i1 i1
二端口网络
2.四端网络 在工程实际中,研究信号及能量的传输和信 号变换时,经常碰到如下形式的电路。称为 四端网络。
=0 U 2
= -Yb - g
I 1
=0 U 1
Ya
I 2
+ U 2 -
gU 1
I Y12 = 1 U2 I Y22 = 2 U2
=0 U 1
= -Yb
= Yb
=0 U 1
二端口网络
解二 + U 1 -
I 1
Ya
Yb
I 2
gU 1
+
U 2
,U . 可解出U 1 2
即:
Y22 - Y12 U1 = I1 Δ Δ U = - Y21 I Y11 2 1 Δ Δ
=Z I I 2 11 1 Z 12 I 2 =Z I I 2 21 1 Z 22 I 2
其中 =Y11Y22 –Y12Y21
线性RLCM 受控源
四端网络
二端口网络
例1 R C 滤波器 n:1
C
三极管
变压器
传输线
二端口网络
3. 二端口(two-port) 如果四端网络的两对端子同时满足端口条件, 则称为二端口网络。 i1 线性RLCM 受控源 i1 i2 i2
+ u1 –
+ u2 –
二端口网络
4. 二端口与四端网络的区别: 二端口的两个端口必须 满足端口条件,四端网 络却没有上述限制。
和I 可视为 端口电流 I 1 2 和U 共同作用产生。 U 1 2
二端口网络
Y 参数的实验测定 I Y11 = 1 自导纳 U 1 U2 =0 I Y21 = 2 转移导纳 U
=Y U Y U I 1 11 1 12 2 I 2 = Y21U1 Y22U 2
二端口网络
第13章 二端口网络
13-1 二端口网络及其参数方程
13-2 二端口网络的等效电路
13-3 二端口网络的网络函数 13-4 二端口网络的连接 13-5 二端口网络的实例
二端口网络
13.1 二端口网络及其参数方程
一、一端口网络和二端口网络的概念 1. 一端口网络 I + U Z (Y)
