二端口网络参数和方程
合集下载
二端口网络的参数
元素为阻抗，
单位是 。
与Y参数方程相同， Z11、Z12、Z21、Z22取决于电路结
构及参数。根据Z参数方程及I1 、I2，可求得 U1 、U 2 。
确定Z参数：
UU12
ZZ1211II11ZZ1222II22
在1-1' 端输入I1 ，将2-2'端开路，即 I2 0 代入上式 有
U1
Z11I1
有
A
U1 U 2
I2 0
称为输出端开路时传输电压比
C
I1 U 2
I2 0
称为输出端开路时转移导纳（S）
UI11CAUU22DB
( (
II22))
2、在输出端短路，即U 2 0 时
有
B
U1 I2
U2 0
称为输出端短路时转移阻抗（）
对于图所示的一端口网络来说
Z
U I
或者
Y
I U
U Z I (以电流 I 为已知量)
或者 I YU （以电压U 为已知量）
一、Y 参数及方程（短路导纳参数）
已知 U1、U 2 ，求 I1 、I2 。 由替代定理可将 U1 、U 2 所在支路用理想电压源代替。
•
1 I1
•
I2 2
•
U1
N
•
U2
1′
确定Y参数：
II12 YY1211UU11YY1222UU24
在1－1' 端加 U1，将2－2' 端短路，即 U 2 0 代入上式
I1 Y11U1
Y11
I1 U1
U 2 0
称为输出端短路时的输入导纳（S）
I2 Y21U1
Y21
I2 U1
U 2 0
【推荐】电路原理基础：第二章 二端口网络的方程和参数
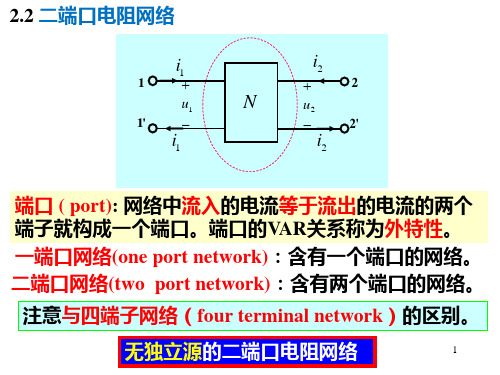
D
i1 i2
u2 0, 10
四、H参数方程： 已知i1和 u2求u1和 i2
u1 H11i1 H12u2 i2 H 21i1 H 22u2
1 i1
u1
1' i1
i2 2
N
u2
i2 2'
u1
i2
H11 H 21
H12 H 22
i1 u2
T
0.5 0.75S
0.6
0.5
将其变换为其它参数方程，则可求得其他参数，
注意变换时有些参数可能不存在。
12
六、二端口网络参数的互易性（reciprocal）
若网络中只含有R、 L、 C、 M 等线性元件而不 含有受控源，则网络参数就具有如下性质：
(1) R12 R21 (3) T AD - BC 1
注意与四端子网络（four terminal network）的区别。
无独立源的二端口电阻网络
1
第一节 二端口网络的方程和参数
i1
1
u1
1'
i1
i2
2
N
u2
2'
i2
二端口的外特性决定于网络的本身与外部所接
电路无关，用端口电压、电流（共四个量）间的关 系反映，共六种情况。
2
一、R参数方程：
i1
u1
i2
Rl
u2
R
Rl Rl
Rl
Rl
但G不存在
二端口网络参数和方程和等效电路相关知识讲解培训
（1） H 参数
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
矩阵形式:
UI21
H11
H
21
H12 H 22
UI12
（2） H 参数的计算与测定
H11
U 1 I1
U 2 0
H21
I2 I1
U 2 0
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
Y21
I2 U 1
U 2 0 Yb Y12
Ya Yb Y11 即：Yb Y12 Y21
Yb Yc Y22
解之得
Ya Y11 Y12 Yb Y12 Yc Y22 Y12
注意： (1) 等效只对两个端口的电压，电流关系成立。对端 口间电压则不一定成立。
(2) 适用于互易网络。
I2
Y12U1 Y22U 2
Y21 Y12
U 1
I2
其中
I1 I'2
Y11U 1 Y12U 1
Y12U 2 Y22U 2
相当于一互易二端口，
可求出其等效电路(型)：
(计算见前例)
•
I1
+
•
U1
Yb
Ya
Yc
I2
+
•
U2
而I2 I2 Y21 Y12 U1相 当 于 在 端 口2并 入 一 受 控 源.
C
I1 U 2
I2 0
D
I1 I2
U 2 0
U1 AU 2 BI2
I1
CU 2
DI2
（3） 互易二端口 Y12 Y21
T 参数满足: AD BC 1
电路原理13.1.4二端口网络及其参数方程 - 二端口网络及其参数方程2
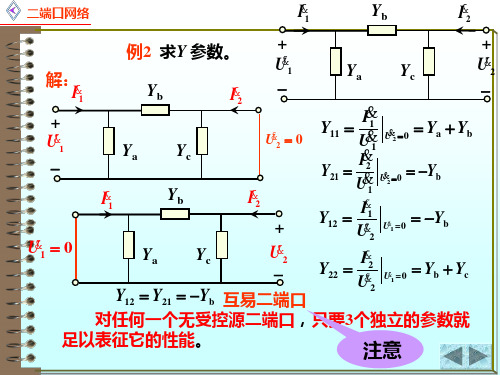
II&&12
Y
UU&&12
Y 1
II&&12
UU&&12
对称二端口 Z11 Z22 (Z12 Z21 )
Z11
Z
21
Z12 Z22
Y11 Y21
Y12 1
Y22
1 ΔY
Y22 Y21
Y12
Y11
若矩阵 Z 与 Y 非奇异
Y Z 1 Z Y 1
二端口网络
+ U1
解一： I1 1
+ U1
2 I2
+
2
U2
2
+ 2 U2
UI11
T11 T21
T12
T22
U2 I2
I1 1
+ U1
2 I2 2
T11
U1 U2
1 2 I2 0 2 1.5
T21
I1 U2
I2 =0 0.5S
T12
U1 I2
U2 =0
I1[1 + (2//2)] 4Ω 0.5I1
Yb
Y22
I&2 U&2
U&1 =0 Yb Yc
对任何一个无受控源二端口，只要3个独立的参数就
足以表征它的性能。
注意
二端口网络
Y
Y11 Y21
Y12
Y22
若Y12 Y21，称为互易二端口。 进一步，若Y11 Y22 ，则称为对称二端口。
I&1
Yb
I&2
+ U&1
Ya
Yc
+ U&2
电路 第十六章 二端口网络
第十六章 二端口网络16.1 基本概念16.1.1 二端口网络的端口条件和端口变量1. 端口条件：在端口网络的任意端口上，由一端流入的电流必须等于由另一端流出的电流，这叫做双口网络的端口条件； 2. 端口变量：包括两个端口电压21u u ，和两个端口电流21i i ，。
16.1.2 二端口网络的方程和参数二端口网络的对外电气性能可以用一些参数表示。
即以这些参数组成的方程对外电路表示二端口网络的电气性能。
在分析二端口的参数时，按正弦稳态情况考虑。
本章讨论的二端口是由线性电阻、电感、电容和线性受控源组成，不含任何独立电源。
如图16-1所示为一线性二端口。
11'22'116-图1. Y 参数方程用21U U ∙∙，表示21I I ∙∙，（1） 方程⎪⎩⎪⎨⎧+=+=∙∙∙∙∙∙22212122121111U Y U Y I U Y U Y I （2） 参数的物理意义。
分别把入口和出口短路出口的驱动点导纳导纳入口与出口之间的转移导纳出口与入口之间的转移入口的驱动点导纳----=----=----=----==∙∙=∙∙=∙∙=∙∙∙∙∙∙22220211201221011111122U U U U U I Y U I Y U I Y U I Y由于以上参数是在入口和出口分别短路情况下的参数，所以称为短路参数。
对于线性无源网络（指即不包含独立电源，也不包含受控源），2111Y Y =，只有三个独立参数，又称互易双口；当2211Y Y =时，称为对称双口，只有两个独立参数。
2. Z 参数方程用∙∙21I I ，表示∙∙21U U ， （1）⎪⎩⎪⎨⎧+=+=∙∙∙∙∙∙22212122121111I Z I Z U I Z I Z U （2）参数的物理意义。
分别把入口和出口开路，出口驱动点阻抗入口对出口的转移阻抗出口对入口的转移阻抗入口驱动点阻抗----=----=----=----==∙∙=∙∙=∙∙=∙∙∙∙∙∙22220211201221011111122I I I I I U Z I U Z I U Z I U Z对于互易双口，2112Z Z = ，只有三个独立参数； 对于对称双口，1211Z Z =，只有两个独立参数。
电流电路的二端口网络方程和参数
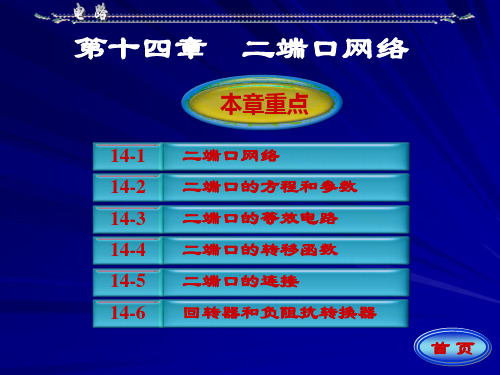
U2 Zc I2 Zb (I1 I2 ) Zb I1 (Zb Zc )I2
Z
Za Zb
Zb
Zb
Zb
Zc
返回 上页 下页
例2-5 求图示二端口的Z参数。
•
•
I1
Za
Zc
Z
I1
+
•
I2
+
+
解
•
U1
Zb
•
U2
列KVL方程：
U1 Za I1 Zb (I1 I2 ) (Za Zb )I1 Zb I2 U2 Zc I2 Zb (I1 I2 ) ZI1
第十四章 二端口网络
本章重点
14-1 二端口网络 14-2 二端口的方程和参数 14-3 二端口的等效电路 14-4 二端口的转移函数 14-5 二端口的连接 14-6 回转器和负阻抗转换器
首页
重点
1. 二端口的参数和方程 2. 二端口的等效电路 3. 二端口的转移函数
返回
14.1 二端口网络
•
I1
Za
+
•
U1
Zc Zb
•
I2
+
•
U2
Z11
U1 I1
I20 Za Zb
Z21
U2 I1
I2 0 Zb
Z12
U1 I2
I10 Zb
Z22
U2 I2
I10 Zb Zc
返回 上页 下页
解法2
•
I1
Za
Zc
+
•
U1
Zb
列KVL方程。
•
I2
+
•
U2
U1 Za I1 Zb (I1 I2 ) (Za Zb )I1 Zb I2
14.2 二端口网络的方程和参数
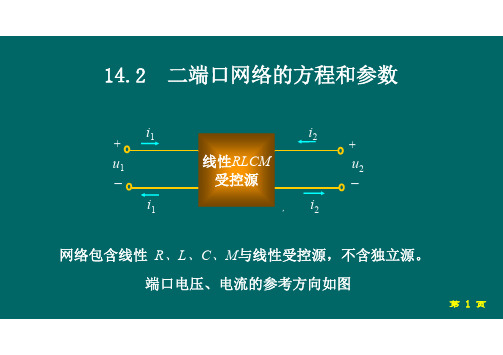
Z
Za Zb
Zb
Zb
Zb
Zc
第 20 页
例题 求二端口Z、Y 参数
I1 R1 j M R2 I2
+
U1
jL1
*
*
jL2
+ U 2
–
U1 R1 jL1 I1 jMI2
U2 jMI1 R2 jL2 I2
Z
R1 jL1
jM
jM
R2
j L2
R2 jL2
Y Z 1
Z I2 0
b
解法1
U1 Z11I1 Z12 I2 U 2 Z21I1 Z22I2
Z12
U1 I2
Z I10
b
Z22
U 2 I2
I10 Zb Zc
第 18 页
解法2
I1 Za
+
U1
Zc Zb
I2
+
U2
列KVL方程：
U1 ZaI1 Zb I1 I2 Za Zb I1 ZbI2
第2页
I1 I1 I1 Y11U1 Y12U2
I2
I2
I2
Y21U1
Y22U 2
I1 Y11U1 Y12U 2
I2
Y21U1
Y22U 2
I1
I2
Y11 Y21
Y12 U1
Y22
U
2
注意 Y参数的值由网络内部元件参数及连接关系决定。
第3页
② Y参数的物理意义
Y11
=
u1
i1
n 0
0
1
u2
i2
n
n 0
T 0
1
n
第 27 页
38第三十八讲 二端口网络方程和参数
1
1/
由Ｚ参数方程可得： U1 Z12 I 2 I1 0 U2 Z 22 I1 0 I
2
（３）、 Y参数矩阵与Ｚ参数矩阵之间的关系
Z 参数矩阵与Y 参数矩阵互为逆矩阵。
YZ
即：
1
Z Y
1
Z11 Z12 1 Y22 Y12 Z Y Y11 21 21 Z 22 Y
可求得： I1 Y11 Ya Yb U1
Y21
I2
Yb g
U1
将１－１／短路， 在２－２／外加电压可得：
U1 0
可求得：
1 I1
Yb Ya Yc
I2 2
g U 1
U1
_
U2
_
Y12 Y22
I1
Yb Yb Yc
1/
2/
0 u s 0 is R2 L2
或 : x Ax Bv
（２）、拓扑法
每个元件为一支路，选一棵特有树。
（３）、列写状态方程的步骤：
① 、线性电路以iL ,uc为状态变量。 ②、对含有电容的支路，选择节点（割集）列出KCL方程，
duc 在方程中包括 项； dt
(注意符号）
A T C
B D
称为T 参数矩阵
（２）、 T 参数的计算或测定
U1 A U2 I1 C U2
I2 0
U1 B I2 I1 D I2
U 2 0
I2 0
U 2 0
U 1 AU 2 BI 2 I 1 CU 2 DI 2
1/
由Ｚ参数方程可得： U1 Z12 I 2 I1 0 U2 Z 22 I1 0 I
2
（３）、 Y参数矩阵与Ｚ参数矩阵之间的关系
Z 参数矩阵与Y 参数矩阵互为逆矩阵。
YZ
即：
1
Z Y
1
Z11 Z12 1 Y22 Y12 Z Y Y11 21 21 Z 22 Y
可求得： I1 Y11 Ya Yb U1
Y21
I2
Yb g
U1
将１－１／短路， 在２－２／外加电压可得：
U1 0
可求得：
1 I1
Yb Ya Yc
I2 2
g U 1
U1
_
U2
_
Y12 Y22
I1
Yb Yb Yc
1/
2/
0 u s 0 is R2 L2
或 : x Ax Bv
（２）、拓扑法
每个元件为一支路，选一棵特有树。
（３）、列写状态方程的步骤：
① 、线性电路以iL ,uc为状态变量。 ②、对含有电容的支路，选择节点（割集）列出KCL方程，
duc 在方程中包括 项； dt
(注意符号）
A T C
B D
称为T 参数矩阵
（２）、 T 参数的计算或测定
U1 A U2 I1 C U2
I2 0
U1 B I2 I1 D I2
U 2 0
I2 0
U 2 0
U 1 AU 2 BI 2 I 1 CU 2 DI 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
等效电路
16 Z1-1 U2=0=2(5//10)=3
Y11
=
1 Z1-1
= 3S 16
16 Z 2-2U 1=0=10//[10(5//2)]=3
13
Y22
=
Z2-2
=S 16
故
Y11
= Y22
=
3S 16
电气 对称
二端口网络
例4
解一 I1
+ U1 -
I1 + U1 Yb
Ya gU1
Yb gU 1
整理可得
I1 =(Y1Y2)U1-Y2U2 I2 =-Y2U1(Y2Y3)U2
I2
+ U2 -
二端口网络
江苏大学电路教学组
I1
I2
+ U 1-
1
线性 网络
2
+ U-2
如果线性网络内部不含独立源，且有 l 个独立回路， 则可列写l个回路电流方程：
Z11I1 Z12 I2 Z1l Il = U 1
4. 二端口与四端网络的区别：
二端口的两个端口必须 满足端口条件，四端网 络却没有上述限制。
i1
i2
i1
i2
二端口
i1
i2
i1
i2
具有公共端的二端口
i2 i1
i3 i4
四端网络
二端口网络
江苏大学电路教学组
二端口的两个端口间若有外部连接，则会破坏原二端口的 端口条件。
1
i1
i 3
R
4 i2 2
u1
2Y2 1-Y1 Y2 1
1Y2
2
-1 T12 = Y 21
T22Leabharlann =-Y11 Y21
其矩阵形式
U I11=T T1211 T T1222-U I22
注意负号
T
=
T11 T21
T12
T2
2
称为T 参数矩阵
二端口网络
江苏大学电路教学组
互易二端口 Y12 =Y21 T11 T22 - T12 T21
二端口网络
江苏大学电路教学组
第13章 二端口网络
13-1 二端口网络及其参数方程 13-2 二端口网络的等效电路 13-3 二端口网络的网络函数 13-4 二端口网络的连接 13-5 二端口网络的实例
二端口网络
江苏大学电路教学组
13.1 二端口网络及其参数方程
一、一端口网络和二端口网络的概念
1. 一端口网络
江苏大学电路教学组
Y 参数的实验测定
Y11
=
I1 U1
U2 =0
Y21
=
I2 U1
U2 =0
Y12
=
I1 U2
U1 =0
Y22
=
I2 U2
U1 =0
自导纳 转移导纳 转移导纳 自导纳
I1 + U 1-
I1
I1 =Y11U1 Y12U2 I2 =Y21U1 Y22U2
线性 无源
线性 无源
I2
I2 +
U2
I1
L1
M U1
R L2
I2
U2
-
-
解：在二个端口分别加电压源 U 1 和 U 2 ，列回路电压方 程
U 1= jL 1 I 1 jM (I 1 I 2 ) jL 2 (I 1 I 2 ) jM I 1 U 2= R I 2 jL 2 (I 1 I 2 ) jM I 1
二端口网络
-
Y参数是在一个端口短路情况下通过计算或测试求得的， 所以又称为短路导纳参数。
二端口网络
江苏大学电路教学组
I1 =11U121U2 I2 =12U122U2
I1 I2
=YY1211
Y12 Y22
U1 U2
若网络内部无受控源（满足互易定理），则导纳矩阵Y对称
12 = 21 Y12 = Y21
互易二端口网络四个参数中只有三个是独立的。
(Z12=Z21)
若矩阵 Z 与 Y 非奇异
Y=Z-1 Z=Y-1
二端口网络
江苏大学电路教学组
即
Z11 Z21
ZZ1222=Δ1Y-YY2221
-Y12
Y11
I 1 Za 例5
+
Zc - r I 1 + I 2 +
U1
Zb
U2
-
-
U 1 = Z a I 1 Z b ( I 1 I 2 ) = ( Z a Z b ) I 1 Z b I 2
-Yb
Yb
非互易二端口网络（网络内部有受控源）有四个独立参数。
二端口网络
江苏大学电路教学组
三、Z参数和方程
I1 + U1 -
线性 无源
I2
U2 -
由Y 参数方程
I1 =Y11U1 Y12U2 I2 =Y21U1 Y22U2
可解 U 1,U 出 2.
即：
U1 =YΔ22I1-ΔY12I2 =Z11I1Z12I2
i1
i2
u2
-
-
1 i1 3
4 i2 2
1-1’ 2-2’是二端口 3-3’ 4-4’不是二端口，是四端网络
i1 = i1 - i i1 i2 = i2 i i2
端口条件破坏
二端口网络
江苏大学电路教学组
5.约定 (1)讨论范围
含线性R、L、C、M与线性受控源；
不含独立源(运算法分析时，不包含附加电源)。
Ya I2
U2 = 0
I1 U1 = 0
Yb Ya g U 1
I2 +
U2
-
江苏大学电路教学组
I2
+ U2 -
Y Y1211==U U II1211
U 2=0 =YaYb U 2=0 =-Yb-g
Y12=UI12 U1=0 =-Yb
Y2 2=UI22
=Y U1=0
b
二端口网络
江苏大学电路教学组
解二
U 2 = r I 1 + Z c I 2 + Z b ( I 1 + I 2 ) = ( r + Z b ) I 1 + ( Z b + Z c ) I 2
则
Z=ZraZZbb
Zb Zb Zc
二端口网络
江苏大学电路教学组
例6：图示电路，已知R=3Ω， L1= L2=3Ω， M=1Ω，求二
端口网络的Z参数。
Z 21
=
U2 I1
I2 =0
开路输入阻抗 开路转移阻抗
二端口网络
江苏大学电路教学组
Z 12
=
U1 I2
I1 =0
Z 22
=
U2 I2
I1 =0
开路转移阻抗 开路输入阻抗
Z参数是在一个端口开路情况下通过计算或测试求得
的，所以Z参数又称开路阻抗参数。
互易二端口 对称二端口
Z12=Z21 Z11=Z22
I2 U2
U1=0 = Yb + Yc
Y12=Y21=-Yb 互易二端口
对任何一个无源线性二端口，只要3个独立的参数就
足以表征它的性能。
注意
二端口网络
江苏大学电路教学组
Y
=
Ya Yb
-Yb
-Yb
Yb
Yc
若 Ya = Yc 有 Y12 = Y21 ，又Y11 = Y22 （电气对称），称为对称二端口。 对称二端口只有2个参数是独立的。
I
+
U
Z
-
（Y）
表征一端口网络电特性的独立 参数：输入阻抗Z或输入导纳Y。 且 Z = Y -1 。
i1 +
u1
i1
–
端口的概念：
端口由一对端子构成，且满足如下 条件：从一个端子流入的电流等于 从另一个端子流出的电流。此称为 端口条件。
二端口网络
江苏大学电路教学组
2.四端网络 在工程实际中，研究信号及能量的传输和信 号变换时，经常碰到如下形式的电路。称为 四端网络。
比较上式与Z参数方程的标准形式，可得
Z11 =j8，Z12 =j4 Z21 =j4，Z22 =3j3
二端口网络
江苏大学电路教学组
四、T参数（传输参数）和方程
I1=Y11U1Y12U2 I2=Y21U1Y22U2
由(2)得 U 1=-Y Y2221U 2Y121I2
将(3)代入(1)得
(1) (2)
T1 2 T22
-U I22
i1
+ u1 -
n:1
i2
+ u2 -
二端口网络
江苏大学电路教学组
例8 求T参数。
I1 1
+ U1
-
解： I1 1
+ U1
-
2 I2
+
2
U2
-
2
+ 2 U2
-
U I11=T T1211 T T1222-U I22
I1 1
+ U1
-
2 I2 2
T11=U U1 2 I2=0=1 22=1.5 T 12=- U I12U 2=0=I1[1 0 + .5 (I21 //2)]=4Ω
例2 求Y 参数。
I1
+
U1 -
Yb
Ya
Yc
I2
+
U2
-
二端口网络
江苏大学电路教学组
解： I1
+ U1 -
I1
Yb
Ya
Yc
Yb
U1 = 0
Ya