最新13二端口网络参数和方程汇总
演示文稿二端口网络参数和方程

二端口网络参数和方程
13.1 二端口网络及其参数方程
一、一端口网络和二端口网络的概念
1. 一端口网络
I
+
U
Z
-
(Y)
表征一端口网络电特性的独立 参数:输入阻抗Z或输入导纳Y。 且 Z = Y -1 。
i1 +
u1
i1
–
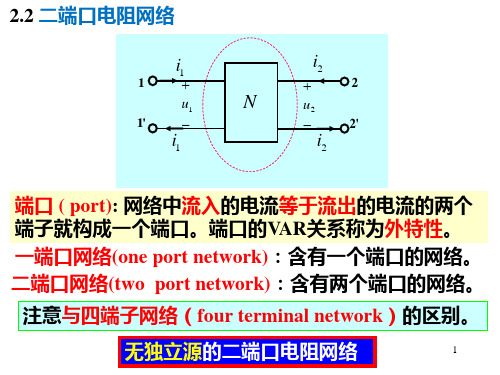
端口的概念:
端口由一对端子构成,且满足如下 条件:从一个端子流入的电流等于 从另一个端子流出的电流。此称为 端口条件。
i2 +
u2 – i2
4. 二端口与四端网络的区别:
二端口的两个端口必须 满足端口条件,四端网 络却没有上述限制。
i1
i2
i1
i2
二端口
i1
i2
i1
i2
具有公共端的二端口
i2 i1
i3 i4
四端网络
二端口的两个端口间若有外部连接,则会破坏原二端口的 端口条件。
1
i1
i 3
R
4 i2 2
u1
i1
2.四端网络 在工程实际中,研究信号及能量的传输和信 号变换时,经常碰到如下形式的电路。称为 四端网络。
线性RLCM 受控源
四端网络
例1
R
C
C
滤波器 n:1
变压器
三极管 传输线
3. 二端口(two-port)
如果四端网络的两对端子同时满足端口条件, 则称为二端口网络。
+
i1
u1 –
i1
线性RLCM 受控源
整理可得
I1 = (Y1 Y2 )U1 - Y2U2 I2 = -Y2U1 (Y2 Y3 )U2
【推荐】电路原理基础:第二章 二端口网络的方程和参数
D
i1 i2
u2 0, 10
四、H参数方程: 已知i1和 u2求u1和 i2
u1 H11i1 H12u2 i2 H 21i1 H 22u2
1 i1
u1
1' i1
i2 2
N
u2
i2 2'
u1
i2
H11 H 21
H12 H 22
i1 u2
T
0.5 0.75S
0.6
0.5
将其变换为其它参数方程,则可求得其他参数,
注意变换时有些参数可能不存在。
12
六、二端口网络参数的互易性(reciprocal)
若网络中只含有R、 L、 C、 M 等线性元件而不 含有受控源,则网络参数就具有如下性质:
(1) R12 R21 (3) T AD - BC 1
注意与四端子网络(four terminal network)的区别。
无独立源的二端口电阻网络
1
第一节 二端口网络的方程和参数
i1
1
u1
1'
i1
i2
2
N
u2
2'
i2
二端口的外特性决定于网络的本身与外部所接
电路无关,用端口电压、电流(共四个量)间的关 系反映,共六种情况。
2
一、R参数方程:
i1
u1
i2
Rl
u2
R
Rl Rl
Rl
Rl
但G不存在
二端口网络参数和方程和等效电路相关知识讲解培训

(1) H 参数
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
矩阵形式:
UI21
H11
H
21
H12 H 22
UI12
(2) H 参数的计算与测定
H11
U 1 I1
U 2 0
H21
I2 I1
U 2 0
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
Y21
I2 U 1
U 2 0 Yb Y12
Ya Yb Y11 即:Yb Y12 Y21
Yb Yc Y22
解之得
Ya Y11 Y12 Yb Y12 Yc Y22 Y12
注意: (1) 等效只对两个端口的电压,电流关系成立。对端 口间电压则不一定成立。
(2) 适用于互易网络。
I2
Y12U1 Y22U 2
Y21 Y12
U 1
I2
其中
I1 I'2
Y11U 1 Y12U 1
Y12U 2 Y22U 2
相当于一互易二端口,
可求出其等效电路(型):
(计算见前例)
•
I1
+
•
U1
Yb
Ya
Yc
I2
+
•
U2
而I2 I2 Y21 Y12 U1相 当 于 在 端 口2并 入 一 受 控 源.
C
I1 U 2
I2 0
D
I1 I2
U 2 0
U1 AU 2 BI2
I1
CU 2
DI2
(3) 互易二端口 Y12 Y21
T 参数满足: AD BC 1
三、二端口网络的T方程和T参数(精)

三、 二端口网络的T 方程和T 参数在上述内容中我们已经介绍了Y 参数和Z 参数的求法,Y 参数和Z 参数都可用来描述一个二端口网络的端口外特性。
但在许多工程实际问题中,往往还要求知道一个端口的电流、电压与另一个端口的电流、电压之间的直接关系。
若把Y 参数方程:22212122121111U Y U Y I U Y U Y I +=+=的第二式化为2212212211I Y U Y Y U +-= 代入Y 参数方程第一式中,整理可得:221112212211121)(I Y Y U Y Y Y Y I +-= 把以上两式写成下列形式⎪⎩⎪⎨⎧-=-=221221I D U C I I B U A U式中 ⎪⎪⎩⎪⎪⎨⎧-=-=-=-=2111212211212121221Y Y D Y Y Y Y C Y B Y Y AA 、B 、C 、D 称为二端口网络的一般参数、传输参数、T 参数或A 参数。
它们的具体含义可用下式说明:0221==I U U A A 是输出端开路时,输入电压与输出电压的比值;0221=-=I I U B B 是输出端短路时,输入端对输出端的转移阻抗;0221==I U I C C 是输出端开路时,输入端对输出端的转移导纳;0221==U I I D D 是输出端短路时,输入电流与输出电流的比值。
可见,A 是一个量纲为一的量纲;B 的量纲为Ω;C 的量纲为s ;D 也是量纲为一的量。
对于无源线性二端口网络A 、B 、C 、D 只有3个是独立的,因为Y 11=Y 22,故A =D 。
所以T 参数方程为:其中 ⎥⎦⎤⎢⎣⎡=D C B A T ,称为T 参数矩阵。
AD BC 可逆时,-=1AD BC A D =对称时满足:-=1,【例】 求例1中电路的T 参数【解】:方法一:根据定义求解(略)方法二:根据KCL 直接列方程求解(略)方法三:根据T 参数与Y 参数或Z 参数的转换公式(可在表6-1中查到)求⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-∆---=2111212121221Y Y Y Y Y Y Y T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∆=1222212121111Z Z Z Z Z Z Z T 其中 2112221122211211Y Y Y Y Y Y Y Y Y -==∆2112221122211211Z Z Z Z Z Z Z Z Z -==∆因为已知例1的 s Y ⎥⎦⎤⎢⎣⎡--=4.02.02.04.0 12.004.016.0=-=∆Y所以 ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=26.0522.04.02.012.02.012.04.0T⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡2211D I U C B A I U【例 】:已知...1111122...2211222(1)(2)U Z I Z I U Z I Z I =+=+ ,求T 参数。
3.1 二端口网络方程与参数

I2 2
U2 2
U1 I2R U2
I1 I2
1 R
T 0
1
1 I1 U1 1
I2 2
U2 2
U1 U2
I1 I2
1 0
T
0
1
参数的求法 二:列方程法
写出图示四种受控源的T参数矩阵
i1=0
+
(1)u1
-
i2
+
+
uCS= u1 u2
-
-
i1
+
(2)u1=0
-
u1 u2
i1 0
U1 T11U2 T12 (I2 ) I1 T21U2 T22 (I2 )
1 I1
输
入 U1
N
端
1
I2I2 2 输 U2 出 端
2
U1
I1
T11 T21
T12 U2
T22
I2
T
T11 T21
T12
T22
1
T参数矩阵(A参数) 单位 S
1
传输参数矩阵
参数的求法 一:定义法
I1 ,U 2
U1 H11I1 H12U 2
I2 H 21I1 H 22U 2
U1பைடு நூலகம்
I2
H11
H
21
H12 I1
H
22
U
2
1 I1 U1 1
H
H11
H
21
H12
H
22
H参数矩阵 混合参数矩阵
I2 2
N
U 2
2
1
单位
1
S
传输参数
传输参数方程
电路分析基础课件第13章 二端口网络

•
I
•
2I
2
+
NN
•
U2
••
I 1I 1
•+
U1
••
II2 2
++
NN
••
UU2 2
Y12
I1 U 2
U1 0
Y22
I2 U 2
U1 0
转移导纳 输入导纳
Y → 短路导纳参数
例2-1 求图示二端口的Y 参数。
解
•
I I I •
•
1 11
Yb YbYb
•
I I I •
•
2
2
2
++
•
••
UU1
1U01
第13章 二端口网络
13-1 13-2 13-3 13-4 13-5 13-6
二端口网络 二端口的方程和参数 二端口的等效电路 二端口的转移函数 二端口的连接 回转器和负阻抗转换器
重点
1. 二端口的参数和方程 2. 二端口的等效电路 3. 二端口的转移函数
13-1 二端口网络
在工程实际中,研究信号及能量的传输和 信号变换时,经常碰到如下二端口电路。
•
I1
例2-8 求二端口T 参数。 +
•
U1
解
n 0
T
0
1
n
1
2
•
I2
+
2
•
U2
A U1 U2
I2 0 1.5
B
U1 I2
U2 0
4Ω
C I1 U2
I2 0 0.5 S
D I1 I2
U2 0
2
二端口网络的网络参数

测量原理:利用频谱分析仪的频率扫描功能,对二端口网络的传输函数进行测量。
测量步骤:将二端口网络接入频谱分析仪,设置合适的频率范围和分辨率,进行频率扫描, 记录传输函数的幅度和相位信息。
测量精度:频谱分析仪的频率精度和幅度分辨率决定了测量精度,高精度的频谱分析仪可以 提高测量准确性。
参数计算的意义:通过计算电压反射 系数,可以了解网络对不同频率和幅 值的入射电压的响应特性,从而优化 网络设计。
定义:电流反射系数是描述二端口 网络输入端口对入射波和反射波的 幅度和相位变化的参数
物理意义:电流反射系数反映了网 络对入射波的反射能力,其值范围 在-1到1之间
添加标题
添加标题
添加标题
影响因素:网络阻抗与源阻抗的差异越大,电压反射系数越大
意义:电压反射系数是二端口网络的重要参数,用于分析网络的性能和稳定性
定义:电流反射系数是指入射波 与反射波的幅度之比
意义:电流反射系数反映了网络 对入射波的反射能力,是二端口 网络的重要参数之一
计算公式:反射系数 = (Z_2 Z_1) / (Z_2 + Z_1),其中 Z_2为输出阻抗,Z_1为输入 阻抗
调整网络分析仪的 参数设置
记录测量结果并进 行数据处理
验证测量结果的准 确性和可靠性
测量步骤:将信号发生器连接到二端口网络的输入端,将示波器连接到输出端,调整信号发生器输出信号的幅度 和频率,观察示波器上的输出波形
注意事项:确保信号发生器和示波器的性能良好,连接正确,避免外界干扰对测量结果的影响
测量结果:通过示波器观察到的输出波形可以计算出二端口网络的参数,如电压放大倍数、输入阻抗等
添加标题
二端口网络

第五部分 二端口网络(一)基本概念和基本定理1、二端口网络的端口方程和参数 (1)端口特性方程在两个端口的四个变量1U 、2U 、1I 、2I 中任取两个为变量,另两个为函数构成的方程。
电压、电流方向如图示。
(2)描述二端口的四个参数矩阵Z 参数对于由线性R 、L (M )、C 元件组成的任意二端口无源网络都有1221Z Z =,即Z 参数矩阵是对称的。
对于对称二端口有1221ZZ =、1122Z Z =Y 参数对于由线性R 、L (M )、C 元件组成的任意二端口无源网络都有1221Y Y =,即Y 参数矩阵是对称的。
对于对称二端口有1221YY =、1122Y Y =T 参数对于由线性R 、L (M )、C 元件组成的任意二端口无源网络都有1AD BC -=,即T 参数矩阵是对称的。
对于对称二端口有A D =.H 参数2、二端口等效电路(1)T 型电路11112Z Z Z =-212Z Z =32212Z Z Z =-(2) π型电路11112Y Y Y =+2122Y Y Y =-=- 3221Y Y Y =+ (3)如果二端口不互易,则等效T 型电路含有受控电压源,如图(4)如果二端口不互易,则等效π型电路含有受控电流源,如图3、二端口的连接(1)级联(2)并联(3)串联4、回转器和复阻抗变换器(1)回转器是一种线性非互易的多端元件。
互易定理不适应回转器。
r 和g分别称为回转电阻和回转电导,简称回转常数。
(2)负阻抗变换器电流反向型:1212,UU I kI ==,电压的大小和方向均不改变;但电流1I 经传输后变为2kI ,即改变了方向;电压反向型:1212,UkU I I =-=-,电压改变了极性(方向),但电流方向不变;NIC 可把正阻抗变为负阻抗。
(二)典型例题及解题方法分析例题1:图示电路二端口网络是由线性电阻构成的,此对称二端口的传输参数A=2,B=30,若将电阻LR并联在22'-两端,输入端11'-的入端电阻为将电阻LR 并联在11'-两端的入端电阻的6倍,求LR解法1:由于二端口网络是由线性电阻构成的,所以有AD-BC=1,又是对称二端口,有A=D=2,C=(AD-1)/B=0.1对于上面左图 22L UR I =-122122U AU BI I CU DI =-⎧⎨=-⎩1212()()L L U AR B I I R C D I =-+⎧⇒⎨=-+⎩112300.12L L in L L U AR B R R I CR D R ++⇒===++ 对于上面右图 20I=11'20'//'20LL i n LL L AR U R A C R R A I C R R C⇒====++ 6'in in R R =3in R =Ω解法2由于二端口网络是由线性电阻构成的对称二端口,A=D=2,C=(AD-1)/B=0.1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I1
I2
=
Y11 Y21
Y12
Y22
U1
U2
若网络内部无受控源(满足互易定理),则导纳矩阵Y对称
12 21 Y12 Y21
互易二端口网络四个参数中只有三个是独立的。
例2 求Y 参数。
I1
+ U1
Yb
Ya
Yc
I2
+ U2
二端口网络
江苏大学电路教学组
解:
I1
+ U1
I1
Yb
Ya
Yc
Yb
U1 0
Ya
Yc
I2
U
2
0
Y11UI11 U20 Ya Yb Y21UI21 U20 Yb
I2
+
Y12
=
I1 U2
U1=0 = Yb
U2
Y22
=
I2 U2
U1=0 = Yb + Yc
Y12Y21Yb 互易二端口
对任何一个无源线性二端口,只要3个独立的参数就
足以表征它的性能。
注意
二端口网络
江苏大学电路教学组
令
Y
Y11 Y 2 1
Y12
Y
22
称为Y参数矩阵。
I1 Y11U1 Y12U2 I2 Y21U1 Y22U2
端口电流 I 1 和 I 2 可视为
U
和
1
U
2
共同作用产生。
二端口网络
江苏大学电路教学组
Y 参数的实验测定
Y11
I1 U1
U20
Y 21
I2 U1
U20
Y12
I1 U2
U10
Y 22
I1 11U121U2 I2 12U122U2
Z l1 I1 Z l 2 I 2 Z ll I1 0
二端口网络
江苏大学电路教学组
分别用Y11、Y12、 Y21、 Y22表示这些系数,上式可写为:
I1 Y11U1 Y12U2 I2 Y21U1 Y22U2
矩阵形式: II12YY1211 YY1222UU12
i1 i1 i i1 i2 i2 i i2
端口条件破坏
二端口网络
江苏大学电路教学组
5.约定 (1)讨论范围
含线性R、L、C、M与线性受控源;
不含独立源(运算法分析时,不包含附加电源)。
(2)参考方向
+
i1
u1
– i1
线性RLCM 受控源
i2 +
u2 – i2
本章中二端口的参考方向,一般都如上图所示。 因此,引用公式时一定要注意端口的参考方向。
二端口网络
江苏大学电路教学组
13二端口网络参数和方程
二端口网络
江苏大学电路教学组
2.四端网络 在工程实际中,研究信号及能量的传输和信 号变换时,经常碰到如下形式的电路。称为 四端网络。
线性RLCM 受控源
四端网络
二端口网络
例1
R
C
C
滤波器 n:1
变压器
江苏大学电路教学组
三极管 传输线
二端口网络
江苏大学电路教学组
I1
I2
+ U1
1
线性 网络
2
+ U2
如果线性网络内部不含独立源,且有 l 个独立回路, 则可列写l个回路电流方程:
Z11I1 Z12 I2 Z1l Il U 1
Z 21I1 Z 22 I2 Z 2l Il U 2 Z 31 I 1 Z 32 I 2 Z 3 l I l 0 解得
= Y22
=ห้องสมุดไป่ตู้
3S 16
电气 对称
二端口网络
例4
解一
I1
I1
+ U1
Yb
Yb gU 1
Ya
I2
+
U1
Ya gU1
U2 0
I1
U1 0
Yb Ya g U 1
I2
+
U2
江苏大学电路教学组
I2
+
U2
Y Y1211U U II1211
U20 U20
Ya Yb Ybg
Y12 Y22
U UII1222
U10 Yb U10 Yb
I2 U2
U10
自导纳 转移导纳 转移导纳 自导纳
I1
+ U1
I1
I1 Y11U1 Y12U2 I2 Y21U1 Y22U2
线性 无源
线性 无源
I2
I2
+ U2
Y参数是在一个端口短路情况下通过计算或测试求得的, 所以又称为短路导纳参数。
二端口网络
江苏大学电路教学组
I1 11U121U2 I2 12U122U2
二端口网络
江苏大学电路教学组
例3 I 1 2
10
I2
I 1 2
I2
+
U1
5
10
++
U2
U1
+
2
4
2
U2
互易二端口 Y12 Y12
等效电路
16 Z11 U202(5//10)3
Y11
=
1 Z1-1
= 3S 16
16 Z 22U 1010//[10(5//2)]3
13
Y22
=
Z2-2
=S 16
故
Y11
i1
i2
二端口
i1
i2
i1
i2
具有公共端的二端口
i2 i1
i3 i4
四端网络
二端口网络
江苏大学电路教学组
二端口的两个端口间若有外部连接,则会破坏原二端口的 端口条件。
1
i1
i 3
R
4 i2 2
u1
i1
i2
u2
1 i1 3
4 i2 2
1-1’ 2-2’是二端口 3-3’ 4-4’不是二端口,是四端网络
江苏大学电路教学组
3. 二端口(two-port)
如果四端网络的两对端子同时满足端口条件, 则称为二端口网络。
+
i1
u1 –
i1
线性RLCM 受控源
i2 +
u2 – i2
二端口网络
江苏大学电路教学组
4. 二端口与四端网络的区别:
二端口的两个端口必须 满足端口条件,四端网 络却没有上述限制。
i1
i2
二端口网络
江苏大学电路教学组
6. 二端口的端口变量
I1
+ U1
线性 无源
I2
U2
端口物理量4个:I1 I2 U 1 U 2 四个端口变量之间存在着反映二端口网络特性的
约束方程。任取两个作自变量(激励),两个作
因变量(响应),可得6组方程。即可用6套参数
描述二端口网络。
二端口网络
江苏大学电路教学组
Y
Ya Yb
Yb
Yb
Yb
Yc
若 Ya Yc 有 Y12 Y21 ,又Y11 Y22 (电气对称),称为对称二端口。 对称二端口只有2个参数是独立的。
对称二端口是指两个端口电气特性上对称。电路结构 左右对称的,端口电气特性对称;电路结构不对称的二端 口,其电气特性也可能是对称的。这样的二端口也是对称 二端口。
二、Y参数和方程
右图所示Π形电路,
I1
I1 I2 U 1 U 2的参考
+
方向如图所示。由基 尔霍夫电流定律,可
U1
列写方程:
Y2
Y1
Y3
Y1U1 Y2(U1 U2)I1 Y2(U2 U1)Y3U2 I2
整理可得
I1 (Y1Y2)U1Y2U2 I2 Y2U1(Y2Y3)U2
I2
+ U2
二端口网络
二端口网络
江苏大学电路教学组
解二
I1
+ U1
Yb gU 1
Ya
I2
+
U2
I 1Y a U 1Y b(U 1U 2)
I 2Y b(U 2U 1)g U 1
I1(Y aY b)U 1Y bU 2
I 2(gY b)U 1Y b U 2
注意
则
YYagYYbb
Yb
Yb
非互易二端口网络(网络内部有受控源)有四个独立参数。
