二端口网络的传输参数矩阵
二端口网络的特性阻抗、回转器与负阻抗变换器相关知识培训讲解

+ u2
电流反向型
ui11
u2 ki2
u1
i1
1 0
0 u2
k
i
2
T 参数矩阵
(2) 阻抗变换器关系 (以INIC为例)
I1
I2
U+
1
INIC
U+ 2
ZL
UI11
U 2 kI2
U 2 ZL I2
(1)
INIC变换器
(2)
(3)
UI11
U 2 kI2
(1) (2)
U 2 ZL I2 (3)
端口1入端阻抗为
B ZS D
AB B ZDZS C D C
A D
ZC Z0ZS
2. 传播常数
•
1 I1
•
I2 2
+
+
•
U1
N
•
U2
ZC
1'
2'
一对称二端口,端口2接特性阻抗ZC时,其端口电压、 电流关系为:
UI11
AU 2 BI2 CU 2 DI2
U 2 ZC I2
(1) ( 2) ( 3)
二端口网络的特性阻抗、回 转器与负阻抗变换器相关知
识培训讲解
二端口的特性阻抗
1. 二端口的特性阻抗
•
1 I1
•
I2 2
+
+
•
U1
N
•
U2
ZL
1'
2'
T
参数方程
UI11
AU 2 CU 2
BI2 DI2
当端口2接阻抗ZL时,U 2 Z L I2
•
二端口网络z参数求解技巧

二端口网络z参数求解技巧二端口网络是指由两个端口组成的网络,其中一个端口为输入端口,另一个端口为输出端口。
在分析和设计二端口网络时,我们常常使用参数化方法,其中最常见的是使用z参数。
z参数是指输入端口和输出端口之间的电压和电流之间的关系。
在二端口网络中,输入端口的电流I1和电压V1以及输出端口的电流I2和电压V2之间存在以下关系:```V1 = Z11 * I1 + Z12 * I2V2 = Z21 * I1 + Z22 * I2```其中,Z11、Z12、Z21和Z22是参数矩阵,代表了电路元件的特性。
我们可以利用这些参数来分析和计算二端口网络的性能。
接下来,我将介绍一些求解二端口网络z参数的技巧。
1. 网络简化:首先,我们要对二端口网络进行简化,即将网络中的电路元件替换为等效电路,以便更方便地分析。
我们可以使用电路分析方法,如电压分压法、电流分流法等,将网络简化为电阻、电容和电感等基本元件的串并联组合。
2. 确定输入和输出量:在分析二端口网络时,我们需要确定输入和输出量。
输入和输出量可以是电流和电压之间的关系,也可以是功率和电阻之间的关系。
通过确定输入和输出量,我们可以更准确地描述和计算二端口网络的特性。
3. 确定参数值:在求解z参数时,我们需要确定参数矩阵Z11、Z12、Z21和Z22的具体值。
参数值可以通过实验或仿真等方式获取。
如果我们已经知道了电路元件的数值,我们可以直接使用电路分析方法求解参数值。
如果我们只知道电路的结构和拓扑关系,我们可以使用矩阵分析方法求解参数值。
4. 参数矩阵运算:一旦确定了参数值,我们就可以进行参数矩阵的运算。
参数矩阵的运算包括矩阵加法、矩阵减法、矩阵乘法和矩阵逆运算等。
通过参数矩阵的运算,我们可以得到输入端口和输出端口之间的关系。
5. 分析和计算:最后,我们可以利用参数矩阵进行分析和计算。
例如,如果我们已知输入端口的电流和电压,我们可以使用参数矩阵得到输出端口的电流和电压。
二端口网络的传输参数、混合参数方程

放大小信号时的交流微变等效电路
U1 H11I1 H12U2 rbeI1
I2
H 21I1
H 22U 2
I1
1 rce
U2
忽 略
H
H11 H 21
H12 H 22
rbe
0
1
rce
P66 [例7-7]
解:求 H参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
P66 [例7-7]续 解:再求 T 参数。该电路中包含一个 理想变压器,先将各部分伏安关系式列出。
U1 2U 2
,
I1
I2 2
I1
I1
U1 3
即
I1
I2 2
2U 2 3
先列出 T 参数方程的结构,再具体化
U1 AU2 B( I2) 2U2 2U2 0
I1
CU2
D(
I
)=
2
U1 3
I1
2 3
电流 放大倍数
转移电导
转移电阻
二 端 口 网 络 参 数 方 程 小 结
二端口网络参数方程小结
互易二端口网络不含受控源,从互易网络应满足的 条件可知,四个参数中只有三个是独立的。
第7章 二端口网络的概念
7.1 二端口网络的端口条件及导纳参数、阻 抗参数方程
7.2 二端口网络的传输参数、混合参数方程 7.3 互易二端口网络的等效电路与级联
二端口网络的导纳参数、阻抗参数是基本参数, 而传输参数、混合参数是工程中的应用参数。
7.2.1 二端口网络的传输参数方程
U1
AU 2
B(
I
)
2
A
C、D的定义为:
三、二端口网络的T方程和T参数(精)

三、 二端口网络的T 方程和T 参数在上述内容中我们已经介绍了Y 参数和Z 参数的求法,Y 参数和Z 参数都可用来描述一个二端口网络的端口外特性。
但在许多工程实际问题中,往往还要求知道一个端口的电流、电压与另一个端口的电流、电压之间的直接关系。
若把Y 参数方程:22212122121111U Y U Y I U Y U Y I +=+=的第二式化为2212212211I Y U Y Y U +-= 代入Y 参数方程第一式中,整理可得:221112212211121)(I Y Y U Y Y Y Y I +-= 把以上两式写成下列形式⎪⎩⎪⎨⎧-=-=221221I D U C I I B U A U式中 ⎪⎪⎩⎪⎪⎨⎧-=-=-=-=2111212211212121221Y Y D Y Y Y Y C Y B Y Y AA 、B 、C 、D 称为二端口网络的一般参数、传输参数、T 参数或A 参数。
它们的具体含义可用下式说明:0221==I U U A A 是输出端开路时,输入电压与输出电压的比值;0221=-=I I U B B 是输出端短路时,输入端对输出端的转移阻抗;0221==I U I C C 是输出端开路时,输入端对输出端的转移导纳;0221==U I I D D 是输出端短路时,输入电流与输出电流的比值。
可见,A 是一个量纲为一的量纲;B 的量纲为Ω;C 的量纲为s ;D 也是量纲为一的量。
对于无源线性二端口网络A 、B 、C 、D 只有3个是独立的,因为Y 11=Y 22,故A =D 。
所以T 参数方程为:其中 ⎥⎦⎤⎢⎣⎡=D C B A T ,称为T 参数矩阵。
AD BC 可逆时,-=1AD BC A D =对称时满足:-=1,【例】 求例1中电路的T 参数【解】:方法一:根据定义求解(略)方法二:根据KCL 直接列方程求解(略)方法三:根据T 参数与Y 参数或Z 参数的转换公式(可在表6-1中查到)求⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-∆---=2111212121221Y Y Y Y Y Y Y T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∆=1222212121111Z Z Z Z Z Z Z T 其中 2112221122211211Y Y Y Y Y Y Y Y Y -==∆2112221122211211Z Z Z Z Z Z Z Z Z -==∆因为已知例1的 s Y ⎥⎦⎤⎢⎣⎡--=4.02.02.04.0 12.004.016.0=-=∆Y所以 ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=26.0522.04.02.012.02.012.04.0T⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡2211D I U C B A I U【例 】:已知...1111122...2211222(1)(2)U Z I Z I U Z I Z I =+=+ ,求T 参数。
9-4 二端口网络的参数

有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
(9) (10)
U1
= R +
1 jωC
I1
+
1 jωC
I2
= U 2
1 jωC
I1
+
1 jωC
I2
(11)
对照式(11)与式(1),通过对号入座,可得 Z 参数为
(1)二端口网络内部结构和参数已知 以一个例子来说明二端口网络参数的确定方法。 例题:求图 3 所示二端口网络的 Z 参数和 Y 参数。
I1
R1
U 1
I2
1
jωC U 2
图 3 二端口网络参数例题电路图
由图 3,根据 KCL 可得
U2 = 1
I1 + I2
jωC
根据 KVL 可得
U=1 RI1 + U2
对照式(13)与式(3),通过对号入座,可得 Y 参数为
1 Y = −RR1
1 R
− +
1 R
1 jωC
(14)
以上求二端口网络网络参数的过程可以简单总结为:列方程→整理方程→对号入座。 (4)二端口网络为黑匣子 如果图 2 中二端口网络为黑匣子,此时需要通过实验测量的方法来确定二端口网络的参 数。 以 Z 参数的确定为例。图 2 中二端口网络 Z 参数的定义方程组在式(1)中已给出,为 了便于后面进行分析,此处重写一遍。
U1= T11U2 + T12 (−I2 ) I1= T21U2 + T22 (−I2 )
将式中的四个系数组合为一个矩阵
(7)
T
第五章 微波网络基础 传输(ABCD)矩阵(转移矩阵)

B1 V2 I D1 2
V2 A2 I C 2 2
B2 V3 D2 I 3
V1 A1 I C 1 1
B1 A2 D1 C2
B2 V3 M个二端口网络级联 [ A] [ A1 ][ A2 ] [ AM ] D2 I 3
I1 D I2
V2 0
2
(端口2短路)
传输矩阵应用
传输矩阵的应用——二端口网络的级联
I1
+ -
I2
V1
I3
A1 B1 C D 1 1
二端口网络1
+ -
V2
A2 B2 C D 2 2
二端口网络2
+ -
V3
V1 A1 I C 1 1
传输矩阵参量计算
变压器:
传输矩阵与阻抗矩阵之间的关系
阻抗矩阵线性方程组
V1 Z11 V Z 2 21
A
B
注意负号意义!
Z12 I1 I Z 22 2
I1Z11 Z11 / Z 21 I1Z 21
V1 I1Z11 I 2 Z12 V2 I1Z 21 I 2 Z 22
若网络是互易的, Z12 Z 21
I1 D I2
I 2 Z 22 / Z 21 Z 22 / Z 21 I2 V 0
2
AD BC 1
11
二端口网络
二端口网络——微波电路中最常见
衰减器
移相器 匹配器 滤波器 ……
12
失配损耗 耗散损耗
V1 AV2 BI 2 I1 CV2 DI 2
电路元件伏安特性的测量实验报告答案

实验一电路元件伏安特性的测量一、实验目的1.学习测量电阻元件伏安特性的方法;2.掌握线性电阻、非线性电阻元件伏安特性的逐点测试法;3.掌握直流稳压电源和直流电压表、直流电流表的使用方法。
二、实验原理在任何时刻,线性电阻元件两端的电压与电流的关系,符合欧姆定律。
任何一个二端电阻元件的特性可用该元件上的端电压U与通过该元件的电流I之间的函数关系式I=f(U)来表示,即用I-U平面上的一条曲线来表征,这条曲线称为电阻元件的伏安特性曲线。
根据伏安特性的不同,电阻元件分为两大类:线性电阻和非线性电阻。
线性电阻元件的伏安特性曲线是一条通过坐标原点的直线,如图1-1(a)所示。
该直线的斜率只由电阻元件的电阻值R决定,其阻值R为常数,与元件两端的电压U和通过该元件的电流I无关;非线性电阻元件的伏安特性曲线不是一条经过坐标原点的直线,其阻值R不是常数,即在不同的电压作用下,电阻值是不同的。
常见的非线性电阻如白炽灯丝、普通二极管、稳压二极管等,它们的伏安特性曲线如图1-1(b)、(c)、(d)所示。
在图1-1中,U >0的部分为正向特性,U<0的部分为反向特性。
(a)线性电阻(b)白炽灯丝绘制伏安特性曲线通常采用逐点测试法,电阻元件在不同的端电压U 作用下,测量出相应的电流I ,然后逐点绘制出伏安特性曲线I =f (U ),根据伏安特性曲线便可计算出电阻元件的阻值。
三、实验设备与器件1 台2.直流电压表 1 块3.直流电流表 1 块4.万用表 1 块5.白炽灯泡 1 只6. 二极管 1 只7.稳压二极管 1 只8.电阻元件 2 只四、实验内容1.测定线性电阻的伏安特性 按图1-2接线。
调节直流稳压电源的输出电压U ,从0伏开始缓慢地增加(不得超过10V ),在表1-1中记下相应的电压表和电流表的读数。
表1-1 测定线性电阻的伏安特性U (V ) 0 1 2 3 4 5 6 7 8 9 10 I (mA ) 012.测定白炽灯泡的伏安特性将图1-2中的1kΩ线性电阻R 换成一只的灯泡,重复1的步骤,在表1-2中记下相应的电压表和电流表的读数。
第10章 习题解答
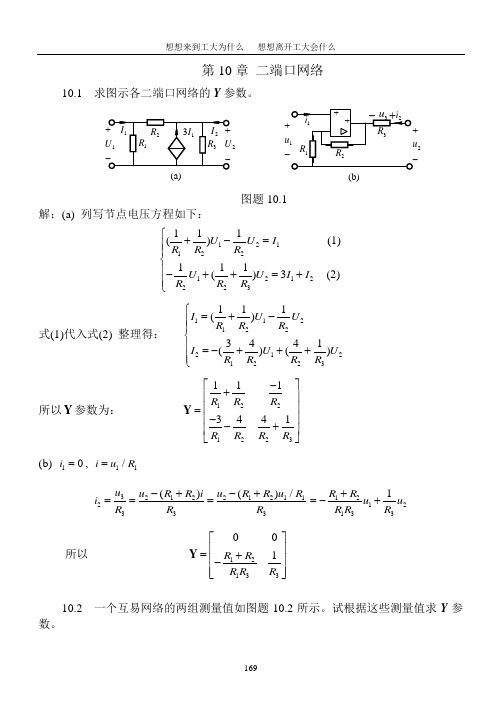
第10章 二端口网络10.1 求图示各二端口网络的Y 参数。
22u (b)图题10.1解:(a) 列写节点电压方程如下:1211221212223111() (1)111()3 (2)U U I R R R U U I I R R R ⎧+-=⎪⎪⎨⎪-++=+⎪⎩ 式(1)代入式(2) 整理得: 1121222121223111()3441()()I U U R R R I U U R R R R ⎧=+-⎪⎪⎨⎪=-+++⎪⎩所以Y 参数为:12212231113441R R R R RR R -⎡⎤+⎢⎥⎢⎥=-⎢⎥-+⎢⎥⎣⎦Y (b) 10i =, 11/i u R =3212212112333()()/u u R R i u R R u R i R R R -+-+===12121331R R u u R R R +=-+ 所以12133001R R R R R ⎡⎤⎢⎥=+⎢⎥-⎢⎥⎣⎦Y10.2 一个互易网络的两组测量值如图题10.2所示。
试根据这些测量值求Y 参数。
(a)(b)22-+U图题10.2解:图(a)中11222A,j2V 2j5j 10V j5A I U U I ===⨯==-,,由Y 参数方程得:11112221222j2j 10 (1)j5j2j 10 (2)I Y Y I Y Y ⎧==⨯+⨯⎨=-=⨯+⨯⎩ 由图(b)得 222jA 1V I Y ==⨯ (3) 对互易网络有:1221Y Y = (4)由式(3) 得: 22j 1S Y =,代入式(2) 得:2112( 2.5j5)S Y Y ==-- 再代入式(1)得:11(12.5j24)S Y =+ 所以12.5j2425j52.5j5j1.+--⎡⎤=⎢⎥--⎣⎦Y S 10.3 求图示各二端口网络的Z 参数。
(b)图题10.3解 (a):按网孔列写KVL 方程得1211221(2)2 (1)2(2)3 (2)R R I RI U RI R R I U U ++=⎧⎨++=+⎩ 将式(1)代入式(2)整理得1122123273U RI RI U RI RI =+⎧⎨=--⎩ 所以 3273RR R R ⎡⎤=⎢⎥--⎣⎦Z(b) 将∆联接的三个阻抗转换成Y 形联接,如图(c)所示,由此电路可直接写出Z 参数1j j j 0+⎡⎤=⎢⎥⎣⎦Z Ω10.4求图示各二端口网络的A 参数。
