第2讲 流体静力学基本方程式
化工原理公式及各个章节总结汇总

第一章 流体流动与输送机械1. 流体静力学基本方程:gh p p ρ+=022. 双液位U 型压差计的指示: )21(21ρρ-=-Rg p p )3. 伯努力方程:ρρ222212112121p u g z p u g z ++=++4. 实际流体机械能衡算方程:f W p u g z p u g z ∑+++=++ρρ222212112121+ 5. 雷诺数:μρdu =Re6. 范宁公式:ρρμλfp d lu u d l Wf ∆==⋅⋅=22322 7. 哈根-泊谡叶方程:232d lup f μ=∆ 8. 局部阻力计算:流道突然扩大:2211⎪⎭⎫ ⎝⎛-=A A ξ流产突然缩小:⎪⎭⎫ ⎝⎛-=2115.0A A ξ第二章 非均相物系分离1. 恒压过滤方程:t KA V V V e 222=+令A V q /=,A Ve q e /=则此方程为:kt q q q e =+22第三章 传热1. 傅立叶定律:n t dAdQ ϑϑλ-=,dxdt A Q λ-= 2. 热导率与温度的线性关系:)1(0t αλλ+= 3. 单层壁的定态热导率:bt t AQ 21-=λ,或mA b tQ λ∆=4. 单层圆筒壁的定态热传导方程: )ln1(21221r r t t l Q λπ-=或m A b tt Q λ21-=5. 单层圆筒壁内的温度分布方程:C r l Qt +-=ln 2λπ(由公式4推导)6. 三层圆筒壁定态热传导方程:34123212141ln 1ln 1ln 1(2r r r r r r t t l Q λλλπ++-=7. 牛顿冷却定律:)(t t A Q w -=α,)(T T A Q w -=α8. 努塞尔数λαl Nu =普朗克数λμCp =Pr 格拉晓夫数223μρβtl g Gr ∆= 9. 流体在圆形管内做强制对流:10000Re >,1600Pr 6.0<<,50/>d lk Nu Pr Re 023.08.0=,或kCp du d ⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=λμμρλα8.0023.0,其中当加热时,k=,冷却时k= 10. 热平衡方程:)()]([1222211t t c q T T c r q Q p m s p m -=-+=无相变时:)()(12222111t t c q T T c q Q p m p m -=-=,若为饱和蒸气冷凝:)(12221t t c q r q Q p m m -== 11. 总传热系数:21211111d d d d b K m ⋅+⋅+=αλα 12. 考虑热阻的总传热系数方程:212121211111d d R R d d d d b K s s m ⋅++⋅+⋅+=αλα 13. 总传热速率方程:t KA Q ∆=14. 两流体在换热器中逆流不发生相变的计算方程:⎪⎪⎭⎫⎝⎛-=--22111112211lnp m p m p m c q c q c q KA t T t T 15. 两流体在换热器中并流不发生相变的计算方程:⎪⎪⎭⎫ ⎝⎛+=--22111122111lnp m p m p m c q c q c q KA t T t T 16. 两流体在换热器中以饱和蒸气加热冷流体的计算方程:2221ln p m c q KAt T t T =--第四章 蒸发1. 蒸发水量的计算:110)(Lx x W F Fx =-=2. 水的蒸发量:)1(1x x F W -= 3. 完成时的溶液浓度:WF F x -=4. 单位蒸气消耗量:rr D W '=,此时原料液由预热器加热至沸点后进料,且不计热损失,r 为加热时的蒸气汽化潜热r ’为二次蒸气的汽化潜热5. 传热面积:mt K QA ∆=,对加热室作热量衡算,求得Dr h H D Q c =-=)(,1t T t -=∆,T 为加热蒸气的温度,t 1为操作条件下的溶液沸点。
流体静力学方程式

流体静力学方程式流体静力学是研究流体在静止状态下的力学性质的学科。
它是流体力学的一个分支,研究流体静止时的压力、密度、重力等因素对流体的影响。
本文将介绍流体静力学的方程式及其应用。
正文流体静力学方程式是描述流体静止时的力学行为的数学表达式。
主要包括两个方程式:流体静力平衡方程和流体连续性方程。
一、流体静力平衡方程流体静力平衡方程是基于力的平衡原理得出的。
它可以用来描述流体内外压力的均衡状态。
在一个封闭的容器中,流体的压力在各个方向上必须保持平衡。
这个平衡关系可以用以下方程式表示:P = ρg其中,P是压力场的梯度,ρ是流体的密度,g是重力加速度。
这个方程式表明流体中各个点的压力梯度与密度和重力加速度之间存在着一定的关系。
二、流体连续性方程流体连续性方程是基于流体质量守恒原理得出的。
它描述了流体在任意两个点之间质量的守恒关系。
对于一个不可压缩的流体(密度恒定),流体连续性方程可以用以下方程式表示:·v = 0其中,·v表示流体速度场的散度。
这个方程式表明流体在任意两个点之间的流量守恒,流出的质量等于流入的质量。
这两个方程式是流体静力学中的基本方程,通过它们可以计算流体静止时的压力分布和速度分布。
在实际的工程应用中,它们被广泛用于分析和设计涉及流体静力学的系统,如水坝、水管等。
总结起来,流体静力学方程式是描述流体静止时力学行为的基本数学表达式。
通过流体静力平衡方程和流体连续性方程,我们可以了解流体静态时的压力分布和速度分布,进而应用于实际工程中的设计和分析。
这些方程式为我们提供了深入理解流体静力学的基础,有助于我们更好地应对与流体静力学相关的问题。
流体力学中的流体静力学方程

流体力学中的流体静力学方程流体力学是研究流体运动和流体行为的物理学科。
它涉及到各种复杂的力学现象,其中之一就是流体静力学方程。
流体静力学方程描述了静止流体中各个点的力学平衡条件,它是流体力学的基础。
在介绍流体静力学方程之前,我们先来了解一下流体静力学的基本概念。
流体是一种无固定形状的物质,包括液体和气体。
流体的特性在很大程度上受到压力的影响。
流体静力学研究的是流体在静止状态下的力学行为,即不考虑流体的运动情况。
流体静力学方程可以通过两个基本方程来描述,分别是压力方程和流体压强分布方程。
1. 压力方程:在流体静力学中,压力是一个非常重要的参数。
它可以通过以下方程来描述:∇P = -ρg其中P是压力,∇P表示压力梯度,ρ是流体的密度,g是重力加速度。
上述方程意味着压力梯度的方向是压力降低的方向。
当流体静止时,压力在任意两点之间的变化只受到重力的影响。
这是因为重力会使流体向下运动,从而导致压力的变化。
2. 流体压强分布方程:流体压强分布方程是描述流体静止状态下压强分布的方程。
它可以通过以下方程来表示:P = P0 + ρgz其中P是流体某一点的压强,P0是参考点的压强,ρ是流体的密度,g是重力加速度,z是从参考点到目标点的垂直距离。
上述方程表明了流体压强随着高度的增加而递减。
这是因为在静止流体中,压强的变化只取决于液体的密度和重力的作用。
除了上述两个基本方程外,流体静力学还涉及到一些附加的方程,如流体的静力平衡方程和流体的表面张力方程。
这些方程在一些特殊情况下起到重要的作用,能够进一步描述流体静止时的行为。
总结起来,流体静力学方程是描述流体静止状态下的力学平衡条件的方程。
它们包括压力方程和流体压强分布方程,能够很好地描述流体静态行为。
在流体力学的研究中,深入理解和应用这些方程对于解决各种与流体静力学相关的问题非常重要。
中南大学《流体力学》课件第二章静力学.

证明
质量力 表面力
1 f x dxdydz 6
1 p 0 0 p A cos( n , x ) x dydz n n 2
导出关系式 得出结论
F 0
x
px pn
第一节 平衡流体中的应力特征
第二节 流体平衡微分方程
压强在流体运动、流体与固体相互作用中扮演重要角色,如 机翼升力、高尔夫球及汽车的尾流阻力,龙卷风产生强大的 负压强作用,液压泵和压缩机推动流体做功等都与压强有关。 然而,压强在静止流体、相对静止流体及粘性运动流体中的 分布规律将明显不同。
如图所示的密闭容器中,液面压强 问题1: p0=9.8kPa,A点压强为49kPa, 则B点压强为多少 ,在液面下的深度为多少? 答案 39.2kPa;
3m
问题2: 露天水池水深5m处的相对压强为:
答案
49kPa
图示容器内 A、B 两点同在一水 问题3:平面上,其压强分别为 pA 及 pB。 因 h1 h 2,所以 pA pB。 答案
• 点压强的定义及特性 • 微元体法推导出流体平衡微分方程 即流体平衡的规律 • 重力作用下流体的平衡
p p ( U U ) 0 0
pp gh 0
等压– 绝对压强p‘ 绝对压强不可为负 – 相对压强(表压强)p 相对压强可正可负 – 真空压强(真空值)pv 真空压强恒为正值
自由面上 p 0 所以 AB 上各点的压强均为 0
[例]试标出如图所示盛液容器内A、B、C三点的位置水头、 测压管高度、测压管水头。以图示0-0为基准面。
pC g pB g
A
pA g
Z
Z
c
ZB
C 因为 ,所以,以A点的测压管水头为依据, g 可以确定B点的位置水头为2m和测压管高度为6m ;C点的 位置水头6m,测压管高度为2m.
流体流动02-(静力学方程式及应用+连续性方程)
2. 平衡器里的液面高度维持在容器液面容许到达的最大高度处。
读数越小。当液面达到最大高度时,压差计的读数为零。
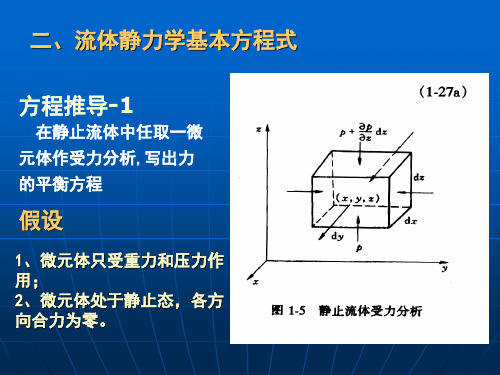
例 2 为了确定容器中石油产品的液面,采用如附图所示的装置。 压缩空气用调节阀1调节流量,使其流量控制得很小,只要在鼓
泡观察器 2内有气泡缓慢逸出即可。因此,气体通过吹气管 4的 流动阻力可忽略不计。吹气管内压力用U管压差计3来测量。压 差计读数 R的大小,反映贮罐 5 内液面高度。指示液为汞。 1、 分别由a管或由b管输送空气时,压差计读数分别为 R1或R2,试 推导R1、R2分别同Z1、Z2的关系。 2、当( Z1 - Z2)= 1.5m, R1= 0.15m, R2=0.06m时,试求石 油产品的密度ρP及Z1。已知Hg密度为13600kg/m3。
该液柱在垂直方向上受到的作用力有: (1)作用在液柱上端面上的总压力P1 P1= p1 A (N) (2)作用 在液柱下端面上的总压力 P2 P2= p2 A (N) (3)作用于整个液柱的重力G G =gA(Z1-Z2) (N)
由于液柱处于静止状态,在垂直方向上的三 个作用力的合力为零, 即 : p1 A+ gA(Z1 - Z2)–p2 A = 0 令: h= (Z1 -Z2) 整理得: p2 = p1 + gh 若将液柱上端取在液面,并设液面上方的压 强为 p0 ; 则: p0 = p1 + gh 以上二式均称为流体静力学基本方程式,它 阐明了静止流体内部任一点流体静压力的大小与 其位置的关系。
扩张室:扩张室的截面积远大于U型管截面积(直径比1:10以
上),当读数R变化时,两扩张室中液面不致有明显的 变化。
按静力学基本方程式可推出:
流体力学(张景松版)第二章 流体静力学

工程大气压 98066.5 0.98067 1
0.9678 735.6 10.000 735.6 14.22
标准大气压 101325 1.01325 1.033
1
760 10.332 760
14.7
托
133.3 0.00133 0.00136 0.00132 1
13.6
1 0.01934
毫米水柱 9.8067 0.000098 0.0001 0.0000968 0.07356 1 0.07356 0.00142
一、压强的计量
p
1、绝对压强
以完全真空为基准计量的压强
绝对 压强
2、计示(相对)压强
以当地大气压强为基准计量的压强
o
计示 压强
计示 压强 (真空)
p>pa
大气压强 p=pa
p<pa 绝对 压强
完全真空 p=0
表压: p pa pe p pa gh
真空: p pa pv pa p pe
p p dx x 2
o y
dz
b ac
dy dx
p p dx x 2
x
为得到b面和c面的压强,利用a点压强进行泰勒展开:
b(x dx , y, z) : 2
pb
p
p x
dx 2
c(x dx , y, z) : 2
pc
p
p x
dx 2
2 流体静力学
z
p p dx x 2
一、流体的静压强
流体处于绝对静止或相对静止时的压强。
P dP p lim
A0 A dA
2.2 流体的静压力及其特性
流体静力学基本方程
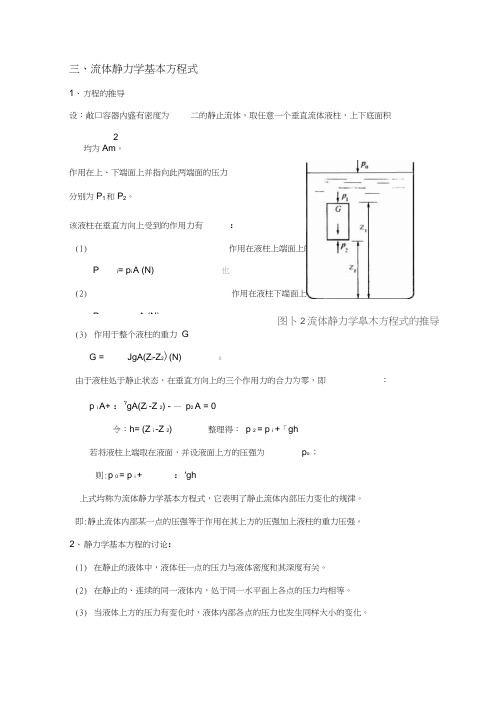
图卜2流体静力学皐木方程式的推导(3) 作用于整个液柱的重力 GG = JgA(Z i -Z 2)(N) 0由于液柱处于静止状态,在垂直方向上的三个作用力的合力为零,即 :p i A+ :?gA(Z i -Z 2) - — p 2 A = 0令:h= (Z i -Z 2) 整理得: p 2 = p i +「gh若将液柱上端取在液面,并设液面上方的压强为p o ; 则:p 0 = p i + :'gh上式均称为流体静力学基本方程式,它表明了静止流体内部压力变化的规律。
即:静止流体内部某一点的压强等于作用在其上方的压强加上液柱的重力压强。
2、 静力学基本方程的讨论:(1) 在静止的液体中,液体任一点的压力与液体密度和其深度有关。
(2) 在静止的、连续的同一液体内,处于同一水平面上各点的压力均相等。
(3) 当液体上方的压力有变化时,液体内部各点的压力也发生同样大小的变化。
三、流体静力学基本方程式1、 方程的推导设:敞口容器内盛有密度为 二的静止流体,取任意一个垂直流体液柱,上下底面积2均为Am 。
作用在上、下端面上并指向此两端面的压力分别为P 1和P 2。
该液柱在垂直方向上受到的作用力有: (1) 作用在液柱上端面上的总压力 P iPi = p i A (N) 也 (2) 作用在液柱下端面上的总压力 P 2P = p A (N)压强差的也大小可利用一定高度的液体柱来表示。
p P (5) 整理得:z 1g1二z 2g 也为静力学基本方程P g (6) 方程是以不可压缩流体推导出来的,对于可压缩性的气体,只适用于压强变 化不大的情况。
3、静力学基本方程的应用(1)测量流体的压差或压力①U 管压差计U 管压差计的结构如图。
对指示液的要求:指示液要与被测流体不互溶,不起 A化学作用,且其密度:7指应大于被测流体的密度:、。
通常采用的指示液有:水、油、四氯化碳或汞等。
I测压差:设流体作用在两支管口的压力为 p 1和P 2,且P i > P 2 , A-B 截面为等压面 即:P A 二P B 根据流体静力学基本方程式分别对 U 管左侧和U 管右侧进行计算整理得: P i - P 2 =:〔'指一'Rg讨论: (a )压差(p i -P 2)只与指示液的读数 R 及指示液冋被测流体的密度差有关。
广东石油化工学院化工原理流体静力学基本方程2

在静止液体中,上述三力之合力应为零, 在静止液体中,上述三力之合力应为零,即: p2dA-p1dA-ρgdA(Z1-Z2)=0 p2=p1+ρg(Z1-Z2) 将等号两边除以ρ并加以整理可得: 将等号两边除以 并加以整理可得: 并加以整理可得
p p 1 2 gZ1 + ρ = gZ2 + ρ
上两式即为液体静力学基本方程式 上两式即为液体静力学基本方程式
3、 压力的测定 、 压力的测定——压力表 压力表 当系统的实际压力大于1 当系统的实际压力大于 1 大气压时, 采用压力表 测压, 压力表测压 大气压时 , 采用 压力表 测压 , 压力表读数称为表压。 压力表读数称为表压。
当系统的实际压力小于1 当系统的实际压力小于1 大气压时,采用真空表测压, 真空表测压 大气压时,采用真空表测压, 真空表读数称为真空度。 真空表读数称为真空度。
R‘与R的关系为 的关系为: 的关系为
R'=R/sinα '=R/sinα
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
或该截面处流体的真空度为:101330-64840=36490Pa
与被测流体密度不同,不互溶,不反应,且易于观察。 常用指示液:测量液体——用Hg(ρ=13600kg/m3)
测量气体——用H2O
几种常用的压差计 ①普通U形管压差计
U管压差计是一根U形玻璃管,内装有液体作为指示液。 要求:指示液ρA>被测流体ρ,如图示,则:
pA p1 gz1 pA' p2 g(z2 R) 0gR
第2讲 第1章 流体流动
本章总教学目的和要求: 掌握流体流动过程的基本原理及流体在管内的流动规
律,并运用这些原理与规律去分析和计算流体的输送问题。 本节教学内容:
1.1流体静止的基本方程式。 教学重点: 1、流体静止的基本方程式推导 教学难点: 无
概念:
(1)流体:液体、气体 特质:不定形、易于流动。 (2)质点:大量分子构成的集团,但其大小与管路或容器的几 何尺寸相比仍然微不足道,常称为微团。
例:水在如图示的管道内流动。 在管道截面处连接一U管压差计, 指示液为水银,读数R=200mm、 h=1000mm。当地大气压强为 101.33×105Pa,试求流体在该截 面的压强。如右图示。
解:选取A-A’为等压面,则:
pA pA' pa
PA p H2 0 gh Hg gR
p pa H2 0 gh Hg gR
流体压强测量仪表
【例1-2】在兰州操作的苯乙烯真空蒸馏塔顶的真空表读数为 80×103Pa。在天津操作时,若要求塔内维持相同的绝对压 强,真空表的读数应为若干?兰州地区的平均大气压强为 85.3×103Pa,天津地区的平均大气压强为101.33×103Pa。
解:绝对压强=大气压强-真空度 实际操作过程中塔内压强不变,改变的只是真空表的读数。
或 绝压=大气压+表压 真空表——真空度:表内压 强(实际压强)比表外大气 压强低出的值。 关系:真空度=大气压-绝压
绝压=大气压-真空度
说明: 压强计量:因大气压强随温度、
湿度和当地海拔高度而变,因此, 为了防止混淆,对表压强、真空度 应加以标注。否则,视表压。 例:3kgf/cm2 、 3kgf/cm2(表压) 真空度50KPa(或记表压:-50KPa)
Z向:FZ 0
pz
(
pz
p z
dz)
d得: p g 0 ……①
z
——静止流体的欧拉(Euler)方程。
y向: Fy 0
py
(
py
p y
dy)
dxdz
0
整理,得: p 0 …… ② y
x向: Fx 0
px
(
px
p x
dx)
dydz
0
整理,得: p 0 ……③ x
m
m V
A xVA
B xVB
n xVn
或
m
pM m RT
n
( Mm Mi yi —— 平均摩尔质量) i 1
注:气体的密度必须注明状态(温度、压强)。
④ 混合液体:若各组分混合前后体积不变,已知各组分质量
分数xwi。以1kg混合液为基准:
m
m V
xwA
1 xwB
A B
xwn
n
或:
m
1
m
F1
F1 mg F2
A
用单位面积(A)上的力表示,即压强
F1 mg F2 AA A
p1
mg A
p2
P1
p1
A(z1
A
z2 ) g
p2
P2
Z1 Z2
p2 p1 g(z1 z2 )
W=mg
0
23:22:10
F2
10 流体静力学 (41)
2.流体静力学基本方程
如右图示,重力场中,在密度为ρ 的静止流体中取一微元立方体dxdydz。 (1)分析受力情形:
( 2)等压面 当容器液面上方的压强p0一定时,静止液体内部任一点的
压强p与液体本身的ρ及该点距液面的深度h有关。因此,在静 止的、连续的同一液体内,处于同一水平面上各点的压强都 相等,压强相等的水平面称为等压面。
(3)传递定律
由
p
p o
gh 知,
po
改变时,液体内部各点的压强也
以液同体样 内大部小的变任化一。点即(液帕面斯上卡方原的理压)强。能1以同样大小传递到2
(2) ρ的计算
① 一般液、固体:ρ=Δm/ΔV (kg/m3 )
② 气体:在压强不太高、温度不太低时,按理想气体处理
ρ=m/V=nM/V=pM/RT
0
p p0
T0 T
或
o
pTo poT
MT0 p 22.4Tp0
③ 混合气体:若各组分混合前后质量不变,已知体积
分数xVi(或摩尔分数yi)。以1m3混合气为基准:
……⑤
图1-7 静止液体内部的压强分布
3、流体静力学基本方程的物理意义
(1)总势能守恒(p1/ρ+ gZ1 = p2/ρ+ gZ2 = 常数) p/ρ和 gz 分别表示单位质量流体所具有的静压能(J/kg)和
位能(J/kg); ( p/ρ+ gZ )——总势能。在同一种静止流 体中不同高度上的点其静压能和位能各不相同,但总势能保 持不变。
(1) 扩大室内径应大于U形管内径的10倍 以上,以维持两扩大室内液面等高。 (2) 指示液要求:A、C不互溶,不起化学 反应,B与C亦不互溶,且A、C密度差越 小,R值就越大,读数精度也越高。
注:若两小室内液面差不可忽略时,则: p p1 p2 (A C )gR RC g
式中 ΔR=R(d/D)2为小室的液面差,d为U管内径,D为小室内径。
0
由: pA pA'
得:p p1 p2 g(z2 z1) (0 )gR
特殊地:若Z1=Z2,则:
A
p p1 p2 (0 )gR
若被测流体为气体,ρ很小,则: p 0 gR
2双液体U形管压差计(微差压差计) 目的:在测量微压差Δp时,可得到较大的读数R。
要求: p p1 p2 (A C )gR
1.2.3 流体静力学基本方程式的应用
流体静力学原理应用非常广泛,它是连通器和液柱压差计 工作原理的基础,还用于容器内液位的测量,液封装置等。解 题的基本要领是正确确定等压面。 1、压强或压强差的测量
液柱压差计——利用流体静力学原理测量流体压强或压强 差的仪器。特殊地:若差压计的一端与被测流体相连,另一端 与大气相通,则显示值是测点处流体的绝对压强与大气压强之 差,即为表压强或真空度。 指示液要求:
若任一静止液体中,对应:z1→p1;z2→p2,则由④式得:
p1
gz1
p2
gz2
……液体静力学基本方程
或: p2 p1 g z1 z2 p1 gh
或: p p2 p1 gh h
特殊地:若p1=p0, Z1=Z0则
p p g(Z Z ) p gh
2
0
0
2
0
p p gh 0
(4)液柱高度表示压强(或压强差)大小
p p
由
p p gh 0
0 h
g
知,压强或压强差的大小可以用
一定高度的液体柱表示(液柱压差计原理),但必须注明是何
种液体。例:760mmHg、10mH2O柱 。
注意适用条件:静止的连通着的同一种连续流体。
pA pa 1gh1 2 gh2 pA' pa 2 gh
(3)连续介质:流体是由大量的彼此无间隙的流体质点构成,流 体质点连续布满整个空间,从而流体的物理性质和运动参数 在空间上也是连续分布的,即为连续介质假定。
(4)流体分类 ①不可压缩流体:p改变,ρ基本不变或变化小。例:液体 ②可压缩流体:p改变,ρ变化大。例:气体
1.1流体的密度
(1)定义:①密度ρ:单位体积流体的质量 。ρ=Δm/ΔV (kg/m3) ②比容υ:单位质量流体的体积。υ=1/ρ( m3/kg)
=10330kgf/m2=1.033kgf/cm2=10.33mH2O=760mmHg 1at=1kgf/cm2=98070N/m2=10mH2O=735.6mmHg=0.9807bar
3.压强测量: 常用测压仪器:压力表(或
真空表)、液柱压差计。 压力表——表压:表内压强 (实际压强)比表外大气压 强高出的值。 关系:表压=绝压-大气压
n i 1
xwi
i
注:液体的密度基本上不随压强而变化,随温度略有改变。
1.2 流体静力学基本方程
1.压强定义 p=ΔP/ΔA——垂直作用于流体单位面积上的压力称为压
强。静止流体中的压强称为静压强。
2.压强表示方法 atm(标准大气压)、at(工程大气压)、流体柱高度、 N/m2(Pa)、kgf/cm2等。 ※注:1标准大气压(0℃、纬度45°海平面为基准) 1atm=101325Pa=101.3KPa=0.1013MPa
先计算兰州操作时塔内绝对压强: 绝对压强=85.3×103-80×103=5.3×103Pa
计算在天津时真空度 真空度=101.33×103-5.3×103=96.03×103Pa
1.2.2 流体静力学基本方程式
概述:流体在重力与压力作用下达到平衡,呈现静止状态, 否则,将产生流动。流体静力学基本方程——探讨 静止流体在重力作用下内部压强的变化规律。
1、流体的静力平衡 静止流体内部任一点的压强,称为该点流体的静压强。
特点: ① 从各个方向作用于某一点的流体静压强相等。 ② 若通过该点指定一作用平面,则压强的方向垂直指向该平面。 ③ 在重力场中,同一水平面上各点的流体静压强相等,但随位 置高低而变。
