螺旋压缩弹簧的稳定性分析
截锥螺旋压缩弹簧静力及模态分析

《工程结构分析专题》课程设计 截锥螺旋压缩弹簧静力及模态分析戴繁 2008301890053 工程力学二班摘要:利用ANSYS 软件对截锥螺旋压缩弹簧进行静力分析和模态分析,练习ANSYS 的建模、加载、求解、结果分析等的过程,并与理论解进行比较,判断求解精度。
关键词:ANSYS ,截锥螺旋压缩弹簧,静力分析,模态分析,理论解。
静力分析与模态分析均属于结构分析。
结构分析是有限元方法最常用的一个应用领域。
结构包括,土木工程结构,如桥梁和建筑物;汽车结构,如车身骨架;海洋结构,如船舶结构;航空结构,如飞机机身等。
同时,还包括机械零部件,如活塞,传动轴等。
结构分析中计算得出的基本未知量(节点自由度)是位移,其他的一些未知量,如应变,应力,和反作用力等,均可通过节点位移到处。
在ANSYS 产品家族中有七种结构分析的类型:静力分析,模态分析,谐波分析,瞬态动力学分析,谐分析,屈曲分析,显式动力分析等。
其中,静力分析用于求解静力荷载作用下结构的位移和应力等。
静力分析包括线性分析与非线性分析。
而非线性分析涉及塑型、应力刚化、大变形、大应变、超弹性、接触和蠕变分析。
模态分析用于计算结构的固有频率和模态。
问题描述变刚度弹簧以其独特的刚度特性在工业各领域得到广泛应用,截锥螺旋弹簧是这种非线性特性螺旋弹簧的典型代表。
这种弹簧在受荷载初期,特性线是直线,即刚度不变,当荷载逐渐增大时,弹簧从大圈开始逐渐接触,有效工作圈数随之减少,而刚度逐渐增大,直到所有弹簧圈压并为止。
该弹簧的变刚度特性引起了弹簧自振频率变化,使得在不同外扰频率作用力下弹簧变刚度运行,从而实现较宽频率范围内为共振峰,可以有利于消除或缓和共振,多用于承受较大的荷载和减震。
为此,为了充分利用变刚度弹簧的这种特性,通过现代的数值仿真模拟弹簧在各种工况下的静力状态和动力学响应,对于实际应用有很大的好处。
图1为截锥螺旋压缩弹簧及其特性线。
这种弹簧在受力后特性线的OA 段是直线,当荷载逐渐增大时弹簧的大圈开始逐渐接触,有效工作圈数减少而刚度逐渐增大,一直到所有的弹簧圈完全压并为止。
调整螺栓、弹簧的作用_概述说明以及解释

调整螺栓、弹簧的作用概述说明以及解释1. 引言1.1 概述本文主要讨论螺栓和弹簧的作用以及它们配合使用的效果。
螺栓是一种常用的紧固件,可以将物体牢固地连接在一起,不易松动;而弹簧则是一种具有弹性变形特性的零部件,在很多领域中发挥重要作用。
通过对螺栓和弹簧的描述和分析,我们可以了解它们在调整、固定等方面的作用,并掌握其应用场景和注意事项。
1.2 文章结构本文分为五个部分进行讨论。
引言部分(第1节)将介绍文章的概述、结构和目的;调整螺栓的作用(第2节)将简要介绍螺栓调整的背景和原理,以及其使用场景和注意事项;接着介绍弹簧的作用(第3节),包括基本原理、在不同领域中的应用以及选择要点;随后是螺栓与弹簧配合使用效果的解释(第4节),包括联合作用原理、实际应用案例分析与解释,以及协同工作优势和适用情况描述;最后是结论部分(第5节),对螺栓和弹簧的作用进行总结。
1.3 目的本文旨在全面介绍螺栓和弹簧的作用,帮助读者理解这两种零部件在实际应用中的重要性和功能。
通过了解螺栓和弹簧的基本原理、使用场景和注意事项,读者可以更好地选择适合自己需求的螺栓和弹簧,并掌握它们联合使用的效果和优势。
最终目标是提高读者对螺栓与弹簧以及其配合使用方面知识的认识水平,为实际工程问题提供参考依据。
2. 调整螺栓的作用:2.1 简介螺栓调整:螺栓是一种常见的机械连接件,常用于连接两个或多个零部件。
在一些特定情况下,需要对零部件进行位置调整或者紧固力的控制,这时候就需要使用调整螺栓。
2.2 作用和原理:调整螺栓可以实现以下几个作用:- 位置调整:通过旋转螺纹来改变零部件之间的相对位置。
通过加紧或松开螺栓,可以使得零部件的相对位置发生微小的移动。
- 紧固力控制:通过对螺栓进行加紧或松开来控制连接处的紧固力大小。
适当调整螺栓的紧度可以确保零部件之间的连接牢固且不会轻易松动。
这些作用都是基于螺纹副(由外螺纹和内螺纹组成)的原理实现的。
通过旋转外螺纹,在内、外侧摩擦面上产生压力,从而实现位置调整和紧固力控制。
圆柱形螺旋弹簧弹力影响因素研究报告参考模板
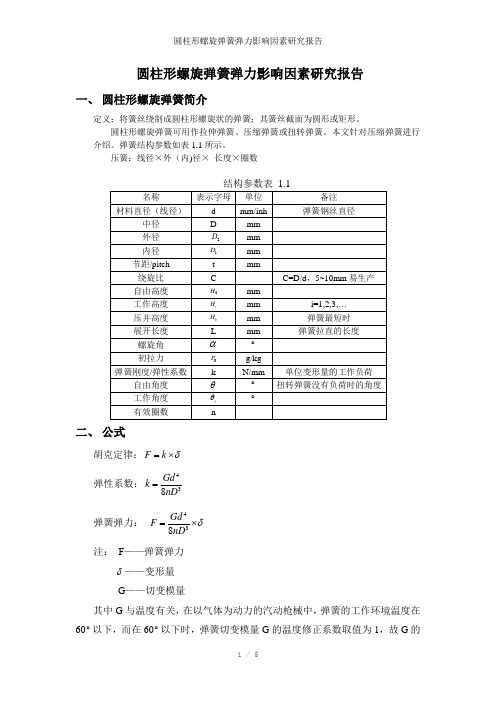
圆柱形螺旋弹簧弹力影响因素研究报告一、圆柱形螺旋弹簧简介定义:将簧丝绕制成圆柱形螺旋状的弹簧;其簧丝截面为圆形或矩形。
圆柱形螺旋弹簧可用作拉伸弹簧、压缩弹簧或扭转弹簧。
本文针对压缩弹簧进行介绍。
弹簧结构参数如表1.1所示。
压簧:线径×外(内)径×长度×圈数二、公式胡克定律:F kδ=⨯弹性系数:438Gd knD =弹簧弹力:438GdFnDδ=⨯注:F——弹簧弹力δ——变形量G——切变模量其中G与温度有关,在以气体为动力的汽动枪械中,弹簧的工作环境温度在60︒以下,而在60︒以下时,弹簧切变模量G的温度修正系数取值为1,故G的大小至于弹簧选用材料有关,可由机械设计手册第二卷查到。
三、 分析(1) G 由弹簧材料决定,取值参照d 在机械设计手册第二卷中选取。
在室温条件下切变模量温度修正系数为1,公司产品中弹簧材料多选用琴钢丝和热轧弹簧钢,则前者G 取79GPa ,后者G 取78GPa;虽然随着G 的增加,弹簧弹力F 线性增大,但考虑到弹簧成本和结构尺寸限制,而且常用弹簧材料中G 取79GPa 已经最大,故不考虑改变G 来实现弹簧弹力的改进。
(2) 弹簧有效圈数增加,弹簧弹性系数变小,弹力减小。
弹簧有效圈数n的变化直接影响压并高b H 和自由高度0H ,以及最大压缩变形量。
在同样的工作高度的条件下,n n →+∆则 :0()3i H H n t d t δδ→-=+∆+=+∆444444333333()(3)(3)8888()88()i i Gd Gd Gd Gd t Gd Gd F d H F d H D n D D n D n D D n δδ+∆==+-→==+-+∆+∆,F 是减小的;反之n n →-∆则t δδ→-∆,F 是增加的。
(3) 在弹性系数及其他条件不变的情况下,F k δ=⨯,有F 随着δ的变大而线性增加。
一般产品结构确定的条件下,弹簧压缩行程固定,不通过改变变形量来实现弹力的改变。
影响弹簧疲劳强度的几个因素-推荐下载

2)感应加热或保护气氛感应加热热处理。
这项工艺一般在螺旋弹簧成形前的线材上进行,有些弹簧工厂把线材料热处理和弹簧制作放在一起以降低成本。
感应加热处理具有较好的强化效果,感应加热速度快,有助细化晶粒和减少表面脱碳,可以充分发挥和提高材料的强度和韧性。
3)表面氮化热处理工艺技术。
近年来,高应力气门弹簧或其他高应力离合器弹簧为了达到可靠的疲劳寿命,也采用表面氮化工艺技术,现在比较先进的工艺是低温气体氮化技术,一般氮化温度为(450~470)℃,气体氮化时间为(5~20)h。
(2)弹簧的喷丸强化工艺 1)组合喷丸工艺技术。
组合喷丸,一般也称多次喷丸工艺。
大多数经济的工艺是采用二次喷丸。
通过采用不同直径的丸粒喷丸来实现。
第一次采用较大丸粒来获得残余压应力和表面光洁度。
2)应力喷丸工艺。
应力喷丸工艺也是一项比较经典的喷丸工艺,只是因为难以应用于大批量生产,但近年来由于应力喷丸设备的快速发展,在高应力汽车悬架弹簧大批量生产中得到了较大发展。
特别是应力强化喷丸与其他喷丸工艺的组合应用具有很好的强化效果。
应力喷丸的预应力一般设定在(700~800)MPa,经应力抛丸后,残余应力的峰值可以达到(1200~1500)MPa,从而得到高的抗疲劳强度。
(3)弹簧的热强压工艺热强压工艺主要应用在要求高的抗永久变形量的螺旋弹簧上,是作为高级的防永久变形的稳定化处理工艺。
热强压工艺除可以显着提高抗永久变形外,还可以提高疲劳寿命。
拉簧、压簧的设计方法阅读:3179人次 更新时间:2009-12-23 8:57:54弹簧设计的任务是要确定弹簧丝直径d、工作圈数n以及其它几何尺寸,使得能满足强度约束、刚度约束及稳定性约束条件,进一步地还要求相应的设计指标(如体积、重量、振动稳定性等)达到最好。
具体设计步骤为:先根据工作条件、要求等,试选弹簧材料、弹簧指数C。
由于sb与d有关,所以往往还要事先假定弹簧丝的直径d。
接下来计算d、n的值及相应的其它几何尺寸,如果所得结果与设计条件不符合,以上过程要重复进行。
螺旋弹簧横向静刚度计算及动刚度频变分析

Lateral Static Stiffness Calculation and Dynamic Stiffness Frequency Variety Analysis of Helical Spring
ZHANG Mingyang, ZHANG Kailin, YAO Yuan (State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China) Abstract:To explore the lateral static stiffness and dynamic stiffness characteristics of cylindrical helical compression spring with
且最终都趋于无垂向压缩时的刚度值。当兀远大于Z
时,弹簧垂向变形占主导地位,故价随兀的增加呈线性增 加/减小,且随着ft的增加,仰变化速度减缓。
由上述分析可知,螺旋弹簧受载端的Z和都会对
弹簧附产生影响,而Krettek刚度公式仅考虑了 的影 响,故其存在一定偏差。
.UIUIZ/
/
(一. 500
E E Z
肖绯雄[ll]发现横向载荷的加载方向会对螺旋弹簧垂 向静刚度亿产生影响。为探究加载方向对k是否有影 响,在受载端以A点为坐标原点,建立如图2所示的坐标 系。y轴与受载端切口平面S|的法向相平行,且向外为 正。通过改变有效圈和支撑圈的圈数,调整受载端切口平 面S|和约束端切口平面S2的相对位置,将两切口平面所 夹角度0分为4个区间。通过有限元计算,定性分析不同 加载方向下k i随fl和兀的变化趋势,如表1所示。
(-.alalz
液压可变刚度螺旋弹簧设计与分析
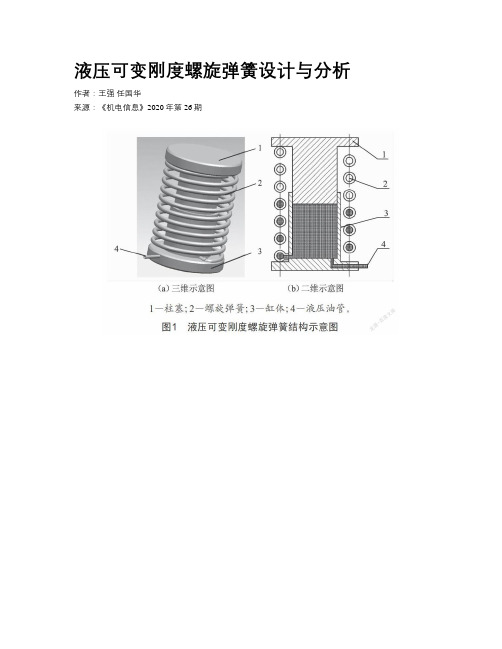
液压可变刚度螺旋弹簧设计与分析作者:王强任国华来源:《机电信息》2020年第26期摘要:针对目前可变刚度螺旋弹簧存在的缺陷,设计了一种液压可变刚度螺旋弹簧。
该弹簧通过螺旋弹簧丝内部的液体压力变化,实现螺旋弹簧刚度可变,为设计出新的汽车悬架系统提供了新的参考方案。
关键词:螺旋弹簧;刚度;液压;ANSYS Workbench0 引言在机械工程中,螺旋弹簧种类繁多,应用范围广,是一种可靠性很强的机械元件,它普遍应用于交通运输工具、电器、航空航天、造船、仪表、内燃机等机械工程领域,主要用于元件复位、限位、缓冲吸振、控制振动、储存能量。
螺旋弹簧通过合理选择设计参数,即可得到优良的综合性能,包括承压稳定性、轴向变形、应力强度、侧向变形、动力特性以及疲劳强度等,以适应不同的工况要求。
近年来,国内不少学者都在螺旋弹簧的工艺加工技术和理论研究方面做出了很大贡献,随着科学技术的进步,不断涌现出各种型式的螺旋弹簧。
弹簧在整个变形过程中,弹簧刚度可能是常量,也可能是变量。
弹簧柔度的定义是单位力使弹簧所产生的变形,即弹簧的柔度是其刚度的倒数。
弹簧特性曲线是指载荷与变形之间的关系曲线。
弹簧特性曲线的切线表示弹簧刚度值,即弹簧产生单位变形所需的载荷量。
弹簧的刚度特性曲线对于设计弹簧以及选择弹簧的类型起到了指导性作用。
当弹簧刚度为常量时,其特性曲线为一条线性直线。
对于弹簧特性曲线为直线的弹簧,其刚度也称为弹簧常量或弹性系数。
弹簧刚度为变量时,其特性曲线为曲线,这种弹簧被称为变刚度弹簧目前可变刚度螺旋弹簧主要有变直径可变刚度弹簧和弹簧叠加可变刚度弹簧两种。
变直径可变刚度弹簧存在如下问题:(1)变化的弹簧直径制造相对困难,增加制造成本;(2)在直径较小的地方,当受力较大时,弹簧丝会相互叠加,甚至造成直径较小处发生塑性变形。
弹簧叠加可变刚度弹簧存在如下问题:(1)不同弹簧的连接难度很大,不牢固;(2)对于弹簧丝直径较小的弹簧,当受力较大时,弹簧丝会叠加,造成直径较小处发生塑性变形。
车辆悬架缓冲弹簧的稳定性分析
向弯曲轴线弧高 h 由下式计算 :
h = R - Rcoλs = 19mm
按图 3 ,悬架缓冲弹簧与悬架之间载荷关系参
见图 4 所示 。
Pmj - 悬架缓冲弹簧轴向载荷 ;
·44 ·
图 4 缓冲弹簧载荷关系图
因缓冲弹簧内部安装了减振器 ,按照产品设计 资料 ,弹簧内径与减振器外部零件间的单边间隙为 :
悬架工作原理悬架是轮式车辆行驶系统的重要组成部分其定义是位于车架或车身与车轴或车轮之间缓和并衰减由地面引起的冲击和振动同时传递作用在车轮和车架或车身之间的各种力和力矩的装车辆在行驶中不平路面作用于车轮的垂直反力动载荷往往是冲损坏安全行驶性差
成都航空职业技术学院学报
Journal of Chengdu Aeronautic Vocational and Technical College
·43 ·
车辆悬架缓冲弹簧的稳定性分析
两平面应平行的基本要求 ,也就是弹簧两端面对母 线的垂直度严重超差 ,必然导致弹簧产生较大的侧 向弯曲变形 。缓冲弹簧产生侧向弯曲将导致缓冲弹 簧内径与减振器外部设备摩擦 ,产生噪声及减振器 出现早期漏油等故障 。
按图 1 : Pmj = 35722 N 。 Pmjt2 - 悬架缓冲弹簧法向载荷 ;由下式计算 : Pmjt2 = Pmj ×coλs = 35260 N
Prt - 悬架缓冲弹簧径向载荷 ;由下式计算 :
Prt = Pmj ×sinλ= 5724 N
Prt1 - 悬架缓冲弹簧水平载荷 ;由下式计算 : Prt1 = Prt ×coλs = 5649 N
当悬架处于上心位置时 ,缓冲弹簧水平载荷处
于最大值为 : Prt1max = 11794 N 弹簧弯曲后 ,根据悬架缓冲弹簧法向载荷 Pmjt2
弹簧的强度计算 1、弹簧的受力 图示的压缩弹簧,当弹簧受轴向压力
弹簧的强度计算1、弹簧的受力图示的压缩弹簧,当弹簧受轴向压力F时,在弹簧丝的任何横剖面上将作用着:扭矩 T= FRcosα ,弯矩 M= FRsinα,切向力F Q = Fcosα和法向力 N F = Fsinα (式中R为弹簧的平均半径)。
由于弹簧螺旋角α的值不大(对于压缩弹簧为6~90 ),所以弯矩M和法向力N 可以忽略不计。
因此,在弹簧丝中起主要作用的外力将是扭矩T和切向力Q。
α的值较小时,cosα≈ 1,可取T = FR 和 Q = F。
这种简化对于计算的准确性影响不大。
当拉伸弹簧受轴向拉力F时,弹簧丝横剖面上的受力情况和压缩弹簧相同,只是扭矩T 和切向力Q均为相反的方向。
所以上述两种弹簧的计算方法可以一并讲述。
2、弹簧的强度从受力分析可见,弹簧受到的应力主要为扭矩和横向力引起的剪应力,对于圆形弹簧丝系数K s可以理解为切向力作用时对扭应力的修正系数,进一步考虑到弹簧丝曲率的影响,可得到扭应力式中K为曲度系数。
它考虑了弹簧丝曲率和切向力对扭应力的影响。
一定条件下钢丝直径3、弹簧的刚度圆柱弹簧受载后的轴向变形量式中n为弹簧的有效圈数;G为弹簧的切变模量。
这样弹簧的圈数及刚度分别为对于拉伸弹簧,n>20时,一般圆整为整圈数,n<20时,可圆整为1/2圈;对于压缩弹簧总圈数n的尾数宜取1/4、1/2或整圈数,常用1/2圈。
为了保证弹簧具有稳定的性能,通常弹簧的有效圈数最少为2圈。
C值大小对弹簧刚度影响很大。
若其它条件相同时,C值愈小的弹簧,刚度愈大,弹簧也就愈硬;反之则愈软。
不过,C值愈小的弹簧卷制愈困难,且在工作时会引起较大的切应力。
此外,k值还和G、d、n有关,在调整弹簧刚度时,应综合考虑这些因素的影响。
4、稳定性计算压缩弹簧的长度较大时,受载后容易发生图a)所示的失稳现象,所以还应进行稳定性的验算。
为了便于制造和避免失稳现象出现,通常建议弹簧的长径比 b =H0/D2 按下列情况取为:弹簧两端均为回转端时,b≤2.6;弹簧两端均为固定端时,b≤5.3 ;弹簧两端一端固定而另一端回转时,b≤3.7。
压缩螺旋弹簧的断裂分析
欢迎访问中国金相分析网您现在位置:失效分析 > 弹簧失效分析压缩螺旋弹簧的断裂分析于志伟1,季士军1,史雅琴1,孙俊才1,张 晓2(1.大连海事大学金属材料工艺研究所,辽宁大连 116026;2.沈阳工学院专科学校 辽宁沈阳 110015)摘要:通过观察断口的宏观痕迹、微观形态以及金相组织,并辅以测定表面宏观残余应力、硬度梯度等试验,对一动力机械上的圆柱形压缩螺旋弹簧的断裂原因进行了较为细致的分析.结果表明,此批弹簧断裂是由磨削加工不当在磨剂端面下亚表层产生了氢致沿晶开裂带,弹簧服役承载时在正应力的作用下发生了氢滞后脆性断裂.改进磨削工艺后弹簧脆断现象完全消除.关键词:弹簧;磨削加工;氢致脆断弹簧是机械产品中的重要基础元件之一,弹簧的性能质量直接影响着整个设备的运行安全和效率.有关结构设计、材料、生产工艺过程以及服役环境等方面原因而导致弹簧失效的故障分析有许多报导[1],但从材料工艺角度细致的观测分析工作并不多见.由于弹簧的种类繁多,应用面广,随着各种新技术、新工艺引入弹簧的生产制造,弹簧的失效形式、部位也常常表现各异,尽管对某一具体弹簧的失效分析并不一定具有普遍的指导意义,但找到失效原因,对提高产品质量,避免类似事故发生仍有很强的实用性.本文通过较细致地观测一例弹簧断裂特征来分析失效原因.1 情况概述某厂生产的动力机械设备弹簧材料为60Si2Mn,制造工序依次为:将直径为Φ52mm的钢棒两端加热拔尖,整体加热卷制成外径为Φ237mm的等径螺旋形簧坯,然后将其置于热处理炉中870℃加热1h,取出空冷1min随即水淬冷至150℃,再入炉430℃回火8h.簧坯两端面在磨簧机上磨平,因磨削时温度很高,所以始终采用喷水冷却磨面.最后经整体喷丸处理便制成圆柱形压缩螺旋弹簧成品.按以上工艺流程制造的一批弹簧装机试运行10多分钟便发生断裂,检验发现裂纹源位于磨面附近,整个磨面布满了网状微裂纹,磨面下出现约0.4mm厚白亮层,其硬度达HRC=61~63.厂方认为这批弹簧的断裂原因是由磨削加工时表层发生淬火现象引起的,表层马氏体受拉应力而开裂形成表面微裂纹从而导致了弹簧断裂.基于这样认识,为挽救余下尚未使用的成品弹簧,便改用干磨削加工以去除表面微裂纹和硬化层,磨面再重新喷丸处理,经检验合格后装机使用,在1.8t正常负荷下运行了几小时也相继发生了断裂,如图1所示.图1 断裂弹簧的实物照片 图2 断口的宏观形貌2 观测试验及结果2.1断口宏观观察此批弹簧的断裂部位均出现在端面上第一圈与第二圈并圈附近,如图1所示.从断口的宏观形貌可见,断口上出现两个裂纹扩展面Ⅰ、Ⅱ,两面夹角约90°,根据断口上遗留的裂纹扩展痕迹可判断出两宏观断面的断裂次序:断面Ⅰ→断面Ⅱ,主裂纹源位于主断面Ⅰ与磨削面交界线上的中点A,主裂纹自端面起向下扩展,外侧扩展速度较快,内侧扩展速度较慢,当主裂纹前缘扩展至下部边缘B点,便引发二次裂纹在二次断面Ⅱ沿箭头所指方向扩展,直至完全断裂.两次断裂均属瞬时断裂.仔细观察还可发现,在靠近断口的磨削面上还出现了许多径向表面微裂纹,这些微裂纹的方向与该处的磨削方向垂直,与主断面Ⅰ约成45°角.2.2断口微观观察采用JSM235CF扫描电子显微镜观察断口的微观形貌.在主裂纹源A观察到一个半径为0.5mm的半圆形凹坑[图3(a)],坑壁形貌呈沿晶断裂特征——冰糖状花样[图3(b)],此外,在距磨削面下0.5~2mm深度内的主断面É上还观察到一个带状的沿晶开裂区[图3(c)],在此区内的断面下层仍呈现沿晶开裂[图3(d)],在其后的裂纹快速扩展区及二次断面Ê的整个区域,断口形貌以准解理和萘状断口为主.2.3金相组织观察在断口附近的磨削面上沿周向垂直于表面微裂纹截取一金相试样,经抛光,4%硝酸酒精溶液浸蚀后置于扫描电镜下观察金相组织及表面裂纹.观察发现靠近磨削面的微裂纹粗而宽,内含一些氧化物杂质[图4(a)],这些微裂纹沿晶界曲折向内延伸变细[图4(b)],微裂纹总深度约为015mm,这些微裂纹是典型的磨削裂纹.从图4(a)还可看出磨削面下的金相组织为回火屈氏体,心部金相组织以珠光体为主.2.4硬度测试为了解热处理弹簧的淬硬层深度,在断口附近沿径向取一横截面,抛光成金相试样后测洛氏硬度梯度,结果见图5.对照金相观察,淬硬层深度——半马氏体深度约为17mm,表层硬度HRC=53,心部为HRC=35,这表明弹簧未被淬透,经计算断裂源处最大的磨削深度约为215mm.图3 断口的微观形貌图4 断簧表层的金相组织图5 弹簧表层的硬度分布2.5表面应力测定采用日本理学MSF-2M型X射线应力仪测定断簧表面的周向残余应力.以CrKα辐照α-Fe的(211)晶面,用sin2ψ法将ψ0分别固定在0°、15°、30°及45°.多处测定结果显示,经热处理及喷丸处理后整个弹簧表面均处于压应力状态.内侧弧面未径喷丸,仅热处理产生的周向应力为-256MPa,端面再径磨削加工,喷丸处理后平均周向应力为-805MPa.由于热处理时整个弹簧未被淬透,淬火过程表层产生的周向热应力与组织应力均为压应力[2],迭加后总的热处理应力为残余压应力.磨削后再经喷丸处理,测磨削应力基本已消除.因此,测得的端面周向应力与内侧弧面周向应力的差值-549MPa应是由喷丸产生的.3 断裂原因分析3.1表层缺陷的形成前已述及,磨削加工时原端面产生了新的马氏体相变层,这表明磨削时表层温度已大于弹簧材料60Si2Mn的Ac1点755℃,这样高的温度足以使磨面上的冷却水汽化,一部分氧原子,尤其是氢原子很容易被带入处于磨削拉应力状态的表层中并向内部扩散.尽管后续不断的磨加工也会削掉扩散到表层内的氧、氢原子,但具有很强扩散能力的氢原子仍会有部分残留在磨削面下的基体中,并随着磨加工的进行逐渐积累.表面新马氏体层形成时产生的残余压应力场还会把氢原子封入其下的亚表层中,使其不易向外逃逸.后来喷丸处理时,表层的残余应力场将重新分布.一般喷丸处理后外表层产生残余压应力,内表层伴生一相当的残余拉应力场[3].此间,残存在淬硬层内处于压应力区域的氢原子会向拉应力区上坡扩散[4],并稳定地富集在该区的晶界处,从而大大降低晶界强度,在较低的外力作用下就能导致沿晶开裂,形成表面网状微裂纹.虽然随后采取了干磨削以去除表面网状微裂纹和硬化层,但已残留在亚表层内的氢原子仍会沿晶界快速向基体扩散,同样,再次喷丸处理后还会形成氢致表面微裂纹,只不过微裂纹的形态变了,密度降低了.3.2断裂过程的力学分析一般说来,等径的压缩螺旋弹簧承载时,簧丝的任一径向横截面主要受扭转应力τ作用[5].端面向下位移时,由于拔尖区的横截面积较小,易于变形,而端面上第一圈与第二圈并圈处的径向横截面积最大,因此它是整个端面受扭力最大的位置1根据弹性应力分析[6],弹簧横截面上的切应力、正应力的大小、方向均随位置而变,参照断簧实物图1,在裂纹源附近与扭转切应力成45°的最大主应力σ的方向恰与主断面Ⅰ的法向平行(图6),这表明磨面下的实际断裂源是在正应力下沿晶开启的,起裂方向与表面径向磨削裂纹无关.断裂源一旦形成, Ⅰ型裂纹尖端应力场则会诱使周围的氢原子向裂纹前缘富集[7].氢原子富集与主裂纹缓慢扩展交替进行,直到裂纹尺寸达到临界值而失稳扩展.这期间裂纹扩展依赖于时间,表现为滞后断裂.主裂纹向下失稳扩展时,由于外侧的扩展速度大于内侧的扩展速度,当主张裂纹前端先达主断面底部附近的B点,该处的最大主应力面也刚好与主断面Ⅰ垂直,二次裂纹则以B点为断裂源,仍在正应力下扩展,直至断面分开.断面Ⅰ、Ⅱ均由正断形成.图6 主裂纹源A起裂,扩展过程的受力示意图4 改进措施及结果综上分析,此批弹簧断裂是由高温磨削时冷却水汽化将氢带入基体中引起的.改进磨削工艺应减缓甚至消除氢致脆断.改进磨削工艺后的试验表明,始终采用干磨削加工端面,磨削后期适当降低磨面温度可完全消除表面微裂纹和氢致脆断.由此也印证本文对这批弹簧断裂的原因分析是正确的.若本文对您有所帮助,同时为了让更多人能看到此文章,请多宣传一下本站,支持本站发展;多谢!建议用 IE 1024*768 分辨率浏览本网站版权所有(c) 中国金相分析网。
螺旋弹簧设计
螺旋弹簧设计一、 弹簧设计参数(1)弹簧丝直径d :制造弹簧的钢丝直径。
(2)弹簧外径o D :弹簧的最大外径。
(3)弹簧内径i D :弹簧的最小外径。
(4)弹簧中径D :弹簧的平均直径。
计算公式:()/2o i i D D D D d =+=+(5)弹簧节距p :除支撑圈外,弹簧相邻两圈对应点在中径上的轴向距离。
(6)有效圈数n :弹簧能保持相同节距的圈数。
(7)支撑圈数s n :为了使弹簧在工作时受力均匀,保证轴线垂直端面、制造时,常将弹簧两端并紧。
并紧的圈数仅起支撑作用,称为支撑圈。
一般有 1.5T 、2T 、2.5T ,常用的是2T 。
(8)总圈数t n :有效圈数与支撑圈的和,t s n n n =+。
(9)螺旋方向:有左右旋之分,常用右旋。
二、 弹簧其它参数(1)旋绕比C 〈弹簧指数〉D C d =为了使弹簧本身较为稳定,不致颤动和过软,C 值不能太大;但为避免卷绕时弹簧丝受到强烈弯曲,C 值不应过小。
常用旋绕比C 值(2)计算补偿系数K4144C K C -=- (3)长细比b弹簧自由长度与弹簧中径之比,0H b D=。
三、 弹簧正向设计流程1. 弹簧丝直径dd ≥式中:C :旋绕比;K :计算补偿系数,4144C K C -=-; max F :弹簧所受最大的力,max max s F k λ=;s k :弹簧的刚度。
现代悬架设计过程中,弹性元件的刚度通常不等于悬架系统等效刚度。
当悬架系统存在杠杆比时,弹性元件的刚度近似等于悬架系统等效刚度与杠杆比平方的乘积,即2s k k i =⨯;i :悬架等效刚度作用力的力臂/弹性元件(弹簧)作用力的力臂; max λ:弹簧受力时的最大压缩量,等于弹簧处于平衡位置时的压缩量t sm g x k =与车轮上跳至极限时的弹簧压缩量之和; []τ:弹簧材料的许用应力。
2. 弹簧工作圈数(有效圈数)n对于压缩弹簧,弹簧的工作圈数38sGd n C k =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
螺旋压缩弹簧的稳定性分析
首先用SolidWorks建立某圆柱型螺旋压缩弹簧和中凹型螺旋压缩弹簧的几何模型;其次分别导入MSC.Marc软件生成弹簧的有限元模型,先求出其两端固定时的临界载荷,再对弹簧进行静力分析,绘制出载荷-挠度曲线图。
通过比较,得出其中稳定性较好的弹簧模型。
标签:螺旋压缩弹簧;稳定性分析;有限元
弹簧是通过其自身产生较大弹性变形进行工作的一种弹性元件。
在各类机器中的应用十分广泛。
1 堆垛机建模
1.1 弹簧失稳失效
随着弹簧在许多领域的广泛应用,许多承载用的设备对弹簧的性能要求越来越高。
螺旋压缩弹簧是其中一种最常用的弹簧,对于细长比较大的圆柱型螺旋压缩弹簧,当轴向工作载荷超过其临界载荷时系统会产生侧向弯曲,比如一端固定一端回旋细长比大于3.7,两端都回旋的弹簧细长比大于2.6时都会发生较大的侧向位移,这种失稳屈曲会导致弹簧工作失效。
因此对于细长螺旋压缩弹簧,特别是大型、要害部位使用的螺旋压缩弹簧,其稳定性计算具有重要意义。
本课题利用solidworks建立模型,marc有限元进行分析,通过对等弹簧丝截面,最大中径相等的圆柱型螺旋压缩弹簧和中凹型螺旋压缩弹簧的失稳形态进行分析,得出相对理想的常见承载弹簧的形状。
从而验证了弹簧的稳定性屈曲分析能通過这种方式来分析,具有一定的意义。
1.2 建立模型
首先引进所选弹簧的基本参数及数值,两种弹簧尺寸为:弹簧自由高度(H0):240mm;弹簧中径(D):40mm;弹簧丝直径(d):6mm;有效圈数(n):8,利用SolidWorks建立弹簧的几何模型,完成后将其以“IGS”格式保存一份文件为moxiny.igs。
2 压缩弹簧的稳定性分析
方法描述:分析螺旋压缩弹簧在失稳前后的屈曲形态,可先对两端约束的弹簧进行临界载荷的求解,再在临界失稳载荷的附近加载不同的载荷,得到用以描述弹簧失稳状态的载荷-挠度曲线。
2.1 圆柱型螺旋压缩弹簧的挠度曲线
2.1.1 圆柱型螺旋压缩弹簧的临界载荷
2.2 中凹型螺旋压缩弹簧的挠度曲线
2.2.1 中凹型螺旋压缩弹簧的临界载荷
本课题利用solidworks建立模型,marc有限元进行分析,通过对等弹簧丝截面,最大中径相等的圆柱型螺旋压缩弹簧和中凹型螺旋压缩弹簧的失稳形态进行分析,显然,从以上图表中可见,中凹型螺旋压缩弹簧的稳定性要比圆柱型螺旋压缩弹簧好,是相对理想的常见承载弹簧的形状。
参考文献
[1]王肇民.塔桅结构[M].上海:同济大学出版社,1989(12).
[2]GB50009-2001.建筑结构荷载规范[S].北京:中国建筑工业出版社,2001.
[3]梁清香.有限元与MARC实现(第二版)[M].北京:机械工业出版社,2005.3.
[4]RW克拉夫,彭津,王光远.结构动力学[M].北京:科学出版社,1981.。
