随机过程第三版课后答案
研究生《随机过程》教材课后作业答案

1.1 证明:∵1111,,,,,A F F F F ∈ΩΦ∈ΩΩ∈Φ∈Ω-Φ∈ΩΦ∈ 且∴1F 是事件域。
∵222,,,,cA A F F A F A A ∈Ω∈Ω∈-Φ∈=Ω-∴22222,,,,c c A F A F A F A F A F ∈-Φ∈-Φ∈Ω-∈Ω-∈ 且2,ccA A A A F ΦΩ=ΩΦΩ∈ ∴2F 是事件域。
且12F F ∈。
∵2ΩΩ∈∴3F Ω∈∴3F 是事件域。
且23F F ∈∴123,,F F F 皆为事件域且123F F F ∈∈。
1.2一次投掷三颗均匀骰子可能出现的点数ω为(),,,,,,16,16,16i j k i R j R k R i j k ∈∈∈≤≤≤≤≤≤∴样本空间()61,,6=,,n i j k i j k =≤≤Ω事件(){},,|,,i j k A i j k ωω==,,,,1,,6i R j R k R i j k ∈∈∈≤≤ 事件域2F Ω= 概率测度(),,1P 216i j k A =,,,,1,,6i R j R k R i j k ∈∈∈≤≤ 则(),,F P Ω为所求的概率空间。
1.3 证明:(1)由公理可知()0P Φ=(2)有概率测度的可列可加性将第n+1个集合往后都取为空集,即可得结论()11n nk k k k P A P A ==⎛⎫= ⎪⎝⎭∑∑ (3)∵,,A B F A B ∈⊂ ∴B A F -∈,()A B A -=Φ由概率测度的可列可加性可得:()()()()P B P A B A P A P B A =+-=+-即()()()P B A P B P A -=-有概率测度的非负性可得()()()0P B P A P B A -=-≥,即()()P B P A ≥ (4)若B =Ω,由(3)则有()()1P A P A =- (5)∵()()()()121212P A A P A P A P A A +=+- 假设()()()()()11211111m m m k k i j i j k m k i j m i j k m k P A P A P A A P A A A P A A A +=≤<≤≤<<≤=⎛⎫=-+-+- ⎪⎝⎭∑∑∑ 成立,则()()()()()()()()()11111111111111211111+1m m m m k k m m k m k k k k k mm k iji j k k i j mi j k mm m m m k k m k i j i k i j mP A P A A P A P A P A A P A P A P A A P A A A P A A A P A A P A P A A P A A ++++====+=≤<≤≤<<≤++=+=≤<≤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫==+-= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭+-+-⎛⎫⎛⎫+-- ⎪⎪⎝⎭⎝⎭=-+∑∑∑∑∑()()()()()()()()()()()()1121111121111212111111111n j k m i j k mm i j m i j k m m m i j m i j k m m m k i j i j k m k i j m i j k m A P A A A P A A A P A A A A P A A A A P A P A A P A A A P A A A +≤<<≤++++≤<≤≤<<≤+++=≤<≤+≤<<≤+-+-⎛⎫--+-+- ⎪⎝⎭=-+-+-∑∑∑∑∑∑也成立由数学归纳法可知()()()()()11211111n n n k k i j i j k n k i j n i j k n k P A P A P A A P A A A P A A A +=≤<≤≤<<≤=⎛⎫=-+-+- ⎪⎝⎭∑∑∑()()()()()()111122212123231231n nn n k k k k k k k k n n n k k k k k k nk k nk k P A P A A P A P A P A A P A P A P A P A A P A A P A P A P A P A =========⎛⎫⎛⎫⎛⎫⎛⎫=+=+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫=++-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫≤++ ⎪⎝⎭≤≤∑1.4 (1)()()()()()()()()()()()()()()()()()()()()()21040114P AB P A P B P AB P AB P A P B P AB P A P B P A P AB P A P B P AB P A P A B P A P A P A ≤-≤-≤≤-≤-=-=+-⎡⎤⎡⎤⎣⎦⎣⎦≤-≤(2)()()()()()()()()()()()()()()()()()()()()()()()if =1else if =P AB P BC P AB P BC P AB P AC P A B C P ABC P AB P BC P AC P A B C P ABC P BC P A B C P AB P BC P AB P BC --+=++-+=++-≤+≤--- 可由这个式子的轮换对称性证明这种情况(3)()()()()()()()()()()11111111111n nk k k k n nn nk k k k k k k k nk k nk k A A A AP A P A P A P A n P A P A n P A P A P A n ========⊂∴⊃⎛⎫≤≤=-=- ⎪⎝⎭-≤-∴≥--∑∑∑∑∑1.5()1(1)k nkk A P X k n--== 1.6由全概率公式()()()()()()()()()()()()100112211110101=1424P Y X P Y P X P Y P X P Y P X P Y P Y P Y e -≥=≥=+≥=+≥==+-=+-=-=-1.7 证明: 显然()()()()111111122,,,,,,0n n n n n F x x F x x F y x P x X y x X x X ∆=-=≤≤≤≤≥假设()()121111222,,,,,,,0i n i i i i i n n F x x P x X y x X y x X y x X x X ∆∆∆=≤≤≤≤≤≤≤≤≥ 成立 从而()()()()12+11111222111112221111122211122,,,,,,,,,,,,,,,,,,,0i i n i i i i i n n i i i i i n n i i i i i n n F x x P x X y x X y x X y x X x X P x X y x X y x X y y X x X P x X y x X y x X y x X x X +++++++++∆∆∆∆=≤≤≤≤≤≤≤≤-≤≤≤≤≤≤≤≤=≤≤≤≤≤≤≤≤≥ (分布函数对于每一变元单调不减)也成立有数学归纳法可知()()121111222,,,,0n n n n n F x x P x X y x X y x X y ∆∆∆=≤≤≤≤≤≤≥1.8()()()()()()()()()()()''''''',,0','x y x y x x y x y x y x y x y x x y y h x y eeh x y eeeee e e e x x y y -+-+-+-+-+-+----∆=-∆∆=---=--≥≤≤所以h 是二元单调不减函数。
随机过程课后习题答案

随机过程课后习题答案随机过程课后习题答案随机过程是概率论和数理统计中的一个重要分支,研究的是随机事件在时间上的演变规律。
在学习随机过程的过程中,习题是不可或缺的一部分。
通过解习题,我们可以更好地理解和掌握随机过程的基本概念和性质。
下面是一些随机过程课后习题的答案,希望对大家的学习有所帮助。
1. 假设随机过程X(t)是一个平稳过程,其自协方差函数为Cov[X(t), X(t+h)] =e^(-2|h|),求该过程的自相关函数。
解:首先,自协方差函数Cov[X(t), X(t+h)]可以通过自相关函数R(t, h)来表示,即Cov[X(t), X(t+h)] = R(t, h) - E[X(t)]E[X(t+h)]。
由于该过程是平稳过程,所以E[X(t)]和E[X(t+h)]是常数,可以将其记为μ。
因此,Cov[X(t), X(t+h)] = R(t, h) - μ^2。
根据题目中给出的自协方差函数,我们有e^(-2|h|) = R(t, h) - μ^2。
将μ^2移到等式左边,得到R(t, h) = e^(-2|h|) + μ^2。
所以,该过程的自相关函数为R(t, h) = e^(-2|h|) + μ^2。
2. 假设随机过程X(t)是一个平稳过程,其自相关函数为R(t, h) = e^(-3|h|),求该过程的均值和方差。
解:由于该过程是平稳过程,所以均值和方差是常数,可以将均值记为μ,方差记为σ^2。
根据平稳过程的性质,自相关函数R(t, h)可以表示为R(h) = E[X(t)X(t+h)] =E[X(0)X(h)]。
根据题目中给出的自相关函数,我们有R(h) = e^(-3|h|)。
将t取为0,得到R(h) = E[X(0)X(h)] = μ^2。
所以,该过程的均值为μ。
根据平稳过程的性质,方差可以表示为Var[X(t)] = R(0) - μ^2。
将t取为0,得到Var[X(t)] = R(0) - μ^2 = e^(-3*0) - μ^2 = 1 - μ^2。
随机过程-方兆本-第三版-课后习题答案

习题 4以下如果没有指明变量 t 的取值范围,一般视为 t R ,平稳过程指宽平稳过程。
1. 设 X(t) sinUt ,这里 U 为 (0,2 )上的均匀分布证明:(a)验证宽平稳的性质0,t s21COV ( X (t ), X (t )) Esin 2Ut 1(b) EX(t) 2 t (1 cos(2 t)),与t 有关,11DX(t) sin(2 t),与 t 有关,不平稳 .2 8 tX n (1) X n X n 1,X n (2) X n (1) X n (1)1 , ,证明:这些序列仍是平稳的证明:已知, EX nm,DX n2,COV(X n t ,X t ) (t)EX n(1) EX n EX n 1 0,DX n (1)D(X n 22X n 1 ) 22 (1) 12COV ( X n (1)t ,X (1))COV(X n t X n t 1,X n X n 1) COV(X n t ,X n ) COV(X n t 1,X n ) COV(X n t ,X n 1 ) COV(X n t 1,X n 1)2 (t) (t 1) (t 1)显然, X n (1)为平稳过程同理可证, X n (2) ,X n (3), 亦为平稳过程a) 若 t 1,2, ,证明{ X (t),t 1,2, } 是宽平稳但不是严平稳, b) 设 t [0, ) ,证明 {X(t),t 0} 既不是严平稳也不是宽平稳过程2EX(t) E sin(Ut )21dUCOV ( X (t ), X (s)) E(sinUt ?sinUs)12( cosUt ) 200,t 1 1,2, s)U)1{ 1[cos(ts)U ]02t1s [cos(t2s)U}?21t2. 设 { X n ,n 1,2, } 是 平 稳 序 列定 义 {X n (i),n 1,2, },in3.设Z n k 2(a k n u k) 这里k和a k为正常数, k=1 , n; u1,...u n 是(0,2 )k1上独立均匀分布随机变量。
随机过程课后题答案

第一章习题解答1. 设随机变量X 服从几何分布,即:(),0,1,2,k P X k pq k ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtkk X k f t E eepq ∞===∑()k jtkk p q e∞==∑ =0()1jt kjtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑222()()[()]q D X E X E X P =-=(其中 00(1)nnn n n n nxn x x ∞∞∞====+-∑∑∑)令 0()(1)n n S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰202201()()(1)11(1)1(1)xn n dS x S t dt dxx xnx x x x ∞=∴==-∴=-=---⎰∑同理 2(1)2kkkk k k k k k x k x kx x ∞∞∞∞=====+--∑∑∑∑令20()(1)k k S x k x ∞==+∑ 则211()(1)(1)xkk k k k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为1,0()0,0()0,0p p bxb x e x p x b p p x --⎧>⎪=>>Γ⎨⎪≤⎩(2) 其期望和方差;(3) 证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
解 (1)设X 服从(,)p b Γ分布,则10()()p jtxp bxX b f t ex e dx p ∞--=Γ⎰ 1()0()p p jt b x b x e dx p ∞--=Γ⎰101()()()()(1)p u p p p p p b e u b u jt b x du jt p b jt b jt b∞----==Γ---⎰ 10(())x p p e x dx ∞--Γ=⎰ (2)'1()(0)X p E X f j b∴== 2''221(1)()(0)X p p E X f j b +== 222()()()PD XE X E X b∴===(4) 若(,)i i X p b Γ 1,2i = 则121212()()()()(1)P P X X X X jt f t f t f t b-++==-1212(,)Y X X P P b ∴=+Γ+同理可得:()()iiP X b f t b jt∑=∑-3、设X 是一随机变量,()F x 是其分布函数,且是严格单调的,求以下随机变量的特征函数。
随机过程-方兆本-第三版-课后习题答案

习题4以下如果没有指明变量t 的取值范围,一般视为R t ∈,平稳过程指宽平稳过程。
1. 设Ut t X sin )(=,这里U 为)2,0(π上的均匀分布.(a ) 若 ,2,1=t ,证明},2,1),({ =t t X 是宽平稳但不是严平稳, (b ) 设),0[∞∈t ,证明}0),({≥t t X 既不是严平稳也不是宽平稳过程. 证明:(a )验证宽平稳的性质,2,1,0)cos (2121)sin()sin()(2020==-=•==⎰t Ut tdU Ut Ut E t EX ππππ))cos()(cos(21)sin (sin ))(),((U s t U s t E Us Ut E s X t X COV ---=•=t U s t s t U s t s t πππ21}])[cos(1])[cos(1{212020•+++--= s t ≠=,021Ut Esin ))(),((2==t X t X COV (b) ,)),2cos(1(21)(有关与t t t t EX ππ-=.)2sin(8121DX(t)有关,不平稳,与t t tππ-=2. 设},2,1,{ =n X n 是平稳序列,定义 ,2,1},,2,1,{)(==i n X i n 为,,)1(1)1()2(1)1(---=-=n n n n n n X X X X X X ,证明:这些序列仍是平稳的. 证明:已知,)(),(,,2t X X COV DX m EX t t n n n γσ===+2121)1(1)1()1(2)(,0σγσ≡+=-==-=--n n n n n n X X D DX EX EX EX)1()1()(2),(),(),(),(),(),(111111)1()1(++--=+--=--=--+-+-++--+++t t t X X COV X X COV X X COV X X COV X X X X COV X X COV n t n n t n n t n n t n n n t n t n n t n γγγ显然,)1(n X 为平稳过程.同理可证, ,,)3()2(n n X X 亦为平稳过程.3.设1)nn k k k k Z a n u σ==-∑这里k σ和k a 为正常数,k=1,....n; 1,...n u u 是(0,2π)上独立均匀分布随机变量。
随机过程第三版课后答案

随机过程第三版课后答案【篇一:随机过程习题答案】们的均值分别为mx和my,它们的自相关函数分别为rx(?)和ry(?)。
(1)求z(t)=x(t)y(t)的自相关函数;(2)求z(t)=x(t)+y(t)的自相关函数。
答案:(1)rz(?)?e?z(t??)z(t)??e?x(t??)y(t??)x(t)y(t)?利用x(t)和y(t)独立的性质:rz(?)?e?x(t??)x(t)?e?y(t??)y(t)???rx(?)ry(?)(2)rz(?)?e?z(t??)z(t)??e??x(t??)?y(t??)???x(t)?y(t)?? ?e?x(t??)x (t)?x(t??)y(t)?y(t??)x(t)?y(t??)y(t)?仍然利用x(t)和y(t)互相独立的性质:rz(?)?rx(?)?2mxmy?ry(?)2、一个rc低通滤波电路如下图所示。
假定输入是均值为0、双边功率谱密度函数为n0/2的高斯白噪声。
(1)求输出信号的自相关函数和功率谱密度函数;(2)求输出信号的一维概率密度函数。
电流:i(t)电压:y(t)答案:(1)该系统的系统函数为h(s)?y(s)1? x(s)1?rcs则频率响应为h(j?)?11?jrc?n02而输入信号x(t)的功率谱密度函数为px(j?)?该系统是一个线性移不变系统,所以输出y(t)的功率谱密度函数为:py(j?)?px(j?)h(j?)?2n0/21?rc?2对py(j?)求傅里叶反变换,就得到输出的自相关函数:1ry(?)?2?????py(j?)ej??1d??2?n0/2j?????1?rc?2ed??(2)线性系统输入为高斯随机过程,则输出也一定是高斯的。
因此,为了求输出的一维概率密度函数,仅需知道输出随机过程的均值和方差即可。
均值:已知输入均值mx=0,则输出均值my=mxh(0)=02方差:ry(0)?var(y)?my因为均值为0,所以方差var(y)?ry(0)?一维pdf:略12?n0/2???1?rc2?2d??3、理想带通滤波器的中心频率为fc、带宽为b,其在通带的频率增益为1。
《随机过程》课后习题解答
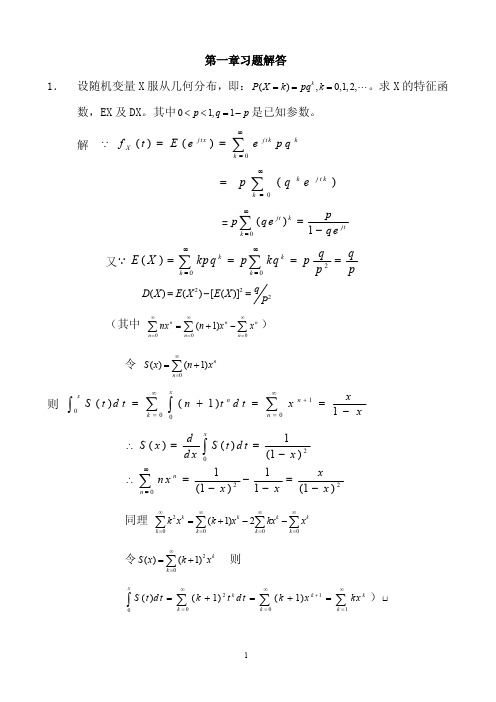
( k 0, 2, n )
1 为一特征函数,并求它所对应的随机变量的分布。 1 t2
n n i
f (t
i 1 k 1
tk )i k
5
=
i 1 k 1
n
n
i k
1 (ti tk )
2
i 1 k 1
n
n
e jti e jti e jti {1 ( jtk )(1 jtk )} n n e jtk e e i k jti = i 1 k 1 e n(1 jtk ) e
1 n n n j ( ti tk ) l ] i k = [e n i 1 k 1 l 1
(2) (3)
其期望和方差; 证明对具有相同的参数的 b 的 分布,关于参数 p 具有可加性。
解 (1)设 X 服从 ( p , b ) 分布,则
f X (t ) e jtx
0
b p p 1 bx x e dx ( p )
bp ( p)
x
0
p 1 ( jt b ) x
i k
1 M 2
0
ti t k } ) ( M 1max{ i , j n
且 f (t ) 连续 f (0) 1 (2) f (t )
f (t ) 为特征函数
1 1 1 1 1 [ ] 2 2 1 t 1 ( jt ) 2 1 jt 1 jt
3
fZ(k)() t (1 )kk! jk (1 jt)(k1)
E (Z k ) 1 (k ) f Z (0) ( 1) k k ! k j
n
钱敏平-龚光鲁-随机过程答案(部分)

随机过程课后习题答案第一章第二题:已知一列一维分布{();1}n F x n ≥,试构造一个概率空间及其上的一个相互独立的随机变量序列{(,);1}n n ξ⋅≥使得(,)n ξ⋅的分布函数为()n F x 。
解:有引理:设ξ为[0, 1]上均匀分布的随机变量,F(x)为某一随机变量的分布函数,且F(x)连续,那么1()F x η-=是以F(x)为分布的随机变量。
所以可以假设有相互独立的随机变量12,,...,n θθθ服从u[0, 1]分布,另有分布{()}n F x , 如果令1(,)()n n n F ξθ-⋅=,则有(,)n ξ⋅为服从分布()n F x 的随机变量。
又由假设条件可知,随机变量{(,),1}n n ξ⋅≥之间相互独立,则其中任意有限个随机变量12(,),(,),...,(,)n i i i ξξξ⋅⋅⋅的联合分布为:11221122{(,),(,),...,(,)}()()()i i n in i i i i in in P i x i x i x F x F x F x ξξξ⋅≤⋅≤⋅≤=⋅⋅⋅⋅再令112{,,...,,...},,{|()[0,1],1,2,...}n i i i i w w w w A A x F x i -Ω=∈=∈=,令F 为Ω所有柱集的σ代数,则由Kolmogorov 定理可知,存在F 上唯一的概率测度P 使得:11221122{(,),(,),...,(,)}()()()i i n in i i i i in in P i w i w i w F w F w F w ξξξ⋅≤⋅≤⋅≤=⋅⋅⋅⋅则所构造的概率空间为(Ω,F , P)。
第八题:令{};1n X n ≥是一列相互独立且服从(0,1)N (正态分布)的随机变量。
又令1n n S X X =++22(1)n S n n ξ+=1(,,)n n F X X σ=试证明:,;1n n F n ξ≥()是下鞅(参见23题)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机过程第三版课后答案【篇一:随机过程习题答案】们的均值分别为mx和my,它们的自相关函数分别为rx(?)和ry(?)。
(1)求z(t)=x(t)y(t)的自相关函数;(2)求z(t)=x(t)+y(t)的自相关函数。
答案:(1)rz(?)?e?z(t??)z(t)??e?x(t??)y(t??)x(t)y(t)?利用x(t)和y(t)独立的性质:rz(?)?e?x(t??)x(t)?e?y(t??)y(t)???rx(?)ry(?)(2)rz(?)?e?z(t??)z(t)??e??x(t??)?y(t??)???x(t)?y(t)?? ?e?x(t??)x (t)?x(t??)y(t)?y(t??)x(t)?y(t??)y(t)?仍然利用x(t)和y(t)互相独立的性质:rz(?)?rx(?)?2mxmy?ry(?)2、一个rc低通滤波电路如下图所示。
假定输入是均值为0、双边功率谱密度函数为n0/2的高斯白噪声。
(1)求输出信号的自相关函数和功率谱密度函数;(2)求输出信号的一维概率密度函数。
电流:i(t)电压:y(t)答案:(1)该系统的系统函数为h(s)?y(s)1? x(s)1?rcs则频率响应为h(j?)?11?jrc?n02而输入信号x(t)的功率谱密度函数为px(j?)?该系统是一个线性移不变系统,所以输出y(t)的功率谱密度函数为:py(j?)?px(j?)h(j?)?2n0/21?rc?2对py(j?)求傅里叶反变换,就得到输出的自相关函数:1ry(?)?2?????py(j?)ej??1d??2?n0/2j?????1?rc?2ed??(2)线性系统输入为高斯随机过程,则输出也一定是高斯的。
因此,为了求输出的一维概率密度函数,仅需知道输出随机过程的均值和方差即可。
均值:已知输入均值mx=0,则输出均值my=mxh(0)=02方差:ry(0)?var(y)?my因为均值为0,所以方差var(y)?ry(0)?一维pdf:略12?n0/2???1?rc2?2d??3、理想带通滤波器的中心频率为fc、带宽为b,其在通带的频率增益为1。
假定输入是均值为0、双边功率谱密度函数为n0/2的高斯白噪声。
(1)求输出信号的自相关函数和功率谱密度函数;(2)求输出信号的平均功率;(3)求输出信号的一维概率密度函数。
答案:类似上一题,仅需注意的是:(a) 此处滤波器的频率响应为h(j?)???1,?02?(fc?b/2)???2?(fc?b/2)otherwise(b) 平均功率等于功率谱密度函数的积分,也即等于输出信号y(t)的自相关在??0处的值,即ry(0)4、设x1(t)与x2(t)为零均值且互不相关的平稳随机过程。
x1(t)通过某个lti系统所得的输出为y1(t),x2(t)通过同一个lti系统的输出为y2(t)。
试证明y1(t)与y2(t)互不相关。
答案:就是要证明y1(t)与y2(t)的协方差为0。
由于x1(t)与x2(t)为零均值,显而易见y1(t)与y2(t)的均值都为0。
所以,我们仅需要证明y1(t)与y2(t)的互相关为0。
设lti系统的单位冲激响应为h(t),则: y1(t)??????x1(t??)h(?)d?y2(t)??x2(t??)h(?)d???所以有:???e?y1(t)y2(t)??e?x1(t??)h(?)d??x2(t?v)h(v)dv????????? ?e?????????x1(t??)x2(t?v)h(?)h(v)d?dv?????12?????????e?x(t??)x(t?v)?h(?)h(v)d?dv?????再利用x1(t)与x2(t)互不相关的性质,则有:e?y1(t)y2(t)????e?x(t??)?e?x(t?v)?h(?)h(v)d?dv?0,从而完成证明。
12?教材:2.8和2.9题 ?答案略【篇二:随机过程答案版 - 副本】机过程x(t)?y?zt,t?0,其中,y,z是相互独立的n(0,1)随机变量,则此随机过程的一维概率密度族为;随机过程第2章第46页例题4 2.对于一个强度为?的poisson过程,在t时间内来k个顾客的概率为;t),t3.设{x(?0}为具有参数?>0的泊松过程,则p{x(t?h)?x(t)?0}?;?0}是具有参数?的泊松分布,tn(n?1)是对应的时间间隔序列,则随机变量tn(n?1,2,?)的概率密度t),t4.设{x(函数为;t),t5.设{wn,n?1}是与泊松过程{x(等待时间序列,则wn服从参数为的?分布。
6.设随机变量关系为;7.设随机过程x(t)??0}对应的一个y)的x,y的数学期望都存在,则e(x)与e(xxh(t)?a(???t??), x是服从正态分布的随机变量,e(x)=0,d(x)=1。
则x(t)的一维分布密度函数f(x)为; 8.设{x(t),t9.设?0}为具有跳跃强度函数?(t)的非齐次泊松过程,马尔可夫链,则对任意整数,n步转移概率(n)pij则此非齐次泊松过程的均值函数为;{xn,n?t}为n?0,0?l?n和i,j?i用一步转移概率表达为; 10.设{xn,n绝对概率pj(n)用初始概率和n步转移概率表达为;(n)11.首达概率可以用一步转移概率来表示:f?_______________; ij(12)设pij(t)是齐次马尔可夫过程的转移概率,qij为齐次马尔可夫过程从状态i到状态j的转移速率,则柯尔莫哥洛夫向后方程为;(13)设随机序列{xn,n?1}均方收敛于随机变量x,则m,n??limxm?xn=;{x(t)?,tt的}相关函数为223r(s,t?)3s?t2则随机过程st{x(t),t?t}与其导数过程{x?(t),t?t}的互相关函数rxx?(s,t)= ;(14)设随机过程15.设{xn,n?1}是相互独立具有相同分布,且均具有二阶矩的随机变量序列,e(xn)??,n?1,2,?,则1limn??xk?k?1n=;16.二阶矩过程{x(t),t?t}在t0?t处均方可微的充要条件是它的相关函数r(s,t)在(t0,t0)处; 17.对一齐次马氏链,其任意n步转移概率之间的关系为。
二、问答题(l)(n)与首达概率fijpij?xy?1、已知随机变量x~n(2,1),y~n(10,4),令1,2z1?x?2y和z2?x?y,试求d(z1)和cov(z1,z2).(完)??求z求x问x2,设z?x?y.的数学期望和方差.与z的相关系数.与z是否相互独立?为什么?(完)3. 设某路公共汽车从早上5时到晚上9时有车发出。
乘客流量如下:5时平均乘客为200人/时;5时至8时乘客线性增加,8时达到1400人/时;8时至18时保持平均到达率不变;18时至21时到达率线性下降,到21时为200人/时。
假定乘客数在不相重叠的时间间隔内是相互独立的。
求12时至14时有2000人来站乘车的概率,并求出这两小时内乘客人数的数学期望。
随机过程第五版p36例题3.94. 设某设备的使用期限为10年,在前5年内它平均2.5年需要维修一次,后5年平均2年需要维修一次,求它在使用期内只维修过一次的概率第3章泊松过程第39页例5.设随机过程x(t)?r?t?c,t?(0,?),c为常数,r服从[0,1]区间上的均匀分布。
求均值函数、自相关函数。
随机过程第2章第44页例题36、设?xn,n?1,2,????是相互独立的随机变量序列,其分布律为?n0??, xn~??121?12?n??n讨论{xn,n?1,2,???}均方连续性. 第三章、随机分析第6页例题1 7设x(t)的均值函数为xm(t)?5sint,相关函数为rx(s,t)?3e求其导数过程的均值函数与相关函数.第三章、随机分析第18页例题3 8.设马尔可夫链的转移概率矩阵为 s)?(t?22,?0.70.10.2???0.80.1p = 0.1????0.050.050.9??求马尔可夫链的平稳分布几各状态的平均返回时间。
随机过程第五版p66页例题4.16 应用随机过程p144 例6-279、顾客到达某商店服从参数??4人/小时的泊松过程,已知商店上午9:00开门,试求1)10:00到12:00没有顾客的概率;2)到9:30时仅到一位顾客,而到11:30时总计已达5位顾客的概率。
第3章_泊松过程第4页例题应用随机过程试卷(a)中的大题10、markov链在经济预测领域里也有其广泛的应用。
如[商品销售情况预测]设某商品在市场上销售情况共有24个季度的数据(“1”表示畅销、“2”表示滞销)112122111212112211212111并假设该商品的销售状态满足齐次markov性。
(1)试确定销售状态的转移概率矩阵;(2)如果现在是畅销,试预测这以后第4个季度的销售状况;(3)如果影响销售的所有因素不变,试预测长期的销售状况。
平稳分布习题课2第13页例5-2011.一质点在1,2,3三个点上作随机游动,1和3是两个吸收壁,当质点处于2时,下一时刻转移到1和3的概率各为1。
写出一步转移概率矩阵,判断此链是否具有遍历性? 2若有,求出极限分布。
随机过程_copy第108页例题312.一质点在1,2,3三个点上作随机游动,1和3是两个反射壁,当质点处于2时,下一时刻转移到1和3的概率各为1。
写出一步转移概率矩阵,判断此链是否具有遍历性,2若有,求出极限分布。
随机过程_copy第107页例题213.一质点在1,2,3三个点上作随机游动,1和3是两个反射壁,当质点处于2时,下一时刻处于1,2,3是等可能的。
写出一步转移概率矩阵,判断此链是否具有遍历性,若有,求出极限分布。
随机过程_copy第106页例题114、设{xn,n?0}是具有三个状态0,1,2的齐次马氏链一步转移概率矩阵为:0 1 20?4?1p?1?2??041340?1??1?4?初始分布pi(0)?p{x0?i}?(1)p{x0?0,x2?1,x4?1};1i?0,1,2试求:3(2)p{x2?1,x4?1,x5?0|x0?0};(3)p{x2?1,x4?1,x5?0};随机过程_copy第97页例题115:某计算机机房的一台计算机经常出故障,研究者每隔15分钟观察一次计算机的运行状态,收集了24个小时的数(共作97次观察),用1表示正常状态,用0表示不正常状态,所得的数据序列如下:111001001111111001111011111100111111111000111101111011 011010111101110111101111110011011111100111设xn为第n(n=1,2,…,97)个时段的计算机状态,可以认为它是一个齐次马氏链. 求(1)一步转移概率矩阵;(2)已知计算机在某一时段(15分钟)的状态为0,问在此条件下,从此时段起,该计算机能连续正常工作45分钟(3个时段) 的条件概率.随机过程_copy第89张例题1016、设{xn}是时齐markov链,i?{0,1,2,3},其一步转移矩阵 ?00.5?00p???00??0.5000.5??10? 01??00.5?随机过程第5章第20页例题1 17、已知一齐次马尔可夫链只有三个状态1,2,3,其一步转移概率矩阵为讨论状态0和3的常返性。
