球面坐标系和柱面坐标系的定义及其应用
柱面坐标变换和球面坐标变换

柱面坐标变换和球面坐标变换
在数学和物理学中,柱面坐标和球面坐标是描述空间中点位置的两种不同坐标系。
通过对这两种坐标系进行变换,可以在不同问题中更好地描述和分析相关的物理现象。
柱面坐标变换
柱面坐标通常用于描述平面内的点位置,其坐标形式为(r, θ, z),其中r是点到z轴的距离,θ是与x轴的夹角,z是点在z轴上的投影位置。
柱面坐标与直角坐标系之间的变换关系如下:
假设直角坐标系中的点为(x, y, z),柱面坐标系中的点为(r, θ, z),则有以下变换关系:
r = √(x^2 + y^2)
θ = arctan(y/x)
z = z
柱面坐标变换在解决某些旋转对称问题时非常有用,比如圆柱体或圆锥体的体积计算和空间内的电场分布等问题。
球面坐标变换
球面坐标通常用于描述空间中的点位置,其坐标形式为(r, θ, φ),其中r是点到原点的距离,θ是与x轴的夹角,φ是与z轴的夹角。
球面坐标与直角坐标系之间的变换关系如下:
假设直角坐标系中的点为(x, y, z),球面坐标系中的点为(r, θ, φ),则有以下变换关系:
r = √(x^2 + y^2 + z^2)
θ = arctan(y/x)
φ = arccos(z/r)
球面坐标变换在处理一些涉及球形对称性问题时非常有用,比如天文学中的行星运动和化学中的原子排列等问题。
综上所述,柱面坐标变换和球面坐标变换是描述空间中点位置的两种重要坐标系,它们在解决不同问题中起着关键作用。
通过深入理解两种坐标系之间的变换关系,我们可以更好地解释和分析物理现象,并在应用中更加灵活地使用不同的坐标系来描述问题。
柱面坐标变换和球面坐标变换一样吗

柱面坐标变换和球面坐标变换一样吗在数学和物理学领域,柱面坐标和球面坐标是常用的坐标系,它们在描述空间中的点和矢量时发挥着重要的作用。
虽然柱面坐标和球面坐标都是三维空间中的坐标系统,但它们之间存在一些显著的不同之处。
柱面坐标变换柱面坐标系是一个应用广泛的坐标系,其中一个点的位置由径向距离、极角和高度组成。
在柱面坐标系中,点的坐标表示为$(r, \\theta, z)$,其中r是点到z轴的距离,$\\theta$是与x轴的夹角,z是点到xy平面的距离。
柱面坐标系到直角坐标系的变换公式如下:$$ \\begin{aligned} x & = r \\cdot \\cos(\\theta) \\\\ y & = r \\cdot\\sin(\\theta) \\\\ z & = z \\end{aligned} $$球面坐标变换球面坐标系是另一种常用的坐标系,其中一个点的位置由半径、极角和方位角组成。
在球面坐标系中,点的坐标表示为$(\\rho, \\phi, \\theta)$,其中$\\rho$是点到原点的距离,$\\phi$是点到z轴的夹角,$\\theta$是与x轴的夹角。
球面坐标系到直角坐标系的变换公式如下:$$ \\begin{aligned} x & = \\rho \\cdot \\sin(\\phi) \\cdot \\cos(\\theta) \\\\ y & = \\rho \\cdot \\sin(\\phi) \\cdot \\sin(\\theta) \\\\ z & = \\rho \\cdot\\cos(\\phi) \\end{aligned} $$比较与总结尽管柱面坐标和球面坐标都用于描述三维空间中的点,但它们之间有一些显著的不同。
柱面坐标主要用于旋转对称的问题,球面坐标则适用于球对称的问题。
在坐标变换公式中,柱面坐标的r是一个平面距离,而球面坐标的$\\rho$是一个空间距离。
坐标系及其关系描述

图2-7 空间点P在直角坐标系中的坐标
2.空间向量的表示
有向线段可以由起始和终止的坐标来表示。如果一个向量起始于点 A,终止于点 B, 则 Ax , Ay 和 Az 是点 A 在直角坐标系中的三个坐标分量, Bx , By 和 Bz 是点 B 在直角坐 标系中的三个坐标分量,则该向量可以表示为
从正 Z 轴来看,自 X 轴按逆时针方向转到 OM 所转过的角,这里 M 为点 P 在 XOY 面上的
投影。我们称 r, , 这三个数为点 P 的球面坐标。
图2-4 球面坐标系
4.其他形式的坐标系 1)参考坐标系
参考坐标系的位置和方向不随工业机器人各关节的运动而变化,对机器人其他坐标系 起参考定位的作用,通常采用三维空间中的固定坐标系 O-XYZ 来描述,如图 2-5 所示。
图2-1 直角坐标系
图2-2 右手坐标系
2.柱面坐标系 如图 2-3 所示,设 M (x ,y ,z) 为空间内一点,并设点 M 在 XOY 面上的投影 P 的极
坐标为 (r , ) ,则 r, ,z 这三个数便称为点 M 的柱面坐标。
图2-3 柱面坐标系
3.球面坐标系 如图 2-4 所示,假设 P (x ,y ,z) 为空间内一点,则点 P 也可用三个有次序的数 (r , ,) 来确定。其中,r 为原点 O 与点 P 间的距离; 为有向线段 OP 与 Z 轴正向的夹角; 为
Omz
则矩阵 M 可简化为
A M
OmO
0 1
也就是说,方向余弦阵 A 表示两坐标系的姿态关系,位置向量 OmO 表示 运动坐标系{m} 的原点 Om 在固定坐标系{O} 中的位置。
2.5利用柱面坐标和球面坐标计算三重积分

0 ≤ θ ≤ 2 π,
z
M ( x,
∞ < z < +∞ .
o
θ
y, z )
r
P (r ,θ )
y
x
如图, 如图,三坐标面分别为
r 为常数
圆柱面; 圆柱面; 半平面; 半平面; 平 面.
z
θ 为常数
z 为常数
M ( x, y , z )
z
柱面坐标与直角坐 标的关系为 x = r cosθ , y = r sinθ , z = z.
o
θ
r
P (r ,θ )
y
x
讨论下列柱坐标系下的曲面方程表示的曲面
Answer : (a ) r = 5 x 2 + y 2 = 55
(b) (c )
Question: In rectangular coordinates the volume element dV is given by dV=dxdydz, dV=dxdydz,
D1 2
8
2π
0
45 dθ ∫ dr ∫r 2 r r 2dz = π , 0 3 2
4 8
I 2 = ∫∫ rdrdθ ∫r 2 fdz = ∫
D2 2
2
2π
0
25 dθ ∫ dr ∫r 2 r r 2dz = π , 0 2 6
2 2
45 25 原式 I = π π = 336π . 3 6
球面坐标与直角坐标的关系为
x = ρ sin cosθ, y = ρ sin sin θ, z = ρ cos.
A
x
ρ M ( x , y, z )
柱面坐标和球面坐标计算定积分
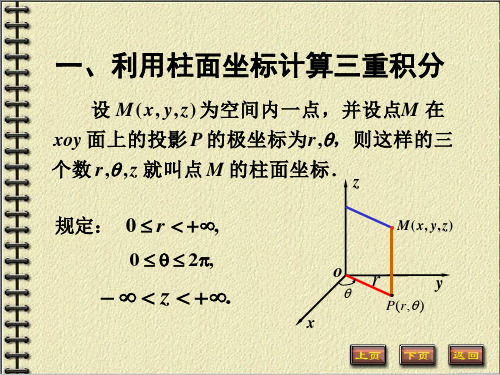
设 M ( x, y, z) 为空间内一点,并设点M 在
xoy 面上的投影 P 的极坐标为r,,则这样的三 个数 r, , z 就叫点 M 的柱面坐标.
z
规定: 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图,三坐标面分别为
r 为常数
三个有次序的数r,, 来确定,其中r 为原 点 O 与点 M 间的距离, 为有向线段 OM与 z 轴正向所夹的角, 为从正 z 轴来看自 x 轴按
逆时针方向转到有向线段 OP 的角,这里 P 为
点 M 在 xoy 面上的投影,这样的三个数 r,, 就叫做点 M 的球面坐标.
规定: 0 r , 0 , 0 2.
y
r
sin
sin
,
z r cos .
如图,
z
球面坐标系中的体积元素为
dv r2 sindrdd ,
f ( x, y, z)dxdydz
dr
d r sin
r
o
d
x
r sind rd
d
y
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
例 3 计算 I ( x2 y2 )dxdydz,其中 是锥面
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
I2 rdrd r2 fdz
D2
2
球面坐标和柱面坐标在计算中的应用 大学毕业设计

(2015届)本科毕业设计(论文)题目名称:球面坐标和柱面坐标在计算中的应用学院(部):理学院专业:数学与应用数学学生姓名:吴永旭班级:1101 学号:11404200413 指导教师姓名:唐亮职称:讲师最终评定成绩:2015年湖南工业大学本科毕业论文(设计)诚信声明本人郑重声明:所呈交的毕业论文(设计),题目《2011年中国各省财政收入数据的主成分分析研究》是本人在指导教师的指导下,进行研究工作所取得的成果。
对本文的研究作出重要贡献的个人和集体,均已在文章以明确方式注明。
除此之外,本论文(设计)不包含任何其他个人或集体已经发表或撰写过的作品成果。
本人完全意识到本声明应承担的责任。
作者签名:日期:2014 年 3 月10 日摘要三重积分和曲面积分是大学数学和数学分析中的重点同时也是难点。
如果当积分的区域是圆柱面、圆锥面、或者是球面时,这个时候我们就可以利用球面坐标和柱面坐标的变换使积分的计算更为简便。
纵观现有各个版本的高等数学和数学分析的系列教材中,应用柱面坐标和球面坐标来计算三重积分和曲面积分都们没有给出具体的设计公式,这使得学生很难掌握。
所以球坐标、柱面坐标在计算中的应用这方面的研究可以帮助学生更好的掌握题目的计算、理清解题的思路。
本文结合了数学分析、解析几何等教材以及相关的文献资料比较全面的给出了运用球面坐标和柱面坐标来简化三重积分和曲面积分的方法。
在运用球面坐标和柱面坐标的基础上充分的运用被积函数的奇偶性和积分区域的对称性省略一部分计算,达到简化的效果。
本文还归纳总结出一些学生常见的求三重积分积分限的类型以及积分域的投影区域,并提出如何确定积分限,对学生计算三重积分有一定的指导意义。
关键词:球面坐标;柱面坐标;三重积分;曲面积分ABSTRACTUniversity of triple integral and surface integral are key points and difficulties in mathematics and mathematical analysis. If when the integral region is a cylinder, cone surface, or spherical, this time we can use spherical coordinates and cylindrical coordinates transform integral calculation more simple. Throughout most of the existing various version of the series of higher mathematics and mathematical analysis teaching material, the application of cylindrical coordinates and spherical coordinates to calculate the triple integral and surface integral are gave no specific design formula, make it hard for students to master. So spherical coordinates and cylindrical coordinates in calculation, the application of this research can help students better grasp the problems of computation, clarify the thinking of the problem solving. This paper combines the mathematical analysis, parsing, how a few materials and relevant literature of using spherical coordinates and cylindrical coordinates is given to simplify the triple integral and surface integral method. In using spherical coordinates and cylindrical coordinates on the basis of fully using the parity of integrand and symmetry of integral area of omit part of calculation, the effect of simplified. This article also summarizes some common for students of triple integral limit type and integral domain projection area, and puts forward how to determine the bounds, for students to have certain guiding significance to the triple integral calculation.Keywords:Spherical coordinates; Cylindrical coordinates; Triple integral.;Surface integral 目录第一章绪论 (1)第二章球坐标、柱面坐标简要简介 (4)2.1球坐标、柱面坐标的概念 (6)2.2球坐标、柱面坐标的性质 (6)第三章球坐标、柱面坐标在三重积分计算中的应用 (6)3.1 三重积分限的确定 (6)3.2球坐标在三重积分计算中的应用3.2.1一般情况下球面坐标三重积分的计算 (6)3.2.2利用对称性和奇偶性简化球面坐标三重积分计算 (6)3.3柱面坐标在三重积分计算中的应用 (6)3.3.1一般情况下三重积分的柱面坐标计算法 (6)3.3.2运用对称性和奇偶性简化柱面坐标三重积分计算 (6)第四章球坐标、柱面坐标在曲面积分计算中的应用 (4)4.1球坐标在曲面积分计算中的应用 (4)4.2柱面坐标在曲面积分计算中的应用 (6)结论 (6)致谢 (6)参考文献 (6)第1章绪论三重积分和曲面积分是大学数学和数学分析中的重点但也是难点。
柱面坐标和球面坐标什么情况下用

柱面坐标和球面坐标何时应用在数学和物理中,柱面坐标和球面坐标是两种常见的坐标系,用于描述三维空间中的点的位置。
在何种情况下选择使用柱面坐标或球面坐标是一个重要的问题,下面将分别讨论这两种坐标系的特点以及在何种情况下应该选择使用。
柱面坐标柱面坐标是一种二维坐标系,通常用$(r, \\theta, z)$表示,其中r表示点到z轴的距离,$\\theta$表示点在x−y平面上的极角,z表示点在z轴上的高度。
柱面坐标系常用于描述具有旋转对称性的问题,如圆柱体、螺旋体等。
在以下情况下使用柱面坐标是比较合适的:- 需要描述具有圆柱对称性的问题,如旋转体、电磁问题等。
- 问题具有明显的旋转对称性,如涡旋问题。
- 问题的解在极坐标下更简洁或更容易求解。
球面坐标球面坐标是一种三维坐标系,通常用$(r, \\theta, \\phi)$表示,其中r表示点到原点的距离,$\\theta$表示点在x−y平面上的极角,$\\phi$表示点从z轴正半轴旋转到该点对应直线的倾角。
球面坐标系常用于描述具有球对称性的问题,如球体、天体运动等。
在以下情况下使用球面坐标是比较合适的: - 需要描述具有球对称性的问题,如天体运动、分子结构等。
- 问题的解在球坐标下更简洁或更容易求解。
- 需要描述三维空间中的全向性问题。
总结根据问题的具体性质,选择适当的坐标系是进行数学建模和物理分析的重要一步。
柱面坐标和球面坐标各有其适用的范围,选择合适的坐标系可以简化问题、提高求解效率,并更好地理解问题的物理本质。
综上所述,柱面坐标适用于具有旋转对称性的问题,而球面坐标适用于具有球对称性的问题。
在实际问题中,根据问题的特点和解题的便捷性来选择使用柱面坐标或球面坐标将更有利于解决问题和得出准确结果。
利用柱面坐标和球面坐标

o
y
为常数 半平
面.
x
球面坐标与直角坐标的关系为
x r sin cos ,
y
r
sin
sin
,
z r cos .
z
r M(x,y,z)
z
o
x
A
y
x
P
y
如图, 球面坐标系中的体积元素为
d vr2sin dd r d,
z
dr
d
rsin
r
rsin d
例3 计算三重积分 (x2y2)dv, 其中 是由曲
面 z x2y2与平 zH 面 (H0)所围成
z
解 将 向 xoy 面投影,得
D: x2y2H2
HH
或
D:
0 2,
0rH.
过 (r, )∈D 做平行于 z 轴
的直线,得
rzH .
o(r,)
r sin cos , r sin sin , r cos.
02d0 co2ssinr551 0d d vr2sin drd d
1 50 2 d0 co 2sin d
1 50 2d0 co 2s d(co ) s
例4 用球面坐标计算 z2dv . 其中
z
: x2y2z21.
解 画 图。
o
y
确定 r, , 的上下限。 x
(1) 将 向 xoy 面投影,得
0 2 .
(2) 任取一 [0,2],过 z 轴作半平面,得
0.
(3) 在半平面上,任取一 [0,], 过原点作
rd
d
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
球面坐标系和柱面坐标系的定义及其应用
球面坐标系和柱面坐标系是数学中关键的方法,经常用来描述
和解决一些几何和物理问题,它们与直角坐标系、极坐标系一样,是一种坐标系的表示方式。
一、球面坐标系
球面坐标系是以球面为基础的坐标系,它是由半径、极角和方
位角确定的。
坐标轴上的点对应着球面上的一个点,可以用三个
参数(r、θ、φ)来描述它的位置。
其中,r是从坐标原点到球面上某一点的距离,是一个实数;θ
是竖直方向的极角,它的范围在0到π之间;φ是水平方向的方位角,它的范围在0到2π之间。
坐标系的原点是球心,竖直方向的
坐标轴是与地球赤道垂直的轴线,水平方向的坐标轴则是经过原
点和北极点的轴线。
球面坐标系在物理学和天文学等领域应用广泛,例如测量地球
上某一点的纬度和经度、描述电磁场的分布等。
二、柱面坐标系
柱面坐标系是一种由高度、半径和角度确定的坐标系,它通常
用来描述长方形坐标系缺陷的问题。
柱面坐标系可以是圆柱面坐
标系或斜柱面坐标系,但都表示同样的信息。
在圆柱坐标系中,一点的坐标为(r,θ,z),其中r表示离坐标
轴的距离,θ表示与x轴的夹角,z表示高度。
而在斜柱面坐标系中,一点的坐标为(r,θ,z'),其中r和θ用同样的方式表示,z'是
某个平面内的高度。
只有当某一平面中的z'为零时,斜柱面坐标
系才与圆柱坐标系相同。
类似于球面坐标系的应用,圆柱坐标系和斜柱坐标系在物理学、工程学和计算机图形学等领域中有广泛的应用。
例如在计算机图
形学中,柱面坐标系被用来描述某些对象的形状和运动,在计算
机辅助设计(CAD)中,也被用来表示机械元件的三维空间位置。
总的来说,球面坐标系和柱面坐标系是一组非常实用的工具,
它们有助于我们更好地理解和描述现实世界中的各种问题。
了解
和掌握这些坐标系的基础和应用,有助于我们更好地应用它们来
解决实际问题。
