三参数、四参数曲线拟合
RTK求解参数(三参、四参、七参)讲解复习过程

站参数,使基准站发射差分信号。 • 3、连接移动站,设置移动站,使得移动站接收到基准站的差分数据,并达到
窄带固定解。 • 4、移动站到测区已知点上测量出窄带固定解状态下的已知点原始坐标。 • 5、根据已知点的原始坐标和当地坐标求解出两个坐标系之间的转换参数。 • 6、打开坐标转换参数,则RTK测出的原始坐标会自动转换成当地坐标。 • 7、到另外你至少一个已知点检查所得到的当地坐标是否正确。 • 8、在当地坐标系下进行测量,放样等操作,得到当地坐标系下的坐标数据。 • 9、将坐标数据在手簿中进行坐标格式转换,得到想要的坐标数据格式。 • 10、将数据经过ActiveSync软件传输到电脑中,进行后续成图操作。
• 平面坐标转换
– 多应用于 – 北京54,国家80 – 与当地自定义 – 坐标系之间的转换
– 四个参数 – X0平移 – Y0平移 – θ 坐标轴旋转 – K 尺度
不同(椭球)坐标系的转换流程
空间直角坐标(X,Y,Z)
椭球转换
大地坐标(B,L,H) 投影反算 平面直角坐标(x,y,h) 平面转换 当地平面坐标(x,y)
• 参数计算是RTK作业中很重要的一个环节,下面就RTK在使用不同的 转换方法时的作业步骤做详细说明。
一:平面四参数+高程拟合(用户常用方法)
• 1、架设基准站 • 基准站可架设在已知点或未知点上(注:如果需要使用求解好的转换
参数,则基准站位置最好和上次位置要一致,打开上次新建好的项目, 在设置基准站,只需要修改基准站的天线高,确定基准站发射差分信 号,则移动站可直接进行工作,不用重新求解转换参数) • 基准站架设点必须满足以下要求: • a、高度角在15度以上开阔,无大型遮挡物; • b、无电磁波干扰(200米内没有微波站、雷达站、手机信号站等, 50米内无高压线); • c、在用电台作业时,位置比较高,基准站到移动站之间最好无大型 遮挡物,否则差分传播距离迅速缩短; • d、至少两个已知坐标点 (已知点可以是任意坐标系下的坐标,最好 为三个或三个以上,可以检校已知点的正确性); • e、不管基站架设在未知点上还是已知点上,坐标系统也不管是国家 坐标还是地方施工坐标,此方法都适用。
RTK求解参数(三参、四参、七参)详解

• 投影讲解 四参数+高程拟合
二、三参数转换
• (1)、架设基准站 • 基准站(基准站架设在已知点上,如果基准站架设在未知点上,手簿 软件使用方法和四参数类似,只是在计算参数时选择计算三参数)。 • 架设点必须满足以下要求: • a、高度角在15度以上开阔,无大型遮挡物; • b、无电磁波干扰(200米内没有微波站、雷达站、手机信号站等, 50米内无高压线); • c、位置比较高,用电台作业时,基准站到移动站之间最好无大型遮 挡物,否则差分传播距离迅速缩短; • d、只需一个已知坐标点 (已知点可以是国家坐标系下的坐标,或坐 标系和WGS-84坐标系之间的旋转很小); • e、此方法都适用于客户对坐标精度要求不是很高的情况,随着移动 站离基准站距离的增加,精度越来越低,一般3KM精度能在5CM以内。
RTK求解参数
罗禹
参数的概念
1、由于GPS所采用的坐标系为WGS-84坐标系,而 在我们国家,实际的工作中所使用的都是BJ-54,国 家-80、或地方坐标系, 因此存在WGS-84和当地坐标系统之间的转换问题。 2、参数转换一般分两种形式: 平面坐标系之间的转换:四参数、校正参数 椭球体之间的转换: 三参数,七参数
• 投影讲解 七参数
四、一步法转换
• 使用要求:至少三个已知坐标点(已知点可以是国家坐标系下的坐标 或自定义坐标系下的坐标,最好三个以上已知点,可以检验已知点的 正确性)。 • 用一步法转换、七参数转换、四参数转换、三参数转换(基准站架设 在未知点)时,仪器和手簿软件操作步骤类似,只是要求的已知点数 据和使用范围不一致。
谢谢
• 一般的:
• • • • 三参数:要求已知一个国家坐标点,精度随传输距离增加而减少 四参数:要求两个任意坐标点,精度在小范围内可靠 七参数:三个国家坐标点,精度高,对已知点要求严格 一步法:三个任意坐标点,在残差不大的情况下,精度可靠
RTK求解参数(三参、四参、七参)讲解

1、架设基准站、设置好GPS主机工作模式 2、打开手簿软件、连接基准站、新建项目、设置坐标系统参数、设置好基准 站参数,使基准站发射差分信号。 3、连接移动站,设置移动站,使得移动站接收到基准站的差分数据,并达到 窄带固定解。 4、移动站到测区已知点上测量出窄带固定解状态下的已知点原始坐标。 5、根据已知点的原始坐标和当地坐标求解出两个坐标系之间的转换参数。 6、打开坐标转换参数,则RTK测出的原始坐标会自动转换成当地坐标。 7、到另外你至少一个已知点检查所得到的当地坐标是否正确。 8、在当地坐标系下进行测量,放样等操作,得到当地坐标系下的坐标数据。 9、将坐标数据在手簿中进行坐标格式转换,得到想要的坐标数据格式。 10、将数据经过ActiveSync软件传输到电脑中,进行后续成图操作。
空间直角坐标(X,Y,Z)
大地坐标(B,L,H) 投影正算 平面直角坐标(x,y,h) 平面转换 当地平面坐标(x,y)
RTK简易操作流程
• 以下只是软件的简易操作流程,详细使用步骤请参照接下来的详细说明。此 流程只是我们提供给的一种解决方案,在熟练使用本软件后,可以不依照此 步骤操作。在作业过程中,通常的使用方法为:
• 投影讲解 三参数
三、七参数转换
一:平面四参数+高程拟合(用户常用方法)
• 1、架设基准站 • 基准站可架设在已知点或未知点上(注:如果需要使用求解好的转换 参数,则基准站位置最好和上次位置要一致,打开上次新建好的项目, 在设置基准站,只需要修改基准站的天线高,确定基准站发射差分信 号,则移动站可直接进行工作,不用重新求解转换参数) • 基准站架设点必须满足以下要求: • a、高度角在15度以上开阔,无大型遮挡物; • b、无电磁波干扰(200米内没有微波站、雷达站、手机信号站等, 50米内无高压线); • c、在用电台作业时,位置比较高,基准站到移动站之间最好无大型 遮挡物,否则差分传播距离迅速缩短; • d、至少两个已知坐标点 (已知点可以是任意坐标系下的坐标,最好 为三个或三个以上,可以检校已知点的正确性); • e、不管基站架设在未知点上还是已知点上,坐标系统也不管是国家 坐标还是地方施工坐标,此方法都适用。
2.RTK求解参数(三参、四参、七参)

一:平面四参数+高程拟合(用户常用方法)
• 1、架设基准站 • 基准站可架设在已知点或未知点上(注:如果需要使用求解好的转换 参数,则基准站位置最好和上次位置要一致,打开上次新建好的项目, 在设置基准站,只需要修改基准站的天线高,确定基准站发射差分信 号,则移动站可直接进行工作,不用重新求解转换参数) • 基准站架设点必须满足以下要求: • a、高度角在15度以上开阔,无大型遮挡物; • b、无电磁波干扰(200米内没有微波站、雷达站、手机信号站等, 50米内无高压线); • c、在用电台作业时,位置比较高,基准站到移动站之间最好无大型 遮挡物,否则差分传播距离迅速缩短; • d、至少两个已知坐标点 (已知点可以是任意坐标系下的坐标,最好 为三个或三个以上,可以检校已知点的正确性); • e、不管基站架设在未知点上还是已知点上,坐标系统也不管是国家 坐标还是地方施工坐标,此方法都适用。
• 2、假设已建好一个项目,参数计算完以后, 正常工作了一段时间,由于客观原因,第 二次作业不想把基准站架设在和第一次同 样的位置,此时,可以用到点校正功能, 只需要将基准站任意架设,打开第一次使 用的项目,到一个已知点上校正坐标即可。 校正方法和第一种情况相同。
• 一般的:
• • • • 三参数:要求已知一个国家坐标点,精度随传输距离增加而减少 四参数:要求两个任意坐标点,精度在小范围内可靠 七参数:三个国家坐标点,精度高,对已知点要求严格 一步法:三个任意坐标点,在残差不大的情况下,精度可靠
五、校正参数
• 用于计算两坐标系统之间的平面、高程平移参数。通常 在以下两种情况,可以使用校正参数
– – – –
– – – – –
多应用于 北京54,国家80 与当地自定义 坐标系之间的转换
如何进行参数计算(四参数高程拟合)?

如何进行参数计算(四参数高程拟合)?定义:四参数是指两个平面坐标系之间的平移(DX、DY),旋转(α),缩放参数(κ)。
四参数是RTK常用的一种坐标转换模式,通过四参数完成WGS84平面到当地平面的转换,通过高程拟合完成WGS84椭球高到当地水准的拟合。
要求:至少两个任意同一坐标系的坐标(通用方法)使用环境:适用于大部分的普通工程测量,工程放样简要步骤1)仪器工作模式设置2)采集控制点坐标3)求解参数4)坐标检核计算参数的详尽流程1、设置基站与移动站(可以选择手机卡或者电台模式),使移动台最终达到固定解;2、采集控制点坐标(如“交186”与“y265”为控制点)在碎部测量中,分别对控制点进行“交186”和“y265”采集坐标(使用平滑采集对控制点进行采集),分别保存为“交186”与“y265”。
3、求解参数1)进入参数求解界面2)、添加控制点对如图操作,分别添加“交186”与“y265”两个点对。
其中源点为刚才采集的坐标,目标点为控制点的已知坐标(需要自己手动添加,或者提前输到控制点库中,再调用)。
3)计算参数点击计算,得到“四参数+高程拟合”的结果点击应用后,即可完成操作。
A为高程固定差改正的差值。
注意:尺度的数据为0.999……或者1.000……4、进行坐标检核找一个控制点进行碎部测量(最好找第三个控制点),对比采集的(N,E,Z)与已知坐标(N,E,Z)检核坐标的正确性。
注意:1、这里的“四参数+高程拟合”计算是针对于基站而言的。
在计算“四参数+高程拟合”之前,必须保证坐标系统中的基准面的“转换模型”,平面转换的“转换模型”,高程拟合“转换模型”均为“无”;2、一个项目只能求解一次参数计算,或者说一个项目求参数前,必须满足前一点条件;3、计算参数的两个点数据必须是接收同一个基站信号采集的固定解坐标;用于计算参数的两个点的已知坐标必须是同一个坐标系统,即计算的尺度(k)为0.999……或者1.000……。
极化曲线测量
极化曲线测量董泽华为了探索电极过程的机理及影响电极过程的各种因素,包括各种水处理剂,缓蚀剂的评价和机理研究,都必须对电极过程进行研究,而在该研究过程中极化曲线的测定又是重要的方法之一。
一般进行进化曲线测量1.实验方法(一)碳钢在弱酸性溶液中的极化曲线(1)工作电极为PTFE或环氧树脂镶嵌的A3钢,面积为0.5cm2,工作电极用200,600,800号金相砂纸逐级打磨至光亮,以无水乙醇和丙酮脱脂后,再用蒸馏水进行冲洗,放入干燥器内干燥30mins,然后浸入被测溶液中15~50mins, 待电位稳定后进行测量。
试验采用密闭的玻璃电解池,并置于恒温水浴中,试验过程中溶液未除氧。
放在丙酮中除去油污,用石腊涂抹剩余面积,备用。
(2)试验介质分别为1000 mg/l H2S+1000 mg/l HCl和1000 mg/l H2S+100 mg/l HCl。
温度为25℃和85℃。
缓蚀剂为某石油化工厂提供的”HT-1”和”WS-1”,主要成分为咪唑啉酰胺为1mmol·L-1的盐酸溶液(pH=3),采用Pt片作为辅助电极,饱和甘汞电极为参比电极。
将工作电极安装到装有250mL介质的四口烧瓶,与Pt辅助电极、饱和甘汞电极组成三电极体系。
电解池的连接参见附件一。
(3)仪器采用华中科技大学研制的CS300型电化学测试系统进行极化曲线测量,测量控制和数据分析才采用corrTest进行。
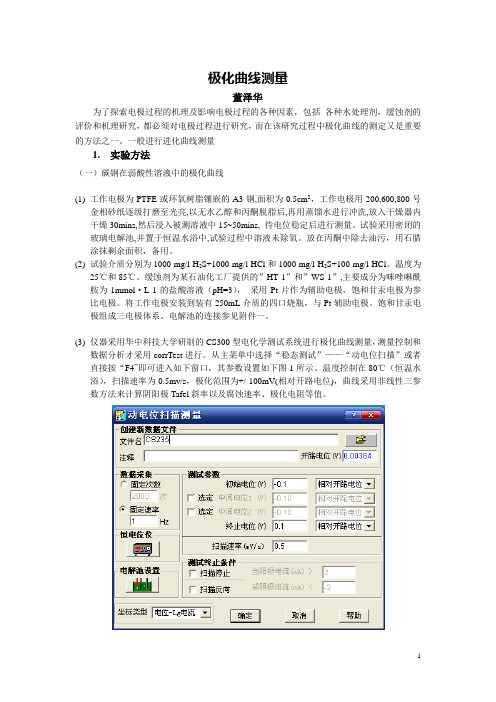
从主菜单中选择“稳态测试”——“动电位扫描”或者直接按“F4”即可进入如下窗口,其参数设置如下图1所示。
温度控制在80℃(恒温水浴),扫描速率为0.5mv/s,极化范围为+/-100mV(相对开路电位),曲线采用非线性三参数方法来计算阴阳极Tafel斜率以及腐蚀速率、极化电阻等值。
图1极化曲线参数设置窗口电解池参数设置如下图2所示,用于设定工作电极的面积,材料化学当量,参比电极类型等,这些参数将用于腐蚀参数的计算。
图2.电极与电解池参数设置窗口此外,恒电位仪的参数设置一般可以依照下图3所示的参数进行,没有特殊需要无需修改。
基于正弦曲线拟合算法的adc测试改进方法

第50卷第2期 2010年2月
电讯技术
Telecommunication Engineering
文章编号:1001—893X(2010)02-0069—04
V01.50 No.2 Feb.2010
基于正弦曲线拟合算法的ADC测试改进方法‘
桑 龙1’2,陈 静3
(1.西北工业大学。西安710072;2.海军装备部,西安710054;3.西安科技大学,西安710054)
摘要:当ADC测试数据与理想模型的偏差为随机的高斯噪声时,基于正弦曲线的ADC测试方法
能够取得较好的拟合效果,然而实际应用时却经常发现标准的正弦曲线测试往往会出现一些偏差。
为了减少拟合时的不确定因素,对正弦曲线拟合过程进行了分析,通过仿真找出了产生偏差的主要
因素,并对其进行了更正。仿真结果表明了该方法的有效性。
参考文献:
[1]DaUet D,Da Silva J M.Dynamic Characterization of Ana. 109ue—to—Digital Conveners[M].[S.1.]:Springer,
2005:66—69.
[2] Eulalia Balestrieri,Pasquale Daponte,Se晒o Rapuano.A state of the art ola ADC error compensation methods[J]. IEEE Transactions Oil Instrumentation and Measurement, 2005,54(4):1388—1394.
正弦信号发生器波形抖动的一种精确测量方法

系统的波动影响, 以及使用数字合成技术时, 抽样间隔
1 引 言
抖动, 是周期信号发生器一种固有的技术特征, 通 常认为, 抖动是信号在时间上相对其理想位置的短期 变动。 在此含义下, 包括信号的周期、 频率、 相位、 占空 比等时间参数的短期不稳定因素, 都可以用抖动指标 给出, 它也涉及多个连续信号周期的稍长时间内的稳 定性评价, 更长时间的稳定性, 常用漂移参数评价。 按统计特性, 抖动可分为随机抖动和确定抖动两 类; 其起源, 主要由随机噪声、 干扰调制、 串扰、 供电源
[1]
设理想正弦信号为:
y ( t ) = A 0 co s ( 2Π ft ) + B 0 sin ( 2Π ft ) + C 0 = A co s ( 2Π ft+ Η 0) + C0 ( 1)
数据记录序列为时刻 t 1 , t 2 …, t n 的采集样本 y 1 ,
y2 , …, yn , 采集速率 v 已知, 采样间隔为 ∃ t, t i= i×∃ t= i v, ( i= 1, …, n ) , 数字角频率 Ξ= 2Π f v, 则公式 ( 1 ) 可
∑ΑiΒi- Α∑Βi
i= 1 n i= 1 n
2 i i
i= 1 n
i= 1 n
;
∑ΑΒ- Β∑Α ∑Β - ΒΑ∑Αi
2
i= 1 n
i= 1 n
-
i= 1
i= 1
∑ΑiΒi- Α∑Βi
i= 1 i= 1
i= 1 n
i= 1 n
;
第 1 期
正弦信号发生器波形抖动的一种精确测量方法
值, 对第 2 个信号点开始的约一个周期的信号的模型 参数进行估计; 依次类推, 直至最后一个完整的信号周 期, 结束估计。 之后, 对众多信号周期的模型参数进行 波形分析和统计分析, 获得它们的抖动特性参数。 下面, 将详细介绍一种三参数正弦曲线拟合算法 和由它改造获得的四参数正弦曲线拟合算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( Ⅴ ) 比较 ( Ⅳ ) 中 2 M + 1 个残差平方和 , 并找出最小残差平方和 对应频率 ( 记为 ω1 ) 、 正弦幅度 ( 记为 A 1 ) 、 余弦幅度 ( 记为 B1 ) 以及直流偏移 ( 记为C1 ) . 这就是正弦信号四参数的第 1 次估计值 , 其中 ,频率估计的最大偏差Δω=Δω0/ M . (Ⅵ)令i=i+1,
四参数拟合的经典算法简介
牛顿法:该方法是基于一阶泰勒展开与误差修正技 术相结合的产物,搜索终止的判据可以是参数增量, 或残差平方和。 顺序搜索法:顺序对每一个参数在初始值上使用增 量搜索法寻找其最优点。
牛顿法简介
牛顿法是对方程四个参数求偏微分,得到E对给 定系数的增量的泰勒级数展开式。用增量对初始值 进行校正,以此方法进行多次迭代,直到相关系数 不再增大,或者设定一个迭代的次数,就可以得出 四个值的最终结果。
1800 A h max|Δp|= (Nh)1.25 A ΔC 0.61 A h max| |= A (Nh)1.21h1.1 A
流量。
拟合参数的不确定度
利用Cramer-Rao界,可以估计出谐波失真造成 的4个测量参数的不确定度。以相位为例,假设 h次 谐波的幅值 A h 造成的参数误差分别在各自的误差界 内均匀分布,则 A h 给 Δp 带来的测量不确定度为:
数学上,幅度、频率、相位和直流偏移4个参数 可以唯一确定一条正弦曲线。曲线拟合的目的就是 通过分析输入的正弦信号,得到正弦波形的四个参 数值,从而得到拟合曲线。
在已知输入正弦波形的前提下,怎样确定它的4 个参数呢?
正弦曲线拟合的总体思路
主要是通过改变拟合正弦函数的幅度、频率、 相位和直流偏移,使拟合函数和采样序列各点的残 差平方和最小,从而获得正弦波形序列最小二乘拟 合结果。
1
其中:
E
2 r i
n
n
2
i 1
由于这是一种闭合算法, 因而收敛是肯定的。
四参数法
当正弦信号的四个参数都不知道时,一般采用 四参数法进行拟合。四参数法也是最常用的一种正 弦波拟合方法。与三参数正弦曲线拟合不同,四参 数正弦曲线拟合是一个非线性迭代过程,没有解析 公式可以直接应用获得结果,需要计算初始值进行 迭代。
( Ⅸ ) 重复 ( Ⅵ ) ~ ( Ⅷ ) , 直到找到满足精度要求的信号频率 , 将其 记为ω, 同时将与它对应的其他三个参数记为 A , B , C , 那么 ω, A , B , C 这四个参数就是正弦信号四参数的估计值. 其中 , 频率估计的最 大误差为Δωmax=Δω0 / Mi 步骤 ( Ⅰ ) ~ ( Ⅸ ) 给出了四参数估计法的一般步骤和频率估计的最 大误差 Δωmax ,可知 , 可以通过增大估计次数 i 来提高估计精度
四参数拟合的算法简介
还有学者使用遗传算法实现总体最优估计,以 此实现四参数正弦参数的最小二乘估计,由于遗传 算法原理本身可保证实现全局最优逼近,可避免收 敛到局部最优点上,从而具有良好的收敛性。
拟合误差
有很多因素会影响到拟合参数的精确度。序列 长度、采样序列中含有的波形周期个数、采样量化 误差、非线性误差等条件,都限制和影响了正弦参 数的估计。
( Ⅶ ) 从区间 [ ωil,ωih] 中等间距地取 2 M + 1 个点 , 分别计算出这些 点对应的 A ij , B ij , Cij 和误差平方和 E ij .
( Ⅷ ) 比较 ( Ⅶ ) 中 2 M + 1 个误差平方和 , 并找出最小误差平方和 对应的四个参数 ( 分别记为 ωi , Ai ,Bi 和 Ci ) , 这就是正弦信号四参 数第 i 次的估计值 ,其中 , 频率估计的最大偏差Δω=Δω0 / Mi.
正弦曲线拟合的三参数法与四 参数法
正弦曲线拟合的意义
由正弦波形的采样序列获得其拟合正弦曲线函 数,是一种基本信号处理方法,在许多场合下获得 了应用,如评价数据采集系统的有效位数、采集速 率、交流增益、通道间延迟、触发特性等,在调制 信号的数字化解调和失真度测量中,也有应用。
曲线拟合的一般过程
正弦信号——采样——A/D变换——信号处理—— 拟合正弦曲线
拟合参数的最小误差界
John P. Deyst1995年给出了正弦波四参数最小 二乘拟合算法获得参数的误差界,使用蒙特卡罗搜 索仿真法等对于各种可以想象的条件变化进行了细 致研究,并分别以经验公式、误差界曲线等形式, 给出4个拟合参数随谐波次数和幅度、噪声、抖动、 序列长度、序列所含信号周期个数等条件参量变化 的规律。基本结论是:拟合获得的4个参数的误差界 随着谐波阶次、序列长度、序列所含信号周期个数 增大而变窄,随着谐波幅度、噪声、波形抖动的降 低而变窄。每个参数的误差界应该在一个确定区间 内变化,最小误差界即是其Cramer-Rao界。
同理也可以得到幅值和直流分量的不确定度。
幅值:
Ah2 u A = u A (A h ) = 2.5 h 2 h 2 3(Nh)
2
直流量:
0.124A h 2 u C = u C (A h ) = 2.42 3.52 h h 2 h 2 N
2
拟合参数的不确定度
对于频率不确定度的估计,可以做一下变换:
D(0)-C p=arcsin( ) A
四参数拟合的算法
四参数拟合有很多种算法。IEEE学会在标准 IEEE std1057-2007 IEEE Standard for Digitizing Waveform Recorders 的 Annex A 中给出了一种方 法,包括两种基本算法:一种通过矩阵运算,另一 种通过迭代过程,二者均需要良好的初始条件估计。
谢 谢!
i=1
n
则,参数A,B,D即为A0,B0,D0的最小二乘拟合值。为寻找出A,B, D,构造矩阵 y1 cos( ) sin( ) 1 A y2 y= cos(2 ) sin(2 ) 1 x = B M 0 D y n
四参数拟合的算法简介
顺序搜索法有一种算法是将四参数拟合过程拆 分成两步走,可以避免四参数非线性迭代带来的收 敛问题。该算法使用一种非线性迭代方法获得信号 频率估计值,然后在已知频率情况下,使用三参数 最小二乘拟合算法获得最终结果。本质上是一种三 参数方法。
四参数顺序搜索算法示例
( Ⅰ ) 令 i = 1 , 确定估计信号频率的大致区间.对于常见的等间隔采样 , 转步骤 ( Ⅱ ) ; 对于非等间隔采样 , 直接转步骤 ( Ⅲ ) . ( Ⅱ ) 利用 D F T 或 F F T 计 算信 号频率 , 设 为ωd , 令迭代区间频 率下限 ,迭代区间频率上限 (其中 ,ωc 为时钟频率 , N为 D F T 或 F F T 的长度) , 转步骤 ( Ⅳ ) . ( Ⅲ ) 观察采样序列过零点时刻 , 设第 m 个过“ 零点” ( 零点指采样 序列的均值位置) 时刻在区间[tkm,tkm+1]中 , 而第L(L>M)个过 “ 零点 ” 时刻在区间 [tkl,tkl+1] 中 , 令 , , 其中m , l 为整数 , 转步骤 ( Ⅳ ). (Ⅳ)令 , 从区间[ω0l,ω0h]中等间距的取 2 M + 1 个点 ( 比如 M = 5) , 利用三参数法分别计算出这些点对应的 A1j , B1j , C1j 和残差平方和 E1j ( j = 1 , 2 , 3 , …, 2 M + 1) .
u p (A h )= Dp m 1800 A h = 1.25 3 (Nh) A 3
由于三角函数基之间的正交性,不同谐波 互不相关,所有谐波带来的总的不确定度为:
2 10800 A h u p = u p 2 (A h ) 2.5 2 A h 2 h 2 (Nh)
拟合参数的不确定度
正弦曲线拟合的总体思路
假设采样点数是L,采样数据是D(I),I: 0,1,…,L-1
拟合函数是S(t)=Asin(2πft+p)+C 则残差的平方和为 E [D(I) S(I t)]2
I 0 L 1
Δt 为采样时间间隔
拟合的目的就是找到让E最小的四个参数A、f、p、 C
三参数法简介
三参数拟合算法示例
设理想正弦信号为 y(t)=C 0cos(2π ft+θ 0 )+D0
=A 0cos(2π ft)+B 0sin(2π ft)+D0
三参数正弦波曲线拟合过程,即为输入信号的数字角频率已知,选取或 寻找A,B,D,使下式所述残差平方和最小:
E= [yi -Acos(ω i)-Bsin(ω i)-D]2
cos(n ) sin(n ) 1
三参数拟合算法示例
残差平方和用矩阵表示为:
T E=E(ω )=(y-Mx0 )(y-Mx ) 0 当式E最小时可得 x0 的最小二乘解为:
x0 =(M M) (M y)
拟合函数的幅度和相位表达形式为:
∧
T
-1
T
y(i) =Ccos(ω i+θ )+D
拟合参数的最小误差界
Cramer-Rao界:在四参数正弦波拟合中,误差界的 指数表达式给出了拟合参数误差随着信号周期个数 和谐波阶次变化而变化的一个公式。 0.9 A h max|ΔN|= 其中:N为采样的周期个 (nh)1.2 A 数,n为采样点数,h为 Ah ΔA 1 谐波次数(整数),A为 max| |= 1.25 A (Nh) A 幅值,p为相位,C为直
三参数正弦曲线拟合,特指信号频率已知时获 取幅度、相位和直流偏移的波形拟合方法,它是一 种闭合算法,无须迭代即能获得结果,没有收敛问 题,具有良好的实用性。
三参数法的算法
在标准IEEE std1057-2007 IEEE Standard for Digitizing Waveform Recorders 的 Annex A 中给出 了一种三参数正弦拟合的算法。
