李子奈 潘文卿 计量经济学第三版课后练习答案
计量经济学(第三版)李子奈 潘文卿 编著 第二章第12题答案
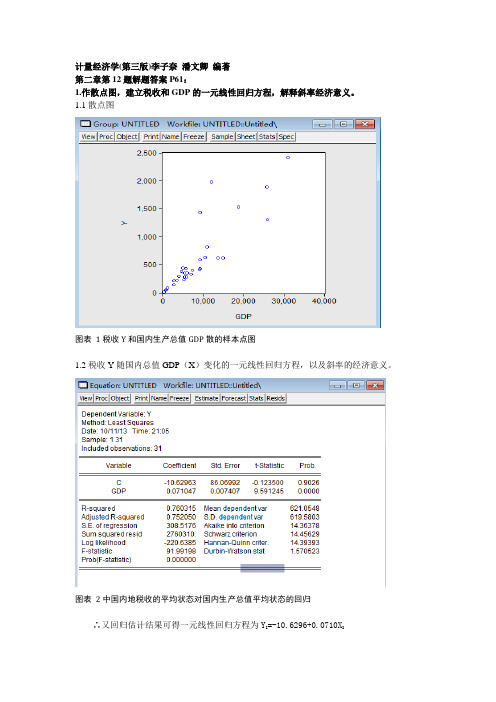
计量经济学(第三版)李子奈潘文卿编著第二章第12题解题答案P61:1.作散点图,建立税收和GDP的一元线性回归方程,解释斜率经济意义。
1.1散点图图表1税收Y和国内生产总值GDP散的样本点图1.2税收Y随国内总值GDP(X)变化的一元线性回归方程,以及斜率的经济意义。
图表2中国内地税收的平均状态对国内生产总值平均状态的回归∴又回归估计结果可得一元线性回归方程为Y I=-10.6296+0.0710X I斜率的经济意义:表示国内生产总值GDP每1元的变化所引起的税收的平均变化为0.071.2.对建立的回归方程进行检验。
2.1拟合优度检验----可决系数R2统计量从回归估计的结果看,模型拟合还行。
可决系数R2=0.7603,表明税收变化的76.03%可以由国内生产总值GDP的变化来解释。
2.2变量的显著性检验假设:H0:βi=0 H1:βi≠0给定显著性性水平0.05,查t分布表得到临界值t(a/2)(31-2)=2.045i.对于β1,从回归分析结果中斜率的t检验值来看9.591245>2.045,所以在95%的置信度下拒绝原假设H0,即变量X是显著的,通过显著性检验。
ii.对于β0,从回归分析结果中截距t检验值来看-0.1235<2.045, 所以在95%的置信度下接受原假设H0,没有通过显著性检验。
3.若2008年某地区GDP为8500亿元,求该地区税收收入的预测值及预测区间?解:由回归方程Y I=-10.6296+0.0710X I可得该地区税收收入的预测值Y=-10.6296+0.0710x8500=592.8704(亿元)由于国民生产总值X的样本均值和样本方差为:E(X)=8891.126 Vax(X)=5782313在给定95%的置信度水平下,该地区税收收入的预测区间为:=592.704±641.288或(-48.584,1233.992)。
李子奈《计量经济学》第三版例题及习题的stata解答

第二章例2.1.1(p24)(1)表2.1.2中E(Y|X=800)即条件均值的求法,将数据直接复制到stata 中。
程序:sum y if x==800程序:程序:sum y if x==1400(2)图2.1.1的做法:程序:twoway(scatter y x )(lfit y x ),title("不同可支配收入水平组家庭消费支出的条件分布图")xtitle("每月可支配收入(元)")ytitle("每月消费支出(元)")xtick(500(500)4000)ytick(0(500)3500)例2.3.1(p37)将数据直接复制到stata 中程序:(1)total xiyireturn listscalars:r(skip) = 0r(first) = 1r(k_term) = 0r(k_operator) = 0r(k) = 0r(k_level) = 0r(output) = 1r(b) = 4974750r(se) = 1507820.761894463g a=r(b) in 1 total xi2 xiyi 4974750 1507821 1563822 8385678Total Std. Err. [95% Conf. Interval]Scatter 表示散点图选项,lfit 表示回归线,title 表示题目,xtick 表示刻度,(500(500)4000)分别表示起始刻度,中间数表示以单位刻度,4000表示最后的刻度。
要注意的是命令中的符号都要用英文字符,否则命令无效。
这个图可以直接复制的,但是由于我的软件出问题,只能直接剪切,所以影响清晰度。
return listg b=r(b) in 1di a/b.67(2)mean Yigen m=r(b) in 1mean Xig n=r(b) in 1di m-n*0.67142.4由此得到回归方程:Y=142.4+0.67Xi例2.6.2(p53)程序:(1)回归reg y x(2)求X的样本均值和样本方差:mean xMean estimation Number of obs = 31 Mean Std. Err. [95% Conf. Interval] x 11363.69 591.7041 10155.27 12572.11sum x ,d(d表示detail的省略,这个命令会产生更多的信息)xPercentiles Smallest1% 8871.27 8871.275% 8920.59 8920.5910% 9000.35 8941.08 Obs 3125% 9267.7 9000.35 Sum of Wgt. 3150% 9898.75 Mean 11363.69Largest Std. Dev. 3294.46975% 12192.24 16015.5890% 16015.58 18265.1 Variance 1.09e+0795% 19977.52 19977.52 Skewness 1.69197399% 20667.91 20667.91 Kurtosis 4.739267di r(Var)(特别注意Var的大小写)10853528例2.6.2(P56)(1)reg Y XSource SS df MS Number of obs = 29F( 1, 27) = 2214.60Model 2.4819e+09 1 2.4819e+09 Prob > F = 0.0000Residual 30259023.9 27 1120704.59 R-squared = 0.9880Adj R-squared = 0.9875Total 2.5122e+09 28 89720219.8 Root MSE = 1058.6Y Coef. Std. Err. t P>|t| [95% Conf. Interval]X .4375268 .0092973 47.06 0.000 .4184503 .4566033_cons 2091.295 334.987 6.24 0.000 1403.959 2778.632(2)图2.6.1的绘制:twoway (line Y X year),title("中国居民可支配总收入X与消费总支出Y 的变动图")第三章例3.2.2(p72)reg Y X1 X2Source SS df MS Number of obs = 31F( 2, 28) = 560.57Model 166971988 2 83485994.2 Prob > F = 0.0000Residual 4170092.27 28 148931.867 R-squared = 0.9756Adj R-squared = 0.9739Total 171142081 30 5704736.02 Root MSE = 385.92Y Coef. Std. Err. t P>|t| [95% Conf. Interval]X1 .5556438 .0753076 7.38 0.000 .4013831 .7099046X2 .2500854 .1136343 2.20 0.036 .0173161 .4828547_cons 143.3266 260.4032 0.55 0.586 -390.0851 676.7383例3.5.1(p85)g lnP1=ln(P1)g lnP0=ln(P0)g lnQ=ln(Q)g lnX=ln(X)Source SS df MS Number of obs = 22 F( 3, 18) = 258.84 Model .765670868 3 .255223623 Prob > F = 0.0000 Residual .017748183 18 .00098601 R-squared = 0.9773 Adj R-squared = 0.9736 Total .783419051 21 .037305669 Root MSE = .0314 lnQ Coef. Std. Err. t P>|t| [95% Conf. Interval]lnX .5399167 .0365299 14.78 0.000 .4631703 .6166631 lnP1 -.2580119 .1781856 -1.45 0.165 -.632366 .1163422 lnP0 -.2885609 .2051844 -1.41 0.177 -.7196373 .1425155 _cons 5.53195 .0931071 59.41 0.000 5.336339 5.727561 drop lnX lnP1 lnP0g lnXP0=ln(X/P0)g lnP1P0=ln(P1/P0)reg lnQ lnXP0 lnP1P0Source SS df MS Number of obs = 22F( 2, 19) = 408.93Model .765632331 2 .382816165 Prob > F = 0.0000Residual .01778672 19 .000936143 R-squared = 0.9773Adj R-squared = 0.9749Total .783419051 21 .037305669 Root MSE = .0306lnQ Coef. Std. Err. t P>|t| [95% Conf. Interval]lnXP0 .5344394 .0231984 23.04 0.000 .4858846 .5829942lnP1P0 -.2753473 .1511432 -1.82 0.084 -.5916936 .040999_cons 5.524569 .0831077 66.47 0.000 5.350622 5.698515练习题13(p105)g lnY=ln(Y)g lnK=ln(K)g lnL=ln(L)reg lnY lnK lnLSource SS df MS Number of obs = 31 F( 2, 28) = 59.66 Model 21.6049266 2 10.8024633 Prob > F = 0.0000 Residual 5.07030244 28 .18108223 R-squared = 0.8099 Adj R-squared = 0.7963 Total 26.6752291 30 .889174303 Root MSE = .42554 lnY Coef. Std. Err. t P>|t| [95% Conf. Interval]lnK .6092356 .1763779 3.45 0.002 .2479419 .9705293 lnL .3607965 .2015915 1.79 0.084 -.0521449 .7737378 _cons 1.153994 .7276114 1.59 0.124 -.33645 2.644439第二问:test b_[lnk]+b_[lnl]==1第四章例4.1.4 (P116)(1)回归g lnY=ln(Y)g lnX1=ln(X1)g lnX2=ln(X2)reg lnY lnX1 lnX2Source SS df MS Number of obs = 31 F( 2, 28) = 49.60 Model 2.9609923 2 1.48049615 Prob > F = 0.0000 Residual .835744123 28 .029848004 R-squared = 0.7799 Adj R-squared = 0.7642 Total 3.79673642 30 .126557881 Root MSE = .17277 lnY Coef. Std. Err. t P>|t| [95% Conf. Interval]lnX1 .1502137 .1085379 1.38 0.177 -.072116 .3725435 lnX2 .4774534 .0515951 9.25 0.000 .3717657 .5831412 _cons 3.266068 1.041591 3.14 0.004 1.132465 5.39967于是得到方程: lnY=3.266+0.1502lnX1+0.4775lnX2(2)绘制参差图:predict e, residg ei2=e^2scatter ei2 lnX2,title("图 4.1.3 异方差性检验图")xtick(6(0.4)9.2)ytick(0(0.04)0.24)predict在回归结束后,需要对拟合值以及残差进行分析,需要使用此命令。
计量经济-学--李子奈-潘文卿版计量经济学-课后习题答案-2

第二章1-为什么计翼经祈字碘型旳理论万桎甲必次包肯隨劝L十耽峡?解答计量经济学模型命離的是貝有因果关系的随机变量间的具体联系方式。
由于起随机变童,意缺着影响被解释变慑的因素是复杂的,除了解释变量的惑响外,还有其他无法在模型中独立列出的各种因素的膨响.这样,理论模型中就必须便用一个称为随机干扰项的变最來代表所有这些无法在模型中独立表示出来的影响因素’以保证模里在理论上的科学性。
2.下列计屋经济学方程哪些暹正确的?鄭些是错课的?为什么?(1) Um⑵K M + 0K + ”…』;⑶y产矗+庐扎+片212…卫$(4)—&f =(5)Y^a^flX t, 212…』;•⑹ 左严心人・2讥…肿⑺Y严时21,2,…冲(8) 乂二&心“兀 r=lA->«.其中带…者表示T古计值3解答计量经济学模型有两种类型:一是总体回归模型;另一是样本回归模樂.两类回归模型都具有确定形武与随机形式两种表达方式=总体回归模型的确定形式£的加=矗十尽r总体回归模型的随机形式样本回归摸型的确定形式S十険样本回归模型的随机形式F =才+芒除此之外,英他的表达形式均是错误的,因此利斷如下J⑴错島(2)正确:(3)错课:(4)错误;(5)错误,(6)正确;(7)正确:(8)错误*4.线性回归模型不=a + 0Xj+隔 F = l,2,…/的零均值假设是否可以表示为丄£Aj=0?为什么?解答线性回归模型中的零均值假设£(A) = 0可以表示为£(^)-0, £(/^) = 0, E(/^) =0,…*1 FL但是不能表示为一理由是*£Or)=°严格说来,随机干扰项的零均值假设是关干疋的条件期望为零:= 其含义为在X取值为疋的条件下.所有其他因素对F的各种可能的影响平均下来为零。
因此,E(H)与丄£殉是两个完全不同的概念。
R J-I乩假设已经得到关系式Y =的最小二乘估计,试回答:(1)假设决定把X变量的单位扩大10倍,这样对原回归的斜率和截距会有什么样的影响?如果把丫变量的单位扩大10倍,又会怎样?(2)假定给X的每个观测值都增加2,对原回归的斜率和截距会有什么样的影响?如果给F的每个观测值都増加2・又会怎样?解答(1)记为原变量北单位扩大10倍的变星,则A*= —,于是10Y =%5XX*胡+0市-=几+辭可见,解释变量的单位扩大1Q倍时,回归的截距项不变,而斜率项将会成为原回归系数的舟*10同样地,记厂为惊变量y单位扩大w倍的变量.则r二于是Y'即r*=io^+io/?t x可见.披解释变量的单位扩大m倍时’截距项与斜率项都会比原回归系数扩大10倍。
李子奈(第三版)计量经济学课后实验作业答案

计量经济学作业第二章 一元线形回归方程模型习题11、下面数据是对X 和Y 的观察值得到的。
∑Y i =1110; ∑X i =1680; ∑X i Y i =204200 ∑X i 2=315400; ∑Y i 2=133300;n=10假定满足所有的古典线性回归模型的假设,要求:(1)b 1和b 2?(2)b 1和b 2的标准差?(3)r 2?(4)对B 1、B 2分别建立95%的置信区间?利用置信区间法,你可以接受零假设:B 2=0吗? (1)168==∑nXX i,111==∑nYY i177201111681011101681111680204200)())((=⨯⨯+⨯-⨯-=+--=--∴∑∑Y X X Y X Y Y X Y Y X X i i i i i i 331601681681031540010102)2()(222222=⨯⨯-=+⨯-=+-=-∑∑∑X X X X X X X X X i i i i 又12()()17720ˆ0.5344()33160i i i X X Y Y X X β--∴===-∑∑ 01ˆˆ1110.534416821.22Y X ββ=-=-⨯= (2)8)ˆˆ2(210)ˆ(2ˆ22222∑∑∑+-=--=-=i i i ii iiY Y Y YYY n eσii X Y 5344.022.21ˆ+= 81.62016805344.022.2123154005344.05344.022.2122.21102042005344.02111022.212133300)25344.0222.212()ˆˆ2(2122221222=⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯-⨯⨯-=+++⨯-⨯-=+-∴∑∑i i i i i i i i i i X X Y X Y Y Y Y Y Y ββββ60.77881.620ˆ2==∴σ22277.60315400ˆ()73.81()1033160iiX Var n X X σβ⨯∴===-⨯∑∑,0ˆ()8.5913se β 21277.60ˆ()0.002333160i Var x σβ===∑,1ˆ()0.0484se β= (3)2221()iieR Y Y =--∑∑,10090123210133300)(,81.62022=-=-=∑∑Y Y e i i 又2620.8110.938510090R ∴=-= (4)%95)306.2(=≤t p ,自由度为8;21.222.306 2.3068.5913β-∴-≤≤,解得:001.408541.0315ββ≤≤为的95%的置信区间。
《计量经济学》第三版课后题答案李子奈

封面作者:Pan Hongliang仅供个人学习第一章绪论参考重点:计量经济学的一般建模过程第一章课后题(1.4.5)1.什么是计量经济学?计量经济学方法与一般经济数学方法有什么区别?答:计量经济学是经济学的一个分支学科,是以揭示经济活动中客观存在的数量关系为内容的分支学科,是由经济学、统计学和数学三者结合而成的交叉学科。
计量经济学方法揭示经济活动中各个因素之间的定量关系,用随机性的数学方程加以描述;一般经济数学方法揭示经济活动中各个因素之间的理论关系,用确定性的数学方程加以描述。
4.建立与应用计量经济学模型的主要步骤有哪些?答:建立与应用计量经济学模型的主要步骤如下:(1)设定理论模型,包括选择模型所包含的变量,确定变量之间的数学关系和拟定模型中待估参数的数值范围;(2)收集样本数据,要考虑样本数据的完整性、准确性、可比性和—致性;(3)估计模型参数;(4)检验模型,包括经济意义检验、统计检验、计量经济学检验和模型预测检验。
5.模型的检验包括几个方面?其具体含义是什么?答:模型的检验主要包括:经济意义检验、统计检验、计量经济学检验、模型的预测检验。
在经济意义检验中,需要检验模型是否符合经济意义,检验求得的参数估计值的符号与大小是否与根据人们的经验和经济理论所拟订的期望值相符合;在统计检验中,需要检验模型参数估计值的可靠性,即检验模型的统计学性质;在计量经济学检验中,需要检验模型的计量经济学性质,包括随机扰动项的序列相关检验、异方差性检验、解释变量的多重共线性检验等;模型的预测检验主要检验模型参数估计量的稳定性以及对样本容量变化时的灵敏度,以确定所建立的模型是否可以用于样本观测值以外的范围。
第二章经典单方程计量经济学模型:一元线性回归模型参考重点:1.相关分析与回归分析的概念、联系以及区别?2.总体随机项与样本随机项的区别与联系?3.为什么需要进行拟合优度检验?4.如何缩小置信区间?(P46)由上式可以看出(1).增大样本容量。
《计量经济学》第三版课后题答案李子奈

第一章绪论【2 】参考重点:计量经济学的一般建模进程第一章课后题(1.4.5)1.什么是计量经济学?计量经济学办法与一般经济数学办法有什么差别?答:计量经济学是经济学的一个分支学科,是以揭示经济运动中客不雅消失的数量关系为内容的分支学科,是由经济学.统计学和数学三者结合而成的交叉学科.计量经济学办法揭示经济运动中各个身分之间的定量关系,用随机性的数学方程加以描写;一般经济数学办法揭示经济运动中各个身分之间的理论关系,用肯定性的数学方程加以描写.4.树立与运用计量经济学模子的重要步骤有哪些?答:树立与运用计量经济学模子的重要步骤如下:(1)设定理论模子,包括选择模子所包含的变量,肯定变量之间的数学关系和拟定模子中待估参数的数值规模;(2)收集样本数据,要斟酌样本数据的完全性.精确性.可比性和—致性;(3)估量模子参数;(4)磨练模子,包括经济意义磨练.统计磨练.计量经济学磨练和模子猜测磨练.5.模子的磨练包括几个方面?其具体寄义是什么?答:模子的磨练重要包括:经济意义磨练.统计磨练.计量经济学磨练.模子的猜测磨练.在经济意义磨练中,须要磨练模子是否相符经济意义,磨练求得的参数估量值的符号与大小是否与根据人们的经验和经济理论所订定的期望值相相符;在统计磨练中,须要磨练模子参数估量值的靠得住性,即磨练模子的统计学性质;在计量经济学磨练中,须要磨练模子的计量经济学性质,包括随机扰动项的序列相干磨练.异方差性磨练.解释变量的多重共线性磨练等;模子的猜测磨练重要磨练模子参数估量量的稳固性以及对样本容量变化时的敏锐度,以肯定所树立的模子是否可以用于样本不雅测值以外的规模.第二章经典单方程计量经济学模子:一元线性回归模子参考重点:1.相干剖析与回归剖析的概念.接洽以及差别?2.总体随机项与样本随机项的差别与接洽?3.为什么须要进行拟合优度磨练?4.若何缩小置信区间?(P46)由上式可以看出(1).增大样本容量.样本容量变大,可使样本参数估量量的标准差减小;同时,在同样置信程度下,n 越大,t 散布表中的临界值越小.(2)进步模子的拟合优度.因为样本参数估量量的标准差和残差平方和呈正比,模子的拟合优度越高,残差平方和应越小.5.以一元线性回归为例,写出β0的假设磨练1).对总体参数提出假设H 0:β0=0,H 1:β0≠02)以原假设H0构造t 统计量,3)由样本盘算其值 4)给定明显性程度α,查t 散布表得临界值t α/2(n-2)0ˆ0ˆββS t =)2(~ˆˆˆ0ˆ0022200--=-=∑∑n t S x n X t i i βββσββαβββββαα-=⨯+<<⨯-1)ˆˆ(ˆˆ22i i s t s t P i i i5)比较,断定若|t|> t α/2(n-2),则谢绝H0,接收H1;若|t|≤ t α/2(n-2),则谢绝H1,接收H0;上届重点:一元线性回归模子的根本假设.随机误差项产生的原因.最小二乘法.参数经济意义.决议系数.第二章PPT里的表(中国居平易近人均花费支出对人均GDP的回归).t磨练(△(平方)代表意义;△(平方)的熟习).可以或许读懂Eviews输出的估量成果第二章课后题(1.3.9.10)1.为什么计量经济学模子的理论方程中必须包含随机干扰项?(经典模子中产生随机误差的原因)答:计量经济学模子考核的是具有因果关系的随机变量间的具体接洽方法.因为是随机变量,意味着影响被解释变量的身分是庞杂的,除了解释变量的影响外,还有其他无法在模子中自力列出的各类身分的影响.如许,理论模子中就必须运用一个称为随机干扰项的变量宋代表所有这些无法在模子中自力表示出来的影响身分,以保证模子在理论上的科学性.3.一元线性回归模子的根本假设重要有哪些?违反根本假设的模子是否不可以估量?答:线性回归模子的根本假设有两大类:一类是关于随机干扰项的,包括零均值,同方差,不序列相干,知足正态散布等假设;另一类是关于解释变量的,重要有:解释变量长短随机的,若是随机变量,则与随机干扰项不相干.现实上,这些假设都是针对通俗最小二乘法的.在违反这些根本假设的情形下,通俗最小二乘估量量就不再是最佳线性无偏估量量,是以运用通俗最小二乘法进行估量己无多大意义.但模子本身照样可以估量的,尤其是可以经由过程最大似然法等其他道理进行估量.假设1. 解释变量X是肯定性变量,不是随机变量;假设2. 随机误差项μ具有零均值.同方差和不序列相干性:E(μi)=0i=1,2, …,nVar (μi)=σμ2 i=1,2, …,nCov(μi, μj )=0i≠j i,j= 1,2, …,n假设3. 随机误差项μ与解释变量X 之间不相干:Cov(X i , μi )=0 i=1,2, …,n假设4.μ屈服零均值.同方差.零协方差的正态散布μi ~N(0, σμ2 ) i=1,2, …,n假设5. 跟着样本容量的无穷增长,解释变量X 的样本方差趋于一有限常数.即∞→→-∑n Q n X X i ,/)(2假设6. 回归模子是精确设定的9.10题为盘算题,见教材P52,答案见P17第三章 经典单方程计量经济学模子:多元线性回归模子上届重点:F 磨练.t 磨练 调剂的样本决议系数.“多元”里为什么要对△(平方)系数进行调剂?第三章课后题(1.2.7.9.10)1.多元线性回归模子的根本假设是什么?在证实最小二乘估量量的无偏性和有用性的进程中,哪些根本假设起了感化?答:多元线性回归模子的根本假定仍然是针对随机干扰项与针对解释变量两大类的假设.针对随机干扰项的假设有:零均值,同方差,无序列相干且屈服正态散布.针对解释量的假设有;解释变量应具有非随机性,假如后随机的,则不能与随机干扰项相干;各解释变量之间不消失(完全)线性相干关系.在证实最小二乘估量量的无偏性中,运用了解释变量非随机或与随机干扰项不相干的假定;在有用性的证实中,运用了随机干扰项同方差且无序列相干的假定.2.在多元线性回归剖析中,t 磨练和F 磨练有何不同?在一元线性回归剖析中二者是否有等价感化?(见教材P70)答:在多元线性回归剖析中,t 磨练常被用作磨练回归方程中各个参数的明显性,而F 磨练则被用作磨练全部回归关系的明显性.各解释变量结合起来对被解释变量有明显的线性关系,并不意味着每一个解释变量分离对被解释变量有明显的线性关系.在一元线性回归剖析中,二者具有等价感化,因为二者都是对配合的假设——解释变量的参数等于零一一进行磨练.7.9.10题为盘算题,见教材P91,答案见P53第四章经典单方程计量经济学模子:放宽根本假定的模子重点控制:参考重点:1.以多元线性回归为例解释异方差性会产生如何的后果?(可能为阐述题)2.磨练.修改异方差性的办法?3.以多元线性回归为例解释序列相干会产生如何的后果?(猜测,矩阵表达式推到)4.磨练.修改序列相干的办法?5.什么是DW磨练法(前提前提)?6.以多元线性回归为例解释多重共线性会产生如何的后果7.磨练.修改多重共线性的办法?8.随机解释变量问题的三种分类?分离造成的后果是什么?9.对象变量法的前提假设1)与所替代的随机解释变量高度相干2)与随机干扰项不相干3)与模子中其他解释变量不相干,以避免消失多重共线性上届重点:异方差.序列相干.多重共线性等违反根本假设的情形产生原因.后果.辨认方法办法.D.W.广义差分法第四章课后题(1.2)1.2题为盘算题,见教材P134,答案见P84第五章经典单方程计量经济学模子:专门问题上届重点:虚拟变量的寄义与设定.滞后变量的寄义.为何参加滞后和虚拟变量第五章课后题(1.3.4.10)1.回归模子中引入虚拟变量的感化是什么?有哪几种根本的引入方法?它们各合实用于什么情形?答:在模子中引入虚拟变量,主如果为了查找某(些)定性身分对解释变量的影响.加法方法与乘法方法是最重要的引入方法.前者重要实用于定性身分对截距项产生影响的情形,后者重要实用于定性身分对斜率项产生影响的情形.除此外,还可以加法与乘法组合的方法引入虚拟变量,这时可测度定性身分对截距项与斜率项同时产生影响的情形.3.滞后变量模子有哪几种类型?散布滞后模子运用OLS办法消失哪些问题?答:滞后变量模子有散布滞后模子和自回归模子两大类,前者只有解释变量及其滞后变量作为模子的解释变量,不包含被解释变量的滞后变量作为模子的解释变量;尔后者则以当期解释变量与被解释变量的若干期滞后变量作为模子的解释变量.散布滞后模子有无穷期的散布滞后模子和有限日的散布滞后模子;自回归模子又以Coyck模子.自顺应预期模子和局部调剂模子最为多见.散布滞后模子运用OLS法消失以下问题:(1)对于无穷期的散布滞后模子,因为样本不雅测值的有限性,使得无法直接对其进行估量.(2)对于有限日的散布滞后模子,运用OLS办法会碰到:没有先验准则肯定滞后期长度,对最大滞后期的肯定往往带有主不雅随便性;假如滞后期较长,因为样本容量有限,当滞后变量数量增长时,必然使得自由度削减,将缺少足够的自由度进行估量和磨练;同名变量滞后值之间可能消失高度线性相干,即模子可能消失高度的多重共线性.4.产生模子设定偏误的重要原因是什么?模子设定偏误的后果以及磨练办法有哪些?答:产生模子设定偏误的原因重要有:模子制订者不熟习响应的理论常识;对经济问题本身熟习不够或不熟习前人的相干工作:模子制订者手头没有相干变量的数据;解释变量无法测量或数据本身消失测量误差.模子设定偏误的后果有:(1)假如漏掉了重要的解释变量,会造成OLS估量量在小样本下有偏,在大样本下非一致;对随机干扰项的方差估量也是有偏的.(2)假如包含了无关的解释变量,尽管OLS估量量具有无偏性与一致性,但不具有最小方差性.(3)假如选择了错误的函数情势,则后果是全方位的,不但会造成估量的参数具有完全不同的经济意义,并且估量成果也不同.对模子设定偏误的磨练办法有:磨练是否含有无关变量,可以运用t磨练与F磨练完成:磨练是否有相干变量的漏掉或函数情势设定偏误,可以运用残差图示法,Ramsey提出的RESET磨练来完成.10.简述约化建模理论与传统理论的异同点?答:Hendry的约化建模理论的焦点是“从一般到简略”的建模思惟,即起首提出一个包括各类身分在内的“一般”模子,然后再经由过程不雅测数据,运用各类磨练对模子进行磨练并化简,最后得到一个相对简略的模子.传统建模理论的主导思惟是“从简略到庞杂”的建模思惟,它起首提出一个简略的模子,然后从各类可能的备选变量中选择恰当的变量进入模子,最后得到一个与数据拟合较好的较为庞杂的模子.从二者的重要接洽上看,它们都以对经济现象的解释为目的,以已有的经济理论为建模根据,以对数据的拟合程度作为模子好坏的重要的剖断标准之一,也都有若干磨练标推.从二者的重要差别上看,传统的建模理论往往更依附于某种单一的经济理论,旧“从一般到简略”的建模理论则更重视将各类不同经济理论纳入到最初的“一般”模子中,甚至更多地是从直觉和经验来树立“一般”的模子;尽管两者都有若干种磨练标准,但约化建模理论从实践上有更大量的诊断性磨练来看每一步建模的可行性,或查找改良模子的路径:与传统建模实践中消失的过渡“数据开采”问题比拟,因为约化建模理论的初估模子是一个包括所有可能变量的“一般”模子,是以也就避免了过度的“数据开采”问题;别的,因为初始模子的“一般”性,所有研讨者在建模的初期往往有着雷同的“起点”,是以,在雷同的约化程序下,最后得到的最终模子也应当是雷同的.而传统建模实践中对统一经济问题往往有各类不同经济理论来解释,假如不同的研讨者采用不同的经济理论建模,得到的最终模子也会不同.当然,因为约化建模理论有更多的磨练,使得建模进程更庞杂,比拟之下,传统建模方轨则加倍“灵巧”.第六章联立方程计量经济学模子理论与办法上届重点:内生变量.外生变量.先定变量.构造式模子.简化式模子.参数关系体系.模子辨认第六章课后题(1.2.3.)1.为什么要树立联立方程计量经济学模子?联立方程计量经济学模子实用于什么样的经济现象?答:经济现象是极为庞杂的,个中诸身分之间的关系,在许多情形下,不是单一方程所能描写的那种简略的单向因果关系,而是互相依存,互为因果的,这时,就必须用联立的计量经济学方程才能描写清晰.所以与单方程实用于单一经济现象的研讨比拟,联立方程计量经济学模子实用于描写庞杂的经济现象,即经济体系.2.联立方程计量经济学模子的辨认状态可以分为几类?其寄义各是什么?答:联立方程计量经济学模子的辨认状态可以分为可辨认和不可辨认,可辨认又分为正好辨认和过度辨认.假如联立方程计量经济学模子中某个构造方程不具有肯定的统计情势,则称该方程为不可辨认,或者根据参数关系体系,在已知简化式参数估量值时,假如不能得到联立方程计量经济学模子中某个构造方程的肯定的构造参数估量值,称该方程为不可辨认.假如一个模子中的所有随机方程都是可以辨认的,则以为该联立方程计量经济学模子体系是可以辨认的.反过来,假如一个模子体系中消失一个不可辨认的随机方程,则以为该联立方程汁量经济学模子体系是不可以辨认的.假如某一个随机方程具有独一一组参数估量量,称其为正好辨认;假如某一个随机方程具有多组参数估量量,称其为过度辨认.3.联立方程计量经济学模子的单方程估量有哪些重要办法?其实用前提和统计性质各是什么?答:单方程估量的重要办法有:狭义的对象变量法(IV),间接最小二乘法(ILS),两阶段最小二乘法(2SLS).狭义的对象变量法(IV)和间接最小二乘法(ILS)只实用于正好辨认的构造方程的估量.两阶段最小二乘法(2SLs)既实用于正好辨认的构造方程,又实用于过度辨认的构造方程.用对象变量法估量的参数,一般情形下,在小样本下是有偏的,但在大样本下是渐近无偏的.假如拔取的对象变量与方程随机干扰项完全不相干,那么其参数估量量是无偏估量量.对于间接最小二乘法,对简化式模子运用通俗最小二乘法得到的参数估量量具有线性性.无偏性.有用性.经由过程多半关系体系盘算得到构造方程的构造参数估量量在小样本下是有偏的,在大样本下是渐近无偏的.采用二阶段最小二乘法得到构造方程的构造参数估量量在小样本下是有偏的,在大样本下是渐近无偏的.补充材料盘算题(一)给出多元线性回归的成果1.断定模子估量的成果若何,拟合后果若何?2.解释每一个参数所代表的经济意义?3.断定有没有违反四个根本假设?盘算题(二)给出数值,盘算:1.t磨练,F磨练的自由度2.在给定明显性程度下参数是否明显?3.估量值是有偏.无偏.有用?盘算题(三)参加虚拟变量D1,D2,D3问:虚拟变量的经济寄义?。
李子奈 潘文卿 计量经济学第三版课后练习答案

第2章练习12下表是中国2007年各地区税收Y和国内生产总值GDP的统计资料。
1.做出散点图,建立税收随国内生产总值GDP变化的一元线性回归方程,并解释斜率的经济意义。
2.对所建立的回归方程进行检验。
3.若2008年某地区国内生产总值为8500,求该地区税收收入的预测值及预测区间。
(置信度为90%)(1)散点图如图所示:我们假设拟建立如下一元回归模型:μGDP ββY ++=10根据Eviews 软件对表中数据进行回归分析的计算结果可得:GDP ..Y i07106310ˆ+-=7603.02=R 99.91=F斜率的经济意义:国内生产总值GDP 每增加1亿元,国内税收增加亿元。
(2)从回归估计的结果看,模型拟合较好。
可决系数7603.02=R ,表明国内税收变化的%可由国内生产总值GDP 的变化来解释。
从斜率项的t 检验值看,大于10%显著性水平下自由度为292=-n 的临界值699.1)29(05.0=t ,且该斜率值满足1071.00<<,符合经济理论中税收乘数在0与1之间的说法,表明2007年,国内生产总值GDP 每增加1亿元,国内税收增加亿元。
(3)有上述回归方程可得中国国内税收的预测值:87.5928500071.063.10ˆ0=⨯+-=Y (元) 下面给出国内生产总值90%置信度的预测区间126.8891=E )(GDP在90%的置信度下,某地区)E(0Y 的预测区间为:),())()((5.11253.606.53287.5922-3164.578231272-318891.126-850031112760310699.187.5922=±=⨯++⨯⨯±。
计量经济学---第三版-李子奈---课后习题--答案

ÿÿÿÿÿ************************************************************************* *****************************************************************************ÿÿÿÿÿÿÿÿÿÿÿÿ第一章绪论(一)基本知识类题型1-1.什么是计量经济学1-3.计量经济学方法与一般经济数学方法有什么区别它在经济学科体系中的作用和地位是什么1-6.计量经济学的研究的对象和内容是什么计量经济学模型研究的经济关系有哪两个基本特征1-7.试结合一个具体经济问题说明建立与应用计量经济学模型的主要步骤。
1-9.计量经济学模型主要有哪些应用领域各自的原理是什么1-12.模型的检验包括几个方面其具体含义是什么1-17.下列假想模型是否属于揭示因果关系的计量经济学模型为什么⑴ S t其中S t为第t年农村居民储蓄增加额(亿元)、R t为第t年城镇居民可支配收入总额(亿元)。
⑵ S t1其中S t1为第(t1)年底农村居民储蓄余额(亿元)、R t为第t年农村居民纯收入总额(亿元)。
1-18.指出下列假想模型中的错误,并说明理由:(1)RS t RI t其中,RS t为第t年社会消费品零售总额(亿元),RI t为第t 年居民收入总额(亿元)(城镇居民可支配收入总额与农村居民纯收入总额之和),IV t为第t年全社会固定资产投资总额1(亿元)。
(2)C t 180其中,C、Y分别是城镇居民消费支出和可支配收入。
(3) ln Y t ln K t L t其中,Y、K、L分别是工业总产值、工业生产资金和职工人数。
1-19.下列假想的计量经济模型是否合理,为什么(1) GDP i GDP i其中, GDP i (i 1,2,3) 是第i产业的国内生产总值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章练习12
下表是中国2007年各地区税收Y和国内生产总值GDP的统计资料。
1.做出散点图,建立税收随国内生产总值GDP变化的一元线性回归方程,并解释斜率的经济意义。
2.对所建立的回归方程进行检验。
3.若2008年某地区国内生产总值为8500,求该地区税收收入的预测值及预测区间。
(置信度为90%)
(1)散点图如图所示:
我们假设拟建立如下一元回归模型:
μGDP ββY ++=10
根据Eviews 软件对表中数据进行回归分析的计算结果可得:
GDP ..Y i
07106310ˆ+-= (-0.12) (9.59)
7603.02=R 99.91=F
斜率的经济意义:国内生产总值GDP 每增加1亿元,国内税收增加0.071亿元。
(2)从回归估计的结果看,模型拟合较好。
可决系数7603.02
=R ,表明国内税收变化的76.03%可由国内生产总值GDP 的变化来解释。
从斜率项的t 检验值看,大于10%显著性水平下自由度为292=-n 的临界值699.1)29(05.0=t ,且该斜率值满足1071.00<<,符合经济理论中税收乘数在0与1之间的说法,表明2007年,国内生产总值GDP 每增加1亿元,国内税收增加0.071亿元。
(3)有上述回归方程可得中国国内税收的预测值:
87.5928500071.063.10ˆ0
=⨯+-=Y (元) 下面给出国内生产总值90%置信度的预测区间
126.8891=E )(GDP
64.57823127)Var(=GDP
在
90%的置信度下,某地区
)
E(0Y 的预测区间为:
)
,()
)()
((5.11253.606.53287.5922
-3164.578231272-318891.126-850031112760310699.187.5922
=±=⨯++⨯⨯
±。
