对数函数及其性质(一)[
对数函数及其性质(一)

2.2.2 对数函数及其性质(一)一、教学目的和要求【知识与技能目标】通过具体实例,直观了解对数函数模型刻画的数量关系,初步理解对数函数的概念,并能画出具体对数函数的图像,掌握对数函数的图象和性质。
【过程与方法】通过从具体到一般的过程,数形结合的方法,体会研究具体函数及其性质的过程和方法。
【情感、态度与价值观】培养学生数形结合的思想,学会研究函数性质的方法,能应用对数函数的性质解有关问题。
二、重点难点教学重点:对数函数的概念,图像和性质教学难点:利用数形结合的方法从具体到一般地探究,理解对数函数的图象及其性质。
三、教学过程(一)复习引入2.2.1例6 生物机体内碳14的“半衰期”为5730年,湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%,试推算马王堆古墓的年代。
死亡年数t 就是要得到的碳14的含量P 的函数。
这个函数写成对数的形式是 。
(二)讲授新课 1. 对数函数的定义:函数y =log ax (a >0且a ≠1)叫做对数函数,定义域为(0,+∞),值域为(-∞,+∞)。
提问:①.在函数的定义中,为什么要限定a >0且a ≠1。
②.为什么对数函数log a y x =(a >0且a ≠1)的定义域是(0,+∞).组织学生充分讨论、交流,使学生更加理解对数函数的含义,从而加深对对数函数的理解。
判断下列函数是不是对数函数:例1 求下列函数的定义域:2. 对数函数的图象: P t 573021log =x y 2log )1(2=x y 2log )2(-=1log )3(2+=x y 2log )1(x y a =)4(log )2(x y a -=)9(log )3(2x y a -=通过列表、描点、连线作x y 2log =与x y 21log =的图像。
思考:两图像有什么关系?因为x x y x 2log log log log 212221-===,所以两图像关于x 轴对称。
课题对数函数及其性质

课题:对数函数及其性质(1)
大同中学王培
一、教案设计的指导思想:
本教案依据洋思中学教学模式,以及根据本校的实际情况进行设计,废弃陈旧的“一堂课”、“满堂灌”的教学方式。
使学生始终把握教学方向,领悟教学全过程,并以互动的方式完成教学任务,力求突出学生的主体地位,体现教师的主导作用,使学生在知识的发生、发展过程中,自然获得思维、能力、心理,思想品德诸方面的提高。
同时,借助多媒体的教育技术手段,为学生营造一个平等、竞争、自主、创新的学习氛围.
二、三维目标
(一)知识与技能
使学生理解对数函数的定义并了解其图象的特征及对应函数性质;
(二)过程与方法
培养学生动手操作的能力以及自主探究数学问题的素养;
(三)情感态度与价值观
构造和谐的教学氛围,增加互动,促进师生情感交流。
三、【教学重点】掌握对数函数的图象和性质;
【教学难点】底数对对数函数值变化的影响.
【教学方法】启发、引导、讨论.
四、课前准备:布置学生课前预习和发放预习稿.
五、教学过程设计及意图
引导学生通过观察图形得出结论:当两个对数函数的底为
轴对称。
并提出问题:能否
x的图象关于x轴对称
然后利用几何画板在同一坐标系中画出当①a=3、4、5、
……的对数函数的图象。
让学生在感
由教师引导学生,学生互相讨论,。
高中数学:2.2.2对数函数及其性质 (1)

2.2.2对数函数及其性质第二课时对数函数及其性质的应用(习题课)比较对数值的大小[例1]比较下列各组数中两个值的大小:(1)log23.4,log28.5;(2)log0.31.8,log0.32.7;(3)log a5.1,log a5.9(a>0,且a≠1).[解](1)考察对数函数y=log2x,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是log23.4<log28.5.(2)考察对数函数y=log0.3x,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是log0.31.8>log0.32.7.(3)当a>1时,y=log a x在(0,+∞)上是增函数,于是log a5.1<log a5.9;当0<a<1时,y=log a x在(0,+∞)上是减函数,于是log a5.1>log a5.9.比较对数值大小时常用的4种方法(1)同底的利用对数函数的单调性.1.比较下列各题中两个值的大小: (1)lg 6,lg 8; (2)log 0.56,log 0.54; (3)log 132与log 152;(4)log 23与log 54.解:(1)因为函数y =lg x 在(0,+∞)上是增函数,且6<8,所以lg 6<lg 8. (2)因为函数y =log 0.5x 在(0,+∞)上是减函数,且6>4,所以log 0.56<log 0.54. (3)由于log 132=1log 213,log 152=1log 215. 又∵对数函数y =log 2x 在(0,+∞)上是增函数,且13>15,∴0>log 2 13>log 2 15,∴1log 213<1log 215.∴log 132<log 152. (4)取中间值1,∵log 23>log 22=1=log 55>log 54,∴log 23>log 54.[例2] (1)已知log a 12>1,求a 的取值范围;(2)已知log 0.7(2x )<log 0.7(x -1),求x 的取值范围. [解] (1)由log a 12>1得log a 12>log a a .求解对数不等式①当a >1时,有a <12,此时无解.②当0<a <1时,有12<a ,从而12<a <1.∴a 的取值范围是⎝⎛⎭⎫12,1.(2)∵函数y =log 0.7x 在(0,+∞)上为减函数, ∴由log 0.72x <log 0.7(x -1) 得⎩⎪⎨⎪⎧2x >0,x -1>0,2x >x -1,解得x >1.∴x 的取值范围是(1,+∞).常见对数不等式的2种解法(1)形如log a x >log a b 的不等式,借助y =log a x 的单调性求解,如果a 的取值不确定,需分a >1与0<a <1两种情况讨论.(2)形如log a x >b 的不等式,应将b 化为以a 为底数的对数式的形式,再借助y =log a x 的单调性求解.2.已知log a (3a -1)恒为正,求a 的取值范围. 解:由题意知log a (3a -1)>0=log a 1. 当a >1时,y =log a x 是增函数,∴⎩⎪⎨⎪⎧ 3a -1>1,3a -1>0,解得a >23,∴a >1;当0<a <1时,y =log a x 是减函数,∴⎩⎪⎨⎪⎧3a -1<1,3a -1>0,解得13<a <23.∴13<a <23. 综上所述,a 的取值范围是⎝⎛⎭⎫13,23∪(1,+∞).有关对数型函数的值域与最值问题[例3] 求下列函数的值域.(1)y =log 2(x 2+4);(2)y =log 12(3+2x -x 2).[解] (1)y =log 2(x 2+4)的定义域是R. 因为x 2+4≥4,所以log 2(x 2+4)≥log 24=2, 所以y =log 2(x 2+4)的值域为[2,+∞). (2)设u =3+2x -x 2=-(x -1)2+4≤4. 因为u >0,所以0<u ≤4.又y =log 12u 在(0,+∞)上为减函数,所以log 12u ≥log 124=-2,所以y =log 12(3+2x -x 2)的值域为[-2,+∞).(1)求对数型函数的值域,一般需根据对数函数的单调性及真数的取值范围求解. (2)求函数的值域时,一定要注意定义域对它的影响,结合函数的单调性求解,当函数中含有参数时,有时需讨论参数的取值.3.已知f (x )=2+log 3x ,x ∈[1,9],求函数y =[f (x )]2+f (x 2)的最大值及此时x 的值. 解:y =[f (x )]2+f (x 2)=(2+log 3x )2+log 3x 2+2=(log 3x )2+6log 3x +6=(log 3x +3)2-3. ∵f (x )的定义域为[1,9], ∴y =[f (x )]2+f (x 2)中,x必须满足⎩⎪⎨⎪⎧1≤x ≤9,1≤x 2≤9,∴1≤x ≤3,∴0≤log 3x ≤1,∴6≤y ≤13. ∴当x =3时,y 取得最大值,为13.[例4] 已知函数f (x )=log a (1+x ),g (x )=log a (1-x ),其中(a >0且a ≠1),设h (x )=f (x )-g (x ).求函数h (x )的定义域,判断h (x )的奇偶性,并说明理由. [解] ∵f (x )=log a (1+x )的定义域为{x |x >-1}, g (x )=log a (1-x )的定义域为{x |x <1},∴h (x )=f (x )-g (x )的定义域为{x |x >-1}∩{x |x <1}={x |-1<x <1}. ∵h (x )=f (x )-g (x )=log a (1+x )-log a (1-x ),∴h (-x )=log a (1-x )-log a (1+x )=-[log a (1+x )-log a (1-x )]=-h (x ), ∴h (x )为奇函数. [一题多变]1.[变条件]若f (x )变为log a 1+x1-x (a >1):求f (x )的定义域.解:因为f (x )=log a 1+x1-x,需有1+x1-x >0,即⎩⎪⎨⎪⎧ 1+x >0,1-x >0,或⎩⎪⎨⎪⎧1+x <0,1-x <0,所以-1<x <1.所以函数f (x )的定义域为(-1,1).2.[变设问]在本例条件下,若f (3)=2,求使h (x )<0成立的x 的集合. 解:∵f (3)=log a (1+3)=log a 4=2,∴a =2. ∴h (x )=log 2(1+x )-log 2(1-x ), ∴h (x )<0等价于log 2(1+x )<log 2(1-x ),对数函数性质的综合应用∴⎩⎪⎨⎪⎧1+x <1-x ,1+x >0,1-x >0,解得-1<x <0.故使h (x )<0成立的x 的集合为{x |-1<x <0}.层级一 学业水平达标1.若lg(2x -4)≤1,则x 的取值范围是( ) A .(-∞,7] B .(2,7] C .[7,+∞)D .(2,+∞)解析:选B ∵lg(2x -4)≤1,∴0<2x -4≤10,解得2<x ≤7,∴x 的取值范围是(2,7],故选B.2.已知log 12m <log 12n <0,则( )A .n <m <1B .m <n <1C .1<m <nD .1<n <m解析:选D 因为0<12<1,log 12m <log 12n <0,所以m >n >1,故选D.3.函数f (x )=|log 12x |的单调递增区间是( )A.⎝⎛⎦⎤0,12 B .(0,1] C .(0,+∞)D .[1,+∞)解析:选D f (x )的图象如图所示,由图象可知单调递增区间为[1,+∞).4.已知实数a =log 45,b =⎝⎛⎭⎫120,c =log 30.4,则a ,b ,c 的大小关系为( ) A .b <c <a B .b <a <c C .c <a <bD .c <b <a解析:选D 由题知,a =log 45>1,b =⎝⎛⎭⎫120=1,c =log 30.4<0,故c <b <a . 5.函数f (x )=lg ⎝ ⎛⎭⎪⎫1x 2+1+x 是( ) A .奇函数 B .偶函数 C .既奇又偶函数D .非奇非偶函数解析:选A f (x )定义域为R ,f (-x )+f (x )=lg ⎝ ⎛⎭⎪⎫1x 2+1-x +lg ⎝ ⎛⎭⎪⎫1x 2+1+x =lg1(x 2+1)-x 2=lg 1=0,∴f (x )为奇函数,故选A. 6.比较大小: (1)log 22______log 23; (2)log 3π______log π3.解析:(1)因为函数y =log 2x 在(0,+∞)上是增函数,且2>3,所以log 22>log 2 3. (2)因为函数y =log 3x 增函数,且π>3,所以log 3π>log 33=1. 同理1=log ππ>log π3,所以log 3π>log π3. -=-=答案=-=-:(1)> (2)>7.不等式log 13(5+x )<log 13(1-x )的解集为________.解析:由⎩⎪⎨⎪⎧5+x >0,1-x >0,5+x >1-x ,得-2<x <1.-=-=答案=-=-:{x |-2<x <1}8.设a >1,函数f (x )=log a x 在区间[a,2a ]上的最大值与最小值之差为12,则a =________.解析:∵a >1,∴f (x )=log a x 在[a,2a ]上递增, ∴log a (2a )-log a a =12,即log a 2=12,∴a 12=2,a =4. -=-=答案=-=-:49.已知对数函数f (x )的图象过点(4,2),试解不等式f (2x -3)>f (x ). 解:设f (x )=log a x (a >0且a ≠1), 因为f (4)=2,所以log a 4=2,所以a =2,所以f (x )=log 2x ,所以f (2x -3)>f (x )⇒log 2(2x -3)>log 2x ⇒⎩⎪⎨⎪⎧2x -3>0,x >0,2x -3>x ⇒x >3,所以原不等式的解集为(3,+∞).10.求函数y =log 12(1-x 2)的单调增区间,并求函数的最小值.解:要使y =log 12(1-x 2)有意义,则1-x 2>0,∴x 2<1,则-1<x <1,因此函数的定义域为(-1,1). 令t =1-x 2,x ∈(-1,1).当x ∈(-1,0]时,x 增大,t 增大,y =log 12t 减小,∴x ∈(-1,0]时,y =log 12(1-x 2)是减函数;同理当x ∈[0,1)时,y =log 12(1-x 2)是增函数.故函数y =log 12(1-x 2)的单调增区间为[0,1),且函数的最小值y min =log 12(1-02)=0.层级二 应试能力达标1.若a >0,且log 0.25(a 2+1)>log 0.25(a 3+1),则实数a 的取值范围是( )A .(0,1)∪(1,+∞)B .(0,1)C .(1,+∞)D .[1,+∞)解析:选C ∵log 0.25(a 2+1)>log 0.25(a 3+1),∴a 2<a 3,即a 2(1-a )<0,∴a >1,故选C.2.设a =log 54,b =log 53,c =log 45,则( ) A .a <c <b B .b <c <a C .a <b <cD .b <a <c解析:选D 由于b =log 53<a =log 54<1<log 45=c ,故b <a <c . 3.关于函数f (x )=log 12(1-2x )的单调性的叙述正确的是( )A .f (x )在⎝⎛⎭⎫12,+∞内是增函数 B .f (x )在⎝⎛⎭⎫12,+∞内是减函数 C .f (x )在⎝⎛⎭⎫-∞,12内是增函数 D ..f (x )在⎝⎛⎭⎫-∞,12内是减函数 解析:选C 由于底数12∈(0,1),所以函数f (x )=log 12(1-2x )的单调性与y =1-2x 的单调性相反.由1-2x >0,得x <12,所以f (x )=log 12(1-2x )的定义域为(-∞,12).因为y =1-2x 在(-∞,+∞)内是减函数,所以f (x )在⎝⎛⎭⎫-∞,12内是增函数,故选C. 4.(2017·全国卷Ⅱ)函数f (x )=ln(x 2-2x -8)的单调递增区间是( ) A .(-∞,-2) B .(-∞,1) C .(1,+∞)D .(4,+∞)解析:选D 由x 2-2x -8>0,得x >4或x <-2.因此,函数f (x )=ln(x 2-2x -8)的定义域是(-∞,-2)∪(4,+∞).注意到函数y =x 2-2x -8在(4,+∞)上单调递增,由复合函数的单调性知,f (x )=ln(x 2-2x -8)的单调递增区间是(4,+∞).5.若y =log (2a -3)x 在(0,+∞)上是增函数,则实数a 的取值范围为________. 解析:由y =log (2a -3)x 在(0,+∞)上是增函数,所以2a -3>1,解得a >2. -=-=答案=-=-:(2,+∞)6.已知f (x )是定义在R 上的偶函数,且在[0,+∞)上为增函数,f ⎝⎛⎭⎫13=0,则不等式f (log 18x )>0的解集为________________.解析:∵f (x )是R 上的偶函数,∴它的图象关于y 轴对称.∵f (x )在[0,+∞)上为增函数,∴f (x )在(-∞,0]上为减函数,做出函数图象如图所示.由f ⎝⎛⎭⎫13=0,得f ⎝⎛⎭⎫-13=0. ∴f (log 18x )>0⇒log 18x <-13或log 18x >13⇒x >2或0<x <12, ∴x ∈⎝⎛⎭⎫0,12∪(2,+∞). -=-=答案=-=-:⎝⎛⎭⎫0,12∪(2,+∞) 7.求函数f (x )=log 2(4x )·log 14x 2,x ∈⎣⎡⎦⎤12,4的值域. 解:f (x )=log 2(4x )·log 14x 2 =(log 2x +2)·⎣⎡⎦⎤-12(log 2x -1) =-12[](log 2x )2+log 2x -2. 设log 2x =t .∵x ∈⎣⎡⎦⎤12,4,∴t ∈[-1,2],则有y =-12(t 2+t -2),t ∈[-1,2], 因此二次函数图象的对称轴为t =-12, ∴它在⎣⎡⎦⎤-1,-12上是增函数,在⎣⎡⎦⎤-12,2上是减函数, ∴当t =-12时,有最大值,且y max =98. 当t =2时,有最小值,且y min =-2.∴f (x )的值域为⎣⎡⎦⎤-2,98.8.已知函数f (x )=log a (1-x )+log a (x +3),其中0<a <1.(1)求函数f (x )的定义域;(2)若函数f (x )的最小值为-4,求a 的值.解:(1)要使函数有意义,则有⎩⎪⎨⎪⎧1-x >0,x +3>0, 解得-3<x <1,所以函数的定义域为(-3,1).(2)函数可化为:f (x )=log a (1-x )(x +3)=log a (-x 2-2x +3)=log a [-(x +1)2+4], 因为-3<x <1,所以0<-(x +1)2+4≤4. 因为0<a <1,所以log a [-(x +1)2+4]≥log a 4,即f (x )min =log a 4,由log a 4=-4,得a -4=4,所以a =4-14=22.。
对数函数及其性质

当 0 < a < 1 时, y loga x 是减函 数. (4)当 a >1 时
x >1,则 loga x >0
(4)当 a >1 时,函数图象在(1, 0< x <1, loga x <0 0)点右边的纵坐标都大于 0,在(1, 0)点左边的纵坐标都小于 0. 当 0 当 0< a <1 时 < a <1 时,图象正好相反,在(1, x >1,则 loga x <0 0)点右边的纵坐标都小于 0,在(1, 0)点左边的纵坐标都大于 0 . 0< x <1, loga x <0
对数函数及其性质(一)
1. 画出 y 2x 、 y ( ) x 的图像,并以这两个函数为例,说说指数函数的性质. 讲授新课: 1.对数函数的图象和性质: ① 定义:一般地,当 a>0 且 a≠1 时,函数 y=loga x 叫做对数函数(logarithmic function). 自变量是 x; 函数的定义域是(0,+∞) ② 辨析: 对数函数定义与指数函数类似,都是形式定义,注意辨别,如: y 2log 2 x , y log5 (5 x) 都 不是对数函数,而只能称其为对数型函数;对数函数对底数的限制 (a 0 ,且 a 1) .
5.1
0.9
)
二、填空题 3 -3 3 -3 4 -4 -1 13.化简:(a +a )(a -a )÷[(a +a +1)(a-a )]=_____. 2 x x 14.f(x)=x -bx+c 满足 f(1+x)=f(1-x)且 f(0)=3,则 f(b )与 f(c )的大小关系是_. 1 |x+1|+|x-2| 15.y=( ) 的递增区间是____递减区间是___. 3 16.(2005.北京)对于函数 f(x)定义域中任意的 x1≠x2,有如下结论: ①f(x1+x2)=f(x1)·f(x2) ②f(x1·x2)=f(x1)+f(x2) f(x1)-f(x2) x1+x2 (x1)+f(x2) ③ >0 ④f( )< x1-x2 2 2 当 f(x)=lgx 时,上述结论中正确的序号是______. 三、解答题 a -1 17.已知函数 f(x)= x (a>0 且 a≠1) a +1 ①求 f(x)的定义域和值域.②讨论 f(x)的单调性.
对数函数及其图象与性质(一)1课件人教新课标

1、类比思想 2、数形结合的思想 3、分类讨论思想
作业设置: 学案中【课后作业】
分别以y log2 x 和 y log 1 x 为例,用描点法画图.
y2
x y log2 x
1 -1
2
10 21
42 6 2.6 83
1
3
y log 2 x
2
0
1
-1
0 1 2 3 45678x
-2
-1
-2.6 -2
-3
-3
y log 1 x
2
知识探究:对数函数y=logax(a>0且a≠1)的图象和性质
3. 指数函数的图象和性质
y=ax
图 象
定义域
a>1
y y=ax
(0,1)
y=1
O
x
R
0<a<1
y=ax y (0,1) y=1 Ox
值域
定点 单调性 函数值 的符号
(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数
x>0时,y>1; x<0时,0<y<1
在R上是减函数
x>0时,0<y<1; x<0时,y>1
所以,t 是关于P的函数。
知识探究:
1、对数函数定义:形如 y loga x(a 0, 且a 1) 的函数叫
做对数函数,其中 x 是自变量;
定义域是(0, +∞). 对数函数的情势:
练习:1、判断下列函数是否是对数函数(1)系数为1
(1)y
lo2)底数是大于0且不等于
课堂导学:求对数函数定义域问题
应用一:求下列函数的定义域
课堂导学:求对数函数定义域问题
应用一:求下列函数的定义域
对数函数及其性质(1)

2.2.2 对数函数及其性质(1)学习目标1.理解对数函数的概念,知道对数函数是一类重要的函数模型;2.理解对数函数的单调性,掌握对数函数图像通过的特殊点;重点难点重点:对数函数的定义、图象及其性质;难点:由对数函数图象总结归纳出对数函数性质。
自主学案预习学案1. 定义:一般地,我们把函数log (0a y x a =>,且1)a ≠叫做对数函数,其中 是自变量,函数的定义域是2. 对数函数图象与性质a>10<a<1图 象 y0 xy0 x性 质①定义域: ②值域: ③过定点: ④增区间:④减区间:预习思考1. 函数log (0a y x a =>,且1)a ≠的图象过定点2.函数2()log 2f x x =-的定义域3.函数5()2+log f x x =(1x ≥)值域是合作探究探究点一:对数函数的概念 一、概念一般地,我们把函数log (0a y x a =>,且1)a ≠叫做对数函数,其中x 是自变量,函数的定义域是()0+∞,. 二、概念理解1、在函数的定义中,为什么要限定0,a >且1a ≠?2、为什么对数函数log (0a y x a =>且1)a ≠的定义域是()0+∞,?3、下列函数是不是对数函数?①2-log y x =,②212log y x =,③3log (1)y x =+,④31log y x=,⑤log 5x y = 三、典例剖析例1. 求下列函数的定义域(1)22log (45)y x x =-- (2) log (22)y x =-(5-x)类题突破2 (1) 23log (31)2x y x x +=++-2 (2)0.5log (43)y x =-探究点二:对数函3数的图象和性质 一、对数函数2log y x =与12log y x =的图象请用描点法分别作出两个函数图象! “列表——描点——连线”x121 2 4 8 162log y x =12log y x =y y2log y x = 12log y x =0 1 x 0 1 x思考:函数2log y x =与12log y x =的图象有什么关系?y 1.注意结合x 、y 对应值表以及2log y x = 函数图象观察分析!关系:2.如何证明这种关系?1 x12log y x =二、探究对数函数的性质在同一直角坐标系下分别作出函数13log y x =,12log y x =,2log y x =,3log y x =的图象,观察图象,你能发现它们有哪些共同特征?y0 1 x三、对数函数log (0a y x a =>,且1)a ≠的图象及性质a>1 0<a<1图 象性 质①定义域: ②值域:③过定点 ,即当x= 时,y= ④在(0,+∞)上是 函数④在(0,+∞)上是 函数四、典例剖析例3、比较大小:①2log 3与2log 4;②12log 5与12log 3;③log 2a 与log 5a .例4、已知下述4个函数图象是底数分别为 A 、B 、C 、D 的对数函数图象,试比较 A 、B 、C 、D 的大小.例5、若函数log (34)a y x =+(0<a<1)的函数值恒大于0,求x 的取值范围?类题突破6 求使函数log (34)a y x =+的值恒为负值的x 的取值范围?概括整合1、对数函数的概念,底数、真数的取值范围;2、对数函数的图象及其性质的应用;3、用数形结合的方法解决问题.4、。
2.2.2对数函数及其性质(1) (2)

例6.函数y 2 loga x 1, x [2,4](a 0, 且a 1) 最大值比最小值大 1, 求a的取值.
1 练习、(1)若loga <1,求实数aห้องสมุดไป่ตู้取值范围; 2
(2)若loga2<logb2<0,则(
A、0<a<b<1 C、0<b<a<1 B、a>b>1 D、b>a>1
(1) log2 3 , log2 3.5 (3) log3 2 , log3.5 2 (2) log0.7 1.6 , log0.7 1.8 (4) log1.6 0.7 , log1.8 0.7
解: (3) 0 log2 3
log2 3.5 ,
1 1 即 0 , log3 2 log3.5 2 log3 2 log3.5 2 .
x=log2y
如果用x表示自变量,y表示函 数,这个函数就是 y=log2x.
1.对数函数的定义: 一般地,我们把函数 y=logax (a>0且 a≠1)叫做对数函数,其中x是自变量,函数的
定义域是 (0,+∞).
对数函数模型(一)
火箭的最大速度v和燃料质 量M、火箭质量m的函数关 系是:
M v 2000 ln(1 ) m
a
)
D.y=4lg x
答案: C
1.已知下列函数: ①y=log1(-x)(x<0);
2
②y=2log4(x-1)(x>1); ③y=ln x(x>0); ④y=log(a2+a)x(x>0,a 是常数). ③ .(只填序号) 其中,是对数函数的是________
函数y=logax(a>0,且a≠1)叫做对数函数,
对数函数及性质 (1)
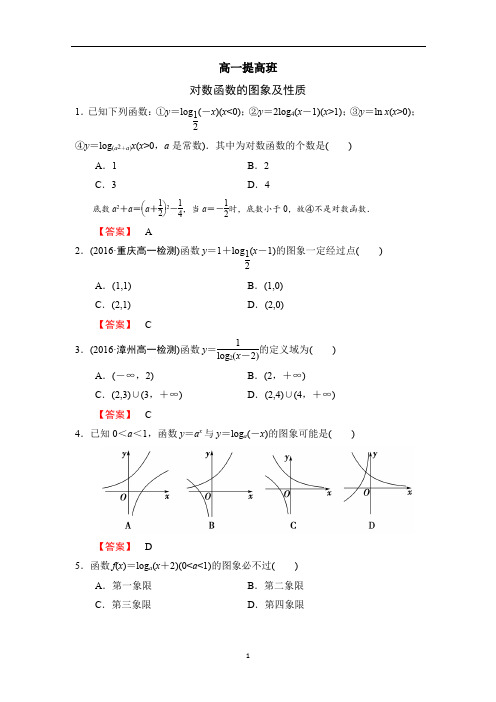
高一提高班 对数函数的图象及性质1.已知下列函数:①y =log 12(-x )(x <0);②y =2log 4(x -1)(x >1);③y =ln x (x >0);④y =log (a 2+a )x (x >0,a 是常数).其中为对数函数的个数是( )A .1B .2C .3D .4底数a 2+a =⎝⎛⎭⎫a +122-14,当a =-12时,底数小于0,故④不是对数函数. 【答案】 A2.(2016·重庆高一检测)函数y =1+log 12(x -1)的图象一定经过点( )A .(1,1)B .(1,0)C .(2,1)D .(2,0)【答案】 C3.(2016·漳州高一检测)函数y =1log 2(x -2)的定义域为( )A .(-∞,2)B .(2,+∞)C .(2,3)∪(3,+∞)D .(2,4)∪(4,+∞) 【答案】 C4.已知0<a <1,函数y =a x 与y =log a (-x )的图象可能是( )【答案】 D5.函数f (x )=log a (x +2)(0<a <1)的图象必不过( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】 A 6.函数f (x )=log 12(3x -2)的定义域是________. 【答案】 ⎝ ⎛⎦⎥⎤23,17.函数y =log 2(x 2-6x +8)的增区间为________.8.已知函数y =log 22-x2+x,下列说法:①关于原点对称;②关于y 轴对称;③过原点.其中正确的是________. 【答案】 ①③9.若函数f (x )为定义在R 上的奇函数,且x ∈(0,+∞)时,f (x )=lg(x +1),求f (x )的表达式,并画出大致图象.【解】 ∵f (x )为R 上的奇函数,∴f (0)=0. 又当x ∈(-∞,0)时,-x ∈(0,+∞),∴f (-x )=lg(1-x ).又f (-x )=-f (x ),∴f (x )=-lg(1-x ),∴f (x )的解析式为f (x )=⎩⎨⎧lg (x +1),x >00,x =0-lg (1-x ),x <0,∴f (x )的大致图象如图所示:[能力提升]1.满足“对定义域内任意实数x ,y ,f (x ·y )=f (x )+f (y )”的函数可以是( )A .f (x )=x 2B .f (x )=2xC .f (x )=log 2xD .f (x )=e ln x【答案】 C2.(2016·台州高一检测)已知函数f (x )=(x -a )(x -b )(其中a >b ),若f (x )的图象如图222所示,则函数g (x )=a x +b 的图象大致为( )图222【答案】 A3.(2016·长春模拟)已知函数y =f (x )(x ∈R )满足f (x +2)=f (x ),且当x ∈[-1,1]时,f (x )=x 2,则y =f (x )与y =log 7x 的图象的交点的个数为( )A .3B .4C .5D .6【答案】 D4.(1)已知函数y =lg(x 2+2x +a )的定义域为R ,求实数a 的取值范围;(2)已知函数f (x )=lg [(a 2-1)x 2+(2a +1)x +1],若f (x )的定义域为R ,求实数a 的取值范围.【解】 (1)因为y =lg(x 2+2x +a )的定义域为R ,所以x 2+2x +a >0恒成立,所以Δ=4-4a <0,所以a >1.故a 的取值范围是(1,+∞).(2)依题意(a 2-1)x 2+(2a +1)x +1>0对一切x ∈R 恒成立. 当a 2-1≠0时,⎩⎨⎧a 2-1>0Δ=(2a +1)2-4(a 2-1)<0, 解得a <-54.当a 2-1=0时,显然(2a +1)x +1>0,对x ∈R 不恒成立.所以a 的取值范围是⎝ ⎛⎭⎪⎫-∞,-54. 对数函数及其性质的应用1.(2016·荆州高一检测)若a =20.2,b =log 4(3.2),c =log 2(0.5),则( )A .a >b >cB .b >a >cC .c >a >bD .b >c >a【答案】 A2.设函数f (x )在(0,+∞)上是增函数,则a =f ⎝ ⎛⎭⎪⎫232,b =f ⎝ ⎛⎭⎪⎫log 232的大小关系是( ) A .a >b B .a <b C .a ≥b D .a ≤b 【答案】 A3.若函数f (x )=a x +log a (x +1)在[0,1]上的最大值和最小值之和为a ,则a 的值为( )A.14 B.12 C .2 D .4 【答案】 B4.已知log a 13>log b 13>0,则下列关系正确的是( )A .0<b <a <1B .0<a <b <1C .1<b <aD .1<a <b 【答案】 A5.当0<x ≤12时,4x <log a x ,则a 的取值范围是( )A .(2,2)B .(1,2) C.⎝ ⎛⎭⎪⎫22,1 D.⎝⎛⎭⎪⎫0,22【答案】 C6.函数y =log 0.4(-x 2+3x +4)的值域是________.【答案】 [-2,+∞)7.(2016·东莞高一检测)已知函数f (x )=m +log 2x 2的定义域是[1,2],且f (x )≤4,则实数m 的取值范围是________.【答案】 (-∞,2] 8.关于函数f (x )=lgxx 2+1有下列结论: ①函数f (x )的定义域是(0,+∞); ②函数f (x )是奇函数; ③函数f (x )的最小值为-lg 2;④当0<x <1时,函数f (x )是增函数;当x >1时,函数f (x )是减函数. 其中正确结论的序号是________. 【答案】 ①④9.已知定义域为[1,2]的函数f (x )=2+log a x (a >0,a ≠1)的图象过点(2,3).(1)求实数a 的值;(2)若g (x )=f (x )+f (x 2),求函数g (x )的值域.【解】 (1)∵函数f (x )=2+log a x (a >0,a ≠1)的图象过点(2,3), ∴3=2+log a 2,即log a 2=1,解得a =2. (2)∵g (x )=f (x )+f (x 2)=4+3log 2x ,故g (x )的定义域满足⎩⎨⎧1≤x ≤21≤x 2≤2⇒1≤x ≤2,且函数g (x )在定义域[1,2]上为增函数,由g (1)=4,g (2)=112, 故g (x )的值域为⎣⎢⎡⎦⎥⎤4,112.10.已知函数f (x )=ln(3+x )+ln(3-x ).(1)求函数y =f (x )的定义域; (2)判断函数y =f (x )的奇偶性;(3)若f (2m -1)<f (m ),求m 的取值范围.【解】 (1)要使函数有意义,则⎩⎨⎧3+x >03-x >0,解得-3<x <3,故函数y =f (x )的定义域为(-3,3).(2)由(1)可知,函数y =f (x )的定义域为(-3,3),关于原点对称. 对任意x ∈(-3,3),则-x ∈(-3,3), ∵f (-x )=ln(3-x )+ln(3+x )=f (x ),∴由函数奇偶性可知,函数y =f (x )为偶函数. (3)∵函数f (x )=ln(3+x )+ln(3-x )=ln(9-x 2),由复合函数单调性判断法则知,当0≤x <3时,函数y =f (x )为减函数. 又函数y =f (x )为偶函数,∴不等式f (2m -1)<f (m ),等价于|m |<|2m -1|<3, 解得-1<m <13或1<m <2.[能力提升]1.函数f (x )=log 12(x 2-4)的单调递增区间为( )A .(0,+∞)B .(-∞,0)C .(2,+∞)D .(-∞,-2)【答案】 D2.若log a 34<1(a >0且a ≠1),则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫0,34B.⎝ ⎛⎭⎪⎫0,34∪(1,+∞) C .(1,+∞) D .(0,1) 【答案】 B3.若函数f (x )=log (a 2-3)(ax +4)在[-1,1]上是单调增函数,则实数a 的取值范围是________.【解析】 设t =g (x )=ax +4,则y =f (x )=log (a 2-3)t ,若a >0,则函数t =ax +4递增,要使函数f (x )=log (a 2-3)(ax +4)在[-1,1]上是单调增函数,则有y =log (a 2-3)t 递增,所以有⎩⎨⎧ a 2-3>1g (-1)=-a +4>0,即⎩⎨⎧a >2或a <-2a <4,所以2<a <4.若a <0,则函数t =ax +4递减,要使函数f (x )=log (a 2-3)(ax +4)在[-1,1]上是单调增函数,则有y =log (a 2-3)t 递减,所以有⎩⎨⎧ 0<a 2-3<1g (1)=a +4>0,即⎩⎨⎧3<a 2<4a >-4,解得-2<a <- 3.综上,实数a 的取值范围是(-2,-3)∪(2,4). 【答案】 (-2,-3)∪(2,4) 4.设函数f (x )=lg(ax )·lg ax 2.(1)当a =0.1时,求f (1 000)的值; (2)若f (10)=10,求a 的值;(3)若对一切正实数x 恒有f (x )≤98,求a 的范围. 【解】 (1)当a =0.1时,f (x )=lg(0.1x )·lg 110x 2, ∴f (1 000)=lg 100·lg 1107=2×(-7)=-14.(2)∵f (10)=lg(10a )·lg a100=(1+lg a )(lg a -2)=lg 2a -lg a -2=10, ∴lg 2a -lg a -12=0,∴(lg a -4)(lg a +3)=0, ∴lg a =4或lg a =-3,即a =104或a =10-3. (3)∵对一切正实数x 恒有f (x )≤98, ∴lg(ax )·lg a x 2≤98对一切正实数恒成立. 即(lg a +lg x )(lg a -2lg x )≤98,∴2lg 2x +lg a lg x -lg 2a +98≥0对任意正实数x 恒成立,∵x >0,∴lg x ∈R ,由二次函数的性质可得,Δ=lg 2a -8⎝ ⎛⎭⎪⎫98-lg 2a ≤0, ∴lg 2a ≤1,∴-1≤lg a ≤1,∴110≤a ≤10.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2.2 对数函数及其性质(1)
教学目标:
1、理解对数函数的概念;
2、掌握对数函数的性质,了解对数学函数初步应用;
3、通过师生间,学生与学生之间互相交流,使学生逐步学会共同学习;
4、通过探究、思考、培养学生思维迁移能力和主动参予能力。
教学重点:
1、对数函数的定义、图象和性质;
2、对数函数性质的初步应用。
教学难点:
底数a 对对数函数性质的影响
教具准备:多媒体课件、投影仪
教学过程:
一、创设情景,引入新课
古谚云:一尺之木,日截其半,万世不竭……若设木长为x ,则其与经过的天数y 存在着一种关系,这个关系应如何表示呢?
(师):则x 与y 的关系式为x=(2
1)y …… 那能否根据(*)式把经过天数y 表示出来?(学生讨论并回答) (师):经过的天数y 可以表示为y=2
1log x
研究发现:在关系式y=2
1log x 中,把木长x 看作自变量,则每一个确定x
值,都有唯一一个经过的天数y 的值与之对应,由函数的定义,经过的天数y 就可以看作木长x 的函数,这样的函数称作为对数函数,即为本节课所要研究的内容。
(引入新课,书写课题:对数函数)
二、讲解新课
(一)对数函数的概念
问题1.1:由实例一我们是不否能得到对数函数的一般式吗? 问题1.2 :y=x
a log 式中的底数a 有什么具体限制条件吗?请给合指数式给以解释。
问题1.3:你能否根据指数函数的定义给出对数函数的定义吗?
(生交流,师结合学生回答总结、归纳并多媒体显示对数函数定义) 定义:一般地,函数y=x a log (a>0,且a ≠1)叫做对数函数,由对数概念可知,对数函数y=x a log 的定义域是(0,+∞),值域为R 。
问题1.4:为什么对数函数的定义域是(0,+∞)?
问题1.5:函数y=x a log 和函数y=x a log (a>0,a ≠1)的定义域,值域之间有什么关系?
(二)对数函数的图象和性质
(1)讨论对数函数的图象
1、利用“几何画板4.03”软件在同一坐标系中画出下列两组函灵敏图象并观察图象,探究它们之间关系。
(1)y=2x (2)y=x
a log (3)y=(21)x y=x 21log 2、当a>0、a ≠1时,函数y=a x 、y=x a log 的图象之间有何种关系?
(多媒体函数图像,提示(1)(2)两组图象之间的关系,由老师引导,学生讨论总结。
)
Ⅱ对数函数的性质
分析两组函数的图象,对照指数函数的性质,总结归纳对数函数性质。
(老师引导,学生相互讨论交流总结、归纳)
问题2.1 对数函数x a log (a>0,a ≠1)是否具有奇偶性?为什么? 问题2.2对数函数x a log (a>0,a ≠1),当a>1时,x 取何值,y>0?x 取何值,y<0?当0<a<1时呢?
问题2.3 对数式b a log 的值符号与a 、b 的取值之间有什么关系?请一句话来叙述。
(三)例题选讲
[例1]求下列函数的定义域
(1)3log x a (2)y=x a -4log
(师生共同完成该题解答,师规范板书或多媒体显示解题过程) 解:(1)由x 3>0得x>3
∴正数y=logx 2的定义域为{x|x >0}
(2)由题意可得04x >-,又∵偶次根号下为非负
∴4-x >0 即x <4 ∴函数x y a -=4log (a >0,a ≠1)的定义域为{x|x <4=
例2、比较下列各组数中两个值的大小
(1)021.1log 023.1log 023.1023.1,,
(2)9859.0log 9861.0log 9861.09861.0,
(3)09.5log 01.5log a a ,(a >0,且a ≠1)
解:(1)因为函数y =log 1.023x 在(0,+∞)上是增函数,且1.023>1.021
∴021.1log 023.1log 023.1023.1>
(2)因为函数y =log 0.9861x 在(0,+∞)上是减函数,且0.9861>0.9859 ∴9859.0log 9861.0log 9861.09861.0<
(3)对数函数的增减性决定于对数的底数a 是大于1还是小于1,因此需要对底数a 进行讨论
(i )当a >1时,因为函数y=log a x 在(0,+∞)上是增函数,且5.01<5.09 ∴09.5log 01.5log a a <
(ii )当0<a <1时,因为函数y=log a x 在(0,+∞)上是减函数,且5.01<5.09
>
∴09
log
.5
01
log
.5
a
a
(四)课堂练习(由学生来完成)
课本P81-练习题2,3
三、课堂小结
1、对数函数的定义
2、对数函数的图象和性质
3、利用对数函数的性质比较大小的一般方法和步骤
四、布置作业
课本P81-练习1,P86习题2 2.A组第7、8、10题
板书设计。
