高中数学一对一讲义——函数
高中数学讲义 第二章 函数A (超级详细)
分析:运用配方法,逆求法,换元法等方法求函数值域.
(1) 解: y x2 4x 2 (x 2)2 2 , x [0,3) ,函数的值域为[2, 2] ;
(2)
解法一:由
y
x2 x2 1
1
x
1 2
1
,
0
1 x2 1
1 ,则 1
1 x2 1
0
, 0
y
1,故函
数值域为[0,1) .
解法二:由
求函数的值域应注意新元的取值范围.
第 3页 【辅导专用】共 16页
【反馈演练】
1.函数 f(x)= 1 2 x 的定义域是__(____,_0_]___.
2.函数
f
(x)
1 log 2 (x 2
4x
3)
的定义域为___(_1_, _2_)___(_2_, _3_)___.
3.
函数
y
1 1 x2
它的值域也就确定,故判断两个函数是否为同一函数,只需判断它的定义域和对应法则是否相同即可.
例 2.求下列函数的定义域:① y 1 x 2 1 ; 2 x
② f (x)
x
;
log 1 (2 x)
2
解:(1)①
2 由题意得:
x
0, 解得 x 1且 x
2 或 x
1且 x
2,
x2 1 0,
1.设有函数组:① y x ,y
x2 ;② y x ,y 3 x3 ;③ y
x ,y
x x
;④
y
1 1
(x 0),
,
(x 0),
y x ;⑤ y lg x 1 , y lg x .其中表示同一个函数的有___②④⑤___.
高三复习 高中数学复习讲义 第一课时函数概念及其性质

高中数学复习讲义 第一课时函数概念及其性质第1课 函数的概念【基础练习】1. 设有函数组:①y x =,y =y x =,y =;③y,y =;④1(0),1(0),x y x >⎧=⎨-<⎩,x y x =;⑤lg 1y x =-,lg 10xy =.其中表示同一个函数的有2. 2.设集合{02}M x x =≤≤,{02}N y y =≤≤,从M 到N 有四种对应如图所示:其中能表示为M 到N 的函数关系的有________. 3.写出下列函数定义域:(1) ()13f x x =-的定义域为______________; (2) 21()1f x x =-的定义_______; (3)1()f x x =的定义域为_________; (4)0()f x =________.4.已知三个函数:(1)()()P x y Q x =;(2)y =(*)n N ∈; (3)()log ()Q x y P x =.写出使各函数式有意义时,()P x ,()Q x 的约束条件:(1)___________________(2)______________________(3)______________________________. 5.写出下列函数值域:(1) 2()f x x x =+,{1,2,3}x ∈;值域是{2,6,12}. (2) 2()22f x x x =-+; 值域是[1,)+∞.①②③④(3) ()1f x x =+,(1,2]x ∈. 值域是(2,3].【范例解析】例 1.设有函数组:①21()1x f x x -=-,()1g x x =+;②()f x =,()g x =③()f x =()1g x x =-;④()21f x x =-,()21g t t =-.其中表示同一个函数的有 . 例2.求下列函数的定义域:①12y x =+- ②()f x =例3.求下列函数的值域:(1)242y x x =-+-,[0,3)x ∈;(2)221x y x =+()x R ∈; (3)y x =-【反馈演练】1.函数f (x )=x 21-的定义域是___________. 2.函数)34(log 1)(22-+-=x x x f 的定义域为_________________. 3. 函数21()1y x R x =∈+的值域为________________. 4.函数23y x =-+_____________. 5.函数)34(log 25.0x x y -=的定义域为_____________________.6.记函数f (x )=132++-x x 的定义域为A ,g (x )=lg [(x -a -1)(2a -x )](a <1) 的定义域为B . (1) 求A ;(2) 若B ⊆A ,求实数a 的取值范围.第2课 函数的表示方法【考点导读】1.会根据不同的需要选择恰当的方法(如图像法,列表法,解析法)表示函数.2.求解析式一般有四种情况:(1)根据某个实际问题须建立一种函数关系式;(2)给出函数特征,利用待定系数法求解析式;(3)换元法求解析式;(4)解方程组法求解析式. 【基础练习】1.设函数()23f x x =+,()35g x x =-,则(())f g x =_________;(())g f x =__________.2.设函数1()1f x x=+,2()2g x x =+,则(1)g -=_________;[(2)]f g = ;[()]f g x = .3.已知函数()f x 是一次函数,且(3)7f =,(5)1f =-,则(1)f =_____.4.设f (x )=2|1|2,||1,1, ||11x x x x--≤⎧⎪⎨>⎪+⎩,则f [f (21)]=_____________.5.如图所示的图象所表示的函数解析式为__________________________. 【范例解析】例1.已知二次函数()y f x =的最小值等于4,且(0)(2)6f f ==,求()f x 的解析式.例2.甲同学家到乙同学家的途中有一公园,甲从家到公园的距离与乙从家到公园的距离都是2km ,甲10时出发前往乙家.如图,表示甲从出发到乙家为止经过的路程y (km )与时间x (分)的关系.试写出()y f x =的函数解析式.第5题【反馈演练】1.若()2x x e e f x --=,()2x xe e g x -+=,则(2)f x =()A. 2()f x B.2[()()]f x g x + C.2()g x D. 2[()()]f x g x ⋅ 2.已知1(1)232f x x -=+,且()6f m =,则m 等于________.3. 已知函数f (x )和g (x )的图象关于原点对称,且f (x )=x 2+2x .求函数g (x )的解析式.第3课 函数的单调性【考点导读】1.理解函数单调性,最大(小)值及其几何意义;2.会运用单调性的定义判断或证明一些函数的增减性. 【基础练习】 1.下列函数中: ①1()f x x=; ②()221f x x x =++; ③()f x x =-; ④()1f x x =-.其中,在区间(0,2)上是递增函数的序号有______. 2.函数y x x =的递增区间是___ ___.3.函数y =的递减区间是__________.4.已知函数()y f x =在定义域R 上是单调减函数,且(1)(2)f a f a +>,则实数a 的取值范围__________.5.已知下列命题:①定义在R 上的函数()f x 满足(2)(1)f f >,则函数()f x 是R 上的增函数;②定义在R 上的函数()f x 满足(2)(1)f f >,则函数()f x 在R 上不是减函数;③定义在R 上的函数()f x 在区间(,0]-∞上是增函数,在区间[0,)+∞上也是增函数,则函数()f x 在R 上是增函数;④定义在R 上的函数()f x 在区间(,0]-∞上是增函数,在区间(0,)+∞上也是增函数,则函数()f x 在R 上是增函数.其中正确命题的序号有___________. 【范例解析】例 . 求证:(1)函数2()231f x x x =-+-在区间3(,]4-∞上是单调递增函数;(2)函数21()1x f x x -=+在区间(,1)-∞-和(1,)-+∞上都是单调递增函数.例2.确定函数()f x =【反馈演练】1.已知函数1()21xf x =+,则该函数在R 上单调递__ __,(填“增”“减”)值域为_________. 2.已知函数2()45f x x mx =-+在(,2)-∞-上是减函数,在(2,)-+∞上是增函数,则(1)f =_____.3. 函数y =的单调递增区间为 .4. 函数2()1f x x x =-+的单调递减区间为 .5. 已知函数1()2ax f x x +=+在区间(2,)-+∞上是增函数,求实数a 的取值范围.第4课 函数的奇偶性【考点导读】1.了解函数奇偶性的含义,能利用定义判断一些简单函数的奇偶性;2.定义域对奇偶性的影响:定义域关于原点对称是函数为奇函数或偶函数的必要但不充分条件;不具备上述对称性的,既不是奇函数,也不是偶函数. 【基础练习】1.给出4个函数:①5()5f x x x =+;②421()x f x x -=;③()25f x x =-+;④()x x f x e e -=-.其中奇函数的有_____;偶函数的有_______;既不是奇函数也不是偶函数的有________. 2. 设函数()()()xa x x x f ++=1为奇函数,则实数=a .3.下列函数中,在其定义域内既是奇函数又是减函数的是( )A .R x x y ∈-=,3B .R x x y ∈=,sinC .R x x y ∈=,D .R x x y ∈=,)21( 【范例解析】例1.判断下列函数的奇偶性:(1)2(12)()2x xf x +=; (2)()lg(f x x =;(3)221()lg lgf x x x =+; (4)()(1f x x =- (5)2()11f x x x =+-+; (6)22(0),()(0).x x x f x x x x⎧-+≥⎪=⎨<+⎪⎩例2. 已知定义在R 上的函数()f x 是奇函数,且当0x >时,2()22f x x x =-+,求函数()f x 的解析式,并指出它的单调区间.【反馈演练】1.已知定义域为R 的函数()x f 在区间()+∞,8上为减函数,且函数()8+=x f y 为偶函数,则( )A .()()76f f >B .()()96f f >C .()()97f f >D .()()107f f > 2. 在R 上定义的函数()x f 是偶函数,且()()x f x f -=2,若()x f 在区间[]2,1是减函数,则函数()x f ( )A.在区间[]1,2--上是增函数,区间[]4,3上是增函数B.在区间[]1,2--上是增函数,区间[]4,3上是减函数C.在区间[]1,2--上是减函数,区间[]4,3上是增函数D.在区间[]1,2--上是减函数,区间[]4,3上是减函数 3. 设⎭⎬⎫⎩⎨⎧-∈3,21,1,1α,则使函数αx y =的定义域为R 且为奇函数的所有α的值为_____.4.设函数))((R x x f ∈为奇函数,),2()()2(,21)1(f x f x f f +=+=则=)5(f ________. 5.若函数)(x f 是定义在R 上的偶函数,在]0,(-∞上是减函数,且0)2(=f ,则使得0)(<x f 的x 的取值范围是 .6. 已知函数21()ax f x bx c+=+(,,)a b c Z ∈是奇函数.又(1)2f =,(2)3f <,求a ,b ,c 的值;【真题演练】1(2012福建7).设函数⎩⎨⎧=为无理数为有理数x x x D ,0,1)(,则下列结论错误的是( )A .)(x D 的值域为}1,0{B .)(x D 是偶函数C .)(xD 不是周期函数 D .)(x D 不是单调函数 2.(2012广东4). 下列函数中,在区间(0,)+∞上为增函数的是( )()A ln(2)y x =+ ()B y = ()C ()x y 1=2()D y x x1=+3.陕西2. 下列函数中,既是奇函数又是增函数的为( )A .1y x =+B .3x y -=C .1y x=D .||y x x = 4.上海9.已知2)(x x f y +=是奇函数,且1)1(=f ,若2)()(+=x f x g ,则=-)1(g .5、(2012年高考江苏卷5) 函数()f x =的定义域为 ▲ .6、(2012年高考上海卷理科7)已知函数||)(a x e x f -=(a 为常数).若)(x f 在区间),1[+∞上是增函数,则a 的取值范围是 .7.(2012年高考上海卷理科9)已知2)(x x f y +=是奇函数,且1)1(=f ,若2)()(+=x f x g ,则=-)1(g .。
高中数学讲义:利用导数解函数的最值

函数的最值一、基础知识:1、函数的最大值与最小值:(1)设函数()f x 的定义域为D ,若0x D $Î,使得对x D "Î,均满足()()0f x f x £,那么称0x x =为函数()f x 的一个最大值点,()0f x 称为函数()f x 的最大值(2)设函数()f x 的定义域为D ,若0x D $Î,使得对x D "Î,均满足()()0f x f x ³,那么称0x x =为函数()f x 的一个最小值点,()0f x 称为函数()f x 的最小值(3)最大值与最小值在图像中体现为函数的最高点和最低点(4)最值为函数值域的元素,即必须是某个自变量的函数值。
例如:()[)ln ,1,4f x x x =Î,由单调性可得()f x 有最小值()10f =,但由于x 取不到4,所以尽管函数值无限接近于ln 4,但就是达不到。
()f x 没有最大值。
(5)一个函数其最大值(或最小值)至多有一个,而最大值点(或最小值点)的个数可以不唯一,例如()sin f x x =,其最大值点为()22x k k Z pp =+Î,有无穷多个。
2.“最值”与“极值”的区别和联系右图为一个定义在闭区间[]b a ,上的函数)(x f 的图象.图中)(1x f 与3()f x 是极小值,2()f x 是极大值.函数)(x f 在[]b a ,上的最大值是)(b f ,最小值是3()f x (1)“最值”是整体概念,是比较整个定义域内的函数值得出的,具有绝对性;而“极值”是个局部概念,是比较极值点附近函数值得出的,具有相对性.(2)从个数上看,一个函数在其定义域上的最值是唯一的;而极值不唯一;(3)函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个(4)极值只能在定义域内部取得,而最值可以在区间的端点处取得,有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值只要不在端点必定是极值.3、结论:一般地,在闭区间[]b a ,上函数()y f x =的图像是一条连续不断的曲线,那么函数()y f x =在[]b a ,上必有最大值与最小值.4、最值点只可能在极值点或者边界点处产生,其余的点位于单调区间中,意味着在这些点的周围既有比它大的,也有比它小的,故不会成为最值点5、利用导数求函数的最值步骤:一般地,求函数)(x f 在[]b a ,上的最大值与最小值的步骤如下:(1)求)(x f 在(,)a b 内的极值;(2)将)(x f 的各极值与端点处的函数值)(a f 、)(b f 比较,其中最大的一个是最大值,最小的一个是最小值,得出函数)(x f 在[]b a ,上的最值6、求函数最值的过程中往往要利用函数的单调性,所以说,函数的单调区间是求最值与极值的基础7、在比较的过程中也可简化步骤:(1)利用函数单调性可判断边界点是否能成为最大值点或最小值点(2)极小值点不会是最大值点,极大值点也不会是最小值点8、最值点的作用(1)关系到函数的值域(2)由最值可构造恒成立的不等式:例如:()ln 1f x x x =-+,可通过导数求出()()min 10f x f ==,由此可得到对于任意的0x >,均有()()min 0f x f x ³=,即不等式ln 1x x £-二、典型例题:例1:求函数()x f x xe -=的最值思路:首先判定定义域为R ,对函数进行求导,根据单调区间求出函数的最值解:()()'1x fx x e -=-,令()'0f x >,解得:1x <()f x \的单调区间为:x (),1-¥()1,+¥'()f x +-()f x Z ]()()max 11f x f e\==,无最小值小炼有话说:函数()xf x xe-=先增再减,其最大值即为它的极大值点,我们可以将这种先增再减,或者先减再增的函数成为“单峰函数”,在单峰函数中,极值点即为函数的某个最值点。
初高中数学衔接教学课程讲义----第6节函数的定义

初高中数学衔接课讲义——函数第六讲 函数的定义【映射】1.定义一般地,设B A ,是两个非空集合,如果按某一个确定的对应关系f ,使对于集合A 中的任意一个元素x ,在集合B 中都有唯一确定的元素y 与之对应,那么就称对应B A f →:为从集合A 到集合B 的一个映射.记作“f (对应关系):A (原象)B →(象)”2.映射的特性(1)存在性:对集合A 中任一个元素a ,在集合B 中都存在元素b 与之对应;(2)唯一性:集合A 中的任一元素在集合B 中的对应元素是唯一的;(3)封闭性:集合A 中任一个元素的对应元素都必须在集合B 中;(4)确定性:非空集合B A ,及对应关系都是确定的;(5)方向性:集合A 到集合B 的对应与集合B 到集合A 的对应所确定的映射是不同的.3.一一映射的概念如果映射f 是集合A 到集合B 的映射,并且对于集合A 中的任何一个元素在集合B 中都有象,集合B 中的每一个元素在A 中都有象,那么就说两个集合之间存在着一一对应关系,并把这个映射叫做一一映射.【提示】(1)函数一定是映射,但是映射不一定是函数.(2)在函数中,B A ,是两个数集,即B A ,中的元素都是实数,但在映射中,B A ,中的元素不一定是实数.【例题1】下列对应是映射的有__________.【例题2】下列各个对应中,构成映射的是( )A.B. C. D.【例题3】下列不能表示}40|{≤≤=x x P 到}20|{≤≤=y y Q 的映射的是( ) A.x y x f 21:=→ B.x y x f 31:=→ C.x y x f 23:=→ D.x y x f =→:【例题4】若),y x (在映射f 作用下的象是),xy y x +(,则()3,2-在f 作用下的象是_________;()3,2-在f 作用下的原象是__________.【例题5】设集合A 和B 都是实数集,映射B A f →:把集合A 中的元素x 映射到集合B 中的元素13+-x x ,则在映射f 下,象1的原象组成的集合是( ) A.}1{B.}210{--,,C.}0{D.}11{0-,,【例题6】设},|),{(R y R x y x B A ∈∈==,),(),(:b y kx y x f +→是从集合A 到集合B 的映射,若B 中元素)(2,6在映射f 下对应A 中元素)13(,,则=k _________,=b __________.【函数的定义】设集合B A 、是两个非空数集,对于A 中的任意数x ,按照某种关系的对应关系f ,在集合B 中都有唯一确定的数)(x f 与它对应,那么就称B A f →:为从集合A 到集合B 的一个函数,记作A x x f y ∈=),(.其中,x 叫做自变量,x 的取值范围A 叫做的定义域,与x 的值相对应)(x f 的值叫做函数值,所有函数值构成的集合}|)({A x x f ∈叫做函数的值域.【提示】(1)B A 、都是非空数集,故定义域(或值域)为空集的函数是不存在的.(2)B 不一定是函数的值域,如函数12+=x y 可称为实数集到实数集的函数,但函数的值域不是实数集R .(3)函数三要素的定义域、对应关系和值域.其中对应关系是核心,定义域是根本.(4)函数符合)(x f 的含义:)(x f 表示一个整体,一个函数,而符号“f ”可以看作是对“x ”施加的某种法则(或运算).【例题1】判断正误:(1)函数值域中的每一个数都有定义域中的数与之对应; ( )(2)函数的定义域可以为空集; ( )(3)定义域和对应关系确定后,函数值域也就确定; ( )(4)若函数的定义域只有一个元素,则值域也只有一个元素; ( )(5)对于不同的x , y 的值也不同; ( )(6)函数23)(x x x f +=,则2)1(=f ; ( )【例题2】已知函数213)(+++=x x x f ,求))3((),3(--f f f 的值.【例题3】函数6)(+=x x f ,则=)3(f __________.【例题4】函数1)1()(3099-+-=x xx f ,则=-)2(f __________.【例题5】已知函数213)(+++=x x x f ,当0>a 时,求)1(),(-a f a f 的值.【例题6】下列图象能表示函数图象的是( )A.B. C. D.【例题7】下列图中能作为函数图象的是( )A.B. C. D.【例题8】下列四个图象中,不是函数图象的是( )A.B. C. D.【例题9】图中能作为函数图象的是( )A. B. C. D.【例题10】)(x f y =定义在[]3,2-上,则函数)(x f y =图象与直线2=x 的交点个数有( )A.0个B.1个C.2个D.不能确定【例题11】函数)(x f y =的图象与直线1=x 的公共点数目是( )A.1B.0C.0或1D.1或2【课堂练习】【练习】设集合A 和集合B 都是自然数集合N ,映射B A f →:把集合A 中的元素n 映射到集合B 中的元素n n+2,则在映射f 下,象20的原象是( )A.2B.3C.4D.5【练习】判断下列说法是否正确:(1)表达式相同的两个函数是相同函数;( ) (2)定义域、值域均相同的函数是同一函数; ( ) (3)函数的定义域、值域均是无限集; ( )【练习】关于函数)(x f y =与函数)1(+=x f y 的叙述一定正确的是( )A.定义域相同B.对应关系相同C.值域相同D.三要素都不可以不同【练习】下列图形可以表示为以}10|{≤≤=x x M 为定义域,以}10|{≤≤=x x N 为值域的函数是( )A.B. C. D.【练习】函数11)(22+-=x x x f ,则=)21()2(f f ( ) A.1B.-1C.53 D.53-【练习】设|||1|)(x x x f --=,则=)]21([f f ( ) A.21-B.0C.21D.1初高中数学衔接课讲义——函数第六讲 函数的定义 【映射】4.定义一般地,设B A ,是两个非空集合,如果按某一个确定的对应关系f ,使对于集合A 中的任意一个元素x ,在集合B 中都有唯一确定的元素y 与之对应,那么就称对应B A f →:为从集合A 到集合B 的一个映射.记作“f (对应关系):A (原象)B →(象)”5.映射的特性(1)存在性:对集合A 中任一个元素a ,在集合B 中都存在元素b 与之对应;(2)唯一性:集合A 中的任一元素在集合B 中的对应元素是唯一的;(3)封闭性:集合A 中任一个元素的对应元素都必须在集合B 中;(4)确定性:非空集合B A ,及对应关系都是确定的;(5)方向性:集合A 到集合B 的对应与集合B 到集合A 的对应所确定的映射是不同的.6.一一映射的概念如果映射f 是集合A 到集合B 的映射,并且对于集合A 中的任何一个元素在集合B 中都有象,集合B 中的每一个元素在A 中都有象,那么就说两个集合之间存在着一一对应关系,并把这个映射叫做一一映射.【提示】(1)函数一定是映射,但是映射不一定是函数.(2)在函数中,B A ,是两个数集,即B A ,中的元素都是实数,但在映射中,B A ,中的元素不一定是实数.【例题1】下列对应是映射的有__________.答案:①④【例题2】下列各个对应中,构成映射的是( )A.B. C. D.答案:B 【例题3】下列不能表示}40|{≤≤=x x P 到}20|{≤≤=y y Q 的映射的是( ) A.x y x f 21:=→ B.x y x f 31:=→ C.x y x f 23:=→ D.x y x f =→: 答案:B【例题4】若),y x (在映射f 作用下的象是),xy y x +(,则()3,2-在f 作用下的象是_________;()3,2-在f 作用下的原象是__________.答案:),(61-; ),)或((133,1-- 【例题5】设集合A 和B 都是实数集,映射B A f →:把集合A 中的元素x 映射到集合B 中的元素13+-x x ,则在映射f 下,象1的原象组成的集合是( ) A.}1{B.}210{--,,C.}0{D.}11{0-,,答案:D【例题6】设},|),{(R y R x y x B A ∈∈==,),(),(:b y kx y x f +→是从集合A 到集合B 的映射,若B 中元素)(2,6在映射f 下对应A 中元素)13(,,则=k _________,=b __________.答案:2; 1【函数的定义】设集合B A 、是两个非空数集,对于A 中的任意数x ,按照某种关系的对应关系f ,在集合B 中都有唯一确定的数)(x f 与它对应,那么就称B A f →:为从集合A 到集合B 的一个函数,记作A x x f y ∈=),(.其中,x 叫做自变量,x 的取值范围A 叫做的定义域,与x 的值相对应)(x f 的值叫做函数值,所有函数值构成的集合}|)({A x x f ∈叫做函数的值域.【提示】(1)B A 、都是非空数集,故定义域(或值域)为空集的函数是不存在的.(2)B 不一定是函数的值域,如函数12+=x y 可称为实数集到实数集的函数,但函数的值域不是实数集R .(3)函数三要素的定义域、对应关系和值域.其中对应关系是核心,定义域是根本.(4)函数符合)(x f 的含义:)(x f 表示一个整体,一个函数,而符号“f ”可以看作是对“x ”施加的某种法则(或运算).【例题1】判断正误:(1)函数值域中的每一个数都有定义域中的数与之对应; ( )(2)函数的定义域可以为空集; ( )(3)定义域和对应关系确定后,函数值域也就确定; ( )(4)若函数的定义域只有一个元素,则值域也只有一个元素; ( )(5)对于不同的x , y 的值也不同; ( )(6)函数23)(x x x f +=,则2)1(=f ; ( ) 答案:(1)√ (2)× (3)√ (4)√ (5)× (6)√【例题2】已知函数213)(+++=x x x f ,求))3((),3(--f f f 的值. 解析:由题意可得:123133)3(-=+-++-=-f 1221131)1())3((+=+-++-=-=-∴f f f 答案:12;1+- 【例题3】函数6)(+=x x f ,则=)3(f __________.答案:3 【例题4】函数1)1()(3099-+-=x x x f ,则=-)2(f __________.解析:由题意可得:当2-=x 时,()()01299≠--,()[]112099=--∴ ()8121)2(3-=--+=-∴f 答案:8-【例题5】已知函数213)(+++=x x x f ,当0>a 时,求)1(),(-a f a f 的值. 解析:由题意可得:当0>a 时,213213)(+++=+++=a a a a a f 11221131)1(+++=+-++-=-a a a a a f 答案:213)(+++=a a a f ; 112)1(+++=-a a a f 【例题6】下列图象能表示函数图象的是( )A.B. C. D.答案:C 【例题7】下列图中能作为函数图象的是( )A.B. C. D.答案:D 【例题8】下列四个图象中,不是函数图象的是( )A.B. C. D.答案:B 【例题9】图中能作为函数图象的是( )A.(1)、(2)B.(1)、(3)C.(2)、(4)D.(3)、(4)答案:A【例题10】)(x f y =定义在[]3,2-上,则函数)(x f y =图象与直线2=x 的交点个数有( )A.0个B.1个C.2个D.不能确定答案:B【例题11】函数)(x f y =的图象与直线1=x 的公共点数目是( )A.1B.0C.0或1D.1或2答案:C【课堂练习】【练习】设集合A 和集合B 都是自然数集合N ,映射B A f →:把集合A 中的元素n 映射到集合B 中的元素n n+2,则在映射f 下,象20的原象是( )A.2B.3C.4D.5答案:C【练习】判断下列说法是否正确:(4)表达式相同的两个函数是相同函数;( ) (5)定义域、值域均相同的函数是同一函数; ( ) (6)函数的定义域、值域均是无限集; ( ) 答案:(1)× (2)× (3)×【练习】关于函数)(x f y =与函数)1(+=x f y 的叙述一定正确的是( )A.定义域相同B.对应关系相同C.值域相同D.三要素都不可以不同答案:C【练习】下列图形可以表示为以}10|{≤≤=x x M 为定义域,以}10|{≤≤=x x N 为值域的函数是( )A.B. C. D.答案:C 【练习】函数11)(22+-=x x x f ,则=)21()2(f f ( ) A.1B.-1C.53 D.53- 解析:由题意可得:531212)2(22=+-=f ,53121121)21(22-=+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=f∴15353)21()2(-=-=f f . 答案:B【练习】设|||1|)(x x x f --=,则=)]21([f f ( ) A.21-B.0C.21 D.1 解析:由题意可得:0|21||121|)21(=--=f ,1|0||10|)0()]21([=--==∴f f f . 答案:D。
高中数学讲义:零点存在的判定与证明

零点存在的判定与证明一、基础知识:1、函数的零点:一般的,对于函数()y f x =,我们把方程()0f x =的实数根0x 叫作函数()y f x =的零点。
2、零点存在性定理:如果函数()y f x =在区间[],a b 上的图像是连续不断的一条曲线,并且有()()0f a f b ×<,那么函数()y f x =在区间(),a b 内必有零点,即()0,x a b $Î,使得()00f x =注:零点存在性定理使用的前提是()f x 在区间[],a b 连续,如果()f x 是分段的,那么零点不一定存在3、函数单调性对零点个数的影响:如果一个连续函数是单调函数,那么它的零点至多有一个。
因此分析一个函数零点的个数前,可尝试判断函数是否单调4、几个“不一定”与“一定”(假设()f x 在区间(),a b 连续)(1)若()()0f a f b ×<,则()f x “一定”存在零点,但“不一定”只有一个零点。
要分析()f x 的性质与图像,如果()f x 单调,则“一定”只有一个零点(2)若()()0f a f b ×>,则()f x “不一定”存在零点,也“不一定”没有零点。
如果()f x 单调,那么“一定”没有零点(3)如果()f x 在区间(),a b 中存在零点,则()()f a f b ×的符号是“不确定”的,受函数性质与图像影响。
如果()f x 单调,则()()f a f b ×一定小于05、零点与单调性配合可确定函数的符号:()f x 是一个在(),a b 单增连续函数,0x x =是()f x 的零点,且()0,x a b Î,则()0,x a x Î时,()0f x <;()0,x x b Î时,()0f x >6、判断函数单调性的方法:(1)可直接判断的几个结论:① 若()(),f x g x 为增(减)函数,则()()f x g x +也为增(减)函数② 若()f x 为增函数,则()f x -为减函数;同样,若()f x 为减函数,则()f x -为增函数③ 若()(),f x g x 为增函数,且()(),0f x g x >,则()()f x g x ×为增函数(2)复合函数单调性:判断()()y f g x =的单调性可分别判断()t g x =与()y f t =的单调性(注意要利用x 的范围求出t 的范围),若()t g x =,()y f t =均为增函数或均为减函数,则()()y f g x =单调递增;若()t g x =,()y f t =一增一减,则()()y f g x =单调递减(此规律可简记为“同增异减”)(3)利用导数进行判断——求出单调区间从而也可作出图像7、证明零点存在的步骤:(1)将所证等式中的所有项移至等号一侧,以便于构造函数(2)判断是否要对表达式进行合理变形,然后将表达式设为函数()f x (3)分析函数()f x 的性质,并考虑在已知范围内寻找端点函数值异号的区间(4)利用零点存在性定理证明零点存在例1:函数()23x f x e x =+-的零点所在的一个区间是( )A.1,02æö-ç÷èø B.10,2æöç÷èø C.1,12æöç÷èø D.31,2æöç÷èø思路:函数()f x 为增函数,所以只需代入每个选项区间的端点,判断函数值是否异号即可解:1211234022f e -æöæö-=+×--=-<ç÷ç÷èøèø,()020f =-<11232022f æö=+×-=-<ç÷èø()12310f e e =+-=->()1102f f æö\×<ç÷èø01,12x æö\Îç÷èø,使得()00f x =答案:C例2:函数()()ln 1f x x x =-+的零点所在的大致区间是( )A.31,2æöç÷èø B.3,22æöç÷èøC.()2,eD.(),e +¥思路:先能判断出()f x 为增函数,然后利用零点存在性判定定理,只需验证选项中区间端点函数值的符号即可。
高中数学 函数指数函数的概念讲义 新人教A版必修一第一册
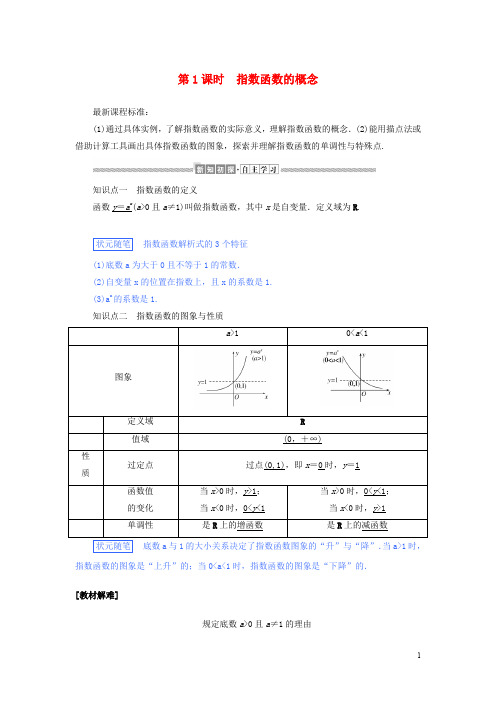
第1课时指数函数的概念最新课程标准:(1)通过具体实例,了解指数函数的实际意义,理解指数函数的概念.(2)能用描点法或借助计算工具画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点.知识点一指数函数的定义函数y=a x(a>0且a≠1)叫做指数函数,其中x是自变量.定义域为R.状元随笔指数函数解析式的3个特征(1)底数a为大于0且不等于1的常数.(2)自变量x的位置在指数上,且x的系数是1.(3)a x的系数是1.知识点二指数函数的图象与性质状元随笔底数a与1的大小关系决定了指数函数图象的“升”与“降”.当a>1时,指数函数的图象是“上升”的;当0<a<1时,指数函数的图象是“下降”的.[教材解难]规定底数a>0且a≠1的理由(1)如果a =0,则⎩⎪⎨⎪⎧当x >0时,a x恒为0;当x <0时,a x无意义.(2)如果a <0,比如y =(-2)x,这时对于x =12,14,18,116,…在实数范围内函数值不存在.(3)如果a =1,那么y =1x=1是常量,对此就没有研究的必要. [基础自测]1.下列各函数中,是指数函数的是( ) A .y =(-3)xB .y =-3xC .y =3x -1D .y =⎝ ⎛⎭⎪⎫13x解析:根据指数函数的定义y =a x(a >0且a ≠1)可知只有D 项正确. 答案:D 2.函数f (x )=12x-1的定义域为( ) A .R B .(0,+∞) C .[0,+∞) D.(-∞,0)解析:要使函数有意义,则2x-1>0,∴2x>1,∴x >0. 答案:B3.在同一坐标系中,函数y =2x与y =⎝ ⎛⎭⎪⎫12x 的图象之间的关系是( )A .关于y 轴对称B .关于x 轴对称C .关于原点对称D .关于直线y =x 对称解析:由作出两函数图象可知,两函数图象关于y 轴对称,故选A. 答案:A4.函数f (x )=1-e x的值域为________.解析:由1-e x≥0得e x≤1,故函数f (x )的定义域为{x |x ≤0},所以0<e x≤1,-1≤-e x<0,0≤1-e x<1,函数f (x )的值域为[0,1).答案:[0,1)题型一 指数函数概念的应用[经典例题]例1 (1)若函数f (x )=(2a -1)x是R 上的减函数,则实数a 的取值范围是( ) A .(0,1) B .(1,+∞)C.⎝ ⎛⎭⎪⎫12,1 D .(-∞,1)(2)指数函数y =f (x )的图象经过点⎝ ⎛⎭⎪⎫-2,14,那么f (4)·f (2)等于________. 【解析】 (1)由已知,得0<2a -1<1,则12<a <1,所以实数a 的取值范围是⎝ ⎛⎭⎪⎫12,1. (2)设y =f (x )=a x (a >0,a ≠1),所以a -2=14,所以a =2,所以f (4)·f (2)=24×22=64. 【答案】 (1)C (2)64(1)根据指数函数的定义可知,底数a>0且a≠1,a x的系数是1.(2)先设指数函数为f(x)=a x,借助条件图象过点(-2,14)求a ,最后求值.方法归纳(1)判断一个函数是指数函数的方法①看形式:只需判定其解析式是否符合y =a x(a >0,且a ≠1)这一结构特征.②明特征:指数函数的解析式具有三个特征,只要有一个特征不具备,则不是指数函数. (2)已知某函数是指数函数求参数值的基本步骤跟踪训练1 (1)若函数y =(3-2a )x为指数函数,则实数a 的取值范围是________; (2)下列函数中是指数函数的是________.(填序号)①y =2·(2)x②y =2x -1③y =⎝ ⎛⎭⎪⎫π2x ④y =x x⑤y =31x -⑥y =x13.解析:(1)若函数y =(3-2a )x为指数函数,则⎩⎪⎨⎪⎧3-2a >0,3-2a ≠1,解得a <32且a ≠1.(2)①中指数式(2)x的系数不为1,故不是指数函数;②中y =2x -1=12·2x ,指数式2x 的系数不为1,故不是指数函数;④中底数为x ,不满足底数是唯一确定的值,故不是指数函数;⑤中指数不是x ,故不是指数函数;⑥中指数为常数且底数不是唯一确定的值,故不是指数函数.故填③.答案:(1)(-∞,1)∪⎝ ⎛⎭⎪⎫1,32 (2)③ 1.指数函数系数为1. 2.底数>0且≠1.题型二 指数函数[教材P 114例1]例2 已知指数函数f (x )=a x(a >0,且a ≠1),且f (3)=π,求f (0),f (1),f (-3)的值.【解析】 因为f (x )=a x ,且f (3)=π,则a 3=π,解得a =π13,于是f (x )=π3x .所以,f (0)=π0=1,f (1)=π13=3π,f (-3)=π-1=1π. 状元随笔 要求f(0),f(1),f(-3)的值,应先求出f(x)=a x的解析式,即先求a 的值.教材反思求指数函数的解析式时,一般采用待定系数法,即先设出函数的解析式,然后利用已知条件,求出解析式中的参数,从而得到函数的解析式,其中掌握指数函数的概念是解决这类问题的关键.因为底数a 是大于0且不等于1的实数,所以a =-3应舍去.跟踪训练2 若指数函数f (x )的图象经过点(2,9),求f (x )的解析式及f (-1)的值. 解析:设f (x )=a x (a >0,且a ≠1),将点(2,9)代入,得a 2=9,解得a =3或a =-3(舍去).所以f (x )=3x .所以f (-1)=3-1=13.设f(x)=a x,代入(2,9)求出a.一、选择题1.下列函数中,指数函数的个数为( )①y =⎝ ⎛⎭⎪⎫12x -1;②y =a x (a >0,且a ≠1);③y =1x;④y =⎝ ⎛⎭⎪⎫122x -1.A .0B .1C .3D .4解析:由指数函数的定义可判定,只有②正确. 答案:B 2.已知f (x )=3x -b(b 为常数)的图象经过点(2,1),则f (4)的值为( )A .3B .6C .9D .81解析:由f (x )过定点(2,1)可知b =2, 所以f (x )=3x -2,f (4)=9.可知C 正确.答案:C3.当x ∈[-1,1]时,函数f (x )=3x-2的值域是( )A.⎣⎢⎡⎦⎥⎤1,53 B .[-1,1] C.⎣⎢⎡⎦⎥⎤-53,1 D .[0,1] 解析:因为指数函数y =3x在区间[-1,1]上是增函数,所以3-1≤3x ≤31,于是3-1-2≤3x-2≤31-2,即-53≤f (x )≤1.故选C.答案:C4.在同一平面直角坐标系中,函数f (x )=ax 与g (x )=a x的图象可能是( )解析:需要对a 讨论:①当a >1时,f (x )=ax 过原点且斜率大于1,g (x )=a x是递增的;②当0<a <1时,f (x )=ax 过原点且斜率小于1,g (x )=a x是减函数,显然B 正确.答案:B 二、填空题 5.下列函数中:①y =2·(2)x;②y =2x -1;③y =⎝ ⎛⎭⎪⎫π2x;④y =31x -;⑤y =x13.是指数函数的是________(填序号). 解析:①中指数式的系数不为1;②中y =2x -1=12·2x的系数亦不为1;④中自变量不为x ;⑤中的指数为常数且底数不是唯一确定的值.答案:③6.若指数函数y =f (x )的图象经过点⎝ ⎛⎭⎪⎫-2,116,则f ⎝ ⎛⎭⎪⎫-32=________. 解析:设f (x )=a x(a >0且a ≠1). 因为f (x )过点⎝ ⎛⎭⎪⎫-2,116,所以116=a -2,所以a =4. 所以f (x )=4x,所以f ⎝ ⎛⎭⎪⎫-32=432-=18. 答案:187.若关于x 的方程2x-a +1=0有负根,则a 的取值范围是________. 解析:因为2x=a -1有负根, 所以x <0, 所以0<2x<1. 所以0<a -1<1. 所以1<a <2. 答案:(1,2) 三、解答题8.若函数y =(a 2-3a +3)·a x是指数函数,求a 的值.解析:由指数函数的定义知⎩⎪⎨⎪⎧a 2-3a +3=1,①a >0且a ≠1,②由①得a =1或2,结合②得a =2. 9.求下列函数的定义域和值域:(1)y =21x-1;(2)y =⎝ ⎛⎭⎪⎫13222x -.解析:(1)要使y =21x-1有意义,需x ≠0,则21x≠1;故21x-1>-1且21x-1≠0,故函数y =21x-1的定义域为{x |x ≠0},函数的值域为(-1,0)∪(0,+∞).(2)函数y =⎝ ⎛⎭⎪⎫13222x -的定义域为实数集R ,由于2x 2≥0,则2x 2-2≥-2.故0<⎝ ⎛⎭⎪⎫13222x -≤9,所以函数y =⎝ ⎛⎭⎪⎫13222x -的值域为(0,9]. [尖子生题库]10.设f (x )=3x,g (x )=⎝ ⎛⎭⎪⎫13x .(1)在同一坐标系中作出f (x ),g (x )的图象;(2)计算f (1)与g (-1),f (π)与g (-π),f (m )与g (-m )的值,从中你能得到什么结论?解析:(1)函数f (x )与g (x )的图象如图所示:(2)f (1)=31=3,g (-1)=⎝ ⎛⎭⎪⎫13-1=3;f (π)=3π,g (-π)=⎝ ⎛⎭⎪⎫13-π=3π;f (m )=3m ,g (-m )=⎝ ⎛⎭⎪⎫13-m =3m .从以上计算的结果看,两个函数当自变量取值互为相反数时,其函数值相等,即当指数函数的底数互为倒数时,它们的图象关于y 轴对称.。
高中数学一对一讲义——函数

3, 4 )
分式中的分母不为零; 偶次方根下的数(或式)大于或等于零; 指数式的底数大于零且不等于一; 对 数式的底数大于零且不等于一,真数大于零。
正切函数
y
tan x
x
R, 且 x
k
2
,k
余切函数
y
cot x
x
R, 且 x
k ,k
反三角函数的定义域
函数 y = arcsinx 的定义域是
[- 1, 1]
ab , a+b+c≥ 3 3 abc ( a, b , c ∈
R
) ,求函数的最值,其题型特征解析式是
和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。 例:
x
2
2 x
(x 1 x 1 x
0) 3
3
=x (
2
x
2
1 x 3
3
1 x
3 3 者的乘积变成常数)
应用公式
如: f
x
1
ex
x ,求 f ( x).
13. 反函数存在的条件是什么?
(一一对应函数) 求反函数的步骤掌握了吗? (①反解 x ;②互换 x 、 y;③注明定义域)
如:求函数
f ( x)
1 x
x
2
x x
0 0
的反函数
在更多时候,反函数的求法只是在选择题中出现,这就为我们这些喜欢偷懒的人提供了大方便。请看这个例题: (2004.全国理 )函数
值是( )
0 ,函数 f ( x)
x
3
ax在 1,
17. 函数 f(x) 具有奇偶性的必要(非充分)条件是什么? ( f(x) 定义域关于原点对称)
高中数学竞赛讲义第三章 函数

第三章 函数一、基础知识定义1 映射,对于任意两个集合A ,B ,依对应法则f ,若对A 中的任意一个元素x ,在B 中都有唯一一个元素与之对应,则称f : A →B 为一个映射。
定义2 单射,若f : A →B 是一个映射且对任意x , y ∈A , x ≠y , 都有f (x )≠f (y )则称之为单射。
定义3 满射,若f : A →B 是映射且对任意y ∈B ,都有一个x ∈A 使得f (x )=y ,则称f : A →B 是A 到B 上的满射。
定义4 一一映射,若f : A →B 既是单射又是满射,则叫做一一映射,只有一一映射存在逆映射,即从B 到A 由相反的对应法则f -1构成的映射,记作f -1: A →B 。
定义5 函数,映射f : A →B 中,若A ,B 都是非空数集,则这个映射为函数。
A 称为它的定义域,若x ∈A , y ∈B ,且f (x )=y (即x 对应B 中的y ),则y 叫做x 的象,x 叫y 的原象。
集合{f (x )|x ∈A }叫函数的值域。
通常函数由解析式给出,此时函数定义域就是使解析式有意义的未知数的取值范围,如函数y =3x -1的定义域为{x |x ≥0,x ∈R}.定义6 反函数,若函数f : A →B (通常记作y =f (x ))是一一映射,则它的逆映射f -1: A →B 叫原函数的反函数,通常写作y =f -1(x ). 这里求反函数的过程是:在解析式y =f (x )中反解x 得x =f -1(y ),然后将x , y 互换得y =f -1(x ),最后指出反函数的定义域即原函数的值域。
例如:函数y =x -11的反函数是y =1-x1(x ≠0). 定理1 互为反函数的两个函数的图象关于直线y =x 对称。
定理2 在定义域上为增(减)函数的函数,其反函数必为增(减)函数。
定义7 函数的性质。
(1)单调性:设函数f (x )在区间I 上满足对任意的x 1, x 2∈I 并且x 1< x 2,总有f (x 1)<f (x 2) (f (x )>f (x 2)),则称f (x )在区间I 上是增(减)函数,区间I 称为单调增(减)区间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学函数知识点总结8. 函数的三要素是什么?如何比较两个函数是否相同? (定义域、对应法则、值域)相同函数的判断方法:①表达式相同;②定义域一致 (两点必须同时具备) 9. 求函数的定义域有哪些常见类型?()()例:函数的定义域是y x x x =--432lg()()()(答:,,,)022334函数定义域求法:● 分式中的分母不为零;● 偶次方根下的数(或式)大于或等于零; ● 指数式的底数大于零且不等于一;●对数式的底数大于零且不等于一,真数大于零。
●正切函数x y tan = ⎪⎭⎫⎝⎛∈+≠∈Z ππk k x R x ,2,且● 余切函数x y cot = ()Z π∈≠∈k k x R x ,,且●反三角函数的定义域函数y =arcsinx 的定义域是 [-1, 1] ,值域是,函数y =arccosx 的定义域是 [-1, 1] ,值域是 [0, π] ,函数y =arctgx 的定义域是 R ,值域是.,函数y =arcctgx 的定义域是 R ,值域是 (0, π) .当以上几个方面有两个或两个以上同时出现时,先分别求出满足每一个条件的自变量的范围,再取他们的交集,就得到函数的定义域。
10. 如何求复合函数的定义域?[]如:函数的定义域是,,,则函数的定f x a b b a F(x f x f x ())()()>->=+-0义域是_____________。
[](答:,)a a -复合函数定义域的求法:已知)(x f y =的定义域为[]n m ,,求[])(x g f y =的定义域,可由n x g m ≤≤)(解出x 的范围,即为[])(x g f y =的定义域。
例 若函数)(x f y =的定义域为⎥⎦⎤⎢⎣⎡2,21,则)(log 2x f 的定义域为 。
11、函数值域的求法1、直接观察法对于一些比较简单的函数,其值域可通过观察得到。
例 求函数y=x1的值域2、配方法配方法是求二次函数值域最基本的方法之一。
例、求函数y=2x -2x+5,x ∈[-1,2]的值域。
3、判别式法对二次函数或者分式函数(分子或分母中有一个是二次)都可通用,但这类题型有时也可以用其他方法进行化简,不必拘泥在判别式上面下面,我把这一类型的详细写出来,希望大家能够看懂.112..22222222ba y 型:直接用不等式性质k+x bxb. y 型,先化简,再用均值不等式x mx nx 1 例:y 1+xx+xx m x n c y 型 通常用判别式x mx n x mx nd. y 型x n法一:用判别式 法二:用换元法,把分母替换掉x x 1(x+1)(x+1)+1 1例:y (x+1)1211x 1x 1x 1==++==≤''++=++++=+++-===+-≥-=+++4、反函数法直接求函数的值域困难时,可以通过求其原函数的定义域来确定原函数的值域。
例 求函数y=6543++x x 值域。
5、函数有界性法直接求函数的值域困难时,可以利用已学过函数的有界性,来确定函数的值域。
我们所说的单调性,最常用的就是三角函数的单调性。
例 求函数y=11+-x x e e ,2sin 11sin y θθ-=+,2sin 11cos y θθ-=+的值域。
6、函数单调性法通常和导数结合,是最近高考考的较多的一个内容 例求函数y=+-25x log31-x (2≤x ≤10)的值域7、换元法通过简单的换元把一个函数变为简单函数,其题型特征是函数解析式含有根式或三角 函数公式模型。
换元法是数学方法中几种最主要方法之一,在求函数的值域中同样发 挥作用。
例 求函数y=x+1-x 的值域。
8 数形结合法其题型是函数解析式具有明显的某种几何意义,如两点的距离公式直线斜率等等,这 类题目若运用数形结合法,往往会更加简单,一目了然,赏心悦目。
例:已知点P (x.y )在圆x 2+y 2=1上,2,(2),2(,20, (1)的取值范围 (2)y-2的取值范围解:(1)令则是一条过(-2,0)的直线. d 为圆心到直线的距离,R 为半径)(2)令y-2即也是直线d dyx x yk y k x x R d x b y x b R +==+-≤=--=≤例求函数y=)2(2-x +)8(2+x 的值域。
例求函数y=1362+-x x+ 542++x x的值域注:求两距离之和时,要将函数 9 、不等式法利用基本不等式a+b ≥2ab ,a+b+c ≥3abc 3(a ,b ,c ∈R+),求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。
例:33()13()32x (3-2x)(0<x<1.5)x x+3-2x =x x (3-2x) (应用公式abc 时,应注意使3者之和变成常数)a b c +⋅⋅≤=++≤ 倒数法有时,直接看不出函数的值域时,把它倒过来之后,你会发现另一番境况例 求函数y=32++x x 的值域多种方法综合运用总之,在具体求某个函数的值域时,首先要仔细、认真观察其题型特征,然后再选择恰当的方法,一般优先考虑直接法,函数单调性法和基本不等式法,然后才考虑用其他各种特殊方法。
12. 求一个函数的解析式或一个函数的反函数时,注明函数的定义域了吗?切记:做题,特别是做大题时, 一定要注意附加条件,如定义域、单位等东西要记得协商,不要犯我当年的错误,与到手的满分失之交臂()如:,求fx e x f x x +=+1().13. 反函数存在的条件是什么?2(0)113322x =x (应用公式a+b+c 者的乘积变成常数)x xx x +>++≥=≥(一一对应函数)求反函数的步骤掌握了吗?(①反解x ;②互换x 、y ;③注明定义域) ()()如:求函数的反函数f x xx xx ()=+≥-<⎧⎨⎪⎩⎪1002在更多时候,反函数的求法只是在选择题中出现,这就为我们这些喜欢偷懒的人提供了大方便。
请看这个例题:(2004.全国理)函数)1(11≥+-=x x y 的反函数是( B )A .y=x 2-2x +2(x <1)B .y=x 2-2x +2(x ≥1)C .y=x 2-2x (x <1)D .y=x 2-2x (x ≥1)14. 反函数的性质有哪些? 反函数性质: 1、 反函数的定义域是原函数的值域 (可扩展为反函数中的x 对应原函数中的y ) 2、 反函数的值域是原函数的定义域(可扩展为反函数中的y 对应原函数中的x )3、反函数的图像和原函数关于直线=x 对称(难怪点(x,y )和点(y ,x )关于直线y=x 对称①互为反函数的图象关于直线y =x 对称; ②保存了原来函数的单调性、奇函数性;③设的定义域为,值域为,,,则y f(x)A C a A b C f(a)=b f 1=∈∈⇔=-()b a[][]∴====---f f a f b a f f b f a b 111()()()(),由反函数的性质,可以快速的解出很多比较麻烦的题目,如 (04. 上海春季高考)已知函数)24(log )(3+=xx f ,则方程4)(1=-x f 的解=x __________.15 . 如何用定义证明函数的单调性? (取值、作差、判正负) 判断函数单调性的方法有三种: (1)定义法:根据定义,设任意得x 1,x 2,找出f(x 1),f(x 2)之间的大小关系 可以变形为求1212()()f x f x x x --的正负号或者12()()f x f x 与1的关系(2)参照图象:①若函数f(x)的图象关于点(a ,b)对称,函数f(x)在关于点(a ,0)的对称区间具有相同的单调性; (特例:奇函数)②若函数f(x)的图象关于直线x =a 对称,则函数f(x)在关于点(a ,0)的对称区间里具有相反的单调性。
(特例:偶函数)(3)利用单调函数的性质:①函数f(x)与f(x)+c(c 是常数)是同向变化的②函数f(x)与cf(x)(c 是常数),当c >0时,它们是同向变化的;当c <0时,它们是反向变化的。
③如果函数f1(x),f2(x)同向变化,则函数f1(x)+f2(x)和它们同向变化;(函数相加)④如果正值函数f1(x),f2(x)同向变化,则函数f1(x)f2(x)和它们同向变化;如果负值函数f1(2)与f2(x)同向变化,则函数f1(x)f2(x)和它们反向变化;(函数相乘)⑤函数f(x)与1()f x 在f(x)的同号区间里反向变化。
⑥若函数u =φ(x),x[α,β]与函数y =F(u),u ∈[φ(α),φ(β)]或u ∈[φ(β),φ(α)]同向变化,则在[α,β]上复合函数y =F[φ(x)]是递增的;若函数u =φ(x),x[α,β]与函数y =F(u),u ∈[φ(α),φ(β)]或u ∈[φ(β),φ(α)]反向变化,则在[α,β]上复合函数y =F[φ(x)]是递减的。
(同增异减)⑦若函数y =f(x)是严格单调的,则其反函数x =f -1(y)也是严格单调的,而且,它们的增减性相同。
()如:求的单y x x =-+log 122216. 如何利用导数判断函数的单调性?()在区间,内,若总有则为增函数。
(在个别点上导数等于a b f x f x '()()≥0零,不影响函数的单调性),反之也对,若呢?f x '()≤0[)如:已知,函数在,上是单调增函数,则的最大a f x x ax a >=-+∞013()值是( )17. 函数f(x)具有奇偶性的必要(非充分)条件是什么? (f(x)定义域关于原点对称) 若总成立为奇函数函数图象关于原点对称f x f x f x ()()()-=-⇔⇔若总成立为偶函数函数图象关于轴对称f x f x f x y ()()()-=⇔⇔注意如下结论:(1)在公共定义域内:两个奇函数的乘积是偶函数;两个偶函数的乘积是偶函数;一个偶函数与奇函数的乘积是奇函数。
()若是奇函数且定义域中有原点,则。
2f(x)f(0)0=如:若·为奇函数,则实数f x a a a x x()=+-+=2221又如:为定义在,上的奇函数,当,时,,f x x f x xx ()()()()-∈=+1101241()求在,上的解析式。
f x ()-11判断函数奇偶性的方法 一、定义域法一个函数是奇(偶)函数,其定义域必关于原点对称,它是函数为奇(偶)函数的必要条件.若函数的定义域不关于原点对称,则函数为非奇非偶函数.二、 奇偶函数定义法在给定函数的定义域关于原点对称的前提下,计算)(x f -,然后根据函数的奇偶性的定义判断其奇偶性.这种方法可以做如下变形f(x)+f(-x) =0 奇函数f(x)-f(-x)=0 偶函数f(x)1 偶函数f(-x)f(x)1 奇函数f(-x)==-三、复合函数奇偶性18. 你熟悉周期函数的定义吗?()(若存在实数(),在定义域内总有,则为周期T T f x T f x f x ≠+=0()()函数,T 是一个周期。
