电路理论基础第四版 孙立山 陈希有主编 第7章习题答案详解
电路习题第六七章含答案

习题第六、七章1. 根据元件的V AR 直接填写图中的未知量。
当i =4A 时,则u =___________,当i =2e -2t A 时,则u =____________。
2. 图示电路,电感上的电流波形如图所示,求电压u (t)和电感吸收的功率p(t), 并绘出它们的波形。
3. 图示电路中:R 1=10Ω,R 2=4Ω,R 3=15Ω,L=1H ,电压u 1的初始值为u 1(0+) = 15V ,求零输入响应u L (t)。
4. 根据元件的V AR 直接填写图旁的未知量。
当u =5V 时,则i =___________, 当u =7e -2ti =___ ________,5. 图示RC 电路,原处于直流稳态,当t=0时,开关从1投向2。
试按u C (t) 的三要素定性作出u C (t) 的波形图。
)6. 根据元件的V AR 直接填写图中的未知量。
当u c=3V 时, 则i = ,当uc =e -3t V 时,则u = 。
7. 图示电路中,开关合在1时已达稳态。
t=0时开关由1合向2,求t>0时的u L (t)。
8. 图示电路,电容上的电流波形如图所示, u (0)=0,求电压u (t),并画波形。
9. 图示电路中,U c =50V ,R 1 =5Ω,R 2 = R 3=10Ω,C= 0.5F ,I s =2A ,电路换路前已达到稳态,求s 闭合后电容上的电压u c (t)。
10. 按元件的V AR 直接填写图旁的未知量。
当i L =1A 时,则i =__________, 当 i L =e -t A 时,则i =__________。
11. 图示RC 电路,原处于直流稳态,当t=0时,开关从1投向2,试按u C (t)的三要素定性作出u C (t)的波形图。
)12. 图示电路中,u s =2V ,R 1=1K Ω,R 2=2KΩ,C=300μF ,t <0时电路处于稳态,在t = 0时,将开关s 闭合,求u c (t)。
电路理论基础第四版孙立山陈希有主编第5章习题答案详解

教材习题5答案部分(p151)答案略答案负载各相阻抗化为星形联接为设A相电源相电压为,A相负载线电流与电源相电流相等由三角形联接得相电流与线电流关系得即负载相电流为。
答案解:电路联接关系如图(a)所示。
负载断开时电源的输出线电压等于图中相电压的倍。
下面计算相电压。
设负载A相电压为,对于感性负载,由,得,则采用单相分析法,如图(b)所示。
电源相电压为当负载断开时,电源输出电压为答案略答案略答案略答案解:设电源为星形联接,电源A相电压相量为则电源线电压分别为,,。
(1)设电路联接如图(a)所示,化为单相计算,如图(b)所示。
因为负载为星形联接,所以负载相电压,,又因为,相电流电压、电流相量图如图(c)所示。
(2) C相断线时,,电源线电压降落在AB相上。
如图(d)所示。
(3) C相负载短路时,如图(e)所示。
,答案解:(1)电路模型如图(a)所示。
图题负载相电流负载线电流(2)设A相负载断路,如图(b)所示。
由图(b)可见,,B、C相负载因相电压不变,均为电源线电压,故电流(3)设端线A断路,如图(c)所示。
由图(c)可见答案解:电路如图所示:图题因为三相负载平均功率等于每相负载平均功率的3倍,所以答案解:星形接法时,三角形接法时负载每相承受电压为380V,是星形接法时的倍。
根据功率与电压的平方成正比关系可知,三角形联接时负载的平均功率是星形联接的3倍。
即解:由已知功率因数,可求得星形和三角形负载的阻抗角分别为:,方法一:因为负载端线电压所以星形负载相电流为星形负载阻抗三角形负载相电流为三角形负载阻抗将三角形联接等效成星形联接,设负载阻抗为,化为单相分析法,则电路如图 (b)所示。
设V,,A由KVL方程得,电源相电压为则电源线电压为V方法二:负载总平均功率负载总无功功率负载总功率因数因为负载线电流电源发出平均功率为无功功率为电源视在功率为答案略答案解:设电源电压则设负载为星形联接,如图(b)所示。
阻抗角为,则A相负载电流滞后电压的角度为,滞后的角度为,即功率表的读数由对称三相负载无功功率的计算公式得。
第7章+静电场+习题和思考题

1 E d S 根据高斯定理
0
q
S内
i
S
Q
q q
习题图7-1
第七章 习题解答 第七章 习题解答
C 3. 关于电场线,以下说法哪个正确。 (A)电场线上各点的电场强度大小相等; (B) 电场线是一条曲线,曲线上的每一点的切线方向都与该点 的电场强度方向平行; (C) 匀强电场中开始处于静止的电荷,在电场力的作用下运动 的轨迹必与一条电场线重合; (D) 在无电荷的电场空间,电场线可以相交。 答 :电场线上任意点的切线方向为该点处电场强度的方向; 电场线密度表针该点处电场强度的大小;电场为有源场,任 意电场线不相交;在均匀场中,电场强度处处相等;电荷在 均匀电场中静止开始运动,其运动轨迹必沿与一条电场线运 动。
解: (1) (0,a)处点电荷在 O 点产生的电场方向从 O 点指 向 y 轴正向;(0,-a)处点电荷在 O 点产生的电场方向从 O 点 指向 y 轴负向;(2a,0)处点电荷在 O 点产生的电场方向从 O 点指向 x 轴正向。 (2)
Eao 2Q Q j j 2 2 40 a 20a 1
1 2Q Q j j 2 2 40 a 20a
y
E ao
a
2Q
Q
a
O
2Q
a 2a
x
E2ao
Q Q i i 2 2 40 ( 2a) 160a 1
第七章 习题解答 第七章 习题解答
(3)
Eo Eao Eao E2ao Q Q Q j ( j) i 2 2 2 20a 20a 160a
第七章 习题解答 第七章 习题解答 球心电势
U E dl
电路第四版课后习题答案

电路第四版课后习题答案第一章:电路基础1. 确定电路中各元件的电压和电流。
- 根据基尔霍夫电压定律和电流定律,我们可以列出方程组来求解未知的电压和电流值。
2. 计算电路的等效电阻。
- 使用串联和并联电阻的计算公式,可以求出电路的等效电阻。
3. 应用欧姆定律解决实际问题。
- 根据欧姆定律 \( V = IR \),可以计算出电路中的电压或电流。
第二章:直流电路分析1. 使用节点电压法分析电路。
- 选择一个参考节点,然后对其他节点应用基尔霍夫电流定律,列出方程组并求解。
2. 使用网孔电流法分析电路。
- 选择电路中的网孔,对每个网孔应用基尔霍夫电压定律,列出方程组并求解。
3. 应用叠加定理解决复杂电路问题。
- 将复杂电路分解为简单的子电路,然后应用叠加定理计算总的电压或电流。
第三章:交流电路分析1. 计算交流电路的瞬时值、有效值和平均值。
- 根据交流信号的表达式,可以计算出不同参数。
2. 使用相量法分析交流电路。
- 将交流信号转换为复数形式,然后使用复数运算来简化电路分析。
3. 计算RLC串联电路的频率响应。
- 根据电路的阻抗,可以分析电路在不同频率下的响应。
第四章:半导体器件1. 分析二极管电路。
- 根据二极管的伏安特性,可以分析电路中的电流和电压。
2. 使用晶体管放大电路。
- 分析晶体管的共发射极、共基极和共集电极放大电路,并计算放大倍数。
3. 应用场效应管进行电路设计。
- 根据场效应管的特性,设计满足特定要求的电路。
第五章:数字逻辑电路1. 理解逻辑门的工作原理。
- 描述不同逻辑门(如与门、或门、非门等)的逻辑功能和电路实现。
2. 使用布尔代数简化逻辑表达式。
- 应用布尔代数的规则来简化复杂的逻辑表达式。
3. 设计组合逻辑电路。
- 根据给定的逻辑功能,设计出相应的组合逻辑电路。
第六章:模拟集成电路1. 分析运算放大器电路。
- 根据运算放大器的特性,分析电路的增益、输入和输出关系。
2. 设计滤波器电路。
发电厂电气部分第四版课后习题答案第1章---第7章

发电厂电气部分第四版课后习题答案第1章---第7章第一章能源和发电1-1 人类所认识的能量形式有哪些?并说明其特点。
答:第一、机械能。
它包括固体一流体的动能,势能,弹性能及表面张力能等。
其中动能和势能是大类最早认识的能量,称为宏观机械能。
第二、热能。
它是有构成物体的微观原子及分子振动与运行的动能,其宏观表现为温度的高低,反映了物体原子及分子运行的强度。
第三、化学能。
它是物质结构能的一种,即原子核外进行化学瓜是放出的能量,利用最普遍的化学能是燃烧碳和氢,而这两种元素是煤、石油、天然气等燃料中最主要的可燃元素。
第四、辐射能。
它是物质以电磁波形式发射的能量。
如地球表面所接受的太阳能就是辐射能的一种。
第五、核能。
这是蕴藏在原子核内的粒子间相互作用面释放的能。
释放巨大核能的核反应有两种,邓核裂变应和核聚变反应。
第六、电能。
它是与电子流动和积累有关的一种能量,通常是电池中的化学能而来的。
或是通过发电机将机械能转换得到的;反之,电能也可以通过电灯转换为光能,通过电动机转换为机械能,从而显示出电做功的本领。
1-2 能源分类方法有哪些?电能的特点及其在国民经济中的地位和作用?答:一、按获得方法分为一次能源和二次能源;二、按被利用程度分为常规能源和新能源;三、按能否再生分为可再生能源和非再生能源;四、按能源本身的性质分为含能体能源和过程性能源。
电能的特点:便于大规模生产和远距离输送;方便转换易于控制;损耗小;效率高;无气体和噪声污染。
随着科学技术的发展,电能的应用不仅影响到社会物质生产的各个侧面,也越来越广泛的渗透到人类生活的每个层面。
电气化在某种程度上成为现代化的同义词。
电气化程度也成为衡量社会文明发展水平的重要标志。
1-3 火力发电厂的分类,其电能生产过程及其特点?答:按燃料分:燃煤发电厂;燃油发电厂;燃气发电厂;余热发电厂。
按蒸气压力和温度分:中低压发电厂;高压发电厂;超高压发电厂;亚临界压力发电厂;超临界压力发电厂。
电路分析基础第四版课后习题答案
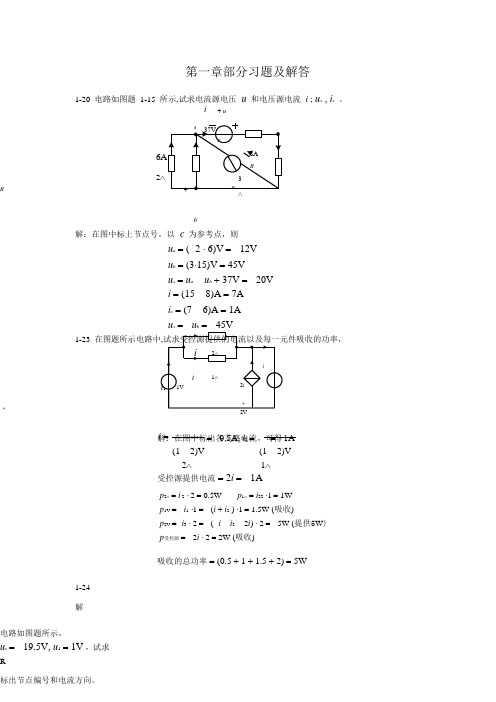
i = = 0.5A, i 2 = =1A 第一章部分习题及解答1-20 电路如图题 1-15 所示,试求电流源电压 u 和电压源电流 i ; u x , i x 。
i+ u2Rb解:在图中标上节点号,以 c 为参考点,则u a = ( 2 ⋅ 6)V = 12V u b = (3⋅15)V = 45V u x = u a u b + 37V = 20V i = (15 8)A = 7A i x = (7 6)A = 1A x b 1-23+解:在图中标出各支路电流,可得(1 2)V (1 2)V 2∧ 1∧受控源提供电流 = 2i = 1Ap 2∧ = i 2 ⋅ 2 = 0.5Wp 1∧ = i 22 ⋅1 = 1Wp 1V = i 1 ⋅1 = (i + i 2 ) ⋅1 = 1.5W (吸收)p 2V = i 3 ⋅ 2 = ( i i 2 2i ) ⋅ 2 = 5W (提供5W ) p 受控源 = 2i ⋅ 2 = 2W (吸收)吸收的总功率 = (0.5 + 1 + 1.5 + 2) = 5W1-24 解电路如图题所示,u s = 19.5V, u 1 = 1V ,试求R标出节点编号和电流方向。
ai +3∧u∧b+ui2∧4∧i+10ucRiiei1 =u11= 1A, u bc = u1 10u1 = 9Vu bc2u ab = i s ⋅ 3 = 10.5Vu ce = u cb + u ba + u s = (9 + 10.5 19.5) = 0V为确定R,需计算i4,u ce = u cd + u de = 0 ® u de = u cd = 10u1 = 10V故1-33 试用支路电流法求解图题所示电路中的支路电流i1, i2 , i3。
a 1∧ci+6Vb解求解三个未知量需要三个独立方程。
由KCL可得其中之一,即i1 + i2 + i3 = 5对不含电流源的两个网孔,列写KVL方程,得网孔badb网孔bdacb2i1 3i2 + 8 = 08 + 3i2 i3 + 6 = 0i 2 = = 4.5A, i s = i 1 + i 2 = 3.5Ai 3 = = 2.5A, i 4 = i s i 3 = ( 3.5 + 2.5)A = 1A整理得: ♦ 2i 1 2 = 8+ 3i ® ♦i 2 = 2A♥♥♣i 1 + i 2 + i 3 = 5 ♣i 1 = 1A ♠ ♠♠3i 2 i 3 = 2 ♠i 3 = 4A♦ i1 + 8i2 3i3 = 9 ® ♦i2 = 1A♥i3 = 1A® ♦♠(R +R)i M2 R1i M 1 R2i M 3 =u ♠♠♠==0♣i M 1 = 24 u® ♦(3 + 4)i M 3 = u ® ♦ ♥i M 3 i M 1 = 8♥ 第二章部分习题及解答2-1试用网孔电流法求图题所示电路中的电流i和电压u ab。
电路理论基础习题答案

电路理论基础习题答案第一章1-1. (a)、(b)吸收10W ;(c)、(d)发出10W. 1-2. –1A; –10V; –1A; – 4mW.1-3. –0.5A; –6V; –15e –t V; 1.75cos2t A; 3Ω; 1.8cos 22t W.1-4. u =104 i ; u = -104 i ; u =2000i ; u = -104 i ; 1-5.1-6. 0.1A. 1-7.1-8. 2F; 4C; 0; 4J. 1-9. 9.6V,0.192W, 1.152mJ; 16V , 0, 3.2mJ.1-10. 1– e -106t A , t >0 取s .1-11. 3H, 6(1– t )2 J; 3mH, 6(1–1000 t ) 2 mJ;1-12. 0.4F, 0 .1-13. 供12W; 吸40W;吸2W; (2V)供26W, (5A)吸10W. 1-14. –40V , –1mA; –50V, –1mA; 50V , 1mA. 1-15. 0.5A,1W; 2A,4W; –1A, –2W; 1A,2W. 1-16. 10V ,50W;50V ,250W;–3V ,–15W;2V ,10W. 1-17. (a)2V;R 耗4/3W;U S : –2/3W, I S : 2W; (b) –3V; R 耗3W; U S : –2W, I S :5W; (c)2V ,–3V; R 耗4W;3W;U S :2W, I S :5W; 1-18. 24V , 发72W; 3A, 吸15W;24V 电压源; 3A ↓电流源或5/3Ω电阻. 1-19. 0,U S /R L ,U S ;U S /R 1 ,U S /R 1 , –U S R f /R 1 . 1-20. 6A, 4A, 2A, 1A, 4A; 8V, –10V , 18V . 1-21. K 打开:(a)0, 0, 0; (b)10V , 0, 10V; (c)10V,10V ,0; K 闭合: (a)10V ,4V ,6V; (b)4V ,4V ,0; (c)4V,0,4V; 1-22. 2V; 7V; 3.25V; 2V. 1-23. 10Ω.1-24. 14V .1-25. –2.333V , 1.333A; 0.4V , 0.8A.1-26. 12V , 2A, –48W; –6V , 3A, –54W . ※第二章2-1. 2.5Ω; 1.6R ; 8/3Ω; 0.5R ; 4Ω; 1.448Ω; . R /8; 1.5Ω; 1.269Ω; 40Ω; 14Ω. 2-2. 11.11Ω; 8Ω; 12.5Ω. 2-3. 1.618Ω.2-4. 400V;363.6V;I A =.5A, 电流表及滑线电阻损坏. 2-6. 5k Ω. 2-7. 0.75Ω.2-8. 10/3A,1.2Ω;–5V ,3Ω; 8V ,4Ω; 0.5A,30/11Ω. 2-9. 1A,2Ω; 5V,2Ω; 2A; 2A; 2A,6Ω. 2-10. –75mA; –0.5A.2-11. 6Ω; 7.5Ω; 0; 2.1Ω. 2-12. 4Ω; 1.5Ω; 2k Ω. 2-13. 5.333A; 4.286A. 2-14. (a) –1 A ↓; (b) –2 A ↓, 吸20W. 2-16. 3A. 2-17. 7.33V . 2-18. 86.76W. 2-19. 1V , 4W. 2-20. 64W.2-21. 15A, 11A, 17A. 2-23. 7V , 3A; 8V ,1A. 2-24. 4V , 2.5V, 2V. 2-26. 60V . 2-27. 4.5V. 2-28. –18V .2-29. 原构成无解的矛盾方程组; (改后)4V ,10V . 2-30. 3.33 k , 50 k . 2-31. R 3 (R 1 +R 2 ) i S /R 1 .2-32. 可证明 I L =-u S /R 3 . 2-33. –2 ; 4 .2-34. (u S1 + u S2 + u S3 )/3 . ※第三章3-1. –1+9=8V; 6+9=15V; sin t +0.2 e – t V. 3-2. 155V . 3-3. 190mA.i A0 s 1 12 3 1-e -t t 0 t ms i mA 410 0 t ms p mW 4 100 2 25i , A 0.4 .75 t 0 .25 1.25 ms -0.4 (d) u , V 80 0 10-20 t , ms(f ) u , V 1000 10 t , ms (e)p (W) 100 1 2 t (s) -103-4. 1.8倍.3-5. 左供52W, 右供78W. 3-6. 1; 1A; 0.75A.3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A. 3-8. 20V , –75.38V.3-9. –1A; 2A; –17.3mA. 3-10. 5V , 20; –2V, 4. 3-12. 4.6. 3-13. 2V; 0.5A. 3-14. 10V , 5k .3-15. 4/3, 75W; 4/3, 4.69W. 3-16. 1, 2.25W. 3-18. 50. 3-19. 0.2A. 3-20. 1A. 3-21. 1.6V . 3-22. 4A; –2A.3-23. 23.6V; 5A,10V . 3-24. 52V . ※第四章4-1. 141.1V , 100V , 50Hz, 0.02s,0o , –120o ; 120 o.4-2. 7.07/0 o A, 1/–45 o A, 18.75/–40.9 oA. 4-3. 3mU , 7.75mA .4-4. 10/53.13o A, 10/126.87o A, 10/–126.87oA,10/–53.13oA ;各瞬时表达式略。
电路理论基础习题答案

电路理论基础习题答案第一章1-1. (a)、(b)吸收10W ;(c)、(d)发出10W. 1-2. –1A; –10V; –1A; – 4mW.1-3. –0.5A; –6V; –15e –t V; 1.75cos2t A; 3Ω; 1.8cos 22t W.1-4. u =104 i ; u = -104 i ; u =2000i ; u = -104 i ;1-8. 2F; 4 C; 0; 4 J. 1-9. 9.6V,0.192W, 1.152mJ; 16V , 0, 3.2mJ.1-10. 1– e -106t A , t >0 取s .1-11. 3H, 6(1– t )2 J; 3mH, 6(1–1000 t ) 2 mJ;1-12. 0.4F, 0 .1-13. 供12W; 吸40W;吸2W; (2V)供26W, (5A)吸10W. 1-14. –40V , –1mA; –50V, –1mA; 50V , 1mA. 1-15. 0.5A,1W; 2A,4W; –1A, –2W; 1A,2W. 1-16. 10V ,50W;50V ,250W;–3V ,–15W;2V ,10W. 1-17. (a)2V;R 耗4/3W;U S : –2/3W, I S : 2W; (b) –3V; R 耗3W; U S : –2W, I S :5W; (c)2V ,–3V; R 耗4W;3W;U S :2W, I S :5W; 1-18. 24V , 发72W; 3A, 吸15W;24V 电压源; 3A ↓电流源或5/3Ω电阻. 1-19. 0,U S /R L ,U S ;U S /R 1 ,U S /R 1 , –U S R f /R 1 . 1-20. 6A, 4A, 2A, 1A, 4A; 8V, –10V , 18V . 1-21. K 打开:(a)0, 0, 0; (b)10V, 0, 10V; (c)10V,10V ,0; K 闭合: (a)10V ,4V ,6V; (b)4V ,4V ,0; (c)4V ,0,4V; 1-22. 2V; 7V; 3.25V; 2V. 1-23. 10Ω.1-24. 14V .1-25. –2.333V , 1.333A; 0.4V , 0.8A. 1-26. 80V . ※第二章2-1. 2.5Ω; 1.6R ; 8/3Ω; 0.5R ; 4Ω; 1.448Ω; . R /8; 1.5Ω; 1.269Ω; 40Ω; 14Ω.2-2. W P 484=低,W P 4484⨯=高. 2-3. 1.618Ω.2-4. 400V;363.6V;I A =.5A, 电流表及滑线电阻损坏. 2-6. 5k Ω. 2-7. 0.75Ω.2-8.R 1=38K Ω,R 2=10/3K Ω 2-9. 10/3A,1.2Ω;–5V,3Ω; 8V ,4Ω; 0.5A,30/11Ω. 2-10. 1A,2Ω; 5V ,2Ω; 2A; 2A; 2A,6Ω. 2-11. –75mA; –0.5A. 2-12. 6Ω; 7.5Ω; 0; 2.1Ω. 2-13. 4Ω; 1.5Ω; 2k Ω. 2-14.1.6V ,-24V 2-15. (a) (b) –2 A ↓, 吸20W. 2-16. 2-17. 3A. 2-18. 7.33V . 2-19. 86.76W. 2-20. 1V, 4W. 2-21. 64W.2-22.电压源发50W ,电流源发1050W 2-232-24. 7V, 3A; 8V ,1A. 2-25. 4V, 2.5V, 2V. 2-26.2Ω 2-27. 60V . 2-28. 4.5V. 2-29. –18V .2-30. 原构成无解的矛盾方程组; (改后)4V,10V . 2-312-32.2.5A2-33. 3.33 k , 50 k .2-34 加法运算 )(3210i i i u u u u ++-= 2-35. R 3 (R 1 +R 2 ) i S /R 1 . 2-36. 可证明 I L =- u S /R 3 . 2-37. –2 ; 4 . ※第三章3-1. 44V;–1+9=8V; 6+9=15V; sin t +0.2 e – t V.3-2. 155V.3-3. 190mA.3-4. 1.8倍.3-5. 左供52W, 右供78W.3-6. 1 ; 1A; 0.75A.3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A.3-8. 20V, –75.38V.3-9. –1A; 2A; 1A.3-10. 5V, 20 ; –2V, 4 .3-12. 4.6 .3-13. 2V; 0.5A.3-14. 10V, 5k .3-15.3-16.22.5V3-17. 4/3 , 75W; 4/3 , 4.69W.3-18. 3 , 529/12W.; 1 , 2.25W.3-193-20. 50 .3-21. 0.2A.3-22. 1A.3-23. 1.6V.3-24. 4A;3-25. 23.6V; 5A,10V.3-26.3-27 4V3-28. ※第四章4-1. 141.1V, 100V, 50Hz, 0.02s,0o, –120o; 120 o. 4-2. 7. o A, 1/–45 o A, 18.75/–40.9 o A.4-3. U, 7.75mA .4-4. 10/53.13A, 10/126.87o A, 10/–126.87o A, 10/–53.13o A;各瞬时表达式略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《电路理论基础》习题7答案答案7.1解:由阻抗并联等效公式得:Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为:233)10(110)j (ωω-+=Z ,)10arctan()(3ωωθ--=令2/1)j (c=ωZ 求得截止角频率rad/s 103c=ω,故通带及阻带分别为: 通带=ω0~rad/s 103,阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
1234O(b)|)j (|ωZ 10.7(c)1234O)(ωθο45-ο90-c/ωωc/ωω答案7.2解: RC 并联的等效阻抗RC RC R C R Z RCωωωj 1j /1j /+=+= RCRC Z L Z U U H +==ωωj /)j (12&& RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时, 1)j (=ωH ;当∞→ω时,0)j (=ωH所以它具有低通特性。
答案7.3解:设1111111j j 1//C R R R C R Z ωω+==, 2222222j j 1//C R R R C R Z ωω+== 由分压公式得:12122U Z Z Z U &&+= )j 1()j 1()j 1()j (11222111212C R R C R R C R R U U H ωωωω++++==&& 当R 1C 1=R 2C 2时,得212)j (R R R H +=ω,此网络函数模及辐角均不与频率无关。
答案7.4解:因为电路处于谐振状态,故电感与电容串联电路相当于短路,因此有50S12121==+I U R R R R Ω代以Ω=1001R ,解得Ω=1002R 又因为电路处于谐振状态 , 所以 Ω==100C L X X 故有V 5021S12=⨯+==L L L X R R I R X I U 答案7.5解:(1)根据题意,电路发生谐振时,存在下列关系:⎪⎩⎪⎨⎧======V10A1/rad/s 10/14LI U R U I LC L ωω 解得 ⎪⎩⎪⎨⎧==Ω=F 10mH 11.0μC L R 品质因数 1001.010===U U Q L(2)V 9010V 901001)(j ︒-∠=︒-∠⨯︒∠==C I U Cω&& 即有V )90cos(210︒-=t u Cω 答案9.9解:由串联谐振规律得:⎪⎪⎩⎪⎪⎨⎧===∆==Ω=RL Q Q LC R /rad/s 100/rad/s 10/1100030ωωωω 解得 ⎪⎩⎪⎨⎧==Ω=1μμC H 1100L R答案7.6解:(1)F 10034.132.0)8752(117220-⨯=⨯⨯==πωL C Qωω=∆ , 5.3250/875/0==∆=ωωQ R L Q /0ω=, Ω=⨯⨯==65.5025.3/32.08752/0πωQ L R 谐振频率为Hz 759)14121(021c ≈⨯++-=f Q Q f Hz 1009)14121(02c2≈⨯++=f QQ f(2) 谐振时电路的平均功率为:W 071.165.502)65.502/2.23(2200=⨯==R I P 在截止频率处,电流下降至谐振电流0I 的2/1,故功率减小到0P 的一半,所以当Hz 759=f 和Hz 1009=f 时,电路平均功率均为W 535.02/0==P P (3)V 2.812.235.3=⨯===QU U U CL 答案7.7解:由谐振时阻抗为Ω310得 Ω=1000RRLC 并联电路带宽:Q/0ωω=∆(参考题9.16) 由带宽与谐振角频率及品质因数的关系得:10/0=∆=ωωQ RLC 并联电路的品质因数为10/0==G C Q ω 由上式求得:μF10)10001000/(10/100=⨯==ωG C 由C L 00/1ωω=得 H1.0H )1010/(1/15620=⨯==-C L ω答案7.8略 答案7.9解:当两线圈顺接时,等效电感H 05.0221=++=M L L L 谐振角频率s rad 10102005.011361=⨯⨯==-LC ω 取V06︒∠=U &,则谐振时的电流 A 04.0A 1050621︒∠=+︒∠=+=R R U I && 由互感的元件方程得: j124(0.4]V j100.4j20)10[(j )j (j8)V 2(0.4]V j100.4j10)5[(j )j (1212211111+=⨯+⨯+=++=+=⨯+⨯+=++=I M I L R U I M I L R U &&&&&&ωωωω两线圈电压的有效值分别为V 24.882221=+=U ,V 65.12124222=+=U 当两线圈反接时,等效电感H 01.0221'=-+=M L L L 谐振角频率rad/s 10236.2102001.01362⨯=⨯⨯=-ω j8.94(0.4A j22.36)10(j )j (2V A 4.05j )j (2222221211+=⨯Ω+=-+==⨯Ω=-+=I M I L R U I M I L R U &&&&&&ωωωω此时两线圈电压的有效值分别为V 21=U ,V 8.995.84222=+=U 答案7.10略答案7.11图示电路,V )cos(22S t u ω=,角频率rad/s 100=ω,Ω=1R ,F 1021-=C ,F 105.022-⨯=C 。
求:(1)L 为何值时电流I 为最大??max =I 并求此时电压1u 。
(2)L 为何值时电流I 为最小??min =I 并求此时电压1u 。
解:S 20U =∠︒&,电路的相量模型如图所示,其中S eqU I Z =(1分)(1)当L 与1C 发生串联谐振时,并联部分相当于短路,此时I 取最大值。
2110.01H L C ω==,m 2A S ax U I R ==(1分)设20I︒=∠&,则21211j 2011j j j I C I I L C C ωωωω===∠︒++&&&111290j U I C ω==∠-︒&&122cos(90)V u t ω∴=-︒ (2分)(2)当并联部分发生谐振时,I 取最小值,此时min 0I =211j 01j j eq Y C L C ωωω=+=+12211C C LC ω+=- 解得0.03H L = (1分)此时 112111j 1201180V11j j SC U U LC L C ωωωω︒==⋅∠=∠︒-+&&12cos(180)V u t ω=+︒(2分)答案7.12略答案7.13解:(1)消去互感后,得图(b )所示等效电路。
1C +-1u Su R 2C L i1+-1U S U R j L ωIj 21C ω1j C ωZeq 1IML -1ML -2M CSI &R I &ab(b)当等效电感M 和电容C 发生串联谐振时,即μF 1110/1/162=⨯==M C ω, ab 端相当于短路,端电压为零,则电流I 也为零。
所以电流I 的最小值为0min =I (2)先分析ab 端的等效导纳,由图(b)得C M M L R Y ωωω/j j 1)(j 12ab-+-+= ])()(/11[j )(222222222M L R M L M C M L R R -+---+-+=ωωωωω由于电容C 变化时,ab Y 的实部不变,所以,当并联部分发生谐振时,ab Y 最小,电压ab S ab /Y I U =为最大,因此电流I 也为最大。
令0)()(/1122222=-+---M L R M L M C ωωωω 得μF 2.0F 102342)(622222=⨯⨯+=-+-=-M L L R M L C ω 由分流公式求得:︒-∠=--=-++--=4522j 24j )(j )/1(j )/1(j 2S S S I I I M L R C M C M I &&&&ωωωωω 故当μF 2.0=C 时,mA 14.142S max ==I I 答案7.14图示电路,V )cos(210t u ω=,角频率rad/s 100=ω,Ω=10R ,H 3.01=L ,H 2.02=L ,H 1.0=M 。
求:(1)当开关断开时,C 为何值时电压U &与电流I &同相位?并求此时电压1u 。
(2)当开关短接时,C 为何值时电压U &与电流I &同相位?**R C1L 2L U&I&+-M+-1u RCeqL U &I &-R CeqL 'U&I &-解:开关断开时,应用串联消互感等效,此时eq 12(2)L L L M =+-,由串联谐振特点,当C 与eq L 发生串联谐振时,电压U &与电流I &同相位,此时 (2分)eq 111000.3L C C==解得43.310C F -=⨯ (2分)1110010102090U I R U j L I j M I ωω︒∠===∠︒=⋅-⋅=∠︒&&&&& 解得1202cos(90)u t ω=+︒ (2分) 开关闭合时,应用并联消互感等效,此时2eq12()()M L M L L M M L M -'=-++-,由串联谐振特点,当C 与eq L '发生串联谐振时,电压U &与电流I &同相位,此时 由谐振产生条件eq1j 0j L C ωω'+= (2分) 4410F C -=⨯ (2分)答案7.15略 答案7.16解:端口等效阻抗]1)(j[)()(j j j 1)j (222222CL R LR L R R L L R R L C Z ωωωωωωωωω-+++=+⨯+= (1) 令 []0ZIm =;解得谐振角频率 220LLC R R -=ω将0ω代回式(1),得RC L Z =)j (0ω 答案7.17略答案7.18解:由分压公式求得:LLCR R RCR R L CRRC R C R L C R C R U U H ωωωωωωωωωωωj )j 1j (j 1)j 1j j (j 1j )j (2iO +-=+++=+++==&&若输出电压u o 中正弦分量占滤波前的5%,则相当于%5)()()j (222=+-=L LCR R RH ωωω 代入数值解得F183.0μ≈C答案7.19解:当1L 、C 对基波发生并联谐振时,滤波器能够阻止电流的基波通至负载,由此得:CL ωω11= (1) 解得mH 254.0)2(11221≈==Cf C L πω 当1L 、C 与2L 组成的电路对九次谐波发生串联谐振时,九次谐波可以顺利 地通至负载,由此得到:0j9)9j /(1j9121=++L L C ωωω (2) 将式(1)代入式(2)解得H 17.3181112μω≈-=CL L L。
