第二章 线性规划习题课
合集下载
《管理运筹学》第四版 第2章 线性规划的图解法 课后习题解析
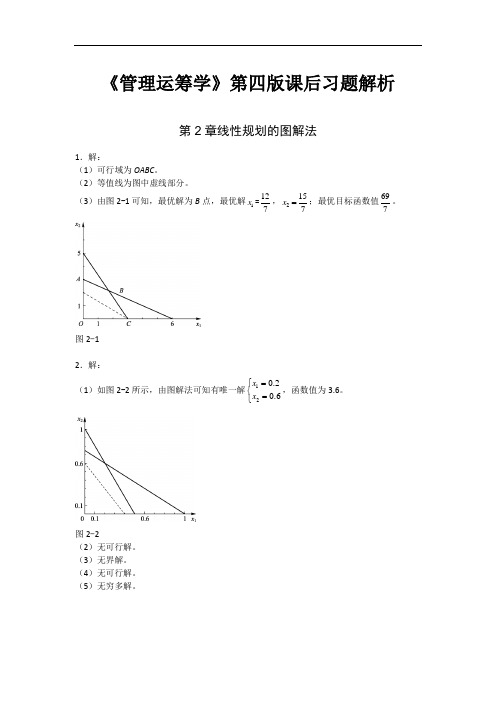
《管理运筹学》第四版课后习题解析第2章线性规划的图解法1．解：（1）可行域为OABC 。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B 点，最优解1x =127，2157x =；最优目标函数值697。
图2-12．解：（1）如图2-2所示，由图解法可知有唯一解120.20.6x x =⎧⎨=⎩，函数值为3.6。
图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
（5）无穷多解。
（6）有唯一解1220383x x ⎧=⎪⎪⎨⎪=⎪⎩，函数值为923。
3．解：（1）标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥（2）标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥（3）标准形式12212min 2200f x x x s s ''''=-+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4．解： 标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥ 松弛变量（0，0） 最优解为1x =1，x 2=3/2。
5．解：标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量（0, 0, 13） 最优解为x 1=1，x 2=5。
北航刘红英数学规划教材课后习题参考答案
ri(x)∇ri(x)
=
2A(x)T r(x),
∇2f (x)
= =
2 2
∑m ∑mi=1
i=1
ri(x)∇2ri(x) ri(x)∇2ri(x)
+ +
2
∑n
i=1
∇ri
(x)(∇ri
(x))T
2A(x)T A(x).
1.6 考虑向量值函数 f (x) : Rn → Rm ，设 f 的每个分量函数 fi(x) 在 x′ 都可微. 写出 f 在 x′ 的Taylor展式，请用 A(x)T 表示 ∇f (x)T (= [∇f1(x), · · · , ∇fm(x)]).
maximize 200x + 60y + 206z
subject to 3x + y + 5z ≤ 8000000
5x + y + 3z ≤ 5000000
x, y, z ≥ 0, 且 x, y, z 是整数.
忽略掉整性要求后，调用 Matlab 中的 linprog.m 函数求解，得最优解 x = 0, y = 500000, z = 1500000，自动满足整性要求.
的最优值相同，将这个问题的最优解投影到 (x, y, z) 所在的空间可以得到原问题的解. 这个问题可以写成线性规划问题：
minimize t1 + t2 + t3 subject to x + y ≤ 1,
2x + z = 3, −t1 ≤ x ≤ t1, −t2 ≤ y ≤ t2, −t3 ≤ z ≤ t3.
解:
(a) ∇f (x) = a, ∇2f (x) = 0n×n; (b) ∇f (x) = (A + AT )x, ∇2f (x) = A + AT ;
第二章 线性规划(管理运筹学,李军)
2014-1-28
5
构建线性规划数学模型
习题1：人力资源规划问题 2：00~ 6：00 2名； 6：00~10：00 12名； 10：00~14：00 20名； 14：00~18：00 6名； 18：00~22：00 26名； 22：00~ 2：00 4名。
2014-1-28
6
构建线性规划数学模型：习题1
2014-1-28
2
资源合理利用问题：第5页例2-1
1. 决策变量：x1和x2 2. 目标函数：max Z = 2 x1+3 x2 3. 约束条件： x1+2 x2 8 s.t. 4 x1 16 4 x2 12 x 1， x 2 0
2014-1-28
3
质量检验问题：第6页例2-2
③ ①
1 2 3 4 5 6 7 8
x1
25
图解法求解线性规划
1. 决策变量：x1和x2 2. 目标函数：max Z = 2 x1+4 x2 3. 约束条件： x1+2 x2 8 s.t. 4 x1 16 4 x2 12 x1，x2 0
2014-1-28
26
图解法求解线性规划:习题1
时间段 2：00~ 6：00 6：00~10：00 10：00~14：00 14：00~18：00 18：00~22：00 22：00~ 2：00
2014-1-28
需要人数 2名 12名 20名 6名 26名 4名
上班人数 X1 X2 X3 X4 X5 X6
7
构建线性规划数学模型：习题1
min Z = X1 + X2 +X3+ X4 + X5 + X6 X6 + X1 ≥ 2 X1 + X2 ≥ 12 s.t. X2 + X3 ≥ 20 X3 + X4 ≥ 6 X4 + X5 ≥ 26 X5 + X6 ≥ 4 X1,X2,X3,X4, X5,X6≥ 0
5
构建线性规划数学模型
习题1：人力资源规划问题 2：00~ 6：00 2名； 6：00~10：00 12名； 10：00~14：00 20名； 14：00~18：00 6名； 18：00~22：00 26名； 22：00~ 2：00 4名。
2014-1-28
6
构建线性规划数学模型：习题1
2014-1-28
2
资源合理利用问题：第5页例2-1
1. 决策变量：x1和x2 2. 目标函数：max Z = 2 x1+3 x2 3. 约束条件： x1+2 x2 8 s.t. 4 x1 16 4 x2 12 x 1， x 2 0
2014-1-28
3
质量检验问题：第6页例2-2
③ ①
1 2 3 4 5 6 7 8
x1
25
图解法求解线性规划
1. 决策变量：x1和x2 2. 目标函数：max Z = 2 x1+4 x2 3. 约束条件： x1+2 x2 8 s.t. 4 x1 16 4 x2 12 x1，x2 0
2014-1-28
26
图解法求解线性规划:习题1
时间段 2：00~ 6：00 6：00~10：00 10：00~14：00 14：00~18：00 18：00~22：00 22：00~ 2：00
2014-1-28
需要人数 2名 12名 20名 6名 26名 4名
上班人数 X1 X2 X3 X4 X5 X6
7
构建线性规划数学模型：习题1
min Z = X1 + X2 +X3+ X4 + X5 + X6 X6 + X1 ≥ 2 X1 + X2 ≥ 12 s.t. X2 + X3 ≥ 20 X3 + X4 ≥ 6 X4 + X5 ≥ 26 X5 + X6 ≥ 4 X1,X2,X3,X4, X5,X6≥ 0
2线性规划的图解法
16
建模练习
P25,T7(1)建立线性规划模型
17
图解法
目标函数：max Z=50x1+100x2 满足约束条件：x1 +x2≤300
2 x1+x2≤400 x2≤250 x1≥0, x2≥0
18
问题1 ，即不等式组，由于只包含两个决策变量，
可以用图解法来求解。多于两个决策变量不能用图 解法解。 图解法.首先把每个约束条件（代表一个平面） 画在二维坐标轴上。
9
常见的线性规划问题
管理上有很多问题可建立线性规划模型来解决，如 合理利用线材问题。现有一批长度一定的钢管，由于 生产的需要，要求截出不同规格的钢管若干。试问应 如何下料，既满足了生产的需要，又使得使用的原材 料钢管的数量最少。 配料问题。用若干种不同价格不同成分含量的原料， 用不同的配比混合调配出一些不同价格不同规格的产 品，在原料供应量的限制和保证产品成分的含量的前 提下，如何获取最大的利润。
松弛变量和线性规划标准化
为了把一个线性规划标准化，需要有代表没使用的
资源或能力的变量，称之为松弛变量，记为Si。显 然这些松弛变量对目标函数不会产生影响，可以在 目标函数中把这些松弛变量的系数看成零，加了松 弛变量后我们得到如下的例1的数学模型： 目标函数： max Z=50x1+100x2+0s1+0s2+0s3， 约束条件： x1+x2+s1=300, 2x1+x2+s2=400, x2+s3=250, x1,x2,s1,s2,s3≥0
x1 X1+X2=300
100
300
x1 X1+X2=300
21
2，即线 性规划问 题，其解 与问题1 的解有什 么关系？
运筹学课件 第二章线性规划
2020/11/23
广东工业大学管理学院
10
配料问题：由若干种不同价格、不同成分含量的原料，用 不同的配比混合调配出一些不同规格的产品，在原料的供 应量限制和保证产品成分含量的前提下，如何进行配料来 获取最大利润或使总成本最低。
投资问题：如何从不同的投资项目中选出一个投资方案， 使得投资的回报达到最大。
甲
乙
丙
A B C 加工费
x11 60%以上 x12 20%以下 x13 0.50
x21 15%以上 x22 60%以下 x23 0.40
x31 x32 50%以下 x33 0.30
售价
3.40
2.85
2.25
原料成本 2.00 1.50 1.00
限制用量 2000 2500 1200
设该厂每月生产甲品牌糖果(x11 x12 x13)千克，其中用原料A x11千克，用原料B x12千克，用原料C x13千克; 生产乙品牌糖果(x21 x22 x23)千克，其中用原料A x21千克，用原料B x22千克，用原料C x23千克; 生产丙品牌糖果(x31 x32 x33)千克，其中用原料A x31千克，用原料B x32千克，用原料C x33千克。
设一共植了y棵树，男生中有x1人挖坑, x2人栽树, x3人浇水； 女生中有x4人挖坑, x5人栽树, x6人浇水.
max z y
20x1 10x4 y 0 30x2 20x5 y 0
s.t.
25x3
x1
x2
15x6 x3
y 30
0
x4
x5
x6
20
x1, x2 , x3 , x4 , x5 , x6 , y 0
松弛变量
xs 2 (2x1 3x2 x3)
线性规划习题课
车间3：设车间3的能力增加10单位，即第三个约束条件为
2x1 + 2x2≤ 450 此时，最优解变为：x1** = 150 x2** = 75 最大值：z** = 105000(元) 车间3的对偶价格为(105000-103000)/10=200
Solution
(5)从（2）中的图可以看出，目标函数的斜率在约束1和约束3的直线斜率
500
如果产品II的利润为400不变，有 即当产品I的利润取值范围为[400,∞]；
c1 400
1
400
c1
习题
1.用单纯形法求解
目标函数 约束条件
max z x1 2x2 x3 x1 x2 x3 12, 2x1 x2 x3 6, x1 3x2 9, x1, x2 , x3 0.
由此可知：车间2的能力还有剩余，剩余540-210=330； 车间4的能力也有剩余，剩余300-285=15；
在这个线性规划中称为松弛变量。
Solution
(4)车间2和车间4的能力有剩余，对偶价格为0；
车间1：设车间1的能力增加10单位，即第一个约束条件为
2x1≤ 310 此时，最优解变为：x1** = 155 x2** = 65 最大值：z** = 103500(元) 车间1的对偶价格为(103500-103000)/10=50
车间
ⅠⅡ
限制
1
2
0
300
2
0
3
540
3
2
2
440
4
1.2 1.5
300
利润 500 400
Solution
解：产品Ⅰ生产x1件，产品Ⅱ生产x2件。z为利润函数，建立线性规划模型 目标函数： max z = 500x1 + 400x2 约束条件： 2x1≤ 300 3x2≤ 540 2x1 + 2x2≤ 440 1.2x1+1.5x2≤ 300 x1,x2 ≥ 0 每个约束条件上加上一个松弛变量si，此线性规划模型的标准型为： 目标函数： max z = 500x1 + 400x2+ 0s1+0s2+0s3+0s4 约束条件： 2x1+s1=300 3x2+s2=540 2x1+2x2+s3=440 1.2x1+1.5x2+s4=300 x1,x2,s1,s2,s3,s4 ≥ 0
2x1 + 2x2≤ 450 此时，最优解变为：x1** = 150 x2** = 75 最大值：z** = 105000(元) 车间3的对偶价格为(105000-103000)/10=200
Solution
(5)从（2）中的图可以看出，目标函数的斜率在约束1和约束3的直线斜率
500
如果产品II的利润为400不变，有 即当产品I的利润取值范围为[400,∞]；
c1 400
1
400
c1
习题
1.用单纯形法求解
目标函数 约束条件
max z x1 2x2 x3 x1 x2 x3 12, 2x1 x2 x3 6, x1 3x2 9, x1, x2 , x3 0.
由此可知：车间2的能力还有剩余，剩余540-210=330； 车间4的能力也有剩余，剩余300-285=15；
在这个线性规划中称为松弛变量。
Solution
(4)车间2和车间4的能力有剩余，对偶价格为0；
车间1：设车间1的能力增加10单位，即第一个约束条件为
2x1≤ 310 此时，最优解变为：x1** = 155 x2** = 65 最大值：z** = 103500(元) 车间1的对偶价格为(103500-103000)/10=50
车间
ⅠⅡ
限制
1
2
0
300
2
0
3
540
3
2
2
440
4
1.2 1.5
300
利润 500 400
Solution
解：产品Ⅰ生产x1件，产品Ⅱ生产x2件。z为利润函数，建立线性规划模型 目标函数： max z = 500x1 + 400x2 约束条件： 2x1≤ 300 3x2≤ 540 2x1 + 2x2≤ 440 1.2x1+1.5x2≤ 300 x1,x2 ≥ 0 每个约束条件上加上一个松弛变量si，此线性规划模型的标准型为： 目标函数： max z = 500x1 + 400x2+ 0s1+0s2+0s3+0s4 约束条件： 2x1+s1=300 3x2+s2=540 2x1+2x2+s3=440 1.2x1+1.5x2+s4=300 x1,x2,s1,s2,s3,s4 ≥ 0
第二章 线性规划习题课
单位成本
甲 乙 丙 丁
1 2 1 1
(元／吨) 5 6 7 8
3. 约束条件：
x1 + 2x2 + x3 + x4 ≥160 2x1 +4 x0单位；B种药物恰好200单 位，C种药物不超过180单位， 且使原料总成本最小。
3x1 ＋ x2 + x3 +2 x4 ≤180 x1、x2 、x3 、x4 ≥0
解：设总利润为z，
max z = 4 x1 + 10 x2 + 3 x3 － 2 x4 2 x1 + 3x2 ≤ 12 3x1 + 4x2 ≤ 24 －4x2 +x3 + x4 = 0 x3 ≤5 x1、x2 、x3 、x4≥ 0
A、B产品销量为x1、x2，
产品C的销售量为x3 ， 报废量为x4，则：
0 x 7 0 x 8 100 1 x 7 0 x 8 100 3 x 7 4 x 8 100 0
Ⅵ Ⅶ Ⅷ
方
案 长度m 2.9 2.1 1.5 合计
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
x1
x2
x3
x4
x5
x6
x7
x8
2 0 1
7.3 0.1
1 2 0
1 1 1
1 0 3
7.4 0.0
0 3 0
x1 +
2x1
x2 + 2x3 +
+ 2x3
x4≤ 30
≤ 34
4x2 + 4x3 + 4x4 ≤ 52 25x1 + 20x2 ＝ 200 40x3 + 20x4＝ 400
运筹学第三版课后习题答案 (2)
运筹学第三版课后习题答案第一章：引论1.1 课后习题习题1a)运筹学是一门应用数学的学科，旨在解决实际问题中的决策和优化问题。
它包括数学模型的建立、问题求解方法的设计等方面。
b)运筹学可以应用于各个领域，如物流管理、生产计划、流程优化等。
它可以帮助组织提高效率、降低成本、优化资源分配等。
c)运筹学主要包括线性规划、整数规划、指派问题等方法。
习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。
它可以帮助制定最佳的生产计划，优化供应链管理，提高运输效率等。
运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题，优化医疗资源分配等。
1.2 课后习题习题1运筹学方法可以应用于各个领域，如物流管理、生产计划、供应链管理、流程优化等。
在物流管理中，可以使用运筹学方法优化仓储和运输的布局，提高货物的运输效率。
在生产计划中，可以使用运筹学方法优化产品的生产数量和生产周期，降低生产成本。
在供应链管理中，可以使用运筹学方法优化订单配送和库存管理，提高供应链的效率。
在流程优化中，可以使用运筹学方法优化业务流程，提高整体效率。
习题2在物流管理中，可以使用运筹学方法优化车辆的调度和路线规划，以提高运输效率和降低成本。
在生产计划中，可以使用运筹学方法优化生产线的安排和产品的生产量，以降低生产成本和提高产能利用率。
在供应链管理中，可以使用运筹学方法优化供应链各个环节的协调和调度，以提高整体效率和减少库存成本。
在流程优化中，可以使用运筹学方法优化业务流程的排布和资源的分配，以提高流程效率和客户满意度。
第二章：线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法，用于解决包含线性约束和线性目标函数的优化问题。
其一般形式为：max c^T*xs.t. Ax <= bx >= 0其中，c是目标函数的系数向量，x是决策变量向量，A是约束矩阵，b是约束向量。
习题2使用线性规划方法可以解决许多实际问题，如生产计划、供应链管理、资源分配等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
min z = 5 x1 + 6 x2 + 7 x3 + 8 x4 3. 约束条件：
丙 141 7 丁 122 8
要求：生产A种药物至少 160单位；B种药物恰好200单 位，C种药物不超过180单位， 且使原料总成本最小。
x1 + 2x2 + x3 + x4 ≥160
2x1
+4 x3 +2 x4 ＝200
j 1，2，3，4，5
例6 某厂生产三种药物， 解：
这些药物可以从四种不同的 原料中提取。下表给出了单 位原料可提取的药物量
1. 决策变量：设四种原料的使
用量分别为：x1、x2 、x3 、x4
药物
单位成本
原料
A B C (元／吨)
甲 123 5
乙 201 6
2. 目标函数：设总成本为z， 则有：
线性规划问题求解程序设计要求
1. 线性规划问题的数学模型
max(min) z c1 x1 c2 x2 cn xn
a11 x1 a12 x2 a1n xn ( ，)b1
a21 x1 a22 x2 a2n xn ( ，)b2
am1 x1
例3 合理利用线材问题
现要做100套钢架，每套用长2.9m，2.1m，1.5m， 的圆钢各一根。已知原料长7.4m，问应如何下料，使用 的原材料最省？
解：所有下料方案如下表：
方 案 长度m
2.9 2.1 1.5 合计 料头
ⅠⅡ Ⅲ ⅣⅤ Ⅵ ⅦⅧ
x1 x2 x3 x4 x5 x6 x7 x8
2 1 11 00 00 0 2 10 32 10 1 0 13 02 34
a11 x1 a12 x2 a1n xn ( ，) b1
a21 x1 a22 x2 a2n xn ( ，) b2
am1 x1 am2 x2 amn xn ( ，) bm
x1
，x2
， ，xn
产品名称
规格要求
单价（元/kg）
A
C不少于50%，P不超过25%
50
B
C不少于25%，P不超过50%
35
D
不限
25
原材料名称
C P H
每天最多供应量（kg） 单价（元/kg）
100
65
100
25
60
35
解： 原料
产品
C
P
H 单价
x1 A x2 B x3 D
x AC x AP x AH
50
xBC xBP xBH
项目D， 5年内每年初可购买公债，与当年末归还， 并加利息6%。
该部门现有资金10万元，问他应如何确定给这些项 目每年的投资额，使到五年末拥有资金的本利总额为最 大？
解： 确定决策变量如下表：
年份
项目
1
2
3
4
5 5年末
A
x A1
xA2
x A3
x A4
1.15 x A4
B
xB3
1.25 x B 3
C
2 x1 + 3x2
≤ 12
3x1 + 4x2
≤ 24
－4x2 +x3 + x4 = 0
x3 ≤ 5
x1、x2 、x3 、x4≥ 0
例2 某航运局现有船只种类、数量以及计划期内各 条航线的货运量、货运成本如下表所示：问：应如何 编队，才能既完成合同任务，又使总货运成本为最小？
航线 船队 号 类型
1 1
x1 x2 x3 x4 x5 x6 x7 x8
2 1 11 00 00 0 2 10 32 10 1 0 13 02 34
7.3 7.1 6.5 7.4 6.3 7.2 6.6 6.0
0.1 0.3 0.9 0.0 1.1 0.2 0.8 1.4
例4 配料问题。
某工厂要用三种原材料C、P、H混合调配出三种 不同规格的产品A、B、D。已知产品的规格要求，产 品单价，每天供应的原材料数量及原材料单价如下表， 该厂应如何安排生产，使利润收入为最大？
min z = 36x1 + 36x2 + 72x3 + 27x4
x1 + x2 + 2x3 + x4≤ 30
2x1
+ 2x3
≤ 34
4x2 + 4x3 + 4x4 ≤ 52
25x1 + 20x2
＝ 200
40x3 + 20x4＝ 400
xj ≥ 0 j = 1,2,3,4
用单纯形法可求得：x1 = 8，x2 = 0 ，x3 = 7， x4 = 6 最优值：z = 954，即：四种船队类型的队数分别是8、 0、7、6，此时可使总货运成本为最小，为954千元。
2 找出所有限定条件：即决策变量受到的所有 的约束；
3 写出目标函数：即问题所要达到的目标，并 明确是max 还是 min。
三、建 模 案 例
例1 某工厂生产A、B两种产品，有关资料如下表所示：
工序 产品
A
C
工时限
B
销售 报废
制
工序 1 2
3
—
—
12
工序 2 3
4
—
—
24
单位利润生产单位产品 B 可得到 4 单位副产品 C， 据预测，市场上产品 C 的最大销量为 5 单位，若
产品 C 销售不出去，则报废。
解：设总利润为z， max z = 4 x1 + 10 x2 + 3 x3 － 2 x4
A、B产品销量为x1、x2， 产 品 C 的 销 售 量 为 x3 ， 报废量为x4，则：
am2 x2
amn xn
( ，)bm
x1，x2， ，xn 0 (无约束)
2. 线性规划问题的求解方法 采用两阶段法求解
3. 求解程序的输入与输出
变量个数n= ( ) 约束条件个数m= ( )
max(min) z c1 x1 c2 x2 cn xn
0
x1 x1
2x2 0x2
x3 x3
0x4 3x4
3x5 0x5
2x6 2x6
1x7 3x7
0x8 4x8
100 100
x1，x2，x3，x4，x5，x6，x7，x8 0
方 案 长度m
2.9 2.1 1.5 合计
ⅠⅡ Ⅲ ⅣⅤ Ⅵ ⅦⅧ
2 3 2 4
编队形式
拖轮
A型 驳船
B型 驳船
1
2
—
1
—
4
2
2
4
1
—
4
货运成本 （千元／队）
36 36 72 27
货运量 （千吨）
25 20 40 20
船只种类 拖轮 A型驳船 B型驳船
船只数 30 34 52
航线号 1 2
合同货运量 200 400
解：设 xj 为第 j 号类型船队的队数( j = 1,2,3,4 ), z 为总货运成本,则：
35
xDC xDP xDH
25
单 价 65 25
35 max z 15xAC 25xAP 15xAH 30xBC 10xBP 0xBH 40xDC 0xDP 10xDH
xAC 0.50( xAC xAP xAH )
xAP 0.25( xAC xAP xAH )
xC 2
1.40xC 2
D
xD1
xD2
xD3
xD4
x D5 1.06x D5
年初拥有 10 1.06xD1 1.06xD2 1.06xD3 1.06xD4
资金
1.15xA1 1.15xA2 1.15xA3
max z 1.15xA4 1.25xB3 1.40xC 2 1.06xD5
3x1 ＋ x2 + x3 +2 x4 ≤180
x1、x2 、x3 、x4 ≥0
线性规划研究的主要问题
一类是已有一定数量的资源（人力、物质、 时间等），研究如何充分合理地使用它们，才能 使完成的任务量为最大。
另一类是当一项任务确定以后，研究如何统 筹安排，才能使完成任务所耗费的资源量为最少。
—— 实际上，上述两类问题是一个问题的两个不同 的方面，都是求问题的最优解（ max 或 min ）。
(1) 线性规划问题的标准型 (2) 第一阶段的所有单纯形表( ) (3) 第二阶段的所有单纯形表( )
xBP 0.50( xBC xBP xBH )
xBC 0.25( xBC xBP xBH )
xAC xBC xDC 100 xAP xBP xCP 100 xAH xBH xDH 60
xij 0 i A, B, D J C , P, H
7.3 7.1 6.5 7.4 6.3 7.2 6.6 6.0
0.1 0.3 0.9 0.0 1.1 0.2 0.8 1.4
min z 0.1x1 0.3x2 0.9x3 0x4 1.1x5 0.2x6 0.8x7 1.4x8
2x1 x2 x3 x4 0x5 0x6 0x7 0x8 100
xA1 xD1 10
xA2 xC 2 xD2 1.06xD1
xA3
xB3
xD3
1.06 x D 2
1.15xA1
丙 141 7 丁 122 8
要求：生产A种药物至少 160单位；B种药物恰好200单 位，C种药物不超过180单位， 且使原料总成本最小。
x1 + 2x2 + x3 + x4 ≥160
2x1
+4 x3 +2 x4 ＝200
j 1，2，3，4，5
例6 某厂生产三种药物， 解：
这些药物可以从四种不同的 原料中提取。下表给出了单 位原料可提取的药物量
1. 决策变量：设四种原料的使
用量分别为：x1、x2 、x3 、x4
药物
单位成本
原料
A B C (元／吨)
甲 123 5
乙 201 6
2. 目标函数：设总成本为z， 则有：
线性规划问题求解程序设计要求
1. 线性规划问题的数学模型
max(min) z c1 x1 c2 x2 cn xn
a11 x1 a12 x2 a1n xn ( ，)b1
a21 x1 a22 x2 a2n xn ( ，)b2
am1 x1
例3 合理利用线材问题
现要做100套钢架，每套用长2.9m，2.1m，1.5m， 的圆钢各一根。已知原料长7.4m，问应如何下料，使用 的原材料最省？
解：所有下料方案如下表：
方 案 长度m
2.9 2.1 1.5 合计 料头
ⅠⅡ Ⅲ ⅣⅤ Ⅵ ⅦⅧ
x1 x2 x3 x4 x5 x6 x7 x8
2 1 11 00 00 0 2 10 32 10 1 0 13 02 34
a11 x1 a12 x2 a1n xn ( ，) b1
a21 x1 a22 x2 a2n xn ( ，) b2
am1 x1 am2 x2 amn xn ( ，) bm
x1
，x2
， ，xn
产品名称
规格要求
单价（元/kg）
A
C不少于50%，P不超过25%
50
B
C不少于25%，P不超过50%
35
D
不限
25
原材料名称
C P H
每天最多供应量（kg） 单价（元/kg）
100
65
100
25
60
35
解： 原料
产品
C
P
H 单价
x1 A x2 B x3 D
x AC x AP x AH
50
xBC xBP xBH
项目D， 5年内每年初可购买公债，与当年末归还， 并加利息6%。
该部门现有资金10万元，问他应如何确定给这些项 目每年的投资额，使到五年末拥有资金的本利总额为最 大？
解： 确定决策变量如下表：
年份
项目
1
2
3
4
5 5年末
A
x A1
xA2
x A3
x A4
1.15 x A4
B
xB3
1.25 x B 3
C
2 x1 + 3x2
≤ 12
3x1 + 4x2
≤ 24
－4x2 +x3 + x4 = 0
x3 ≤ 5
x1、x2 、x3 、x4≥ 0
例2 某航运局现有船只种类、数量以及计划期内各 条航线的货运量、货运成本如下表所示：问：应如何 编队，才能既完成合同任务，又使总货运成本为最小？
航线 船队 号 类型
1 1
x1 x2 x3 x4 x5 x6 x7 x8
2 1 11 00 00 0 2 10 32 10 1 0 13 02 34
7.3 7.1 6.5 7.4 6.3 7.2 6.6 6.0
0.1 0.3 0.9 0.0 1.1 0.2 0.8 1.4
例4 配料问题。
某工厂要用三种原材料C、P、H混合调配出三种 不同规格的产品A、B、D。已知产品的规格要求，产 品单价，每天供应的原材料数量及原材料单价如下表， 该厂应如何安排生产，使利润收入为最大？
min z = 36x1 + 36x2 + 72x3 + 27x4
x1 + x2 + 2x3 + x4≤ 30
2x1
+ 2x3
≤ 34
4x2 + 4x3 + 4x4 ≤ 52
25x1 + 20x2
＝ 200
40x3 + 20x4＝ 400
xj ≥ 0 j = 1,2,3,4
用单纯形法可求得：x1 = 8，x2 = 0 ，x3 = 7， x4 = 6 最优值：z = 954，即：四种船队类型的队数分别是8、 0、7、6，此时可使总货运成本为最小，为954千元。
2 找出所有限定条件：即决策变量受到的所有 的约束；
3 写出目标函数：即问题所要达到的目标，并 明确是max 还是 min。
三、建 模 案 例
例1 某工厂生产A、B两种产品，有关资料如下表所示：
工序 产品
A
C
工时限
B
销售 报废
制
工序 1 2
3
—
—
12
工序 2 3
4
—
—
24
单位利润生产单位产品 B 可得到 4 单位副产品 C， 据预测，市场上产品 C 的最大销量为 5 单位，若
产品 C 销售不出去，则报废。
解：设总利润为z， max z = 4 x1 + 10 x2 + 3 x3 － 2 x4
A、B产品销量为x1、x2， 产 品 C 的 销 售 量 为 x3 ， 报废量为x4，则：
am2 x2
amn xn
( ，)bm
x1，x2， ，xn 0 (无约束)
2. 线性规划问题的求解方法 采用两阶段法求解
3. 求解程序的输入与输出
变量个数n= ( ) 约束条件个数m= ( )
max(min) z c1 x1 c2 x2 cn xn
0
x1 x1
2x2 0x2
x3 x3
0x4 3x4
3x5 0x5
2x6 2x6
1x7 3x7
0x8 4x8
100 100
x1，x2，x3，x4，x5，x6，x7，x8 0
方 案 长度m
2.9 2.1 1.5 合计
ⅠⅡ Ⅲ ⅣⅤ Ⅵ ⅦⅧ
2 3 2 4
编队形式
拖轮
A型 驳船
B型 驳船
1
2
—
1
—
4
2
2
4
1
—
4
货运成本 （千元／队）
36 36 72 27
货运量 （千吨）
25 20 40 20
船只种类 拖轮 A型驳船 B型驳船
船只数 30 34 52
航线号 1 2
合同货运量 200 400
解：设 xj 为第 j 号类型船队的队数( j = 1,2,3,4 ), z 为总货运成本,则：
35
xDC xDP xDH
25
单 价 65 25
35 max z 15xAC 25xAP 15xAH 30xBC 10xBP 0xBH 40xDC 0xDP 10xDH
xAC 0.50( xAC xAP xAH )
xAP 0.25( xAC xAP xAH )
xC 2
1.40xC 2
D
xD1
xD2
xD3
xD4
x D5 1.06x D5
年初拥有 10 1.06xD1 1.06xD2 1.06xD3 1.06xD4
资金
1.15xA1 1.15xA2 1.15xA3
max z 1.15xA4 1.25xB3 1.40xC 2 1.06xD5
3x1 ＋ x2 + x3 +2 x4 ≤180
x1、x2 、x3 、x4 ≥0
线性规划研究的主要问题
一类是已有一定数量的资源（人力、物质、 时间等），研究如何充分合理地使用它们，才能 使完成的任务量为最大。
另一类是当一项任务确定以后，研究如何统 筹安排，才能使完成任务所耗费的资源量为最少。
—— 实际上，上述两类问题是一个问题的两个不同 的方面，都是求问题的最优解（ max 或 min ）。
(1) 线性规划问题的标准型 (2) 第一阶段的所有单纯形表( ) (3) 第二阶段的所有单纯形表( )
xBP 0.50( xBC xBP xBH )
xBC 0.25( xBC xBP xBH )
xAC xBC xDC 100 xAP xBP xCP 100 xAH xBH xDH 60
xij 0 i A, B, D J C , P, H
7.3 7.1 6.5 7.4 6.3 7.2 6.6 6.0
0.1 0.3 0.9 0.0 1.1 0.2 0.8 1.4
min z 0.1x1 0.3x2 0.9x3 0x4 1.1x5 0.2x6 0.8x7 1.4x8
2x1 x2 x3 x4 0x5 0x6 0x7 0x8 100
xA1 xD1 10
xA2 xC 2 xD2 1.06xD1
xA3
xB3
xD3
1.06 x D 2
1.15xA1