现代控制理论第八章
现代控制理论(浓缩版)

现代控制理论(浓缩版)绪论1.经典控制理论与现代控制理论的比较。
经典控制理论也称为古典控制理论,多半是用来解决单输入-单输出的问题,所涉及的系统大多是线性定常系统,非线性系统中的相平面法也只含两个变量。
经典控制理论是以传递函数为基础、在频率域对单输入单输出控制系统进行分析和设计的理论。
它明显具有依靠手工进行分析和综合的特点,这个特点是与20世纪40~50年代生产发展的状况,以及电子计算机的发展水平尚处于初级阶段密切相关的。
在对精度要求不高的场合是完全可用的。
最大成果之一就是PID 控制规律的产生,PID 控制原理简单,易于实现,具有一定的自适应性与鲁棒性,对于无时间延时的单回路控制系统很有效,在工业过程控制中仍被广泛采用。
现代控制理论主要用来解决多输入多输出系统的问题,系统可以是线性或非线性的、定常或时变的。
确认了控制系统的状态方程描述法的实用性,是与状态方程有关的控制理论。
现代控制理论基于时域内的状态空间分析法,着重实现系统最优控制的研究。
从数学角度而言,是把系统描述为四个具有适当阶次的矩阵,从而将控制系统的一些问题转化为数学问题,尤其是线性代数问题。
而且,现代控制理论是以庞得亚金的极大值原理、别尔曼的动态规划和卡尔曼的滤波理论为其发展里程碑,揭示了一些极为深刻的理论结果。
面对现代控制理论的快速发展及成就,人们对这种理论应用于工业过程寄于乐期望。
但现代控制在工业实践中遇到的理论、经济和技术上的一些困难。
所以说,现代控制理论还存在许多问题,并不是“完整无缺”,这是事物存在矛盾的客观反应,并将推动现代控制理论向更深、更广方向发展。
如大系统理论和智能控制理论的出现,使控制理论发展到一个新阶段。
2.控制一个动态系统的几个基本步骤有四个基本步骤:建模,基于物理规律建立数学模型;系统辨识,基于输入输出实测数据建立数学模型;信号处理,用滤波、预报、状态估计等方法处理输出;综合控制输入,用各种控制规律综合输入。
拉普拉斯变换

拉普拉斯变换定义式:设有一时间函数f(t) [0,∞] 或 0≤t≤∞单边函数 ,其中,S=σ+jω是复参变量,称为复频率。
左端的定积分称为拉普拉斯积分,又称为f(t)的拉普拉斯变换;右端的F(S)是拉普拉斯积分的结果,此积分把时域中的单边函数f(t)变换为以复频率S为自变量的复频域函数F(S),称为f(t)的拉普拉斯象函数。
以上的拉普拉斯变换是对单边函数的拉普拉斯变换,称为单边拉普拉斯变换。
如f(t)是定义在整个时间轴上的函数,可将其乘以单位阶跃函数,即变为f(t)ε(t),则拉普拉斯变换为F(s),=mathcal left =int_ ^infty f(t),e^ ,dt 其中积分下标取0-而不是0或0+ ,是为了将冲激函数δ(t)及其导函数纳入拉普拉斯变换的范围。
z变换可将分散的信号(现在主要用于数字信号)从时域转换到频域。
作用和拉普拉斯变换(将连续的信号从时域转换到频域)是一样的。
拉普拉斯变换是将时域信号变换到“复频域”,与傅里叶变换的“频域”有所区别。
FT[f(t)]=从负无穷到正无穷对[f(t)exp(-jwt)]积分 ,LT[f(t)]=从零到正无穷对[f(t)exp(-st)]积分 ,(由于实际应用,通常只做单边拉普拉斯变换,即积分从零开始) .具体地,在傅里叶积分变换中,所乘因子为exp(-jwt),此处,-jwt显然是为一纯虚数;而在拉普拉斯变换中,所乘因子为exp(-st),其中s为一复数:s=D+jw,jw是为虚部,相当于Fourier变换中的jwt,而D则是实部,作为衰减因子,这样就能将许多无法作Fourier变换的函数(比如exp(at),a>0)做域变换。
拉普拉斯变换主要用于电路分析,作为解微分方程的强有力工具(将微积分运算转化为乘除运算)。
但随着CAD的兴起,这一作用已不怎么受重视了,但关于其收敛域的分析(零极点图)依然常用。
Fourier 变换则随着FFT算法(快速傅立叶变换)的发展已经成为最重要的数学工具应用于数字信号处理领域。
现代控制理论(修改最终版)

《现代控制理论基础》课程教学大纲课程编号:课程名称:现代控制理论英文名称: Modern Control Theory课程性质: 考试学时: 42学时(讲授36学时+6学时实验)适用对象: 工业自动化先修课程:自动控制理论,线性代数,工程数学一、编写说明(一)本课程的性质、地位和作用现代控制理论是自动化专业的主干技术基础课,它是在经典控制理论的基础上建立和发展起来的。
本课程是以状态空间理论为核心,对动态系统进行分析和研究。
它不但可以解决单变量线性定常系统,还可以解决多变量、时变、非线性系统的问题。
通过本门课程的学习,使学生掌握线性控制系统的状态空间描述,能够对线性系统的几种模型进行互相转化; 掌握线性控制系统的运动规律及连续系统的离散化;熟悉线性控制系统的能控性与能观测性概念及其判定准则;了解控制系统的李亚普诺夫稳定性理论; 掌握线性控制系统的状态反馈与状态观测器的设计方法。
通过对本课程的学习,要求学生系统地获得现代控制理论的基本知识,切实掌握所涉及的基本概念、基本理论和基本方法,为后继课程的学习奠定良好的理论基础.(二)教学基本要求1. 掌握现代控制理论的基本知识及其分析方法,能够用状态空间表达式来描述系统,并根据系统的微分方程建立其状态空间表达式的方法。
2. 掌握系统特征值的求取方法,掌握线性定常系统非齐次方程的解和线性时变系统的解的求取方法,以及离散时间系统状态方程的两种解法。
3. 掌握能控性、能观性的定义及各自的判别准则。
4.掌握用李雅普诺夫第一法和第二法分析系统的稳定性的方法。
5. 对线性系统理论的新发展有所了解。
6. 为学生进一步的学习打下必要的基础。
(三)课程教学方法与手段以课堂讲授为主,辅以习题、实验等环节。
(四)实践环节通过计算机仿真,主要运用Matlab软件使学生能初步掌握MATLAB工具包,并用它在计算机环境中进行控制‘实验’,对控制系统进行分析与综合,以提高学生的系统分析和综合能力。
现代控制理论Modern Control Theory

c(t)
s(s 1)(4s 1)
试分析系统的稳定性
解 非线性环节为库仑摩擦加黏性摩擦
查表得描述函数 N ( A) K 4M
Chapter 8 Analysis and design of nonlinear system
非线性系统的分析与设计
2
The Principle of Automatic Control 2008
第八章、非线性控制系统分析
8.1 非线性控制系统概述 8.2 相平面法 8.3 描述函数法 8.4 改善非线性系统性能的措施及非线性特
8.1 非线性控制系统概述
8.1.3 非线性系统运动的特殊性
• 不满足叠加原理— 线性系统理论原则上不能运用
• 稳定性问题 — 不仅与自身结构参数,且与输 入,初条件有关,平衡点可能不惟一
• 自振运动
— 非线性系统特有的运动形式
没有外界周期变化信号的作用时,系统内产生的具 有固定振幅和频率的稳定周期运动,简称自振
性的利用(稳定性判别)
3
The Principle of Automatic Control 2008
8.1 非线性控制系统概述
8.1.1 非线性现象的普遍性
非线性是宇宙间的普遍规律 非线性系统的运动形式多样,种类繁多 线性系统只是在特定条件下的近似描述
E.g. 欧姆定律U=IR
4
The Principle of Automatic Control 2008
j
G( j)
1 N ( A)
1 N ( A)
0
当гG曲线包围
1 N ( A)
,系统不稳定
当гG曲线不包围 N (1A),系统稳定
25
The Principle of Automatic Control 2008
现代控制理论课件教材

2. 1895年劳斯(Routh)与赫
尔维茨(Hurwitz)把马克 斯韦尔的思想扩展到高阶微 分方程描述的更复杂的系 统中,各自提出了两个著名
的稳定性判据—劳斯判据
和赫尔维茨判据。基本上 满足了二十世纪初期控制 赫尔维茨(Hurwitz)
工程师的需要。
同济大学汽车学院 2013
1.1 现代控制理论的产生与发展
水 运 仪 象 台
2. 公元1086-1089年 (北宋哲宗元祐初年), 我国发明的水运仪象台, 就是一种闭环自动调节系 统。
同济大学汽车学院 2013
1.1 现代控制理论的产生与发展
二 起步阶段
随着科学技术与工业生 产的发展,到十八世纪, 自动控制技术逐渐应用到 现代工业中。其中最卓越 的代表是瓦特(J.Watt) 发明的蒸汽机离心调速器, 加速了第一次工业革命的 步伐。
•成绩:
• 期终考试: 70% • 作业: 15% • 出席: 15%
同济大学汽车学院 2013
同济大学 汽车学院
College of Automotive, Tongji University
课程内容:
• 绪论 • 控制系统的状态空间描述 • 线性控制系统的运动分析 • 线性控制系统的能控性和能观性 • 控制系统的李雅普诺夫稳定性分析 • 状态反馈和状态观测器 • 最优控制
3.由于第二次世界大战需要 控制系统具有准确跟踪与补 偿能力,1932年奈奎斯特 (H.Nyquist)提出了频域 内研究系统的频率响应法, 为具有高质量的动态品质和 静态 准确度的军用控制系 统提供了所需的分析工具。
奈奎斯特
同济大学汽车学院 2013
1.1 现代控制理论的产生与发展
4.1948年伊万斯(W.R.Ewans)提出了复数域内 研究系统的根轨迹法。 建立在奈奎斯特的频率响应法和伊万斯的根轨 迹法基础上的理论,称为经典(古典)控制理论 (或自动控制理论)。
第八章 状态方程

化简,得
d eAtλ t eAt Bet
dt
两边取积分,并考虑起始条件,有
eAtλ tλ 0
t eA Be( ) d
0
对上式两边左乘 e A,t 并考虑到 eAteAt I ,可得
λ为t方 程eA的tλ 一0般解0t eAt Be d eAtλ 0 eAt B et
求输出方程r(t)
et b1
dk 1 dt k1
et
bk1
d dt
et bket
此系统为k 阶系统,输入信号的最高次导数也为
k 次系统函数为
H
s
b0sk b1sk1 bk1s bk sk a1sk1 ak1s ak
为便于选择状态变量,系统函数表示成
H
s
b0
b1s1
bk
s1k
1
bk sk
d λ t, 输出为 λ t。
dt
若 A,B,C矩, D阵是 的函t数,表明系统是线性时变
的,对于线性时不变系统,A,B,C的, D各元素都为常
数,不随 t改变。
状态变量的特性
每一状态变量的导数是所有状态变量和输 入激励信号的函数;
每一微分方程中只包含有一个状态变量对 时间的导数;
输出信号是状态变量和输入信号的函数;
1 a1s1
ak
s1k
1
ak sk
当用积分器来实现该系统时,其流图如下
et 1
b0
1 s k a1
b1 b2
1 sk1
a2
bk 2
bk 1
3 1 s 2 1 s 1 bk
r t
ak2 ak1
ak
取积分器的输出作为状态变量,如图中所标的
(完整版)现代控制理论
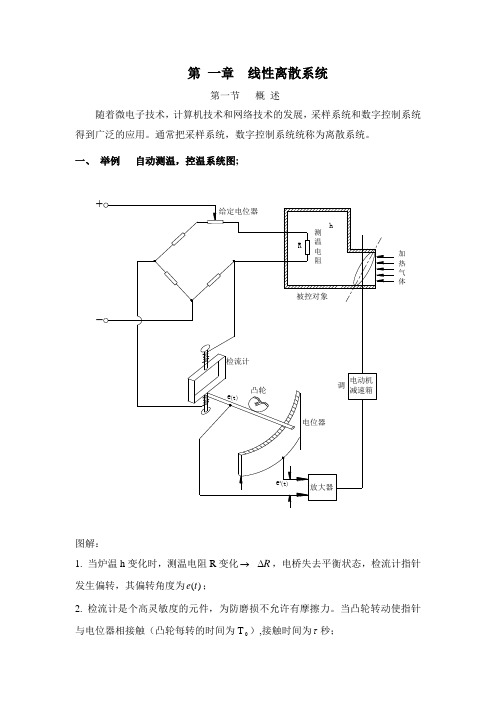
第一章线性离散系统第一节概述随着微电子技术,计算机技术和网络技术的发展,采样系统和数字控制系统得到广泛的应用。
通常把采样系统,数字控制系统统称为离散系统。
一、举例自动测温,控温系统图;加热气体图解:1. 当炉温h变化时,测温电阻R变化→R∆,电桥失去平衡状态,检流计指针发生偏转,其偏转角度为)e;(t2. 检流计是个高灵敏度的元件,为防磨损不允许有摩擦力。
当凸轮转动使指针),接触时间为τ秒;与电位器相接触(凸轮每转的时间为T3. 当炉温h 连续变化时,电位器的输出是一串宽度为τ的脉冲信号e *τ(t);4.e *τ(t)为常值。
加热气体控制阀门角度调速器电动机放大器h →→→→→→ϕ 二、相关定义说明(通过上例来说明) 1. 信号采样偏差)(t e 是连续信号,电位器的输出的e *τ(t)是脉冲信号。
连续信号转变为脉冲信号的过程,成为采样或采样过程。
实现采样的装置成为采样器。
To —采样周期,f s =--To1采样频率,W s =2πf s —采样角频率 2.信号复现因接触时间很小,τo T 〈〈τ,故可把采样器的输出信号)(t e *近似看成是一串强度等于矩形脉冲面积的理想脉冲,为了去除采样本身带来的高额分量,需要把离散信号)(t e *恢复到原信号)(t e 。
实现方法:是在采样器之后串联一个保持器,及信号复现滤波器。
作用:是把)(t e *脉冲信号变成阶梯信号e h (t)3.采样系统结构图r(t),e(t),c(t),y(t)为连续信号,)(t e *为离散信号)(s G h ,)(s G p ,)(s H 分别为保持器,被控对象和反馈环节的传递函数。
(t)r4.采样系统工作过程⇒由保持器5. 采样控制方式采样周期To ⎪⎩⎪⎨⎧=≠=⇒相位不同步采样常数常数6. 采样系统的研究方法(或称使用的数字工具)因运算过程中出现s 的超越函数,故不用拉式变换法,二采用z 变换方法,状态空间法。
《现代控制理论基础》第八章(3)

计算行列式得: Qo = 0, 事实上 rankQo = 2 < 3 det 该系统不完全能观。
16
2 [Jordan标准型判据 标准型判据] 标准型判据 1) 若系统(2)为对角标准型,其矩阵 A 的特征 值 λ1 , λ2 ,L , λn 两两互异,
λ1 0 L 0 0 λ O M 2 x = x & M O O 0 0 L 0 λn y = Cx
满足条件:
AII = A
T I
BII = C
T I
CII = B
T I
则称系统 ∑ 1 与系统 ∑ 2 是互为对偶的系统。
23
注意
∑
∑
1
2
r 输入 m 输出 n 阶系统 m 输入 r 输出 n 阶系统
BI
∑ u I
1
+
∫
AI
xI
CI
yI
∑ u II
2
C
T I
+
∫
AIT
xII
BIT
yII
对偶系统结构原理图
答:能控
1 0 u 1 0 u 2 0 2
答:能控
11
& x1 λ1 1 0 x1 1 7 u (3) x2 = 0 λ1 0 x2 + 0 0 1 & u x3 0 0 λ3 x3 −3 2 2 &
答:不完全能观
22
8.3.3
能控性与能观性的关系 ——对偶原理 对偶原理
一. 对偶系统的概念
& xI = AI xI + BI uI & xII = AII xII + BII uII 若系统 ∑ 1 : 与系统 ∑ 2 : yI = C I x I yII = CII xII
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ˆ 8.3.1 X ( Z ) a BZ 称为 x 的线性估计,其中 为常量, 为 n m 常阵,Z 为m维观测向量。
定义8.3.2 使误差方差阵
% ˆ ˆ DX X X (Z ) X X (Z )
8.2 最小方差估计
% % 定义8.2.1 使误差方差阵 EXX 最小的估计
ˆ X v (Z )
X 叫 X 最小方差估计,ˆ (Z ) 是一个随机向量。
设 X 的概率密度为 f ( x),Z的概率密度为 g ( z),
二者的联合概率密度为 ( x, z ),则在Z=z 条件
X 下, 的条件概率密度为 p x z ( x, z ) / g ( z ) ˆ X (Z )的误差方阵为
估计误差的方差为
1 2 2 1 1 3 3 1 1 2 2 1 5 ˆ E ( X X V )2 10 3 10 3 10 4 10 4 10 3 10 3 24
进而求得
5 5 ˆ X L (Z ) EX cov( X , Z )( DZ )1 (Z EZ ) 0 1 Z Z 2 2
2005-11-5
第八章 状态估计
ˆ 例8.3.2 已知 X 和 Z的联合分布如表8-2,试求 X L ( Z )
解: EX 1 (1) 3 1 1 1 2 2 7
最小。注意到
ˆ ˆ ( X X ( z ))( X X ( z)) p( x / z)dx
ˆ ˆ [ X E ( X z ) E ( X z ) X ( z )] [ X E ( X z ) E ( X z ) X ( z )] p( x / z )dx
1 1
DX cov( X , Z )( DZ )1 cov(Z , X )
在右边加减 cov( X , Z )( DZ )1 cov(Z , X ) 后配方,得
E X a BZ X a BZ bb B cov( X , Z )(DZ ) DZ B cov( X , Z )(DZ )
2005-11-5
第八章 状态估计 =
[ X E( X
z )][ X E ( X z )] p( X z )dx
ˆ ˆ ( z ) E ( X z )][ X ( z ) E ( X z )] p ( X z )dx [X +
= [ X E ( X z)][ X E ( X z)] p( X z)dx
ˆ ( Z )] DX cov( X , Z )( DZ ) 1 cov( Z , X ) 81 3 21 D[ X X L 100 5 100
2005-11-5
第八章 状态估计 小于前面最小方差估计时的误差方差
ˆ ) 5 D( X X V 24
线性最小方差估计的统计性质为:
2005-11-5
第八章 状态估计
X 的线性最小方差估计为
ˆ X L (Z ) EX cov( X , Z )( DZ )1 (Z EZ )
3 10 , z 1 7 7 Z , z0 10 10 17 10 , z 1
估计误差为方差
= DX bb BD(Z ) B cov( X , Z ) B B cov(Z , X )
2005-11-5
第八章 状态估计
E X a BZ X a BZ bb B cov( X , Z )(DZ ) DZ B cov( X , Z )(DZ )
% % ˆ ˆ EXX E( X X (Z )) ( X X (Z ))
ˆ ˆ ( X X ( z ))( X X ( z)) ( x, z)dxdz
[
ˆ ˆ ( X X ( z )) ( X X ( z)) p( x / z)dx] g ( z)dz
8.1.2差分方程模型
随机差分方程模型
y(k ) a1 y(k 1) an y(k n)
b0u (k ) b1u(k 1) bmu(k m) (k ) c1 (k 1) c p (k p)
2005-11-5
第八章 状态估计
% % 阵 EXX 最小
2005-11-5
第八章 状态估计
ˆ ˆ E X X MV ( Z ) X X MV ( Z )
例8.2.1 设被估计量 x 和观测量 z 的联合分布 如表8-1所示, 试求 x 的最小方差估计。 表8-1 x z -1 1 -3 1/4 0 -2 1/4 0 2 0 1/4 3 0 1/4
2005-11-5
第八章 状态估计 表8-2
z x -1 -1 0 0 1 1 2
1/10 2/10
0
1
ˆ 解: XV E( X / Z )
1/10 3/10
1/10 2/10
2005-11-5
第八章 状态估计
1 3 , z 1 3 , z0 4 5 3, z 1
D( X
z )g ( z )dz
2005-11-5
第八章 状态估计
ˆ 解 XV E( X / Z )
5 2 , 当 z -1 时 5 , 当 z 1时 2
例8.2.2
已知被估计量 x 和观测量 z 的联合分布
如表8-2所示,试求 x的最小方差估计和线性最小 方差估计。
ˆ ˆ ( z ) E ( X z )] [ X ( z ) E ( X z )] [X
[ X E( X
z)][ X E ( X z )] p( X z )dx D( X z )
ˆ ˆ 可知,当且仅当 X ( z ) E ( X z ) X MV (Z ) 时,方差
L
2005-11-5
第八章 状态估计 例8.3.1 设被估计量 X和 Z观测量的联合分布如表 8-1,试求 X 的线性最小方估计
解: 根据表中数据可以求出:
1 1 EX (2 3 2 3) 0 EZ (1 1 1 1) 0 4 4 1 13 DX [22 32 (2) 2 (3) 2 ] 4 2 1 2 2 DZ [1 1 (1) 2 (1) 2 ] 1 4 5 cov( X , Z ) [1 2 1 3 (1)(2) (1)(3)] Z 2
(1)线性
ˆ X L a BZ
ˆ (2)无偏性 EX L E[ EX cov( X , Z )( DZ )1 (Z EZ )] EX
(3)正交性
ˆ E ( X X L )Z 0
ˆ 由于 E ( X X L )( BZ ) 0 ˆ 所以 E( X X )(Z EZ )
第八章 状态估计
第八章 状态估计(卡尔曼滤波)
8.1 系统的描述 8.2 最小方差估计 8.3 线性最小方差估计
8.4 波-状态估计
2005-11-5
第八章 状态估计
8.1 系统的描述
8.1.1状态空间模型
随机状态空间模型描述:
X k k ,k 1 X k 1 Bk 1Uk 1 k 1Wk 1
EZ EX , =P , H DX
D(Z ) HPH, R
再根据正态分布中的条件概率可知
ˆ XV E ( X z ) PH [ HPH R]1 (Z H )
2005-11-5
第八章 状态估计
8.3 线性最小方差估计
最小方差是最理想的估计,但需要知道 X , Z 的联
10 10 10 10 10 1 2 1 2 EZ (1) 1 0 10 10 10 10
2 2 2 2 2 2
1 17 2 7 1 7 3 3 1 3 2 173 81 DX 10 10 10 10 10 10 10 10 10 10 10 10 100
1 1
DX cov( X , Z )( DZ )1 cov(Z , X )
要方差 DX最小,必须令 b 0 ,B cov( X , Z )( DZ )1 由此推得:
ˆ X L (Z ) EX cov( X , Z )( DZ )1 (Z EZ )
2005-11-5
% % EXX
第八章 状态估计
ˆ 定理8.2.1X 的最小方差估计 X (Z ) 等于 X 的条件 ˆ 条件均值为 X (Z ) E( X / Z )
证:
% % 使 EXX 最小,等价于使
ˆ ˆ ( X X ( z)) ( X X ( z)) p( x / z)dx
2005-11-5
第八章 状态估计
ˆ 最小的线性估计 X ( Z ) a BZ 称为线性最小方差 ˆ 估计 ,记为 X L (Z )
令 则 于是有
b aEx BEZ
a b EX BEZ
ˆ ˆ X X (Z ) X X (Z ) E X a BZ X a BZ E = E X EX b B[Z EZ ] X EX b B[Z EZ ]
