初二数学(人教版)全等三角形的性质与判定的综合运用第三课时练习题

合集下载

人教版八年级上第十二章《三角形全等的性质和判定的综合应用》练习题

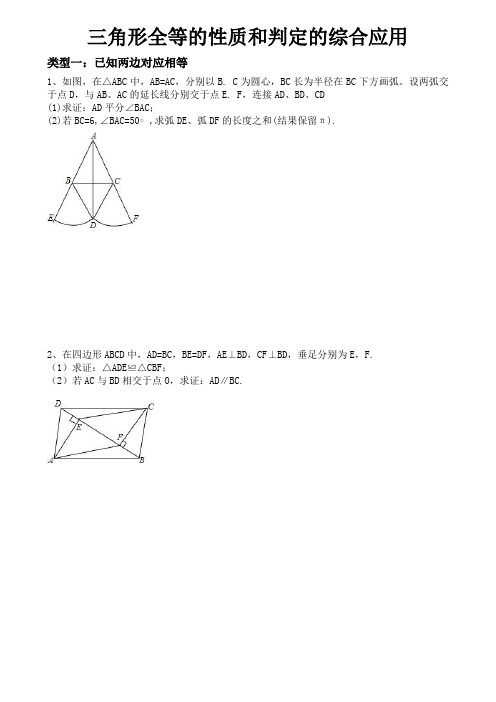
三角形全等的性质和判定的综合应用类型一：已知两边对应相等1、如图，在△ABC中，AB=AC，分别以B. C为圆心，BC长为半径在BC下方画弧。

设两弧交于点D，与AB、AC的延长线分别交于点E. F，连接AD、BD、CD(1)求证：AD平分∠BAC；(2)若BC=6,∠BAC=50∘,求弧DE、弧DF的长度之和(结果保留π).2、在四边形ABCD中，AD=BC，BE=DF，AE⊥BD，CF⊥BD，垂足分别为E，F.（1）求证：△ADE≌△CBF；（2）若AC与BD相交于点O，求证：AD∥BC.3、如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=90∘，且BC=CE，AB=DE.求证：△ABC≌△DEC.类型二：已知两角对应相等4、如图，点A. C. D. B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF.5、已知：如图，∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB的平分线，求证：AB=DC．类型三：已知一角一边对应相等6、如图所示，AB=DB，∠ABD=∠CBE，∠E=∠C，求证：DE=AC.7、已知如图,点F. A. E. B在一条直线上,∠C=∠F,BC∥DE，AB=DE求证：AC=DF.8、如图,∠ACB=90∘，AC=BC，AE⊥CE于E，BD⊥CE于D，AE=5cm，BD=2cm，则DE的长是多少？类型四：两次应用全等9、如图，在△ABC与△DCB中，AC与BD交于点E，且∠BAC=∠CDB，∠ACB=∠DBC，分别延长BA与CD交于点F，求证：BF=CE。

10、已知：如图，D是△ABC中BC边上一点，且AD⊥BC，E是AD上的一点，EB=EC，求证：∠BAE=∠CAE.。

12.2 三角形全等的判定(第3课时)人教版数学八年级上册同步练习(含答案)

第十二章全等三角形12.2 三角形全等的判定第3课时1. 下列各图中a,b,c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（）A．甲和乙B．乙和丙C．甲和丙D．只有丙2. 在△ABC与△A′B′C′中，已知∠A＝44°，∠B＝67°，∠C′＝69° ，∠A′＝44°，且AC＝A′C′，那么这两个三角形（　）A．一定不全等　B．一定全等 C．不一定全等 D．以上都不对3.如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是___________.　4. 如图，已知∠ACB=∠DBC，∠ABC=∠CDB，判别下面的两个三角形是否全等，并说明理由.5. 已知：如图，AB⊥BC，AD⊥DC，∠1=∠2,求证：AB=AD.6. 如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗? 如果可以,带哪块去合适?你能说明其中理由吗?7. 已知：如图，△ABC ≌△A′B′C′，AD，A′D′分别是△ABC和△A′B′C′的高.试说明AD＝A′D′，并用一句话说出你的发现.参考答案：1.B2.B3. AC=BC4. 不全等，因为BC虽然是公共边，但不是对应边.5. 证明：∵AB⊥BC，AD⊥DC，∴∠B=∠D=90 °.在△ABC和△ADC中，∠1=∠2（已知），∠B=∠D（已证），AC=AC （公共边），∴△ABC≌△ADC (AAS)，∴AB=AD.6. 答：带1去，因为有两角且夹边相等的两个三角形全等.7. 解：因为△ABC ≌△A′B′C′，所以AB=A'B'（全等三角形对应边相等），∠ABD=∠A'B'D'（全等三角形对应角相等）.因为AD⊥BC，A'D'⊥B'C'，所以∠ADB=∠A'D'B'.在△ABD和△A'B'D'中，∠ADB=∠A'D'B'（已证），∠ABD=∠A'B'D'（已证），AB=AB（已证），所以△ABD≌△A'B'D'.所以AD=A'D'.。

八年级上数学小专题全等三角形的性质与判定同步练习(人教版带答案)

八年级上数学小专题全等三角形的性质与判定同步练习（人教版带答案）小专题(四) 全等三角形的性质与判定 1．如图所示，D、E是△ABC 中BC边上的点，AD＝AE，∠ADC＝∠AEB，EB＝DC，那么∠1和∠2之间是什么关系？说你的理由．2．已知：如图，D是△ABC的边AB上一点，DF交AC于点E，DE＝FE，FC∥AB.求证：AE＝CE.3．已知：如图，AB，CD交于点O，E，F为AB上两点，OA＝OB，OE ＝OF，∠A＝∠B，∠ACE＝∠BDF.求证：△ACE≌△BDF. 4．如图，已知AC交BD于点O，AB＝DC，∠A＝∠D. (1)请写出符合上述条件的五个结论(并且不再添加辅助线，对顶角除外)；(2)从你写出的5个结论中，任选一个加以证明．5．如图，点C，F在线段BE上，BF＝EC，∠1＝∠2.请你添加一个条件，使△ABC≌△DEF，并加以证明．(不再添加辅助线和字母) 6．如图，在△ABC中，MN⊥AC，垂足为N，且MN平分∠AMC，△ABM 的周长为9 cm，AN＝2 cm，求△ABC的周长．7．如图所示，要测量湖中小岛E距岸边A和D的距离，作法如下：(1)任作线段AB，取中点O；(2)连接DO并延长使DO＝CO；(3)连接BC；(4)用仪器测量E，O在一条线上，并交CB于点F，要测量AE，DE，只需测量BF，CF即可，为什么？8．两个大小不同的等腰直角三角板如图1所示方式放置，图2是由它抽象出的几何图形，B，C，E在同一直线上，连接DC. (1)请找出图2中的全等三角形，并予以证明；(2)求证：DC⊥BE.9．如图，在Rt△ABC中，∠BAC＝90°，点D、E在边BC上，∠CAE ＝∠B，E是CD的中点，且AD平分∠BAE，试问：BD与AC相等吗？请说说你的理由． 10．(南京中考)(1)如图1，在△ABC和△DEF中，AC＝DF，BC＝EF，∠ABC＝∠DEF，且∠ABC、∠DEF都是钝角，求证：△ABC≌△DEF.(2)在△ABC和△DEF中，AC＝DF，BC＝EF，∠ABC＝∠DEF，且∠ABC、∠DEF都是锐角，请你用尺规在图2中作出△DEF，使△DEF和△ABC 不全等．(不写作法，保留作图痕迹) 参考答案 1．在△ADC和△AEB 中，AD＝AE，∠ADC＝∠AEB，DC＝EB，所以△ADC≌△AEB(SAS)．所以∠DAC＝∠EAB. 因为∠EA B－∠DAE＝∠DAC－∠DAE，所以∠1＝∠2. 2.证明：∵FC∥AB，∴∠ADE＝∠CFE. 在△ADE和△CFE中，∠ADE＝∠CFE，DE＝FE，∠AED＝∠CEF，∴△ADE≌△CFE(ASA)．∴AE ＝CE. 3.证明：∵OA＝OB，OE＝OF，∴OA－OE＝OB－OF，即AE＝BF.在△ACE和△BDF中，∠A＝∠B，∠ACE＝∠BDF，AE＝BF，∴△ACE≌△BDF(AAS)． 4.(1)五个结论：OB＝OC；OA＝OD；AC＝DB；∠ABO＝∠DCO；∠ABC＝∠DCB. (2)选证OB＝OC.在△ABO和△DCO 中，∠AOB＝∠DOC，∠A＝∠D，AB＝DC，∴△ABO≌△DCO(AAS)．∴OB ＝OC. 5.答案不唯一，可以是∠E＝∠B，∠D＝∠A，FD＝CA，AB∥ED 等．以DF＝AC加以证明．∵BF＝EC，∴BF－CF＝EC－CF，即BC＝EF. 在△ABC和△DEF中，BC＝EF，∠1＝∠2，CA＝FD，∴△ABC≌△DEF(SAS)． 6.因为MN平分∠AMC，所以∠AMN＝∠CMN，因为MN⊥AC，所以∠MNA＝∠MNC＝90°. 在△AMN和△CMN中，∠AMN ＝∠CMN，MN＝MN，∠MNA＝∠MNC，所以△AMN≌△CMN(ASA)．所以AN＝NC，AM＝CM. 因为AN＝2 cm，所以AC＝2AN＝4 cm. 又因为△ABM 的周长为9 cm，所以△ABC的周长为9＋4＝13(cm)． 7．由条件可知，△AOD≌△BOC，∴BC＝AD. 又∠A＝∠B，∠AOE＝∠BOF，AO＝BO，故△AOE≌△BOF. ∴AE＝BF. ∴DE＝CF. 因此只要测出BF，CF即可知AE，DE的长度了． 8.(1)图2中△ABE≌△ACD .证明：∵△ABC 和△AED都是等腰直角三角形，∴AB＝AC，AE＝AD，∠BAC＝∠EAD ＝90°. ∴∠BAC＋∠CAE＝∠EAD＋∠CAE，即∠BAE＝∠CAD.∴△ABE≌△ACD(SAS)． (2)证明：由(1)知△ABE≌△ACD，∴∠ACD ＝∠B＝45°. 又∵∠ACB＝45°，∴∠BCD＝∠ACB＋∠ACD＝90° .∴DC⊥BE. 9．BD＝AC，理由如下：过D点作AC的平行线交AE的延长线于F，则∠CAE＝∠F. 又∵∠AEC＝∠DEF，E是CD的中点，∴CE＝DE.∴△AEC≌△FED. ∴AC＝FD. 又∵AD平分∠BAE，∴∠DAE＝∠BAD. 又∵∠B＝∠F，AD为公共边，∴△ABD≌△AFD. ∴BD＝DF. ∴BD＝AC. 10.(1)证明：过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H，∵∠ABC＝∠DEF，且∠ABC、∠DEF都是钝角，∴180°－∠ABC＝180°－∠DEF，即∠CBG ＝∠FEH. 在△CBG和△FEH中，∠G＝∠H＝90°，∠CBG＝∠FEH，BC ＝EF，∴△CBG≌△FEH(AAS)．∴CG＝FH .在Rt△A CG和Rt△DFH 中，AC＝DF，CG＝FH，∴Rt△ACG≌Rt△DFH(HL)．∴∠A＝∠D. 在△ABC和△DEF中，∠ABC＝∠DEF，∠A＝∠D，AC＝DF，∴△ABC≌△DEF(AAS)． (2)略。

八年级初二上册数学人教版课时练《三角形全等的判定》03(含答案)

《12．2 三角形全等的判定》课时练一、选择题（本大题共12道小题）1．如图，已知AB＝AD，若利用SSS证明△ABC≌△ADC，则需要添加的条件是()A．AC＝ACB．∠B＝∠DC．BC＝DCD．AB＝CD2．如图所示，∠C＝∠D＝90°，若要用“HL”判定Rt△ABC与Rt△ABD全等，则可添加的条件是()A．AC＝AD B．AB＝ABC．∠ABC＝∠ABD D．∠BAC＝∠BAD3．如图，点B，E，C，F在同一直线上，AB∥DE，∠A＝∠D，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是()A．BE＝CF B．∠ACB＝∠FC．AC＝DF D．AB＝DE4．如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带哪一块去()A．①B．②C．③D．①和②5．如图，在正方形ABCD中，连接BD，点O是BD的中点．若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有()A．2对B．3对C．4对D．5对6．如图，点B，E在线段CD上，若∠C=∠D，则添加下列条件，不一定能使△ABC≌△EFD的是()A．BC=FD，AC=ED B．∠A=∠DEF，AC=EDC．AC=ED，AB=EF D．∠A=∠DEF，BC=FD7．如图，已知∠ABC＝∠DCB，添加以下条件，不能判定△ABC≌△DCB的是()A．∠A＝∠DB．∠ACB＝∠DBCC．AC＝DBD．AB＝DC8．如图，AB＝AC，AD＝AE，BE＝CD，∠2＝110°，∠BAE＝60°，则下列结论错误的是()A．△ABE≌△ACD B．△ABD≌△ACEC．∠C＝30°D．∠1＝70°9．如图，点A，E，B，F在同一直线上，在△ABC和△FED中，AC＝FD，BC＝ED，当利用“SSS”来判定△ABC和△FED全等时，下面的4个条件中：①AE＝FB；②AB＝FE；③AE ＝BE；④BF＝BE，可利用的是()A．①或②B．②或③C．①或③D．①或④10．如图，在等腰直角△ABC中，∠C＝90°，点O是AB的中点，且AB＝6，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为D、E，则CD＋CE等于()A． 2 B． 3 C．2 D．611．现已知线段a，b(a<b)，∠MON=90°，求作Rt△ABO，使得∠O=90°，OA=a，AB=b．小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求．小雷:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求．则下列说法中正确的是()A．小惠的作法正确，小雷的作法错误B．小雷的作法正确，小惠的作法错误C．两人的作法都正确D．两人的作法都错误12．如图，∠AOB＝120°，OP平分∠AOB，且OP＝2．若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有()A．1个B．2个C．3个D．3个以上二、填空题（本大题共6道小题）13．如图，在△ABC中，AD⊥BC于点D，要使△ABD≌△ACD，若根据“HL”判定，还需要添加条件：____________．14．如图，已知CD＝CA，∠1＝∠2，要使△ECD≌△BCA，需添加的条件是__________(只需写出一个条件)．15．如图，在四边形ABCD 中，∠B ＝∠D ＝90°，AB ＝AD ，∠BAC ＝65°，则∠ACD 的度数为________．16．如图，在△ABC 中，∠C ＝90°，AC ＝BC ，AD 是∠BAC 的平分线，DE ⊥AB ，垂足为E ．若△DBE 的周长为20，则AB ＝________．17．如图，在Rt ABC △中，90C ∠=︒，以顶点B 为圆心，适当长度为半径画弧，分别交AB BC ，于点M N ，，再分别以点M N ，为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线BP 交AC 于点D ．若30A ∠=︒，则BCDABDS S =△△__________．18．如图，∠C ＝90°，AC ＝10，BC ＝5，AX ⊥AC ，点P 和点Q 是线段AC 与射线AX 上的两个动点，且AB ＝PQ ，当AP ＝________时，△ABC 与△APQ 全等．三、解答题（本大题共3道小题）19．如图，BD ，CE 是△ABC 的高，且BE ＝CD ．求证：Rt △BEC ≌Rt △CDB ．20．如图，AD ∥BC ，AB ⊥BC 于点B ，连接AC ，过点D 作DE ⊥AC 于点E ，过点B 作BF ⊥AC 于点F ．(1)若∠ABF ＝63°，求∠ADE 的度数； (2)若AB ＝AD ，求证：DE ＝BF ＋EF ．21．如图，ABC △中，点E 在BC 边上，AE AB =，将线段AC 绕点A 旋转到AF 的位置，使得CAF BAE ∠=∠，连接EF ，EF 与AC 交于点G ． (1)求证：EF BC =；(2)若65ABC ∠=︒，28ACB ∠=︒，求FGC ∠的度数．参考答案一、选择题1．C 2．A 3．B 4．C 5．C 6．C 7．C 8．C 9．A 10．B11．A12．D二、填空题 13．AB ＝AC14．答案不唯一，如CE ＝CB 15．25° 16．20 17．1218．5或10 三、解答题19．证明：∵BD ，CE 是△ABC 的高， ∴∠BEC ＝∠CDB ＝90°．在Rt △BEC 和Rt △CDB 中，⎩⎪⎨⎪⎧BC ＝CB ，BE ＝CD ，∴Rt △BEC ≌Rt △CDB(HL)．20．解：(1)∵AD ∥BC ，AB ⊥BC ， ∴∠ABC ＝∠BAD ＝90°． ∵DE ⊥AC ，BF ⊥AC ， ∴∠BFA ＝∠AED ＝90°．∴∠ABF ＋∠BAF ＝∠BAF ＋∠DAE ＝90°． ∴∠DAE ＝∠ABF ＝63°．∴∠ADE ＝27°．(2)证明：由(1)得∠DAE ＝∠ABF ，∠AED ＝∠BFA ＝90°．在△DAE 和△ABF 中，⎩⎪⎨⎪⎧∠DAE ＝∠ABF ，∠AED ＝∠BFA ，AD ＝BA ，∴△DAE ≌△ABF(AAS)． ∴AE ＝BF ，DE ＝AF ．∴DE ＝AF ＝AE ＋EF ＝BF ＋EF ．21．(1)∵CAF BAE ∠=∠， ∴BAC EAF ∠=∠，∵AE AB AC AF ==，， ∴BAC EAF △≌△， ∴EF BC =．(2)∵65AB AE ABC =∠=︒，， ∴18065250BAE ∠=︒-︒⨯=︒， ∴50FAG ∠=︒， ∵BAC EAF △≌△， ∴28F C ∠=∠=︒， ∴502878FGC ∠=︒+︒=︒．。

人教版数学八年级上册：12.2.3 三角形全等的判定(三)ASA、AAS 同步练习(附答案)

第十二章全等三角形12.2.3 三角形全等的判定(三)ASA、AAS1．如图，已知△ABC三条边、三个角，则甲、乙两个三角形中和△ABC全等的是( ) A．甲B．乙C．甲和乙都是D．都不是2．如图，∠ABC＝∠DCB，BD，CA分别是∠ABC，∠DCB的平分线．求证：AB＝DC.3．如图，BD⊥AC于点D，CE⊥AB于点E，AD＝AE.求证：BE＝CD.4．如图，在△ABC中，∠B＝∠C，D为BC的中点，过点D分别向AB，AC作垂线段，则能够说明△BDE≌△CDF的理由是( )A．SSS B．SASB．C．ASA D．AAS5．如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，CE＝BF，∠A ＝∠D.求证：AB＝CD.6．如图，∠B＝∠DEF，AB＝DE，要说明△ABC≌△DEF.(1)若以“SAS”为依据，还需添加的条件为；(2)若以“ASA”为依据，还需添加的条件为；(3)若以“AAS”为依据，还需添加的条件为．7．如图，AE∥DF，AE＝DF，则添加下列条件还不能确定△EAC≌△FDB( ) A．AB＝CD B．CE∥BF C．CE＝BF D．∠E＝∠F第7题图第8题图第9题图第10题图8．如图，已知D是△ABC的边AB上一点，DF交AC于点E，DE＝EF，FC∥AB，若BD ＝2，CF＝5，则AB的长为( )A．2 B．5C．7 D．39．如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC(不添加其他字母及辅助线)，你添加的条件是．10．如图，要测量河两岸相对的两点A，B的距离，在AB的垂线BF上取两点C，D，使BC＝CD，过点D作BF的垂线DE，与AC的延长线交于点E，则∠ABC＝∠CDE＝90°，BC＝DC，∠1＝，△ABC≌．若测得DE的长为25米，则河宽AB的长为．11．如图，已知点A，F，E，C在同一直线上，AB∥CD，∠ABE＝∠CDF，AF＝CE.(1)从图中任找两组全等三角形；(2)从(1)中任选一组进行证明．12．已知△ABN和△ACM位置如图所示，AB＝AC，AD＝AE，∠1＝∠2.求证：(1)BD＝CE；(2)∠M＝∠N.13．如图1，在△ABC中，∠ACB＝90°，AC＝BC，过点C在△ABC外作直线MN，AM⊥MN 于点M，BN⊥MN于点N.(1)求证：MN＝AM＋BN；(2)如图2，若过点C作直线MN与线段AB相交，AM⊥MN于点M，BN⊥MN于点N(AM＞BN)，(1)中的结论是否仍然成立？说明理由．参考答案1．B2．证明：∵∠ABC ＝∠DCB ，BD ，CA 分别是∠ABC ，∠DCB 的平分线，∴∠DBC ＝∠ACB.在△ABC 和△DCB 中，⎩⎪⎨⎪⎧∠ABC ＝∠DCB ，BC ＝CB ，∠ACB ＝∠DBC ，∴△ABC ≌△DCB(ASA )．∴AB ＝DC.3．证明：∵BD ⊥AC 于点D ，CE ⊥AB 于点E ，∴∠ADB ＝∠AEC ＝90°.在△ABD 和△ACE 中，⎩⎪⎨⎪⎧∠ADB ＝∠AEC ，AD ＝AE ，∠A ＝∠A ，∴△ABD ≌△ACE(ASA )．∴AB ＝AC.又∵AD ＝AE ，∴AB －AE ＝AC －AD ，即BE ＝CD.4．D5．证明：∵AB ∥CD ，∴∠B ＝∠C.∵CE ＝BF ，∴CE ＋EF ＝BF ＋EF ，即CF ＝BE.在△ABE 和△DCF 中，⎩⎪⎨⎪⎧∠A ＝∠D ，∠B ＝∠C ，BE ＝CF ，∴△ABE ≌△DCF(AAS )，∴AB ＝CD.6． (1) BC ＝EF 或BE ＝CF ；(2) ∠A ＝∠D ；(3) ∠ACB ＝∠F ．7．C8．C9．AC ＝BC ．10．25米．11．解：(1)△ABE ≌△CDF ，△AFD ≌△CEB.(2)选△ABE ≌△CDF ，证明：∵AB ∥CD ，∴∠BAE ＝∠DCF.∵AF ＝CE ，∴AF ＋EF ＝CE ＋EF ，即AE ＝CF.在△ABE 和△CDF 中，⎩⎪⎨⎪⎧∠BAE ＝∠DCF ，∠ABE ＝∠CDF ，AE ＝CF ，∴△ABE ≌△CDF(AAS )．12．证明：(1)在△ABD 和△ACE 中，⎩⎪⎨⎪⎧AB ＝AC ，∠1＝∠2，AD ＝AE ，∴△ABD ≌△ACE(SAS )．∴BD ＝CE.(2)∵∠1＝∠2，∴∠1＋∠DAE ＝∠2＋∠DAE ，即∠BAN ＝∠CAM.由(1)，得△ABD ≌△ACE ，∴∠B ＝∠C. 在△ACM 和△ABN 中，⎩⎪⎨⎪⎧∠C ＝∠B ，AC ＝AB ，∠CAM ＝∠BAN ，∴△ACM ≌△ABN(ASA )．∴∠M ＝∠N.13．解：(1)证明：∵∠ACB ＝90°，∴∠ACM ＋∠BCN ＝90°.又∵AM ⊥MN ，BN ⊥MN ，∴∠AMC ＝∠CNB ＝90°.∴∠BCN ＋∠CBN ＝90°.∴∠ACM ＝∠CBN. 在△ACM 和△CBN 中，⎩⎪⎨⎪⎧∠ACM ＝∠CBN ，∠AMC ＝∠CNB ，AC ＝CB ，∴△ACM ≌△CBN(AAS )．∴MC ＝NB ，MA ＝NC.∵MN ＝MC ＋CN ，∴MN ＝AM ＋BN.(2)(1)中的结论不成立，结论为MN ＝AM －BN. 理由如下：同(1)中证明可得△ACM ≌△CBN ，∴CM＝BN，AM＝CN.∵MN＝CN－CM，∴MN＝AM－BN.。

八年级初二上册数学人教版课时练《全等三角形》03(含答案)

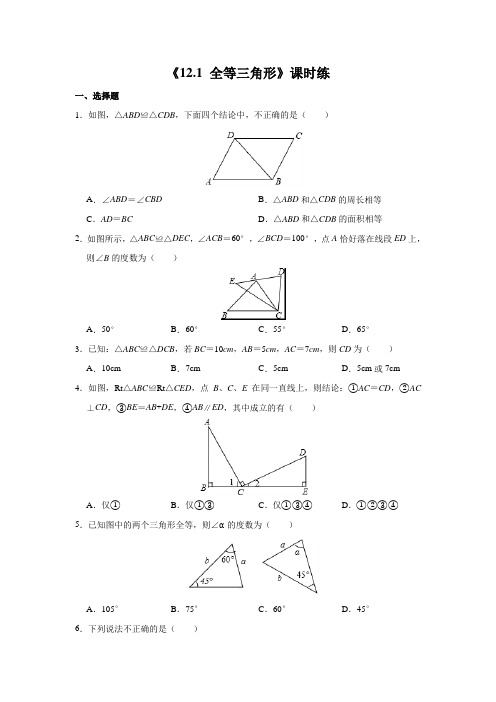
《12.1 全等三角形》课时练一、选择题1．如图，△ABD≌△CDB，下面四个结论中，不正确的是（）A．∠ABD＝∠CBD B．△ABD和△CDB的周长相等C．AD＝BC D．△ABD和△CDB的面积相等2．如图所示，△ABC≌△DEC，∠ACB＝60°，∠BCD＝100°，点A恰好落在线段ED上，则∠B的度数为（）A．50°B．60°C．55°D．65°3．已知：△ABC≌△DCB，若BC＝10cm，AB＝5cm，AC＝7cm，则CD为（）A．10cm B．7cm C．5cm D．5cm或7cm 4．如图，Rt△ABC≌Rt△CED，点B、C、E在同一直线上，则结论：①AC＝CD，②AC ⊥CD，③BE＝AB+DE，④AB∥ED，其中成立的有（）A．仅①B．仅①③C．仅①③④D．①②③④5．已知图中的两个三角形全等，则∠α的度数为（）A．105°B．75°C．60°D．45°6．下列说法不正确的是（）A．全等三角形对应角平分线相等，对应边上的高、中线也分别相等B．全等三角形的周长和面积都相等C．全等三角形的对应角相等，对应边相等D．全等三角形是指周长和面积都相等的三角形7．如图，△ABC≌△DEF，BE＝2，AE＝1，则BD的长是（）A．5B．4C．3D．28．已知：如图，△ABC≌△ADE，AB与AD是对应边，AC与AE是对应边，若∠B＝31°，∠C＝95°，∠EAB＝20°，则∠BAD等于（）A．77°B．74°C．47°D．44°9．已知△ABC与△DEF全等，BC＝EF＝4cm，△ABC的面积是12cm2，则EF边上的高是（）A．3cm B．4cm C．6cm D．无法确定10．如图，已知△ABC≌△EDF，点F，A，D在同一条直线上，AD是∠BAC的平分线，∠EDA＝20°，∠F＝60°，则∠DAC的度数是（）A．50°B．60°C．100°D．120°二．填空题11．如图，△ABC≌△DEF，∠A＝35°，∠B＝50°，则∠DFE＝．12．已知：如图，△ABC≌△DEF，∠A＝85°，∠B＝60°，AB＝8，EH＝2．则∠F的度数；DH的长．13．已知△ABC≌△DEF，AB＝DE＝8cm，△DEF的面积为20cm2，则△ABC的边AB上的高为cm．14．如图，已知△ABC≌△DEF，AD＝1cm，则BE的长为cm．15．如图，已知△ABC≌△DBE，如果∠CBD＝96°，∠CBE＝28°，那么∠ABC＝．三．解答题16．如图，A，D，E三点在同一直线上，且△BAD≌△ACE．（1）求证：BD＝DE+CE；（2）请你猜想△ABD满足什么条件时，BD∥CE．17．如图，已知△ABF≌△CDE．（1）若∠B＝30°，∠DCF＝40°，求∠EFC的度数；（2）求证：AE＝CF．18．如图，△ACF≌△DBE，其中点A、B、C、D在同一条直线上．（1）若BE⊥AD，∠F＝63°，求∠A的大小．（2）若AD＝11cm，BC＝5cm，求AB的长．19．已知：如图，△ABC≌△DEF，AM、DN分别是△ABC、△DEF的对应边上的高．求证：AM＝DN．参考答案一、选择题1．A 2．A 3．C 4．D 5．B 6．D 7．A 8．B 9．C 10．A 二、填空题11．95°12．35° 6 13．5 14．1 15．68°三、解答题16．（1）证明：∵△BAD≌△ACE，∴AD＝CE，BD＝AE，∵A，D，E三点在同一直线上，∴AE＝AD+DE，∴BD＝CE+DE；（2）解：假如BD∥CE，则∠BDE＝∠E，∵△BAD≌△ACE，∴∠ADB＝∠E，∴∠ADB＝∠BDE，又∵∠ADB+∠BDE＝180°，∴∠ADB＝∠BDE＝90°，∴当∠ADB＝∠E＝90°时，BD∥CE．17．（1）解：∵△ABF≌△CDE，∴∠D＝∠B＝30°，∴∠EFC＝∠D+∠DCF＝70°；（2）证明：∵△ABF≌△CDE，∴∠AFB＝∠CED，AF＝CE，在△AFE和△CEF中，，∴△AFE≌△CEF（SAS），∴AE＝CF．18．解：（1）∵BE⊥AD，∴∠EBD＝90°，∵△ACF≌△DBE，∴∠FCA＝∠EBD＝90°，∴∠A＝90°﹣∠F＝27°；（2）∵△ACF≌△DBE，∴CA＝BD，∴CA﹣CB＝BD﹣BC，即AB＝CD，∵AD＝11cm，BC＝5cm，∴AB+CD＝11﹣5＝6cm，∴AB＝3cm．19．方法一：证明：∵△ABC≌△DEF，∴AB＝DE，∠B＝∠E，∵AM，DN分别是△ABC，△DEF的对应边上的高，即AM⊥BC，DN⊥EF，∴∠AMB＝∠DNE＝90°，在△ABM和△DEN中，∴△ABM≌△DEN（AAS），∴AM＝DN．方法二：∵△ABC≌△DEF。

人教版八年级数学(上册)12.2三角形全等的判定(第3课时) 课时习题(附参考答案)

12.2三角形全等的判定（第3课时）1.判断：①两角及其夹边对应相等的两三角形全等（）②两角和其中一角的对边对应相等的两三角形全等（）③两角及其一边对应相等的两三角形全等（）④两角及其一边相等的两三角形全等（）2.选择：①能判定△ABC≌△DEF的条件是( )A.AB=DE,∠C=∠E,BC=EFB.AB=DE,∠A=∠E,BC=EFC.∠A=∠E,AB=EF,∠B=∠DD.∠A=∠D,AB=DE,∠B=∠E②如图，下列条件中，不能判定△ABD和△CBD全等的条件是( )A.AD∥BC,AB=CDB.AB∥DC,AB=CDC.AB=CD,AD=BCD.AB=BC,AD=CD3.如下图，已知∠B=∠C,①若AB=AC,则△ABD≌，其理由是②若AD=AE,也可证与全等，其理由是4.如果要使△ABC≌△DEF，下列各种情况中，将还需补充的条件加在题后的横线上.①AB=DE,∠B=∠E, .其理由是：.②∠A=∠D,∠C=∠F, .其理由是：③AC=DF,BC=EF,其理由是：5.已知∠A=∠B,∠E=∠F,AC=BD.求证：AF=BE.6.如图所示，已知OA=OB,OC=OD,且OB平分∠AOC，OC平分∠BOD，OB交AC 于M，OC交BD于N，求证：①∠OAC=∠OBD ②OM=ON参考答案1.对对对错2.D A3. △ACE，ASA，△ABD≌△ACE，SAS.4.BC=EF，SAS；AC=DF，ASA；AB=DE，SSS；5.证明：AC=BD，AD=BC，在△ADF与△BCE中，∠A=∠B,∠E=∠F, AD=BC，所以△ADF≌△BCE.6.①先证明∠AOB=∠BOC=∠COD，即∠AOC=∠BOD，又OA=OB,OC=OD, △AOC≌△BOD. ∠OAC=∠OBD②在△OAM与△OBN中，∠AOB=∠BOCOA=OB, ∠OAC=∠OBD所以△OAM≌△OBN.即OM=ON.。

【整合】数学人教版八年级上册122三角形全等的判定第三课时同步练习.doc

12. 2三角形全等的判定（3）一、选择题1.如图，玻璃三角板摔成三块，现在到玻璃店在配一块同样大小的三角板，最省事的方法（）A.带①去B.带②去C.带③去D.带①②③去2.如图，已知Z1二Z2,则不一定能使△ ABD^AACD的条件是（）A. AB=ACB. BD=CDC. ZB=ZCD.ZBDA二ZCDA3•如图，给出下列四组条件：① AB = DE, BC=EF, AC = DF ；②AB = DE, ZB = ZE, BC = EF ；③ZB = ZE, BC = EF, ZC = ZF；④AB = DE, AC = DF, ZB = ZE.其中，能使△ ABC竺5DEF的条件共有（）A・1组B・2组C・3组D・4组4.如图，ZE = ZF = 90c, ZB = ZC , AE = AF ,结论：① EM = FN ；②CD = DN ；③ ZFAN = ZEAM；④厶ACN竺£\ABM .其中正确的有（）A. 1个B.2个C・3个 D. 4个5.如图，在下列条件中，不能证明厶ABD^/\ACD的是（）N.BD=DC, AB=AC B.ZADB=ZADC, BD=DCC.ZB=ZC, ZBAD=ZCAD D・ZB=" BD=DC6•如图，已知ZVIBC屮，ZABC = 45°, F是高AD和BE的交点，CE> = 4,则线段DF的长度为（）•A. 2>/2B. 4C. 3V2D. 4>/2A7.如图，点B、C、E在同一条直线上，AABC与厶CDE都是等边三角形，则下列结论不一定成立的是（）A. AACE^ABCDB. ABGC^ AAFCC.ADCG^AECFD. AADB^ACEA8.如图，在厶ABC中，AB=AC, ZABC. ZACB的平分线BD, C£相交于O点，且BD交AC于点D, CE交AB于点E・某同学分析图形后得出以下结论：②、BAD竺/\BCD；③△BDA今Z\CE4；④“BOE竺/\COD；⑤厶ACE竺厶BCE；上述结论一定正确的是（）A.①②③B.②③④C.①③⑤D.①③④二.填空题9•如图，已知AABC的六个元素，则下列甲、乙、丙三个三角形中和AABC全等的图形是___________ 10•如图，AABC 屮，BD二EC, ZADB=ZAEC, ZB=ZC> 则ZCAE= ____________ .11.如图，点B、E、F、C在同一直线上，已知ZA二ZD ZB二ZC,要使△ ABF^/\DCE,以“AAS"需要补充的一个条件是___________________________ （写出一个即可）.12•如图，AD=BC, AC=BD,则图中全等三角形有__________ 对.13.如图,已知AB〃CF,E为DF的中点•若AB=9 cm,C.F=5 cm,则BD的长度为__________ cm.14.如图，ZA=ZD, OA=OD, ZDOC=50°,贝iJZDBO _____________ 度.15.如图，ZB AC = ZABD，请你添加一个条件：______________ ,使O C = OD（只添一个即可）.16.如图，RtAABC 4', ZBAC=90°, AB=AC,分别过点B, C作过点A的直线的垂线BD, CE,垂足分别为点D,E.若BD=2, CE=3,则AE二_______________ , AD= _____________ .17.如图，有一块边长为4的正方形塑料摸板ABCD.,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F ,与CB延长线交于点E .则四边形AECF的面积是 _____________ .18.如图，两块完全相同的含30。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2.
2.如图，C是路段AB的中点，两人从C同时出发，以相同的速度分别沿两条直线行走，并同时到达D，E两地，此时，DA⊥AB，EB⊥AB，D、E与路段AB的距离相等吗？为什么？
课程Hale Waihona Puke 本信息课例编号学科
数学
年级
八年级
学期
QJ
课题
全等三角形的性质与判定的综合运用（第三课时）
教科书
书名：义务教育教科书八年级上册
出版社：人民教育出版社出版日期： 2013 年 6 月
学生信息
姓名
学校
班级
学号
课后练习
1.如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠ABC和∠DEF的大小有什么关系？为什么？