三角函数公式及其记忆方法
三角函数公式大全及记忆口诀.docx
三角函数公式大全、定义正弦(sin)sinA 二—£ 二—r余弦(cos) ceisA-— c £050 =-T正切（tan tan A = ?b 伽少=—或tg) X余切（cot cotA --cot0 =—或 ctg) a P 正割(sec)t secA =-b sec &=-X 余割(CSC)€cscA 二一rcscP 二一>■二、函数关系倒数关系：tan<rcota= 1 ； - 1: cosaseca = 1平方关系：sin^a +cos^a = 1 ； l-rtdn2<r = 5e^a ； 1 +cot 2a=c5c 2«图形锐角三角函数tana =独商数关系：COSff gmcola =― ----- sinrrC任意角三角函数对边G三、诱导公式口诀：奇变偶不变，符号看彖限公式一：设CT为任意角，终边相同的角的同一三角函数的值相等:4 ^) = sina,fc eZcos(2faf? + 纹)=ms 纽k w Ntan(^T7? + a) = tana, k € 更cotffcn + ff] = cota f fc €Z公式二：设&为任意角，觅牛*与◎的三角函数值之间的关系：sin(7? + a] = -sin<r€OS(H + a] = -COSfftan(7? + a) =tan(rC€>t(7T + ffj =C€>ttf公式三：任意角-旳与a的三角函数值Z间的关系：sin(-aj =-sina cos(-aj = cosa t5n(-a} =-tancjr cot(-a) =-cota 公式四：71-cr与心的三角函数值Zl'可的关系：sin(7T 一a) = sina- aj = -<vscrtan(7i-ff) = -tana公式五：的三角函数值Z间的关系：sin(2n - a) =-sinacos(2n - a) =cosa \tan(2n 一a)二-tan acot(2n-a) =-cota71 3—i ft-—77 i公式六：2 及2 与農的三角函数值之间的关系：bj- ■a +天-2兀2n-27?-2l27?-2l:: -2-- -} «)a ut cn siI d>四、基本公式1 .和差角公式口诀：正余同余正，余余反正正sintit 4 — sin a + cos a sin p. sin(a -^) = sin acos^-costrsin^cos(a+^l = cosacos^cos(a - = cosa cos^F+sin a sin2.和弄化积口诀：正加正，正在前。
三角函数公式记忆方法
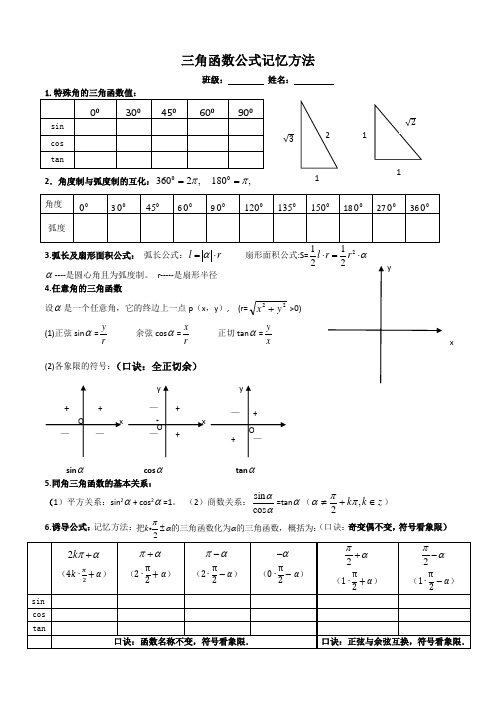
9、辅助角公式：������ = ������������������������ ������ + ������ ������������������ ������
√������2 + ������2 b
a
3.弧长及扇形面积公式： 弧长公式： l = r
----是圆心角且为弧度制。 r-----是扇形半径
4.任意角的三角函数
扇形面积公式:S= 1 l r = 1 r2
22
y
设 是一个任意角，它的终边上一点 p（x，y）, (r= x2 + y 2 >0)
(1)正弦 sin = y
余弦 cos = x
正切 tan = y
r
r
x
x
(2)各象限的符号：（口诀：全正切余）
y
+
+
O
x
+—
—
y
—+
+
x
—O +
y
—+ O
+—
sin
cos
tan
5.同角三角函数的基本关系：
（1）平方关系：sin2 + cos2 =1。 （2）商数关系： sin =tan （ + k , k z ）
奇偶性
减区间： 增区间：
增区间：
8、两角和差公式：口诀（正弦：正余余正，符号相同。 余弦：余余正正，符号相反）
+
−
2
sin
cos
tan
降幂公式： 1+cos = 2 cos 2
2
1-cos = 2sin2
2
升幂公式 ： cos2 = 1 + cos 2
三角函数记忆顺口溜
三角函数记忆顺口溜
三角函数的记忆口诀之一：
三角函数是函数象限符号坐标注。
函数图像单位圆，周期奇偶增减现。
同角关系很重要，化简证明都需要。
正六边形顶点处，从上到下弦切割:中心记上数字一，连结顶点三角形。
三角函数的记忆口诀之二：
余弦积减正弦积，换角变形众公式。
和差化积须同名，互余角度变名称。
计算证明角先行，注意结构函数名，保持基本量不变繁难向着简易变。
逆反原则作指导，升幂降次和差积。
条件等式的证明，方程思想指路明。
万能公式不一般，化为有理式居先。
公式顺用和逆用，变形运用加巧用。
一加余弦想余弦一减余弦想正弦，幕升一次角减半，升幕降次它为范。
三角函数反函数，实质就是求角度，先求三角函数值，再判角取值范围。
利用直角三角形形象直观好换名，简单三角的方程，化为最简求解集。
三角函数必背公式记忆技巧
三角函数必背公式记忆技巧
三角函数的必背公式有很多，记忆技巧包括以下几点：
1. 理解公式的含义：不仅仅是死记硬背，更要理解公式的意义和用途。
例如，sin函数代表一个角度的正弦值，cos函数代表一个角度的余弦值。
2. 利用图形记忆：可以通过画图的方式，将公式与图形联系起来，从
而更容易记忆和理解。
例如，sin函数的图形是一个周期性的波形，可以将公式与这个图形联系起来记忆。
3. 创造联想记忆：将公式与一些容易记住的关键词或形象相联系，可
以帮助记忆。
例如，sin(a + b) = sina*cosb + cosa*sinb，可以将
"a + b"联想成"阿爸"，然后将每个字母与对应的公式部分联系起来记忆。
4. 划分为小块记忆：将公式划分为几个小块，分别记忆每个小块的内容，然后逐渐合并起来。
例如，sin(a + b)可以拆分为sin(a)*cos(b) + cos(a)*sin(b)，分别记忆这两个部分，然后合并起来记忆整个公式。
5. 多练习：通过反复练习来巩固记忆，可以进行一些练习题或者实际
应用来加深对公式的理解和记忆。
记忆三角函数的公式需要耐心和坚持，通过不断的练习和巩固，相信
可以掌握并记忆好这些公式。
三角函数公式及其记忆方法
三角函数公式及其记忆方法一、同角三角函数得基本关系式(一)基本关系1、倒数关系2、商得关系3、平方关系(二)同角三角函数关系六角形记忆法构造以"上弦、中切、下割;左正、右余、中间1"得正六边形为模型。
1、倒数关系对角线上两个函数互为倒数;2、商数关系六边形任意一顶点上得函数值等于与它相邻得两个顶点上函数值得乘积。
(主要就是两条虚线两端得三角函数值得乘积,下面4个也存在这种关系。
)。
由此,可得商数关系式。
3、平方关系在带有阴影线得三角形中,上面两个顶点上得三角函数值得平方与等于下面顶点上得三角函数值得平方。
二、诱导公式得本质所谓三角函数诱导公式,就就是将角n·(π/2)±α得三角函数转化为角α得三角函数。
(一)常用得诱导公式1、公式一: 设α为任意角,终边相同得角得同一三角函数得值相等:2、公式二:α为任意角,π+α得三角函数值与α得三角函数值之间得关系:3、公式三:任意角α与 -α得三角函数值之间得关系:4、公式四:利用公式二与公式三可以得到π-α与α得三角函数值之间得关系:5、公式五:利用公式一与公式三可以得2π-α与α得三角函数值之间得关系:sin(2π－α)=－sinα cos(2π－α)=cosαtan(2π－α)=－tanα cot(2π－α)=－cotαsec (2π—α) = secαcsc (2π—α) =—cscα6、公式六:+α与α得三角函数值之间得关系:sin(+α)=cosα cos(+α)=－sinαtan(+α)=－cotα cot(+α)=－tanαsec (+α) =—cscα csc (+α) = secα7、公式七:-α与α得三角函数值之间得关系:sin(－α)=cosα cos(－α)=sinαtan(－α)=cotα cot(－α)=tanαsec (—α) = cscα csc (—α) = secα8、推算公式:+α与α得三角函数值之间得关系:sin(+α)=－cosα cos(+α)=sinαtan(+α)=－cotα c ot(+α)=－tanαsec (+α) = cscα csc (+α) =—secα9、推算公式:—α与α得三角函数值之间得关系:sin(－α)=－cosα cos(－α)=－sinαtan(－α)=cotα cot(－α)=tanαsec(-α) =—cscα csc(—α) =—secα诱导公式记忆口诀:“奇变偶不变,符号瞧象限”。
三角函数记忆顺口溜 记忆的方法和技巧
三角函数记忆顺口溜记忆的方法和技巧
三角函数是基本初等函数之一，是以角度为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
也可以等价地用与单位圆有关的各种线段的长度来定义。
1 三角函数记忆口诀三角函数是函数，象限符号坐标注。
函数图像单位圆，周期奇偶增减现。
同角关系很重要，化简证明都需要。
正六边形顶点处，从上到下弦切割;
中心记上数字一，连结顶点三角形。
向下三角平方和，倒数关系是对角，顶点任意一函数，等于后面两根除。
诱导公式就是好，负化正后大化小，变成锐角好查表，化简证明少不了。
二的一半整数倍，奇数化余偶不变，将其后者视锐角，符号原来函数判。
两角和的余弦值，化为单角好求值，余弦积减正弦积，换角变形众公式。
和差化积须同名，互余角度变名称。
计算证明角先行，注意结构函数名，保持基本量不变，繁难向着简易变。
逆反原则作指导，升幂降次和差积。
条件等式的证明，方程思想指路明。
万能公式不一般，化为有理式居先。
公式顺用和逆用，变形运用加巧用;
一加余弦想余弦，一减余弦想正弦，幂升一次角减半，升幂降次它为范;
三角函数反函数，实质就是求角度，先求三角函数值，再判角取值范围;
利用直角三角形，形象直观好换名，简单三角的方程，化为最简求解集。
1 三角函数万能公式怎幺记1）正弦：1 加切方除切倍。
要注意‘除’的含义。
2）余弦：阴阳相比是余弦。
三角函数公式及其记忆方法
三角函数公式及其记忆方法4、公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：ααπsin )sin(=- ααπcos )cos(-=-ααπtan )tan(-=- ααπcot )cot(-=-ααπsec )sec(-=- ααπcsc )csc(=-5、公式五：利用公式一和公式三可以得2π-α与α的三角函数值之间的关系：sin （2π－α）=－sinα cos （2π－α）= cosαtan （2π－α）=－tanα cot （2π－α）=－cotαsec (2π—α) = secα csc (2π—α) =—cscα6、公式六：2π+α与α的三角函数值之间的关系：sin （2π+α）= cosα cos （2π+α）=－sinα tan （2π+α）=－cotα cot （2π+α）=－tanαsec (2π+α) =—cscα csc (2π+α) = secα7、公式七：2π-α与α的三角函数值之间的关系：sin（π－α）= cosα2cos（π－α）= sinα2tan（π－α）= cotα2cot（π－α）= tanα2sec (π—α) = cscα2csc (π—α) = secα28、推算公式：3π+α与α的三角函数值2之间的关系：sin（23π+α）=－cosα cos （23π+α）= sinαtan（23π+α）=－cotα cot （23π+α）=－tanαsec (23π+α) = cscαcsc (3π+α) =—secα29、推算公式：23π—α与α的三角函数值之间的关系：sin（23π－α）=－cosα cos （23π－α）=－sinαtan（23π－α）= cotα cot （23π－α）= tanαsec（3π-α) =—cscα2csc（23π—α) =—secα诱导公式记忆口诀：“奇变偶不变，符号看象限”。
“奇、偶”指的是π的倍数的奇偶，“变2与不变”指的是三角函数的名称的变化：“变”是指正弦变余弦，正切变余切。
高中数学常用三角函数公式及口诀
常用三角函数公式及口诀常用的诱导公式有以下几组：公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin(2kπ+α)=sinα (k∈Z)cos(2kπ+α)=cosα (k∈Z)tan(2kπ+α)=tanα (k∈Z)cot(2kπ+α)=cotα (k∈Z)公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三：任意角α与-α的三角函数值之间的关系：sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)注意：在做题时，将a看成锐角来做会比较好做。
诱导公式记忆口诀规律总结上面这些诱导公式可以概括为：对于π/2*k ±α(k∈Z)的三角函数值，①当k是偶数时，得到α的同名函数值，即函数名不改变;②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot，cot→tan.(奇变偶不变)然后在前面加上把α看成锐角时原函数值的符号。
三角函数公式大全(方便记忆)
倒数关系: 商的关系：平方关系：tanα ·cotα＝1sinα ·cscα＝1cosα ·secα＝1 sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα sin2α＋cos2α＝11＋tan2α＝sec2α1＋cot2α＝csc2α（六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”）诱导公式（口诀:奇变偶不变，符号看象限。
）sin（－α）＝－sinαcos（－α）＝cosα tan（－α）＝－tanαcot（－α）＝－cotαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotαsin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotαsin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin（α＋β）＝sinαcosβ＋cosαsinβsin（α－β）＝sinαcosβ－cosαsinβcos（α＋β）＝cosαcosβ－sinαsinβcos（α－β）＝cosαcosβ＋sinαsinβtanα＋tanβtan（α＋β）＝——————1－tanα ·tanβtanα－tanβtan（α－β）＝——————1＋tanα ·tanβ2tan(α/2)sinα＝——————1＋tan2(α/2)1－tan2(α/2)cosα＝——————1＋tan2(α/2)2tan(α/2)tanα＝——————1－tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α2tanαtan2α＝—————1－tan2αsin3α＝3sinα－4sin3αcos3α＝4cos3α－3cosα3tanα－tan3αtan3α＝——————1－3tan2α三角函数的和差化积公式三角函数的积化和差公式α＋βα－βsinα＋sinβ＝2sin———·cos———2 2α＋βα－βsinα－sinβ＝2cos———·sin———2 2α＋βα－βcosα＋cosβ＝2cos———·cos———2 2α＋βα－βcosα－cosβ＝－2sin———·sin———2 2 1sinα ·cosβ＝-[sin（α＋β）＋sin（α－β）]21cosα ·sinβ＝-[sin（α＋β）－sin（α－β）]21cosα ·cosβ＝-[cos（α＋β）＋cos（α－β）]21sinα ·sinβ＝— -[cos（α＋β）－cos（α－β）]2化asinα ±bcosα为一个角的一个三角函数的形式（辅助角的三角函数的公式）。
三角函数公式定理记忆口诀
三角函数知识点公式定理记忆口诀三角函数是函数，象限符号坐标注。
函数图象单位圆，周期奇偶增减现。
同角关系很重要，化简证明都需要。
正六边形顶点处，从上到下弦切割；中心记上数字1，连结顶点三角形；向下三角平方和，倒数关系是对角，顶点任意一函数，等于后面两根除。
诱导公式就是好，负化正后大化小，变成税角好查表，化简证明少不了。
二的一半整数倍，奇数化余偶不变，将其后者视锐角，符号原来函数判。
两角和的余弦值，化为单角好求值，余弦积减正弦积，换角变形众公式。
和差化积须同名，互余角度变名称。
计算证明角先行，注意结构函数名，保持基本量不变，繁难向着简易变。
逆反原则作指导，升幂降次和差积。
条件等式的证明，方程思想指路明。
万能公式不一般，化为有理式居先。
公式顺用和逆用，变形运用加巧用；1加余弦想余弦，1减余弦想正弦，幂升一次角减半，升幂降次它为范；三角函数反函数，实质就是求角度，先求三角函数值，再判角取值范围；利用直角三角形，形象直观好换名，简单三角的方程，化为最简求解集。
【文字：大小】口口之和仍口口赛赛之和赛口留口口之差负赛赛赛赛之差口赛收高中数学三角函数公式定理口诀三角函数是函数，象限符号坐标注。
函数图象单位圆，周期奇偶增减现。
同角关系很重要，化简证明都需要。
正六边形顶点处，从上到下弦切割；中心记上数字1，连结顶点三角形；向下三角平方和，倒数关系是对角，顶点任意一函数，等于后面两根除。
诱导公式就是好，负化正后大化小，变成税角好查表，化简证明少不了。
二的一半整数倍，奇数化余偶不变，将其后者视锐角，符号原来函数判。
两角和的余弦值，化为单角好求值，余弦积减正弦积，换角变形众公式。
和差化积须同名，互余角度变名称。
计算证明角先行，注意结构函数名，保持基本量不变，繁难向着简易变。
逆反原则作指导，升幂降次和差积。
条件等式的证明，方程思想指路明。
万能公式不一般，化为有理式居先。
公式顺用和逆用，变形运用加巧用；1加余弦想余弦，1减余弦想正弦，幂升一次角减半，升幂降次它为范；三角函数反函数，实质就是求角度，先求三角函数值，再判角取值范围；利用直角三角形，形象直观好换名，简单三角的方程，化为最简求解集三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)倍角公式tan2A = 2tanA/(1-tan^2 A)Sin2A=2SinA•CosACos2A = Cos^2 A--Sin^2 A=2Cos^2 A—1=1—2sin^2 A三倍角公式sin3A = 3sinA-4(sinA)^3;cos3A = 4(cosA)^3 -3cosAtan3a = tan a • tan(π/3+a)• tan(π/3-a)半角公式sin(A/2) = √{(1--cosA)/2}cos(A/2) = √{(1+cosA)/2}tan(A/2) = √{(1--cosA)/(1+cosA)}cot(A/2) = √{(1+cosA)/(1-cosA)}tan(A/2) = (1--cosA)/sinA=sinA/(1+cosA) 和差化积sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] sin(a)-sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b) = -2sin[(a+b)/2]sin[(a-b)/2] tanA+tanB=sin(A+B)/cosAcosB积化和差sin(a)sin(b) = -1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b) = 1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b) = 1/2*[sin(a+b)+sin(a-b)] cos(a)sin(b) = 1/2*[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sin(a)cos(-a) = cos(a)sin(π/2-a) = cos(a)cos(π/2-a) = sin(a)sin(π/2+a) = cos(a)cos(π/2+a) = -sin(a)sin(π-a) = sin(a)cos(π-a) = -cos(a)sin(π+a) = -sin(a)cos(π+a) = -cos(a)tgA=tanA = sinA/cosA万能公式sin(a) = [2tan(a/2)] / {1+[tan(a/2)]^2}cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]^2}tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2}其它公式a•sin(a)+b•cos(a) = [√(a^2+b^2)]*sin(a+c) [其中，tan(c)=b/a] a•sin(a)-b•cos(a) = [√(a^2+b^2)]*cos(a-c) [其中，tan(c)=a/b]1+sin(a) = [sin(a/2)+cos(a/2)]^2;1-sin(a) = [sin(a/2)-cos(a/2)]^2;;其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tg h(a) = sin h(a)/cos h(a)公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）= sinαcos（2kπ＋α）= cosαtan（2kπ＋α）= tanαcot（2kπ＋α）= cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）= -sinαcos（π＋α）= -cosαtan（π＋α）= tanαcot（π＋α）= cotα公式三：任意角α与-α的三角函数值之间的关系：sin（-α）= -sinαcos（-α）= cosαtan（-α）= -tanαcot（-α）= -cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π-α）= sinαcos（π-α）= -cosαtan（π-α）= -tanαcot（π-α）= -cotα公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π-α）= -sinαcos（2π-α）= cosαtan（2π-α）= -tanαcot（2π-α）= -cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2+α）= cosαcos（π/2+α）= -sinαtan（π/2+α）= -cotαcot（π/2+α）= -tanαsin（π/2-α）= cosαcos（π/2-α）= sinαtan（π/2-α）= cotαcot（π/2-α）= tanαsin（3π/2+α）= -cosαcos（3π/2+α）= sinαtan（3π/2+α）= -cotαcot（3π/2+α）= -tanαsin（3π/2-α）= -cosαcos（3π/2-α）= -sinαtan（3π/2-α）= cotαcot（3π/2-α）= tanα(以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ) =√{(A^2 +B^2 +2ABcos(θ-φ)} • sin{ ωt + arcsin[ (A•sinθ+B•sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} }√表示根号,包括{……}中的内容。
常用三角函数公式及口诀
常用三角函数公式及口诀-CAL-FENGHAI.-(YICAI)-Company One1常用三角函数公式及口诀常用的诱导公式有以下几组：公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin(2kπ+α)=sinα (k∈Z)cos(2kπ+α)=cosα (k∈Z)tan(2kπ+α)=tanα (k∈Z)cot(2kπ+α)=cotα (k∈Z)公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin(π+α)=-sinαcos(π+α)=-cosαta n(π+α)=tanαcot(π+α)=cotα公式三：任意角α与 -α的三角函数值之间的关系：sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)注意：在做题时，将a看成锐角来做会比较好做。
三角函数记忆法
三角函数是数学中的重要概念，而其公式和口诀也是学习中的难点。
以下是一些记忆三角函数的方法：
1.口诀记忆：通过编写简洁明快的口诀来记忆复杂的公式。
例如，“奇变偶
不变，符号看象限”用来记忆三角函数的诱导公式。
2.图像记忆：将函数图像和公式相结合，通过图像的直观性来记忆公式。
例
如，对于正弦函数和余弦函数，可以通过观察图像来记忆其周期性、最值等性质。
3.推导记忆：通过不断地进行公式推导，将公式串联起来记忆。
这种方法尤
其适用于同角三角函数的基本关系式和两角和与差的三角函数公式。
4.归纳总结：将学过的三角函数知识进行归纳总结，形成知识体系。
例如，
总结三角函数的定义、图像、性质、应用等，以便于整体把握和记忆。
5.实际应用：通过解决实际问题来加深对三角函数的理解和记忆。
例如，利
用三角函数解决几何问题、物理问题等。
总之，记忆三角函数的方法多种多样，可以根据自己的情况选择适合自己的方法。
同时，多做练习题也是加深理解和记忆的好方法。
三角函数公式及其记忆方法
三角函数公式及其记忆方法三角函数是数学中的一类函数，它们描述了角度和长度之间的关系。
在三角函数中，最常见的三个函数是正弦函数(sin)，余弦函数(cos)和正切函数(tan)。
1. 正弦函数(sin)：在一个直角三角形中，正弦值是指对边与斜边的比值。
正弦函数的记忆方法可以通过以下动作，即“拉橡皮筋”：-首先，将一个橡皮筋固定在一个固定点上；-然后，将橡皮筋的另一端拉向一些角；-最后，角与橡皮筋的拉力之间的关系就是正弦函数的关系。
正弦函数的公式为：sin(θ) = 对边 / 斜边，其中θ为角度。
2. 余弦函数(cos)：在一个直角三角形中，余弦值是指邻边与斜边的比值。
余弦函数的记忆方法可以通过以下动作，即“压缩橡皮筋”：-首先，将一个橡皮筋固定在一个固定点上；-然后，将橡皮筋的另一端向内压缩；-最后，压缩橡皮筋的长度与角之间的关系就是余弦函数的关系。
余弦函数的公式为：cos(θ) = 邻边 / 斜边，其中θ为角度。
3. 正切函数(tan)：在一个直角三角形中，正切值是指对边与邻边的比值。
正切函数的记忆方法可以通过以下动作，即“竖直爬长梯”：-首先，站立在一根垂直的梯子底端；-然后，爬上梯子，爬升的高度与梯子水平的位置之间的关系就是正切函数的关系。
正切函数的公式为：tan(θ) = 对边 / 邻边，其中θ为角度。
除了这三个基本的三角函数之外，还有其它一些相关的三角函数：- 余切函数(cot)：cot(θ) = 1 / tan(θ) = 邻边 / 对边- 正割函数(sec)：sec(θ) = 1 / cos(θ) = 斜边 / 邻边- 余割函数(csc)：csc(θ) = 1 / sin(θ) = 斜边 / 对边这些函数都有各自的定义和性质，但是它们之间存在一些重要的关系- sin²(θ) + cos²(θ) = 1，这是三角函数中的基本恒等式。
- tan(θ) = sin(θ) / cos(θ)，这表明正切是正弦与余弦的比值。
常用三角函数公式与口诀
常用三角函数公式及口诀常用的引诱公式有以下几组：公式一：设α为随意角，终边同样的角的同一三角函数的值相等：sin(2kπ +α )=sin∈Z)α (kcos(2k π +α )=cos∈αZ) (ktan(2k π +α )=tan∈αZ) (kcot(2kπ +α )=cot∈ αZ) (k公式二：设α为随意角，π+α的三角函数值与α的三角函数值之间的关系：sin( π +α-sin)= αcos( π +α-cos)= αtan( π +α )=tan αcot( π +α )=cot α公式三：随意角α与-α的三角函数值之间的关系：sin(-α )=-sin αcos(-α )=cos αtan(-α )=-tan αcot(-α )=-cot α公式四：利用公式二和公式三能够获得π-α与α的三角函数值之间的关系：sin( -πα )=sin αcos( π-α )=-cos αtan( π-α )=-tan αcot( π-α )=-cot α公式五：利用公式一和公式三能够获得2π-α与α的三角函数值之间的关系：sin(2 -πα )=-sin αcos(2 π-α )=cos αtan(2 π-α )=-tan αcot(2 -πα )=-cot α公式六：π/2 ±α及 3π/2 ±α与α的三角函数值之间的关系：sin( π /2+ α )=cos αcos( π /2+ α-sin)= αtan( π /2+ α-cot)= αcot( π /2+ α-tan)=αsin( π-α/2 )=cos αcos( π-/2α )=sin αtan( π-/2α )=cot αcot( π-/2α )=tan αsin(3 π /2+ -αcos)=αcos(3 π /2+ α )=sin αtan(3 π /2+ α-cot)=αcot(3 π /2+ α-tan)=αsin(3 π-α/2 )=-cos αcos(3 π-/2α )=-sin αtan(3 π-/2α )=cot αcot(3 π-/2α )=tan α(以上 k∈Z)注意：在做题时，将 a 当作锐角来做会比较好做。
常用三角函数公式及口诀
常用三角函数公式及口诀常用的诱导公式有以下几组： 公式一： 设α为任意角，终边相同的角的同一三角函数的值相等： sin(2kπ+α)=sinα (k∈Z) cos(2kπ+α)=cosα (k∈Z) tan(2kπ+α)=tanα (k∈Z) cot(2kπ+α)=cotα (k∈Z) 公式二： 设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三： 任意角α与 -α的三角函数值之间的关系： sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα 公式四： 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五： 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系： sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα 公式六： π/2±α及3π/2±α与α的三角函数值之间的关系： sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα (以上k∈Z) 注意：在做题时，将a看成锐角来做会比较好做。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三角函数公式及其记忆方法一、同角三角函数的基本关系式 （一）基本关系1、倒数关系1cot tan =⋅αα 1csc sin =⋅αα 1sec cos =⋅αα 2、商的关系αααtan cos sin = αααtan csc sec = αααcot sin cos = αααcot sec csc = 3、平方关系1cos sin 22=+αα αα22sec tan 1=+ αα22csc cot 1=+（二）同角三角函数关系六角形记忆法构造以"上弦、中切、下割；左正、右余、中间1"的正六边形为模型。
1、倒数关系对角线上两个函数互为倒数； 2、商数关系六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。
（主要是两条虚线两端的三角函数值的乘积，下面4个也存在这种关系。
）。
由此，可得商数关系式。
3、平方关系在带有阴影线的三角形中，上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。
二、诱导公式的本质所谓三角函数诱导公式，就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
（一）常用的诱导公式1、公式一： 设α为任意角，终边相同的角的同一三角函数的值相等：z k k ∈=+,sin )2sin(ααπ z k k ∈=+,cos )2cos(ααπz k k ∈=+,tan )2tan(ααπ z k k ∈=+,cot )2cot(ααπ z k k ∈=+,sec )2sec(ααπ z k k ∈=+,csc )2csc(ααπ2、公式二：α为任意角，π+α的三角函数值与α的三角函数值之间的关系：ααπsin )sin(-=+ ααπcos )cos(-=+ααπtan )tan(=+ ααπcot )cot(=+ ααπsec )sec(-=+ ααπcsc )csc(-=+3、公式三：任意角α与 -α的三角函数值之间的关系：ααsin )sin(-=- ααcos )cos(=-ααtan )tan(-=- ααcot )cot(-=- ααsec )sec(=- ααcsc )csc(-=-4、公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：ααπsin )sin(=- ααπcos )cos(-=-ααπtan )tan(-=- ααπcot )cot(-=- ααπsec )sec(-=- ααπcsc )csc(=-5、公式五：利用公式一和公式三可以得2π-α与α的三角函数值之间的关系： sin （2π－α）=－sinα cos （2π－α）= cosα tan （2π－α）=－tanα cot （2π－α）=－cotα sec (2π—α) = secα csc (2π—α) =—cscα6、公式六：2π+α与α的三角函数值之间的关系：sin （2π+α）= cosα cos （2π+α）=－sinα tan （2π+α）=－cotα cot （2π+α）=－tanαsec (2π+α) =—cscα csc (2π+α) = secα7、公式七：2π-α与α的三角函数值之间的关系：sin （2π－α）= cosα cos （2π－α）= sinα tan （2π－α）= cotα cot （2π－α）= tanαsec (2π—α) = cscα csc (2π—α) = secα8、推算公式：23π+α与α的三角函数值之间的关系：sin （23π+α）=－cosα cos （23π+α）= sinα tan （23π+α）=－cotα cot （23π+α）=－tanα sec (23π+α) = cscα csc (23π+α) =—secα 9、推算公式：23π—α与α的三角函数值之间的关系：sin （23π－α）=－cosα cos （23π－α）=－sinα tan （23π－α）= cotα cot （23π－α）= tanα sec （23π-α) =—cscα csc （23π—α) =—secα 诱导公式记忆口诀：“奇变偶不变，符号看象限”。
“奇、偶”指的是2π的倍数的奇偶，“变与不变”指的是三角函数的名称的变化：“变”是指正弦变余弦，正切变余切。
（反之亦然成立）“符号看象限”的含义是：把角α看做锐角，不考虑α角所在象限，看n·(π/2)±α是第几象限角，从而得到等式右边是正号还是负号。
符号判断口诀：“一全正；二正弦；三两切；四余弦”。
这十二字口诀的意思就是说：第一象限内任何一个角的四种三角函数值都是“+”； 第二象限内只有正弦是“+”，其余全部是“－”；第三象限内只有正切和余切是“+”，其余全部是“－”； 第四象限内只有余弦是“+”，其余全部是“－”。
“ASCT”意即为“all(全部)”、“sin”、“tan ”、“cos ”（二）其他三角函数知识1、两角和差公式βαβαβαsin cos cos sin )sin(+=+βαβαβαsin cos cos sin )sin(-=-βαβαβαsin sin cos cos )cos(-=+βαβαβαsin sin cos cos )cos(+=-βαβαβαtan tan 1tan tan )tan(-+=+βαβαβαtan tan 1tan tan )tan(+-=-记忆方法： S +=SC+CS C +=CC-SS T +=TTTT +-1变号都反转2、二倍角的正弦、余弦和正切公式αααcos sin 22sin ⋅=ααααα2222sin 211cos 2sin cos 2cos -=-=-=ααα2tan 1tan 22tan -=3、半角的正弦、余弦和正切公式2cos 12sin α-±=a 2cos 12cosα+±=a αααααsin cos 1cos 1sin 2tan -=+= αααcos 1cos 12tan 2+-=4、万能公式2tan 12tan2sin 2ααα+=2tan 12tan 1cos 22ααα+-=2tan 12tan2tan 2ααα-=5、三倍角的正弦、余弦和正切公式ααα3sin 4sin 33sin -= αααcos 3cos 43cos 3-=αααα23tan 31tan tan 33tan --= 5.1方法一谐音、联想1) 正弦三倍角：3元 减 4元3角（欠债了(被减成负数)，所以要“挣钱”(音似“正弦”)）2) 余弦三倍角：4元3角 减 3元（减完之后还有“余”） 注意：函数名，即正弦的三倍角都用正弦表示，余弦的三倍角都用余弦表示。
5.2方法二：1) 正弦三倍角 ：3 1 4 3 2) 余弦三倍角：4 3 3 1 注意:①正弦里函数名都为sin, 余弦里函数名都为cos②中间都为减号6、和差化积公式2cos2sin2sin sin βαβαβα-+=+2sin2cos 2sin sin βαβαβα-+=- 2cos2cos 2cos cos βαβαβα-+=+ 2sin2sin 2cos cos βαβαβα-+-=- βαβαβαcos cos )sin(tan tan ⋅±=±βαβαβαsin sin )sin(cot cot ⋅±±=±三角函数和差化积公式快速记忆口诀：正加正，正在前。
正减正，余在前。
余加余，余并肩。
余减余，余不见，负号很讨厌。
7、积化和差公式)]sin()[sin(21cos sin βαβαβα-++=)]sin()[sin(21sin cos βαβαβα--+=)]cos()[cos(21cos cos βαβαβα-++=)]cos()[cos(21sin sin βαβαβα--+-=结合6来记忆三、公式推导过程（一）万能公式推导ααααααα22sin cos cos sin 2cos sin 22sin +⋅=⋅=（因为1sin cos 22=+αα） 再把上面的分式上下同除α2cos ，可得2tan 12tan22sin 2ααα+=然后用2α代替α即可。
同理可推导余弦的万能公式。
正切的万能公式可通过正弦比余弦得到。
（二）三倍角公式推导αααααααααααααααααααααααααααααααααααα233223222222tan 31tan tan 3cos cos sin 2sin cos cos cos sin sin cos cos sin 2cos sin 2sin cos cos sin sin cos cos sin 2cos 2sin sin 2cos sin 2cos cos 2sin 3cos 3sin 3tan --=---+=---+=-+==ααααααααααααααααα33322sin 4sin 3sin 2sin sin 2sin 2sin )sin 21(cos sin 2sin 2cos cos 2sin )2sin(3sin -=-+-=-+=+=+=αααααααααααααααααcos 3cos 4)cos 2cos 2(cos cos 2sin cos 2cos )1cos 2(sin 2sin cos 2cos )2cos(3cos 33322-=-+-=--=-=+=即 ααα3sin 4sin 33sin -= αααcos 3cos 43cos 3-=（三）和差化积公式推导首先,我们知道βαβαβαsin cos cos sin )sin(+=+ βαβαβαsin cos cos sin )sin(-=-我们把两式相加就得到βαβαβαcos sin 2)sin()sin(=-++所以, )]sin()[sin(21cos sin βαβαβα-++=同理,若把两式相减,就得到)]sin()[sin(21sin cos βαβαβα--+=同样的,我们还知道βαβαβαsin sin cos cos )cos(-=+ βαβαβαsin sin cos cos )cos(+=- 所以,把两式相加,我们就可以得到βαβαβαcos cos 2)cos()cos(=-++所以我们就得到, )]cos()[cos(21cos cos βαβαβα-++=同理,两式相减我们就得到)]cos()[cos(21sin sin βαβαβα--+-=这样,我们就得到了积化和差的四个公式:)]sin()[sin(21cos sin βαβαβα-++=)]sin()[sin(21sin cos βαβαβα--+=)]cos()[cos(21cos cos βαβαβα-++=)]cos()[cos(21sin sin βαβαβα--+-=好,有了积化和差的四个公式以后,我们只需一个变形,就可以得到和差化积的四个公式.我们把上述四个公式中的βα+设为χ, βα-设为γ,那么2γα+=, 2γχβ-=把α,β分别用χ,γ表示就可以得到和差化积的四个公式:2cos2sin2sin sin γχγχγχ-+=+2sin2cos 2sin sin γχγχγχ-+=- 2cos 2cos 2cos cos γχγχγχ-+=+2sin 2sin 2cos cos γχγχγχ-+-=-。