小学奥数圆环面积计算练习题
小学六年级圆环的练习题

小学六年级圆环的练习题圆环是小学六年级数学学习中的重点内容之一。
通过练习圆环题目可以帮助学生巩固对圆环的认识和运用,提高数学思维和解题能力。
本文将为大家提供一些小学六年级圆环的练习题,以帮助学生更好地理解和应用相关知识。
1. 题目一:已知圆的半径为3cm,求其周长和面积。
解析:周长的公式为C=2πr,面积的公式为S=πr²。
将半径r=3cm 代入公式中计算即可得到结果。
周长C=2π×3≈18.85cm,面积S=π×3²≈28.27cm²。
2. 题目二:已知一个圆的周长为25.12cm,求其半径和面积。
解析:已知周长C=25.12cm,我们可以通过周长的公式推导出半径的计算公式r=C/(2π)。
将周长C=25.12cm代入计算可得半径r≈4cm。
接下来,我们可以通过半径的公式S=πr²求得面积S≈50.27cm²。
3. 题目三:一个圆的直径等于另一个圆的半径的两倍,如果小圆的周长为18.84cm,求大圆的周长和面积。
解析:我们设小圆的半径为r,由题意可知大圆的半径为2r。
已知小圆的周长C=18.84cm,我们可以通过周长的公式求得小圆的半径r≈3cm。
而大圆的半径为2r≈6cm。
再利用周长的公式C=2πr,我们可以求得大圆的周长C=2π×6≈37.7cm。
同样,根据面积的公式S=πr²,大圆的面积S=π×6²≈113.1cm²。
4. 题目四:已知一个圆的周长与直径的比值为π,求其半径和面积。
解析:已知周长与直径的比值C/d=π,我们可以推导出周长与半径的比值C/r=2π。
由于周长与半径的比值为常数,我们可以设周长为C,半径为r,则C/r=2π。
根据题意,可以得到周长C=r×2π,将此式代入C/r=2π中可得r×2π/r=2π,即2π=2π,该等式恒成立。
因此,我们无法求出具体的半径和面积。
圆环的面积练习题(附答案)

圆环的面积练习题1、一个圆环的外圆半径是10cm ,内圆半径是8cm ,圆环的面积是()平方厘米。
2、一个圆环的外圆直径是8cm ,内圆半径是3cm ,圆环的面积是()平方厘米。
3、先将圆规的两脚叉开 2cm 画一个圆,然后扎在圆心处的圆规的脚不动,将圆规的另一个脚继续叉开,使圆规两脚间的距离是4cm 再画一个圆,形成一个圆环,这个圆环的面积是()平方厘米。
4、一个圆的半径是 6cm ,如果这个圆的直径增加2cm ,那么这个圆的面积增加()平方厘米。
5、一个圆的半径是 6cm ,如果这个圆的半径增加2cm ,那么这个圆的面积增加()平方厘米。
6、在一块直径为 50米的圆形空地,计划在它的中央修一个半径为15米一、填空题。
的圆形水池,剩余部分铺草皮绿地,草皮绿地的面积是( )平方米,圆形水池的面积是( )平方米。
二、计算下面各图中涂色部分的面积。
(单位:厘米)7、环形的外圆直径是24 厘米,环宽是 5 厘米,求环形的面积。
8、环形的外圆周长为78.5 分米,内圆周长为 62.8分米,求环形的面积。
9、环形的外圆周长为 31.4 厘米,环宽 3 厘米,求环形的面积。
10、公园内花圃中的圆形花坛,外圆周长78.5 米,环宽 1.2 米。
求这个花坛的面积。
6cm12cm8cm三、解决问题。
1.某公园内有一座圆形喷水池, 它的半径是3米。
现在要在喷水池周围铺上1米宽的雨路。
雨路的占地面积是多少平方米?2、 一个圆环, 内圆半径是3厘米, 环宽2厘米。
这个圆环的面积是多少?3、 一个圆环, 外圆半径是6厘米, 环宽1厘米,这个圆环的面积是多少?4、在一个直径是6米的圆形花园四周修一条宽1米的小路。
小路的面积是多少平方米?四、判断题。
(1)在圆内剪去一个小圆就成为一个圆环。
( )(2)一个环形,外圆半径是4厘米,内圆直径是2厘米,计算这个环形的面积列式为:3.14X42-3. 14X22 ( )五、拓展一个运动场如右图, 两端是半圆形, 中间是长方形。
求圆环的面积的题典型

求圆环的面积的题典型摘要:一、圆环的面积公式二、圆环面积的典型例题及答案三、判断题:在一个正方形里画一个最大的圆,圆的面积约占正方形面积的78.5%四、求圆环的面积的方法五、总结正文:一、圆环的面积公式圆环的面积公式为:S 环= π(R^2 - r^2),其中R 为外圆半径,r 为内圆半径。
圆环面积也可以用其他形式表示,如S 环= πRr(R - r) 或者S 环= π(R^2 - r^2)。
二、圆环面积的典型例题及答案例题1:一个内圆半径为3cm,外圆半径为5cm 的圆环,求其面积。
解:根据圆环的面积公式S 环= π(R^2 - r^2),代入R = 5cm,r = 3cm,得到S 环= π(25 - 9) = 16π cm。
例题2:一个边长为4cm 的正方形内切一个最大的圆,求圆的面积占正方形面积的百分比。
解:正方形的面积为4 × 4 = 16 cm,最大圆的直径等于正方形的边长,所以圆的半径为2cm。
根据圆的面积公式S 圆= πr,代入r = 2cm,得到S 圆= 4π cm。
圆的面积占正方形面积的百分比为(S 圆/ S 正方形) × 100% = (4π / 16) × 100% = 78.5%。
三、判断题:在一个正方形里画一个最大的圆,圆的面积约占正方形面积的78.5%答案:正确。
四、求圆环的面积的方法1.圆环面积等于外圆面积减去内圆面积:S 环= S 圆R - S 圆r;2.圆环面积等于圆周率乘以大圆半径和小圆半径的平方差:S 环= π(R^2 - r^2);3.圆环面积等于圆周率乘以小圆切线被大圆截得长度的一半的平方:S 环= π(Rr)^2 / 4。
五、总结本篇文章介绍了圆环的面积公式及几种求解方法,并通过典型例题进行了讲解。
环形面积练习题及答案

环形面积练习题及答案标题:环形面积练习题及答案文章:在数学学科中,几何是一个重要的分支,它研究的是空间中的形状和大小关系。
其中,面积是一个常见的概念,用来描述平面图形的大小。
而环形面积是其中的一种特殊情况,它指的是由两个同心圆所围成的区域的面积。
为了帮助大家更好地理解和掌握环形面积的计算方法,下面将给出一些环形面积的练习题及答案。
练习题1:已知一个圆的半径为5cm,另一个圆的半径为3cm,求由这两个同心圆所围成的环形的面积。
解答:首先,我们需要知道计算环形面积的公式:环形面积 = 大圆面积 - 小圆面积。
根据公式,我们可以先计算大圆的面积:大圆面积= π * 大圆半径² = π * 5² =25π cm²。
然后,计算小圆的面积:小圆面积= π * 小圆半径² = π * 3² = 9π cm²。
最后,根据公式计算环形的面积:环形面积 = 大圆面积 - 小圆面积= 25π - 9π = 16π cm²。
练习题2:已知一个圆的半径为8cm,另一个圆的直径为12cm,求由这两个同心圆所围成的环形的面积。
解答:首先,我们需要将直径转换为半径,因为计算环形面积的公式中使用的是半径。
由于直径是半径的两倍,所以小圆的半径为12cm / 2 = 6cm。
然后,我们可以按照练习题1中的方法计算环形的面积。
大圆的面积= π * 大圆半径² = π * 8² = 64π cm²。
小圆的面积= π * 小圆半径² = π * 6² = 36π cm²。
环形面积 = 大圆面积 - 小圆面积= 64π - 36π = 28π cm²。
通过以上两个练习题的解答,我们可以看出,计算环形面积的关键在于正确地使用公式,并将已知条件转化为半径的形式。
同时,我们也需要熟练掌握圆的面积计算方法,以便更好地解决类似的问题。
六年级圆环面积应用题十道

六年级圆环面积应用题十道六年级圆环面积应用题十道如下:1. 一个圆环的面积是 25.12 平方厘米,求这个圆环的半径。
2. 一个长方形的长是3.2 厘米,宽是 2.4 厘米,它的周长和面积各是多少?3. 一个圆的半径是 2 厘米,它的面积是多少?4. 一个正方形的面积是 3.14 平方米,它的周长是多少?5. 一个圆环的面积是 3.14 平方厘米,求这个圆环的半径。
6. 一个长方形的周长是 12.56 厘米,求它的长和宽。
7. 一个正方形的面积是 12.56 平方米,求它的周长和边长。
8. 一个圆的半径是 4 厘米,求它的面积。
9. 一个长方形的长是 5 厘米,宽是 3 厘米,它的周长是多少?10. 一个圆环的面积是 100.24 平方厘米,求这个圆环的半径。
解答:1. 圆环的半径等于直径,即半径为 25.12÷2=12.56 厘米。
2. 长方形的长等于圆周长的一半,即3.2÷2=1.6 厘米。
宽等于圆周长的一半,即 2.4÷2=1.2 厘米。
因此,长方形的面积为 1.6×1.2=1.92 平方厘米。
3. 圆的面积等于半径的平方,即 3.14×半径×半径=3.14×2×2=12.56 平方厘米。
4. 正方形的面积等于边长的平方,即 3.14×边长 2=3.14 平方米。
周长等于边长的平方加 4,即 3.14×边长 2+4=12.56 厘米。
5. 圆环的面积等于半径的平方,即 3.14×半径 2=3.14 平方厘米。
因此,半径等于 3.14÷2=1.57 厘米。
6. 长等于周长乘以 2,即 12.56×2=25.12 厘米。
宽等于周长除以 2,即 12.56÷2=6.28 厘米。
因此,长方形的面积为 25.12×6.28=152.0192 平方厘米。
(完整)圆的周长与面积(奥数)

圆的周长与面积
例1:计算阴影部分的周长。
练一练:计算阴影部分的周长.(单位:厘米)
例2:现有两根圆木,横截面直径都是2分米,如果把它们用铁丝捆在一起,两端各捆一圈(接头不计),那么应准备多长的铁丝?
练一练:求右图阴影部分的周长(每个圆的半径都是2厘米)。
例3:求右图外圆的周长。
(单位:分米)
练一练:求右图阴影部分的周长。
例4:如右图,已知正方形面积是60平方厘米,求圆的面积。
练一练:已知右图中阴影部分的面积是300平方厘米,求圆的面积。
例5:已知右图中阴影部分的面积是40平方厘米,求圆环的面积。
练一练:右图中平行四边形的面积是100平方厘米,求阴影部分的面积。
例6:有一个半圆形零件,周长是20。
56厘米,求这个半圆形零件的面积。
练一练:如右图,一个扇形的圆心角是90°,它的周长是14。
28厘米,求它的面积。
例7:图中ABCD是边长为4米的正方形,分别以AB、BC、CD、AD为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.
练一练:图中三角形ABC是边长为6厘米的正三角形,求阴影部分的面积。
例8:计算阴影部分的面积。
练一练:计算阴影部分的面积。
(单位:厘米)
例9:求出右图中正方形面积与圆的面积比。
练一练:右图圆的面积是942平方分米,那么正方形的面积是多少?如果正方形的面积是360平方厘米,那么圆的面积是多少?。
六年级奥数圆面积1
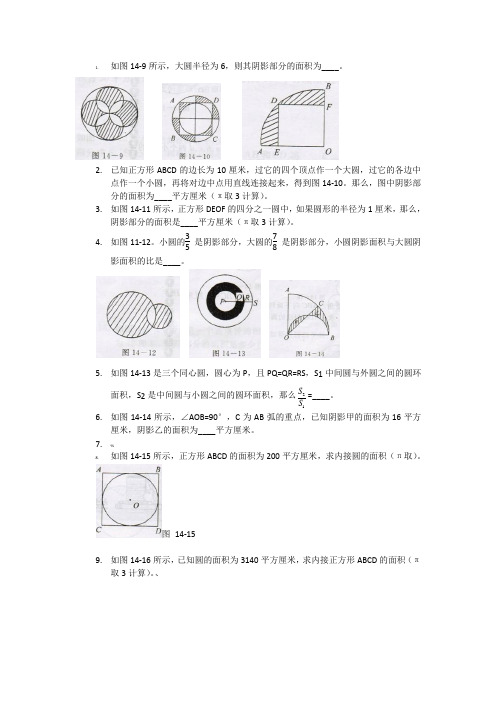
1.如图14-9所示,大圆半径为6,则其阴影部分的面积为____。
2.已知正方形ABCD的边长为10厘米,过它的四个顶点作一个大圆,过它的各边中点作一个小圆,再将对边中点用直线连接起来,得到图14-10。
那么,图中阴影部分的面积为____平方厘米(π取3计算)。
3.如图14-11所示,正方形DEOF的四分之一圆中,如果圆形的半径为1厘米,那么,阴影部分的面积是____平方厘米(π取3计算)。
4.如图11-12。
小圆的35是阴影部分,大圆的78是阴影部分,小圆阴影面积与大圆阴影面积的比是____。
5.如图14-13是三个同心圆,圆心为P,且PQ=QR=RS,S1中间圆与外圆之间的圆环面积,S2是中间圆与小圆之间的圆环面积,那么21SS=____。
6.如图14-14所示,∠AOB=90°,C为AB弧的重点,已知阴影甲的面积为16平方厘米,阴影乙的面积为____平方厘米。
7.%8.如图14-15所示,正方形ABCD的面积为200平方厘米,求内接圆的面积(π取)。
图14-159.如图14-16所示,已知圆的面积为3140平方厘米,求内接正方形ABCD的面积(π取3计算)。
、10.如图14-17所示,已知大圆的半径为20厘米,求a、b、c、d四个小圆的周长之和。
\11.如图14-18所示,将直角三角形ABC向下旋转90°。
已知BC=5厘米,AB=4厘米,AC=3厘米。
求三角形ABC扫过的面积。
)12.如图14-19所示,大圆的半径为100厘米,小圆的半径为1厘米,将小圆沿大圆周长滚动一周。
求(1)小圆的圆心经过的长度;(2)求小圆扫过的面积。
$13.如图14-20所示,已知六个圆的面积相等,而且阴影部分的面积为60平方厘米,求六个圆的面积为多少平方厘米|14.如图14-21所示,已知大正方形的面积为100平方厘米,小正方形面积为50平方厘米,求阴影部分的面积。
【六年级上册数学】 圆环面积的实际应用专项练习

圆环面积的实际应用专项练习1.有一个圆形花坛,半径是8米,围绕花坛一周有一条宽为2米的小路,这条小路的面积是多少平方米?8+2=10(米)3.14×(10²-8²)=113.04(平方米)答:这条小路的面积是113.04平方米。
2.一种零件的横截面是一个圆环,外圈半径是8分米,内圈半径是6.5分米,这种零件横截面的面积是多少平方分米?3.14×(8²-6.5²)=3.14×(64-42.25)=3.14×21.75=68.295(平方分米)答:这种零件横截面的面积是68.295平方分米。
3.一块圆形玉佩(如图)。
外圈是环形玉石,中间镶嵌圆形黄金。
这块玉佩所用玉石的面积是多少平方厘米?小圆半径:3÷2=1.5(厘米)大圆半径:6÷2=3(厘米)3.14×(3²-1.5²)=3.14×(9-2.25)=21.195(平方厘米)答:这块玉佩所用玉石的面积是21.195平方厘米。
圆环面积的实际应用专项练习4.在一个直径是20米的圆形花坛四周修一条2米宽的小路。
(1)这条小路的面积是多少平方米?3.14×[(20÷2+2)²-(20÷2)²]=3.14×44=138.16(平方米)答:这条小路面积是138.16平方米。
(2)花坛里花种类繁多,其中有杜鹃花120棵,,花坛里一共有多少棵花?占总数的13=360(棵)120÷13答:花坛里一共有360棵花。
5.一个圆形花坛的直径是20米,如果要扩建这个花坛,把它的直径增加2米。
花坛的面积增加了多少平方米?(20+2)÷2=11(米)20÷2=10(米);3.14×(11²-10²)=3.14×21=65.94(平方米)答:花坛的面积增加了65.94平方米。
