初二数学矩形菱形经典习题
平行四边形矩形菱形经典例题(8套)

经典例题(附带详细答案)1.如图,E F 、是平行四边形ABCD 对角线AC 上两点,BE DF ∥,求证:AF CE =.【答案】证明:平行四边形ABCD 中,AD BC ∥,AD BC =,ACB CAD ∴∠=∠.又BE DF ∥,BEC DFA ∴∠=∠,BEC DFA ∴△≌△,∴CE AF =2.如图6,四边形ABCD 中,AB ∥CD ,∠B=∠D ,,求四边形ABCD 的周长.【【答案】20、解法一: ∵∴又∵∴∴∥即得是平行四边形∴∴四边形的周长解法二:连接3 ,6==AB BC AB CD ∥︒=∠+∠180C B B D ∠=∠︒=∠+∠180D C AD BC ABCD 36AB CD BC AD ====,ABCD 183262=⨯+⨯=AC A DCBA DC BD C AB EF∵∴又∵∴≌∴∴四边形的周长解法三:连接∵∴又∵∴∴∥即是平行四边形∴∴四边形的周长3.(在四边形ABCD 中,∠D =60°,∠B 比∠A 大20°,∠C 是∠A 的2倍,求∠A ,∠B ,∠C 的大小.【关键词】多边形的内角和【答案】设x A =∠(度),则20+=∠x B ,x C 2=∠.根据四边形内角和定理得,360602)20(=++++x x x .解得,70=x .∴︒=∠70A ,︒=∠90B ,︒=∠140C .4.(如图,E F ,是四边形ABCD 的对角线AC 上两点,AF CE DF BE DF BE ==,,∥. 求证:(1)AFD CEB △≌△.(2)四边形ABCD 是平行四边形.【关键词】平行四边形的性质,判定【答案】证明:(1)DF BE ∥,DFE BEF ∴∠=∠.180AFD DFE ∠+∠=°,180CEB BEF ∠+∠=°,AFD CEB ∴∠=∠.又A F C E D F ==,,AFD CEB ∴△≌△(SAS).AB CD ∥DCA BAC ∠=∠B D AC CA ∠=∠=,ABC △CDA △36AB CD BC AD ====,ABCD 183262=⨯+⨯=BD AB CD ∥CDB ABD ∠=∠ABC CDA ∠=∠ADB CBD ∠=∠AD BC ABCD 36AB CD BC AD ====,ABCD 183262=⨯+⨯=A BDE F C A DCB(2)由(1)知AFD CEB △≌△,DAC BCA AD BC ∴∠=∠=,,AD BC ∴∥.∴四边形ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形)5.)25.如图13-1,在边长为5的正方形ABCD 中,点E 、F 分别是BC 、DC 边上的点,且AE EF ⊥,2BE =.(1)求EC ∶CF 的值;(2)延长EF 交正方形外角平分线CP P 于点(如图13-2),试判断AE EP 与的大小关系,并说明理由;(3)在图13-2的AB 边上是否存在一点M ,使得四边形DMEP 是平行四边形?若存在,请给予证明;若不存在,请说明理由.【关键词】平行四边形的判定【答案】解:(1)AE EF ⊥2390∴∠+∠=°四边形ABCD 为正方形90B C ∴∠=∠=°1390∴∠+∠=°12∠=∠90DAM ABE DA AB ∠=∠==°,DAM ABE ∴△≌△DM AE ∴=AE EP =DM PE ∴=∴四边形DMEP 是平行四边形.解法②:在AB 边上存在一点M ,使四边形DMEP 是平行四边形证明:在AB 边上取一点M ,使AM BE =,连接ME 、MD 、DP .90AD BA DAM ABE =∠=∠=,°Rt Rt DAM ABE ∴△≌△14DM AE ∴=∠=∠,1590∠+∠=°4590∴∠+∠=°AE DM ∴⊥AE EP ⊥ A D C B E B C E DA F P FDM EP ∴⊥∴四边形DMEP 为平行四边形6.(2009年广州市)如图9,在ΔABC 中,D 、E 、F 分别为边AB 、BC 、CA 的中点。
初二菱形矩形正方形练习题

初二菱形矩形正方形练习题题目一:菱形练习题在一张正方形纸上,画一个边长为6厘米的正方形,然后连接相邻顶点,形成四个菱形。
请计算这四个菱形的周长和面积分别是多少?解答:菱形的周长可以通过计算菱形的边长乘以4得到。
已知正方形的边长为6厘米,那么菱形的边长就是正方形边长的一半,即3厘米。
四个菱形的周长分别为3厘米 * 4 = 12厘米。
菱形的面积可以通过计算菱形的对角线长度之积除以2得到。
由于正方形的对角线等于边长乘以√2,所以对角线长度等于6厘米* √2。
四个菱形的面积分别为(6厘米 * √2)^2 / 2 = 18厘米^2。
所以,四个菱形的周长和面积分别是12厘米和18平方厘米。
题目二:矩形练习题已知一个矩形的长为8厘米,宽为4厘米,请计算这个矩形的周长和面积分别是多少?解答:矩形的周长可以通过计算矩形的长和宽的两倍之和得到。
已知长为8厘米,宽为4厘米,那么矩形的周长为(8厘米 + 4厘米)* 2 = 24厘米。
矩形的面积可以通过计算矩形的长和宽的乘积得到。
已知长为8厘米,宽为4厘米,那么矩形的面积为8厘米 * 4厘米 = 32平方厘米。
所以,这个矩形的周长为24厘米,面积为32平方厘米。
题目三:正方形练习题已知一个正方形的边长为5厘米,请计算这个正方形的周长和面积分别是多少?解答:正方形的周长可以通过计算边长的四倍得到。
已知边长为5厘米,那么正方形的周长为5厘米 * 4 = 20厘米。
正方形的面积可以通过计算边长的平方得到。
已知边长为5厘米,那么正方形的面积为5厘米 * 5厘米 = 25平方厘米。
所以,这个正方形的周长为20厘米,面积为25平方厘米。
通过以上练习题,我们可以巩固初二学习过的菱形、矩形和正方形的周长和面积的计算方法。
希望大家能够掌握这些基础知识,为以后的数学学习打下坚实的基础。
(完整版)矩形、菱形与正方形-专题训练(含答案)

矩形、菱形与正方形专题训练(含答案)班级________姓名________成绩________一、选择题(每小题3分,共30分)1.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )A.12 B.24 C.12 3 D.16 3第1题图第2题图第3题图第4题图2.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( ) A.14 B.15 C.16 D.173.如图,将矩形ABCD沿对角线BD折叠,使点C与点C′重合.若AB=2,则C′D的长为( ) A.1 B.2 C.3 D.44.如图,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点.将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )A.矩形B.菱形C.正方形D.梯形5.由菱形的两条对角线的交点向各边引垂线,以各垂足为顶点的四边形是( )A.平行四边形B.矩形C.菱形D.正方形6.如图,▱ABCD的周长为16 cm,AC,BD相交于点O,OE⊥AC交AD于点E,则△DCE的周长为( )A.4 cm B.6 cm C.8 cm D.10 cm第6题图第9题图第10题图7.菱形的周长为8 cm,高为1 cm,则菱形两邻角度数比为( )A.3∶1 B.4∶1 C.5∶1 D.6∶18.用两块完全相同的直角三角形拼下列图形:①平行四边形,②矩形,③菱形,④正方形,⑤等腰三角形,⑥等边三角形,一定能拼成的图形是( )A.①④⑤B.②⑤⑥C.①②③D.①②⑤9.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )A.16 B.17 C.18 D.1910.如图,F为正方形ABCD的边AD上一点,CE⊥CF交AB的延长线于点E,若正方形ABCD 的面积为64,△CEF的面积为50,则△CBE的面积为( )A.20 B.24 C.25 D.26二、填空题(每小题3分,共24分)11.如图所示,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为点E,连结CP,则∠CPB=____度.第11题图第12题图第14题图第15题图12.如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1分别是四边形ABCD 各边中点,如果AC=8,BD=10,则四边形A1B1C1D1的面积为___.13.矩形的对角线相交成的角中,有一个角是60°,这个角所对的边长为20 cm,则其对角线长为____________-_,矩形的面积为_______________.14.如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=4 cm,BD=8 cm,则这个菱形的面积是____cm2.15.如图,矩形ABCD中,点E,F分别是AB,CD的中点,连结DE和BF,分别取DE,BF的中点M,N,连结AM,CN,MN,若AB=22,BC=23,则图中阴影部分的面积为____________.,第16题图第17题第18题图16.如图,▱ABCD的对角线相交于点O,请你添加一个条件______________,使▱ABCD是矩形.17.如图,正方形ABCD中,对角线AC,BD交于点O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G,F,AC=10,则EG+EF=____.18.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为_______________________________.三、解答题(共66分)19.(6分)如图,已知矩形ABCD中,E是AD上一点,F是AB上一点,EF⊥EC且EF=EC,DE =4 cm,矩形ABCD的周长为32 cm,求AE的长.20.(8分)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连结BM,DN.(1)求证:四边形BMDN是菱形;(2)若AB=4,AD=8,求MD的长.21.(8分)如图所示,矩形ABCD中,AE⊥BD于点E,∠DAE∶∠BAE=3∶1,求∠BAE和∠EAO 的度数.22.(10分)如图,已知菱形ABCD中,AB=AC,E,F分别是BC,AD的中点,连结AE,CF.(1)证明:四边形AECF是矩形;(2)若AB=8,求菱形ABCD的面积.23.(12分)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是点E,F,并且DE=DF,求证:(1)△ADE≌△CDF;(2)四边形ABCD是菱形.24.(10分)在四边形ABCD中,AB=CD,M,N,P,Q分别是AD,BC,BD,AC的中点,求证:MN与PQ互相垂直平分.参考答案一、选择题(每小题3分,共30分)1.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( D )A.12 B.24 C.12 D.16第1题图第2题图第3题图第4题图2.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( C ) A.14 B.15 C.16 D.173.如图,将矩形ABCD沿对角线BD折叠,使点C与点C′重合.若AB=2,则C′D的长为( B ) A.1 B.2 C.3 D.44.如图,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点.将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( A )A.矩形B.菱形C.正方形D.梯形5.由菱形的两条对角线的交点向各边引垂线,以各垂足为顶点的四边形是( B )A.平行四边形B.矩形C.菱形D.正方形6.如图,▱ABCD的周长为16 cm,AC,BD相交于点O,OE⊥AC交AD于点E,则△DCE的周长为( C )A.4 cm B.6 cm C.8 cm D.10 cm第6题图第9题图第10题图7.菱形的周长为8 cm,高为1 cm,则菱形两邻角度数比为( C )A.3∶1 B.4∶1 C.5∶1 D.6∶18.用两块完全相同的直角三角形拼下列图形:①平行四边形,②矩形,③菱形,④正方形,⑤等腰三角形,⑥等边三角形,一定能拼成的图形是( D )A.①④⑤B.②⑤⑥C.①②③D.①②⑤9.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( B )A.16 B.17 C.18 D.1910.如图,F为正方形ABCD的边AD上一点,CE⊥CF交AB的延长线于点E,若正方形ABCD 的面积为64,△CEF的面积为50,则△CBE的面积为( B )A.20 B.24 C.25 D.26二、填空题(每小题3分,共24分)11.如图所示,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为点E,连结CP,则∠CPB=__72__度.第11题图第12题图第14题图第15题图12.如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1分别是四边形ABCD 各边中点,如果AC=8,BD=10,则四边形A1B1C1D1的面积为__20__.13.矩形的对角线相交成的角中,有一个角是60°,这个角所对的边长为20 cm,则其对角线长为__40_cm__,矩形的面积为__400_cm2__.14.如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=4 cm,BD=8 cm,则这个菱形的面积是__16__cm2.15.如图,矩形ABCD中,点E,F分别是AB,CD的中点,连结DE和BF,分别取DE,BF的中点M,N,连结AM,CN,MN,若AB=2,BC=2,则图中阴影部分的面积为__2__.,第16题图第17题第18题图16.如图,▱ABCD的对角线相交于点O,请你添加一个条件__AO=BO(答案不唯一)__,使▱ABCD 是矩形.17.如图,正方形ABCD中,对角线AC,BD交于点O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G,F,AC=10,则EG+EF=__5__.18.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为__(8,4),(3,4)或(2,4)__.三、解答题(共66分)19.(6分)如图,已知矩形ABCD中,E是AD上一点,F是AB上一点,EF⊥EC且EF=EC,DE =4 cm,矩形ABCD的周长为32 cm,求AE的长.解:∵∠AFE +∠AEF =∠AEF +∠CED =90°,∴∠AFE =∠DEC .又∵∠A =∠D =90°,EF =EC ,∴△AEF ≌△DCE ,∴AE =CD .设AE =x ,则CD =x ,∴AD +CD =21×32,即x +4+x =16,∴x =6.即AE =6 cm20.(8分)如图,在矩形ABCD 中,对角线BD 的垂直平分线MN 与AD 相交于点M ,与BD 相交于点O ,与BC 相交于点N ,连结BM ,DN .(1)求证:四边形BMDN 是菱形;(2)若AB =4,AD =8,求MD 的长.解:(1)∵MN 是BD 的垂直平分线,∴BO =DO ,∠BON =∠DOM =90°.∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠BNO =∠DMO ,∴△BON ≌△DOM (AAS ),∴OM =ON .∵OB =OD ,∴四边形BMDN 是平行四边形.∵MN ⊥BD ,∴▱BMDN 是菱形(2)设MD =x ,则MB =x ,MA =8-x ,在Rt △ABM 中,∵BM 2=AM 2+AB 2,∴x 2=(8-x )2+42,解得x =5.∴MD 的长为521.(8分)如图所示,矩形ABCD 中,AE ⊥BD 于点E ,∠DAE ∶∠BAE =3∶1,求∠BAE 和∠EAO 的度数.解:提示:由∠DAE ∶∠BAE =3∶1,求出∠BAE =22.5°,而∠ABD =90°-∠BAE =90°-22.5°=67.5°,∵∠BAO =∠ABD =67.5°,∴∠EAO =∠BAO -∠BAE =67.5°-22.5°=45°22.(10分)如图,已知菱形ABCD 中,AB =AC ,E ,F 分别是BC ,AD 的中点,连结AE ,CF .(1)证明:四边形AECF 是矩形;(2)若AB =8,求菱形ABCD 的面积.解:(1)∵四边形ABCD 是菱形,∴AB =BC ,又∵AB =AC ,∴△ABC 是等边三角形.∵E 是BC 的中点,∴AE ⊥BC (等边三角形三线合一),∠AEC =90°.同理,CF ⊥AD .∵E ,F 分别是BC ,AD 的中点,∴AF =21AD ,EC =21BC .∵四边形ABCD 是菱形,∴AD 綊BC ,∴AF 綊EC ,∴四边形AECF 是平行四边形(一组对边平行且相等的四边形是平行四边形).又∵∠AEC =90°,∴四边形AECF 是矩形(有一个角是直角的平行四边形是矩形)(2)在Rt △ABE 中,∵AE ==4,∴S 菱形ABCD =8×4=3223.(12分)如图,已知四边形ABCD 是平行四边形,DE ⊥AB ,DF ⊥BC ,垂足分别是点E ,F ,并且DE =DF ,求证:(1)△ADE ≌△CDF ;(2)四边形ABCD 是菱形.解:证明:(1)∵四边形ABCD 是平行四边形,∴∠A =∠C ,又∵DE =DF ,DE ⊥AB ,DF ⊥BC ,∴∠DEA =∠DFC =90°,∴△ADE ≌△CDF (AAS ) (2)由(1)知AD =DC ,又∵四边形ABCD 是平行四边形,∴四边形ABCD 是菱形24.(10分)在四边形ABCD 中,AB =CD ,M ,N ,P ,Q 分别是AD ,BC ,BD ,AC 的中点,求证:MN 与PQ 互相垂直平分.解:证明:连结MP ,NQ ,PN ,MQ ,∵PM 綊21AB ,同理NQ 綊21AB ,∴PM 綊NQ ,∴四边形MPNQ 为平行四边形,又∵PN 綊21CD ,而CD =AB ,∴PN =PM ,∴四边形MPNQ 为菱形,∴MN 与PQ 互相垂直平分。
中考数学专题训练:矩形、菱形、正方形(附参考答案)

中考数学专题训练:矩形、菱形、正方形(附参考答案)1.下列命题正确的是( )A .正方形的对角线相等且互相平分B .对角互补的四边形是平行四边形C .矩形的对角线互相垂直D .一组邻边相等的四边形是菱形2.如图,D ,E ,F 分别是△ABC 各边的中点,则以下说法错误的是( )A .△BDE 和△DCF 的面积相等B .四边形AEDF 是平行四边形C .若AB =BC ,则四边形AEDF 是菱形D .若∠A =90°,则四边形AEDF 是矩形3.如图,在正方形ABCD 中,E ,F 分别是AB ,BC 的中点,CE ,DF 交于点G ,连接AG .下列结论:①CE =DF ;②CE ⊥DF ;③∠AGE =∠CDF .其中正确的结论是( )A .①②B .①③C .②③D .①②③4.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,E 为BC 的中点,连接EO 并延长交AD 于点F ,∠ABC =60°,BC =2AB .下列结论:①AB ⊥AC ;②AD =4OE ;③四边形AECF 是菱形;④S △BOE =14S △ABC .其中正确结论的个数是( )A .4B .3C .2D .15.如图,在矩形ABCD中,AB=6 cm,BC=9 cm,点E,F分别在边AB,BC上,AE=2 cm,BD,EF交于点G.若G是EF的中点,则BG的长为______cm.6.如图,在菱形ABCD中,AC,BD为菱形的对角线,∠DBC=60°,BD=10,点F为BC的中点,则EF的长为_____.7.已知四边形ABCD是正方形,点E在边DA的延长线上,连接CE交AB于点G,过点B作BM⊥CE,垂足为点M,BM的延长线交AD于点F,交CD的延长线于点H.(1)如图1,求证:CE=BH;(2)如图2,若AE=AB,连接CF,在不添加任何辅助线情况下,请直接写出图2中的四个三角形(△AEG除外),使写出的每个三角形都与△AEG全等.8.如图,在菱形ABCD中,E,F,G,H分别是AB,BC,CD,AD上的点,且BE =BF=CG=AH.若菱形的面积等于24,BD=8,则EF+GH=_____.9.如图,在矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F.(1)若BE平分∠CBD,求证:BF⊥AC;(2)找出图中与△OBF相似的三角形,并说明理由;(3)若OF=3,EF=2,求DE的长度.10.(1)如图1,在矩形ABCD中,点E,F分别在边DC,BC上,AE⊥DF,垂足为点G.求证:△ADE∽△DCF.【问题解决】(2)如图2,在正方形ABCD中,点E,F分别在边DC,BC上,AE=DF,延长BC 到点H,使CH=DE,连接DH.求证:∠ADF=∠H.【类比迁移】(3)如图3,在菱形ABCD中,点E,F分别在边DC,BC上,AE=DF=11,DE=8,∠AED=60°,求CF的长.参考答案1.A 2.C 3.A 4.D5.√13 6.5 7.(1)证明略 (2)略8.6解析:如图,连接AC ,交BD 于点O ,∵四边形ABCD 是菱形,BD =8,∴AB =BC =AD =CD ,AC ⊥BD ,AO =OC =12AC ,BO =OD =12BD =4. ∵S 菱形ABCD =12AC ·BD =24,∴AC =6,∴AO =3,∴AB =√AO 2+BO 2=5=AD .∵BE =BF =CG =AH ,∴AE =CF =DH =DG ,∴BE AE =BF CF ,∴EF ∥AC .同理可得GH ∥AC ,设BE =BF =CG =AH =a ,则有DH =5-a ,∵EF ∥AC ,∴△BEF ∽△BAC ,∴BE AB =EF AC ,即a 5=EF 6,∴EF =65a ,同理可得DH DA =GH CA ,即5−a 5=GH 6,∴GH =6-65a ,∴EF +GH =6.9.(1)证明略(2)与△OBF相似的三角形有△ECF,△BAF,理由略(3)DE=3+√1910.(1)证明:∵四边形ABCD是矩形,∴∠C=∠ADE=90°,∴∠CDF+∠DFC=90°.∵AE⊥DF,∴∠DGE=90°,∴∠CDF+∠AED=90°,∴∠AED=∠DFC,∴△ADE∽△DCF.(2)证明:∵四边形ABCD是正方形,∴AD=DC,AD∥BC,∠ADE=∠DCF=90°.∵AE=DF,∴Rt△ADE≌Rt△DCF(HL),∴DE=CF.∵CH=DE,∴CF=CH.∵点H在BC的延长线上,∴∠DCH=∠DCF=90°.又∵DC=DC,∴△DCF≌△DCH(SAS),∴∠DFC=∠H.∵AD∥BC,∴∠ADF=∠DFC,∴∠ADF=∠H.(3)解:如图3,延长BC至点G,使CG=DE=8,连接DG,∵四边形ABCD是菱形,∴AD=DC,AD∥BC,∴∠ADE=∠DCG,∴△ADE≌△DCG(SAS),∴∠DGC=∠AED=60°,AE=DG. ∵AE=DF,∴DG=DF,∴△DFG是等边三角形,∴FG=DF=11.∵CF+CG=FG,∴CF=FG-CG=11-8=3,即CF的长为3.。
2021年中考数学 专题训练:矩形、菱形 (含答案)

2021中考数学专题训练:矩形、菱形一、选择题1. 已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为()A.2B.2C.4D.22. 如图,矩形纸片ABCD中,AB=4,BC=6,将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是()A. 6B. 3C. 2.5D. 23. 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=2,BD=2,则菱形ABCD的面积为()A. 2 2B. 4 2C. 6 2D. 8 24. 如图,四边形ABCD的对角线相交于点O,且O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为()A.40B.24C.20D.155. 关于▱ABCD的叙述,正确的是()A. 若AB⊥BC,则▱ABCD是菱形B. 若AC⊥BD,则▱ABCD是正方形C. 若AC=BD,则▱ABCD是矩形D. 若AB=AD,则▱ABCD是正方形6. 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处.若∠2=40°,则图中∠1的度数为()A. 115°B. 120°C. 130°D. 140°7. 如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是()A.∠DAB′=∠CAB′B.∠ACD=∠B′CDC.AD=AED.AE=CE8. 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F.在下列结论中,不一定正确的是()A. △AFD≌△DCEB. AF=12ADC. AB=AFD. BE=AD-DF9. 如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的116时,则AEEB为()A. 53 B. 2 C.52 D. 410. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=45,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为()A. (0,0)B. (1,12) C. (65,35) D. (107,57)二、填空题11. 把图①中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图②,图③所示的正方形,则图①中菱形的面积为.图K24-812. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.如果∠ADB =30°,则∠E=________度.13. 如图,将矩形ABCD折叠,折痕为EF,BC的对应边B'C'与CD交于点M,若∠B'MD=50°,则∠BEF的度数为.14. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=________.15. 如图,在△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是形,点P,E,F分别为线段AB,AD,DB上的任意一点,则PE+PF的最小值是.三、解答题16. 如图,AD∥FE,点B、C在AD上,∠1=∠2,BF=BC.(1)求证:四边形BCEF是菱形;(2)若AB=BC=CD,求证:△ACF≌△BDE.17. 如图,在菱形ABCD中,AB=5,sin∠ABD=55,点P是射线BC上一点,连接AP交菱形对角线BD于点E,连接EC.(1)求证:△ABE≌△CBE;(2)如图①,当点P在线段BC上时,且BP=2,求△PEC的面积;(3)如图②,当点P在线段BC的延长线上时,若CE⊥EP,求线段BP的长.18. 如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上的点,连接EF.(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF =3S△EDF,求AE的长;(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M 处,且使MF∥CA.①试判断四边形AEMF的形状,并证明你的结论;②求EF的长.2021中考数学 专题训练:矩形、菱形 -答案一、选择题 1. 【答案】C2. 【答案】C【解析】本题考查了四边形裁剪问题中的最值问题 .使剩余面积最小的剪法如解图所示,S △ABG =12AB ·BG =12×4×4=8,∵AD =6,∴AE =ED =32,∴EF =DF =3,∴S △AED =12AE ·ED =12×32×32=9,S △EDF =12EF ·DF =12×3×3=4.5,∴S 剩余部分=S 矩形ABCD -S △ABG -S △AED -S △EDF =4×6-8-9-4.5=2.5.解图3. 【答案】A【解析】∵E ,F 分别是 AD ,CD 边上的中点,即EF 是△ACD的中位线,∴AC =2EF =22,则菱形ABCD 的面积=12AC ·BD =12×22×2=2 2.4. 【答案】B [解析]∵∠ABD=∠CDB ,∴AB ∥CD , ∵O 是BD 的中点,∴BO=DO , 又∠AOB=∠COD ,∴△AOB ≌△COD , ∴AB=CD ,又AB ∥CD ,∴四边形ABCD 是平行四边形. ∵AB=AD ,∴四边形ABCD 是菱形. ∴AC ⊥BD.在Rt △ABO 中,BO=BD=4,AO===3,∴AC=2AO=6,∴四边形ABCD 的面积为AC ·BD=×6×8=24.故选B .5. 【答案】C【解析】逐项分析如下表:选项 逐项分析正误A 有一个角是直角的平行四边形是矩形,不是菱形 ×B 对角线互相垂直的平行四边形是菱形,不一定是正方形× C 对角线相等的平行四边形是矩形√ D 有一组邻边相等的平行四边形是菱形,不一定是正方形×6. 【答案】A 【解析】由折叠的性质知∠EA ′B ′=∠A =90°,∵∠2=40°,∴∠B ′A ′C=50°,∴∠EA ′D =40°,∠DEA ′=50°,∴∠AEA ′=130°,∴∠AEF =∠FEA ′=12∠AEA ′=65°,∵AD ∥BC ,∴∠1=180°-65°=115°.7. 【答案】D 【解析】∵四边形ABCD 为矩形,∴AB ∥CD ,∴∠ACD =∠BAC ,由折叠的性质可得∠BAC =∠EAC, ∴∠ACD =∠EAC ,∴AE =CE .B 【解析】逐项分析如下表: 选项 逐项分析 正误A ∵四边形ABCD 是矩形,AF ⊥DE ,∴∠C =90°=∠AFD ,AD ∥BC ,∴∠ADF =∠CED ,∵AD =DE ,∴△AFD ≌△DCE (AAS)√B 只有当∠ADF =30°时,才有AF =12AD 成立× C 由△AFD ≌△DCE 可知,AF =DC ,∵矩形ABCD 中,AB=DC ,∴AB =AF√D ∵△AFD ≌△DCE ,∴DF =CE ,∴BE =BC -CE =AD -DF √ 9. 【答案】A 【解析】如解图,由折叠的对称性可知,∠A =∠J ,∠C =∠M ,四边形MNJK 和四边形BENF 都是菱形,则BE =NE ,AE =JE ,∵菱形MNJK 与菱形ABCD 相似,且菱形MNJK 的面积是菱形ABCD 面积的116,∴⎝ ⎛⎭⎪⎫JN AB 2=116,∴JN AB =14,设JN =a ,EN =b ,则AB =4a ,∵AB =AE +EB =EJ +EN =JN +EN+EN =JN +2EN =a +2b ,∴a +2b =4a ,∴a =23b ,AE BE =a +b b =53.10. 【答案】D 【解析】如解图,连接CA 、AD ,CA 与OB 相交于点E ,过点E作EF ⊥OA ,交OA 于点F .由题知点C 关于OB 的对称点是点A ,AD 与BO 的交点即为点P .根据菱形的性质,菱形的对角线互相垂直且平分两组对角,可知△COE ∽△EOF ,∴CO EO =EO OF ,∵OC =OA =5,OE =OB 2=25,∴OF =OE 2CO =(25)25=4,根据勾股定理可得EF =OE 2-OF 2=(25)2-42=2,点E 的坐标为(4,2),易得直线OE 的函数解析式为y =12x ,直线AD 的函数解析式是y =-15x +1,联立得:⎩⎪⎨⎪⎧y =12xy =-15x +1,解得⎩⎪⎨⎪⎧x =107y =57,∴点P 的坐标为(107,57).解图二、填空题11. 【答案】12 [解析]设图①中小直角三角形的两直角边长分别为a ,b (b>a ),则由图②,图③可列方程组解得所以菱形的面积S=×4×6=12.故答案为12.12. 【答案】15【解析】如解图,连接AC.∵四边形ABCD 是矩形,∴AD =BC ,AC =BD ,又∵AB =BA ,∴△DAB ≌△CBA(SSS ),∴∠ACB =∠ADB =30°,∵CE =BD ,∴AC =CE ,∴∠E =∠CAE =12∠ACB =15°.解图13. 【答案】70°[解析]依题意∠B=∠B'=∠B'MD +∠B'EA=90°,所以∠B'EA=90°-50°=40°,所以∠B'EB=180°-∠B'EA=140°,又∠B'EF=∠BEF ,所以∠BEF=∠B'EB=70°,故应填:70°.14. 【答案】4.8【解析】∵S菱形=12AC·BD=2AB·DH,∴AC·BD=2AB·DH.∵四边形ABCD是菱形,∴∠AOB=90°,AO=12AC=4,BO=12BD=3,∴在Rt△AOB中,AB=42+32=5,∴DH=8×62×5=4.8.15. 【答案】菱[解析]∵AC=BC,∴△ABC是等腰三角形.将△ABC沿AB翻折得到△ABD,∴AC=BC=AD=BD,∴四边形ADBC是菱形.∵△ABC沿AB翻折得到△ABD,∴△ABC与△ABD关于AB成轴对称.如图所示,作点E关于AB的对称点E',连接PE',根据轴对称的性质知AB垂直平分EE',∴PE=PE',∴PE+PF=PE'+PF,当E',P,F三点共线,且E'F⊥AC时,PE+PF有最小值,该最小值即为平行线AC与BD间的距离.作CM⊥AB于M,BG⊥AD于G,由题知AC=BC=2,AB=1,∠CAB=∠BAD,∴cos∠CAB=cos∠BAD,即=,∴AG=,在Rt△ABG中,BG===,由对称性可知BG长即为平行线AC,BD间的距离,∴PE+PF的最小值=.三、解答题16. 【答案】证明:(1)∵AD∥EF,∴∠FEB=∠2.∵∠1=∠2,∴∠FEB=∠1.∴BF=EF.∵BF=BC,∴BC=EF.∴四边形BCEF是平行四边形.∵BF =BC.∴四边形BCEF 是菱形. (2)∵EF =BC ,AB =BC =CD ,AD ∥FE.∴四边形ABEF 、四边形CDEF 均为平行四边形, ∴AF =BE ,FC =ED.又∵AC =2BC =BD.∴△ACF ≌△BDE.17. 【答案】(1)证明:∵四边形ABCD 是菱形, ∴AB =BC ,∠ABE =∠CBE .在△ABE 和△CBE 中,AB =BC ,∠ABE =∠CBE ,BE =BE , ∴△ABE ≌△CBE (SAS);(2)解:如解图①,连接AC 交BD 于点O ,分别过点A 、E 作BC 的垂线,垂足分别为点H 、F ,解图①∵四边形ABCD 是菱形, ∴AC ⊥BD ,∵AB =5,sin ∠ABD =55, ∴AO =OC =5, ∴BO =OD =25, ∴AC =25,BD =45, ∵12AC ·BD =BC ·AH , 即12×25×45=5AH , ∴AH =4, ∵AD ∥BC ,∴△AED ∽△PEB , ∴AE PE =AD BP ,∴AE +PE PE =AD +BP BP , 即AP PE =5+22=72,∴AP =72PE , 又∵EF ∥AH ,∴△EFP ∽△AHP , ∴EF AH =PE AP ,∴EF =PE AP ·AH =PE 72PE×4=87,∴S △PEC =12PC ·EF =12×(5-2)×87=127; (3)解:如解图②,连接AC 交BD 于点O ,解图②∵△ABE ≌△CBE ,CE ⊥PE , ∴∠AEB =∠CEB =45°, ∴AO =OE =5,∴DE =OD -OE =25-5=5,BE =3 5. ∵AD ∥BP ,∴△ADE ∽△PBE , ∴AD BP =DE BE , ∴5BP =535,∴BP =15.18. 【答案】(1)如解图①,∵折叠后点A 落在AB 边上的点D 处,解图①∴EF ⊥AB ,△AEF ≌△DEF , ∴S △AEF =S △DEF ,∵S 四边形ECBF =3S △EDF , ∴S 四边形ECBF =3S △AEF ,∵S △ACB =S △AEF +S 四边形ECBF ,∴S △ACB =S △AEF +3S △AEF =4S △AEF ,∴14△△AEF ACB S S=, ∵∠EAF =∠BAC ,∠AFE =∠ACB =90°,∴△AEF ∽△ABC ,∴2△△()AEF ACB S AE ABS =, ∴214()=,AE AB 在Rt △ACB 中,∠ACB =90°,AC =4,BC =3,∴AB 2=AC 2+BC 2,即AB =42+32=5,∴(AE 5)2=14,∴AE =52;(2)①四边形AEMF 是菱形.证明:如解图②,∵折叠后点A 落在BC 边上的点M 处,∴∠CAB =∠EMF ,AE =ME ,又∵MF ∥CA ,∴∠CEM =∠EMF ,∴∠CAB =∠CEM ,∴EM ∥AF ,∴四边形AEMF 是平行四边形,而AE =ME ,∴四边形AEMF 是菱形,解图②②如解图②,连接AM ,与EF 交于点O ,设AE =x ,则AE =ME =x ,EC =4-x , ∵∠CEM =∠CAB ,∠ECM =∠ACB =90°,∴Rt △ECM ∽Rt △ACB ,∴EC AC =EM AB ,∵AB =5,∴445-,x x =解得x =209, ∴AE =ME =209,EC =169,在Rt △ECM 中,∵∠ECM =90°,∴CM 2=EM 2-EC 2,即CM =(209)2-(169)2=43, ∵四边形AEMF 是菱形,∴OE =OF ,OA =OM ,AM ⊥EF , ∴S AEMF 菱形=4S △AOE =2OE ·AO , 在Rt △AOE 和Rt △ACM 中, ∵tan ∠EAO =tan ∠CAM , ∴OE AO =CMAC ,∵CM =43,AC =4,∴AO =3OE ,∴S AEMF 菱形=6OE 2,又∵S AEMF 菱形=AE ·CM ,∴6OE 2=209×43,解得OE =2109, ∴EF =2OE =4109.。
矩形和菱形的性质与判定经典例题试

矩形和菱形的性质与判定经典例题试————————————————————————————————作者:————————————————————————————————日期:第一课时——矩形的性质 矩形的性质:边角对角线对称性练一练: 1、矩形的两条对角线把矩形分成 个等腰三角形.2、矩形具有而平行四边形不具有的性质是( )A .对角线互相平分B .两组对边分别相等C .相邻两角互补D .对角线相等3.已知E 是矩形ABCD 的边BC 的中点,那么S △AED =________S 矩形ABCD ( )A.21B.41C.51D.61 4.在矩形ABCD 的边AB 上有一点E ,且CE =DE ,若AB =2AD ,则∠ADE 等于( )A.45°B.30°C.60°D.75°【探究三】直角三角形斜边上的中线性质1、根据矩形对角线性质可得到直角三角形斜边上的中线性质:2、归纳我们已学过的直角三角形的性质:角:边:斜边上的中线:边与角:练一练:1、已知直角三角形的周长为14,斜边上的中线长为3.则直角三角形的面积为( )A .5B .6C .7D .82、如果一个直角三角形斜边上的中线与斜边上的高所夹的锐角为34°,那么这个直角三角形的较小的内角是 度.精讲精练例1、如图,在矩形ABCD 中,AC 、BD 相较于点O ,AE 平分BAD ∠交BC 于E ,若15CAE ∠=︒,求BOE ∠的度数。
变式:已知矩形ABCD 中,如图2,对角线AC 、BD 相交于O ,AE ⊥BD 于E ,若∠DAE ∶∠BAE =3∶1,则∠EAC =________.例2、如图,在矩形ABCD 中,AB=3,AD=4,P 是AD 上的动点,PE AC ⊥于E ,PF BD ⊥于F ,求PE+PF 的值。
例3、如图,延长矩形的边CB 至E ,使CE=CA,F 是AE 的中点,求证:BF FD ⊥三、用中学习:1.如图,周长为68的矩形ABCD 被分成7个全等的矩形,则矩形ABCD 的面积为( )A.98B.196C.280D.2842.矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长是()A.16B.22C.26D.22或263.矩形的两条对角线的夹角是60°,一条对角线与矩形短边的和为15,那么矩形对角线的长为_______,短边长为_______.4.矩形ABCD的周长是56 cm,它的两条对角线相交于O,△AOB的周长比△BOC 的周长少4 cm,则AB=_______,BC=_______.V的两条高,M、N分别是BC、DE的中点,MN与DE有5、如图,已知BD、CE是ABC怎样的位置关系。
初二数学矩形菱形经典习题
第1页共4页A 、对角线互相垂直且相等的四边形B 、一条对角线平分一组对角的矩形矩形,菱形例1、如图,在平行四边形 ABCD 中,E 是CD 的中点,△ ABE 是等边三角形,求 证:四边形ABCD 是矩形。
角是直角的四边形是矩形;(4)有四个角是直角的四边形是矩形; (5)四个角都相等的四边是矩形;(6)对角线相等, 且有一个直角的四边形是矩形; (7) —组邻边垂直,一组对边平行且相等的四边形是矩形; (8)对角线相等且互相垂直的四边形是矩形”中,正确的个数有() A 、3个B 、4个C 、5个D 、6个3、下列性质中,菱形具有而矩形不一定具有的性质是( )B 、对角线互相平分D 、每一条对角线所在直线都是它的对称轴4、 下列条件中,能判定一个四边形为菱形的条件是( )A 、对角线互相平分的四边形B 、对角线互相垂直且平分的四边形C 、对角线相等的四边形D 、对角线相等且互相垂直的四边形5、 已知四边形ABCD 是平行四边形,下列结论中不一定正确的是( )7、正方形具有而菱形不一定具有的性质是( ) A 、对角线相等 B 、对角线互相垂直平分C 、四条边相等D 、一条对角线平分一组对角8、下列条件中不能判定四边形是正方形的条件是()例3、如图①,四边形 ABCDI 正方形,点G 是BC 上任意一点,DEL AG 于点E BF 丄AG 于点F . 求证:DE-BF = EF .当点G 为BC 边中点时,试探究线段EF 与GF 之间的数量关系, 并说明理由. 若点G 为CB 延长线上一点,其余条件不变•请你在图②中画出图形,写出此时 (不需要证明).DE BF EF 之间的数量关系D图① (一)选择题1、 矩形具有而一般平行四边形不具有的性质是( ). A 、对角线相等 B 、对边相等 C 、对角相等 D 、对角线互相平分2、 下列对矩形的判定:“(1)对角线相等的四边形是矩形; (2)对角线互相平分且相等的四边形是矩形; B图②(3)有一个A 、对边平行且相等 C 、内角和等于外角和A 、AB=CDB 、AC=BDC 、当AC 丄BD 时,它是菱形 6、正方形具有而矩形不一定具有的性质是()A.四个角都是直角B •对角线互相平分C •对角线相等D 、当/ ABC=90 °时,它是矩形D •对角线互相垂直9、下列命题中,假命题是(C 对角线相等的棱形第2页共4页 对角线互相垂直的矩形A 、四个内角都相等的四边形是矩形 、四条边都相等的平行四边形是正方形 C 既是菱形又是矩形的四边形是正方形、对角线互相垂直的平行四边形是菱形10、在四边形ABCD 中,O 是对角线的交点, 能判定四边形是正方形的条件是(AC=BD AB//CDB 、AD//BC £A = £C C AO = BO =CO = DO , AC _ BDD 、AO = CO , BO = DO ,AB 二 BC120°,若一条对角线的长为 2,那么矩形的周长为( (1+ 3 )D 5.2ABCD 勺周长为8,两邻角的比为2 : 1,则对角线的长分别为 (12 ~513 TD 、224、已知:如图,在 □ ABCD 中, O 为边AB 的中点,且/ AOD M BOC 求证:□ ABCD 是矩形.25、已知菱形ABCD 中, AC 与BD 相交O 点,若/ BDC=0° 菱形的周长为20厘米,求菱形的面积.矩形的两条对角线所成的钝角是 11、C 、2 A B 、5.812、A 13、C 、矩形D 正方形 ) 、6 如图,菱形 、4和2 如图,矩形 的形状最准确的判断是( )A 、2015、如图,在矩形 B 、 24C 、 25D 、 26ABCD 中 ,AB=3,AD=4,P 是 AD 上一动点,PF 丄 AC 于 F,PE 丄 BD 于 E,则 PE+PF 的B 、1 和 2 3C 、2 和 2 3D 、2 和 3 ABCD 勺对角线AC 的中垂线与 AD BC 分别交于F 、E,则四边形 14、如图,设F则 S A CBE =( AD 上一点,CEC23、如图,E 是正方形 ABCD 内一点,如果△ ABE 为等边三角形,那么/ DCE=22、点M 为矩形ABCD 勺边AD 的中点,P 为BC 上一点,且PE! MC,P 吐MB,当AB AD 满足 条件_______________ 时,四边形PEMF 是矩形。
初二数学菱形、矩形复习题(含答案)汇编

初二数学菱形、矩形复习题矩形:定义:有一个是直角的平行四边形是矩形性质:判定:菱形:定义:有一组邻边相等的平行四边形是菱形性质:判定:1.如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为____________2.如图,在矩形ABCD中,AB=3,AD=4,点P在AB上,PE⊥AC于E,PF⊥BD于F,则PE+PF 等于________3.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=8,则DE的长度是_______________4.如图,E,F分别是矩形ABCD边AD、BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为________________5.若菱形两条对角线长分别为6和8,则这个菱形的面积为________________6.若菱形的周长为16,两邻角度数之比为1:2,则该菱形的面积为_________________7.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有________________8.如果矩形一条较短的边是5,两条对角线的夹角是60°,则对角线长是.9.Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为.10.如图,四边形ABCD为矩形,H、F分别为AD、BC边的中点,四边形EFGH为矩形,E、G 分别在AB、CD边上,则图中四个直角三角形面积之和与矩形EFGH的面积之比为.11.如图,在矩形ABCD中,AD=5,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于.12.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为.13.如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是;若将△ABP的PA边长改为,另两边长度不变,则点P到原点的最大距离变为.14.如图,在菱形ABCD中,AD=8,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为.15.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则BG= .16.下列命题:①矩形的对角线互相平分且相等;②对角线相等的四边形是矩形;③菱形的每一条对角线平分一组对角;④一条对角线平分一组对角的平行四边形是菱形.其中正确的命题为(注:把你认为正确的命题序号都填上)17.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足(关系)时,四边形EFGH为矩形.18.如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=6,AF=BF,则四边形BCDE的面积是.19.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D是斜边AB上任意一点,DE⊥AC,DF⊥BC,垂足分别是点E、F,点Q是EF的中点,则线段DQ长的最小值等于.20.如图,矩形ABCD中,AB=20cm,BC=4cm,点P从A 开始沿折线A﹣B﹣C﹣D以4cm/s的速度运动,点Q从C开始沿CD边以1cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s),当t= 时,四边形APQD也为矩形.21.如图,在菱形ABCD中,∠BAD=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是.(把所有正确结论的序号都填在横线上)①OG=AB;②与△EGD全等的三角形共有5个;③S四边形CDGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.22.如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是.23.如图,已知四边形ABCD是平行四边形,并且∠A=∠D.(1)求证:四边形ABCD为矩形;(2)点E是AB边的中点,F为AD边上一点,∠1=2∠2,若CE=4,CF=5,求DF的长.24.已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC 的平行线与CE的延长线交于点F,连接DF.(1)求证:AF=DC;(2)请问:AD与CF满足什么条件时,四边形AFDC是矩形,并说明理由.25.如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.(1)求证:四边形DEBF是菱形;(2)请判断四边形AGBD是什么特殊四边形?并加以证明.26.如图,四边形ABCD中,AB=AC=AD,BC=CD,锐角∠BAC的角平分线AE交BC于点E,AF 是CD边上的中线,且PC⊥CD与AE交于点P,QC⊥BC与AF交于点Q.求证:四边形APCQ 是菱形.27.矩形ABCD中,E是CD上一点,且AE=CE,F是AC上一点FH⊥AE于H,FG⊥CD于G,求证:FH+FG=AD.28.如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB 于点H.(1)求证:四边形AGPH是矩形;(2)在点P在运动过程中,GH是否存在最小值?若存在,请求出,若不存在,请说明理由.29.如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P (点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE.(1)求证:四边形AEPQ为菱形;(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半?30.在△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC交AD于E,交AC于G,GF⊥BC 于F,连接EF.(1)如图1,求证:四边形AEFG是菱形;(2)如图2,若E为BG的中点,过点E作EM∥BC交AC于M,在不添加任何辅助线的情况下,请直接写出图2中是CM长倍的所有线段.31.阅读下面短文:如图①,△ABC是直角三角形,∠C=90°,现将△ABC补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个矩形ACBD和矩形AEFB(如图②)解答问题:(1)设图②中矩形ACBD和矩形AEFB的面积分别为S1、S2,则S1S2(填“>”“=”或“<”).(2)如图③,△ABC是钝角三角形,按短文中的要求把它补成矩形,那么符合要求的矩形可以画个,利用图③把它画出来.(3)如图④,△ABC是锐角三角形且三边满足BC>AC>AB,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出个,利用图④把它画出来.(4)在(3)中所画出的矩形中,哪一个的周长最小?为什么?32.如图1,菱形ABCD中,点E、F分别为AB、AD的中点,连接CE、CF.(1)求证:CE=CF;(2)如图2,若H为AB上一点,连接CH,使∠CHB=2∠ECB,求证:CH=AH+AB.33.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.34.将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;(2)若AB=8,AD=4,求四边形DHBG的面积.35.如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.(1)求证:四边形ABCF是矩形;(2)若EA=EG,求证:ED=EC.36.如图1,平行四边形ABCD,DE⊥AB.垂足E在BA的延长线上,BF⊥DC,垂足F在DC 的延长线上.(1)求证:四边形BEDF是矩形;(2)如图2,若M、N分别为AD、BC的中点,连接EM、EN、FM、FN,求证:四边形EMFN 是平行四边形.37.如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;(2)如图1,当点G和点M、C不重合时,求证:DG=DN.参考答案矩形:定义:有一个是直角的平行四边形是矩形性质:判定:菱形:定义:有一组邻边相等的平行四边形是菱形性质:1.如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为__________【解答】解:∵四边形ABCD是矩形,∴AB=DC,BC=AD,OA=OC=OB=OD,AD∥BC,∴∠EDO=∠FBO,.∵矩形ABCD的周长为20cm,∴BC+DC=10cm,∵EF⊥AC,∴CE=CF,在△ODE和△OBF中,,∴△ODE≌△OBF(ASA),∴DE=BF,∴△CDE的周长=DE+CE+DC=BF+CF+DC=BC+DC=10cm.2.如图,在矩形ABCD中,AB=3,AD=4,点P在AB上,PE⊥AC于E,PF⊥BD于F,则PE+PF 等于______【解答】解:方法一:设AP=x,PB=3﹣x.∵∠EAP=∠EAP,∠AEP=∠ABC;∴△AEP∽△ABC,故=①;同理可得△BFP∽△DAB,故=②.①+②得=,∴PE+PF=.方法二:(面积法)如图,作BM⊥AC于M,则BM==,∵S△AOB=S△AOP+S△POB,∴•AO•BM=•AO•PE+•OB•PF,∵OA=OB,∴PE+PF=BM=.3.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=8,则DE的长度是______________【解答】解:∵四边形ABCD是矩形,∴∠ADC=90°,AC=BD=8,OA=OC=AC=4,OB=OD=BD=4,∴OC=OD,∴∠ODC=∠OCD,∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,∴∠EDC=22.5°,∠EDA=67.5°,∵DE⊥AC,∴∠DEC=90°,∴∠DCE=90°﹣∠EDC=67.5°,∴∠ODC=∠OCD=67.5°,∴∠ODC+∠OCD+∠DOC=180°,∴∠COD=45°,∴OE=DE,∵OE2+DE2=OD2,∴2DE2=OD2=16,∴DE=2.4.如图,E,F分别是矩形ABCD边AD、BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为_____________【解答】解:连接EF,∵S△ABF=S△EBF∴S△EFG=S△ABG=15;同理:S△EFH=S△DCH=20∴S阴影=S△EFG+S△DCH=15+20=35.5.若菱形两条对角线长分别为6和8,则这个菱形的面积为________________ 【解答】解:菱形的面积为:×6×8=24.6.若菱形的周长为16,两邻角度数之比为1:2,则该菱形的面积为___________ 【解答】解:如图,∵两邻角度数之比为1:2,两邻角和为180°,∴∠ABC=60°,∠BAD=120°,∵周长为16,∴边长AB=4,∴菱形的对角线AC=4,BD=2×4sin60°=4,∴面积=AC•BD=×4×4=8.7.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有___________【解答】解:①正确∵E、F分别是OA、OC的中点.∴AE=OE.∵S△ADE=×AE×OD=×OE×OD=S△EOD∴S△ADE=S△EOD.②正确∵四边形ABCD是菱形,E,F分别是OA,OC的中点.∴EF⊥OD,OE=OF.∵OD=OD.∴DE=DF.同理:BE=BF∴四边形BFDE是菱形.③正确∵菱形ABCD的面积=AC×BD.∵E、F分别是OA、OC的中点.∴EF=AC.∴菱形ABCD的面积=EF×BD.④不正确由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.⑤正确∵EF⊥OD,OE=OF,OD=OD.∴△DEO≌△DFO.∴△DEF是轴对称图形.∴正确的结论有四个,分别是①②③⑤8.如果矩形一条较短的边是5,两条对角线的夹角是60°,则对角线长是10 .【解答】解:如图,在矩形ABCD中,AO=BO,∵AC、BD的夹角是60°,∴△ABO是等边三角形,∴AO=AB=5,∴对角线AC=2AO=2×5=10.故答案为:10.9.Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为.【解答】解:由题意知,四边形AFPE是矩形,∵点M是矩形对角线EF的中点,则延长AM应过点P,∴当AP为直角三角形ABC的斜边上的高时,即AP⊥BC时,AM有最小值,此时AM=AP,由勾股定理知BC==5,∵S△ABC=AB•AC=BC•AP,∴AP==,∴AM=AP=.10.如图,四边形ABCD为矩形,H、F分别为AD、BC边的中点,四边形EFGH为矩形,E、G 分别在AB、CD边上,则图中四个直角三角形面积之和与矩形EFGH的面积之比为1:1 .【解答】解:连接HF,∵四边形ABCD为矩形,∴AD=BC,AD∥BC,∠D=90°∵H、F分别为AD、BC边的中点,∴DH=CF,DH∥CF,∵∠D=90°,∴四边形HFCD是矩形,∴△HFG的面积是CD×DH=S矩形HFCD,即S△HFG=S△DHG+S△CFG,同理S△HEF=S△BEF+S△AEH,∴图中四个直角三角形面积之和与矩形EFGH的面积之比是1:1,故答案为:1:1.11.如图,在矩形ABCD中,AD=5,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于.【解答】解:连接FH、EG;∵AF=CG=2,AE=CH=4﹣1=3,∠A=∠C=90°,∴△AEF≌△CHG,S△AEF=S△CHG=3;同理可证:△FHD≌△GEB,S△FHD=S△GEB=1.5;∴FH=EG,EF=GH,即四边形EFHG是平行四边形;且S平行四边形=S矩形﹣2S△AEF﹣2S△FHD=11;过P作EF、GH的垂线,交EF于M,GH于N;则S△EFP+S△GHP=EF(PM+PN)=EF•MN=S▱EFHG=.故答案为:.12.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为.【解答】解:∵四边形ABCD是矩形,点G是DF的中点,∴AG=DG,∴∠ADG=∠DAG,∵AD∥BC,∴∠ADG=∠CED,∴∠AGE=∠ADG+∠DAG=2∠CED,∵∠AED=2∠CED,∴∠AED=∠AGE,∴AE=AG=4,在Rt△ABE中,AB===.故答案为:.13.如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是1+;若将△ABP的PA边长改为,另两边长度不变,则点P到原点的最大距离变为1+.【解答】解:取AB的中点M,连OM,PM,在Rt△ABO中,OM==1,在等边三角形ABP中,PM=,无论△ABP如何运动,OM和PM的大小不变,当OM,PM在一直线上时,P距O最远,∵O到AB的最大值是AB=1,此时在斜边的中点M上,由勾股定理得:PM==,∴OP=1+,将△AOP的PA边长改为,另两边长度不变,∵22+22=,∴∠PBA=90°,由勾股定理得:PM==,∴此时OP=OM+PM=1+.故答案为:1+,1+.14.如图,在菱形ABCD中,AD=8,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为4.【解答】解:连接BD,DE,∵四边形ABCD是菱形,∴B、D关于直线AC对称,∴DE的长即为PE+PB的最小值,∵ABC=120°,∴∠BCD=60°,∴△BCD是等边三角形,∵E是BC的中点,∴DE⊥BC,CE=BC=×8=4,∴DE===4.故答案为:4.15.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则BG= 5 .【解答】解:∵AG∥BD,BD=FG,∴四边形BGFD是平行四边形,∵CF⊥BD,∴CF⊥AG,又∵点D是AC中点,∴BD=DF=AC,∴四边形BGFD是菱形,设GF=x,则AF=13﹣x,AC=2x,∵在Rt△ACF中,∠CFA=90°,∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,解得:x=5,即BG=5.故答案是:5.16.下列命题:①矩形的对角线互相平分且相等;②对角线相等的四边形是矩形;③菱形的每一条对角线平分一组对角;④一条对角线平分一组对角的平行四边形是菱形.其中正确的命题为①③④(注:把你认为正确的命题序号都填上)【解答】解:①矩形的对角线互相平分且相等;故正确;②对角线相等的四边形是矩形,不能正确判定,故错误;③菱形的每一条对角线平分一组对角,这是菱形的一条重要性质,故正确;④一条对角线平分一组对角的平行四边形是菱形,故正确.故答案为:①③④.17.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足AB=AD (关系)时,四边形EFGH为矩形.【解答】解:∵四边形ABCD是矩形,∴∠A=90°.∵AE=AF,∴∠AFE=∠AEF=45°.又∵EH⊥EF,FG⊥EF∴∠GFB=∠HED=45°,∴△DHE和△BGF都是等腰直角三角形.如果四边形EFGH是矩形,则EH=FG,∴ED=FB又∵AE=AF,∴AD=AB.故答案是:AD=AB.18.如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=6,AF=BF,则四边形BCDE的面积是18.【解答】解:∵AF=BF,即F为AB的中点,又DE垂直平分AC,即D为AC的中点,∴DF为三角形ABC的中位线,∴DE∥BC,DF=BC,又∠ADF=90°,∴∠C=∠ADF=90°,又BE⊥DE,DE⊥AC,∴∠CDE=∠E=90°,∴四边形BCDE为矩形,∵BC=6,∴DF=BC=3,在Rt△ADF中,∠A=30°,DF=3,∴tan30°=,即AD=3,∴CD=AD=3,则矩形BCDE的面积S=CD•BC=18.故答案为:18.19.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D是斜边AB上任意一点,DE⊥AC,DF⊥BC,垂足分别是点E、F,点Q是EF的中点,则线段DQ长的最小值等于 2.4 .【解答】解:∵在△ABC中,∠ACB=90°,AC=6,BC=8,∴AB=10,连接CD,∵DE⊥AC,DF⊥BC,∴四边形EDFC是矩形,∴EF=CD,∠EDF=90°,∵点Q是EF的中点,∴DQ=EF=CD,当CD最小时,则DQ最小,根据垂线段最短可知当CD⊥AB时,则CD最小,∴DQ=EF=CD=×=2.4,故答案为:2.4.20.如图,矩形ABCD中,AB=20cm,BC=4cm,点P从A 开始沿折线A﹣B﹣C﹣D以4cm/s的速度运动,点Q从C开始沿CD边以1cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s),当t= 4 时,四边形APQD也为矩形.【解答】解:根据题意,当AP=DQ时,四边形APQD为矩形.此时,4t=20﹣t,解得t=4(s).故答案是:4.21.如图,在菱形ABCD中,∠BAD=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是①④.(把所有正确结论的序号都填在横线上)①OG=AB;②与△EGD全等的三角形共有5个;③S四边形CDGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.【解答】解:∵四边形ABCD是菱形,∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,∵CD=DE,∴AB=DE,在△ABG和△DEG中,,∴△ABG≌△DEG(AAS),∴AG=DG,∴OG是△ACD的中位线,∴OG=CD=AB,①正确;∵AB∥CE,AB=DE,∴四边形ABDE是平行四边形,∵∠BCD=∠BAD=60°,∴△ABD、△BCD是等边三角形,∴AB=BD=AD,∠ODC=60°,∴OD=AG,四边形ABDE是菱形,④正确;∴AD⊥BE,由菱形的性质得:△ABG≌△BDG≌△DEG,在△ABG和△DCO中,,∴△ABG≌△DCO(SAS),∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正确;∵OB=OD,AG=DG,∴OG是△ABD的中位线,∴OG∥AB,OG=AB,∴△GOD∽△ABD,△ABF∽△OGF,∴△GOD的面积=△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,∴△AFG的面积=△OGF的面积的2倍,又∵△GOD的面积=△AOG的面积=△BOG的面积,∴S四边形ODGF=S△ABF;不正确;正确的是①④.故答案为:①④.22.如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.【解答】解:∵五边形ABCDE是正五边形,∴AB∥CE,AD∥BC,∴四边形ABCF是平行四边形,又∵AB=BC=CD=DE=EA,∴四边形ABCF是菱形,∴AC⊥BF,∴OB2+OC2=BC2,∵AC=2OC,BF=2OB,∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,又∵BC=CD,∴AC2+BF2=4CD2.故答案为:AC2+BF2=4CD2.23.如图,已知四边形ABCD是平行四边形,并且∠A=∠D.(1)求证:四边形ABCD为矩形;(2)点E是AB边的中点,F为AD边上一点,∠1=2∠2,若CE=4,CF=5,求DF的长.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A+∠D=180°,又∠A=∠D,∴∠A=∠D=90°,∴平行四边形ABCD为矩形;(2)解:延长DA,CE交于点G,∵四边形ABCD是矩形,∴∠DAB=∠B=90°,AD∥BC,∴∠GAE=90°,∠G=∠ECB,∵E是AB边的中点,∴AE=BE,在△AGE和△BCE中,,∴△AGE≌△BCE(AAS),∴AG=BC,若CE=4,CF=5,设DF=x,根据勾股定理得:CD2=CF2﹣DF2=CG2﹣DG2,即52﹣x2=82﹣(5+x)2,解得:x=,即DF=.24.已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC 的平行线与CE的延长线交于点F,连接DF.(1)求证:AF=DC;(2)请问:AD与CF满足什么条件时,四边形AFDC是矩形,并说明理由.【解答】(1)证明:∵AF∥BC,∴∠AFE=∠DCE,又∵E为AD的中点,∴AE=DE,在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=DC;(2)解:当AD=CF时,四边形AFDC是矩形;理由如下:由(1)得:AF=DC且AF∥DC,∴四边形AFDC是平行四边形,又∵AD=CF,∴四边形AFDC是矩形(对角线相等的平行四边形是矩形).25.如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.(1)求证:四边形DEBF是菱形;(2)请判断四边形AGBD是什么特殊四边形?并加以证明.【解答】(1)证明:∵四边形ABCD是平行四边形∴AB∥CD且AB=CD,AD∥BC且AD=BCE,F分别为AB,CD的中点,∴BE=AB,DF=CD,∴BE=DF,∴四边形DEBF是平行四边形在△ABD中,E是AB的中点,∴AE=BE=AB=AD,而∠DAB=60°∴△AED是等边三角形,即DE=AE=AD,故DE=BE∴平行四边形DEBF是菱形.(2)解:四边形AGBD是矩形,理由如下:∵AD∥BC且AG∥DB∴四边形AGBD是平行四边形由(1)的证明知AD=DE=AE=BE,∠EDB=∠DBE=30°故∠ADB=90°∴平行四边形AGBD是矩形.26.如图,四边形ABCD中,AB=AC=AD,BC=CD,锐角∠BAC的角平分线AE交BC于点E,AF 是CD边上的中线,且PC⊥CD与AE交于点P,QC⊥BC与AF交于点Q.求证:四边形APCQ 是菱形.【解答】证明:∵AC=AD,AF是CD边上的中线,∴∠AFC=90°,∴∠ACF+∠CAF=90°,∵∠ACF+∠PCA=90°,∴∠PCA=∠CAF,∴PC∥AQ,同理:AP∥QC,∴四边形APCQ是平行四边形.∵AF∥CP,AE∥CQ,∵AB=AC,AE平分∠BAC,∴CE=BE=CB(等腰三角三线合一),∵AF是CD边上的中线,∴CF=CD,∵CB=DC,∴CE=CF,∵PC⊥CD,QC⊥BC,∴∠ECP+∠PCQ=∠QCF+∠PCQ=90°,∴∠PCE=∠QCF,∴△PEC≌△QFC(AAS),∴PC=QC,∴四边形APCQ是菱形.27.矩形ABCD中,E是CD上一点,且AE=CE,F是AC上一点FH⊥AE于H,FG⊥CD于G,求证:FH+FG=AD.【解答】证明:连接EF,如图所示:∵FH⊥AE于H,FG⊥CD于G,∴△ACE的面积=△AEF的面积+△CEF的面积=AE•FH+CE•FG,∵AE=CE,∴△ACE的面积=CE(FH+FG),又∵四边形ABCD是矩形,∴AD⊥CD,∴△ACE的面积=CE•AD,∴FH+FG=AD.28.如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB 于点H.(1)求证:四边形AGPH是矩形;(2)在点P在运动过程中,GH是否存在最小值?若存在,请求出,若不存在,请说明理由.【解答】(1)证明∵AC=9 AB=12 BC=15,∴AC2=81,AB2=144,BC2=225,∴AC2+AB2=BC2,∴∠A=90°.∵PG⊥AC,PH⊥AB,∴∠AGP=∠AHP=90°,∴四边形AGPH是矩形;(2)存在.理由如下:连结AP.∴GH=AP.∵当AP⊥BC时AP最短.∴9×12=15•AP.∴AP=.29.如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P (点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE.(1)求证:四边形AEPQ为菱形;(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半?【解答】(1)证明:∵EF∥AB,PQ∥AC,∴四边形AEPQ为平行四边形,∴∠BAD=∠EPA,∵AB=AC,AD平分∠CAB,∴∠CAD=∠BAD,∴∠CAD=∠EPA,∴EA=EP,∴四边形AEPQ为菱形.(2)解:P为EF中点,即AP=AD时,S菱形AEPQ=S四边形EFBQ∵四边形AEPQ为菱形,∴AD⊥EQ,∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴EQ∥BC,又∵EF∥AB,∴四边形EFBQ为平行四边形.作EN⊥AB于N,如图所示:则S菱形AEPQ=EP•EN=EF•EN=S四边形EFBQ.30.在△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC交AD于E,交AC于G,GF⊥BC 于F,连接EF.(1)如图1,求证:四边形AEFG是菱形;(2)如图2,若E为BG的中点,过点E作EM∥BC交AC于M,在不添加任何辅助线的情况下,请直接写出图2中是CM长倍的所有线段.【解答】(1)证明:∵AD⊥BC,GF⊥BC,∴∠ADF=∠GFC=90°,∴AE∥GF,在△ABG和△FBG中,,∴△ABG≌△FBG,∴AG=FG,∵∠FBG+∠BED=90°,∵∠BED=∠AEG,∴∠FBG+∠AEG=90°,∵∠ABG+∠AGE=90°,∵∠ABG=∠FBG,∴∠AEG=∠AGE,∴AE=AG,∴AE=FG,∴四边形AEFG是平行四边形,∵AE=AG∴四边形AEFG是菱形.(2)解:∵四边形AEFG是菱形,∴AE=AG,∵BE=EG,∠BAG=90°,∴AE=BE=EG,∴△AEG是等边三角形,∴∠AGE=60°,在RT△ABG中,∵∠ABG=30°,∴AB=AG,∵∠C=30°,∴BC=2AB,∴BE=GE,EF∥AC,EM∥BC,∴BF=FC,CM=GM,在RT△AEM中,∵∠AME=∠C=30°,∠GEM+∠GME=60°,∴∠GEM=∠GME=30°,∴EG=AG=GM=CM,∵EM∥FC,EF∥CM,∴四边形EFCM是平行四边形,∴AB=BF=CF=EM=CM,∴是CM长倍的所有线段有AB、BF、CF、EM.31.阅读下面短文:如图①,△ABC是直角三角形,∠C=90°,现将△ABC补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个矩形ACBD和矩形AEFB(如图②)解答问题:(1)设图②中矩形ACBD和矩形AEFB的面积分别为S1、S2,则S1= S2(填“>”“=”或“<”).(2)如图③,△ABC是钝角三角形,按短文中的要求把它补成矩形,那么符合要求的矩形可以画 1 个,利用图③把它画出来.(3)如图④,△ABC是锐角三角形且三边满足BC>AC>AB,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出 3 个,利用图④把它画出来.(4)在(3)中所画出的矩形中,哪一个的周长最小?为什么?【解答】解:(1)=(2)1(3)3(4)以AB为边长的矩形周长最小,设矩形BCED,ACHQ,ABGF的周长分别为L1,L2,L3,BC=a,AC=b,AB=c.易得三个矩形的面积相等,设为S,∴L1=+2a;L2=+2b;L3=+2c.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩形,菱形
例1、如图,在平行四边形ABCD中,E是CD的中点,△ABE是等边三角形,求证:四边形ABCD是矩形。
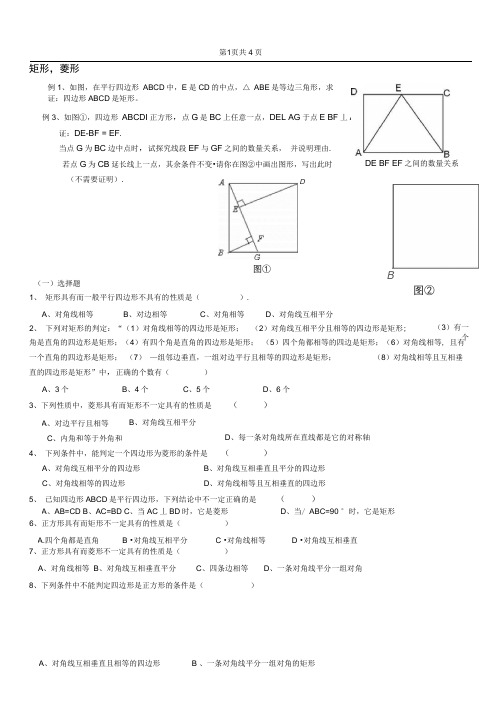
例3、如图①,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1) 求证:DE-BF = EF.
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系,并说明理由.
(3) 若点G为CB延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE、BF、EF之间的数量关
系(不需要证明).
(一)选择题
1、矩形具有而一般平行四边形不具有的性质是().
A、对角线相等
B、对边相等
C、对角相等
D、对角线互相平分
2、下列对矩形的判定:“(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(4)有四个角是直角的四边形是矩形;(5)四个角都相等的四边是矩形;(6)对角线相等,且有一个直角的四边形是矩形;(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;(8)对角线相等且互相垂直的四边形是矩形”中,正确的个数有()
A、3 个
B、4个
C、5个
D、6个
3、下列性质中,菱形具有而矩形不一定具有的性质是( )
A、对边平行且相等
B、对角线互相平分
C、内角和等于外角和
D、每一条对角线所在直线都是它的对称轴
4、下列条件中,能判定一个四边形为菱形的条件是( )
A、对角线互相平分的四边形
B、对角线互相垂直且平分的四边形
C、对角线相等的四边形
D、对角线相等且互相垂直的四边形
5、已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
A、AB=CD
B、AC=BD
C、当AC⊥BD时,它是菱形
D、当∠ABC=90°时,它是矩形
6、正方形具有而矩形不一定具有的性质是()。
A.四个角都是直角B.对角线互相平分C.对角线相等D.对角线互相垂直
7、正方形具有而菱形不一定具有的性质是()。
A、对角线相等
B、对角线互相垂直平分
C、四条边相等
D、一条对角线平分一组对角
B E
D
C
F
A 8、下列条件中不能判定四边形是正方形的条件是( )。
A 、对角线互相垂直且相等的四边形
B 、一条对角线平分一组对角的矩形
C 、对角线相等的棱形
D 、对角线互相垂直的矩形 9、下列命题中,假命题是( )。
A 、四个内角都相等的四边形是矩形
B 、四条边都相等的平行四边形是正方形
C 、既是菱形又是矩形的四边形是正方形
D 、对角线互相垂直的平行四边形是菱形 10、在四边形ABCD 中,O 是对角线的交点,能判定四边形是正方形的条件是( )。
A 、BD AC =,CD A
B // B 、B
C A
D //,C A ∠=∠
C 、
DO CO BO AO ===,BD AC ⊥ D 、CO AO =,DO BO =,BC AB =
11、矩形的两条对角线所成的钝角是120°,若一条对角线的长为2,那么矩形的周长为( ) A 、6 B 、5.8
C 、2(1+ 3 )
D 、5.2
12、如图,菱形ABCD 的周长为8,两邻角的比为2∶1,则对角线的长分别为( )
A 、4和2
B 、1和2 3
C 、2和2 3
D 、2和 3
13、如图,矩形ABCD 的对角线AC 的中垂线与AD 、BC 分别交于F 、E,则四边形AFCE 的形状最准确的判断是( ) A 、平行四边形
B 、菱形
C 、矩形
D 、正方形
14、如图,设F 为正方形ABCD 的边AD 上一点,CE ⊥CF 交AB 的延长线于E,若S 正方形ABCD =64,S △CEF =50,
则S △CBE =( ) A 、20
B 、24
C 、25
D 、26
15、如图,在矩形ABCD 中,AB=3,AD=4,P 是AD 上一动点,PF ⊥AC 于F,PE ⊥BD 于E,则PE+PF 的值为( )
A 、12
5
B 、13
5
C 、52
D 、2
24、已知:如图,在□ABCD 中,O 为边AB 的中点,且∠AOD=
∠BOC .求证:□ABCD 是矩形.
A
B C
D
O 第13题
第14题 第15题 第
B
A
C
D
O
P
H
D C
B
A
F
E
D
C
B A
F
E
D C
B
A
25、已知菱形ABCD 中,AC 与BD 相交O 点,若∠BDC=030,菱形的周长为20厘米,求菱形的面积.
23、如图,E 是正方形ABCD 内一点,如果△ABE 为等边三角形,那么∠DCE= _______________
22、点M 为矩形ABCD 的边AD 的中点,P 为BC 上一点,且PE ⊥MC,PF ⊥MB,当AB 、AD 满足条件__________时,四边形PEMF 是矩形。
1. 如图, 在矩形ABCD 中, AP=DC, PH=PC, 求证: PB 平分∠CBH.
2. 如图, 矩形ABCD 的周长为16cm, DE=2cm, 若△CEF 是等腰直角三角形, 那么这个三角形的面积为______________.
3. 如图, 在矩形ABCD 中, AD=12, AB=7, DF 平分∠ADC, AF ⊥EF, (1)求EF 长; (2)在平面上是
否存在点Q, 使得QA=QD=QE=QF? 若存在, 求出QA 的长; 若不存在, 说明理由.
11.如图,在矩形ABCD 中,AB=3,BC=4,如果将该矩形沿对角线BD 重叠,求图中阴影部分的面积.
A
B C
D
O A
B
C
D E
第23题图
C D
A
B
E
12.如图,已知在四边形ABCD 中,AC DB ⊥交于O ,E 、F 、G 、H 分别是四边的中点, 求证:四边形EFGH 是矩形.
13. 如图,平行四边形ABCD 中,AQ 、BN 、CN 、DQ 分别是DAB ∠、ABC ∠、BCD ∠、CDA ∠的平分线,AQ 与BN 交于P ,CN 与DQ 交于M , 求证:四边形PQMN 是矩形.
★14. 如图矩形ABCD 中,延长CB 到E ,使CE AC =,F 是AE 中点. 求证:BF DF ⊥.
★15. 如图,矩形ABCD 中,CE BD ⊥于E ,AF 平分BAD ∠交EC 于F , 求证:CF BD =.
H
G O
F
E
D
C
B A
N
M
Q
P
D
C
B
A
A
B
C
E F
D
D
A
B
C
E
10.如图,四边形ABDC中,∠ABC=∠ADC=90°,M、E分别是AC,BD的中点,
求证:(1)MD=MB;(2)ME⊥BD
E
M
C D
B A。
