北京市各区2018届中考一模数学试卷精选汇编：二次函数综合(含答案)

合集下载

北京市各区2018届中考一模数学试卷精选汇编：函数计算及运用(含答案)

函数计算及运用专题东城区22. 已知函数()30y x x=＞的图象与一次函数()20y ax a =-≠的图象交于点A ()3,n . （1）求实数a 的值；(2) 设一次函数()20y ax a =-≠的图象与y 轴交于点B .若点C 在y 轴上，且=2ABC AOB S S △△，求点C 的坐标.22.解：（1）∵点()3,A n 在函数()30y x x=＞的图象上， ∴=1n ，点()3,1A .∵直线()20y ax a =-≠过点()3,1A ， ∴ 321a -= .解得 1a =. ----------------------2分 (2)易求得()0,2B -.如图，12AOB A S OB x =⋅△，1=2ABC A S BC x ⋅△∵=2ABC AOB S S △△， ∴=24BC OB =.∴()10,2C ,或()20,6C -. ----------------------5分西城区22．如图，在平面直角坐标系xOy 中，直线y x m =+与x 轴的交点为0()4,A -，与y 轴的交点为B ，线段AB 的中点M 在函数ky x=（0k ≠）的图象上（1）求m ，k 的值;（2）将线段AB 向左平移n 个单位长度（0n >）得到线段CD ，A ，MB 的对应点分别为C ，N ，D ．①当点D 落在函数ky x=（0x <）的图象上时，求n 的值． ②当MD MN ≤时，结合函数的图象，直接写出n 的取值范围．【解析】（1）如图．∵直线y x m =+与x 轴的交点为0()4,A -， ∴4m =．∵直线y x m =+与y 轴的交点为B ， ∴点B 的坐标为(0,4)B ． ∵线段AB 的中点为M ， ∴可得点M 的坐标为(2,2)M -． ∵点M 在函数ky x=（0k ≠）的图象上， ∴4k =-．（2）①由题意得点D 的坐标为(,4)D n -， ∵点D 落在函数ky x=（0k ≠）的图象上， ∴44n -=-，解得1n =．②n 的取值范围是2n ≥．海淀区22．在平面直角坐标系xOy 中，已知点P （2，2），Q （－1，2），函数my x=.（1）当函数my x=的图象经过点P 时，求m 的值并画出直线y x m =+．（2）若P ，Q 两点中恰有一个点的坐标（x ，y ）满足不等式组,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0），求m 的取值范围．22．解：（1）∵函数my x=的图象经过点()22P ，， ∴2=2m，即4m =． ………………1分图象如图所示. ………………2分（2）当点()22P ，满足,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0）时，解不等式组2222m m⎧>⎪⎨⎪<+⎩，得04m <<． ………………3分当点()12Q -，满足,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0）时，解不等式组221m m>-⎧⎨<-+⎩，得3m >． ………………4分∵P Q ，两点中恰有一个点的坐标满足,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0）， ∴m 的取值范围是：03m <≤，或4m ≥． ………………5分丰台区22．在平面直角坐标系xOy 中，反比例函数2y x=的图象与一次函数y kx b =+的图象的交点分别为P (m ，2)，Q (-2，n ). （1）求一次函数的表达式；（2）过点Q 作平行于y 轴的直线，点M 为此直线上的一点，当MQ = PQ 时，直接写出点M 的坐标.22．（1）解： ∵反比例函数2y x=的图象经过点(,2)P m ，Q (-2，n )， ∴1m =，1n =-．∴点P ，Q 的坐标分别为(1，2)，(-2，-1). …….…….…….……2分 ∵一次函数y kx b =+的图象经过点P (1，2)，Q (-2，-1)，∴2,2 1.k b k b +=⎧⎨-+=-⎩ 解得1,1.k b =⎧⎨=⎩ ∴一次函数的表达式为1y x =+． .…….…….…….……3分（2）点M 的坐标为（-2，）或（-2，）……………5分石景山区22．在平面直角坐标系xOy 中，函数a y x=（0x >）的图象与直线1l y x b =+：交于点(3,2)A a -．（1）求a ，b 的值；（2）直线2l y x m =-+：与x 轴交于点B ，与直线1l 交于点C ，若S △ABC 6≥，求m 的取值范围．22．解：（1）∵函数()0a y x x=>的图象过点()3,2A a -，∴23a a -=，解得3a =． ………………1分∵直线1l y x b =+：过点()3,1A ,∴2b =-． ………………2分（2）设直线2y x =-与x 轴交于点D ，则(2,0)D ，直线y x m =-+与x 轴交于点(,0)B m ，与直线y x b =+交于点22(,)22m m C +-． ①当S △ABC =S △BCD +S △ABD =6时，如图1. 可得211(2)(242m m -+- 解得2m =-，8m =②当S △ABC =S △BCD -S △ABD =6时，如图2.可得211(2)(2)1642m m ---⨯=，解得8m =，2m =-（舍）.综上所述，当8m ≥或2m -≤时，S △ABC 6≥. ………………5分朝阳区22. 如图，在平面直角坐标系xOy 中，直线AB 与x 轴、y 轴分别交于点A 、B ，与反比例函数xky =的图象在第四象限交于点C ，CD ⊥x 轴于点D ，tan ∠OAB ＝2，OA ＝2，OD ＝1．（1）求该反比例函数的表达式；（2）点M 是这个反比例函数图象上的点，过点M作MN ⊥y 轴，垂足为点N ，连接OM 、AN ，如果 S △ABN ＝2S △OMN ，直接写出点M 的坐标.22. 解：（1）∵AO ＝2，OD ＝1，∴AD ＝AO+ OD ＝3. ………………………………………………1分 ∵CD ⊥x 轴于点D ， ∴∠ADC ＝90°.在Rt △ADC 中，6tan =∠⋅=OAB AD CD ..∴C （1，－6）. ……………………………………………………2分 ∴该反比例函数的表达式是xy 6-=. ……………………………………3分（2）点M 的坐标为（－3,2）或（53，－10）. ……………………5分 ∴OM 27=215 OM=715∴⊙O 的半径是715…………………………………6′门头沟区20. 如图，在平面直角坐标系xOy 中，一次函数y x =与反比例函数ky x=（k ≠0）的图象相交于点)A a . （1）求a 、k 的值；（2）直线x =b （0b >）分别与一次函数y x =、反比例函数ky x=的图象相交于点M 、N ，当MN =2时,画出示意图并直接写出b 的值.20．（本小题满分5分）（1）∵直线y x =与双曲线ky x=（k ≠0）相交于点)A a .∴a =1分∴A3k =………………………2分（2）示意图正确………………………………3分 3b =或1 ………………………………5分大兴区22．如图，点A 是直线2y x =与反比例函数1m y x-=（m 为常数）的图象的交点．过点A 作x 轴的垂线，垂足为B ，且OB =2．（1）求点A 的坐标及m 的值；(2)已知点P (0，n) (0＜n ≤8) ，过点P 作平行于x 轴的直线，交直线2y x =于点C 11(,)x y , 交反比例函数1m y x-=（m 为常数）的图象于点D 22(,)x y ,交垂线AB 于点E 33(,)x y , 若231x x x <<，结合函数的图象，直接写出123++x x x 的取值范围．22．（1）解：由题意得，可知点A 的横坐标是2，……………………1分由点A 在正比例函数2y x =的图象上，∴点A 的坐标为（2，4）……………………………………2分又点A 在反比例函数1m y x-=的图象上，142m -∴=，即9m =．……………………………………… 3分（2）6<x 1+x 2+x 3≤7 ……………………………………………… 5分平谷区22．如图，在□ABCD 中，BF 平分∠ABC 交AD 于点F ，AE ⊥BF 于点O ，交BC 于点E ，连接EF ．（1）求证：四边形ABEF 是菱形；（2）连接CF ，若∠ABC=60°， AB= 4，AF =2DF ，求CF 的长．22．（1）证明：∵BF 平分∠ABC ，∴∠ABF =∠CBF ． (1)∵□ABCD ，∴AD ∥BC ． ∴∠AFB =∠CBF ．OF ODF∴∠ABF =∠AFB ． ∴AB=AF ． ∵AE ⊥BF ，∴∠ABF +∠BAO =∠CBF +∠BEO =90°． ∴∠BAO =∠BEO ． ∴AB=BE ． ∴AF=BE ．∴四边形ABEF 是平行四边形．∴□ABEF 是菱形． (2)（2）解：∵AD=BC ，AF=BE ，∴DF=CE ． ∴BE =2CE ． ∵AB =4，∴BE =4． ∴CE =2．过点A 作AG ⊥BC 于点G ． (3)∵∠ABC =60°，AB=BE ， ∴△ABE 是等边三角形． ∴BG=GE =2．∴AF=CG =4． ········································································· 4 ∴四边形AGCF 是平行四边形． ∴□AGCF 是矩形． ∴AG=CF ．在△ABG 中，∠ABC =60°，AB =4，∴AG =∴CF =怀柔区22．在平面直角坐标系xOy 中,一次函数y=kx+b 的图象与y 轴交于点B （0,1），与反比例函数xmy的图象交于点A(3，-2). (1)求反比例函数的表达式和一次函数表达式；(2)若点C 是y 轴上一点，且BC=BA ，直接写出点C 的坐标.y x–1–2–3–4–512345–1–2–3–4–512345O22．(1)∵双曲线x m y =过A （3，-2），将A （3，-2）代入xmy =，解得：m= -6.∴所求反比例函数表达式为: y=x6-. …………………………………1分 ∵点A （3，-2）点B （0,1）在直线y=kx+b 上，∴-2=3k+1. …………………………………………………………………………………2分 ∴k=-1.∴所求一次函数表达式为y=-x+1. …………………………………………………………3分 (2)C(0，123+ )或 C(0，231- ). ……………………………………………………5分延庆区22．在平面直角坐标系xOy 中，直(0)y kx b k =+≠ 与x 轴交于点A ，与y 轴交于点B ，与反比例函数(0)my m x=≠的图象在第一象限交于点P （1，3），连接OP ．（1）求反比例函数(0)my m x=≠的表达式；（2）若△AOB 的面积是△POB 的面积的2倍，求直线y kx b =+的表达式．-1-2-3-3-2-1y123456x54321O22．（1）3y x……1分错误!未找到引用源。

2018北京二次函数代数综合题例讲(解析版)

二次函数的图象和性质重点落实什么能力？2019北京中考26题重点题型------------ 必须会!!!!!!例1 在平面直角坐标系xOy 中，抛物线2443(0)y ax ax a a =-+-≠的顶点为A ．（1）求顶点A 的坐标；（2）过点(0,5)且平行于x 轴的直线l ，与抛物线2443(0)y ax ax a a =-+-≠交于B ，C 两点．①当2a =时，求线段BC 的长；②当线段BC 的长不小于6时，直接写出a 的取值范围．代数变形能力：2443(0)y ax ax a a =-+-≠通过配方转化为2(2)(0)3y a x a =-≠- 几何作图能力：考点：二次函数的性质分析：（1）配方得到y=ax2-4ax+4a-3=a （x-2）2-3，于是得到结论；（2）①当a=2时，抛物线为y=2x2-8x+5，如图．令y=5得到2x2-8x+5=5，解方程即可得到结论；②令y=5得到ax2-4ax+4a-3=5，解方程即可得到结论．解答：(1)∵y =ax 2−4ax +4a −3=a (x −2)2−3， ∴顶点A 的坐标为(2,−3)；(2)①当a =2时,抛物线为y =2x 2−8x +5，如图。

令y =5，得 2x 2−8x +5=5，解得,x 1=0,x 2=4， ∴a2a4线段BC 的长为4， ②令y =5,得ax 2−4ax +4a −3=5，解得,x 1=a a a 222 ,x 2=aaa 22-2∴线段BC 的长为a2a4 ∵线段BC 的长不小于6，∴a2a4≥6，∴0<a ≤8/9. 例2 已知：二次函数1422-++=m x x y ，与x 轴的公共点为A ，B .（1）如果A 与B 重合，求m 的值；（2）横、纵坐标都是整数的点叫做整点； ①当1=m 时，求线段AB 上整点的个数； ②若设抛物线在点A ，B 之间的部分与线段AB所围成的区域内（包括边界）整点的个数为n ，当1<<8n 时，结合函数的图象，求m 的取值范围.代数变形能力：1422-++=m x x y 通过配方转化为22(1)3y x m =++-*考点：抛物线与x 轴的交点，二次函数图象上点的坐标特征分析：（1）当A 、B 重合时，抛物线与x 轴只有一个交点，此时△=0，从可求出m 的值．（2）①m=1代入抛物线解析式，然后求出该抛物线与x 轴的两个交点的坐标，从而可求出线段AB 上的整点；②根据二次函数表达式可以用带m 表达出两根之差，根据1<两根之差<8，即可解题．解答：(1)∵A 与B 重合，∴二次函数y =2x 2+4x +m −1的图象与x 轴只有一个公共点， ∴方程2x 2+4x +m −1=0有两个相等的实数根， ∴△=42−4×2(m −1)=24−8m =0，解得：m =3.∴如果A 与B 重合，m 的值为3.(2)①当m =1时,原二次函数为y =2x 2+4x +m −1=2x 2+4x ，令y =2x 2+4x =0,则x 1=0,x 2=−2， ∴线段AB 上的整点有(−2,0)、(−1,0)和(0,0). 故当m =1时，线段AB 上整点的个数有3个。

北京市【中考真题】2018年全国各地中考数学真题汇编全系列13套,134页,含答案)

中考数学真题汇编:二次函数一、选择题1.给出下列函数：①y=﹣3x+2；②y= ；③y=2x2；④y=3x，上述函数中符合条作“当x＞1时，函数值y随自变量x增大而增大“的是（）A. ①③B. ③④C. ②④D. ②③【答案】B2.如图,函数和( 是常数,且)在同一平面直角坐标系的图象可能是（）A. B. C. D.【答案】B3.关于二次函数，下列说法正确的是（）A. 图像与轴的交点坐标为B. 图像的对称轴在轴的右侧C. 当时，的值随值的增大而减小D. 的最小值为-3【答案】D4.二次函数的图像如图所示，下列结论正确是( )A. B. C. D. 有两个不相等的实数根【答案】C5.若抛物线与轴两个交点间的距离为2，称此抛物线为定弦抛物线，已知某定弦抛物线的对称轴为直线，将此抛物线向左平移2个单位，再向下平移3个单位，得到的抛物线过点( )A. B. C. D.【答案】B6.若抛物线y=x2+ax+b与x轴两个交点间的距离为2，称此抛物线为定弦抛物线。

已知某定弦抛物线的对称轴为直线x=1，将此抛物线向左平移2个单位，再向下平移3个单位，得到的抛物线过点（）A. （-3，-6）B. （-3，0）C. （-3，-5）D. （-3，-1）【答案】B7.已知学校航模组设计制作的火箭的升空高度h（m）与飞行时间t（s）满足函数表达式h ＝﹣t2＋24t＋1．则下列说法中正确的是（）A. 点火后9s和点火后13s的升空高度相同B. 点火后24s火箭落于地面C. 点火后10s的升空高度为139mD. 火箭升空的最大高度为145m【答案】D8.如图，若二次函数y=ax2+bx+c（a≠0）图象的对称轴为x=1，与y轴交于点C，与x轴交于点A、点B（﹣1，0），则①二次函数的最大值为a+b+c；②a﹣b+c＜0；③b2﹣4ac＜0；④当y＞0时，﹣1＜x＜3，其中正确的个数是（）A. 1B. 2C. 3D. 4【答案】B9.如图是二次函数（，，是常数，）图象的一部分，与轴的交点在点和之间，对称轴是.对于下列说法：①；②；③；④（为实数）；⑤当时，，其中正确的是（）A. ①②④B. ①②⑤C. ②③④D. ③④⑤【答案】A10.如图，二次函数y=ax2+bx的图象开口向下，且经过第三象限的点P．若点P的横坐标为-1，则一次函数y=（a-b）x+b的图象大致是（）A. B. C. D.【答案】D11.四位同学在研究函数（b，c是常数）时，甲发现当时，函数有最小值；乙发现是方程的一个根；丙发现函数的最小值为3；丁发现当时，．已知这四位同学中只有一位发现的结论是错误的，则该同学是（）A. 甲B. 乙C. 丙D. 丁【答案】B12.如图所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜边DF上一动点,过B作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,则y与x之间的函数图象大致为（）A. （B.C. D. （【答案】B二、填空题13.已知二次函数，当x＞0时，y随x的增大而________（填“增大”或“减小”）【答案】增大14.右图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，水面下降2m，水面宽度增加________m。

【中考汇编】北京市各区2018届中考一模数学试卷精选汇编88页含答案

北京市各区2018届中考一模数学试卷精选汇编目录北京市各区2018届中考一模数学试卷精选汇编：解不等式组（含答案）北京市各区2018届中考一模数学试卷精选汇编：计算题（含答案）北京市各区2018届中考一模数学试卷精选汇编：解四边形（含答案）北京市各区2018届中考一模数学试卷精选汇编：几何证明（含答案）北京市各区2018届中考一模数学试卷精选汇编：几何综合（含答案）北京市各区2018届中考一模数学试卷精选汇编：函数计算及运用（含答案）北京市各区2018届中考一模数学试卷精选汇编：二次函数综合（含答案）北京市各区2018届中考一模数学试卷精选汇编：统计（含答案）解不等式组专题东城区18．解不等式组4+6,23x x x x ⎧⎪+⎨⎪⎩＞≥，并写出它的所有整数解. 18. 解：4+6,23x x x x ⎧⎪⎨+⎪⎩①②＞≥，由①得，-x ＞2，------------------1分由②得，1x ≤， ------------------2分∴不等式组的解集为-1x 2＜≤.所有整数解为-1, 0, 1. ---------------------5分西城区18．解不等式组3(2)4112x x x ++⎧⎪⎨-<⎪⎩≥，并求该不等式组的非负整数解．【解析】解①得，364x x ++≥，22x -≥，1x -≥，解②得，12x -<，3x <，∴原不等式解集为13x -<≤，∴原不等式的非负整数解为0，，2．海淀区18．解不等式组：()5331,263.2x x x x +>-⎧⎪⎨-<-⎪⎩ 18.解：() 5331, 263. 2x x x x +>-⎧⎪⎨-<-⎪⎩①② 解不等式①，得3x >-. …2分解不等式②，得2x <. ………4分所以原不等式组的解集为32x -<<. ………5分18．解不等式组：341,51 2.2x x x x ≥-⎧⎪⎨->-⎪⎩ 18．解：解不等式①，得1x ≤， ……………………2分解不等式②，得1x >-. ……………………4分∴原不等式组的解集是11x -<≤．………5分石景山区18．解不等式组：3(1)45622x x x x +>++<⎧⎪⎨⎪⎩，． 18．解：原不等式组为3(1)45,62.2x x x x +>++<⎧⎪⎨⎪⎩ 解不等式①，得2x <-． ………………2分解不等式②，得2x <． ………………4分 ∴原不等式组的解集为<2x -． ………………5分朝阳区18. 解不等式组：⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x18. 解：原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式①，得 5<x . ………………………………………2分解不等式②，得 21>x .………………………………………………4分 ∴ 原不等式组的解集为521<<x . …………………………………5分① ②18．解不等式组：⎩⎪⎨⎪⎧x －32<1，2（x ＋1）≥x －1.18．解：由（1）得，x-3<2X<5 ……………………….2′（2）得 2x+2≥x-1x ≥-3 ……………………….4′所以不等式组的解是-3≤x ＜5……………………….5′ 门头沟区18. 解不等式组：1031+1.x x x ⎧-<⎪⎨⎪-⎩，≤3(）18．（本小题满分5分）解不等式①得，x ＜3， …………………………………………2分解不等式②得，x ≥﹣2， ………………………………4分所以，不等式组的解集是﹣2≤x ＜3． ………………5分大兴区17.解不等式组：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 并写出它的所有整数解. 17. 解：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 由①，得21-≥x . ………………………………………………………1分由②，得2<x . …………………………………………………………2分 ∴原不等式组的解集为221<≤-x . ………………………………………4分它的所有整数解为0，1. …………………………………………………5分① ②18．解不等式组3(1)45,513x x x x -≥-⎧⎪-⎨->⎪⎩，并写出它的所有整数解．．．． 18．解：3(1)455 3 1x x x x -≥-⎧⎪⎨-->⎪⎩①② 解不等式①，得 x ≤2． ·········································································1 解不等式②，得 x ＞-1． ·······································································3 ∴原不等式组的解集为12x -<≤． ························································4 ∴适合原不等式组的整数解为0,1,2． ·······················································5 怀柔区18.解不等式组:()⎪⎩⎪⎨⎧<+-<-.1213,213x x x x 18.解：由①得：3x < . ………………………………………………………………………2分由②得：9x >- …………………………………………………………………………4分原不等式组的解集为93x -<< ………………………………………………………5分延庆区18．解不等式组：523(2)53.2x x x x -<+⎧⎪⎨+≤⎪⎩，并写出它的所有整数解． 18．解：由①得，x <4． ……1分由②得，x ≥1 ． ……3分∴ 原不等式组的解集为1≤x <4． ……4分∴ 原不等式组的所有整数解为1，2，3． ……5分18．解不等式组：()7+1,2315 1.x x x x +⎧≥-⎪⎨⎪+<-⎩18．解不等式组：()7+12315x x x x +⎧≥-⎪⎨⎪+<-⎩解：解不等式①得 x ≥3- ……………………………………………………………2分解不等式②得 2x > ………………………………………………………………4分不等式组的解集是 2x > …………………………………………………………5分计算题专题东城区17．计算：()2012sin 60-π-2++1-3-⎛⎫︒ ⎪⎝⎭. =217.解：原式分分西城区17114sin 3015-⎛⎫+︒- ⎪⎝⎭．【解析】原式1541)52122=+⨯-=+=．海淀区17．计算：11()3tan 302|3-︒+． 17.解：原式=3323-⨯+- ………………4分=5- ………………5分丰台区1702cos 45(3π)|1-︒+-+-．1702cos 45(3π)|1︒+-+．=211++ ……………………4分= ……………………5分石景山区17．计算：012sin 455(3--++° 17．解：原式=2512⨯-+- ………………4分4=-- ………………5分朝阳区17. 计算：2sin30°+ .8)4()31(01+-+-π17. 解：原式 2213212+++⨯= …………………………………………………4分 225+=. ……………………………………………………………5分燕山区17．计算：4cos30°－12 + 20180 + ||1－317．4cos30°－12 + 20180 + ||1－3 =13132234-++-⨯=3 门头沟区17．计算：()201254sin 603π-⎛⎫--++-︒ ⎪⎝⎭．平谷区17．计算：(1013132sin 603-⎛⎫-+-︒ ⎪⎝⎭π.17．解：(1013132sin 603-⎛⎫-+--︒ ⎪⎝⎭π=331312-- ···········································································4 =1 ····································································································5 怀柔区17.计算：102130tan 3)3(31-︒⎪⎭⎫ ⎝⎛-+---π. 17.解：原式331132=--+ …………………………………………………4分.…………………………………………………………………5分延庆区17．计算：0113tan 301(2)()3π-︒+---．17．原式=3⨯33+3-1+1-3 ……4分=23-3 ……5分顺义区17．计算：()01312sin 452π--︒+-．17．解：()01312sin 452π--︒+-112132=-⨯+ (4)分13= ……………………………………………………………………………… 5分4=-解四边形专题东城区21．如图，已知四边形ABCD 是平行四边形，延长BA 至点E ，使AE = AB ，连接DE ，AC .（1）求证：四边形ACDE 为平行四边形;（2）连接CE 交AD 于点O . 若AC=AB =3，1cos 3B =，求线段CE 的长.21.(1) 证明：∵平行四边形ABCD ，∴=AB DC ，AB DC ∥.∵AB =AE ，∴=AE DC ，AE DC ∥.∴四边形ACDE 为平行四边形. -------------------2分(2) ∵=AB AC ，∴=AE AC .∴平行四边形ACDE 为菱形.∴AD ⊥CE .∵AD BC ∥，∴BC ⊥CE.在Rt △EBC 中，BE =6, 1cos 3BC B BE ==, ∴=2BC . 根据勾股定理，求得=42BC 分西城区21．如图，在ABD △中，ABD ADB ∠=∠，分别以点B ，D 为圆心，AB 长为半径在BD 的右侧作弧，两弧交于点C ，分别连接BC ，DC ，AC ，记AC 与BD 的交点为O ．（1）补全图形，求AOB ∠的度数并说明理由;（2）若5AB =，3cos 5ABD ∠=，求BD 的长．BDA【解析】（1）补全的图形如图所示．90AOB ∠=︒．证明：由题意可知BC AB =，DC AB =， ∵在ABD △中，ABD ADB ∠=∠， ∴AB AD =，∴BC DC AD AB ===， ∴四边形ABCD 为菱形， ∴AC BD ⊥， ∴90AOB ∠=︒．（2）∵四边形ABCD 为菱形， ∴OB OD =．在Rt ABO △中，90AOB ∠=︒，5AB =，3cos 5ABD ∠=，∴cos 3OB AB ABD =⋅∠=， ∴26BD OB ==．ABCDO海淀区21．如图，□ABCD 的对角线,AC BD 相交于点O ，且AE ∥BD ，BE ∥AC ，OE = CD . （1）求证：四边形ABCD 是菱形；（2）若AD = 2，则当四边形ABCD 的形状是__________时，四边形AOBE 的面积取得最大值是_______.C B EOAD21．（1）证明：∵AE BD ∥，BE AC ∥，∴四边形AEBO 是平行四边形. ………………1分 ∵四边形ABCD 是平行四边形，∴DC AB =. ∵OE CD =, ∴OE AB =.∴平行四边形AEBO 是矩形. ………………2分 ∴90BOA ∠=︒. ∴AC BD ⊥.∴平行四边形ABCD 是菱形. ………………3分 (2) 正方形； ………………4分2. ………………5分丰台区21．已知：如图，菱形ABCD ，分别延长AB ，CB 到点F ，E ，使得BF = BA ，BE = BC ，连接AE ，EF ，FC ，CA ．（1）求证：四边形AEFC 为矩形；（2）连接DE 交AB 于点O ，如果DE ⊥AB ，AB = 4，求DE 的长．ABCEDF21．（1）证明：∵BF =BA ，BE =BC ，∴四边形AEFC 为平行四边形. ………………………1分 ∵四边形ABCD 为菱形， ∴BA =BC .∴BE =BF .∴BA + BF = BC + BE ，即AF =EC .∴四边形AEFC 为矩形. ………………………2分（2）解：连接DB .由（1）知，AD ∥EB ，且AD =EB . ∴四边形AEBD 为平行四边形 ∵DE ⊥AB ，∴四边形AEBD 为菱形.∴AE =EB ，AB =2AG ，ED =2EG . ………………………4分 ∵矩形ABCD 中，EB =AB ，AB=4， ∴AG =2，AE =4.∴Rt △AEG 中，EG=23.∴ED=43. ………………………5分（其他证法相应给分）石景山区21．如图，在四边形ABCD 中，90A BCD ∠=∠=°，210BC CD ==，CE AD ⊥于点E ．（1）求证：AE CE =；（2）若tan 3D =，求AB 的长．BA CE D21．（1）证明：（法一）过点B 作BH ⊥CE 于H ，如图1． ∵CE ⊥AD ，∴∠BHC ＝∠CED ＝90°，190D ∠+∠=︒． ∵∠BCD ＝90°， ∴1290∠+∠=︒， ∴2D ∠=∠．又BC ＝CD∴BHC △≌CED △． ∴BH CE =．∵BH ⊥CE ，CE ⊥AD ，∠A ＝90°， ∴四边形ABHE 是矩形， ∴AE BH =．∴AE CE =． ………………3分（法二）过点C 作CH ⊥AB 交AB 的延长线于H ．图略，证明略．（2）解： ∵四边形ABHE 是矩形， ∴AB HE =．∵在Rt CED △中，tan 3CE D DE==,设,3DE x CE x ==，∴10210CD x ==． ∴2x =．∴2DE =,6CE =． ………………4分 ∵2CH DE ==．∴624AB HE ==-=． ………………5分朝阳区21. 如图，在△ABC 中，D 是AB 边上任意一点，E 是BC 边中点，过点C作AB 的平行线，交DE 的延长线于点F ，连接BF ，CD ．（1）求证：四边形CDBF 是平行四边形；（2）若∠FDB =30°，∠ABC =45°，BC =，求DF 的长．21.（1）证明：∵CF ∥AB ，∴∠ECF ＝∠EBD . ∵E 是BC 中点， ∴CE ＝BE .∵∠CEF ＝∠BED ， ∴△CEF ≌△BED . ∴CF ＝BD .∴四边形CDBF 是平行四边形. ………………………2分（2）解：如图，作EM ⊥DB 于点M ，∵四边形CDBF 是平行四边形，BC ＝24，∴2221==BC BE ，DE DF 2=. 在Rt △EMB 中，2sin =∠⋅=ABC BE EM . ……………………3分在Rt △EMD 中，42==EM DE . …………………4分∴DF ＝8. ………………………………………………………5分燕山区23．如图，在△ABC 错误!未找到引用源。

北京市各区2018届九年级中考一模数学试卷精选汇编：代数综合专题

朝阳区
20. 已知关于 x 的一元二次方程 x2 (k 1)x k 0 ．
（ 1）求证：方程总有两个实数根；
（ 2）若该方程有一个根是正数，求 k 的取值范围 .
20. （ 1）证明：依题意，得
(k 1)2 4k ………………… 1 分
(k 1)2. ………………………………… 2 分
∵ (k 1)2 0 ，
∴方程总有两个实数根 . ……………………… 3 分
（ 2）解：由求根公式，得 x1 1， x2
∵方程有一个根是正数，
∴ k 0. ∴ k 0 .……………………………… 5 分
k . ………………………… 4 分
3/ 7
∴
2
m
2
2mm .
3
(2) b2 4ac 12m 5 .
∵ m 0，
∴ 12m 0 .
∴
12m 5 0 .
………………３分 ………………４分
∴此方程有两个不相等的实数根 .
丰台区
20．已知：关于 x 的一元二次方程 x2 - 4x + 2m = 0 有两个不相等的实数根．（ 1）求 m 的取值范围；
当 m=0 时，方程为 x2 4 x 0 ，解得方程的根为 x1 0 ， x2 4 ，符合题意；当 m=1 时，方程为 x2 4 x 2 0 ，它的根不是整数，不合题意，舍去 .
综上所述， m=0.
……………………… 5 分
2/ 7
石景山区
20．关于 x的一元二次方程 mx 2 (3m 2) x 6 0 ．（ 1）当 m 为何值时，方程有两个不相等的实数根；（ 2）当 m 为何整数时，此方程的两个根都为负整数．
m3 m1

北京市各区2018届中考数学一模试卷精选汇编函数操作专题

C
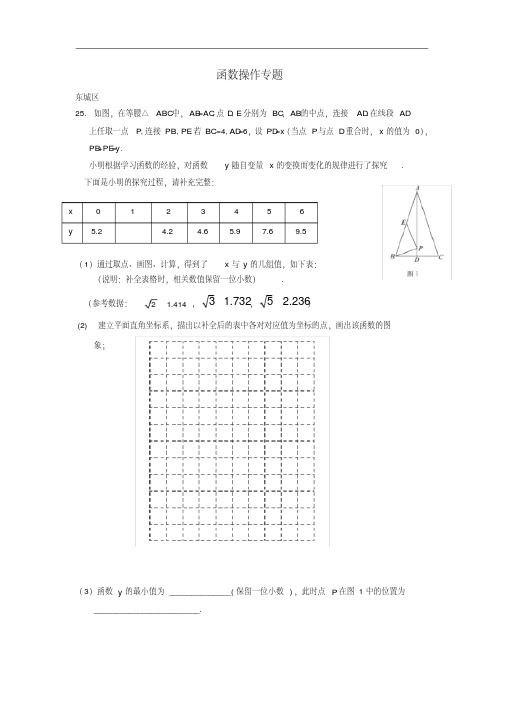
E
AD
B
小东根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行了探究．
下面是小东的探究过程，请补充完整：
（ 1）通过取点、画图、测量，得到了 x 与 y 的几组值，如下表：
（说明：补全表格时相关数值保留一位小数）（ 2）在下面的平面直角坐标系 xOy 中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
规律 .
（ 1）通过取点、画图、测量，得到了 x 与 y 的几组对应值，如下表：
x/cm
0
0.40
0.55
1.00
1.80
2.29
2.61
3
y/cm
2
3. 68
3.84
3.65
3.13
2.70
2
（ 2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的
图象；
（ 3）结合画出的函数图象，解决问题：点 F 与点 O重合时， DE长度约为
(3) 在画出的函数图象上标出 x=2 时所对应的点，并写出 m=
(4) 结合函数的图象，写出该函数的一条性质：
____________
．
3 26. 解： (1) 当自变量是 -2 时，函数值是 2
（ 2）如图 , 该函数的图象； ( 略)
………………………………… 1′ ………………………………… 3′
图5
（ 3） 2.42 ．
海淀区
25．在研究反比例函数
1 y 的图象与性质时，我们对函数解析式进行了深入分析
.
x
首先，确定自变量 x 的取值范围是全体非零实数，因此函数图象会被 y 轴分成两部分；其次，

北京市各区2018届中考数学一模试卷精选汇编压轴题专题(附答案)

压轴题专题东城区28．给出如下定义：对于⊙O的弦MN和⊙O外一点P（M，O，N三点不共线，且P，O在直线MN的异侧），当∠MPN ＋∠MON=180°时，则称点 P是线段MN关于点O的关联点．图1是点P为线段MN关于点O的关联点的示意图.在平面直角坐标系xOy中，⊙O的半径为1.（1）如图2，2222M⎛⎫⎪⎪⎝⎭，2222N⎛-⎝⎭.在A（1，0），B（1，1），)2,0C三点中, 是线段MN关于点O的关联点的是；（2）如图3， M（0，1），N312⎫-⎪⎪⎝⎭，点D是线段MN关于点O的关联点.①∠MDN的大小为°；②在第一象限内有一点E)3,m m，点E是线段MN关于点O的关联点，判断△MNE的形状，并直接写出点E的坐标；③点F在直线323y x=-+上，当∠MFN≥∠MDN时，求点F的横坐标Fx的取值范围．28. 解：（1）C ； --------------2分（2）① 60°；② △MNE 是等边三角形，点E 的坐标为)；--------------5分③ 直线32y x =+交 y 轴于点K （0，2），交x 轴于点()3T ，0. ∴2OK =，23OT =. ∴60OKT ∠=︒.作OG ⊥KT 于点G ,连接MG . ∵()M 0，1， ∴OM =1. ∴M 为OK 中点 . ∴ MG =MK =OM =1.∴∠MGO =∠MOG =30°，OG 3∴33.2G ⎫⎪⎪⎝⎭， ∵120MON ∠=︒, ∴ 90GON ∠=︒. 又3OG 1ON =， ∴30OGN ∠=︒. ∴60MGN ∠=︒.∴G 是线段MN 关于点O 的关联点. 经验证，点)31E，在直线32y =+上. 结合图象可知，当点F 在线段GE 上时，符合题意. ∵G F E x x x ≤≤， ∴33F x ≤分西城区28．对于平面内的⊙C 和⊙C 外一点Q ，给出如下定义：若过点Q 的直线与⊙C 存在公共点，记为点A ，B ，设AQ BQk CQ+=，则称点A （或点B ）是⊙C 的“k 相关依附点”，特别地，当点A 和点B 重合时，规定AQ BQ =，2AQ k CQ =（或2BQCQ）．已知在平面直角坐标系xOy 中，(1,0)Q -，(1,0)C ，⊙C 的半径为r ．（1）如图，当r =①若1(0,1)A 是⊙C 的“k 相关依附点”，则k 的值为__________．②2(1A 是否为⊙C 的“2相关依附点”．答：__________（填“是”或“否”）．（2）若⊙C 上存在“k 相关依附点”点M ， ①当1r =，直线QM 与⊙C 相切时，求k 的值．②当k r 的取值范围．（3）若存在r 的值使得直线3y x b =-+与⊙C 有公共点，且公共点时⊙C 3b 的取值范围．图1CyxO A 1A 2Q【解析】（12（2）①如图，当1r =时，不妨设直线QM 与⊙C 相切的切点M 在x 轴上方（切点M 在x 轴下方时同理），连接CM ，则QM CM ⊥，x∵(1,0)Q -，(1,0)C ，1r =， ∴2CQ =，1CM =，∴MQ = 此时23MQk CQ== ②如图，若直线QM 与⊙C 不相切，设直线QM 与⊙C 的另一个交点为N （不妨设QN QM <，点N ，M 在x 轴下方时同理），作CD QM ⊥于点D ，则MD ND =，x∴()222MQ NQ MN NQ NQ ND NQ DQ +=++=+=， ∵2CQ =， ∴2MQ NQ DQk DQ CQ CQ+===，∴当k 3DQ = 此时221CD CQ DQ -，假设⊙C 经过点Q ，此时2r =， ∵点Q 早⊙C 外，∴r 的取值范围是12r <≤．（3）33b <．海淀区28．在平面直角坐标系xOy 中，对于点P 和C ，给出如下定义：若C 上存在一点T 不与O 重合，使点P 关于直线OT 的对称点'P 在C 上，则称P 为C 的反射点．下图为C 的反射点P 的示意图．（1）已知点A 的坐标为(1,0)，A 的半径为2，①在点(0,0)O ，(1,2)M ，(0,3)N -中，A 的反射点是____________；②点P 在直线y x =-上，若P 为A 的反射点，求点P 的横坐标的取值范围；（2）C 的圆心在x 轴上，半径为2，y 轴上存在点P 是C 的反射点，直接写出圆心C 的横坐标x 的取值范围．28．解（1）①A 的反射点是M ，N ． ………………1分②设直线y x =-与以原点为圆心，半径为1和3的两个圆的交点从左至右依次为D ，E ，F ，G ，过点D 作⊥DH x 轴于点H ，如图．可求得点D 的横坐标为32．同理可求得点E ，F ，G 的横坐标分别为2232 点P 是A 的反射点，则A 上存在一点T ，使点P 关于直线OT 的对称点'P 在A 上，则'OP OP =.∵1'3≤≤OP ，∴13≤≤OP ．反之，若13≤≤OP ，A 上存在点Q ，使得OP OQ =，故线段PQ 的垂直平分线经过原点，且与A 相交．因此点P 是A 的反射点．∴点P 的横坐标x的取值范围是≤xx ．………………4分（2）圆心C 的横坐标x 的取值范围是44≤≤x -． ………………7分丰台区28．对于平面直角坐标系xOy 中的点M 和图形1W ，2W 给出如下定义：点P 为图形1W 上一点，点Q 为图形2W 上一点，当点M 是线段PQ 的中点时，称点M 是图形1W ，2W 的“中立点”．如果点P (x 1，y 1)，Q (x 2，y 2)，那么“中立点”M 的坐标为⎪⎭⎫⎝⎛++2,22121y y x x ．已知，点A (-3，0)，B (0，4)，C (4，0)．（1）连接BC ，在点D (12，0)，E (0，1)，F (0，12)中，可以成为点A 和线段BC 的“中立点”的是____________；（2）已知点G (3，0)，⊙G 的半径为2．如果直线y = - x + 1上存在点K 可以成为点A 和⊙G 的“中立点”，求点K 的坐标；（3）以点C 为圆心，半径为2作圆．点N 为直线y = 2x + 4上的一点，如果存在点N ，使得y 轴上的一点可以成为点N 与⊙C 的“中立点”，直接写出点N 的横坐标的取值范围．54411231213xOy6654327654326528．解：（1）点A 和线段BC（2）点A 和⊙G 的“中立点”在以点O 为圆心、半径为1的圆上运动. 因为点K 在直线y =- x +1上，设点K 的坐标为（x ，- x +1），则x 2+（- x +1）2=12，解得x 1=0，x 2=1.所以点K 的坐标为（0，1）或（1，0）. ………5分（3）（说明：点N 与⊙C 的“中立点”在以线段NC 的中点P 为圆心、半径为1的圆上运动.圆P 与y 轴相切时，符合题意.）所以点N 的横坐标的取值范围为-6≤x N ≤-2. ………8分石景山区28．对于平面上两点A ，B ，给出如下定义：以点A 或B 为圆心，AB 长为半径的圆称为点A ，B 的“确定圆”．如图为点A ，B 的“确定圆”的示意图．．．． AB（1）已知点A 的坐标为(1,0)-，点B 的坐标为(3,3)，则点A ，B 的“确定圆”的面积为_________；（2）已知点A 的坐标为(0,0)，若直线y x b =+上只存在一个点B ，使得点A ，B 的“确定圆”的面积为9π，求点B 的坐标；（3）已知点A 在以(0)P m ，为圆心，以1为半径的圆上，点B 在直线33y =+ 若要使所有点A ，B 的“确定圆”的面积都不小于9π，直接写出m 的取值范围．28．解：（1）25π； ………………… 2分（2）∵直线y x b =+上只存在一个点B ，使得点,A B 的“确定圆”的面积为9π，∴⊙A 的半径3AB =且直线y x b =+与⊙A 相切于点B ，如图， ∴AB CD ⊥，45DCA ∠=°．xy xy①当0b >时，则点B 在第二象限．过点B 作BE x ⊥轴于点E ，∵在Rt BEA ∆中，45BAE ∠=°，3AB =， ∴322BE AE ==．∴323222B -（，． ②当0b <时，则点'B 在第四象限．同理可得3232'22B -（．综上所述，点B 的坐标为323222-（，或323222-（． ………………… 6分（3）5m -≤或11m ≥． ………………… 8分朝阳区28. 对于平面直角坐标系xOy 中的点P 和线段AB ，其中A (t ，0)、B (t +2，0)两点，给出如下定义：若在线段AB 上存在一点Q ，使得P ，Q 两点间的距离小于或等于1，则称P 为线段AB 的伴随点．（1）当t =-3时，①在点P 1（1，1），P 2（0，0），P 3（-2，-1）中，线段AB 的伴随点是；②在直线y =2x +b 上存在线段AB 的伴随点M 、N ，且MN =b 的取值范围；（2）线段AB 的中点关于点（2，0）的对称点是C ，将射线CO 以点C 为中心，顺时针旋转30°得到射线l ，若射线l 上存在线段AB 的伴随点，直接写出t 的取值范围．28. 解：（1）①线段AB的伴随点是:23,P P. …………………2分②如图1，当直线y=2x+b经过点（-3，-1）时，b=5，此时b取得最大值.…………………………………………4分如图2，当直线y=2x+b经过点（-1，1）时，b=3，此时b取得最小值.……………………………………………5分∴b的取值范围是3≤b≤5. ……………………………………6分（2）t的取值范围是-12.2t≤≤…………………………………………8分燕山区28．在Rt△ABC中, ∠ACB=90°,CD是AB边的中线，DE⊥BC于E, 连结CD，点P在射线CB上（与B，C不重合）．（1）如果∠A=30°①如图1，∠DCB= °②如图2，点P在线段CB上，连结DP，将线段DP绕点D逆时针旋转60°，得到线段DF,连结BF，补全图2猜想CP、BF之间的数量关系，并证明你的结论；( 2 )如图3，若点P在线段CB的延长线上，且∠A=α（0°<α<90°），连结DP, 将线段DP绕点逆时针旋转α2得到线段DF,连结BF, 请直接写出DE、BF、BP三者的数量关系（不需证明）．图1图228.解：(1) ①∠DCB=60°…………………………………1′②补全图形CP=BF …………………………………3′△ DCP ≌△ DBF …………………………………6′（2）BF-BP=2DE ⋅tan α…………………………………8′门头沟区28. 在平面直角坐标系xOy 中，点M 的坐标为11(,)x y ，点N 的坐标为22(,)x y ，且12x x ≠，12y y =,我们规定：如果存在点P ，使MNP ∆是以线段MN 为直角边的等腰直角三角形，那么称点P 为点M 、N 的 “和谐点”. （1）已知点A 的坐标为)3,1(，①若点B 的坐标为)3,3(，在直线AB 的上方，存在点A ，B 的“和谐点”C ，直接写出点C 的坐标； ②点C 在直线x =5上，且点C 为点A ，B 的“和谐点”，求直线AC 的表达式.（2）⊙O 的半径为r ，点D (1,4)为点E (1,2)、F ),(n m 的“和谐点”，若使得△DEF 与⊙O 有交点，画出示意．．图直接．．．写出半径r 的取值范围.备用图1 备用图228．（本小题满分8分）解： (1)①)5,3()5,1(21C C 或. ……………………………………………2分②由图可知，B )3,5( ∵A (1,3) ∴AB =4∵ABC ∆为等腰直角三角形 ∴BC =4∴)1,5()7,5(21-C C 或设直线AC 的表达式为(0)y kx b k =+≠ 当)7,5(1C 时，⎩⎨⎧=+=+753b k b k ⎩⎨⎧==∴21b k2+=∴x y …………………………………3分当)1,5(2-C 时，⎩⎨⎧-=+=+153b k b k ⎩⎨⎧=-=∴41b k4+-=∴x y …………………………………4分 ∴综上所述，直线AC 的表达式是2+=x y 或4+-=x y(2)当点F 在点E 左侧时：大兴区28.在平面直角坐标系xOy 中，过y 轴上一点A 作平行于x 轴的直线交某函数图象于点D ，点P 是x 轴上一动点，连接D P ，过点P 作DP 的垂线交y 轴于点E （E 在线段OA 上，E 不与点O 重合），则称∠DPE 为点D ，P ,E 的“平横纵直角”.图1为点D ，P ,E 的“平横纵直角”的示意图.图图2如图2，在平面直角坐标系xOy 中，已知二次函数图象与y 轴交于点与x 轴分别交于点B （3-，(0,)F m ，0），C （12，0）. 若过点F 作平行于x 轴的直线交抛物线于点N .（1）点N 的横坐标为；（2）已知一直角为点,,N M K 的“平横纵直角”，若在线段OC 上存在不同的两点1M 、2M ，使相应的点1K 、2K 都与点F 重合，试求m 的取值范围；（3）设抛物线的顶点为点Q ，连接BQ 与FN 交于点H ,当4560QHN ︒≤≤︒∠时，求m 的取值范围． 28.（1）9 ………………………………………………………………… 1分（2）方法一:MK ⊥MN ，∴要使线段OC 上存在不同的两点M 1、M 2，使相应的点K 1、K 2都与点F 重合，也就是使以FN 为直径的圆与OC 有两个交点，即m r >．29=r ，29<∴m ．又0>m ， 290<<∴m ． ………………………………………………4分方法二：0>m ，∴点K 在x 轴的上方．过N 作NW ⊥OC 于点W ，设OM x =，OK y =，则 CW ＝OC －OW ＝3，WM ＝9x -．由△MOK ∽△NWM ，得，∴9y x x m=-． ∴x mx m y 912+-=．当m y =时，219m x x m m=-+，化为0922=+-m x x ．当△=0，即22940m -=，解得92m =时，线段OC 上有且只有一点M ，使相应的点K 与点F 重合．0>m ，∴ 线段OC 上存在不同的两点M 1、M 2，使相应的点K 1、K 2都与点F 重合时，m 的取值范围为290<<m ． ………………………………………………………………………………4分（3）设抛物线的表达式为：)12)(3(-+=x x a y (a ≠0)，又抛物线过点F （0，m ），a m 36-=∴．m a 361-=∴．m x m x x m y 1625)29(361)12)(3(3612+--=-+-=∴． …………………………………5分过点Q 做QG ⊥x 轴与FN 交于点RFN ∥x 轴∴∠QRH =90°tan BG BQG QG∠=，2516QG m =，152BG =∴，又4560QHN ︒≤∠≤︒，∴3045BQG ︒≤∠≤︒∴当30BQG ∠=︒时，可求出3524=m ，………………………………… 6分当45BQG ∠=︒时，可求出524=m ． ……………………………………7分m ∴的取值范围为2424355m ≤≤…………………………………8分平谷区28. 在平面直角坐标系xOy 中，点M 的坐标为()11,x y ，点N 的坐标为()22,x y ，且12x x ≠，12y y ≠，以MN 为边构造菱形，若该菱形的两条对角线分别平行于x 轴，y 轴，则称该菱形为边的“坐标菱形”. （1）已知点A （2,0），B （3，则以AB 为边的“坐标菱形”的最小内角为_______；（2）若点C （1,2），点D 在直线y =5上，以CD 为边的“坐标菱形”为正方形，求直线CD 表达式；（3）⊙O 2P 的坐标为(3,m ) .若在⊙O 上存在一点Q ，使得以QP 为边的“坐标菱形”为正方形，求m 的取值范围．28．解：（1）60； ····························· 1 （2）∵以CD 为边的“坐标菱形”为正方形， ∴直线CD 与直线y =5的夹角是45°．过点C 作CE ⊥DE 于E ．∴D （4,5）或()2,5-． ............. 3 ∴直线CD 的表达式为1y x =+或3y x =-+． (5)（3）15m ≤≤或51m -≤≤-． ···················7怀柔区28. P 是⊙C 外一点，若射线．．PC 交⊙C 于点A ，B 两点，则给出如下定义：若0＜PAPB≤3，则点P 为⊙C 的“特征点”．(1)当⊙O 的半径为1时．①在点P 1（2,0）、P 2（0,2）、P 3（4，0）中，⊙O 的“特征点”是； ②点P 在直线y=x+b 上，若点P 为⊙O 的“特征点”．求b 的取值范围；(2)⊙C 的圆心在x 轴上，半径为1，直线y=x+1与x 轴，y 轴分别交于点M ，N ，若线段MN 上的所有点都不是．．．⊙C 的“特征点”，直接写出点C 的横坐标的取值范围．yx–1–2–3–4–512345–1–2–3–4–512345O28.(1)①P 1（2,0）、P 2（0,2）…………………………………………………………………2分yxE Hy=x+b 2y=x+b1–1–2–3–41234–1–2–3–41234OD②如图，在y=x+b 上，若存在⊙O 的“特征点”点P ，点O 到直线y=x+b 的距离m≤2. 直线y=x+b 1交y 轴于点E ，过O 作OH ⊥直线y=x+b 1于点H. 因为OH=2，在Rt△DOE 中，可知OE=22. 可得b 1=22.同理可得b 2=-22.∴b 的取值范围是:22-≤b ≤22. …………………………………………………6分 (2)x>3或 3-<x . …………………………………………………………………………8分延庆区28．平面直角坐标系xOy 中，点1(A x ，1)y 与2(B x ，2)y ，如果满足120x x +=，120y y -=，其中12x x ≠，则称点A 与点B 互为反等点．已知：点C (3，4)（1）下列各点中，与点C 互为反等点； D (-3，-4)，E （3，4），F （-3，4）（2）已知点G （-5，4），连接线段CG ，若在线段CG 上存在两点P ，Q 互为反等点，求点P 的横坐标p x 的取值范围；（3）已知⊙O 的半径为r ，若⊙O 与（2）中线段CG 的两个交点互为反等点，求r 的取值范围．28．(1)F ……1分(2) -3≤p x ≤3 且p x ≠0 ……4分(3)4 < r≤5 ……7分顺义区点P 任意引出一条射线分别与1L 、2L 交于1Q 、2Q ，总有12PQ PQ 是定值，我们称曲线1L 与2L “曲似”，定值12PQ PQ 为“曲似比”，点P 为“曲心”．例如：如图2，以点O'为圆心，半径分别为1r 、2r （都是常数）的两个同心圆1C 、2C ，从点O'任意引出一条射线分别与两圆交于点M 、N ，因为总有12''r O M O N r =是定值，所以同心圆1C 与2C 曲似，曲似比为12r r ，“曲心”为O'．（1）在平面直角坐标系xOy 中，直线y kx =与抛物线2y x =、212y x =分别交于点A 、B ，如图3所示，试判断两抛物线是否曲似，并说明理由；（2）在（1）的条件下，以O 为圆心，OA 为半径作圆，过点B 作x 轴的垂线，垂足为C ，是否存在k 值，使⊙O 与图2C 2C 1N MO'直线BC 相切？若存在，求出k 的值；若不存在，说明理由；（3）在（1）、（2）的条件下，若将“212y x =”改为“21y x m=”，其他条件不变，当存在⊙O 与直线BC 相切时，直接写出m 的取值范围及k 与m 之间的关系式．28．（1）是．。

2018北京市中考数学一模分类27题二次函数及答案解析

2017年北京中考数学一模 27题“二次函数综合题”西城. 在平面直角坐标系xOy 中，二次函数5)12(2-++-=m x m mx y 的图象与x 轴有两个公共点. （1）求m 的取值范围；（2）若m 取满足条件的最小的整数，①写出这个二次函数的解析式；②当n ≤x ≤1时，函数值y 的取值范围是-6≤y ≤4-n ，求n 的值；③将此二次函数图象平移，使平移后的图象经过原点O . 设平移后的图象对应的函数表达式为k h x a y +-=2)(，当x ＜2时，y 随x 的增大而减小，求k 的取值范围东城．二次函数2(2)2(2)5y m x m x m =+-+-+，其中20m +>．（1）求该二次函数的对称轴方程；（2）过动点C (0, n )作直线l ⊥y 轴.① 当直线l 与抛物线只有一个公共点时, 求n 与m 的函数关系；② 若抛物线与x 轴有两个交点，将抛物线在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象. 当n =7时，直线l 与新的图象恰好有三个公共点，求此时m 的值；（3）若对于每一个给定的x 的值，它所对应的函数值都不小于1，求m 的取值范围．xy直线lCBA–1–21234–1–2–31234O朝阳．在平面直角坐标系中xOy 中，抛物线2211222y x mx m m =-++-的顶点在x 轴上．（1）求抛物线的表达式；（2）点Q 是x 轴上一点，①若在抛物线上存在点P ，使得∠POQ =45°，求点P 的坐标；②抛物线与直线y =2交于点E ，F （点E 在点F 的左侧），将此抛物线在点E ，F （包含点E 和点F ）之间的部分沿x 轴平移n 个单位后得到的图象记为G ，若在图象G 上存在点P ，使得∠POQ =45°，求n 的取值范围．房山. 在平面直角坐标系xOy 中，直线32-=x y 与y 轴交于点A ，点A 与点B 关于x 轴对称，过点B 作y 轴的垂线l ，直线l 与直线32-=x y 交于点C.（1）求点C 的坐标；（2）如果抛物线n nx nx y 542+-= (n ＞0)与线段BC 有唯一公共点，求n 的取值范围．顺义．如图，已知抛物线28(0)y ax bx a =++≠与x 轴交于A （-2，0），B 两点，与y 轴交于C点，tan ∠ABC =2．（1）求抛物线的表达式及其顶点D 的坐标；（2）过点A 、B 作x 轴的垂线，交直线CD 于点E 、F ，将抛物线沿其对称轴向上平移m 个单位，使抛物线与线段EF （含线段端点）只有1个公共点．求m 的取值范围．平谷．直线33y x =-+与x 轴，y 轴分别交于A ，B 两点，点A 关于直线1x =-的对称点为点C ．（1）求点C 的坐标；（2）若抛物线()230y mx nx m m =+-≠经过A ，B ，C 三点，求该抛物线的表达式；（3）若抛物线()230y ax bx a =++≠ 经过A ，B 两点，且顶点在第二象限，抛物线与线段AC 有两个公共点，求a 的取值范围．yx–2–112345–5–4–3–2–112O门头沟. 在平面直角坐标系xOy 中，抛物线()()13y a x x =+-与x 轴交于A ,B 两点，点A 在点B 的左侧，抛物线的顶点为P ,规定：抛物线与x 轴围成的封闭区域称为“G 区域”（不包含边界）.（1）如果该抛物线经过（1, 3），求a 的值，并指出此时“G 区域”有______个整数点；（整数点就是横纵坐标均为整数的点）（2）求抛物线()()13y a x x =+-的顶点P 的坐标（用含a 的代数式表示）；（3）在（2）的条件下，如果G 区域中仅有4个整数点时，直接写出a 的取值范围.海淀．平面直角坐标系xOy 中，抛物线2222y mx m x =-+交y 轴于A 点，交直线x =4于B 点．（1）抛物线的对称轴为x = （用含m 的代数式表示）；（2）若AB ∥x 轴，求抛物线的表达式；（3）记抛物线在A ，B 之间的部分为图象G （包含A ，B 两点），若对于图象G 上任意一点P （P x ，P y ），2P y ≤，求m 的取值范围．丰台．在平面直角坐标系xOy 中，抛物线()01242≠-+-=m m mx mx y 与平行于x 轴的一条直线交于A ，B 两点．（1）求抛物线的对称轴；（2）如果点A 的坐标是（-1，-2），求点B 的坐标；（3）抛物线的对称轴交直线AB 于点C ，如果直线AB 与y 轴交点的纵坐标为-1，且抛物线顶点D 到点C 的距离大于2，求m 的取值范围．石景山．在平面直角坐标系xOy 中，抛物线2443(0)y ax ax a a =-+-≠的顶点为A ．（1）求顶点A 的坐标；（2）过点(0,5)且平行于x 轴的直线l ，与抛物线 2443(0)y ax ax a a =-+-≠交于B ，C 两点． ①当2a =时，求线段BC 的长；②当线段BC 的长不小于6时，直接写出a 的取值范围．通州．在平面直角坐标系xOy 中，抛物线2222+-+-=m m mx x y 的顶点为D.线段AB 的两个端点分别为A （-3，m ），B （1，m ）.（1）求点D 的坐标（用含m 的代数式表示）；（2）若该抛物线经过点B （1，m ），求m 的值；（3）若线段AB 与该抛物线只有一个公共点，结合函数的图象，求m 的取值范围.怀柔．已知二次函数122-++=a ax axy （a>0）.（1）求证：抛物线与x 轴有两个交点；（2）求该抛物线的顶点坐标；（3）结合函数图象回答：当x ≥1时，其对应的函数值y 的最小值范围是2≤y ≤6，求a 的取值范围.西城.解：（1）∵ 二次函数5)12(2-++-=m x m mx y 的图象与x 轴有两个交点，∴≠0[]054122>)()+(---m m m解得 241->m 且m ≠0. ∴m 的取值范围是241->m 且m ≠0. ·············· 2分（2）①m 取满足条件的最小的整数，由（1）可知m =1.∴ 二次函数的表达式为234y x x =--. ··········· 3分② 图象的对称轴为直线23=x .当n ≤x ≤1＜32时，函数值y∵ 函数值y 的取值范围是-6≤y ∴ 当x =1时，函数值为- 6. 当x =n 时，函数值为4-n.∴ n 2– 3n - 4 = 4-n.，解得n ∴ n 的值为- 2.③由①可知，a =1.又函数图像经过原点，∴k =-h 2，∵当x ＜2时，y 随x 的增大而减小， ∴h ≥ 2 ∴k ≤-4.··································· 7分东城.解：（1）对称轴方程：2(2)12(2)m x m -+=-=+. …………1分（2）①∵直线l 与抛物线只有一个公共点,∴23n m =-+. …………3分 ② 依题可知：当237m -+=-时，直线l 与新的图象恰好有三个公共点. ∴5m =. …………5分（3）抛物线2(2)2(2)5y m x m x m =+-+-+的顶点坐标是(1,23)m -+.依题可得 20,23 1.m m +>⎧⎨-+≥⎩解得2,1.m m >-⎧⎨≤⎩∴ m 的取值范围是21m -<≤. …………7分朝阳．解：（1）222111-2()2222y x mx m m x m m =++-=-+-. 由题意，可得m -2=0． ∴2m =． ∴21(2)2y x =-．（2）①由题意得，点P 是直线y x =与抛物线的交点.∴21-222x x x =+. 解得 135x =+，235x =-. ∴P 点坐标为(35,35)++或 (35,35)--.②当E 点移动到点（2,2）时，n =2.当F 点移动到点（-2,2）时，n =-6. 由图象可知，符合题意的n 的取值范围是26-≤≤n .房山解：（1）∵直线y=2x-3与y 轴交于点A （0，-3） ------1分 ∴点A 关于x 轴的对称点为B （0，3），l 为直线y=3 ∵直线y=2x-3与直线l 交于点C ，∴点C 的坐标为（3，3） ------2分（2）∵抛物线n nx nx y 542+-= (n ＞0) ∴y = nx2-4nx+4n+n = n(x-2)2+n∴抛物线的对称轴为直线x=2，顶点坐标为（2，n ） ------3分 ∵点B （0，3），点C （3，3）①当n ＞3时，抛物线最小值为n ＞3，与线段BC 无公共点； ②当n=3时，抛物线顶点为（2，3），在线段BC 上，此时抛物线与线段BC 有一个公共点； ------4分 ③当0＜n ＜3时，抛物线最小值为n ，与直线BC 有两个交点如果抛物线y=n(x-2)2+ n 经过点B （0，3），则3=5n ，解得53=n由抛物线的对称轴为直线x=2，可知抛物线经过点（4，3）点（4，3）不在线段BC 上，此时抛物线与线段BC 有一个公共点B ------5分如果抛物线y=n(x-2)2+ n 经过点C （3，3），则3=2n ，解得23=n 由抛物线的对称轴为直线x=2，可知抛物线经过点（1，3）点（1，3）在线段BC 上，此时抛物线与线段BC 有两个公共点 ------6分综上所述，当53≤n ＜23或n=3时，抛物线与线段BC 有一个公共点. ------7分顺义27．解：（1）由抛物线的表达式知，点C （0，8），即 OC =8；Rt△OBC 中，OB =OC •tan∠ABC =8×12=4，则点B （4，0）． ………………………… 1分将A 、B 的坐标代入抛物线的表达式中，得：428016480a b a b -+=⎧⎨++=⎩，解得12a b =-⎧⎨=⎩， ∴抛物线的表达式为228y x x =-++．…… 3分∵2228(1)9y x x x =-++=--+ ，∴抛物线的顶点坐标为D （1，9）． ………… 4分（2）设直线CD 的表达式为y =kx +8,∵点D （1，9），∴直线CD 表达式为y =x +8．∵过点A 、B 作x 轴的垂线，交直线CD 于点E 、F ，可得：E （-2，6），F （4，12）． ………… 6分设抛物线向上平移m 个单位长度（m ＞0），则抛物线的表达式为：2(1)9y x m =--++；当抛物线过E （-2，6）时，m =6，当抛物线过F （4，12）时，m =12， ∵抛物线与线段EF （含线段端点）只有1个公共点，∴m 的取值范围是6<m ≤12． ………………………………………… 7分平谷27．解：（1）令y =0，得x =1．∴点A 的坐标为（1,0）． ······················ 1 ∵点A 关于直线x =﹣1对称点为点C ， ∴点C 的坐标为（﹣3,0）． ······ 2 （2）令x =0，得y =3．∴点B 的坐标为（0,3）． ∵抛物线经过点B ，∴﹣3m =3，解得m =﹣1． ······· 3 ∵抛物线经过点A ， ∴m+n ﹣3m =0，解得n =﹣2．∴抛物线表达式为223y x x =--+． ·· 4 （3）由题意可知，a <0．根据抛物线的对称性，当抛物线经过（﹣1,0）时，开口最小，a =﹣3， ·· 5 此时抛物线顶点在y 轴上，不符合题意.当抛物线经过（﹣3,0）时，开口最大，a =﹣1. ............. 6 结合函数图像可知，a 的取值范围为31a -<≤-. (7)门头沟27. （1）()()3a 1113=+- ……………1分解得：34a =-………………………2分 6个 ………………………3分（2）由()()y a 13x x =+-配方或变形()()()2y a 13=14x x a x a =+--- .所以顶点P 的坐标为（1，-4a ）. ……………………………………5分2132a --≤＜（3） a ＜0时，； ………………………………………6分a ＞0时， . 7分．m ；------- 2分（2）∵ 抛物线2222y mx m x =-+与y 轴交于A 点， ∴A （0，2）．------------------------------------------------------------------------------------- 3分∵ AB ∥x 轴，B 点在直线x =4上， ∴B （4，2），抛物线的对称轴为直线x =2.--------------------------------------------- 4分 ∴ m =2． ∴抛物线的表达式为2282y x x =-+． --------------------------------------------------- 5分（3）当0m >时，如图1．∵()02A ，，∴要使04P x ≤≤时，始终满足2P y ≤，只需使抛物线2222y mx m x =-+的对称轴与直线图112a ＜≤x=2重合或在直线x=2的右侧．∴2m ≥． -------------------------------------------- 6分当0m <时，如图2，m <时，2P y ≤恒成立． ------------------- 7分综上所述，0m <或2m ≥．丰台27. 解：（1）∵抛物线()12212422---=-+-=m x m m mx mx y ，∴对称轴为x = 2．…………………………………2分（2）①∵抛物线是轴对称图形，∴点A 点B 关于x = 2轴对称，∵A (﹣1，-2) ，∴B （5，-2）．……………………………………………3分②∵抛物线()12212422---=-+-=m x m m mx mx y ，∴顶点D （2，﹣2m -1）． …………………………………………………4分∵直线AB 与y 轴交点的纵坐标为-1，∴C （2，-1）． ……………………………………………………………5分∵顶点D 到点C 的距离大于2，∴﹣2m ﹣1 +1 > 2或﹣1+ 2m +1 > 2，∴m <﹣1或m > 1．………………………………………………………… 7分石景山27．解：（1）解法一： ∵2443y ax ax a =-+-2(2)3a x =--， ………………………………… 1分∴顶点A 的坐标为(2,3)-． ………………………………… 2分解法二：图2∵244(43)(4)2,324a a a a aa-⨯----==-，∴顶点A 的坐标为(2,3)-． ………………………………… 2分（2）①当2a =时，抛物线为2285y x x =-+，如图．令5y =，得22855x x -+=， ……………… 3分解得，1204x x ==，．……………… 4分∴线段BC 的长为4． ……………… 5分② 80<9a ≤． ……………… 7分通州27. 解：（1）D (m ，-m +2) （2）m =3或m =1 ……………………..(5分) （3）1≤m ≤3 ……………………..(7分)怀柔27．解：（1）令y=0.∴0122=-++a ax ax .∵△=)1(442--a a a=4a,……………………………1分 ∵a>0,∴4a>0.∴△>0.∴抛物线与x 轴有两个交点. …………………2分（2）212ax a=-=-.……………………………3分把x=-1代入122-++=a ax ax y .∴y=-1.∴顶点坐标（-1，-1）.…………………4分（3）①把（1,2）代入122-++=a ax ax y . ∴43=a .……………………………5分 ②把（1,6）代入122-++=a ax axy . ∴74a =.……………………………6分 ∴由图象可知：43≤a ≤74.……………………………7分 y xB x =2–1–2–3–4–512345–1–2–3–41234567CA (2,-3)O。

北京市各区2018届九年级中考一模数学试卷精选汇编：函数计算及运用专题(有答案)

函数计算及运用专题东城区22. 已知函数()30y x x=＞的图象与一次函数()20y ax a =-≠的图象交于点A ()3,n . （1）求实数a 的值；(2) 设一次函数()20y ax a =-≠的图象与y 轴交于点B.若点C 在y 轴上，且=2ABC AOB S S △△，求点C 的坐标.22.解：（1）∵点()3,A n 在函数()30y xx=＞的图象上， ∴=1n ，点()3,1A .∵直线()20y ax a =-≠过点()3,1A ， ∴ 321a -= .解得 1a =. ----------------------2分 (2)易求得()0,2B -.如图，12AOB A S OB x =⋅△，1=2ABC A S BC x ⋅△∵=2ABC AOB S S △△， ∴=24BC OB =.∴()10,2C ,或()20,6C -. ----------------------5分西城区22．如图，在平面直角坐标系xOy 中，直线y x m =+与x 轴的交点为0()4,A -，与y 轴的交点为B ，线段AB 的中点M 在函数ky x=（0k ≠）的图象上（1）求m ，k 的值;（2）将线段AB 向左平移n 个单位长度（0n >）得到线段CD ，A ，MB 的对应点分别为C ，N ，D ． ①当点D 落在函数ky x=（0x <）的图象上时，求n 的值． ②当MD MN ≤时，结合函数的图象，直接写出n 的取值范围．【解析】（1）如图．∵直线y x m =+与x 轴的交点为0()4,A -， ∴4m =．∵直线y x m =+与y 轴的交点为B ， ∴点B 的坐标为(0,4)B ． ∵线段AB 的中点为M ， ∴可得点M 的坐标为(2,2)M -． ∵点M 在函数ky x=（0k ≠）的图象上， ∴4k =-．（2）①由题意得点D 的坐标为(,4)D n -， ∵点D 落在函数ky x=（0k ≠）的图象上， ∴44n -=-，解得1n =．②n 的取值范围是2n ≥．海淀区22．在平面直角坐标系xOy 中，已知点P （2，2），Q （－1，2），函数my x=. （1）当函数my x=的图象经过点P 时，求m 的值并画出直线y x m =+．（2）若P ，Q 两点中恰有一个点的坐标（x ，y ）满足不等式组,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0），求m 的取值范围．22．解：（1）∵函数my x=的图象经过点()22P ，， ∴2=2m，即4m =． ………………1分图象如图所示. ………………2分（2）当点()22P ，满足,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0）时，解不等式组2222m m⎧>⎪⎨⎪<+⎩，得04m <<． ………………3分当点()12Q -，满足,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0）时，解不等式组221m m>-⎧⎨<-+⎩，得3m >． ………………4分∵P Q ，两点中恰有一个点的坐标满足,m y xy x m⎧>⎪⎨⎪<+⎩（m ＞0）， ∴m 的取值范围是：03m <≤，或4m ≥． ………………5分丰台区22．在平面直角坐标系xOy 中，反比例函数2y x=的图象与一次函数y kx b =+的图象的交点分别为 P(m ，2)，Q(-2，n). （1）求一次函数的表达式；（2）过点Q 作平行于y 轴的直线，点M 为此直线上的一点，当MQ = PQ 时，直接写出点M 的坐标.22．（1）解： ∵反比例函数2y x=的图象经过点(,2)P m ，Q(-2，n)， ∴1m =，1n =-．∴点P ，Q 的坐标分别为(1，2)，(-2，-1). …….…….…….……2分 ∵一次函数y kx b =+的图象经过点P(1，2)，Q(-2，-1)，∴2,2 1.k b k b +=⎧⎨-+=-⎩ 解得1,1.k b =⎧⎨=⎩ ∴一次函数的表达式为1y x =+． .…….…….…….……3分（2）点M 的坐标为（-2，-2，分石景山区22．在平面直角坐标系xOy 中，函数a y x=（0x >）的图象与直线1l y x b =+：交于点(3,2)A a -．（1）求a ，b 的值；（2）直线2l y x m =-+：与x 轴交于点B ，与直线1l 交于点C ，若S △ABC6≥，求m 的取值范围．22．解：（1）∵函数()0a y x x=>的图象过点()3,2A a -，∴23a a -=，解得3a =． ………………1分∵直线1l y x b =+：过点()3,1A ,∴2b =-． ………………2分（2）设直线2y x =-与x 轴交于点D ，则(2,0)D ，直线y x m =-+与x 轴交于点(,0)B m ，与直线y x b =+交于点22(,)22m m C +-． ①当S △ABC =S △BCD +S △ABD =6时，如图1. 可得211(2)(242m -+- 解得2m =-，8m =②当S △ABC =S △BCD -S △ABD =6时，如图2. 可得211(2)(2)1642m m ---⨯=，解得8m =，2m =-（舍）.综上所述，当8m ≥或2m -≤时，S△ABC6≥. ………………5分朝阳区22. 如图，在平面直角坐标系xOy 中，直线AB 与x 轴、y 轴分别交于点A 、B ，与反比例函数xky =的图象在第四象限交于点C ，CD ⊥x 轴于点D ，tan ∠OAB ＝2，OA ＝2，OD ＝1．（1）求该反比例函数的表达式；（2）点M 是这个反比例函数图象上的点，过点M 作MN ⊥y 轴，垂足为点N ，连接OM 、AN ，如果 S △ABN ＝2S △OMN ，直接写出点M 的坐标.22. 解：（1）∵AO ＝2，OD ＝1，∴AD ＝AO+ OD ＝3. ………………………………………………1分 ∵CD ⊥x 轴于点D ， ∴∠ADC ＝90°.在Rt △ADC 中，6tan =∠⋅=OAB AD CD ..∴C （1，－6）. ……………………………………………………2分 ∴该反比例函数的表达式是xy 6-=. ……………………………………3分（2）点M 的坐标为（－3,2）或（53，－10）. ……………………5分 ∴OM 27=215 OM=715∴⊙O 的半径是715…………………………………6′ 门头沟区20. 如图，在平面直角坐标系xOy 中，一次函数y x =与反比例函数k y x=（k ≠0）的图象相交于点)A a .（1）求a 、k 的值；（2）直线x=b （0b >）分别与一次函数y x =、反比例函数k y x=的图象相交于点M 、N ，当MN=2时,画出示意图并直接写出b 的值.20．（本小题满分5分）（1）∵直线y x =与双曲线ky x=（k ≠0）相)A a .∴a =1分 ∴A 3k =………………………2分（2）示意图正确………………………………3分 3b =或1 ………………………………5分大兴区22．如图，点A 是直线2y x =与反比例函数1m y x-=（m 为常数）的图象的交点．过点A 作x 轴的垂线，垂足为B ，且OB =2．（1）求点A 的坐标及m 的值；(2)已知点P (0，n) (0＜n ≤8) ，过点P 作平行于x 轴的直线，交直线2y x =于点C 11(,)x y , 交反比例函数1m y x-=（m 为常数）的图象于点D 22(,)x y ,交垂线AB 于点E 33(,)x y ,若231x x x <<，结合函数的图象，直接写出123++x x x 的取值范围．22．（1）解：由题意得，可知点A 的横坐标是2，……………………1分由点A 在正比例函数2y x =的图象上，∴点A 的坐标为（2，4）……………………………………2分又点A 在反比例函数1m y x-=的图象上，142m -∴=，即9m =．……………………………………… 3分（2）6<x 1+x 2+x 3≤7 ……………………………………………… 5分平谷区22．如图，在□ABCD 中，BF 平分∠ABC 交AD 于点F ，AE ⊥BF 于点O ，交BC 于点E ，连接EF ．（1）求证：四边形ABEF 是菱形；（2）连接CF ，若∠ABC=60°， AB= 4，AF =2DF ，求CF 的长．22．（1）证明：∵BF 平分∠ABC ，∴∠ABF=∠CBF ． (1)∵□ABCD ，∴AD ∥BC ． ∴∠AFB=∠CBF ． ∴∠ABF=∠AFB ． ∴AB=AF ． ∵AE ⊥BF ，∴∠ABF+∠BAO=∠CBF+∠BEO=90°． ∴∠BAO=∠BEO ． ∴AB=BE ． ∴AF=BE ．∴四边形ABEF 是平行四边形．∴□ABEF 是菱形． (2)（2）解：∵AD=BC ，AF=BE ，∴DF=CE ． ∴BE=2CE ． ∵AB=4，∴BE=4． ∴CE=2．过点A 作AG ⊥BC 于点G ． (3)∵∠ABC=60°，AB=BE ， ∴△ABE 是等边三角形． ∴BG=GE=2．∴AF=CG=4． ························ 4 ∴四边形AGCF 是平行四边形． ∴□AGCF 是矩形． ∴AG=CF ．在△ABG 中，∠ABC=60°，AB=4，∴AG=∴CF=怀柔区22．在平面直角坐标系xOy 中,一次函数y=kx+b 的图象与y 轴交于点B （0,1），与反比例函数xmy 的图象交于点A(3，-2).(1)求反比例函数的表达式和一次函数表达式；(2)若点C 是y 轴上一点，且BC=BA ，直接写出点C 的坐标.y x–1–2–3–4–512345–1–2–3–4–512345O22．(1)∵双曲线x m y =过A （3，-2），将A （3，-2）代入xmy =，解得：m= -6.∴所求反比例函数表达式为: y=x6-. …………………………………1分 ∵点A （3，-2）点B （0,1）在直线y=kx+b 上，∴-2=3k+1. …………………………………………………………………………………2分 ∴k=-1.∴所求一次函数表达式为y=-x+1. …………………………………………………………3分 (2)C(0，123+ )或 C(0，231- ). ……………………………………………………5分延庆区22．在平面直角坐标系xOy 中，直(0)y kx b k =+≠ 与x 轴交于点A ，与y 轴交于点B ，与反比例函数(0)my m x=≠的图象在第一象限交于点P （1，3），连接OP ．（1）求反比例函数(0)my m x=≠的表达式；（2）若△AOB 的面积是△POB 的面积的2倍，求直线y kx b =+的表达式．22．（1）3y x ……1分（2）如图22（1）：∵∴OA=2PE=2∴A（2,0） ……2分将A （2,0），P （1,3）代入y=kx+b可得∴ ……3分图22（1）∴直线AB 的表达式为：y=-3x+6同理：如图22（2）直线AB 的表达式为：y=x+2 ……4分综上：直线AB 的表达式为y=-3x+6或y=x+2 ……5分图22（2）顺义区22．如图，在平面直角坐标系xOy 中，直线24y x =+与双曲线ky x =（k ≠0）相交于A （-3，a ），B 两点．（1）求k 的值；（2）过点P （0，m ）作直线l ，使直线l 与y 轴垂直，直线l 与直线AB 交于点M ，与双曲线ky x =交于点N ，若点P 在点M 与点N 之间，直接写出m 的取值范围．22．解：（1）∵点A （-3，a ）在直线24y x =+上，∴2(3)42a =⨯-+=-．∴点A 的坐标为（-3，-2）． …………………………………… 1分 ∵点A （-3，-2）在双曲线ky x =上，∴23k-=-， ∴6k =． …………………………………… 3分（2）m 的取值范围是 04m <<． ……………………………… 5分。

(8)2018-2020年北京中考数学复习各地区模拟试题分类(8)——二次函数参考答案

（8）——二次函数参考答案与试题解析一．选择题（共2小题）1．【解答】解：由图象可得，该函数的对称轴x ＞18+542且x ＜54，∴36＜x ＜54，故选：C ．2．【解答】解：∵y ＝﹣n 2+14n ﹣24＝﹣（n ﹣2）（n ﹣12），1≤n ≤12且n 为整数，∴当y ＝0时，n ＝2或n ＝12，当y ＜0时，n ＝1，故选：D ．二．填空题（共5小题）3．【解答】解：（1）∵y ＝kx 2+（2k +1）x +1（k 为实数）．∴当x ＝﹣2时，y ＝4k +（2k +1）×（﹣2）+1＝﹣1，当x ＝0时，y ＝0+0+1＝1，∴对于任意实数k ，函数图象一定经过点（﹣2，﹣1）和点（0，1），故答案为：（0，1）；（2）∵k 为任意正实数，∴k ＞0，∴函数图象开口向上，∵函数y ＝kx 2+（2k +1）x +1的对称轴为x=−2k+12k =−1−12k ＜−1，∴在对称轴右侧，y 随x 的增大而增大，∵x ＞m 时，y 随x 的增大而增大，∴m ≥﹣1−12k ，故m ＝0时符合题意．（答案不唯一，m ≥﹣1即可）．故答案为：0．4．【解答】解：将点A 、B 、C 的坐标代入抛物线表达式得：−2=4a −2b +c c =33=9a +3b +c ，解得：a =−12b =32c =3，故抛物线y 1的表达式为：y 1=−12x 2+32x +3，顶点（32，338）；同理可得：y 2=−54x 2+154x +3，顶点坐标为：（32，9316）；y 3=−58x 2+54x +3，顶点坐标为（1，298）；y 4＝﹣x 2+2x +6，与y 轴的交点为：（0，6）；①由函数表达式知，四条抛物线的开口方向均向下，故正确，符合题意；②当x ＜0时，y 3随x 的增大而增大，故错误，不符合题意；③由顶点坐标知，抛物线y 1的顶点在抛物线y 2顶点的下方，错误，不符合题意；④抛物线y 4与y 轴的交点（0，6）在B 的上方，正确，符合题意．故答案为：①④．5．【解答】解：y ＝x 2﹣3x +2，答案不唯一．故答案为：y ＝x 2﹣3x +2，答案不唯一．6．【解答】解：符合的表达式是y ＝（x ﹣1）2，故答案为：（x ﹣1）2．7．【解答】解：y ＝3x 2+2＝3（x +0）2+2，所以将抛物线y ＝3（x +2）2﹣1先向右平移2个单位长度，再向上平移3个单位长度得到抛物线y ＝3x 2+2．故答案为：将抛物线y ＝3（x +2）2﹣1先向右平移2个单位长度，再向上平移3个单位长度得到抛物线y＝3x 2+2三．解答题（共32小题）8．【解答】解：（1）∵抛物线的对称轴是直线x ＝1，∴m 2=1，∴m ＝2，∴抛物线的解析式为y ＝﹣x 2+2x +3，令y ＝0，则﹣x 2+2x +3＝0，∴x ＝﹣1或x ＝3，∴A （﹣1，0），B （3，0），画出图象如图1所示；（2）∵P （m ，2），Q （﹣m ，2m ﹣1），当x ＝m 时，y ＝﹣m 2+m 2+3＝3，∴点P 在抛物线与x 轴围成的图象的内部，∵当x ＝﹣m 时，y ＝﹣m 2﹣m 2+3＝﹣2m 2+3，当m ≥0时，点P 在第一象限内，∴点P 在抛物线与x 轴围成的图象的内部，∴线段PQ 只有和在x ＝m 左侧的抛物线相交，∵抛物线与线段PQ 恰有一个公共点，∴﹣2m 2+3≤2m ﹣1，∴m ≤﹣2或m ≥1，∵m ≥0，∴m ≥1，当m ＜0时，点P 在第二象限内，∴点P 在抛物线与x 轴围成的图象的内部，∴线段PQ 只有和在x ＝m 右侧的抛物线相交，∵抛物线与线段PQ 恰有一个公共点，∴﹣2m 2+3≤2m ﹣1，∴m ≤﹣2或m ≥1，∵m ＜0，∴m ≤﹣2，即满足条件的m 的范围为m ≤﹣2或m ≥1．9．【解答】（1）x 取任意实数；故答案为：x 取任意实数；（2）把x ＝1代入y=12x 3﹣4x +1得，y=12−4+1=−52，故答案为：−52；（3）根据列表、描点、连线得出函数y=12x 3−4x +1的图象，所画的图象如图所示：（4）通过图象直观得出函数的图象与x 轴正半轴交点的横坐标．故答案为：0.3或2.7．10．【解答】解：（1）∵y＝x2﹣2ax+a2＝（x﹣a）2，∴顶点A（a，0）；（2）①当a＝0时，则抛物线y＝x2，如图所示，观察图形，可知：区域W内的整点个数是4；②如图所示：当抛物线经过（0，2），区域W内有1个整点；当抛物线经过（0，1），区域W内有3个整点；观察图形，可知：如果区域W 内有2个整点，a 的取值范围为−2＜a ≤﹣1．11．【解答】解：（1）∵抛物线y ＝ax 2+a 2x +c 与y 轴交于点（0，2），∴c 的值为2；（2）当a ＝2时，抛物线为y ＝2x 2+4x +2＝2（x +1）2，∴抛物线顶点的坐标为（﹣1，0）；（3）当a ＞0时，①当a ＝2时，如图1，抛物线与AB 只有一个交点；②当a ＝1+2时，如图2，抛物线与线段AB 有两个交点，结合函数图象可知：2＜a ≤1+2；当a ＜0时，抛物线与线段AB 只有一个交点或没有交点，综上所述，a 的取值范围为2＜a ≤1+2．12．【解答】解：（1）把m ＝3代入y ＝mx 2﹣3（m ﹣1）x +2m ﹣1中，得y ＝3x 2﹣6x +5＝3（x ﹣1）2+2，∴抛物线的顶点坐标是（1，2）．（2）当x ＝1时，y ＝m ﹣3（m ﹣1）+2m ﹣1＝m ﹣3m +3+2m ﹣1＝2．∵点A （1，2），∴抛物线总经过点A ．（3）∵点B （0，2），由平移得C （3，2）．①当抛物线的顶点是点A （1，2）时，抛物线与线段BC 只有一个公共点．由（1）知，此时，m ＝3．②当抛物线过点B （0，2）时，将点B （0，2）代入抛物线表达式，得2m ﹣1＝2．∴m=32＞0．此时抛物线开口向上（如图1）．∴当0＜m ＜32时，抛物线与线段BC 只有一个公共点．③当抛物线过点C （3，2）时，将点C （3，2）代入抛物线表达式，得9m ﹣9（m ﹣1）+2m ﹣1＝2．∴m ＝﹣3＜0．此时抛物线开口向下（如图2）．∴当﹣3＜m ＜0时，抛物线与线段BC 只有一个公共点．综上，m 的取值范围是m ＝3或0＜m ＜32或﹣3＜m ＜0．13．【解答】解：（1）∵抛物线y ＝x 2+2x +m +1＝（x +1）2+m ，∴抛物线的顶点（﹣1，m ），（2）∵抛物线经过点A （m ，m +1），∴m +1＝m 2+2m +m +1，解得m ＝0或﹣2，∴抛物线的解析式为y ＝x 2+2x +1或y ＝x 2+2x ﹣1．（3）当m ≥0时，如图1中，观察图象可知：m+1≤m2+2m+m+1≤m+3，∴m2+2m≥0且m2+2m﹣2≤0，解得0≤m≤﹣1+3．当m＜0时，如图2中，观察图象可知：m+1≤m2+2m+m+1≤m+3，∴m2+2m≥0且m2+2m﹣2≤0，解得﹣1−3≤m≤﹣2，综上所述，满足条件的m的值为：0≤m≤﹣1+3或﹣1−3≤m≤﹣2．14．【解答】解：（1）∵抛物线y＝ax2+bx﹣1交y轴于点P，∴点P（0，﹣1），∵PQ＝4，PQ∥x轴，∴点Q（4，﹣1），（﹣4，﹣1）当点Q为（4，﹣1），∴﹣1＝16a+4b﹣1，∴ba=−4，当点Q（﹣4，﹣1）∴﹣1＝16a﹣4b﹣1，∴ba=4；（2）当a＜0时，当抛物线过点（2，2）时，a=−34，当抛物线过点（2，3）时，a ＝﹣1，∴﹣1≤a ＜−34，当a ＞0时，当抛物线过点（2，﹣2）时，a=14，当抛物线过点（1，﹣2）时，a=13，∴14＜a ≤13；综上所述：14＜a ≤13或﹣1≤a ＜−34．15．【解答】解：（1）抛物线的对称轴为：x ＝2，故答案为：x ＝2；（2）解：∵抛物线的对称轴直线为x ＝2，∴顶点在1≤x ≤5范围内，∵y 的最小值是﹣1，∴顶点坐标为（2，﹣1）．∵a ＞0，开口向上，∴当x ＞2时，y 随x 的增大而增大，即x ＝5时，y 有最大值，∴把顶点（2，﹣1）代入y ＝ax 2﹣4ax +1，∴4a ﹣8a +1＝﹣1，解得a=12，∴y=12x 2﹣2x +1，∴当x ＝5时，y=72，即y 的最大值是72；（3）当x ＝﹣2时，P （﹣2，5），把P （﹣2，5）代入y ＝ax 2﹣4ax +1，∴4a +8a +1＝5，解得a=13，当x 1＝﹣1时，P （﹣1，4），把P （﹣1，4）代入y ＝ax 2﹣4ax +1，∴a +4a +1＝4，解得a=35，∴13≤a ＜35．16．【解答】解：（1）∵点A （﹣1，0）在抛物线y ＝ax 2+bx ﹣3a （a ≠0）上，∴a ﹣b ﹣3a ＝0，即b ＝﹣2a ，∴y ＝ax 2﹣2ax ﹣3a ＝a （x ﹣1）2﹣4a ，∴抛物线的顶点坐标为（1，﹣4a ）；（2）∵y ＝ax 2﹣2ax ﹣3a ＝a （x 2﹣2x ﹣3）＝a （x +1）（x ﹣3），∴抛物线与x 轴交于点A （﹣1，0），D （3，0），与y 轴交于点E （0，﹣3a ）．由题意得，点C （0，4），又∵B （3，4），如图，当a ＞0时，显然，抛物线与线段BC 无公共点，当a ＜0时，若抛物线的顶点在线段BC 上，则顶点坐标为（1，4），∴﹣4a ＝4，∴a ＝﹣1．若抛物线的顶点不在线段BC 上，由抛物线与线段BC 恰有一个公共点，得﹣3a ＞4，∴a ＜−43，综上，a 的取值范围是a ＜−43，或a ＝﹣1．17．【解答】解：（1）①当G 在原点下方时，b ＝﹣3，②当G 在原点上方时，(x −0)2+(x 2−b)2=3，整理得：x 4+（1﹣2b ）x 2+b 2﹣9＝0，△＝（1﹣2b ）2﹣4（b 2﹣9）＝0，解得：b=374（舍去），故答案为：﹣3；（2）如图1，作直线y＝x+3与x轴交于点B（﹣3，0），过点M作MN⊥BN交于点N，则MN的长度为所求值，则△BMN为等腰直角三角形，故MN=＝32，故点M（3，0）到直线y＝x+3的距离为32；（3）①当点N在直线BH和x＝2的交点下方时，如图2，作直线y＝x+4交x轴于点B，过点N作NH⊥BH于点H，过点N作MN∥x轴交直线BH于点M，则HN＝4，由（2）同理可知，△HMN为等腰直角三角形，MN=2HN＝42，故x M＝2﹣42，y M＝x M+4＝6﹣42=y N，故点N的坐标为：（2，6﹣42）；②当点N在直线BH和x＝2的交点上方时，同理可得：点N的坐标为：（2，6+42）；综上，点N的坐标为：（2，6﹣42）或（2，6+42）．18．【解答】解：（1）把点A（0，﹣4）和B（﹣2，2）分别代入y＝ax2+bx+c中，得c＝﹣4，4a﹣2b+c＝2．∴b＝2a﹣3；（2）当a＜0时，依题意抛物线的对称轴需满足−2a−32a≤−2，解得−32≤a＜0．当a＞0时，依题意抛物线的对称轴需满足−2a−32a≥0，解得0＜a ≤32．∴a 的取值范围是−32≤a ＜0或0＜a ≤32；（3）设直线AB 的表达式为：y ＝mx +n ，则n =−42=−2m +n ，解得：m =−3n =−4，故直线AB 表达式为y ＝﹣3x ﹣4，把C （m ，5）代入得m ＝﹣3．∴C （﹣3，5），由平移得D （1，5）．①当a ＞0时，若抛物线与线段CD 只有一个公共点（如图1），y ＝ax 2+bx +c ＝ax 2+（2a ﹣3）x ﹣4，当x ＝1时，y ＝3a ﹣7，则抛物线上的点（1，3a ﹣7）在D 点的下方，∴a +2a ﹣3﹣4＜5．解得a ＜4．∴0＜a ＜4；②当a ＜0时，若抛物线的顶点在线段CD 上，则抛物线与线段只有一个公共点（如图2），∴4ac−b 24a =5．即4a×(−4)−(2a−3)24a =5．解得a =−3+a =−3−综上，a 的取值范围是0＜a ＜4或a =−3−19．【解答】解：（1）当x ＝0时，则y=1m x 2﹣2x +1＝1，∴A （0，1），∵y=1m x 2﹣2x +1=1m (x −m)2+1−m ，∴B （m ，1﹣m ），故答案为（0，1）；（m ，1﹣m ）；（2）当m ＞0时，1﹣m ＜1，∴抛物线的对称轴在y 轴右边，顶点在y ＝4的下方，若抛物线与线段MN ×(−6)2−2×(−6)+1≥4×32−2×3+1＜4，解得，m ＞1；当m ＜0时，1﹣m ＞1，若1＜1﹣m ＜4，即﹣3＜m ＜0时，抛物线开口向下，顶点在直线y ＝4的下方，则抛物线与线段MN 无交点；若1﹣m ＝4，即m ＝﹣3时，抛物线的顶点在线段MN 上，此时抛物线与线段MN 只有一个公共点；若1﹣m ＞4，即m ＜﹣3时，抛物线的对称轴在直线x ＝﹣3的左边，顶点在直线y ＝4的上方，若抛物线与线段MN ×(−6)2−2×(−6)+1＞4×32−2×3+1≤4，解得，m ＜﹣4，综上，m ＜﹣4或m ＝﹣3或m ＞1．20．【解答】解：（1）①如图1，∵矩形ACBD 是点A ，B 的“相关矩形”，∴AD ∥CB ，∵点A （1，0），B （2，5），∴点C （2，0），BC ＝5，∴AC ＝2﹣1＝1，∴点A ，B 的“相关矩形”的周长为2（AC +BC ）＝2×（1+5）＝12；②如图2，∵点C 在直线x ＝3上，∴点C 的横坐标为3，∵点A （1，0），C 的“相关矩形”为正方形，∴BC ∥AD ，AB ＝BC ，∴点B 的坐标为（3，0），∴BC ＝AB ＝3﹣1＝2∴点C 的坐标为（3，2）或（3，﹣2），∵抛物线y ＝x 2+mx +n 经过点A 和点C ，∴1+m +n =09+3m +n =2或1+m +n =09+3m +n =−2∴m =−3n =2或m =−5n =4∴抛物线的解析式为y ＝x 2﹣3x +2或y ＝x 2﹣5x +4，令x ＝0，则y ＝0，或y ＝4∴点D 的坐标为（0，2）或（0，4）；（2）如图3，当点F 在y 轴的右侧时，点E 在点M 的右侧时，点E 的横坐标大，连接OM ，OF ，设OG ＝m ，∵点E ，F 的“相关矩形”为正方形，∴FM ＝ME ，∵点E 在直线y ＝3上，∴MG ＝3，在Rt △OGF 中，FG=OF 2−OG 2=16−m 2，∴点E 的横坐标为OG +ME ＝OG +MF ＝OG +MG +FG ＝OG +3+FG＝m+16−m 2+3＝（m ）2+16−m 2）2﹣2m 16−m 2+2m 16−m 2+3＝（m −16−m 2）2+2m 16−m 2+3≥2m 16−m 2+3（当且仅当m =16−m 2时，取等号），即m ＝22时，点E 的横坐标为（OG +ME ）最大＝（m+16−m 2）最大+3＝42+3，∴点E 的横坐标最大是42+3，由圆的对称性得，点E 的横坐标的最小值为﹣（42+3），即点E 的横坐标的范围是大于等于﹣（42+3）而小于等于（42+3）．21．【解答】解：（1）∵二次函数y ＝ax 2﹣2kx +k 2+k 图象的对称轴为直线x ＝k ，∴−−2k 2a =k ，∴a ＝1；（2）把a ＝1代入y ＝ax 2﹣2kx +k 2+k 得，y ＝x 2﹣2kx +k 2+k ，当x ＝k 时，y ＝k 2﹣2k 2+k 2+k ＝k ，∴顶点P （k ，k ）；（3）∵函数y ＝ax 2﹣2kx +k 2+k ＝x 2﹣2kx +k 2+k ＝（x ﹣k ）2+k ，∴抛物线的开口向上，抛物线的对称轴为x ＝k ，顶点为（k ，k ），∵点A （0，1），B （2，1），∴①当k ＞1时，抛物线的顶点在直线AB 的上方，抛物线与直线AB 没有公共点，则函数y ＝ax 2﹣2kx +k 2+k （k ﹣1≤x ≤k +1）的图象与线段AB 没有公共点；②当k ＝1时，顶点（1，1）在线段AB 上，即函数y ＝ax 2﹣2kx +k 2+k （k ﹣1≤x ≤k +1）的图象与线段AB恰有一个公共点；③当k ＜0时，则x ＝k +1或k ﹣1时，y ＝1+k ＜1，函数y ＝ax 2﹣2kx +k 2+k （k ﹣1≤x ≤k +1）的图象在线段AB 下方，没有公共点；④当k ＝0时，函数y ＝ax 2﹣2kx +k 2+k ＝x 2，与线段AB 恰有一个公共点（1，1）；⑤当0＜k ＜1时，若函数图象过A （0，1）时，k 2+k ＝1，解得k=0（舍去），或k=∵01，∴根据抛物线的对称性知，当−1+52≤k ＜1时，函数y ＝ax 2﹣2kx +k 2+k （k ﹣1≤x ≤k +1）的图象与线段AB 有两个公共点，当0＜k y ＝ax 2﹣2kx +k 2+k （k ﹣1≤x ≤k +1）的图象与线段AB 恰有一个公共点；综上所述：若函数y ＝ax 2﹣2kx +k 2+k （k ﹣1≤x ≤k +1）的图象与线段AB 恰有一个公共点，则0≤k 或k ＝1；22．【解答】解：（1）∵x 轴是图形l ，△PAB 是边长为2的等边三角形，∴P 点纵坐标为±3，y ＝x 上存在点（3，3）或（−3，−3）是x 轴的“美好点”，y=1x 上存在点（33，3）或（−−3）是x 轴的“美好点”y ＝x 2+2中y 的最小是2，∴y ＝x 2+2上不存在x 轴的“美好点”，故选A 、B ；（2）①∵M （3n ，0），N （0，n ），n ＞0，设直线MN 的解析式为y ＝kx +b ，则有b =n 0=3nk +b ，解得b =nk =−∴y=−+n ，如图1：∵M （3n ，0），N （0，n ），其中n ＞0，∴∠MNO ＝60°，∵△ABD 与△ACB 是边长为2的等边三角形，∴∠BAD ＝60°，∴AD ∥BC ∥y 轴，设过点C 与MN 平行的直线为y=+c ，过点D 与MN 平行的直线为y=+d ，当直线y=+c 与⊙O 相切时，c ＝4，∴n ＝4+2＝6，此时⊙O 上恰好存在1个直线MN 的“美好点”，如图2：当直线y=+d 与⊙O 相切时，d ＝4，∴n ＝4﹣2＝2，此时当直线y=−+c 经过原点O ，则c ＝0，∴此时⊙O 上恰好存在3个直线MN 的“美好点”，∴2＜n ＜6时，⊙O 上恰好存在2个直线MN 的“美好点”；②如图3：∵n ＝4，∴M （43，0），N （0，4），∴∠OMN ＝30°，设AB ＝2在圆O 上，C 与D 是MN 上的点，则△ABC与△ABD是边长为2的等边三角形，当MN与D点所在圆相切时，OD＝23，∴r＝2，此时线段MN上存在⊙O的“美好点”，如图4：当OC＝OM时，OC＝43，∴MH=3，AH＝1，∴OA＝219，此时线段MN上存在⊙O的“美好点”，∴2≤r≤219，线段MN上存在⊙O的“美好点”．23．【解答】解：（1）令y ＝0，即0＝ax 2﹣4ax ，解得x 1＝0，x 2＝4，∴A （0，0），B （4，0）．答：点A 、B 的坐标为：（0，0），（4，0）；（2）①设直线PC 解析式为y ＝kx +b ，将点C （2，1），P （1，−32a ）代入解得：k ＝1+32a ，b ＝﹣3a ﹣1，∴直线PC 解析式为y ＝（1+32a ）x ﹣3a ﹣1，当x ＝4时，y ＝3a +3，所以点Q 的纵坐标为3a +3．②∵当点Q 在B 上方或与点B 重合时，抛物线与线段PQ 恰有一个公共点，3a +3≥0，∴a ≥﹣1∴当a ＜0时，抛物线开口向下，抛物线只能与点Q 相交，∴﹣1≤a ＜0当a ＞0时，抛物线开口向上，只能与点P 相交，当x ＝1时，y=−32a ，y ＝﹣3a ，所以抛物线与点P 不相交．综上：a 的取值范围是：﹣1≤a ＜024．【解答】解：（1）根据题意量取数据m 为2.6，故答案为：2.6（2）根据已知数据描点连线得（3）①由图象可得，当0.8＜x ＜3.5时，y ＞2．故答案为：0.8＜x ＜3.5②不存在，理由如下：若BQ ＝BP∴∠BPQ ＝∠BQP∵∠BQP ＝∠APQ +∠PAQ ＞90°∴∠BPQ +∠BQP +∠QBP ＞180°与三角形内角和为180°相矛盾．∴不存在点P ，使得BQ ＝BP ．故答案为不存在．25．【解答】解：（1）观察对应数值表可知：m ＝0，（2）用平滑的曲线依次连接图中所描的点，如下图所示：（3）观察函数图象，发现该函数图象关于y 轴对称，（答案不唯一），故答案为：函数图象关于y 轴对称；（4）①∵函数的图象与x 轴有4个交点，∴方程x 4﹣5x 2+4＝0有4互不相等的实数根，故答案为4；②函数图象可知，当x 2＞x 1＞2时，y 1＜y 2；故答案为＜；③观察函数图象，结合对应数值表可知：﹣2.2＜a ＜4，故答案为：﹣2.2＜a ＜4．26．【解答】解：（1）根据顶点坐标公式得：x=−b 2a =−−2n 2n =1，y ＝n ﹣2n +n +2＝2；∴顶点D （1，2）；答：D 点坐标为（1，2）．（2）直线y ＝kx +b 经过点D （1，2）和点C （0，1），∴k +b =2b =1，解得：k ＝1，b ＝1；∴直线的解析式为y ＝x +1．答：直线CD 的解析式为y ＝x +1．（3）如图所示，∵x 1+x 2＝3，∴P 、Q 关于直线x=32对称，当t ＝1时，P 在C 处，即x 1＝0，∵x 1+x 2＝3，∴x 2＝3，∴Q （3，1），代入抛物线y ＝nx 2﹣2nx +n +2中得：9n ﹣6n +n +2＝1，n=−14，当t ＝﹣1时，y ＝﹣1＝x +1，即x 1＝﹣2，∵x 1+x 2＝3，∴x 2＝5，∴Q （5，﹣1），代入抛物线y ＝nx 2﹣2nx +n +2中得：25n ﹣10n +n +2＝﹣1，n=−316，∵抛物线的顶点不变，且开口向下，随Q 的移动开口大小不改变，答：n 的取值范围是：−14＜n ＜−316．27．【解答】解：（1）∵抛物线M ：y ＝ax 2﹣4ax +a ﹣1（a ≠0），∴抛物线的对称轴直线为：x=−b 2a =−−4a 2a =2．故答案为：x ＝2．（2）∵抛物线M ：y ＝ax 2﹣4ax +a ﹣1（a ≠0）的对称轴为直线，抛物线M 与x 轴的交点为点A ，点B ，（点A 在点B 的左侧），AB ＝2∴点A 、B 的坐标分别为（1，0），（3，0），∵点A 在抛物线M 上，∴将A 的坐标代入抛物线的函数表达式，得a ﹣4a +a ﹣1＝0，解得a=−12，∴抛物线M 的解析式为：y=−12x 2+2x −32，∴直线l 与y 轴的交点在y 轴的上方，∴b ＞2，k ＜0∵抛物线M 的解析式为：y=−12x 2+2x −32=−12（x ﹣2）2+12∴顶点坐标D 为（2，12）．（3）如图，由（2）知点D 的坐标为（2，12）．∵直y ＝n 与直线l 的交点横坐标记为x 3，（x 3＜4），且当﹣2≤n ≤﹣1时，总有x 1﹣x 3＜x 3﹣x 2＜0，∴可以得出x 1＜x 3x 3＜x 2，∵x 3＜4∴2＜x 3＜4当直线l ：y ＝kx +b （k ≠0）经过抛物线的顶点D （2，12）和（4，﹣2）时，2k +b =124k +b =−2，解得k=−54故k 的取值范围：k ＜−54．28．【解答】解：（1）抛物线y ＝ax 2﹣2a 2x 的对称轴是直线x =−−2a 22a=a ，∴点P 的坐标是（a ，0）；（2）由题意可知图形M 为线段AB ，A （﹣1，3），B （3，0）．当抛物线经过点A 时，解得a =−32或a ＝1；当抛物线经过点B 时，解得a =32．……………………………………………………（3分）如图1，当a =−32时，抛物线与图形M 恰有一个公共点．如图2，当a ＝1时，抛物线与图形M 恰有两个公共点．如图3，当a =32时，抛物线与图形M 恰有两个公共点．结合函数的图象可知，当a ≤−32或0＜a ＜1或a ＞32时，抛物线与图形M 恰有一个公共点．29．【解答】解：（1）∵抛物线y ＝mx 2+2mx ﹣3（m ＞0）的顶点D 的纵坐标是﹣4，∴−12m−4m 24m =−4，解得m ＝1，∴y ＝x 2+2x ﹣3，令y ＝0，则x ＝﹣3或1，∴A （﹣3，0）B （1，0）；（2）∵y ＝x 2+2x ﹣3＝（x +1）2﹣4，∴抛物线的对称轴为x ＝﹣1，∵点C （0，﹣3）关于抛物线的对称轴的对称点坐标是E （﹣2，﹣3），点A （﹣3，0）关于该抛物线的对称轴的对称点坐标是B （1，0），设直线的表达式为y ＝kx +b ，∵点E （﹣2，﹣3）和点B （1，0）在直线上∴−2k +b =−3k +b =0，解得k =1b =−1，∴直线的表达式为y ＝x ﹣1；（3）由对称性可知x 1+x 22=−1，∴x 1+x 2＝﹣2，∵x 1＜x 3＜x 2，∴﹣2＜x 3＜1，∴﹣4＜x 1+x 2+x 3＜﹣1．30．【解答】解：（1）函数的对称轴为：x=−b 2a=m ；（2）函数对称轴为x ＝m ，函数开口向上，x ＝m 时函数取得最小值，故：y 3＞y 1＞y 2；（3）把点A 的坐标代入y ＝﹣x +b 的表达式并解得：b ＝3，则点B （0，3），直线表达式为：y ＝﹣x +3，当y ＝3时，y ＝x 2﹣2mx +m 2﹣1＝3，则x ＝m ±2，则点P （m +2，3），当△OAP 为钝角三角形时，则m +2＜0或m +2＞3，解得：m ＜﹣2或m ＞1．31．【解答】解：（1）∵y ＝x 2﹣2ax +a 2+2＝（x ﹣a ）2+2，∴抛物线顶点C 的坐标为（a ，2）．（2）∵1＞0，∴抛物线开口向上，又∵点C （a ，2）到直线l 的距离为2，直线l 垂直于y 轴，且与抛物线有交点，∴直线l 的解析式为y ＝4．当y ＝4时，x 2﹣2ax +a 2+2＝4，解得：x 1＝a −2，x 2＝a+2，∴点E 的坐标为（a −2，4），点F 的坐标为（a+2，4），∴EF ＝a+2−（a −2）＝22．（3）当y ＝t 时，x 2﹣2ax +a 2+2＝t ，解得：x 1＝a −t −2，x 2＝a+t −2，∴EF ＝2t −2．又∵存在实数m ，使得x 1≥m ﹣1且x 2≤m +5成立，∴t −2＞02t −2≤6，解得：2＜t ≤11．32．【解答】解：（1）∵抛物线y ＝ax 2+bx +c （a ＞0）经过点A （0，﹣3）和B （3，0）．∴−3=c 0=9a +3b +c ，∴c ＝﹣3，3a +b ﹣1＝0．（2）由1可得：y ＝ax 2+（1﹣3a ）x ﹣3，对称轴为x=−1−3a 2a ，∵抛物线在A 、B 两点间从左到右上升，当a ＞0时，对称轴在A 点左侧，如图：即：−1−3a 2a ≤0，解得：a ≤13，∴0＜a ≤13．A 、B 两点间从左到右上升，∴当0＜a ≤13时，抛物线在A 、B 两点间从左到右上升，（3）抛物线不能同时经过点M （﹣1+m ，n ）、N （4﹣m ，n ）．理由如下：若抛物线同时经过点M （﹣1+m ，n ）、N （4﹣m ，n ）．则对称轴为：x =(−1+m)+(4−m)2=32，由抛物线经过A 点可知抛物线经过（3，﹣3），与抛物线进过B （3，0）相矛盾，故：抛物线不能同时经过点M （﹣1+m ，n ）、N （4﹣m ，n ）33．【解答】解：（1）∵y ＝kx ﹣4k +4＝k （x ﹣4）+4，即k （x ﹣4）＝y ﹣4，而k 为任意实数，∴x ﹣4＝0，y ﹣4＝0，解得x ＝4，y ＝4，∴直线过定点（4，4）；（2）当k=−12时，直线解析式为y=−12x +6，解方程组y =−12x +6y =14x 2−x 得x =−4y =8或x =6y =3，则A （6，3）、B （﹣4，8）；①如图1，作PQ ∥y 轴，交AB 于点Q ，设P （x ，14x 2﹣x ），则Q （x ，−12x +6），∴PQ ＝（−12x +6）﹣（14x 2﹣x ）=−14（x ﹣1）2+254，∴S △P AB =12（6+4）×PQ=−54（x ﹣1）2+1254=20，解得x 1＝﹣2，x 2＝4，∴点P 的坐标为（4，0）或（﹣2，3）；②设P （x ，14x 2﹣x ），如图2，由题意得：AO ＝35，BO ＝45，AB ＝55，∵AB 2＝AO 2+BO 2，∴∠AOB ＝90°，∵∠AOB ＝∠PCO ，∴当CP CO =OA OB 时，△CPO ∽△OAB ，即|14x 2−x||x|=35，整理得4|14x 2﹣x |＝3|x |，解方程4（14x 2﹣x ）＝3x 得x 1＝0（舍去），x 2＝7，此时P 点坐标为（7，214）；解方程4（14x 2﹣x ）＝﹣3x 得x 1＝0（舍去），x 2＝1，此时P 点坐标为（1，−34）；当CP OC =OB OA 时，△CPO ∽△OBA ，即|14x 2−x||x|=45，整理得3|14x 2﹣x |＝4|x |，解方程3（14x 2﹣x ）＝4x 得x 1＝0（舍去），x 2=283，此时P 点坐标为（283，1129）；解方程3（14x 2﹣x ）＝﹣4x 得x 1＝0（舍去），x 2=−43，此时P 点坐标为（−43，169）综上所述，点P 的坐标为：（7，214）或（1，−34）或（−43，169）或（283，1129）．34．【解答】（1）证明：△＝（5﹣m ）2﹣4×（﹣1）（6﹣m ）＝m 2﹣14m +49＝（m ﹣7）2≥0，∴该抛物线与x 轴总有交点；（2）解：由（1）△＝（m ﹣7）2，根据求根公式可知，方程的两根为：x =m−5±(m−7)2−2，即x 1＝﹣1，x 2＝﹣m +6，由题意，有3＜﹣m +6＜5，∴1＜m ＜3；（3）解：令x ＝0，y ＝﹣m +6，∴M （0，﹣m +6），由（2）可知抛物线与x 轴的交点为（﹣1，0）和（﹣m +6，0），它们关于直线y ＝﹣x 的对称点分别为（0，1）和（0，m ﹣6），由题意，可得：﹣m +6＝1或﹣m +6＝m ﹣6，∴m ＝5或m ＝6．35．【解答】解：（1）∵二次函数y ＝ax 2﹣2ax ﹣2（a ≠0），∴该二次函数图象的对称轴是直线x=−−2a 2a =1，故答案为：x ＝1；（2）∵该二次函数的图象开口向上，对称轴为直线x ＝1，﹣1≤x ≤5，∴当x ＝5时，y 取得最大值，即M （5，112），∴112=a ×52−2a ×5−2，得a=12，∴该二次函数的表达式为y ＝ax 2﹣2ax ﹣2＝a （x ﹣1）2﹣a ﹣2=12（x ﹣1）2−52，即点N 的坐标为（1，−52）．（3）当a ＞0时，该函数的图象开口向上，对称轴为直线x ＝1，无法保证t ≤x 1≤t +1，当x 2≥3时，具有y 1≥y 2；当a ＜0时，该函数的图象开口向下，对称轴为直线x ＝1，∵t ≤x 1≤t +1，当x 2≥3时，具有y 1≥y 2，点A （x 1，y 1）B （x 2，y 2）在该函数图象上，∴t +1≤3t ≥1−(3−1)，∴﹣1≤t ≤2．36．【解答】解：（1）∵抛物线y ＝ax 2+4x +c （a ≠0）经过点A （3，﹣4）和B （0，2），可得：9a +12+c =−4c =2解得：a =−2c =2∴抛物线的表达式为y ＝﹣2x 2+4x +2．∵y ＝﹣2x 2+4x +2＝﹣2（x ﹣1）2+4，∴顶点坐标为（1，4）；（2）设点B （0，2）关于x ＝3的对称点为B ′，则点B ′（6，2）．若直线y ＝kx +b 经过点C （9，4）和B '（6，2），可得b ＝﹣2．若直线y ＝kx +b 经过点C （9，4）和A （3，﹣4），可得b ＝﹣8．直线y ＝kx +b 平行x 轴时，b ＝4．综上，﹣8＜b ＜﹣2或b ＝4．37．【解答】解：（1）根据题意得△＝（﹣4）2﹣4（2m ﹣1）＞0，解得m ＜52；（2）m 的最大整数为2，抛物线解析式为y ＝x 2﹣4x +3，当y ＝0时，x 2﹣4x +3＝0，解得x 1＝1，x 2＝3，所以A （1，0），B （3，0）．38．【解答】解：∵抛物线y ＝x 2﹣2ax +b 的顶点在x 轴上，∴4b−(−2a)24=0，∴b ＝a 2．（1）∵a ＝1，∴b ＝1，∴抛物线的解析式为y ＝x 2﹣2x +1．①∵m ＝b ＝1，∴x 2﹣2x +1＝1，解得：x 1＝0，x 2＝2．②设平移后的抛物线为y ＝（x ﹣1）2+k ．∵抛物线的对称轴是x ＝1，平移后与x 轴的两个交点之间的距离是4，∴（3，0）是平移后的抛物线与x 轴的一个交点，∴（3﹣1）2+k ＝0，即k ＝﹣4，∴变化过程是：将原抛物线向下平移4个单位．（2）∵x 2﹣2ax +a 2＝m ，解得：x 1＝a −m ，x 2＝a+m ，∴PQ ＝2m ．又∵x 1≤c ﹣1，x 2≥c +7，∴2m ≥（c +7）﹣（c ﹣1）＝8，∴m ≥16．39．【解答】解：（1）①∵OE=12+12=2，OF==1，OM=22+22=22，∴点F 在⊙上，而点F 的横坐标和纵坐标相等∴⊙O 的“梦之点”为点F ；故答案为F 点；②∵⊙O 的半径为1．∴⊙O 的“梦之点”坐标为（−−）和（22，22），又∵双曲线y=k x （k ≠0）与直线y ＝x 的交点均为双曲线的“梦之点”，∴将（−−k=−（=12，∵点P 位于⊙O 内部．∴0＜k ＜12；（2）设P （x ，x ），∵点C 的坐标为（1，t ），⊙C 的半径为2，∴（x ﹣1）2+（x ﹣t ）2＝2，整理得2x 2﹣2（t +1）x +t 2﹣1＝0，∵△＝4（t +1）2﹣4•2•（t 2﹣1）≥0，∴﹣1≤t ≤3；（3）由“梦之点”定义可得：A （x 1，x 1），B （x 2，x 2）．则x ＝ax 2﹣ax +1．整理得ax 2﹣（a +1）x +1＝0解得x 1＝1，x 2=1a ，把两个根代入|x 1﹣x 2|＝2中得|1−1a |＝2，解得，a 1＝﹣1，a 2=13，当a ＝﹣1时，y ＝﹣x 2+x +1＝﹣（x −12）2+54，其顶点坐标为（12，54）；当a=13时，y=13x 2−13x +1=13（x −12）2+1112，其顶点坐标为（12，1112）．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

二次函数综合专题东城区26．在平面直角坐标系xOy 中，抛物线()02342≠-+-=a a ax ax y 与x 轴交于A ，B 两点（点A 在点B 左侧）．（1）当抛物线过原点时，求实数a 的值；（2）①求抛物线的对称轴；②求抛物线的顶点的纵坐标（用含a 的代数式表示）；（3）当AB ≤4时，求实数a 的取值范围．26.解：(1) ∵点()0,0O 在抛物线上，∴320a -=，23a =.--------------------2分(2)①对称轴为直线2x =；②顶点的纵坐标为 2a --.--------------------4分 (3) （i ）当0a ＞时，依题意，-20320.a a -⎧⎨-⎩＜，≥解得2.3a ≥（ii ）当0a ＜时，依题意，-20320.a a -⎧⎨-⎩＞，≤解得a ＜-2.综上，2a -＜，或23a ≥. --------------------7分西城区26.在平面直角坐标系xOy 中，抛物线G ：221(0)y mx mx m m =++-≠与y 轴交于点C ，抛物线G 的顶点为D ，直线：1(0)y mx m m =+-≠．（1）当1m =时，画出直线和抛物线G ，并直接写出直线被抛物线G 截得的线段长．（2）随着m 取值的变化，判断点C ，D 是否都在直线上并说明理由．（3）若直线被抛物线G 截得的线段长不小于2，结合函数的图象，直接写出m 的取值范围．x【解析】（1）当1m =时，抛物线G 的函数表达式为22y x x =+，直线的函数表达式为y x =，直线被抛物线Gx（2）∵抛物线G ：221(0)y mx mx m m =++-≠与y 轴交于点C ， ∴点C 的坐标为(0,1)C m -，∵2221(1)1y mx mx m m x =++-=+-， ∴抛物线G 的顶点D 的坐标为(1,1)--，对于直线：1(0)y mx m m =+-≠，当0x =时，1y m =-，当1x =-时，(1)11y m m =⨯-+-=-， ∴无论m 取何值，点C ，D 都在直线上．（3）m的取值范围是m ≤m ．海淀区26．在平面直角坐标系xOy 中，已知抛物线22y x ax b =-+的顶点在 x 轴上，1(,)P x m ，2(,)Q x m （12x x <）是此抛物线上的两点．（1）若1a =，①当m b =时，求1x ，2x 的值；②将抛物线沿y 轴平移，使得它与x 轴的两个交点间的距离为4，试描述出这一变化过程；（2）若存在实数c ，使得11x c ≤-，且27x c ≥+成立，则m 的取值范围是．26．解：抛物线22y x ax b =-+的顶点在x 轴上，24(2)04b a --∴=.2b a ∴=. ………………1分（1）1a =，1b ∴=.∴抛物线的解析式为221y x x =-+.①1m b ==，2211x x ∴-+=，解得10x =，22x =. ………………2分②依题意，设平移后的抛物线为2(1)y x k =-+.抛物线的对称轴是1x =，平移后与x 轴的两个交点之间的距离是4，∴(3,0)是平移后的抛物线与x 轴的一个交点.2(31)0k ∴-+=，即4k =-.∴变化过程是：将原抛物线向下平移4个单位. ………………4分（2）16m ≥. ………………6分丰台区26．在平面直角坐标系xOy 中，抛物线243y ax ax a =-+的最高点的纵坐标是2．（1）求抛物线的对称轴及抛物线的表达式；（2）将抛物线在1≤x ≤4之间的部分记为图象G 1，将图象G 1沿直线x = 1翻折，翻折后的图象记为G 2，图象G 1和G 2组成图象G ．过(0，b )作与y 轴垂直的直线l ，当直线l 和图象G 只有两个公共点时，将这两个公共点分别记为P 1(x 1，y 1)，P 2(x 2，y 2)，求b 的取值范围和x 1 + x 2的值．)22a -，∴对称轴为x = 2．………………………………………1分 ∵抛物线最高点的纵坐标是2，∴a = -2． ………………………………………2分∴抛物线的表达式为2286y x x =-+-. ……………3分（2）由图象可知，2b = 或-6≤b <0.………………6分由图象的对称性可得：x 1+x 2=2． ……………… 7分石景山区26．在平面直角坐标系xOy 中，将抛物线21G y mx =+：（0m ≠位长度后得到抛物线2G ，点A 是抛物线2G 的顶点．xy（1）直接写出点A 的坐标；（2）过点0（且平行于x 轴的直线l 与抛物线2G 交于B ，C 两点．①当=90BAC ∠°时，求抛物线2G 的表达式；②若60120BAC <∠<°°，直接写出m 的取值范围．26．解:（1）()A. ………………………………… 2分（2）①设抛物线2G的表达式为2(y m x =-+，如图所示，由题意可得AD ==∵=90BAC ∠°，AB AC =， ∴=45ABD ∠︒.∴BD AD ==∴点B的坐标为. ∵点B 在抛物线2G 上，可得3m =.∴抛物线2G的表达式为23y x =-+，即223y x x =-+ ………………… 5分②m <<-. ………………… 7分朝阳区26. 在平面直角坐标系xOy 中，抛物线()2440y ax ax a =--≠与y 轴交于点A ，其对称轴与x 轴交于点B . （1）求点A ，B 的坐标；（2）若方程()244=00ax ax a --≠有两个不相等的实数根，且两根都在1，3之间（包括1，3），结合函数的图象，求a 的取值范围.26.解：（1）44)2(4422---=--=a x a ax ax y ．∴A （0，－4），B （2，0）．……………………………………2分（2）当抛物线经过点（1，0）时，34-=a ．…………………… 4分当抛物线经过点（2，0）时，1-=a ． …………………………6分结合函数图象可知，a 的取值范围为134<≤-a ．……………… 7分燕山区24．如图，在平面直角坐标系中，直线l : y=kx+k (k ≠0)与x 轴,y 轴分别交于A,B 两点，且点B(0,2)，点P 在y 轴正半轴上运动，过点P 作平行于x 轴的直线y=t ．（1）求 k 的值和点A 的坐标；（2）当t=4时，直线y=t 与直线l 交于点M ，反比例函数xny =（n ≠0）的图象经过点M ，求反比例函数的解析式； (3)当t<4时，若直线y=t 与直线l 和（2）反比例函数的图象分别交于点C ，D ，当CD 间距离大于等于2时，求t 的取值范围.24.解：（1）∵直线l :y=kx+k 经过点B(0,2)，∴k=2∴ y=2x+2∴A(-1,0) ……………………….2′（2）当t=4时，将y=4代入y=2x+2得，x=1∴M(1,4)代入xny =得，n=4 ∴xy 4=……………………….2′ （3）当t=2时，B(0,2) 即C(0,2)，而D(2,2)如图，CD=2，当y=t 向下运动但是不超过x 轴时，符合要求∴ t 的取值范围是 0 <t ≤2 ……………………….5′门头沟区26.有一个二次函数满足以下条件：①函数图象与x 轴的交点坐标分别为(1,0)A ，22(,)B x y (点B 在点A 的右侧)； ②对称轴是3x =； ③该函数有最小值是-2.（1）请根据以上信息求出二次函数表达式；（2）将该函数图象2x x ＞的部分图象向下翻折与原图象未翻折的部分组成图象“G ”，平行于x 轴的直线与图象“G ”相交于点33(,)C x y 、44(,)D x y 、55(,)E x y （345x x x <<），结合画出的函数图象求345x x x ++的取值范围.26. （本小题满分7分）（1）解：有上述信息可知该函数图象的顶点坐标为: (3,2)- 设二次函数表达式为：2(3)2y a x =-- ……………1分 ∵该图象过(1,0)A∴20(13)2a =--，解得12a = ……………2分∴表达式为21(3)22y x =-- （2）图象正确………………………………………………………3分由已知条件可知直线与图形“G ”要有三个交点① 当直线与x 轴重合时，有2个交点,由二次函数的轴对称性可求 346x x += ……………………………………4分 ∴34511x x x ++＞ ……………………………………5分 ②当直线过21(3)22y x =--的图象顶点时，有2个交点，由翻折可以得到翻折后的函数图象为21(3)22y x =--+ ∴令21(3)222x --+=-时，解得3x =±3x =-6分∴3459x x x +++＜综上所述345x x x ++11＜＜…………7分大兴区26. 在平面直角坐标系xOy 中,抛物线22(31)2(0)y x m x m m m =-+++>，与y 轴交于点C ，与x 轴交于点A 1(,0)x ,B 2(,0)x ，且12x x <.（1）求1223-+x x 的值；（2）当m=1223-+x x 时，将此抛物线沿对称轴向上平移n 个单位，使平移后得到的抛物线顶点落在△ABC 的内部（不包括△ABC 的边），求n 的取值范围（直接写出答案即可）．26.（1）解关于x 的一元二次方程，()223120x m x m m -+++=得x =2m +1, x =m ………………………………………………………2分 ∵m ＞0, x 1＜x 2∴x 1=m , x 2=2m+1. …………………………………………………… 3分 2x 1-x 2+3=2m -2m -1+3=2 …………………………………………… 4分（2）符合题意的n 的取值范围是. …………………………………7分平谷区26．在平面直角坐标系xOy 中，抛物线223y x bx =-+-的对称轴为直线x =2．（1）求b 的值；（2）在y 轴上有一动点P （0，m ），过点P 作垂直y 轴的直线交抛物线于点A （x 1，y 1），B （x 2 ，y 2），其中 12x x <．①当213x x -=时，结合函数图象，求出m 的值；②把直线PB 下方的函数图象，沿直线PB 向上翻折，图象的其余部分保持不变，得到一个新的图象W ，新图象W 在0≤x ≤5 时，44y -≤≤，求m 的取值范围．26．解：（1）∵抛物线223y x bx =-+-的对称轴为直线x =2，∴b =2． ················································· 1 （2）①∴抛物线的表达式为243y x x =-+-． ∵A （x 1，y ），B （x 2 ，y ）， ∴直线AB 平行x 轴．∵213x x -=， ∴AB =3． ∵对称轴为x =2， ∴AC =12． ············································· 2 ∴当12x =时，54y m ==-． ................... 3 ②当y =m =-4时，0≤x ≤5时，41y -≤≤； (4)当y =m =-2时，0≤x ≤5 时，24y -≤≤；..... 5 ∴m 的取值范围为42m -≤≤-． (6)怀柔区26.在平面直角坐标系xOy 中，抛物线y=nx 2-4nx+4n-1(n ≠0)，与x 轴交于点C ，D(点C 在点D 的左侧)，与y 轴交于点A ．(1)求抛物线顶点M 的坐标；(2)若点A 的坐标为（0，3），AB ∥x 轴，交抛物线于点B ，求点B 的坐标；(3)在(2)的条件下，将抛物线在B ，C 两点之间的部分沿y 轴翻折，翻折后的图象记为G ，若直线m x y +=21与图象G 有一个交点，结合函数的图象，求m 的取值范围． yx –1–2–3–4–512345–1–2–3–4–512345O26.(1)M(2，-1)； ………………………………………………………………………………2分(2)B(4，3)； …………………………………………………………………………………3分(3)∵抛物线y=mx 2-4mx+4m-1(m ≠0)与y 轴交于点A （0,3）,∴4n-1=3.∴n=1. ……………………………………………………………………………………4分 ∴抛物线的表达式为342+-=x x y .由34212++=+x x m x . 由△=0，得: 161-=m ……………………………………………………………………5分 ∵抛物线342+-=x x y 与x 轴的交点C 的坐标为（1,0），∴点C 关于y 轴的对称点C 1的坐标为（-1,0）.把（-1,0）代入m x y +=21，得：21=m .……………………………………………6分把（-4,3）代入m x y +=21，得：5=m . ∴所求m 的取值范围是161-=m 或21＜m ≤ 5. …………………………………………7分延庆区26．在平面直角坐标系xOy 中，抛物线y =ax 2-4ax +3a (a ＞0)与x 轴交于A ，B 两点（A 在B 的左侧）．（1）求抛物线的对称轴及点A ，B 的坐标；（2）点C （t ，3）是抛物线243(0)y ax ax a a =-+>上一点，（点C 在对称轴的右侧），过点C 作x 轴的垂线，垂足为点D ．①当CD AD =时，求此时抛物线的表达式；②当CD AD >时，求t 的取值范围．26．（1）对称轴：x =2 ……1分A （1，0）或B （3，0） ……1分（2）①如图1，∵AD =CD∴AD =3∴C 点坐标为（4，3） ……3分将C （4，3）代入243y ax ax a =-+∴316163a a a =-+∴a =1∴抛物线的表达式为：243y x x =-+ ……4分②34t << ……6分过程略顺义区26．在平面直角坐标系xOy 中，若抛物线2y x bx c =++顶点A 的横坐标是-1，且与y 轴交于点B （0，-1），点P 为抛物线上一点．（1）求抛物线的表达式；（2）若将抛物线2y x bx c =++向下平移4个单位，点P 平移后的对应点为Q ．如果OP =OQ ，求点Q 的坐标．26．解：（1）依题意12-=-b ，b =2, 由B （0，-1），得c=-1,∴抛物线的表达式是221=+-y x x ．…………………… 2分4（2）向下平移4个单位得到225=+-y x x ，……………………… 3分 ∵OP =OQ ，∴P 、Q 两点横坐标相同，纵坐标互为相反数．∴2221250+-++-=x x x x ．∴13=-x ，21=x ．………………………………………………… 5分把13=-x ，21=x 分别代入225=+-y x x ．得出Q 1（-3，-2），Q 2（1，-2）．………………………………… 7分。