应用时间序列分析部分习题答案(1)
人大版应用时间序列分析(第5版)习题答案
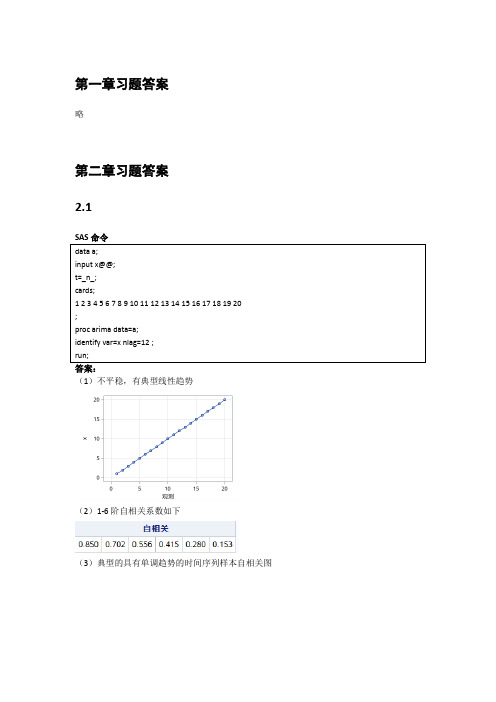
第一章习题答案略第二章习题答案2.1答案:(1)不平稳,有典型线性趋势(2)1-6阶自相关系数如下(3)典型的具有单调趋势的时间序列样本自相关图2.2答案:(1)不平稳(2)延迟1-24阶自相关系数(3)自相关图呈现典型的长期趋势与周期并存的特征2.3答案:(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列2.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列(2)差分后序列为平稳非白噪声序列2.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
(2)单位根检验显示带漂移项0阶延迟的P值小于0.05,所以基于adf检验可以认为该序列平稳(3)如果使用adf检验结果,认为该序列平稳,则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳,那么一阶差分后序列为平稳非白噪声序列2.8答案(1)时序图和自相关图都显示典型的趋势序列特征(2)单位根检验显示该序列可以认为是平稳序列(带漂移项一阶滞后P值小于0.05)(3)一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--() 221112() 1.96110.7t Var x φ===--() 22213=0.70.49ρφ==()12122221110.490.7=0110.71ρρρφρρ-==-(4) 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有:,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=()1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=() 1112223340.70.15=0φρφφφ====-()3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩() ()模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩() 3.5证明:该序列的特征方程为:320c c λλλ--+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
应用统计学时间序列习题及答案

计算题:34323*22562584*22582603*22602502*2250254++++++++++=a = (人计算(1)第一季度该店平均每月商品销售额(2)第一季度平均销售员人数(3)第一季度平均每个销售员的销售额 (4)第一季度平均每月每个销售员的销售额 解:(1)商品销售额为时期总量指标时间序列,4月不属一季度,该数据无用3280350300++=a = (万元)(2) 销售员人数是时点总量指标时间序列,间断间隔相等,用首尾折半法,4月初人数相当于3月末人数,这个数据有用32424045240+++=b = (人) (3)32424045240280350300+++++==平均人数一季度销售额c = (万元/人) (4)3324240452403028350300c d =+++++==平均人数一季度月平均销售额 = (万元/人)要求:(1)根据表中资料 ,计算并填制表中空白栏指标(2)计算该地财政收入的这几年的年平均发展水平、年平均增长水平(水平法)和平均增长速度(几何平均法)(3)超过平均增长速度的年份有哪些年?解:注意平均时项数的确定,写计量单位,我以下省略了单位1430%02.193*430116430%02.193*4307%02.193*4304554301)26n 0010-=-=-='-=-=∆+++=+++=a a V V n a a n a a a a n n n ((3)填全表中各年的环比增长速度,和年平均增长速度进行比较即可4. 某地1980~1990年间(以1979年为基期:a0),地区生产总值以平均 每年25%的速度增长(平均增长速度),而1991~2000年间地区生产总值以平均每年30%的速度增长(平均增长速度),2001~2012年间地区生产总值以平均每年18%的速度增长,则1980~2012年间,该地区的生产总值平均每年的增长速度是多少?(重点:正确确定时间段长短)解:注意是以1979年为基期,经过33年发展到2012年,求这段时间的平均增长速度1%118*%130*%125133121011-=-='V V5. 某地1980年的人口是120万人,1981~2000年间人口平均增长率为1.2%,之后下降到1%,按此增长率到2008年人口会达到多少?如果要求到2012年人口控制在170万以内,则2008年以后人口的增长速度应控制在什么范围内? 解:1)2(%101*%2.101*)140812*******-='==V V V a a a a ((1)分别用最小平方法的普通法和简捷法配合直线方程,并预测2010年该企业产值 (2)比较两种方法得出的结果有无异同。
时间序列分析作业及答案
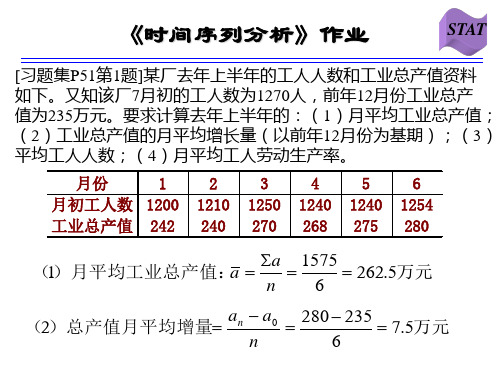
(3) 5500 4000 (1 x ) 5 5500 x 106.58% 甲厂平均发展速度需 106.58% 4000
a1 a2 a3 a4 a5 1 解 : x x 1 x 1 5 a0 a1 a2 a3 a 4
n
5 (1 5.2%) (1 4.8%) (1 3.8%) (1 3.5%) (1 2.4%) 1
平均每年的降低率: x 96.05% 1 3.95%
lg1.375 0.13830 n 14.32年 15年后可达到乙厂水平 lg1.0225 0.00966
《时间序列分析》作业
STAT
[习题集P53第8题]甲、乙两厂各年产量资料如下。要求:(1) 分别计算两厂的平均发展速度;(2)按现在甲厂平均发展速度, 要几年才能达到乙厂1999年的水平?(3)如要求甲厂从1999年 起,在五年内达到乙厂1999年的水平,则甲厂的平均发展速度 必须达到多少?
a1990 25(1 4%)5 30.42 a2000 30.42(1 4.5%)10 47.24
a2000 25(1 4%)5 (1 4.5%)10 47.24 (万吨)
(2)已知:a2000 3 25 75 75 25(1 4%)5 (1 x )10
5
《时间序列分析》作业
STAT
[习题集P54第10题]某地区1995~2001年财政收入资料如下(单位: 亿元)。根据该资料: (1)用最小平方法的简捷式配合直线趋势方程; (2)根据直线趋势方程预测2002年的财政收入。
时间序列分析与预测课后习题答案

22 7336 18 0766 20 2040
第八章 时间序列分析与预测
练习题第五题答案
2000
季度 销售量
长期趋势
一季度 13 1
9 3324
二季度 13 9
9 9722
三季度 79
10 6121
四季度 86
11 2519
2001
Y/T 销售量 长期趋势
1 4037 10 8
11 8918
1 3939 11 5
9
2 10
10
2 50
Y 1 1 = 0 . 3 6 5 3 3 3 + 0 . 1 9 2 6 4 8 1 1 = 2 . 4 8 6 6 6 7
2024/1/18
第八章 时间序列分析与预测
练习题第五题
某县2000—2003年各季度鲜蛋销售量如表所示单位:万公斤 1用移动平均法消除季节变动 2拟合线性模型测定长期趋势 3预测2004年各季度鲜蛋销售量
13 95 0 987174
2024/1/18
第八章 时间序列分析与预测
练习题第五题答案
2用线形趋势模型法测定时间序列的长期趋势
年份 2000 2001 2002 2003
季度 一 二 三 四 一 二 三 四 一 二 三 四 一 二 三 四
2024/1/18
销售量
13 1 13 9
t 1 3 6 , t= 8 .5 , t2 = 1 4 9 6
0 9177 17 5
15 0910 1 1596
20 0 17 6504 1 1331 1 1511 1 1472 20 2099
0 7364 16 0
15 7309 1 0171
16 9 18 2903 0 9240 0 8555 0 8526 20 8497
时间序列分析课后习题答案1

时间序列分析课后习题答案(上机第二章 2、328330332334336338340342(1时序图如上:序列具有明显的趋势和周期性,该序列非平稳。
(2样本自相关系数:(3该样本自相关图上,自相关系数衰减为 0的速度缓慢,且有正弦波状,显示序列具有趋势和周期,非平稳。
3、 (1样本自相关系数:(2序列平稳。
(3因 Q 统计量对应的概率均大于 0.05,故接受该序列为白噪声的假设,即序列为村随机序列。
5、 (1时序图和样本自相关图:50100150200250300350(2序列具有明显的周期性,非平稳。
(3序列的 Q 统计量对应的概率均小于 0.05,该序列是非白噪声的。
6、 (1根据样本相关图可知:该序列是非平稳,非白噪声的。
(2对该序列进行差分运算:1--=t t t x x y {t y }的样本相关图:该序列平稳,非白噪声。
第三章:17、 (1结论:序列平稳,非白噪声。
(2 拟合 MA(2 model:VariableCoefficient Std. Error t-Statistic Prob. C 80.40568 4.630308 17.36508 0.0000 MA(1 0.336783 0.114610 2.938519 0.0047 R-squared0.171979 Mean dependent var 80.29524 Adjusted R-squared 0.144379 S.D. dependent var 23.71981 S.E. of regression 21.94078 Akaike info criterion 9.061019 Sum squared resid 28883.87 Schwarz criterion 9.163073 Log likelihood -282.4221 F-statistic 6.230976 Durbin-Watson stat 2.072640 Prob(F-statistic 0.003477Residual tests(3拟合 AR(2model:C 79.71956 5.442613 14.64729 0.0000 AR(10.2586240.1288102.0077940.0493R-squared0.154672 Mean dependent var 79.50492 Adjusted R-squared 0.125522 S.D. dependent var 23.35053 S.E. of regression 21.83590 Akaike info criterion 9.052918 Sum squared resid 27654.79 Schwarz criterion 9.156731 Log likelihood -273.1140 F-statistic 5.306195 Durbin-Watson stat 1.939572 Prob(F-statistic 0.007651Inverted AR Roots.62-.36Residual tests:(4 拟合 ARMA (2, 1 model :Variable Coefficient Std. Error t-Statistic Prob. C 79.17503 4.082908 19.39183 0.0000 AR(1 -0.586834 0.118000 -4.973170 0.0000 AR(2 0.376120 0.082091 4.581756 0.0000 MA(11.1139990.09712211.470120.0000R-squared0.338419 Mean dependent var 79.50492 Adjusted R-squared 0.303599 S.D. dependent var 23.35053 S.E. of regression 19.48617 Akaike info criterion 8.840611 Sum squared resid 21643.51 Schwarz criterion 8.979029 Log likelihood-265.6386 F-statistic9.719104Inverted AR Roots .39-.97 Inverted MA Roots-1.11Estimated MA process is noninvertible残差检验:(5拟合 ARMA (1, (2 model:Variable Coefficient Std. Error t-Statistic Prob. C 79.52100 4.621910 17.205230.0000 AR(1 0.270506 0.125606 2.153603 0.0354 R-squared0.157273 Mean dependent var 79.55161 Adjusted R-squared 0.128706 S.D. dependent var 23.16126 S.E. of regression 21.61946 Akaike info criterion 9.032242 Sum squared resid 27576.65 Schwarz criterion 9.135167 Log likelihood -276.9995 F-statistic 5.505386 Durbin-Watson stat 1.981887 Prob(F-statistic 0.006423Inverted AR Roots.27残差检验:(6优化根据 SC 准则,最优模型为 ARMA(2,1模型。
应用时间序列分析(试卷一)

应用时间序列分析(试卷一)一、 填空题1、拿到一个观察值序列之后,首先要对它的平稳性和纯随机性进行检验,这两个重要的检验称为序列的预处理。
2、白噪声序列具有性质纯随机性和方差齐性。
3、平稳AR (p )模型的自相关系数有两个显著的性质:一是拖尾性;二是呈负指数衰减。
4、MA(q)模型的可逆条件是:MA(q)模型的特征根都在单位圆内,等价条件是移动平滑系数多项式的根都在单位圆外。
5、AR (1)模型的平稳域是{}11<<-φφ。
AR (2)模型的平稳域是{}11,12221<±<φφφφφ且,二、单项选择题1、频域分析方法与时域分析方法相比(D )A 前者要求较强的数学基础,分析结果比较抽象,不易于进行直观解释。
B后者要求较强的数学基础,分析结果比较抽象,不易于进行直观解释。
C前者理论基础扎实,操作步骤规范,分析结果易于解释。
D后者理论基础扎实,操作步骤规范,分析结果易于解释。
2、下列对于严平稳与宽平稳描述正确的是(D)A宽平稳一定不是严平稳。
B严平稳一定是宽平稳。
C严平稳与宽平稳可能等价。
D对于正态随机序列,严平稳一定是宽平稳。
3、纯随机序列的说法,错误的是(B)A时间序列经过预处理被识别为纯随机序列。
B纯随机序列的均值为零,方差为定值。
C在统计量的Q检验中,只要Q时,认为该序列为纯随机序列,其中m为延迟期数。
D不同的时间序列平稳性检验,其延迟期数要求也不同。
4、关于自相关系数的性质,下列不正确的是(D)A. 规范性;B. 对称性;C. 非负定性;D. 唯一性。
5、对矩估计的评价,不正确的是(A)A. 估计精度好;B. 估计思想简单直观;C. 不需要假设总体分布;D. 计算量小(低阶模型场合)。
6、关于ARMA模型,错误的是(C)A ARMA模型的自相关系数偏相关系数都具有截尾性。
B ARMA模型是一个可逆的模型C 一个自相关系数对应一个唯一可逆的MA模型。
D AR模型和MA模型都需要进行平稳性检验。
统计基础知识第五章时间序列分析习题及答案

D.平均数数列二、多项选择题1.将不同时期的发展水平加以平均而得到的平均数称为 A. 序时平均数2.定基发展速度和环比发展速度的关系是 ( BD A 相邻两个环比发展速度之商等于相应的定基发展速度B. 环比发展速度的连乘积等于定基发展速度一、单项选择题 第五章 时间序列分析1.构成时间数列的两个基本要素是 ( A.主词和宾词 )(20XX 年 1 月) B. 变量和次数 C.现象所属的时间及其统计指标数值 D.时间和次数2.某地区历年出生人口数是一个 ( A 时期数列 B ) (20XX 年 10月)B.时点数列C.分配数列 3. 某商场销售洗衣机, 共销售 6000 台, 年 10) 年底库存 50 台,这两个指标是 ( C ) 20XXA. 时期指标B. 时点指标C. 前者是时期指标,后者是时点指标 4.累计增长量(A ) (20XX 年 10)A. 等于逐期增长量之和 D. 前者是时点指标,后者是时期指标B. 等于逐期增长量之积C. 等于逐期增长量之差D .与逐期增长量没有关系5. 某企业银行存款余额 4 月初为 80 万元, 160 万元,则该企业第二季度的平均存款余额为( 5 月初为 150 万元, 6 月初为 210 万元, 7 月初为10)A.140 万元B.150 万元6. 下列指标中属于时点指标的是 ( A ) C.160 万元 D.170 万元A. 商品库存量 (10)B .商品销售C. 平均每人销售额D .商品销售额 7. 时间数列中,各项指标数值可以相加的是A. 时期数列10)( A )B.相对数时间数列C.平均数时间数列D.时点数列8. 时期数列中各项指标数值( A A. 可以相加 1月)B. 不可以相C.绝大部分可以相加D. 绝大部分不可以相加10. 某校学生人数 比 增长了 8%,增长了( D )( 10 月)比 增长了 15%, 比 增长了 18%,则 2004- 学生人数共A.8%+15%+18%B. 8 %X 15%X 18%C. (108%+115%+118%) -1D.108 %X 115%X 118% -1( ABD B.动态平均数)(20XX 年 1 月) C.静态平均数 D.平均发展水平 E. 般平均数 )(20XX 年 10 月)B. 数列中各个指标数值不具有可加性C. 指标数值是通过一次登记取得的D. 指标数值的大小与时期长短没有直接的联系E.指标数值是通过连续不断的登记取得的 )(20XX 年 1)B. 增加一个百分点所增加的相对量E. 环比增长量除以100再除以环比发展速度7. 增长速度( ADE )( 1 月)A.等于增长量与基期水平之比6. 计算平均发展速度常用的方法有( A.几何平均法(水平法)C.方程式法(累计法)E.加权算术平均法 AC)(10)B.调和平均法 D.简单算术平均法C.累计增长量与前一期水平之比D. 等于发展速度 -1E.包括环比增长速度和定基增长速度 8. 序时平均数是( CE )( 10 月)A.反映总体各单位标志值的一般水平B. 根据同一时期标志总量和单位总量计算C. 说明某一现象的数值在不同时间上的一般水平D.由变量数列计算E. 由动态数列计算三、判断题 1 .职工人数、产量、产值、商品库存额、工资总额指标都属于时点指标。
应用时间序列分析习题标准答案
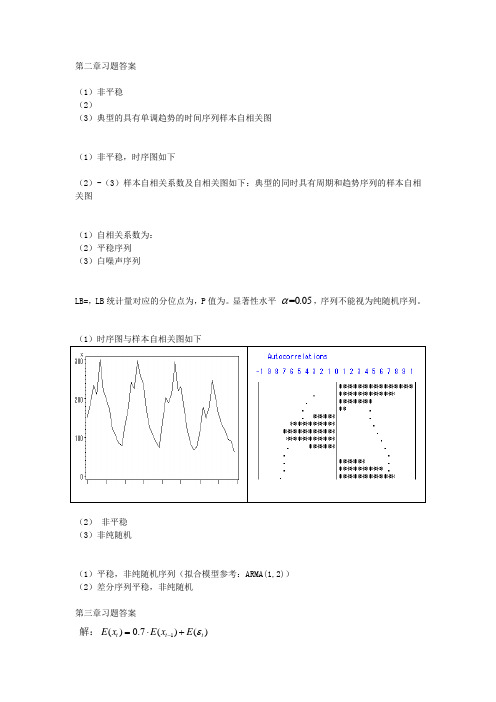
第二章习题答案(1)非平稳(2)(3)典型的具有单调趋势的时间序列样本自相关图(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图(1)自相关系数为: (2)平稳序列 (3)白噪声序列LB=,LB 统计量对应的分位点为,P 值为。
显著性水平 =0.05α,序列不能视为纯随机序列。
(2) 非平稳 (3)非纯随机(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案解:1()0.7()()t t t E x E x E ε-=⋅+0)()7.01(=-t x E 0)(=t x E t t x ε=-)B 7.01(t t t B B B x εε)7.07.01()7.01(221Λ+++=-=- 229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ 022=φ解:对于AR (2)模型:⎩⎨⎧=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ 解得:⎩⎨⎧==15/115/721φφ解:根据该AR(2)模型的形式,易得:0)(=t x E原模型可变为:t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==2σ⎪⎩⎪⎨⎧=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ ⎪⎩⎪⎨⎧=-====015.06957.033222111φφφρφ 解:原模型可变形为:t t x cB B ε=--)1(2由其平稳域判别条件知:当1||2<φ,112<+φφ且112<-φφ时,模型平稳。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间序列分析作业(1)习题2.3.1
编写程序:
运行程序:
【时序图】
【自相关图】
【白噪声检验结果】
结果分析:
1. 从时序图中可以看出,所分析序列有很明显的单调递增趋势,判
断该序列非平稳。
2. 该序列的样本自相关系数分别为:
0.850 0.702 0.556 0.415 0.280 0.153
3. 从自相关图中可以看出,该序列的自相关系数向零衰减的速度比
较缓慢,且到达零点后并非小幅度围绕零轴波动,而是一直向负
方向递增。
综上,该序列是非平稳序列。
习题2.3.3
编写程序:
运行程序:【时序图】【自相关图】
【白噪声检验结果】
结果分析:
1. 该序列的样本自相关系数如白噪声检验图。
2. 先从时序图看出,序列没有明显趋势及规律性,可初步判断为平
稳序列;再从自相关图中可看出,自相关系数迅速衰减为零,并
随后一直在2倍标准差范围以内,可认为自相关系数一直在零轴
附近波动。
综上,该序列为平稳序列。
3. 延迟6期的P值是0.2023>0.05,接受原假设,该序列具有纯随
机性。
习题2.3.4
例题2.4
编写程序:运行程序:。
