MATLAB夫琅禾费衍射课程设计
基于MATLAB的夫琅和费衍射实验的计算机仿真

式 中 J x是 一 阶 贝塞 尔 函 数 , 拟 时 令 f l h 6 0m, ,) ( 模 = m,= 0 n
a 0O 1 利用 MAT A = .0 m, L B编程 , 程序运行完毕后 , 依次得到 以 下图形 7 。圆孔衍射和矩孔衍射的三维 图形基本相 同, 二维 图
平 面 上 会 聚 点 Q(,) xy 的和 振 动 的 相 对 强 度 为 : I I u) Sl ) ( Q) ds (lP m r
u
v
() 1
于学生的理解 。同时通过 多种元 件的夫琅和费衍射 计算机仿
真, 能够动态直观地呈现光学衍射 中各种物 理量之间 的关 系,
有利于大学物理实验中光学部分教学的开展 。因此 , 我们应 当 充分利用计算机软件功 能为教学增添活力 ,为 学生理解复杂
Z agZ i n S uig J n e gh n YagK n L ne g Yag njn h n hf g uY l i g n cu n u iu f n gu e n a F J n Ho
(】潘 柏 根 , 施群 , 志 建 . 于 V +的 夫 琅 和 费 衍 射 仿 真 [] 5 金 刘 基 c+ J.
仪 器 仪表 用 户 ,0 O4: 66 . 2 l()6 —9
[]夏 静 , 6 陆训 毅 , 德 君 . 杨 圆孔 、 方 孔 和 双 矩 孔 夫琅 和 赞 衍 射 的
I tr ̄inN nfr n e n nen o Co ee c o M e s rn Te h lg a d M e h to is a ui g c noo y n c ar nc
Au o a i n Co f r n e o I EE: 0 — 0 . t m to , n e e c f E 9 2 9 5
基于Matlab的夫琅禾费衍射光学仿真设计

基于Matlab的夫琅禾费衍射光学仿真摘要计算机仿真技术是以多种学科和理论为基础,以计算机及其相应的软件为工具,通过虚拟试验的方法来分析和解决问题的一门综合性技术。
计算机仿真早期称为蒙特卡罗方法,是一门利用随机数实验求解随机问题的方法。
关键词:计算机仿真夫琅禾费衍射MatlabFraunhofer Diffraction Optical Simulation Based onMatlabAbstract The computer simulation technology is based on a variety of disciplines and theoretical, with the computer and the corresponding software tools, we can analyze the virtual experimentation and solve the problem of a comprehensive technology. Computer simulation of early known as the Monte Carlo method, is a random problem solved using the method of random number test.Key words:Computer simulation Fraunhofer diffraction Matlab一、引言计算机仿真技术是以多种学科和理论为基础,以计算机及其相应的软件为工具,通过虚拟试验的方法来分析和解决问题的一门综合性技术。
计算机仿真早期称为蒙特卡罗方法,是一门利用随机数实验求解随机问题的方法。
根据仿真过程中所采用计算机类型的不同,计算机仿真大致经历了模拟机仿真、模拟-数字混合机仿真和数字机仿真三个大的阶段。
20世纪50年代计算机仿真主要采用模拟机;60年代后串行处理数字机逐渐应用到仿真之中。
基于MATLAB的圆孔夫朗和费衍射现象

基于MATLAB 的圆孔夫朗和费衍射现象(陈群 20092301069 华南师范大学 物理与电信工程学院)摘要:本文首先回顾了单圆孔的夫朗和费衍射的特点,进而分析了双圆孔的夫朗和费衍射现象,双圆孔的夫朗和费衍射可以看成是两个单圆孔之和的夫朗和费衍射的叠加,所得结果对分析和理解圆孔夫朗和费衍射现象以及圆孔夫朗和费衍射演示实验的设计有参考价值。
关键词: MATLAB ,圆孔,双圆孔,夫朗和费衍射Abstract: The paper first reviews the characteristics of the Fraunhofer diffraction of a single hole and then analyzes the Fraunhofer diffraction phenomenon of the double-hole, the double holes Fraunhofer diffraction can be seen as the superposition of two single-hole Fraunhofer diffraction. The results is valuable to analyzing and understanding the hole Fraunhofer diffraction phenomenon and designing the hole Fraunhofer diffractionKey word: MATLAB, hole, double hole, Fraunhofer diffraction 引言实际应用中许多光学元件的边缘都是圆形的,所以圆孔衍射是光学系统中常见的衍射现象。
它也是基础光学的重要教学环节,而圆孔衍射现象的实验演示是重要的教学环节。
由衍射理论知,当圆孔直径由大变小时,衍射条纹会由密变疏,同时衍射场强度会逐渐变弱,为了在接收屏上获得易于观察的条纹分布,条纹的疏密程度和衍射场的强度都需要达到适于肉眼观察的程度,这就对衍射屏提出了较高的要求。
夫琅禾费矩孔衍射的特征及其MATLAB模拟

##!
万方数据
蓝海江, 潘晓明, 吴建生: 夫琅禾费矩孔衍射的特征及其 %&’(&) 模拟
光强变小, 中央亮斑的面积增大! 这与 (!) 、 (") 式的结果是 一致的! ! ! ! ! ! 矩孔大小对夫琅禾费矩孔衍射的影响 在人机对话窗口中输入数据: " # # ! $ $$, % # # ! $ $$, ! # # ! ###$ $$, 则夫琅禾费矩孔衍射的 %&’(&) 模拟结果如 图 $ 所示! 何光学! ! ! ! ! - 从矩孔衍射到单缝衍射的 %&’(&) 模拟 在人机对话窗口中输入数据: " # # ! " $$, % # " $$, !# # ! ###$ $$, 夫琅禾费矩孔衍射的 %&’(&) 模拟结果如图 , 所示!
[-] 衍射是矩孔衍射的特例 !
! ! " ! ( 衍射反比律及其意义 由 ()) 式可知, ( 或 $!! 与 % 成反比) , $!# 与 $ 成反比 这一反比律具有普遍意义! 若设限制波前的光孔在某方向上 的几何线度为 #, 光波在该方向上的衍射发散角为 $!, 则衍
matlab实现夫朗和费矩形和圆孔衍射
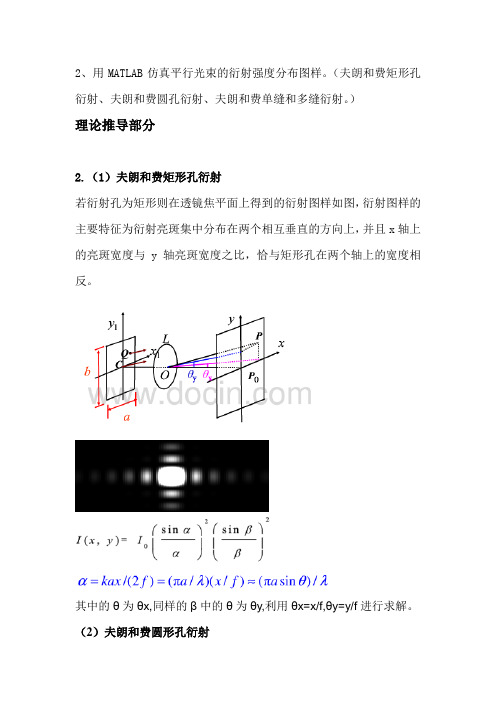
2、用MATLAB仿真平行光束的衍射强度分布图样。
(夫朗和费矩形孔衍射、夫朗和费圆孔衍射、夫朗和费单缝和多缝衍射。
)理论推导部分2.(1)夫朗和费矩形孔衍射若衍射孔为矩形则在透镜焦平面上得到的衍射图样如图,衍射图样的主要特征为衍射亮斑集中分布在两个相互垂直的方向上,并且x轴上的亮斑宽度与y轴亮斑宽度之比,恰与矩形孔在两个轴上的宽度相反。
其中的θ为θx,同样的β中的θ为θy,利用θx=x/f,θy=y/f进行求解。
(2)夫朗和费圆形孔衍射夫朗和费圆孔衍射的讨论方法和矩形孔衍射的讨论方法相同,只是由于圆孔的几何对称性,采用极坐标更为方便。
Ф=kaθ2.(1)夫朗和费矩形孔衍射clear all;lamda=500e-9;a=1e-3;b=1e-3;f=1;m=500;ym=8000*lamda*f;ys=linspace(-ym,ym,m)xs=ys;n=255;for i=1:msinth2=ys./sqrt(ys.^2+f^2);%相当于x/fsinth1=xs(i)/sqrt(xs(i).^2+f^2);%xs(i)作用每给一个ys值,要遍历到所有的x值angleA=pi*a*sinth1/lamda;%相当于书上的alfa=kax/2f k=2*pi/lamdaangleB=pi*b*sinth2./lamda;B(:,i)=(sin(angleA).^2.*sin(angleB).^2.*5000./(angleA.^2.*a ngleB.^2));%光强度公式endsubplot(1,2,1)image(xs,ys,B)colormap(gray(n))subplot(1,2,2)plot(B(m/2,:),ys)(2)夫朗和费圆孔衍射clearlam=500e-9a=1e-3f=1m=300;ym=5*0.61*lam*f/a;%取爱里光斑半径的5倍ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:mr=xs(i)^2+ys.^2;%相当于r的平方sinth=sqrt(r./(r+f^2));%角度fai=2*pi*a*sinth./lam;%fai=k*a*sinthhh=(2*BESSELJ(1,fai)).^2./fai.^2;%贝塞尔函数 b(:,i)=hh.*5000;endsubplot(1,2,1)image(xs,ys,b)colormap(gray(n))subplot(1,2,2)b(:,m/2)plot(ys,b(:,m/2))。
多缝的夫琅和费衍射matlab仿真

4、多缝的夫琅和费衍射,使用平行光照明,观察衍射图样随点光源位置(光源上下移动)的变化 θθθ图4-1 图4-2多缝夫琅禾费衍射如图4-1所示。
由于相邻单缝在P 点产生的夫琅禾费衍射的幅值与中心单缝的相同,只是产生一个相位差θλπδsin 2d =,故,经证明,P 点处的光强为:220)2sin 2sin ()sin ()(δδααN I P I =, 其中θλπαsin a =,θλπδsin 2d =。
因而,程序代码如下:clear %清除原有变量Lambda=600*(1e-9); %设置波长为600nma=0.005*(1e-3); %设置衍射屏参数:缝宽为0.005mm , 缝距为0.02mmd=0.02*(1e-3);f=0.01; %汇聚透镜焦距设置为1cmN=20; %设置缝数为20ni=1000;x=linspace(-0.005,0.005,ni); %将衍射屏按照狭缝方向分为ni 个微元 for k=1:nisn=x(k)/sqrt(x(k).^2+f^2);alpha=pi*a*sn/Lambda; %算各微元对应的α和δ值delta=2*pi*d*sn/Lambda;I(k)=(sin(alpha)/alpha).^2*(sin(N*delta/2)/sin(delta/2)).^2; %求出各处的光强endfigure(gcf); %显示图像NCLevels=250;Br=I*NCLevels;image(0,x,Br);colormap(gray(NCLevels));title('二维强度分布');运行后结果如图4-2所示。
将光源上下移动的结果如图4-3所示:图4-3 图4-4点光源发出的光经过准直透镜后形成倾斜入射的平行光,倾斜角度为i 。
此时,P 点强度的公式为:220)sin ()sin ()(ββααN I P I =, 其中)sin (sin i a -=θλπα,)sin (sin i d -=θλπβ。
应用Matlab模拟光的夫琅禾费衍射的研究

应用Matlab模拟光的夫琅禾费衍射的研究摘要:光的衍射是一种非常重要的光的物理现象。
它指的是:光将障碍物绕过,偏离直线传播路径,然后进入阴影区里的现象。
它也是光的波动表现的一种现象。
衍射系统的组成有三个部分,它们分别是:光源、衍射屏、接收屏(用来接收衍射图样的屏幕)。
通常情况下,我们根据衍射系统当中三个组成部分之间相互距离的大小,将衍射现象分为两类:一类叫做菲涅耳(Fresnel)衍射,剩下的一类叫做夫琅禾费(Fraunhofer,)衍射。
此文通过Matlab软件,进行编程,进而对夫琅禾费衍射过程进行模拟。
然后给出衍射光强分布图形,又通过对光的波长、焦距、缝宽等因素的改变,得到了衍射光强的分布和它的变化规律,并在理论上作出了合理的解释。
从而帮助我们更深刻的理解光的波动性原理。
关键词:Matlab;衍射;光学实验目录1 绪论 (1)1.1光的衍射现象 (1)1.2 Matlab模拟的意义 (1)2 光的衍射理论 (3)2.1 惠更斯原理 (3)2.2 惠更斯——菲涅耳原理 (3)3夫琅禾费衍射原理 (4)3.1 夫琅禾费单缝衍射 (4)3.2 夫琅禾费双缝衍射 (5)4 夫琅禾费衍射模拟 (6)4.1 单缝 (6)4.2 矩孔 (12)5 总结 (15)参考文献 (15)1 绪论1.1光的衍射现象自然界之中有一些光的现象,它们与人们已经发现的光的直线传播现象并不是百分百符合。
这些现象相继在17世纪之后被科学家们发现。
这就是由光的波动性表现出来的。
在这些现象之中,人们第一个发现的光的现象便是衍射现象,而且还在发现的同时做了些实验与理论的研究和探讨。
第一次成功发现衍射现象的科学家是意大利的物理学者格里马第。
在他的一部著作里描写了这样一个实验:让光通过很小的一个孔后射入到一个暗室里面,利用这种方法来形成点光源,然后在光路上面放置根直杆。
这时发现了两个特殊的现象:一个是影子,它投在白色的屏幕之上,以光的直线传播理论假定的影子要比它的宽度要小;另一个就是在这个影子的边缘还呈现出大约2、3个条带,条带是彩色的,随着光的增强,增强到很强的时候,这些条带甚至进入影子里。
基于MATLAB的正三角形夫琅禾费衍射现象

θ
P
P0
L
多缝衍射缝数3
多缝衍射缝数3光强分布
正三角形孔衍射代码
clear all a=0.00004; lmda=500e-9; f=10; H=a*sin(pi/3); x=-1:0.005:1; y=-1:0.005:1; for i=1:1:401 for j=1:1:401 X(i)=2*pi*x(i)/(tan(pi/3)*lmda*f); Y(j)=2*pi*y(j)/(lmda*f); I1(i,j)=(sin(0.5*H*(Y(j)-X(i))))^2/((Y(j)-X(i))^2+eps); I2(i,j)=(sin(0.5*H*(Y(j)+X(i))))^2/((Y(j)+X(i))^2+eps); I3(i,j)=2*cos(H*X(i))*(sin(0.5*H*(Y(j)-X(i))))*(sin(0.5*H*(Y(j)+X(i))))/(Y(j)*Y(j)-
基于MATLAB的正三角形夫 琅禾费衍射现象
理论基础
夫琅禾费衍射振幅公式:
E(x,
y)
C exp[i
S
k f
(x
y)]dd
观察屏上的光强表达式为:
I E(x, y) E(x, y)
其中
C Aexp{ik[ f
(x2 y2agesc(p1)
title('单缝衍射模拟图');
colormap(lgray)
单缝的夫琅和费衍射
单缝衍射实验装置
L1
K
L2
S
*
E屏幕
线光源在透镜L1的物方焦平面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计任务书学生姓名:袁娜专业班级:电子科学与技术1201 班指导教师:工作单位:信息工程学院题目: 夫琅禾费矩孔﹑单缝和圆孔衍射图样一、设计目的了解MATLAB软件的基本知识,基本的程序设计,软件在高等数学和工程数学中的应用,学会使用软件进行数值计算和控制工程中的应用。
二、设计内容和要求1.绘制禾费矩孔、单缝和圆孔衍射图样,可以是二维的或三维的,也可以两种都有。
改变矩孔、单缝和圆孔的参数,比较衍射条纹的变化。
提示:参考《物理光学》教材或冯国英《波动光学》,画二维图时用image和colormap 函数,显示灰度图像时用colromap(gray(255)),255级灰度即可,画出的图和教材上的衍射图样一样。
三维图时就用mesh或surf函数。
2. 学习Matlab语言的概况和Matlab语言的基本知识。
3.学习Matlab语言的程序设计。
三、初始条件计算机;Matlab软件。
四、时间安排1、2015年01月19日,任务安排,课设具体实施计划与课程设计报告格式的要求说明。
2、2015年01月20日,查阅相关资料,学习Matlab语言的基本知识,学习MATLAB语言的应用环境、调试命令,绘图功能函数等。
3、2015年01月21日至2015年01月22日,Matlab课程设计制作和设计说明书撰写。
4、2015年01月23日,上交课程设计成果及报告,同时进行答辩。
指导教师签名:2015年01 月19日系主任(或负责教师)签名:2015年01 月19日目录摘要 (I)1 设计内容及要求 (1)1.1 设计的目的 (1)1.2 设计的要求 (1)2 设计原理及设计思路 (1)2.1 矩孔衍射原理 (1)2.2 单缝衍射原理 (2)2.3圆孔衍射原理 (3)3 程序设计 (3)3.1 矩孔衍射程序 (3)3.2 单缝衍射程序 (4)3.3 圆孔衍射程序 (6)4 图形仿真 (7)4.1 矩孔衍射仿真图样 (7)4.2 单缝衍射仿真图样 (8)4.3 圆孔衍射仿真图样 (8)5 心得体会 (10)参考文献 (11)摘要本文基于衍射理论,利用MATLAB软件编程来实现对夫琅禾费矩孔﹑单缝和圆孔衍射图样的计算机仿真,不仅参数很容易调节、模拟结果直观,而且与实验观测结果也非常吻合。
这为数字化仿真现代光学实验和教学提供了一种极好的手段。
MATLAB是一套高性能的数值分析和计算软件,它将矩阵计算﹑数值分析﹑图形管理和编程技术结合在一起,广泛应用于高校基础和专业课程的教学中。
计算机仿真以其良好的可控性﹑无破性﹑易观察性以及低成本等优点,在光学理论和实验教学中被迅速推广。
根据光学原理设计程序进行实验仿真,简单灵活﹑周期短,而且不受实际试验条件的限制,节约了实验器材,并减少了实验者的操作难度。
利用MATLAB软件对光学现象进行数值仿真能迅速地展示实验现象,验证理论,使学生较直接地接受科学事实,更好地理解理论知识,从而加深对光学原理﹑概念和图像的理解。
关键字:夫琅禾费衍射矩孔单缝圆孔MATLAB 仿真1 设计内容及要求1.1设计的目的利用MATLAB 软件编程来实现对夫琅禾费矩孔﹑单缝和圆孔衍射图样的计算机仿真,对光学现象进行数值仿真,能迅速地展示实验现象,验证理论,使学生较直接地接受科学事实,更好地理解理论知识,从而加深对光学原理﹑概念和图像的理解。
1.2 设计的要求绘制禾费矩孔、单缝和圆孔衍射图样,可以是二维的或三维的,也可以两种都有。
改变矩孔、单缝和圆孔的参数,比较衍射条纹的变化。
2 设计原理及设计思路2.1 矩孔衍射原理设波长为λ的平行光正入射到宽度为a (0x 轴方向),高度为b (0y 轴方向)的矩孔上,若设矩孔上的光场分布均匀,则瞳函数为常数,即Λ=),y (x U 00~,夫琅禾费矩孔衍射的衍射场为)sin ()sin (,~0021ββααθθ•=L ik e c )(U ,式中1θ和2θ分别为x 轴和y 轴方向上的衍射角;A ab f i c )(λ-=;002λπ=k 为真空中的波数;0L 为光波从0x ,0y 坐标的原点出发沿着衍射方向到达场点)(y x P ,的光程,即参考光程,在积分过程中是不变的常量;λθπα1sin a =,λθπβ2sin b =。
由上易得出夫琅禾费矩孔衍射的光强分布为 2221)sin sin ββααθθ()(),(•=I I极小值,...2,1,sin 111±±==m m a λθ ,...2,1,sin 222±±==m m b λθ2.2 单缝衍射原理由惠更斯—菲涅尔原理易得出波的振动表达式为t bdxA dE ωcos 0=,对于单缝衍射,其相位差为θλπϕsin 2x =,其光振动表达式为⎪⎭⎫⎝⎛-=θλπωsin 2cos 0x t b dx A dE 或 ⎪⎭⎫⎝⎛-=wt i e b dx A dE θλπsin 20其复振幅为 θλπsin 2~0x ei b dx A E d =所以光屏上点的合振幅为μμλθλπsin ~-~0sin 2000A e bA r i E x i b ==⎰⎰∑ 其中 λθπμsin b =,因此光强为 μμμ2020*sin sin ~~2c I A E E I =⎪⎪⎭⎫ ⎝⎛=⨯= 所以光强分布为20sin ⎪⎪⎭⎫⎝⎛=μμI I 0=θ时有最大光强 20max A I =...3,2,1,=±=k k πμ时,最小光强 0min =I ,,...47.3,46.2,43.1πππμ±±±=2.3圆孔衍射原理圆孔衍射中间亮纹亮度最大,称为爱里斑,直径为d ,观察平面上任意一点的复振幅为()[]1110cos 20211'~ϕϕϕθπd dr r e C E a ikr ⎰⎰--=,由贝塞尔函数可得 ()()[]()θθπθθθπka ka C a kr kr k C E a r r 121112J 2'J '2~11==== 因此,光强为()()()210212222J 2'⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=Z Z J I ka ka C aI θθπ 爱里斑的半径为afr 222.10λ=3 程序设计3.1 矩孔衍射程序clear all close all clclmda=632.8e-9; %波长 xmax=0.05; %矩孔x 轴宽度 ymax=0.05; %矩孔y 轴宽度def=0.0001; %分析分辨率x=-xmax:def:xmax;y=-ymax:def:ymax;lenm=length(x);lenn=length(y);for m=1:lenmfor n=1:lennalpha=pi*x(m)/(lmda);beta=pi*y(n)/(lmda);I(m,n)=((sin(alpha))/(alpha))^2*((sin(beta))/(beta))^2;endend[X,Y]=meshgrid(x,y);I=I/(max(max(I)));figureimshow(255*I);3.2 单缝衍射程序clear allclose allclclmda=632.8e-9; %波长xmax=0.005; %矩孔x轴宽度ymax=0.05; %矩孔y轴宽度def=0.0001; %分析分辨率x=-xmax:def:xmax;y=-ymax:def:ymax;lenm=length(x);lenn=length(y);for m=1:lenmfor n=1:lennalpha=pi*x(m)/(lmda);beta=pi*y(n)/(lmda);I(m,n)=((sin(beta))/(beta))^2;endendI=I/(max(max(I)));[X,Y]=meshgrid(x,y);figureimshow(255*I);xlabel('x');ylabel('y');3.3 圆孔衍射程序clear allclose allclclam=632.8e-9; %波长a=0.0005; %圆孔直径f=1; %距离m=512; %画的点数ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;for i=1:mr=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lam;hh=(2*besselj(1,x)).^2./x.^2;b(:,i)=(hh)'.*5000;endimage(xs,ys,b)colormap(gray(256))4 图形仿真4.1 矩孔衍射仿真图样x=0.05 , y=0.05时x=0.02 , y=0.05时4.2 单缝衍射仿真图样x=0.005 , y=0.05时x=0.002 , y=0.05时波长=700e-9,x=0.005 , t=0.05时4.3 圆孔衍射仿真图样直径a=0.0005时直径a=0.0003时5 心得体会通过这次的课设,我认识到了MATLAB软件的功能非常强大,对于很多关于光学实验方面都可以用它来实现,这使得我们在使用的时候非常方便及多变。
我也熟悉了MATLAB的工作环境,可以很熟练的对MATLAB进行常规的操作,快速进行程序编辑和仿真。
本文次课设利用MATLAB仿真夫琅禾费矩孔﹑单缝和圆孔衍射图样,方法简单、快捷。
在本次的课程设计中,这个课题看似有点陌生,但是真正做起来才发现不是那么困难。
主要是因为以前做实验时老师对我们要求比较严格,锻炼很多,对软件的用法比较熟悉。
这次的课程设计让我学到了很多知识,不仅仅是对MATLAB软件的学习,对学习编程有很大帮助,对衍射的相关知识也有更深的了解,更有对做课程设计的熟练,通过相互学习中,我也学到了很多其他同学的方法及他们的一些知识,体会到了同学之间的团结。
当然,也有老师的帮助及平时的教导。
经过了课程设计,我也发现了自己的很多不足。
但是通过自己的动手动脑,既增加了知识,又给了我专业知识以及专业技能上的提升,对提高自己的思维能力和操作能力有很大的帮助。
同时我也会更加努力,认真学习,争取在以后的课程中做得更好!参考文献[1] 梁绍荣.普通物理学・光学[M].高等教育出版社,1988[2]姚启钧.光学教程[M].高等教育出版社,2002[3]张兆奎,缪连元,张立.大学物理实验[M].高等教育出版社,2001[4]蓝海江.夫禾费矩孔衍射的光强[J].柳州师专学报,2000[5]谢嘉宁,陈伟成,赵建林.MATLAB在光学信息处理仿真实验中的应用[J].物理实验,2006本科生课程设计成绩评定表指导教师签字:2015年1月23日。
