物化各种公式概念总结
物化期末公式总结

物化期末公式总结一、热力学方面的公式1. 热力学第一定律:ΔU = Q + W这个公式表示了能量的守恒,其中,ΔU是系统内能的变化,Q是系统吸收或释放的热量,W是系统对外界做功。
2. 热力学第二定律:ΔS≥0这个公式表示了熵的增加趋势,系统在无限接近绝对零度时,熵趋于最小。
3. 热力学第三定律:绝对零度熵为0这个公式表示了在绝对零度下,熵为0。
4. 焓的变化:ΔH = ΔU + PΔV这个公式表示了焓的变化,其中,ΔH是焓的变化,ΔU是系统内能的变化,P是压强,ΔV 是体积的变化。
5. 熵的变化:ΔS = Q/T这个公式表示了熵的变化,其中,ΔS是熵的变化,Q是系统吸收或释放的热量,T是温度。
二、化学反应方程的计算1. 物质的量与摩尔质量:物质的量n = m/M其中,n是物质的量,m是物质的质量,M是摩尔质量。
2. 化学反应的平衡常数:Kc = ([C]^c[D]^d) / ([A]^a[B]^b)其中,[C]、[D]、[A]、[B]分别表示化学反应中的物质浓度,a、b、c、d分别表示化学反应中物质的摩尔系数。
3. 反应速率与物质浓度的关系:v = k[A]^a[B]^b其中,v表示反应速率,k表示速率常数,[A]、[B]分别表示反应物质的浓度。
三、电化学方面的公式1. Faraday定律:m = nFz其中,m是电化学反应的产物质量,n是电子数,F是法拉第定数,z是电化学反应的化学当量。
2. 电池方程:Ecell = Ecathode - Eanode这个公式表示了电池的电动势,Ecell是电池的电动势,Ecathode是阴极半反应的标准电势,Eanode是阳极半反应的标准电势。
3. 纳仑方程:Ecell = E°cell - (RT/nF)lnQ这个公式表示了电池的电动势,E°cell是标准电动势,R是理想气体常量,T是温度,n 是电子数,F是法拉第定数,Q是反应物质浓度的比值。
物化公式归纳

物化公式归纳 第一章化学热力学基础公式总结1.体积功 We = -Pe ^V2 •热力学第一定律的数学表达式△U = Q +W 3. n mol 理想气体的定温膨胀过程 .定温可逆时: V iF 2Wmax=-Wmin=nRT ln nRT ln -V 2F4.焓定义式 H = U + FV 在封闭体系中,W =0 ,体系发生一定容过程 Qv = △ U 在封闭体系中,W =0 ,体系发生一定压过程 Qp = H2 -H1 = △ H5.摩尔热容 Cm ( J K-1 mol-1 ):C m 定容热容CV T2 U = T nC v ,m dTT 1(适用条件:封闭体系、无相变、无化学变化、适用对象:任意的气体、液体、固体物质 W' =0定容过程 )定压热容Cp 丁2= T nC p,m dT T1(适用条件:封闭体系、无相变、无化学变化、W' =0的定压过程适用对象:任意的气体、液体、固体物质 ) 单原子理想气体:Cv,m = 1.5R , Cp,m = 2.5R 双原子理想气体:Cv,m = 2.5R, Cp,m = 3.5R 多原子理想气体:Cv,m = 3R , Cp,m = 4R Cp,m = Cv,m + R6.理想气体热力学过程△ U 、△ H 、Q 、W^H A S 的总结C p dT△ Cp ( T2 - T1)10.热机的效率为 对于卡诺热机 W Q 亠 Q 2Q 2--- zzj -------------- =1 "r : Q Q [ ---------------- Q [W Q 1 Q Q 1Q|★ ~T 2 T 1可逆循环过程不可逆循环过程11.熵变定义式 (体系经历一可逆过程的热温商之和等于该过程的熵变.)7. 定义:△ fHm 9 (kJ mol-1)-- 标准摩尔生成焓 △ H —焓变;△ rHm —反应的摩尔焓变 △ rHm 9 — 298K 时反应的标准摩尔焓变;△ fHm 9 (B) — 298K 时物质B 的标准摩尔生成焓; △ cHm 9 (B) — 298K 时物质B 的标准摩尔燃烧焓。
物化公式

1. 理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ,V ,T 及n 单位分别为Pa ,m 3,K 及mol 。
m /V V n =称为气体的摩尔体积,其单位为m 3 · mol -1。
R =8.314510 J · mol -1 · K -1,称为摩尔气体常数。
此式适用于理想气体,近似地适用于低压的真实气体。
2. 气体混合物 (1) 组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B*=V ϕ∑*AVy Am,A式中∑AA n 为混合气体总的物质的量。
Am,*V表示在一定T ,p 下纯气体A 的摩尔体积。
∑*AA m,A V y 为在一定T ,p 下混合之前各纯组分体积的总和。
(2) 摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量,∑=BB n n 为混合气体总的物质的量。
上述各式适用于任意的气体混合物。
(3) V V p p n n y ///B B B B *===式中p B 为气体B ,在混合的T ,V 条件下,单独存在时所产生的压力,称为B 的分压力。
*B V 为B 气体在混合气体的T ,p 下,单独存在时所占的体积。
3. 道尔顿定律p B = y B p ,∑=BB p p上式适用于任意气体。
对于理想气体V RT n p /B B =4. 阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。
5. 范德华方程RT b V V a p =-+))(/(m 2mnRT nb V V an p =-+))(/(22式中a 的单位为Pa · m 6 · mol -2,b 的单位为m 3 · mol -1,a 和b 皆为只与气体的种类有关的常数,称为范德华常数。
物理化学公式总结

物理化学公式总结物理化学是研究物质变化及其中发生的物理现象的学科,公式是物理化学研究的基础工具之一。
本文将对一些常用的物理化学公式进行总结和解析,帮助读者更好地理解这些公式的实际应用。
1. 状态方程状态方程描述了物质的状态及其性质与条件之间的关系。
其中,最为著名的状态方程是理想气体状态方程:PV = nRT。
它表达了气体的压强(P)、体积(V)、摩尔数(n)与温度(T)之间的关系,其中 R 是气体常数。
2. 阿伏伽德罗定律阿伏伽德罗定律是描述理想气体摩尔浓度与分压之间的关系的公式。
根据阿伏伽德罗定律,理想气体的摩尔浓度与其分压成正比:C = kP,其中 C 是摩尔浓度,P 是分压,k 是比例常数。
3. 物质的摩尔浓度物质的摩尔浓度表示单位体积或单位质量物质中包含的物质的量。
它可以用以下公式表示:C = n/V,其中 C 是摩尔浓度,n 是物质的摩尔数,V 是溶液的体积。
4. 热力学公式热力学是研究能量转化和能量变化规律的学科。
热力学公式中最为著名的是热力学第一定律:ΔU = q + w,其中ΔU 是系统内能的变化量,q 是系统吸热量,w 是系统对外做功。
5. 熵的变化熵是描述系统混乱程度的物理量,它可以用来分析物质在化学反应中的状态变化。
熵的变化可以用以下公式表示:ΔS = ΔS_prod - ΔS_react,其中ΔS 是熵的变化量,ΔS_prod 是生成物的总熵变,ΔS_react 是反应物的总熵变。
6. 酸碱中和反应酸碱中和反应是常见的化学反应类型之一。
在酸碱中和反应中,酸和碱反应生成盐和水。
一些重要的酸碱中和反应公式包括酸的离解方程式(例如 HCl -> H+ + Cl-)和碱的离解方程式(例如NaOH -> Na+ + OH-)。
7. 溶解度平衡常数溶解度平衡常数是描述溶液中溶质的溶解程度的物理化学参数。
对于一般的溶液,溶解度平衡常数可以用以下公式表示:Ksp =[A+]^m[B-]^n,其中 Ksp 是溶解度平衡常数,[A+] 是阳离子的浓度,[B-] 是阴离子的浓度,m 和 n 是阳离子和阴离子在化学方程式中的系数。
物化公式归纳

物化公式归纳物化公式归纳第一章化学热力学基础公式总结1.体积功 We = -Pe △V2.热力学第一定律的数学表达式△U = Q + W 3.n mol 理想气体的定温膨胀过程.定温可逆时:Wmax=-Wmin=4.焓定义式 H = U + PV在封闭体系中,W ′= 0,体系发生一定容过程Qv = △U在封闭体系中,W ′= 0,体系发生一定压过程 Qp = H2 – H1 = △H5.摩尔热容Cm ( J ·K-1·mol-1 ): 定容热容 CV(适用条件 :封闭体系、无相变、无化学变化、W ′=0 定容过程适用对象 : 任意的气体、液体、固体物质)定压热容 Cp(适用条件:封闭体系、无相变、无化学变化、W ′=0 的定压过程适用对象 : 任意的气体、液体、固体物质)单原子理想气体: Cv,m = 1.5R , Cp,m = 2.5R 双原子理想气体:Cv,m = 2.5R , Cp,m = 3.5R 多原子理想气体: Cv,m = 3R , Cp,m = 4RCp,m = Cv,m + R6.理想气体热力学过程ΔU 、ΔH 、Q 、W 和ΔS 的总结=21,T T mp dTnCH 1221lnln P P nRT V V nRT =nC C m =?=21,T T m V dTnC U7.定义:△fHm θ(kJ ·mol-1)-- 标准摩尔生成焓△H —焓变;△rHm —反应的摩尔焓变△rHm θ—298K 时反应的标准摩尔焓变;△fHm θ(B)—298K 时物质B 的标准摩尔生成焓;△cHm θ(B) —298K 时物质B 的标准摩尔燃烧焓。
8.热效应的计算由物质的标准摩尔生成焓计算反应的标准摩尔焓变△rH θm = ∑νB △fH θm ,B 由物质的标准摩尔燃烧焓计算反应的标准摩尔焓变△rH θm = -∑νB △cH θm ,B 9.Kirchhoff (基尔霍夫)方程△rHm (T2) = △rHm (T1) + 如果ΔCp 为常数,则△rHm (T2) = △rHm(T1) + △Cp ( T2 - T1)10.热机的效率为对于卡诺热机= 可逆循环过程< 不可逆循环过程11.熵变定义式(体系经历一可逆过程的热温商之和等于该过程的熵变.)12.热力学第二定律的数学表达式(不等式中, ― > ‖号表示不可逆过程, ― = ‖ 号表示可逆过程― T ‖—环境温度 , 对可逆过程也是体系温度. )13.熵增原理 (孤立体系的熵永不减少) △S 孤立≥ 0 > 不可逆过程, 自发过程 = 可逆过程, 体系达平衡.对于封闭体系△S 孤立= △S 封闭+ △S 环境≥ 0 > 不可逆过程, 自发过程 = 可逆过程, 体系达平衡14.定温定压的可逆相变15.化学反应熵变的计算△rS θm = ∑νBS θm ,B16.△rH θm 和△rS θm 与温度的关系:△rH θ m (T2) = △rH θ m (T1) + △rS θ m (T2) = △rS θ m (T1) +1211Q Q Q Q W R +=-=ηdTC p T T ?21121211Q Q Q Q Q Q W +=+=-21T T T -=2211≤+T Q T Q RBAA B TQ S S S (δ?=-=?∑≥?i iiTQ S (δTQdS δ≥环体环环环境T Q T Q S - ==相变,相变T Hn S m ?=dTC p T T ?21TC p T T ??21第二章自由能、化学势和溶液公式1.第一和第二定律的联合公式为2.吉布斯自由能定义式G = U + PV – TS = H – TS△G =△H -T △S(G----体系的状态函数, ( J ) , 绝对值无法测量) 3.在定温定压下,有如下关系:ΔG=W’最大 4.吉布斯自由能判据< 不可逆过程, 自发过程 = 可逆过程, 平衡态 > 反方向为自发过程5.判断过程方向及平衡条件的总结6定压下.对任意相变或化学变化7.定温物理变化?G 的计算(W’=0的封闭体系). 理想气体定温过程0≥'+--W dV P dU dS T e e δ0,,≤'W P T dG 0,,≤?'W P T G S TGP ?-=)(===?212112lnP P P P T P P nRT dP PnRT dP V G. 纯液体或纯固体的定温过程. 定温定压可逆相变 dG = -SdT + VdP dT =0 dP =0 ?G T , P, W' = 0 。
物理化学公式总结

物理化学公式总结物理化学是研究物质的结构、性质和变化的科学,它使用数学和物理的原理来解释化学现象。
在物理化学的研究过程中,涉及到许多重要的公式,这些公式是揭示物质性质和相互作用规律的基础。
下面我将为大家总结一些物理化学中常见的公式。
1. 热力学公式热力学公式描述了物质在热平衡状态下的性质和能量转化规律。
其中最基本的公式是热力学第一定律(能量守恒定律):∆U = q + w其中,∆U表示系统内能的变化,q表示传递给系统的热量,w 表示系统对外界做的功。
2. 热力学第二定律热力学第二定律描述了能量的定向流动规律。
其中最著名的公式是卡诺热机效率公式:η = 1 - Tc/Th其中,η表示卡诺热机的效率,Tc表示冷热源的温度,Th表示热源的温度。
3. 热力学公式一般表达式根据热力学第一定律,可以推导出一般的热力学公式:dU = TdS - PdV其中,dU表示系统内能的微小变化,T表示温度,dS表示系统的熵变化,P表示压力,dV表示体积的微小变化。
4. 热力学常用关系根据热力学公式一般表达式,可以得到一些重要的热力学关系:Gibbs自由能(G)与焓(H)的关系:G = H - TS其中,G表示Gibbs自由能,H表示焓,T表示温度,S表示熵。
5. 气体状态方程气体状态方程描述了理想气体和实际气体之间的关系。
最常见的气体状态方程是理想气体状态方程:PV = nRT其中,P表示压力,V表示体积,n表示气体的摩尔数,R表示气体常数,T表示温度。
6. 麦克斯韦速率分布定律麦克斯韦速率分布定律描述了气体分子速度的分布规律。
根据麦克斯韦速率分布定律,可以得到气体分子的平均动能(等于温度的能量):KE = (3/2) kT其中,KE表示气体分子的平均动能,k表示玻尔兹曼常数,T表示温度。
7. 热容公式热容公式描述了物质温度变化时的热量和温度之间的关系。
最常用的热容公式是:C = q/∆T其中,C表示热容,q表示吸收或释放的热量,∆T表示温度变化。
物化公式总结

1. Ω是热力学概率,K 是玻尔兹曼常数,k=R/N=1.3807×10^(-23)J/K2. 在温度趋近于热力学温度0 K 时的等温过程中,体系的熵值不变。
即:3. 在0 K 时,任何完整晶体的熵等于零。
4.规定熵 4. 摩尔熵5.化学反应熵变任意温度下(无相变),,,,()()r m m G m H m A m B S gS hS aS bS ∆=+-+ln =⋅ΩB S k =⋅log S k w0lim 0→∆=T S n S S T m T =,hH gG bB aA +−→−+,298.15()(298.15K)T p m r m r m C dT S T S T ∆∆=∆+⎰0()(0)T p C S S T S K dTT ∆=-=⎰6. 亥姆霍兹能 -dFT ≥ -δ W吉布斯能当封闭系统在等温、等容、非体积功 W ' = 0 的条件下封闭系统在等温、等压、W ’=0 条件下上式中的W 为总功,为体积功(-P ed V )与非体积功W '之和。
7. 当封闭系统在等温、等容、非体积功 W ' = 0 的条件下: 自发过程可逆过程或处于平衡态F U TS ≡-',,0()0T V W F =∆≤',,0()0T V W F =∆<',,0()0T V W F =∆=',,0()0T V W F =∆>00',,()T P W G =∆<',()T P dG W δ-≥-00',,()T p W G =∆≤G H TS≡-',,0()0T V W F =∆≤00',,()T P W G =∆=不可能自发进行的过程8.9. 封闭系统、组成不变、只做体积功(W ' = 0)。
10. 麦克斯韦(Ma xwell)关系式00',,()T P W G =∆>=-dU TdS pdV=+dH TdS Vdp =--dF SdT pdV=-+dG SdT Vdp∂∂=-∂∂(()S V p T V S ∂∂=∂∂((S p T V p S ∂∂=∂∂((V T p S V T ∂∂=-∂∂((p T S V p T11.理想气体,等温 12.13. 21nRT G dp p ∆=⎰21ln p nRT p =21nRT F dV V ∆=-⎰21ln p nRT p =2()()G H T T T ∆∂∆=-∂212111(()(G G H T T T T ∆∆-=∆-。
物化公式整理整理版
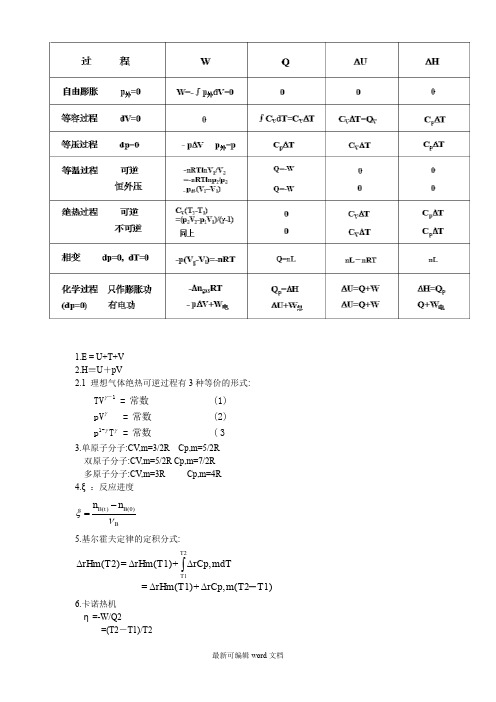
1.E = U+T+V2.H ≡U +pV2.1 理想气体绝热可逆过程有3种等价的形式:(3)常数= T p (2)常数 = pV (1)常数= TV -1-1γγγγ3.单原子分子:CV,m=3/2R Cp,m=5/2R双原子分子:CV,m=5/2R Cp,m=7/2R多原子分子:CV,m=3R Cp,m=4R4.ξ:反应进度B B t B n n νξ)0()(-=5.基尔霍夫定律的定积分式:T1)-m(T2rCp, +rHm(T1)= mdTrCp, +rHm(T1) =rHm(T2)T2T1∆∆∆∆∆⎰6.卡诺热机η=-W/Q2=(T2-T1)/T2=1-(T1/T2)7.熵的微观意义:S=klnWW:宏观状态拥有的微观运动状态的数量k :Boltzmann 常数8.纯物质B 在状态(T,p)的规定熵即为下述过程的熵变:),()0(p T B K B →Kp T B TK p T B S S S S 0,0),(-=∆= 9. 等温过程的熵变: (理想气体)(p1/p2)nRln = S p2/p1=V2/V1∴p2V2=p1V1∵(1) (V2/V1)nRln = S1)/TnRTln(V2/V =-WR/T =QR/T =QR/T ∫=S ∆∆∆δ 10. 绝热过程:绝热可逆过程, 由熵的判别式:0 = S ∆ 绝热可逆 (2)绝热不可逆过程: 对此类过程需设计一条可逆途径, 从相同的始态到相同末态, 再沿可逆途径求算熵变.11. 变温过程: 简单体系A. 等压变温:)Cpln(T2/T1 = (4)(Cp/T)dT =QR/T ∫=SCpdT=QR ⎰∆δδB. 等容变温:ln(T2/T1)C = /T)dT ∫(C =/T Q ∫=SdTC =Q V V R V R δδ∆12.相变过程:平衡相变:平衡相变是一可逆过程, 在等温等压下进行./T Q =Q/T ∫=S R δ∆平衡相变有:H =Qp ∆ 故平衡相变的熵变为:相变H/T =S ∆∆ (6)即:平衡相变的熵变等于相变潜热除以相变温度13.理想气体的混合过程:(1).A, B 先各自等温可逆膨胀到各自的末态;(2).可逆混合.第一步的熵变为:2Rln2= )/V Rln(V +)/V Rln(V =S +S =S1B 1,B 2,A 1,A 2,B A ∆∆∆第二步熵变为零14.赫氏自由能 F ≡U -TS状态函数,广度性质,没有明确的物理意义,具有能量的量纲.15.在等温过程中,一封闭系统所能作的最大功等于系统的亥姆霍兹函数的减少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,能与焓。
二、基本定律 热力学第一定律:ΔU =Q +W 。
三、基本关系式1、体积功的计算 δW = -p 外d V恒外压过程:W = -p 外ΔV定温可逆过程(理想气体):W =nRT 1221ln ln p p nRT V V = 2、热效应、焓:等容热:Q V =ΔU (封闭系统不作其他功)等压热:Q p =ΔH (封闭系统不作其他功)焓的定义:H =U +pV ; ΔH =ΔU +Δ(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容:热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂= 定压热容与定容热容的关系:nR C C =-V p热容与温度的关系:C p ,m =a +bT +cT 2四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p 外d V等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d pC V (㏑T 2-㏑T 1)=nR(㏑V 1-㏑V 2)(T 与V 的关系)C p (㏑T 2-㏑T 1)=nR(㏑P 2-㏑P 1) (T 与P 的关系)不可逆绝热过程:Q =0 ;利用C V (T 2-T 1)=-p 外(V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化 可逆相变化:ΔH =Q =n ΔH ;W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、实际气体节流膨胀:焦耳-汤姆逊系数:μJ-T (理想气体在定焓过程中温度不变,故其值为0;其为正值,则随p 降低气体T 降低;反之亦然)4、热化学标准摩尔生成焓:在标准压力和指定温度下,由最稳定的单质生成单位物质的量某物质的定压反应热(各种稳定单质在任意温度下的生成焓值为0) 标准摩尔燃烧焓:…………,单位物质的量的某物质被氧完全氧化时的反应焓第二章 热力学第二定律一、基本概念 自发过程与非自发过程二、热力学第二定律热力学第二定律的数学表达式(克劳修斯不等式)T Q dS δ≥“=”可逆;“>”不可逆三、熵(0k 时任何纯物质的完美结晶丧子为0)1、熵的导出:卡若循环与卡诺定理(页522、熵的定义:T Q dS rδ=3、熵的物理意义:系统混乱度的量度。
4、绝对熵:热力学第三定律5、 熵变的计算(1)理想气体等温过程:2112ln ln p p nR V V nR T Q S r ===∆ (2)理想气体等压过程:12,ln T T nC S m p =∆ (3)理想气体等容过程:12,ln T T nC S m V =∆ (4)理想气体pTV 都改变的过程:2112,ln ln p p nR T T nC S m p +=∆ (5)可逆相变化过程:T H n S _∆=∆(6)化学反应过程:)298,()298(B S S m B m r ∑=∆θθν四、赫姆霍兹函数和吉布斯函数1、定义:A=U-TS ;G=H-TS等温变化:ΔA=ΔU-T ΔS ;ΔG=ΔH-T ΔS2、应用:不做其他功时,ΔG T ,p ≤0 ;自发、平衡3、热力学重要关系式:dU=TdS-pdV ;dH=TdS+Vdp【页72】 dA=-SdT- pdV ;dG=-SdT+Vdp4、ΔA 和ΔG 的求算(1)理想气体等温过程用公式:ΔA=ΔU-T ΔS ;ΔG=ΔH-T ΔS用基本关系式:d A =-S d T - pdV ;d G =-S d T + Vdp(2)可逆相变过程 ΔA=ΔU-T ΔS =W =-nRT ;ΔG =0(3)化学反应过程的ΔG 标准熵法:ΔG=ΔH-T ΔS标准生成吉布斯函数法:)298,()298(B G G m f B m r θθν∆=∆∑(4)ΔG 与温度的关系ΔG=ΔH-T ΔS ,设ΔH 、ΔS 不随温度变化。
第三章化学势1、化学势的定义。
物理意义:决定物质传递方向的限度的强度因素。
)(,,)(B c c n p T BB n G ≠∂∂=μ ;在T 、p 及其他物质的量保持不变的情况下,增加1molB 物质引起系统吉布斯函数的增量。
(又称偏摩尔量。
1、只有系统的容量性质才有偏摩尔量,故系统强度性质没有偏摩尔量【页8有两种性质定义】2、只有在定稳T ,定压P 下才成为偏摩尔量)2、化学势的应用在等温等压不作其他功时,∑B B μν<0自发;=0平衡;>0逆向自发3、化学时表示式理想气体:)/ln(θθμμp p RT += 纯固体和纯液体:θμμ=拉乌尔定律和亨利定律1、拉乌尔定律p A =p *x A (溶液中该物质蒸汽压=纯该物质蒸汽压*溶液中该物质物质量分数【理想】) 适用于液态混合物和溶液中的溶剂。
2、亨利定律p B =k x,x B (与溶液平衡的溶质蒸汽的分压=亨利系数*溶质在溶液中的摩尔分数)适用于溶液中的溶质。
二、液态混合物和溶液中各组分的化学势1、理想液态混合物x RT T mix p T x ln )(),,(+=θμμ 标准态为:同温下的液态纯溶剂。
2、真实液态混合物x x a RT T mix p T ln )(),,(+=θμμ 标准态为:同温下的液态纯溶剂。
3、理想稀溶液溶剂:A A x A x RT T sln p T ln )(),,(+=θμμ 标准态为:同温下的液态纯溶剂。
溶质:B B x B x RT T sln p T ln )(),,(+=θμμ 标准态为:同温下x B =1且符合亨利定律的溶质。
4、真实溶液 溶剂:A x A x A a RT T sln p T ,,ln )(),,(+=θμμ ;a x,A =f x,A x ; 标准态为:同温下的液态纯溶剂。
溶质:B x B x B a RT T sln p T ,ln )(),,(+=θμμ ; a x,B =γx,B x B ; 标准态为:同温下x B =1且符合亨利定律的溶质。
B b B b B a RT T sln p T ,,ln )(),,(+=θμμ; ab,B =γb,B b B ; 标准态为:同温下b B =1且符合亨利定律的溶质。
理想稀溶液的凝固点降低B A m fus f f f x H T RT T ,*∆=∆第四章 化学平衡一、化学平衡常数与平衡常数表达式二、 标准平衡常数的求算:θθK RT T G m r ln )(-=∆ 三、 特荷夫等温方程θθK RT T G m r ln )(-=∆+RT ㏑Q P(页114 四、平衡常数与温度的关系θθθm r m r m r S T H T G ∆-∆=∆)(;θθK RT T G m r ln )(-=∆五、平衡常数的各种表示方法:(页121K p 、K x 是气相反应的经验平衡常数。
其与标准平衡常数关系为: K θ=K p (p θ)-△V (产物与反应物计量数之差)=K x (p/ p θ)△V =K n (p/ p θn 总)△V若△v=0则K θ=K p =K x =K n分解压:固体物质在一定温度下分解达到平衡时产物中气体的总压力第五章 多相平衡一、相律1、系统中所包含的相的总数称为相数,以Ф表示。
最小值为1。
正整数2、一个系统中无论多少气体都为一个气相;系统一般一两个液相;多少固体物质便有多少固相。
3、系统中所含化学物质书称为“物种数”以S 表示,最小值为1.正整数4、足以表示系统中各相组成所需的最少独立物种数称为系统“组分数”,以K表示。
组分数=物种数-独立化学平衡数-独立浓度关系数 K=S-R-R ,自由度:在不引起旧相消失和新相形成的前提下,可在一定围独立变动的强度性质,以f 表示只考虑温度与压力因素的影响时f =K -φ+2,(f =K -φ+1指定温度或压力)。
最小值为0二、单组分系统 1、克-克方程 )11(ln 2112T T R H p p m vap -∆=2、水的相图 三面、三线、一点。
三、二组分系统 1、步冷曲线(页1702、看相图:有“丁”字型相则说明有不稳定化合物生成。
第六章(没学不考)第七章 电化学通过电极电荷量:Q=nF (n 为电极反应时得失电子的物质的量,F为1mol 电子电荷量,叫法拉第,通常取96.5kC/mol )一、电解质溶液的电导1、电导 G =1/R ; 单位:S(西门子)2、电导率 G =κA /l 或κ=G l /A ; 单位:S/m3、摩尔电导率 Λm =κ/c4、无限稀释摩尔电导率 ∞--∞++∞+=ΛΛΛm νν5、离子的电迁移l E U ∆=++υ ;-++--+++++=+===U U U I IQ Qt υυυ ;1=+-+t t二、电解质溶液的活度(229页表格1、电解质的化学势(电解质溶液的浓度用m B 或b B 表示)B B B a RT ln +=θμμ;)(;)(;/)(;/1/1/1ννννννθννννγγγγ-+-+-+-+±-+±±±-+±±⋅=⋅=⋅=⋅==m m m m m a a a a a B 2、离子强度 ∑=221B B z m I 电池系列 一、可逆电池的构成电池反应互为逆反应;充放电时电流无穷小。
二、可逆电池热力学1、(△r G m )T,P =-nFE=-QE2、p m r T E zF S )(∂∂=∆4、m r r S T Q ∆= ;电池反应做了其他功。
三、能斯特方程四、可逆电极的种类1、第一类电极:金属电极;气体电极2、第二类电极:微溶盐电极;微溶氧化物电极3、第三类电极:氧化还原电极电池表示式(1)以化学式表示电池中各种物质的组成,并需分别注明固液气等物态。
对气体注明压力,对溶液注明浓度(2)以“|”表示不同物相之间的界面,包括电极与溶液的接界和不同溶液间的接界。
盐桥以“||”(3)电池中的负极(氧化反应)写在左边。
五、电极电势的应用1、判断反应趋势2、求化学反应平衡常数3、求微溶盐活度积4、测离子平均活度±γ 六、电动势E=φ(正极电势)-φ(负)= φ(阴)-φ(阳)无论原电池还是电解池,相对于可逆电极电势φ,当有电流通过电极时,由于电极的极化,阳极电势升高,阴极电势降低,即φ(阳)=φ+μ,φ(阴)=φ-μ1、浓差极化:电极反应速度比离子迁移速度快造成的。
