初中几何难度题100道(上)(PDF版 含解答)
初中难度几何100题

第一题:已知:ABC ∆外接于⊙O ,︒=∠60BAC ,BC AE ⊥,AB CF ⊥,AE 、CF 相交于点H ,点D 为弧BC 的中点,连接HD 、AD 。
求证:AHD ∆为等腰三角形第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE。
CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC 。
求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB 。
求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB 。
求ACD ∠。
BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =。
求证:222BD BC AB =+DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D。
求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA 。
求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形。
第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC。
PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFDEB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =。
求证:︒=∠60ACBA第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠。
初中难度几何100题

第一题:已知:ABC ∆外接于⊙O ,︒=∠60BAC ,BC AE ⊥,AB CF ⊥,AE 、CF 相交于点H ,点D 为弧BC 的中点,连接HD 、AD 。
求证:AHD ∆为等腰三角形第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE。
CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC 。
求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB 。
求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB 。
求ACD ∠。
BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =。
求证:222BD BC AB =+DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D。
求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA 。
求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形。
第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC。
PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFDEB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =。
求证:︒=∠60ACBA第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠。
(完整版)初中数学几何题(超难)及答案分析

(完整版)初中数学⼏何题(超难)及答案分析⼏何经典难题1、已知:如图,O 是半圆的圆⼼,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初三)2、已知:如图,P 是正⽅形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三⾓形.(初⼆)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正⽅形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正⽅形.(初⼆)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂⼼(各边⾼线的交点)(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外⼀直线,过O 作OA ⊥MN 于A ,⾃A,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移⾄圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初三)8、如图,分别以△ABC 的AC 和BC 为⼀边,在△ABC 的外侧作正⽅形ACDE 和正⽅形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的⼀半.N9、如图,四边形ABCD 为正⽅形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初⼆)10、如图,四边形ABCD 为正⽅形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正⽅形ABCD ⼀边BC求证:PA =PF .(初⼆)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三⾓形,P 是三⾓形内⼀点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初⼆)14、设P 是平⾏四边形ABCD 内部的⼀点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初⼆)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平⾏四边形ABCD 中,设E 、F 分别是BC 、AB 上的⼀点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 内任⼀点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正⽅形ABCD 内的⼀点,求PA +PB +PC 的最⼩值.19、P 为正⽅形ABCD 内的⼀点,并且PA =a ,PB =2a ,PC =3a ,求正⽅形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH ⊥AB,连接EO 。
初中难度几何100题

已知:ABC ∆外接于⊙O ,︒=∠60BAC ,BC AE ⊥,AB CF ⊥,AE 、CF 相交于点H ,点D 为弧BC 的中点,连接HD 、AD 。
求证:AHD ∆为等腰三角形第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE。
CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC 。
求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB 。
求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB 。
求ACD ∠。
BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =。
求证:222BD BC AB =+DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D。
求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA 。
求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形。
第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC。
PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFDEB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =。
求证:︒=∠60ACBA第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠。
初中难度几何100题

第一题:已知:ABC ∆外接于⊙O ,︒=∠60BAC ,BC AE ⊥,AB CF ⊥,AE 、CF 相交于点H ,点D 为弧BC 的中点,连接HD 、AD 。
求证:AHD ∆为等腰三角形第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE 于点E,连接CE,且AC=AE。
CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC 。
求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB 。
求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB 。
求ACD ∠。
BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =。
求证:222BD BC AB =+DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO 相交于B、D。
求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA 。
求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形。
第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC。
PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFDEB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =。
求证:︒=∠60ACBA第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠。
初中几何难度题100道(上)(PDF版 含解答)

BA=BE,由∠ADB=45°得∠EDB=45°
E
∴A、D、E、B 四点共圆,∠ABE=∠ADE=
90°
即 AB⊥BC。
A
D
C
第五题:
如图,四边形 ABCD 的两条对角线 AC 、 BD 交于点 E , BAC 50 , ABD 60 ,
CBD 20 , CAD 30 , ADB 40 。求 ACD 。
证明:过 C 作 CG⊥PO 于 G,
则由∠AEC=∠PGC=90°得
A
E、B、G、C 四点共圆
同理 F、D、G、C 四点共圆
PC 是⊙O 切线,PC 2 PE PF
P
BG O
D
在 RT△PCO 中,PC 2 PG PO
E
∴PE PF PG PO ,
F
∴E、G、O、F 四点共圆。∴∠OGF
=∠OEF,∠BGE=∠OEF,∴∠
BCP ACQ 30 , ABR BAR 15 。求证: RQ 与 RP 垂直且相等。
简证:以 BR 为边作正三角形(如图)
则△ORA 是等腰直角三角形,
C
△OAB∽△PCB,△OBP∽△ABC
△ORP≌△ARQ
∴RQ=RP,RQ⊥RP。
P
Q
O
A
B
R
第十八题:
如图,已知 AD 是⊙ O 的直径,D 是 BC 中点,AB 、AC 交⊙ O 于点 E 、F ,EM 、FM
C
OGF=∠BGE
又 CG⊥PO 得∠EGC=∠FGC,∠EGF=∠EOF=2∠EAF,∴∠EGC=∠FGC=∠EAF
又∠EGC=∠EBC,∠FGC=∠FDC,∴∠EBC=∠FDC=∠EAF
∴AF∥BC,AE∥CD,∴四边形 ABCD 是平行四边形。
初中难度几何100题学习资料
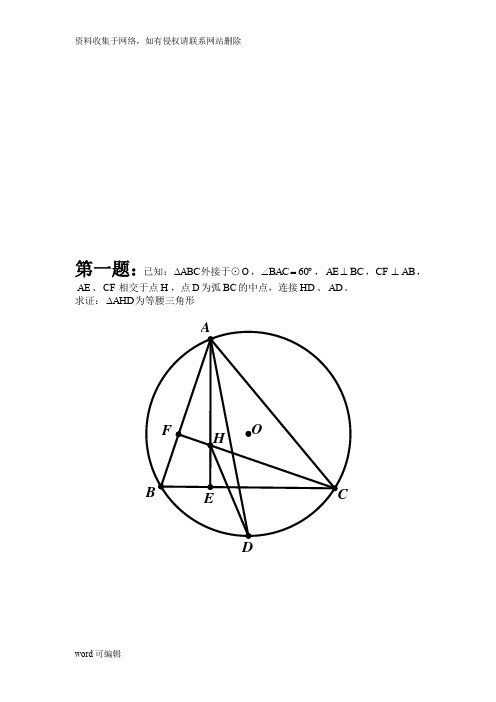
第一题:已知:ABCCF⊥,BAC,BCAE⊥,AB∆外接于⊙O,︒=∠60AE、CF相交于点H,点D为弧BC的中点,连接HD、AD。
求证:AHD∆为等腰三角形第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE。
CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC 。
求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB 。
求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB 。
求ACD ∠。
BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =。
求证:222BD BC AB =+DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D。
求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA 。
求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形。
第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC。
PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFDEB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =。
求证:︒=∠60ACBA第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠。
初中难度几何100题

第一题:已知:ABC ∆外接于⊙O ,︒=∠60BAC ,BC AE ⊥,AB CF ⊥,AE 、CF 相交于点H ,点D 为弧BC 的中点,连接HD 、AD 。
求证:AHD ∆为等腰三角形第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE。
CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC 。
求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB 。
求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB 。
求ACD ∠。
BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =。
求证:222BD BC AB =+DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D。
求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA 。
求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形。
第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC。
PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFDEB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =。
求证:︒=∠60ACBA第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E
简证:以 AD 为边作正三角形 ADE(如图)
易知△ABC≌△CAE
D
∴AD=AE=BC。
B
C
第四题:
已知: ABC 中, D 为 AC 边的中点, A 3C , ADB 45 。求证: AB BC
简证:过 D 作 DE⊥AC 交 BC 于 E
由已知得 AE=EC,∠EAD=∠C
B
又∠A=3∠C,∴∠BAE=∠BEA
B
C
第十题:
已知:正方形 ABCD 中, E 、 F 为 AD 、 DC 的中点,连接 BE 、 AF ,相交于点 P ,连
接 PC 。求证: PC BC
简证:易知△ABE≌△DAF
BE⊥AF,∴B、C、F、P 四点共圆
∠BPC=∠BFC ∠PBC=∠BEA
A
E
D
而∠BEA=∠BFC
∴∠BPC=∠PBC
C
OGF=∠BGE
又 CG⊥PO 得∠EGC=∠FGC,∠EGF=∠EOF=2∠EAF,∴∠EGC=∠FGC=∠EAF
又∠EGC=∠EBC,∠FGC=∠FDC,∴∠EBC=∠FDC=∠EAF
∴AF∥BC,AE∥CD,∴四边形 ABCD 是平行四边形。
第八题:
已知:在 ABC 中, AB AC , A 80 , OBC 10 , OCA 20。
D
A D D A x (y 1)i ,
E
∴
F
AE
i
2A D e 4
2[x (y 1)i]
2
(1
i
)
x
y
1
C
(y
x
1)i
B
2
∴ E A A E i x y 1 (y x 1)i x y 1 (y x )i
∴ DF
2
DC
i
e 4
,
2
∴ F D DF x yi 2 (x yi) 2 (1 i) 1 (x y ) 1 (y x )i
简证:作点 E 关于 AD 对称点 G,则 DE⊥DG
△CDG≌△ADE,△ACG 是等边三角形。
∠GAC=60°,∠DAF=15°,∠CEF=30°,
∠DEF=30°,∠CFE=30°,
∴△CEF 是等腰三角形。CE=CF。
B
G D
F E
C
第三题:
A
已知:ABC 中,AB AC ,BAC 20 ,BDC 30 。 求证: AD BC
证明:过 C 作 CG⊥PO 于 G,
则由∠AEC=∠PGC=90°得
A
E、B、G、C 四点共圆
同理 F、D、G、C 四点共圆
PC 是⊙O 切线,PC 2 PE PF
P
BG O
D
在 RT△PCO 中,PC 2 PG PO
E
∴PE PF PG PO ,
F
∴E、G、O、F 四点共圆。∴∠OGF
=∠OEF,∠BGE=∠OEF,∴∠
初中教师转正必做 100 题
第一题:
已知: ABC 外接于⊙ O ,BAC 60 , AE BC ,CF AB , AE 、CF 相交
于点 H ,点 D 为弧 BC 的中点,连接 HD 、 AD 。求证: AHD 为等腰三角形
简证:易证∠BHC=120°,∠BOC=120°,∴B、H、
O、C 四点共圆。
2
2
2
2
∵ E B x y (y x )i 2F
∴F 是 EB 中点,∴△CDF 是等腰直角三角形,∠CFD=90°。
第十二题:
已知:ABC 中,CBA 2CAB ,CBA 的角平分线 BD 与 CAB 的角平分线 AD 相
则 BC⊥BE, BE 2 BC 2 CE 2
易证△DAB≌△CAE,BD=CE
于是 A B 2 BC 2 BD2 。
A
D
B
C
第七题:
如图, PC 切⊙ O 于 C , AC 为圆的直径, PEF 为⊙ O 的割线, AE 、 AF 与直线 PO 相
交于 B 、 D 。求证:四边形 ABCD 为平行四边形
解:设 AD、BC 交于点 F,过 D 作 DG∥AB
交 BF 于点 G,AG 交 BD 于 H。则
A
△ABF 是等腰三角形,A、B、G、D 四点共
圆。
∠DAG=∠DBG=20°,∴∠BAG=60°
∠BDG=∠BAG=60°,∠AGD=∠ABD =60°∴△GHD 是等边三角形。△ABH 是 B 等边三角形
P
∴PC=BC。
F
B
C
第十一题:
如图,ACB 与 ADE 都是等腰直角三角形,ADE ACB 90 ,CDF 45 ,DF 交 BE 于 F ,求证: CFD 90
A
证明:只要证明△CDF 是等腰直角三角形时,E、F、B 共线即可。
设C 0 ,B 1, A i , D x yi(x,y ) ,则
已知:正方形 ABCD 中, OAD ODA 15 ,求证: OBC 为正三角形。
简证:以 BC 为边作正三角形 BCO'(如图),
则 AB=O'B,∠ABO'=30°,
A
∴∠BAO'=75°,∠DAO'=15°
D O
同理∠ADO'=15°
O'
于是△ADO'≌△ADO
∴O 与 O'重合
∴△OBC 是正三角形。
A
DB=DO=DC,∴DH=DO=OA,又 AH∥OD,∴
AHDO 是菱形
∴AH=HD,△AHD 为等腰三角形。
FH
O
B
E
C
D
第二题:
A
如图,F 为正方形 ABCD 边 CD 上一点,连接 AC 、
AF ,延长 AF 交 AC 的平行线 DE 于点 E ,连接
CE ,且 AC=AE。求证: CE CF
H
D
E
BH=AB=BC,∴∠BHC=80°,∴∠CHG =40°
C G
∴∠HGC=40°,∴HC=GC,∴△HCD≌
△GCD
F
∴∠HDC=30°,∴∠ACD=80°。
第六题:
已知, ABC 30 , ADC 60 , AD DC 。求证: AB2 BC2 BD2
简证:以 AB 为边向外作正三角形 ABE E
BA=BE,由∠ADB=45°得∠EDB=45°
E
∴A、D、E、B 四点共圆,∠ABE=∠ADE=
90°
即 AB⊥BC。
A
D
C
第五题:
如图,四边形 ABCD 的两条对角线 AC 、 BD 交于点 E , BAC 50 , ABD 60 ,
CBD 20 , CAD 30 , ADB 40 。求 ACD 。
பைடு நூலகம்
求证: AB OB
简证:延长 CO 交 AB 于 D,以 OC 为边作正三角
形 OCE(如图)
A
易知 AC=DC,BD=OD,OC=AD
△ACE≌△CAD,△ACO≌△AEO,
D
∠CAO= 1 ∠CAE=10°
2
∴∠BAO=70°,∠ABO=40°
O
∴∠BOA=70°,∴AB=OB。
B
C
E
第九题:
