发动机传动电机的转速控制BP+PI
电机驱动及PID算法
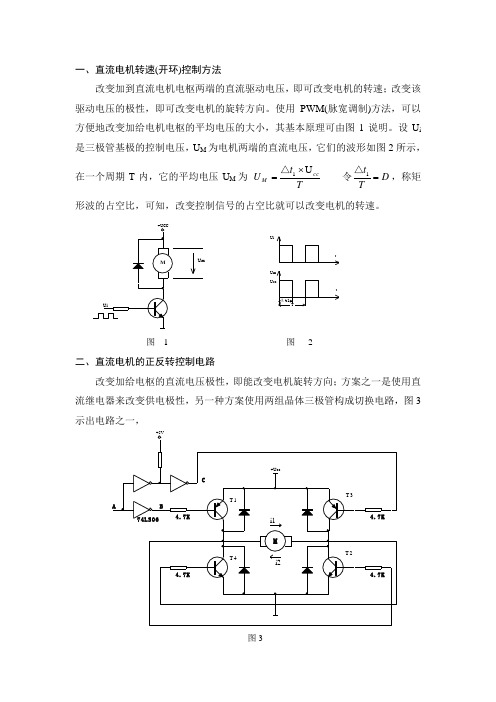
一、直流电机转速(开环)控制方法改变加到直流电机电枢两端的直流驱动电压,即可改变电机的转速;改变该驱动电压的极性,即可改变电机的旋转方向。
使用PWM(脉宽调制)方法,可以方便地改变加给电机电枢的平均电压的大小,其基本原理可由图1说明。
设U i 是三极管基极的控制电压,U M 为电机两端的直流电压,它们的波形如图2所示,在一个周期T 内,它的平均电压U M 为 Tt U ccM U 1⨯=△ 令DTt =1△,称矩形波的占空比,可知,改变控制信号的占空比就可以改变电机的转速。
图 1 图 2二、直流电机的正反转控制电路改变加给电枢的直流电压极性,即能改变电机旋转方向;方案之一是使用直流继电器来改变供电极性,另一种方案使用两组晶体三极管构成切换电路,图3示出电路之一,图3UitUm UccTtΔt1其工作原理简述如下:当A=1(高电平):则B=0 →T1导通→T2导通;C=1 →T3 截上→T4截上;于是电流i1流经由机M的路径为:Ucc→T1→M→T2→地,电机正转若A=0(低电平):则B=1 →T1截上→T2截上;C=0 →T3导通→T4导通;于是电流i2的流径电机M的路径为:Ucc→T3→M→T4→地,电机反转。
图4是正反转控制的另一种电路,图4其工作原理简述如下:当A=1:则B=0 →T1截上→T2导通C=1 →T4导通→T3截上于是电流i1流径电机M的路径为:Vcc→T2→M→D2→T4→地,电机正转。
当A=0:则B=1 →T1导通→T2截上C=0 →T4截上→T3导通于是电流i2流径电机M的路径为:Vcc→T3→M→D1→T1→地,电机反转。
以上两个电路,以图4为例,在T1、T4的控制输入端B、C处分别加入一个与门(或者与非门)引入PWM 信号,则可以把正反转控制和PWM 调整控制结合起来。
三、整形电路为使不规范脉冲波形的前后沿陡峭,并使其幅值规范为某一定值,须使用整形电路。
通常,使用滞回比较器构成整形电路,它具有抗干扰能力强等特点,在一些简单应用中,也可以使用简单的单阈值比较器。
发动机神经网络自适应PID转速控制

时不可能面面俱到 (常会忽略一些不重要的参数,如
进气歧管截面积随温度的变化、 发动机的磨损情况
等), 常造成发动机模型不精确, 且式
进行研究,将神经网络同 PID 控制相结合,很好地解
决了发动机转速与燃油控制问题,可以使发动机在最
优状态下工作,对节能减排具有重要的现实意义。
化的增益参数。
2.3 仿真结果
仿真条件为:仿真软件为 MATLAB;发动机模型
如上所述;参数优化神经网络中 n=2,m1=2,m2=10,i=
32
农业科技与装备
2014 年 1 月
图 4 发动机模型辨识 NN 结构 Figure 4 Engine model identification NN structure
2014 年第 1 期
吴笑伟等:发动机神经网络自适应 PID 转速控制
31
分燃油量之和。
1.2 PID 算法
发 动 机 的 转 速 控 制 采 用 可 变 增 益 的 PID 方 法 ,
具体控制算法为:
α=Kpε+Ki∫εdt+Kddε/dt
(8)
式 中 :α 为 节 气 门 开 度 ;ε 为 转 速 误 差 ;Kp,Ki,Kd
负载小、发动机各种干扰小的转速控制。 仿真结果还
表明,PID 调节器的转速跟踪 (负载较大时) 效果很
差。
2 发动机转速的神经网络控制
2.1 发动机转速的 NC 设计 对如图 3 所示的控制结构进行研究。 神经网络
NN2 用于建立被控系统的动态模型 , 并为神经网络 NN1 的学习训练过程提供必要信息。 神经网络 NN1 根据系统的状态,不断调节 PID 控制器的增益,以达 到所规定的最优性能指标。
电机转速pi调节公式

电机转速pi调节公式电机转速PI调节公式一、引言电机转速调节是工业控制领域中常见且重要的问题之一。
在许多应用中,精确控制电机的转速对于保证系统的稳定性和性能至关重要。
本文将介绍一种常用的电机转速PI调节公式,旨在提供一种有效的方法来实现电机转速的精确控制。
二、电机转速PI调节公式电机转速PI调节公式通常由两个部分组成:比例控制和积分控制。
比例控制用于根据转速误差的大小调整输出信号的幅度,而积分控制则用于根据转速误差的持续时间调整输出信号的持续时间。
1. 比例控制比例控制的目标是根据转速误差的大小来调整输出信号的幅度,以使转速误差逐渐减小。
比例控制公式如下:输出信号 = Kp × 转速误差其中,Kp为比例系数,用于确定输出信号的幅度大小。
较大的Kp 值将导致较大的输出信号,从而更快地减小转速误差,但也可能引发系统的不稳定性。
2. 积分控制积分控制的目标是根据转速误差的持续时间来调整输出信号的持续时间,以使转速误差逐渐趋于零。
积分控制公式如下:输出信号= Ki × ∫转速误差 dt其中,Ki为积分系数,用于确定输出信号的持续时间。
较大的Ki 值将导致较长的输出信号持续时间,从而更快地减小转速误差,但也可能引发系统的震荡和超调。
3. PI调节公式将比例控制和积分控制结合起来,即可得到电机转速PI调节公式:输出信号 = Kp × 转速误差+ Ki × ∫转速误差 dt通过调整比例系数Kp和积分系数Ki的数值,可以实现对电机转速的精确控制。
较小的Kp和Ki值将导致较慢的响应速度,但可以提高系统的稳定性;较大的Kp和Ki值则可以实现更快的响应速度,但可能导致系统的不稳定性和震荡。
三、结论电机转速PI调节公式是一种常用且有效的方法,可用于实现电机转速的精确控制。
通过调整比例系数Kp和积分系数Ki的数值,可以根据实际需求来平衡系统的响应速度和稳定性。
在实际应用中,需要根据具体情况进行参数调整和实时监控,以保证系统的稳定性和性能。
PID控制PWM调节直流电机速度

模板本次设计主要研究的是PID控制技术在运动控制领域中的应用,纵所周知运动控制系统最主要的控制对象是电机,在不同的生产过程中,电机的运行状态要满足生产要求,其中电机速度的控制在占有至关重要的作用,因此本次设计主要是利用PID 控制技术对直流电机转速的控制。
其设计思路为:以AT89S51单片机为控制核心,产生占空比受PID算法控制的PWM脉冲实现对直流电机转速的控制。
同时利用光电传感器将电机速度转换成脉冲频率反馈到单片机中,构成转速闭环控制系统,达到转速无静差调节的目的。
在系统中采128×64LCD显示器作为显示部件,通过4×4键盘设置P、I、D、V四个参数和正反转控制,启动后通过显示部件了解电机当前的转速和运行时间。
因此该系统在硬件方面包括:电源模块、电机驱动模块、控制模块、速度检测模块、人机交互模块。
软件部分采用C语言进行程序设计,其优点为:可移植性强、算法容易实现、修改及调试方便、易读等。
本次设计系统的主要特点:(1)优化的软件算法,智能化的自动控制,误差补偿;(2)使用光电传感器将电机转速转换为脉冲频率,比较精确的反映出电机的转速,从而与设定值进行比较产生偏差,实现比例、积分、微分的控制,达到转速无静差调节的目的;(3)使用光电耦合器将主电路和控制电路利用光隔开,使系统更加安全可靠;(4)128×64LCD显示模块提供一个人机对话界面,并实时显示电机运行速度和运行时间;(5)利用Proteus软件进行系统整体仿真,从而进一步验证电路和程序的正确性,避免不必要的损失;(6)采用数字PID 算法,利用软件实现控制,具有更改灵活,节约硬件等优点; (7)系统性能指标:超调量≤8%;调节时间≤4s ;转速误差≤±1r/min 。
1 PID 算法及PWM 控制技术简介PID 算法控制算法是微机化控制系统的一个重要组成部分,整个系统的控制功能主要由控制算法来实现。
直流电机PI转速控制(基于STC89C52RC)

{
SBUF=weima[na[i]];//静态显示,依次发送
while(TI==0);//未发送完,即等待
TI=0;//标记位置0
}
}
void timer0() interrupt 1//T0中断响应函数
{
TR0=0;//关闭定时器T0
PWM1=1;//高电平
TH0=0x15;//T0初值,60ms
unsigned int err=0,err_l=0;//全局变量,定义err表示err[k],err_1表示err[k-1]
unsigned int pwmh=0xd8;//全局变量,TH1初值
unsigned int pwml=0xf0;//全局变量,TL1初值
unsigned char weima[10]={0xfc,0x60,0xda,0xf2,0x66,0xb6,0xbe,0xe0,0xfe,0xf6};//LED数
na[1]=(pul%100000)/10000;//LED数码管第5位
na[2]=(pul%10000)/1000;//LED数码管第4位
na[3]= (pul%1000)/100;//LED数码管第3位
na[4]=(pul%100)/10;//LED数码管第2位
na[5]= pul%10;//LED数码管第1位
3.2流程图
图xx程序流程图
STC89C52RC(PDIP-40)单片机没有PWM输出口,所以需要用IO口模拟产生PWM信号,而且要求PWM信号的占空比可调,因此需要对单片机内部的T0、T1定时相关寄存器进行设置,PWM频率(1000/60HZ)由T0设置,改变PWM占空比由改变T1设置实现,即T1定时器的初值TH1和TL1两个寄存器的初值设定。电机的转速由光电传感器来采集,选用单片机的外部中断INT1口统计光电码盘的脉冲个数(pulse),因此需要对单片机的INT1相关寄存器进行设置。转速显示采用LED数码管,利用单片机的串口方式0进行静态显示,故需要对串口的相关寄存器进行设置。基于控制框图和以上说明,流程图绘制如下。图中PWM1表示单片机P1^6口,PWM1表示单片机P1^7口(可参考上文电路原理图部分)。
超声波电动机P与PI型迭代学习转速控制_刘玉

Dቤተ መጻሕፍቲ ባይዱ
超声波电动机 P 与 PI 型迭代学习转速控制
驱动控制 2015 年第 43 卷第 1 期 rive and control 得到的, 即控制量与当前的系统输出转速误差 e k + 1 被控对象的向 是在上述每一次的重复运行过程中, 量函数及其相互之间的函数关系是不变的 。 ( t) 无关。从这一点来看, 图 1 系统实质上是一个开 作为普通和精密运动控制执行部件的超声波电 环控制系统。如前述, 迭代学习控制是针对具有可 动机, 经常工作于具有重复性的运动控制场合。 据 重复性的系统提出的, 其可重复性包含被控对象及 采用迭代学习控制方法, 有可能通过相对简单的 其系统 的 时 不 变 性 质。 对 于 时 不 变 系 统, 采用式 此, 控制器形式、 较小的在线计算量, 利用电机运动的重 ( 1 ) 计算控制量, 能够保持控制的有效性, 因为在每 实现电机控制性能的渐进调整, 并在有限次数 一次重复的控制过程中, 控制对象的特性始终保持 复性, 的重复运动之后, 达到较好的控制性能。 这就为降 不变, 变化的只是随机的扰动信号。 由于随机扰动 的量值通常微小, 采用式 ( 1 ) 有可能保证并加快系 低超声波电动机系统的控制复杂度提供了一种新的 可能思路。 统学习过程的收敛。但是超声波电动机具有明显的 : 迭代学习控制的基本控制规律 时变特性, 采用式( 1 ) 与图 1 形式进行控制, 不能保 u k +1 ( t) = u k ( t) + K P e k ( t) ( 1) 证系统控制过程的有效性。 实验表明, 在阶跃转速 e( t) = N ref ( t) - n( t) ( 2) 给定值情况下, 会导致电机转速跟踪过程中的抖动 式中: t 为时间; u k + 1 ( t ) 为系统第 k + 1 次重复运行 和稳态的转速偏差。因而, 本文将式( 1 ) 改为: , t 时刻的控制器输出控制量, 过程中 在 本文取为超 u k +1 ( t) = u k ( t) + K P e k +1 ( t) ( 3) 声波电动机的驱动频率值; u k ( t) 为系统第 k 次运行 式中: e k + 1 ( t) 为系统第 k + 1 次运行过程 t 时刻的转 过程中 t 时刻的控制量; e ( t ) 为系统第 k 次运行过 k 速误差。 对应于式 ( 3 ) 的控制系统框图 如 图 2 所 程中 t 时刻的转速误差 ; N ref ( t ) 为电机转速给定值 ; 示, 控制形式进一步简化。 n( t) 为电机的实际转速值; 比例环节 K 为学习增 P 式 ( 1 ) 的控制规律又称 益。因学习律为比例环节, 为 P 型迭代学习控制。 迭代学习控制的目的是在系统结构和参数都未 知的前提下, 经过多次重复运行, 控制器的输出 图 2 超声波电动机改进迭代学习控制系统基本框图 u ( t ) u ( t ) , 趋近于事先未知的 从而使得电机转速 d 式( 3 ) 控制量与当前转速误差相关。 从单次控 n( t) 趋近于期望的 N ( t ) 。 当达到控制要求的精 ref 具有闭环控制的性质, 为克服超声波电 制过程来看, 停止迭代学习并保存最近一次运行的控制 度之后, 动机的时变特性提供了可能。从多次重复控制过程 器输入输出数据, 就完成了迭代学习过程。 来看, 每次的控制量都是在记忆前次控制量的基础 上, 根据时变对象当前的误差信息进行修正 , 同样具 刘 有迭代学习的特征, 能够通过迭代使控制过程渐好。 玉 考察式( 3 ) 、 图 2 控制过程的在线计算量, 与传统的 等 固定参数 PID 控制器相比, 仅增加了控制量的一次 图 1 超声波电动机迭代学习控制系统基本框图 超 存储与读取操作, 计算量相当。 图 1 给出了超声波电动机迭代学习转速控制系 声 波 统的基本结构框图。 图中“控制量记忆 ” 、 “误差记 2 P 型迭代学习转速控制 电 “延时” 忆” 与 环节用来存储以前运动过程中的控制 动 机 2 . 1 学习增益 K P 的确定 K P 环节表示学习控制律。这些环节构成 量和误差, 了迭代学习控制器, 采用式( 3 ) 对超声波电动机进行转速控制, 学 对应于式 ( 1 ) 。 显然, 采用不同 习增益 K P 是唯一需要确定的控制参数。 该值不仅 可以得到不同的学习过程和控制过 型 的学习控制律, 迭 与单次控制过程的动态性能相关, 而且直接决定了 控制器的输出为超声波电动机频率的 代 程。系统中, 学 迭代学习过程是否能够收敛。为得到学习过程的收 给定值, 通过驱动电路给出具有相应频率的驱动电 习 转 首先取超声波电动 敛条件, 进而确定合适的 K P 值, 压作用于超声波电动机。与电机同轴刚性连接的旋 速 其与转速给 并设为具有普遍意义的 机的模型为状态方程形式, 控 转编码器检测电机转速得到反馈信号 , 制 [4 ] 定值之差作为控制器的输入, 进而通过重复的迭代 全局 Lipschitz 连续动力系统状态方程 : · 得到更好的控制过程。 x( t) = F( x, u, t) 学习控制, ( 4) 考察式( 1 ) 与图 1 , 系统当前控制过程的控制量 n( t) = G( x, u, t) 40 式中: x( t) 为超声波电动机系统的状态变量。 根据 u k + 1 ( t ) 是由前次的控制量 u k ( t ) 和误差 e k ( t ) 计算
pid转速控制系统设计案例

pid转速控制系统设计案例
以下是一个PID转速控制系统设计的案例,这个案例采用了PID控制算法
来调节电机的转速。
1. 系统方案
首先,我们需要确定系统的整体方案。
在这个案例中,我们将采用一个比例-积分-微分(PID)控制器来调节电机的转速。
这个方案的目标是让电机的
转速能够快速地响应系统的需求,同时消除稳态误差,并保持良好的动态性能。
2. 控制器设计
接下来,我们需要设计控制器。
在这个案例中,我们将采用一个PID控制器。
PID控制器由比例(P)、积分(I)和微分(D)三个部分组成,通过调整
这三个部分的参数,可以实现对电机转速的精确控制。
3. 参数整定
在确定了控制器的结构之后,我们需要对控制器进行参数整定。
参数整定的目的是为了找到一组最优的参数,使得电机的转速能够快速地响应系统的需求,同时消除稳态误差,并保持良好的动态性能。
4. 系统测试
最后,我们需要对系统进行测试。
在这个案例中,我们将测试电机的转速是否能够快速地响应系统的需求,同时观察系统是否存在稳态误差和动态性能问题。
如果存在这些问题,我们需要对控制器进行重新整定,直到系统的性能满足要求为止。
通过以上步骤,我们可以完成一个PID转速控制系统的设计。
在实际应用中,我们还需要根据具体的系统需求和实际情况对方案进行调整和优化,以达到更好的控制效果。
转速PI-P控制策略

段 向下 弯 曲的现 象如 图 1所示 。
占; 节器; I 调 计算机仿真 ;I P控制策略 P— 文献标 志码 : A 文章编号 :0 529 ( 0 8 0 -0 30 10 -8 5 2 0 )607 - 4 中图分类号 :P 7 T23
Ro a in l p e I-P Co to t a e y t to a e d P — n r lS r tg S
caat i i f I ot l yt nlzdi tecus f i nA R ( uo ai S edR glt )i bu t h rc r t so —Pcnr s m i a a e oreo agv S 1 A tm t p e euao na rp e sc P os e s y nh e c r
第2 卷 第6 6 期 20 0 8年 1 2月
轻工枕糖 Lg t n ut ciey ih Id sr Mahn r y
V 1 6N . o 2 o6 . D c 20 e.0 8
摘
要: 在分析 I —P转速调节器 参数 变化对系统启动性能影响的基础上 。 提出了一种 P — I P控制 策略 , 给出 P 一 / P控 制
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录一、设计题目 (1)二、系统的工作原理 (2)三、BP神经网络 (3)3.1BP神经网络结构 (3)3.2BP网络学习算法 (4)四、基于BP神经网络的PID控制器 (6)4.1PID控制器 (6)4.2基于BP神经网络的PID控制器 (7)五、程序代码及结果分析 (10)5.1程序代码 (10)5.2仿真结果 (13)六、结论 (15)一、设计题目柴油-电力机车传动电机的转速控制柴油机有着十分广泛的用途,它可用来驱动内燃机车的传动电机,从而保证重型列车的正常运行。
但是柴油机的工作效率对转速非常敏感,因此为了提高其工作效率,应该控制传动电机的转速。
图中给出了柴油内燃机车的电力传动模型。
图1-1 转速控制模型移动输入电位计的游标,可设置控制阀的位置,从而设定传动电机的预期转速w r 。
负载转速w 0是受控变量,其实际值由测速机测量。
测速机由电机轴上的皮带驱动,其输出电压v 0是系统的反馈变量。
由于输入电位计提供了预期参考电压,由此可求得参考电压与反馈电压间的偏差为( v r - v 0 )。
放大器将偏差电压放大后,生成电压信号v f ,并用作直流发电机的线圈磁场电压。
在电力传动系统中,柴油机的输出转速恒为w q ,直流发电机由柴油机驱动,其输出电压V g 是电枢控制直流电机的驱动电压。
此外电枢控制直流电机的励磁磁场电流i 也保持恒定不变。
在上述条件下,由于V R 的作用,直流电机将产生力矩T ,并使负载转速w 0逐渐趋近于预期转速w r 。
已知:● 电机的反电动势系数为Kb =31/50;● 与电机有关的参数为J=1,b=1,La=0.2,Ra=1;● 发电机有关的参数为励磁电阻Rf=1,励磁电感Lf=0.1,Lg=0.1,Rg=1;柴油机 w rv rv 0 v d 常量放大器i f L f R fi a L a R a发电机 电机 测速机 负载w 0,J ,bv fV g●测速机增益Kt=1; ● 发电机常数Kg ,电机常数Km 自定;二、系统的工作原理本系统利用移动输入电位计的游标,可设置控制阀的位置,从而设定传动电机的预期转速w r ,在移动输入电位计两端加有电源,每当游标移动一定距离,电位计上输出电压也跟随变化,该变化的电压(由输入电位计提供的的预期参考电压)与电动机反馈回来的电压值v 0进行比较,得到一个电压差v r - v 0。
电压差V 1输入运算放大器K ,根据放大器“虚短”与“虚亏”方法,放大器K 的放大系数为540,电压差V 1经过放大器K 放大后输出电压信号V 2,并用作直流发电机的线圈磁场电压。
在电力传动系统中,柴油机的输出转速恒为w q ,直流发电机由柴油机驱动,其输出电压V g 是电枢控制直流电机的驱动电压,直流电机带动负载转动并由测速机测量其实际转速w 0。
测速机由电机轴上的皮带驱动,其输出电压v 0是系统的反馈变量。
此外电枢控制直流电机的励磁磁场电流i 也保持恒定不变。
其中,控制系统的被控对象是电动机,发电机;被控量是电压;系统的输入量为转速w r ,输出量为转速w 0;给定量是移动输入电位计,功率放大器K ,测速发电机。
系统模型及结构图如下:图 2-1 系统模型图2-2 系统结构图1()G s 2()G s3()G s 4()G s 1()G s 0(t)系统传递函数求解:由上述框架结构图可以看出该系统为一个四阶系统,为求解方便将其化简成一个二阶系统(除去不大的极点),其结构框图如下图2.3:图2-3 化简后的系统传递函数结构图简化思路如下:由于励磁电感远小于励磁电阻,故励磁电感可以忽略。
建立系统的数学模型和传递函数一般表达式:比较电路 V1=Vr-V0;(Vr 输入电压,V1为偏差电压)回馈电路 电机的反电动势系数为Kb =31/50;放大电路 V 10=1.5(正常工作点);V 2=2e 3v 1 发电机电路:0.11Kg S + 电机电路:1KmS + 测速电路:测速机增益Kt=1;所以系统的开环传递函数为:5400*(10)(10.62)Kg Km G s s Km =+++ 系统的闭环传递函数为: 5400*()(10)(10.62)5400*Kg Km G c s s Km Kg Km=++++ 三、BP 神经网络3.1 BP 神经网络结构大脑是一部不寻常的智能机,它能以惊人的高速度解释感觉器官传来的含糊不清的信息。
它能觉察到喧闹房间内的窃窃私语,能够识别出光线暗淡的胡同中的一张面孔,更能通过不断地学习而产生伟大的创造力。
所谓神经网路系统是利用工程技术手段模拟人脑神经网络的结构和功能的一种技术系统,它是一种大规模并行的非线性动力学系统。
严格地讲神经网络应该称为人工神经网络,为了简化起见,一般省略人工二字直接称神经网络,可简记为 NN(Neural Network)。
由于神经网络具有信息的分布存储、并行处理以及自学习等优点,所以它在信息处理、模式识别,智能控制等领域有着广阔的应用前景。
人工神经网络的着眼点不是利用物理器件来完整的复制生物体中细胞网络,而是采纳其可利用的部分来解决目前计算机或其它系统不能解决的问题,如学习、识别、控制和专家系统等。
随着生物和认知科学的发展,人们对人脑的结构和认知过程的了解越来越深入,促进了人工神经网络技术的发展,越来越多的生物特性将被利用到工程中去。
X1X3X2Y1Y2Y3………图3-1 BP 神经网络结构图BP 神经网络结构如图3-1所示。
由图可见,BP 网络是一种具有三层或三层以上神经元的神经网络,包括输入层、中间层和输出层。
上下层之间实现全连接,而每层神经元之间无连接。
当一对学习样本提供给网络后神经元的激活值从输入层经中间层向输出层传播,在输出层的各神经元获得网络的输入响应。
接下来,按照减少目标输出与实际输出之间误差的方向,从输出层反向经过各中间层回到输入层,从而逐层修正各连接权值,这种算法称为“误差反向传播算法”,即BP 算法。
随着这种误差逆向的传播修正不断进行,网络对输入模式响应的正确率也不断上升。
与感知器不同的是,由于误差反向传播中会对传递函数进行求导计算,BP 网络的传递函数要求必须是可微的,所以不能使用感知器网络中的硬闭值传递函数,常用的有sigmoid 型对数、正切函数或线性函数。
由于传递函数是处处可微的,所以对BP 网络来说,一方面,所划分的区域不再是一个线性划分,而是由一个非线性超平面组成的区域,它是比较平滑的曲面,因而它的分类比线性划分更加精确,容错性也比线性划分更好;另一方面,网络可以严格采用梯度下降法进行学习,权值修正的解析式十分明确。
3.2 BP 网络学习算法设有n 个输入节点1x ,2x ……n x ;q 个输出节点1y ,……n y ;网络层的隐含节点有p 个神经元。
输入层第i 个单元至隐含层第j 个单元连接权j i w ,。
隐含层第j 个单元至输出层第t 个单元连接权t j v ,。
隐含层各单元的阈值为j θ,输出层各个单元的阈值为t γ,在训练该网络的学习阶段,设有N 组训练样本,先假定用其中的某一固定样本k 输入输出模式对网络进行训练。
输入层:n 个输入1x ,2x ……n x ;也就是输入样本。
中间层: j ni i j i j x w s θ+=∑, (1)()j j s S b =;j=1,2……p (2)输出层: ()t t s S =C ;t=1,2,……q (3)t j pj t j t b v L γ+=∑=1, (4)为了模拟生物神经元的非线性特性,激励函数常选用s 函数()xe x S -11+= (5) S 函数不但具有可微分性,而且具有饱和非线性特性,这又增强了网络的非线性映射能力。
S 函数的微分函数为:()x S 。
=()()()x S x S -1 (6) 单元输出闭值是为模拟神经元的闭值电位而设置的,在网络的学习过程中,它和各连接权一样不断的被修正。
阂值的作用反应在S 函数的输出曲线上,使曲线向左平移了阂值大小的单位,它起到了调节神经元兴奋水平的作用。
定义第N 个标准模式的误差函数为:()∑==q t t t k c y E 12-21 (7) 学习过程按使误差Ek 减少最快的方向调整权值系数,直到获得满意的权值为止。
根据梯度下降原则使连接权t j v ,的调整量与tj k v E ,∂∂的负值称比例,连接权的修正公式如下: tj k t j v E v ,,-∂∂=∆η 式中t=l ,2,.……q;j=l,2,……p;0<η<1 ()()j t t t tj t t k t j k t j b L S C d v C C E v E v '=∂∂∂∂=∂∂=∆---,,,ηηη (8)相应的闭值公式为:()()t t t tt t k t k L S C d C C E E '=∂∂∂∂=∂∂=∆---t ηγηγηγ (9) 若连接权值不直接作用于输出层神经元,情况就有所不同了,但仍按梯度下降法ji j j j j kj i j i w s s b b E w E w ,,,--∂∂∂∂∂∂=∂∂=∆ηη (10) ()j j js S s b '=∂∂ (11)()[]()t j t t t j t t t q t t k j k v L S C d b L L C C E b E ,q 1t 1--'=∂∂∂∂∂∂=∂∂∑∑== (12) 于是()()()i j t j t qi t t j i x s S v L S C d w ''=∆∑=,1,-η (13)同理()()()j t j t qi t t j s S v L S C d ''=∆∑=,1-ηθ (14)BP 网络学习算法计算步骤如下:(l)初始化,置所有的连接权值j i w ,,t j v ,,j θ,t γ为随机数(2)提供训练集,即给出顺序赋值的输入向量k X 和期望的输出向量k d 。
(3)计算中间层和输出层的各神经元实际输出。
(4)计算期望输出与实际输出的偏差k E 。
(5)计算t j v ,∆和t γ∆,调整中间层至输出层的连接权和闭值。
(6)计算j i w ,∆和j θ∆,调整输入层至中间层的连接权和闭值。
(7)返回2,直至误差满意为止。
四、基于BP 神经网络的PID 控制器4.1 PID 控制器PID 控制器是一个在工业控制应用中常见的反馈回路部件。
这个控制器把收集到的数据和一个参考值进行比较,然后把这个差别用于计算新的输入值,这个新的输入值的目的是可以让系统的数据达到或者保持在参考值。
和其他简单的控制运算不同,PID 控制器可以根据历史数据和差别的出现率来调整输入值,这样可以使系统更加准确,更加稳定。
