1.1线性规划问题及其数学模型
线性规划

影子价格测算 影子价格就是对偶最优解,它可以从单 纯形最优表中读到,即松弛变量所对应 的检验数的绝对值。
线性规划引例1
派公司是一个生产高尔夫器材的大型公司,公司决 定生产高中价位的高尔夫袋。分销商对新产品十分 感兴趣,并且同意买进派公司下3个月内的全部产品。 在对整个高尔夫袋生产步骤进行了详细的调查以后, 管理阶层明确了高尔夫袋的生产过程:
n
AT m
≤ C
n
§4.2 对偶问题的性质
1、对偶的对偶就是原始问题
min z=CTX s.t. AX≥b X ≥0
对偶的定义
max y=bTW s.t. ATW≤C W ≥0
max z’=-CTX
s.t. -AX≤-b X ≥0
对偶的定义
min y=-bTW s.t. -ATW≥-C W ≥0
某约束条件右端项每增加一个单位而产生的目标函
数最优值的增加,成为相应于此约束条件的影子价 格。(也称对偶变量)
对偶变量的经济解释
对偶变量yi在经济上表示原问题第i种资源的边际贡 献,即当第i种资源增加一个单位时,相应的目标值z的 增量 对偶问题的最优解yi*是原问题第i种资源的影子价格 应用:1.出租资源或设备时,租金价格的设定(至少高于 该资源在企业内的影子价格) 2.企业内资源I的存量设定(当资源I的影子价格>= 市场价格时,可买进该资源;否则卖出) 3.调整资源的分配量以增加利润
问题成型或称问题建模,是将语言文字上的 问题转化为数学问题。可以说,这是一项艺 术创造,只有通过不断的练习才能熟练掌握。 虽然,实际生活中的每个问题都有独特之处, 但其中大部分还是有共性的。所以,我们可 以学习一些具有普遍适用性的方法来帮助我 们建立数学模型,这些方法对初学者尤其有 效。下面我们以派公司为例讲解一下建立数 学模型的方法。
第一章 线性规划

例 1.5 (汽油混合问题) 一种汽油的特性可用两个指标描述:其点火性用“辛烷数” 描述,其挥发性用“蒸汽压力”描述,某炼油厂有四种标准汽油,设其标号分别为 1,2, 3,4,其特性及库存量见表 1.5,将上述标准汽油适量混合,可得到两种飞机汽油,其标 号分别为 1,2,这两种飞机汽油的性能指标及产量需求见表 1.6,问应如何根据库存情况 适量混合各种标准汽油,使既满足飞机汽油的性能指标,而产量又为最高。
注:前苏联的尼古拉也夫斯克城住宅兴建计划采用了上述模型,共用了 12 个变量,10 个约束条件。
表 1.2 资源 住宅体系 砖混住宅 壁板住宅 大模住宅 资源限量 造价 (元/m2) 105 135 120 110000 (千元 钢材 (公斤/m2) 12 30 25 20000 (吨) 例 1.2 的数据表 水泥 (公斤/m2) 110 190 180 150000 (吨) 砖 (块/m2) 210 —— —— 147000 (千块) 人工 (工日/m2) 4.5 3.0 3.5 4000 (千工日)
3.线性规划模型的一般形式 以 MAX 型、≤约束为例 决策变量: x1 ,
(1-4)
, xn
目标函数: Maxz = c1 x1 +
+ cn x n
⎧a11 x1 + + a1n x n ≤ b1 ⎪ ⎪ 约束条件: s.t.⎨ ⎪a m1 x1 + + a mn x n ≤ bm ⎪ ⎩ x1 , , x n ≥ 0
2
Maxz = x1 + x 2 + x3 ⎧0.105 x1 + 0.135 x 2 + 0.120 x3 ≤ 110000 ⎪0.012 x1 + 0.030 x 2 + 0.025 x3 ≤ 20000 数学模型为: ⎪0.110 x1 + 0.190 x 2 + 0.180 x 3 ≤ 150000 (1-3) s.t ⎨ 0.210 x ≤ 147000 ⎪0.00451 x + 0.003x 2 + 0.0035 x 3 ≤ 4000 ⎪x , x , x 1 ≥ 0 ⎩ 1 2 3
线性规划

• 4.2 两阶段法
• 两阶段法是处理人工变量的另一种方法。其具体做 法是在原约束条件中增加人工变量,构造一个新的 目标函数,其中人工变量的系数为-1,其余变量的 系数为0,这样就产生了如下的最优解有三种情形。 (1)这说明在辅助问题的最优解中,还有人工变量是基变量, 且取值不为0,此时原问题无可行解。 (2)且最优解中人工变量均为非基变量,则把它们划去后就得 到了原问题的一个基本可行解。 (3)但最优解中还有人工变量是基变量,其取值为0。这时, 只要选某个不是人工变量的非基变量进基,把在基中的人工 变量替换出来,则情形同(2)。 第二阶段:对于第一阶段的后两种情形,在第一阶段的最优单 纯形表中划去人工变量所在的列,并把检验数行换成原问题 目标函数(消去基变量以后)的系数,从而得到原问题的初 始单纯形表,再继续迭代求解。
2014-6-19 3
例2(运输问题)
• 设有某种物资要从A1,A2,A3三个仓库运往四个 销售点B1,B2,B3,B4。各发点(仓库)的发货 量、各收点(销售点)的收货量以及 到 的单位运 费如表1-2。问如何组织运输才能使总运费最少?
例3(配料问题)
• 在现代化的大型畜牧业中,经常使用工业生产的饲料。 设某种饲料由四种原料B1,B2,B3 ,B4混合而成,要 求它含有三种成份(如维生素、抗菌素等)A1,A2, A3的數量分別不少于25、36、40个单位(这些单位可 以互不相同),各种原料的每百公斤中含三种成份的数 量及各种原料的单价如表1-3.
1.2 线性规划的数学模型
一、一般形式 上述各例具有下列共同特征: 1.存在一组变量 ,称为决策变量,表示某一方案。通 常要求这些变量的取值是非负的。 2.存在若干个约束条件,可以用一组线性等式或线性 不等式来描述。 3.存在一个线性目标函数,按实际问题求最大值或最 小值。
第1章 线性规划

1.1 线性规划问题及其数学模型
线性规划
该公司想达到的目标为:投资 风险最小,每年红利至少为6.5万 元,最低平均增长率为12%,最低 平均信用度为7。请用线性规划方 法求解该问题。
1.1 线性规划问题及其数学模型
解:
(1)决策变量
线性规划
本问题的决策变量是在每种投资项目上的投 资 额 。 设 xi 为 项 目 i 的 投 资 额 ( 万 元 ) ( i=1,2,,6)
(2)目标函数
本问题的目标为总投资风险最小,即
Min z 0.18x1 0.06x2 0.10x3 0.04x4 0.12x5 0.08x6
线性规划
运筹学
线性规划
线性规划
本章内容要点
线性规划问题及其数学模型;
线性规划的电子表格建模; 线性规划的多解分析。
线性规划
本章内容
1.1 线性规划问题及其数学模型
1.2 线性规划问题的图解法
1.3 用Excel“规划求解”功能求解线性规划问题
1.4 线性规划问题求解的几种可能结果
本章主要内容框架图
1.4 线性规划问题求解的 几种可能结果
线性规划
唯一解 无穷多解 无解 可行域无界(目标值不收敛)
1.4 线性规划问题求解的 几种可能结果
线性规划
唯一解
线性规划问题具有 唯一解是指该规划 问题有且仅有一个 既在可行域内、又 使目标值达到最优 的解。例1.1就是一 个具有唯一解的规 划问题
(1-1)
运筹学第1章-线性规划

下一页 返回
图解法步骤:
(1)建立坐标系; (2)将约束条件在图上表示; (3)确立满足约束条件的解的范围; (4)绘制出目标函数的图形 (5)确定最优解
用图解法求解下列线性规划问题
max z 2x1 3x2
4x1 0x2 16
s.t
10xx11
4x2 2x2
12 8
x1, x2 0
1. 1.1问题举例
(1)生产计划问题。 生产计划问题是典型的已知资源求利润最大化的问题,对于此类
问题通常有三个假设:①在某一计划期内对生产做出的安排;②生产 过程的损失忽略不计;③市场需求无限制,即假设生产的产品全部 卖出。
下一页 返回
1.一般线性规划问题的数学模型
例1 用一块连长为a的正方形铁皮做一个容 器,应如何裁剪,使做成的窗口的容积为最 大?
解:设 x1, x2分别表示从A,B两处采购的原油量(单
位:吨),则所有的采购方案的最优方案为:
min z 200x1 290x2
0.15x1 0.50x2 150000
s.t
0.20x1 0.50x1
0.30x2 0.15x2
120000 120000
x1 0, x2 0
1. 1线性规划问题与模型
也可以写成模型(1-6)和模型(1-7)的形式,其中模型(1-7)较为常用。
线性规划问题及其数学模型
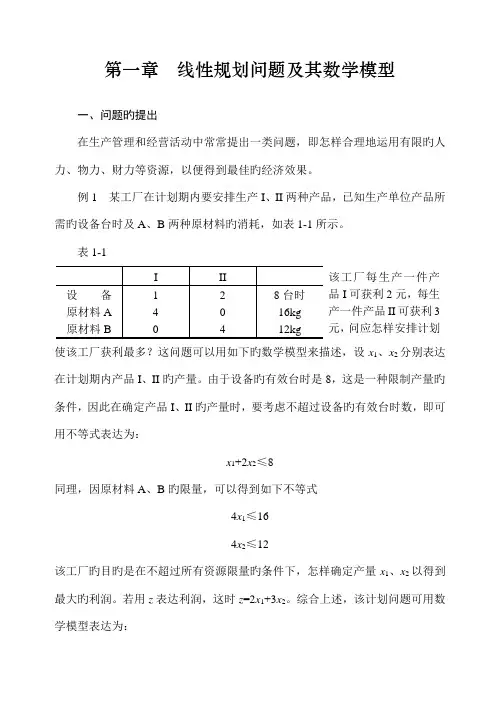
第一章线性规划问题及其数学模型一、问题旳提出在生产管理和经营活动中常常提出一类问题,即怎样合理地运用有限旳人力、物力、财力等资源,以便得到最佳旳经济效果。
例1 某工厂在计划期内要安排生产I、II两种产品,已知生产单位产品所需旳设备台时及A、B两种原材料旳消耗,如表1-1所示。
表1-1该工厂每生产一件产品I可获利2元,每生产一件产品II可获利3元,问应怎样安排计划使该工厂获利最多?这问题可以用如下旳数学模型来描述,设x1、x2分别表达在计划期内产品I、II旳产量。
由于设备旳有效台时是8,这是一种限制产量旳条件,因此在确定产品I、II旳产量时,要考虑不超过设备旳有效台时数,即可用不等式表达为:x1+2x2≤8同理,因原材料A、B旳限量,可以得到如下不等式4x1≤164x2≤12该工厂旳目旳是在不超过所有资源限量旳条件下,怎样确定产量x1、x2以得到最大旳利润。
若用z表达利润,这时z=2x1+3x2。
综合上述,该计划问题可用数学模型表达为:目旳函数 max z =2x 1+3x 2 满足约束条件 x 1+2x 2≤84x 1≤16 4x 2≤12 x 1、x 2≥0例2 某铁路制冰厂每年1至4季度必须给冷藏车提供冰各为15,20,25,10kt 。
已知该厂各季度冰旳生产能力及冰旳单位成本如表6-26所示。
假如生产出来旳冰不在当季度使用,每千吨冰存贮一种季度需存贮费4千元。
又设该制冰厂每年第3季度末对贮冰库进行清库维修。
问应怎样安排冰旳生产,可使该厂整年生产费用至少?解:由于每个季度生产出来旳冰不一定当季度使用,设x ij 为第i 季度生产旳用于第j 季度旳冰旳数量。
按照各季度冷藏车对冰旳需要量,必须满足:⎪⎪⎩⎪⎪⎨⎧++++++33231343221242114144x x x x x x x x x x 。
,,,25201510==== 又每个季度生产旳用于当季度和后来各季度旳冰旳数量不也许超过该季度旳生产能力,故又有⎪⎪⎩⎪⎪⎨⎧++++++33232213121143424144x x x x x x x x x x 。
线性规划-讲义-12章
整数规划
第五章 动态规划
第六章 图论与问题及其数学模型 1.1.1 线性规划问题的数学模型
例1、生产计划问题 I 1 3 0 40 II 2 2 2 50
原材料A 原材料B 台时 利润
例6 max S=2x1+ 4x2 2x1+x2 8
x2
8
-2x1+ x2=2
-2x1+x2 2
x1 , x2 0 无界解(无最优解) 无界解=>可行域无界 <=
6
4
2
0
4
x1
2x1+ x2=8
例7 max S=3x1+2x2 -x1 -x2 1
x1 , x2 0 有解 无可行解 唯一解 无穷多解 无有限最优解 无可行解
(3) 变量 若xj 0, 令 xj = -xjˊ, 其中: xjˊ 0 若xj是无限制变量. 令 xj = xjˊ- xj〞, 其中: xjˊ、 xj〞 0
例 3x1+2x2 8
x1 –4x2 14
x2 0 令x1= x1'- x1 " 3 x1' –3x1 " +2x2 8 x1' - x1 " – 4x2 14 x1' , x1" ,x2 0
2x3 +2x4+ x5=100 3x1+ x2+2x3 +3x5=100
xi 0 (i =1,…,5),且为整数
最优方案是:按方案I-30根, II-10根;III-50根 即只要90根原料--制造100套
运输问题
1.1 72线性规划问题及其数学模型
4 3 2
最优解
8 0 3 4
x1
无穷多最优解(多重最优解)
即可行域的范围延伸到无 例: max z=x1+x2
穷远,目标函数值可以无 穷大或无穷小。 ≤4 s.t. -2x1+ x2 一般来说,这说明模型有 x1 - x2 ≤2 错,忽略了一些必要的约 束条件。 ≥0, x2≥0 x1 x2
无穷 多个最优解
2.可行域为非封闭的无界区域
x2 x2 x2
z
z
x1 x1
Z
x1
唯一最优解
无穷多个最优解
无界解
3、可行域为空集
x2
空集 x1
无可行解
两个变量的LP问题的解的启示:
(1)可行域非空时,它是有界或无界凸多边形 (凸集) ,顶点个数只有有限个。 (2)求解LP问题时,解的情况有: 唯一最优解;无穷多最优解;无界解;无可行解。 (3)若可行域非空且有界则必有最优解, 若可行域无界,则可能有最优解,也可能无最优解。 (4)若最优解存在,则最优解或最优解之一一定是 可行域的凸集的某个顶点。 (5)若在两个顶点上同时取到最优解,则这两点的 连线上 任一点都是最优解
由图解法得到的结论:
求解线性规划问题最优解的方法:
确定可行域 = 凸集(凸多边形) 确定可行域顶点 = 求基可行解 寻找最优解, 如果最优解存在,则必在可行域的某一顶点 = 在基可行解中寻找
图解法优点: 直观、易掌握。有助于了解解的结构。
图解法缺点:
只能解决低维问题,对高维无能为力。
1.3 线性规划问题的标准型式
m i nZ
C
j 1
n j1
n
j
Xj
线性规划
M1 : 目标函数: max z c 1 x 1 c 2 x 2 c n x n a 11 x 1 a 12 x 2 a 1 n x n b1 a x a 22 x 2 a 2 n x n b 2 21 1 约束条件: a x a x a x b m2 2 mn n n m1 1 x 1 , x 2 , , x n 0
24
第2节 应用举例
最终计算表(第3次计算)
c j→ CB 0.1 -0.3 0 XB x2 x4 x1 c j -z j b 10 50 30 0 x1 0 0 1 0 0.1 x2 1 0 0 0 0.2 x3 -1 1 1 0 0.3 x4 0 1 0 0 0.8 x5 -9/10 1/3 13/10 -0.74 -M x6 3/5 0 -1/5 -M + 0.06 -M x7 -3/10 1/3 1/10 -M + 0.12 -M x8 -1/5 0 2/5 -M -0.02 θ
27
第2节 应用举例
表1-7表明这些原材料供应数量的限额。加入到产品A、 B、D的原材料C总量每天不超过100kg,P的总量不超过 100kg,H总量不超过60kg。
表1-7
原材料名称 C P H 每 天 最 多 供 应 量 ( kg) 100 100 60 单 价 /(元 /kg) 65 25 35
29
第2节 应用举例
约束条件可表示为:
1 2 1 4 x1 x1 1 2 3 4 x2 x2 1 2 1 4 x3 x3 x1 x2 x3 x1 , , x 9 0 3 4 1 2 x4 x4 1 4 1 2 x5 x5 1 4 1 2 x6 x6 x7 x5 x6 x8 0 0 0 0 100 100 x 9 60
1-1线性规划问题及模型
西安邮电大学 现代邮政学院
Xi'an post and telecommunications university modern post College
第一章 线性规划与单纯形法
1.1线性规划问题及模型 运 筹 学
主要内容
01 线性规划问题
运
02 线性规划模型及特征
筹
学
一 线性规划问题
二 线性规划模型
2.线性规划模型的一般形式
运 筹 学
二 线性规划模型
简写式
运 筹 学
n
max(或 min)Z c j x j j 1
s.t.
n
aij x j
(或 ,)bi
j1
xj 0
i 1,,m j 1,, n
二 线性规划模型
运向量式 筹 学
max(或 min ) Z CX
星期 需要人数 星期 需要人数
运
一
300
五
480
筹
二
300
六
600
学
三
350
日
550
四
400
应如何安排每天的上班人数,使商场总的营业员最少。
一 线性规划问题
在上班 周 周 周 周 周 周 周 一二三四五六日
开始上班
周一
周二
运
周三
筹
周四
学
周五 周六
周日
一 线性规划问题
解:设xj(j=1,2,…,7)为休息2天后星期一到星
期日开始上班的营业员,则这个问题的线性规划模型为
min Z x1 x2 x3 x4 x5 x6 x7
x1 x4 x5 x6 x7 300
x1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v一 般 形 式
目标函数
minz c1 x1 c2 x2 cn xn
ai1 x1 ai2 x2 ainxn bi ;i 1,2,...,p
蕴含约束:数量非负 xij 0;i 1,2, j 1,2,3,4
v模 型
24
min
cij xij
i1 j1
xi1 xi2 xi3 xi4 ai ;i 1,2
s.t. x1j x2 j bj ; j 1,2,3,4
xij 0;i 1,2, j 1,2,3,4
v规划问题数学模型的三要素
生产计划问题 运输问题
| 线性规划模型
一般形式 规范形式 标准形式 形式转换
生产计划问题
v 常山机械厂制造Ⅰ、Ⅱ两种产品。已知各 制造一件时分别占用的设备A、B、C的台时, 每天可用于这两种家电的能力、各售出一件时的 获利情况如下表所示。问该企业应制造两种产品 各多少件,可使获取的利润最大。
项目
Ⅰ
a 11
A
a 21
a 12
a 22
a 1 n a 2n
a m 1 a m 2 a mn
为系数矩阵。
v规 范 形 式
min c x
Ax b
s
.t
.
x
0
v标 准 形 式
max cx
s.t.
Ax b x 0
v模 型 转 换
❖变量转换
令自由变量 x j
x
j
x
j
,其中
v问 题 分 析
可控因素:从仓库 Ai 运往B j 的产品数量 设为 xij ;i 1,2, j 1,2,3,4 目标:总运费最小
24
费用函数 cij xij i1 j1
受控条件: 从仓库运出总量不超过可用总量,运入零售点的数量不低于需求量。 由于总供给量等于总需求量,所以都是等号。即
xi1 xi2 xi3 xi4 ai ;i 1,2 x1 j x2 j b j ; j 1,2,3,4
x1, x2 0
v模 型
max z 2x1 3x2 2x1 2x2 12
s.t. 4x1 1 6
5x2 15 x1, x2 0
v运 输 问 题
一个制造厂要把若干单位的产品从两个仓库 Ai ;i 1,2 发送到零售点 B j ; j 1,2,3,4 ,仓库 Ai 能供应的产品数量为 ai ;i 1,2 ,零售点 B j 所需的产品的数量为 b j ; j 1,2,3,4 。 假设供给总量和需求总量相等,且已知从仓库 Ai 运一个单 位产品往 B j 的运价为 cij 。问应如何组织运输才能使总运费 最 Ai 小?
v不 等 式 变 等 式
a i 1 x 1 a i 2 x 2 a in x n b i
a i 1 x 1 a i 2 x 2 a in x n s i b i , s i 0
或
a i 1 x 1 a i 2 x 2 a in x2 x 2 a in x n s i b i , s i 0
运筹学课件
运
决
筹
胜
帷
线性规划
千
幄
里
之
之
中
Linear Programming
外
v线 性 规 划
| 线性规划问题及其数学模型 | 图解法 | 单纯形法原理 | 单纯形法计算步骤 | 单纯形法的进一步讨论 | 数据包络 | 其他应用例子 | 案例分析
v线 性 规 划 问 题 及 其 数 学 模 型
| 问题提出与建模
2x1 x2 2
s.t.
x1 x1
2x2 2 x2 5
x1 0
max z x1 (x2 x2)
2
x1
( x2
x2 )
x3
2
s.t.
x1
2( x2
x2 )
x4
2
x1 (x2 x2) x5 5
xi 0;i 1,3, 4,5, x2, x2 0.
v 例1 把问题转化为标准形式
x
j
,
x
j
为非负变量
❖目标转换
求最小可以等价成求负的最大
min cx
❖ 约束转换 ❖ 实例
max cx
v约 束 转 换 ❖等式变不等式
ai1 x1 ai2 x2 ainxn bi
ai1 x1 ai2 x2 ainxn bi ai1 x1 ai2 x2 ainxn bi
❖ 不等式变等式 ❖ 不等式变不等式
s.t.axij1
x1
0;
ai2 x2 ain j 1,2,...,q
xn
bi ;i
p 1,...,m
xj无限制; j 1,2,...,q
约束条件
v注 释
x j ; j 1 , 2 ,..., n 为 待 定 的 决 策 变 量 , c (c1 ,c 2 , ,c n ) 为 价 值 向 量 , c j ; j 1 , 2 ,..., n 为 价 值 系 数 , b ( b 1 , b 2 ,..., b m ) 为 右 端 向 量 , 矩阵
| 变量(决策变量)
它是问题中要确定的未知量,它用以表明规划中用数 量表示的方案、措施,可由决策者决定和控制;
| 目标函数
它是决策变量的函数,按优化目标分别在这个函数前 加上max或min;
| 约束条件
指决策变量取值时受到的各种资源条件的限制,通常 表达为含决策变量的等式或不等式。
v线性规划的数学模型
剩余变量
v不等式变不等式
ai1 x1 ai 2 x2 ain xn bi
ai1 x1 ai2 x2 ain xn bi
或
ai1 x1 ai 2 x2 ain xn bi
ai1 x1 ai2 x2 ain xn bi
v 例1 把问题转化为标准形式
min z x1 x2
设备A(h)
2
设备B(h)
4
设备C(h)
0
利润(元)
2
Ⅱ 每天可用量
2
12
0
16
5
15
3
v问 题 分 析
可控因素:每天生产两种产品的数量,分别设为 x1, x2 目标:每天的生产利润最大
利润函数 2x1 3x2 受制条件:
每天资源的需求量不超过可用量:
设备 A: 2x1 2x2 12 设备 B: 4x1 16 设备 C: 5x2 15 蕴含约束:产量为非负数
