八年级下册数学重难点题型(人教版)专题 动点与特殊三角形存在性问题大视野(原卷版)
八年级下册数学重难点题型(人教版)专题 动点与特殊三角形存在性问题大视野(解析版)

②PE=PD 时,即 DE 为斜边, 3 t+2=-2t, 2
解得:t=-4,
∴P 点坐标为(0,0).
综上所述:当 t= 4 时,△PDE 为等腰直角三角形,此时 P 点坐标为(0, 8 )或(0, 4 );
5
5
5
当 t= 4 时,△PDE 为等腰直角三角形,此时 P 点坐标为(0, 8 );
2
故答案为:(8,4)或( 5 ,7). 2
题型二、直角三角形存在性问题 例 1. 【2019·厦门六中月考】如图,在 RtΔABC 中,∠B=90°,AC=60,∠A=60°.点 D 从点 C 出发沿 CA 方 向以每秒 4 个单位长的速度向点 A 匀速运动,同时点 E 从点 A 出发沿 AB 方向以每秒 2 个单位长的速度向 点 B 匀速运动,设点 D、E 运动的时间是 t 秒(0<t≤15).过点 D 作 DF⊥BC 于点 F,连接 DE、EF. (1)求证:AE=DF; (2)四边形 AEFD 能够成为菱形吗?如果能,求出相应的 t 值;如果不能,说明理由. (3)当 t 为何值时,ΔDEF 为直角三角形?请说明理由.
故答案为 ,(-2,1);
(2)过点 B 作 BH⊥x 轴于 H,
∵∠ACB=90°,AC=CB, ∴△BHC≌△COA,
∴HC=OA=4,BH=CO=1,OH=HC+CO=4+1=5, ∴B(-5,1). 设直线 AB 的表达式为:y=kx+b, 将 A(0,4)和 B(-5,1)代入得, b=4, -5k+b=1,解得:k=0.6,b=4, 即直线 AB 的函数表达式为:y=0.6x+4. (3)设 Q(t,2t-6),分两种情况: ①当点 Q 在 x 轴下方时,Q1M∥x 轴,与 BP 的延长线交于点 Q1.
中(小)学初二三角形四边形动点问题重点知识点重点学习及题标准
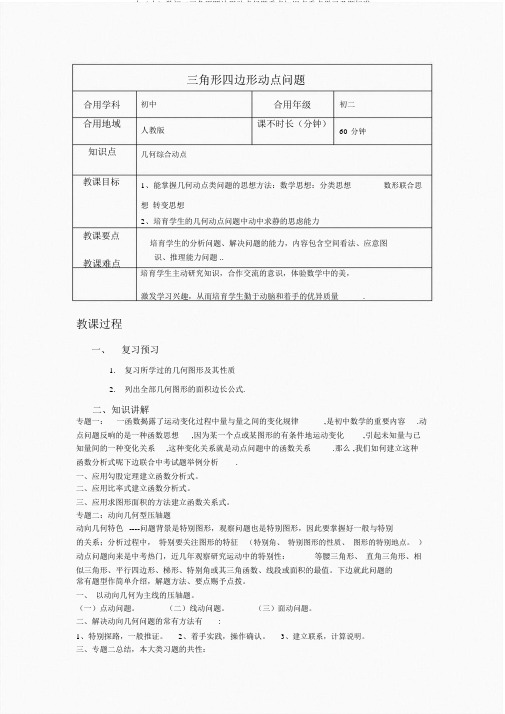
三角形四边形动点问题合用学科合用地域知识点初中人教版几何综合动点合用年级课不时长(分钟)初二60分钟教课目标教课要点1、能掌握几何动点类问题的思想方法:数学思想:分类思想数形联合思想转变思想2、培育学生的几何动点问题中动中求静的思虑能力培育学生的分析问题、解决问题的能力,内容包含空间看法、应意图识、推理能力问题 ..教课难点培育学生主动研究知识,合作交流的意识,体验数学中的美,激发学习兴趣,从而培育学生勤于动脑和着手的优异质量.教课过程一、复习预习1.复习所学过的几何图形及其性质2.列出全部几何图形的面积边长公式.二、知识讲解专题一:一函数揭露了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反响的是一种函数思想,因为某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么 ,我们如何建立这种函数分析式呢下边联合中考试题举例分析.一、应用勾股定理建立函数分析式。
二、应用比率式建立函数分析式。
三、应用求图形面积的方法建立函数关系式。
专题二:动向几何型压轴题动向几何特色----问题背景是特别图形,观察问题也是特别图形,因此要掌握好一般与特别的关系;分析过程中,特别要关注图形的特征(特别角、特别图形的性质、图形的特别地点。
)动点问题向来是中考热门,近几年观察研究运动中的特别性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特别角或其三角函数、线段或面积的最值。
下边就此问题的常有题型作简单介绍,解题方法、要点赐予点拨。
一、以动向几何为主线的压轴题。
(一)点动问题。
(二)线动问题。
(三)面动问题。
二、解决动向几何问题的常有方法有:1、特别探路,一般推证。
2、着手实践,操作确认。
3、建立联系,计算说明。
三、专题二总结,本大类习题的共性:1.代数、几何的高度综合(数形联合);着力于数学实质及中心内容的观察;四大数学思想:数学联合、分类谈论、方程、函数.2.以形为载体,研究数目关系;经过设、表、列获取函数关系式;研究特别状况下的函数值。
初二三角形四边形动点问题知识点及题问题详解

教学过程一、复习预习1.复习所学过的几何图形及其性质2.列出所有几何图形的面积边长公式.二、知识讲解专题一:一函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析.一、应用勾股定理建立函数解析式。
二、应用比例式建立函数解析式。
三、应用求图形面积的方法建立函数关系式。
专题二:动态几何型压轴题动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
一、以动态几何为主线的压轴题。
(一)点动问题。
(二)线动问题。
(三)面动问题。
二、解决动态几何问题的常见方法有:1、特殊探路,一般推证。
2、动手实践,操作确认。
3、建立联系,计算说明。
三、专题二总结,本大类习题的共性:1.代数、几何的高度综合(数形结合);着力于数学本质及核心内容的考查;四大数学思想:数学结合、分类讨论、方程、函数.2.以形为载体,研究数量关系;通过设、表、列获得函数关系式;研究特殊情况下的函数值。
专题三:双动点问题点动、线动、形动构成的问题称之为动态几何问题. 它主要以几何图形为载体,运动变化为主线,集多个知识点为一体,集多种解题思想于一题. 这类题综合性强,能力要求高,它能全面的考查学生的实践操作能力,空间想象能力以及分析问题和解决问题的能力. 其中以灵活多变而著称的双动点问题更成为今年中考试题的热点,现采撷几例加以分类浅析,供读者欣赏.1 以双动点为载体,探求函数图象问题。
八年级下册数学重难点题型(人教版)专题 动点与平行四边形存在性问题大视野(原卷版)

专题动点与平行四边形存在性问题大视野【例题精讲】题型一、平行四边形存在性问题例1.【2019·长沙市天心区期中】如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=3,OB=2OA,C为直线y=2x与直线AB的交点,点D在线段OC上,OD= .(1)求点C的坐标;(2)若P为线段AD上一动点(不与A、D重合).P的横坐标为x,△POD的面积为S,请求出S与x的函数关系式;(3)若F为直线AB上一动点,E为x轴上一点,是否存在以O、D、E、F为顶点的四边形是平行四边形?若存在,写出点F的坐标;若不存在,请说明理由.题型二、特殊平行四边形(矩形)存在性问题例1.【2019·武汉市期中】如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.(1)证明:当E在AO上运动,F在CO上运动,且E与F不重合时,四边形DEBF是平行四边形;(2)点E,F在AC上运动过程中,以D、E、B、F为顶点的四边形是否可能为矩形?如能,求出此时的运动时间t的值;如不能,请说明理由.例2.【2019·禹城市期末】如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB 的角平分线于点E,交∠ACB的外角平分线于点F(1)求证:EO=FO;(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形ABCE的面积为.题型三、特殊平行四边形(菱形)存在性问题例1.【2019·福州市晋安区期末】如图,在平面直角坐标系中,矩形ABCD的顶点A、B、D的坐标分别为(0,5)、(0,2)、(4,5),直线l的解析式为y=kx+2﹣4k(k>0).(1)当直线l经过原点O时,求一次函数的解析式;(2)通过计算说明:不论k为何值,直线l总经过点C;(3)在(1)的条件下,点M为直线l上的点,平面内是否存在x轴上方的点N,使以点O、A、M、N为顶点的四边形是菱形?若存在,请直接写出点M的坐标:若不存在,请说明理由.题型四、特殊平行四边形(正方形形)存在性问题例1.【2019·华蓥市期末】如图,已知一次函数y=12-x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=13 MP,MB=13OM,OE=13ON,ND=13NP.(1)b=______;(2)求证:四边形BCDE是平行四边形;(3)在直线y=12-x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.【刻意练习】1.【2019·阳江市期中】如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3),B 点坐标为(-2,0),C点坐标为(0,-1)(1)AC的长为______;(2)求证:AC⊥BC;(3)若以A、B、C及点D为顶点的四边形组成平行四边形,画出符合条件的所有平行四边形,并写出D 点的坐标______.2.【2018·莆田市期中】已知:在△ABC中,AD是BC边上的中线,点E是AD的中点;过点A作AF∥BC,交BE的延长线于F,连接CF.(1)求证:四边形ADCF是平行四边形;(2)填空:①当AB=AC时,四边形ADCF是______形;②当∠BAC=90°时,四边形ADCF是______形.3.【2018·琼中县期中】如图在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=,平行四边形CDEB为菱形.4.【2019·宿迁市期末】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有______次.5.【2019·惠州市期末】如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P 从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.(1)经过多长时间,四边形PQCD是平行四边形?(2)经过多长时间,四边形PQBA是矩形?6.【2019·武昌期末】如图,在平面直角坐标系中,OA=OB,△OAB的面积是2.(1)求线段OB的中点C的坐标.(2)连结AC,过点O作OE⊥AC于E,交AB于点D,①直接写出点E的坐标.②连结CD,求证:∠ECO=∠DCB.(3)点P为x轴上一动点,点Q为平面内一点,以点A、C、P、Q为顶点作菱形,直接写出点Q的坐标.7.【2018·襄阳市期中】如图,矩形OABC的边OA,OC分别与坐标轴重合,并且点B的坐标为(8,).将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.(1)求证:△OBD为等腰三角形;(2)求点E的坐标;(3)坐标平面内是否存在一点F,使得以点B,E,F,O为顶点的四边形是平行四边形,若存在,请直接写出点F 的坐标;若不存在,请说明理由.8.【2019·天津蓟县期中】如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的一动点,连接EF,过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE、BD.(1)求证:四边形DBEC是平行四边形.(2)若∠ABC=120°,AB=BC=4,则在点E的运动过程中:①当BE=时,四边形BECD是矩形,试说明理由;②当BE=时,四边形BECD是菱形.。
八年级下册数学重难点题型(人教版)专题 勾股定理重难点大视野(解析版)

专题勾股定理重难点大视野Part 1 基本概念1. 什么是勾股定理?2. 什么是原命题?逆命题?怎么将一个命题改成它的逆命题?3. 勾股定理的逆定理内容4. 什么是勾股数?常见的勾股数有哪些?柏拉图提出了哪一对勾股数公式?★5. 勾股定理的证明据说,中世纪时数学系硕士研究生必须提出一种勾股定理的新证明方法才能毕业,足见其重要性,这是几何学上的第一朵“奇葩”!需要掌握住以下几个常见证法:【核心:面积法】(1)毕达哥拉斯证法(2)赵爽弦图证法(3)美国总统证法(4)(了解)欧几里得证法【注:我们现在所学几何为欧式几何,就是根据欧几里得所编著的《几何原本》所提炼而得,作为他的学生,他的论述过程还是要了解的!】6. 勾股定理逆定理是怎么证明的?7. 怎么用勾股定理解释“HL判定定理(SSA)”?Part 2 基本结论及思路1. 含特殊角(30°、45°、60°等)的三角形三边关系及面积a =0.5c c =2ab =3a a =3b a = 22c c = 2 aS =23a (含a 的代数式表示) S =234a (含a 的代数式表示)a =33c c =3 a 2. 遇到特殊角时,将特殊角放在直角三角形中求解,常见辅助线是作出垂线。
Part 3 勾股定理应用1. 勾股数2. 用「尺规」的线段或点。
3. 格点三角形的面积;格点三角形各边的长度及各边上高的求法;平面直角坐标系中一点到一条直线距离的求法。
先求★ABC的面积,再求线段AB的长,利用面积法求解。
【例题精讲】题型一、图形求值问题例1. 【2019·株洲市期末】已知:如图,有一块Rt△ABC的绿地,量得两直角边AC=8m,BC=6m.现在要将这块绿地扩充成等腰△ABD,且扩充部分(△ADC)是以8 m为直角边长的直角三角形,求扩充后等腰△ABD 的周长.(1)在图1中,当AB=AD=10 m时,△ABD的周长为______;(2)在图2中,当BA=BD=10 m时,△ABD的周长为______;(3)在图3中,当DA=DB时,求△ABD的周长.【答案】(1)32m;(2)20+4√5m;(3)见解析.【解析】解:(1)∵AB=AD=10m,AC⊥BD,AC=8 m,在Rt★ACD中,由勾股定理得:DC=√AD2−AC2=6(m),则△ABD的周长为:10+10+6+6=32(m).故答案为:32 m;(2)当BA=BD=10m时,则DC=BD-BC=10-6=4,在Rt★ACD中,由勾股定理得:AD=√AC2+DC2=4√5,则△ABD的周长为:AD+AB+BD=10+4√5+10=(20+4√5)m;故答案为:(20+4√5)m;(3)设DC=x,则AD=6+x,在Rt★ACD中,由勾股定理得:DC2+AC2=AD2,即x2+82=(6+x)2,解得:x=73,由(2)知AB=10,△ABD的周长为:AD+BD+AB=803(m).例2. 【2018·北师大附中期中】如图,在长方形ABCD中,AC是对角线,将长方形ABCD绕点B顺时针旋转90°到长方形GBEF位置,H是EG的中点,若AB=6,BC=8,则线段CH的长为()A. B. C. D.【答案】B.【解析】解:延长CH交FE的延长线于M,过C作CN★EF于N,则CN=BE=AD=8,易证★CHG★★EHM,★NF=CG=EM=BC-BG=8-6=2,★MN=NE+ME=10,在Rt★AMN中,由勾股定理得:CM★CH =12CM 故答案为:B .例3. 【2019·厦门市期中】如图,边长为a 的正方形ABCD ,点M 是正方形内部一点,连接AM 并延长交CD 于N ,连接MC ,★BCM 是等边三角形,则★MNC 的面积为【答案】14a 2. 【解析】解:过M 作MG ★BC 于G ,MH ★CD 于H ,则BG =CG ,AB ★MG ★CD ,★AM =MN ,★MH ★CD ,★D =90°,★MH ★AD ,NH =DH ,★★MBC 是等边三角形,★MC =BC =aMH =12a ,CH =2a ,DH =a -2a ,★CN =CH -NH =)1a ,★MNC 的面积为:12×12a ×)1a 2故答案为:14a 2. 例4. 【2019·汕头市期末】如图,直线y =﹣x +2分别交x 轴、y 轴于点A ,B ,点D 在BA 的延长线上,OD 的垂直平分线交线段AB 于点C .若★OBC 和★OAD 的周长相等,则OD 的长是( )A.2B.C D.4【答案】B.【解析】解:★直线y=﹣x+2分别交x轴、y轴于点A,B,★OA=OB=2.在Rt★BOA中,利用勾股定理求得:AB=.★OBC周长=2+BC+OC,★OAD周长=2+OD+AD,★★OBC和★OAD的周长相等,★BC+OC=OD+AD.★OD的垂直平分线交线段AB于点C,★OC=CD,OC=CA+AD.★BC+CA+AD=OD+AD,即BC+CA=OD,BA=OD.★OD=.故答案为:B.题型二、实际应用问题例1. 【2019·惠州市期末】如图,铁路MN和公路PQ在点O处交汇,★QON=30°.公路PQ上A处距离O 点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,如果A处受噪音影响,求影响的时间.【答案】见解析.【解析】解:过点A作AC★ON于C,以A为圆心,以200为半径画弧,交MN于点B、D,则AB=AD=200,★★QON=30°,OA=240,★AC=120,火车到达B点时对A处产生噪音影响,此时AB=200,AC=120,由勾股定理得:BC=160,CD=160,BD=320,★72 千米/小时=20米/秒,★影响的时间为:320÷20=16秒.例 2. 【2019·厦门六中月考】一棵大树被台风挂断,若树在离地面3m处这段,树顶端落在离树底部4m处,则树折断之前高为()A.7mB.8mC.5mD.10m【答案】B.【解析】解:如图:.在RtΔABC中,AB=3米,BC=4米,由勾股定理,得:AC=√AB2+BC2=5米.★AC+AB=3+5=8米,即大树折断之前有8米高.故答案为:B.题型三、易错问题例1. 【2019·宜城市期末】已知菱形ABCD的边长为4,★B=120°,如果点P是菱形内一点,且P A=PC=√13,那么BP的长为______.【答案】3或1.【解析】解:如图,★菱形ABCD的边长为4,★B=120°,★★ABP=12★ABC=60°,AC★BD,AO=CO,BO=DO,AB=BC=4,★BO=12AB=2,AO=√3BO=2√3,★P A=PC=√13,★点P在AC的垂直平分线上,★PO=√AP2−AO2=1当点P与点D在AC同侧时,BP=OB+OP=3当点P与点D在AC异侧时,BP=OB-OP=1故答案为:3或1.例2. 【2019·阜阳市联考期中】在★ABC中,已知AC=10cm,BC,AB边上的高CD=6cm,则AB=______.【答案】11cm或5cm.【解析】解:(1)如图,在Rt★ACD中,由勾股定理得:AD=8,在Rt★BCD中,由勾股定理得:BD=3,★AB=AD+BD=11(cm),(2)如图,AB=AD-BD=5(cm),则AB=11cm或5cm,故答案为:11cm或5cm.【刻意练习】1. 【2019·禹城市期末】如图,已知OP平分★AOB,★AOB=60°,CP=2,CP★OA,PD★OA于点D,PE★OB 于点E.如果点M是OP的中点,则DM的长是()A.2B C D.【答案】C.【解析】解:★OP平分★AOB,★AOB=60°,★★AOP=★COP=30°,★CP★OA,★★COP =★CPO ,★OC =CP =2,★★PCE =★AOB =60°,PE ★OB ,★★CPE =30°,★CE =12CP =1,由勾股定理得:PE★OP =2PE =★PD ★OA ,点M 是OP 的中点,★DM =12OP 故答案为:C .2.【2019·高密市期末】如图,等边★AOB 中,点B 在x 轴正半轴上,点A 坐标为(1,将★AOB 绕点O 顺时针旋转15°,此时点A 对应点A ′的坐标是 .【答案】).【解析】解:过点A 作AE ★OB 于E ,过点A ’作A ′H ★OB 于H .★A (1,★OE =1,AE由勾股定理得:OA =2,★★OAB 是等边三角形,★★AOA′=15°,★★A′OH=60°﹣15°=45°,★OA′=OA=2,A′H★OH,★A′H=OH,故答案为:).3. 【2018·容县期末】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是()A.B.6C.D.3+【答案】A.【解析】解:连接BC′,由题意得:B在对角线AC′上,★B′C′=AB′=3,在Rt★AB′C′中,AC′=,★BC′=﹣3,在等腰Rt★OBC′中,OB=BC′=3,在直角三角形OBC′中,OC′(﹣3)=6﹣,★OD′=3﹣OC′=3,★四边形ABOD′的周长是:2AD′+OB+OD′=6+﹣3+﹣3=故答案为:A.4. 【2019·株洲市期末】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是______.【答案】20厘米.【解析】如图,解:由翻折知,★HEM=★AEH,★BEF=★FEM,★HEF=★HEM+★FEM=90°,★EHG=★HGF=★EFG=90°,★四边形EFGH为矩形,AD=AH+HD=HM+MF=HF,在Rt★EFH中,由勾股定理,得:HF=√EH2+EF2=√122+162=20,即AD=20厘米.故答案为:20厘米.5. 【2019·成都市期末】如图,在正方形ABCD和正方形CEFG中,BC=1,CE=3,点D是CG边上一点,H是AF的中点,那么CH的长是______.【解析】解:★四边形ABCD 和四边形CEFG 都是正方形,★★ACD =45°,★FCG =45°,AC BC CF CE ,★★ACF =45°+45°=90°,在Rt ★ACF 中,由勾股定理得:AF =√AC 2+CF 2=2,★H 是AF 的中点,★CH =12AF6. 【2019·孝感市期末】如图,将矩形ABCD 的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH ,EH =6cm ,GH =8cm ,则边AB 的长是______.【答案】485cm . 【解析】如图所示,解:★★HEM =★HEB ,★GEF =★CEF ,★★HEF =★HEM +★GEF =12★BEG +12GEC =12×180°=90°, 同理可得:★EHG =★HGF =★EFG =90°,★四边形EFGH 为矩形,★EH =6cm ,GH =8cm ,由勾股定理,得:GE =10,由折叠可知,HM ★GE ,AH =HM ,BH =HM ,HM×GE=EH×GH,★HM=24 5★AB=BH+AH=2HM=48 5.故答案为485cm.7. 【2019·澧县期中】如图是“赵爽弦图”,★ABH、★BCG、★CDF和★DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,EF=2,那么AH等于.【答案】6.【解析】解:由题意得:大正方形的面积是100,小正方形的面积是4,四个直角三角形面积和为:100﹣4=96,设AE=a,DE=b,4×12ab=96,★2ab=96,a2+b2=100,★(a+b)2=a2+b2+2ab=100+96=196,★a+b=14,或a+b=-14(舍),★a﹣b=2,可得:a=8,b=6,★AH=8﹣2=6.故答案为:6.8. 【2019·阜阳市联考期中】公元3世纪,我国数学家赵爽在《周牌算经》中巧妙地运用如图所示的“弦图”来证明勾股定理,该图是由四个全等的直角三角形和一个小正方形拼成一个大正方形,若直角三角形的较长直角边长为a,短直角边长为b,大正方形面积为20,且(a+b)2=32.则小正方形的面积为()A.6B.8C.10D.12【答案】B.【解析】解:如图所示:★(a+b)2=32,★a2+2ab+b2=32,★大正方形的面积为20,2ab=32-20=12,★小正方形的面积为20-12=8.故答案为:B.9. 【2019·阳江市期中】如图,在★ABC中,★A=45°,★B=30°,CD★AB,垂足为D,AD=1,则BD的长为()A.√2B.2C.√3D.3【答案】C.【解析】解:在★ABC中,★A=45°,CD★AB,★★ACD是等腰直角三角形,★CD=AD=1,★★B=30°,在Rt★BCD中,BC=2CD=2,★BD=√BC2−CD2=√3,故答案为:C.10.【2019·武汉市期末】如图,正方形ABCD的面积是2,E,F,P分别是AB,BC,AC上的动点,PE+PF 的最小值等于______.【答案】√2.【解析】解:过点P作MN★AD交AB于点M,交CD于点N,如图所示,★四边形ABCD为正方形,★MN★AB,★PM≤PE(当PE★AB时取等号),PN≤PF(当PF★BC时取等号),★MN=AD=PM+PN≤PE+PF,★正方形ABCD的面积是2,★AD=√2.故答案为:√2.11. 【2019·乐亭县期末】将等边三角形ABC放置在如图的平面直角坐标系中,已知其边长为2,现将该三角形绕点C按顺时针方向旋转90°,则旋转后点A的对应点A′的坐标为()A.(1+√3,1)B.(-1,1-√3)C.(-1,√3-1)D.(2,√3)【答案】A.【解析】解:如图,由题意知,A′C与x轴的夹角为30°,过点A′作AD★x轴,则CD=OA=√3,A′D=1,★OD=1+√3,即A′(1+√3,1).故答案为:A.12. 【2019·汕头市期中】如图,三角形是直角三角形,四边形是正方形,已知正方形A的面积是64,正方形B的面积是100,则半圆C的面积是()A.36B.4.5πC.9πD.18π【答案】B.【解析】解:正方形A的面积是64,正方形B的面积是100,★DE=10,EF=8,由勾股定理得,DF=√DE2−EF2=6,半圆C的面积为:12×π×32=4.5π,故答案为:B.13. 【2019·广州市番禺区期末】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的数为()A.2B.√5−1C.√10−1D.√5【答案】C.【解析】解:由题意得,AC=√AB2+BC2=√AD2+DC2=√10,AM=√10,BM=AM-AB=√10-3,★点B的表示的数为2,★点M表示的数为√10−1.故答案为:C.14. 【2019·厦门六中月考】如图,矩形ABCD中,E是AD的中点,将ΔABE沿直线BE折叠后得到ΔGBE,延长BG交CD于点F.若AB=6,BC FD的长为【答案】4.【解析】解:★E是AD的中点★AE=DE由折叠性质得:AE=EG,AB=BG★ED=EG★在矩形ABCD中★★A=★D=90°★★EGF=90°★在RtΔEDF和RtΔEGF中,ED=EG,EF=EF★RtΔEDF★RtΔEGF(HL)★DF=FG设DF=x,则BF=6+x,CF=6-x在RtΔBCF中,由勾股定理得:(()()222x x+-=+,66解得:x=4,故答案为:4.15. 【2019·广州市番禺区期末】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:★x2+y2=49,★x-y=2,★2xy+4=49,★x+y=9.其中说法正确的是()A.★★B.★★★C.★★★D.★★★★【答案】B.【解析】解:由题意得:x2+y2=49★;(x-y)2=4★,★-★得:2xy=45★,★2xy+4=49,★+★得:x2+2xy+y2=94,★(x+y)2=94,★★★★正确,★错误.故答案为:B.16. 【2018·辽阳市期末】如图,等腰直角三角形ABC的直角边AB的长为6 cm,将★ABC绕点A逆时针旋转15°后得到★AB′C′,AC与B′C′相交于点H,则图中★AHC′的面积等于()A.12﹣6B.14﹣6C.18﹣6D.18+6【答案】C .【解析】解:在Rt ★ABC 中,由勾股定理得:AC 2=62+62,★AC =6;由旋转得:★CAC ’=15°,★★B ’AH =45°﹣15°=30°;★B ’H =★S ★AB ’H =S ★AHC ’=18﹣故答案为:C .17. 【2019·宜昌市期中】如图所示,A ,0)、B (0,1)分别为x 轴、y 轴上的点,△ABC 为等边三角形,点P (3,a )在第一象限内,且满足2S △ABP =S △ABC ,则a 的值为( )A .74BCD .2【答案】C .【解答】解:由题意得:OA OB =1,由勾股定理得:AB =2,★★ABC 是等边三角形,★S ★ABC =4×AB 2 过点P 作PD ★x 轴于D ,S ★ABP =S ★ABO +S 梯形BODP -S ★APD=121+(1+a )×3×12-12×()×a解得:a故答案为:C .18. 【2018·莆田市期中】如图,点P 是平面坐标系中一点,则点P 到原点的距离是( )A . 3B . √2C . √7D . √53【答案】A .【解析】解:连接PO ,★点P 的坐标是(2,7),★点P 到原点的距离=()()2227+=3.故答案为:A .19. 【2019·固始县期末】一阵大风把一根高为9m 的树在离地4m 处折断,折断处仍相连,此时在离树3.9m 处,一头高1m 的小马正在吃草,小马有危险吗?为什么?【答案】见解析.【解析】解:如图,过点C 作CE ★AB 于点E★BE=3在Rt★BCE中,由勾股定理得:BC2=BE2+EC2=32+3.92=24.21树高为9 m,因为52=25>24.21,所以小马有危险.20. 【2019·黄石期中】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100√2米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:√2≈1.41,√3≈1.73,计算结果保留两位小数)【答案】见解析.【解析】解:如图,过点C作CD★AB于点D,★在Rt★ADC中,★ACD=45°,AC=100√2,★CD=AC=100,2AD=CD=100.在Rt★CDB中,★BCD=60°,★BD=√3CD=100√3.★AB=AD+BD=100+100√3=100(√3+1)≈273.小轿车的速度为:273÷13=21(米/秒)=75.6千米/小时.该路段限速为60千米/时<75.6千米/小时★这辆小轿车超速了.21. 【2019·北京101中学期末】如图,在矩形ABCD中,点E在AD上,且EC平分★BED.(1)★BEC是否为等腰三角形?证明你的结论;(2)若AB=2,★DCE=22.5°,求BC长.【答案】见解析.【解析】解:(1)★BEC是等腰三角形;理由如下:★四边形ABCD是矩形,★AD★BC,★★DEC=★BCE,★EC平分★DEB,★★DEC=★BEC,★★BEC=★ECB,★BE=BC,即★BEC是等腰三角形.(2)★四边形ABCD是矩形,★★A=★D=90°,★★DCE=22.5°,★★DEB=135°,★★AEB=180°-★DEB=45°,★★ABE=★AEB=45°,由勾股定理得:BC=BE=22. 【2019·黄石市期中】如图在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米/秒的速度收绳,6秒后船移动到点D的位置问船向岸边移动了大约多少米?(假设绳子是直的结果精确到0.1米. 参考数据:√2≈1.414,√3≈1.732)【答案】见解析.【解析】解:★在Rt★ABC中,★CAB=90°,BC=13 ,AC=5 ,由勾股定理得:AB=√132−52=12 ,由题意得:CD=13-0.5×6=10,★AD=√CD2−AC2=√102−52=5√3,★BD=AB-AD=12-5√3≈3.3.即船向岸边移动了大约3.3m.。
初二数学《三角形、四边形》动点问题分析与讲解

初二数学《三角形、四边形》动点问题分析与讲解初二数学《三角形、四边形》动点问题分析与讲解所谓“动点问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想例题分析与讲解:1. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向D以1cm/s的速度运动;动点Q 从点C开始沿CB边向B以3cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形PQCD为等腰梯形?(3)当t为何值时,四边形PQCD为直角梯形?分析:(1)四边形PQCD为平行四边形时PD=CQ.(2)四边形PQCD为等腰梯形时QC-PD=2CE.(3)四边形PQCD为直角梯形时QC-PD=EC.所有的关系式都可用含有t的方程来表示,即此题只要解三个方程即可.解答:解:(1)∵四边形PQCD平行为四边形∴PD=CQ∴24-t=3t解得:t=6即当t=6时,四边形PQCD平行为四边形.(2)过D作DE⊥BC于E则四边形ABED为矩形∴BE=AD=24cm∴EC=BC-BE=2cm∵四边形PQCD为等腰梯形∴QC-PD=2CE即3t-(24-t)=4解得:t=7(s)即当t=7(s)时,四边形PQCD为等腰梯形.(3)由题意知:QC-PD=EC时,四边形PQCD为直角梯形即3t-(24-t)=2解得:t=6.5(s)即当t=6.5(s)时,四边形PQCD为直角梯形.点评:此题主要考查了平行四边形、等腰梯形,直角梯形的判定,难易程度适中.2.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.分析:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC 于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A 点,P、Q两点同时停止运动.设点Q运动的时间为t秒.(1)求NC,MC的长(用t的代数式表示);(2)当t为何值时,四边形PCDQ构成平行四边形;(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;(4)探究:t为何值时,△PMC为等腰三角形.分析:(1)依据题意易知四边形ABNQ是矩形∴NC=BC-BN=BC-AQ=BC-AD+DQ,BC、AD已知,DQ就是t,即解;∵AB∥QN,∴△CMN∽△CAB,∴CM:CA=CN:CB,(2)CB、CN已知,根据勾股定理可求CA=5,即可表示CM;四边形PCDQ构成平行四边形就是PC=DQ,列方程4-t=t即解;(3)可先根据QN平分△ABC的周长,得出MN+NC=AM+BN+AB,据此来求出t的值.然后根据得出的t的值,求出△MNC的面积,即可判断出△MNC的面积是否为△ABC面积的一半,由此可得出是否存在符合条件的t值.(4)由于等腰三角形的两腰不确定,因此分三种情况进行讨论:①当MP=MC时,那么PC=2NC,据此可求出t的值.②当CM=CP时,可根据CM和CP的表达式以及题设的等量关系来求出t的值.③当MP=PC时,在直角三角形MNP中,先用t表示出三边的长,然后根据勾股定理即可得出t的值.综上所述可得出符合条件的t的值.解答:解:(1)∵AQ=3-t∴CN=4-(3-t)=1+t在Rt△ABC中,AC2=AB2+BC2=32+42∴AC=5在Rt△MNC中,cos∠NCM= = ,CM= .(2)由于四边形PCDQ构成平行四边形∴PC=QD,即4-t=t解得t=2.(3)如果射线QN将△ABC的周长平分,则有:MN+NC=AM+BN+AB即:(1+t)+1+t= (3+4+5)解得:t= (5分)而MN= NC= (1+t)∴S△MNC= (1+t)2= (1+t)2当t= 时,S△MNC=(1+t)2= ≠ ×4×3∴不存在某一时刻t,使射线QN恰好将△ABC的面积和周长同时平分.(4)①当MP=MC时(如图1)则有:NP=NC即PC=2NC∴4-t=2(1+t)解得:t=②当CM=CP时(如图2)则有:(1+t)=4-t解得:t=③当PM=PC时(如图3)则有:在Rt△MNP中,PM2=MN2+PN2而MN= NC= (1+t)PN=NC-PC=(1+t)-(4-t)=2t-3∴[ (1+t)]2+(2t-3)2=(4-t)2解得:t1= ,t2=-1(舍去)∴当t= ,t= ,t= 时,△PMC为等腰三角形点评:此题繁杂,难度中等,考查平行四边形性质及等腰三角形性质.考查学生分类讨论和数形结合的数学思想方法.3.如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.(1)当x为何值时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形;(2)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形;(3)以P,Q,M,N为顶点的四边形能否为等腰梯形?如果能,求x的值;如果不能,请说明理由.分析:以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形的必须条件是点P、N重合且点Q、M不重合,此时AP+ND=AD即2x+x2=20cm,BQ+MC≠BC即x+3x≠20cm;或者点Q、M重合且点P、N不重合,此时AP+ND≠AD即2x+x2≠20cm,BQ+MC=BC即x+3x=20cm.所以可以根据这两种情况来求解x的值.以P,Q,M,N为顶点的四边形是平行四边形的话,因为由第一问可知点Q只能在点M的左侧.当点P在点N的左侧时,AP=MC,BQ=ND;当点P在点N 的右侧时,AN=MC,BQ=PD.所以可以根据这些条件列出方程关系式.如果以P,Q,M,N为顶点的四边形为等腰梯形,则必须使得AP+ND≠AD即2x+x2≠20cm,BQ+MC≠BC即x+3x≠20cm,AP=ND即2x=x2,BQ=MC即x=3x,x≠0.这些条件不能同时满足,所以不能成为等腰梯形.解答:解:(1)当点P与点N重合或点Q与点M重合时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边可能构成一个三角形.①当点P与点N重合时,由x2+2x=20,得x1= -1,x2=- -1(舍去).因为BQ+CM=x+3x=4(-1)<20,此时点Q与点M不重合.所以x= -1符合题意.②当点Q与点M重合时,由x+3x=20,得x=5.此时DN=x2=25>20,不符合题意.故点Q与点M不能重合.所以所求x的值为-1.(2)由(1)知,点Q只能在点M的左侧,①当点P在点N的左侧时,由20-(x+3x)=20-(2x+x2),解得x1=0(舍去),x2=2.当x=2时四边形PQMN是平行四边形.②当点P在点N的右侧时,由20-(x+3x)=(2x+x2)-20,解得x1=-10(舍去),x2=4.当x=4时四边形NQMP是平行四边形.所以当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形.(3)过点Q,M分别作AD的垂线,垂足分别为点E,F.由于2x>x,所以点E一定在点P的左侧.若以P,Q,M,N为顶点的四边形是等腰梯形,则点F一定在点N的右侧,且PE=NF,即2x-x=x2-3x.解得x1=0(舍去),x2=4.由于当x=4时,以P,Q,M,N为顶点的四边形是平行四边形,所以以P,Q,M,N为顶点的四边形不能为等腰梯形.点评:本题考查到三角形、平行四边形、等腰梯形等图形的边的特点.4.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M从点A开始,沿边AD向点D运动,速度为1cm/s;点N从点C开始,沿边CB向点B运动,速度为2cm/s、点M、N分别从点A、C出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒.(1)当t为何值时,四边形MNCD是平行四边形?(2)当t为何值时,四边形MNCD是等腰梯形?分析:(1)根据平行四边形的性质,对边相等,求得t值;(2)根据等腰梯形的性质,下底减去上底等于12,求解即可.解答:解:(1)∵MD∥NC,当MD=NC,即15-t=2t,t=5时,四边形MNCD是平行四边形;(2)作DE⊥BC,垂足为E,则CE=21-15=6,当CN-MD=12时,即2t-(15-t)=12,t=9时,四边形MNCD是等腰梯形点评:考查了等腰梯形和平行四边形的性质,动点问题是中考的重点内容.5.如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q 从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,设运动时间为t(s).(1)设△BPQ的面积为S,求S与t之间的函数关系;(2)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?分析:(1)若过点P作PM⊥BC于M,则四边形PDCM为矩形,得出PM=DC=12,由QB=16-t,可知:s= PM×QB=96-6t;(2)本题应分三种情况进行讨论,①若PQ=BQ,在Rt△PQM中,由PQ2=PM2+MQ2,PQ=QB,将各数据代入,可将时间t求出;②若BP=BQ,在Rt△PMB中,由PB2=BM2+PM2,BP=BQ,将数据代入,可将时间t求出;③若PB=PQ,PB2=PM2+BM2,PB=PQ,将数据代入,可将时间t求出.解答:解:(1)过点P作PM⊥BC于M,则四边形PDCM为矩形.∴PM=DC=12,∵QB=16-t,∴s= •QB•PM= (16-t)×12=96-6t(0≤t≤ ).(2)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分三种情况:①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,由PQ2=BQ2得t2+122=(16-t)2,解得;②若BP=BQ,在Rt△PMB中,PB2=(16-2t)2+122,由PB2=BQ2得(16-2t)2+122=(16-t)2,此方程无解,∴BP≠PQ.③若PB=PQ,由PB2=PQ2得t2+122=(16-2t)2+122得,t2=16(不合题意,舍去).综上所述,当或时,以B、P、Q为顶点的三角形是等腰三角形.点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.6.直线y=- 34x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O⇒B⇒A运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;(3)当S= 485时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.分析:(1)分别令y=0,x=0,即可求出A、B的坐标;(2))因为OA=8,OB=6,利用勾股定理可得AB=10,进而可求出点Q由O 到A的时间是8秒,点P的速度是2,从而可求出,当P在线段OB上运动(或0≤t≤3)时,OQ=t,OP=2t,S=t2,当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,作PD⊥OA于点D,由相似三角形的性质,得PD=48-6t5,利用S= 12OQ×PD,即可求出答案;(3)令S= 485,求出t的值,进而求出OD、PD,即可求出P的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M的坐标.解答:解:(1)y=0,x=0,求得A(8,0)B(0,6),(2)∵OA=8,OB=6,∴AB=10.∵点Q由O到A的时间是81=8(秒),∴点P的速度是6+108=2(单位长度/秒).当P在线段OB上运动(或O≤t≤3)时,OQ=t,OP=2t,S=t2.当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,如图,做PD⊥OA于点D,由PDBO=APAB,得PD= 48-6t5.∴S= 12OQ•PD=- 35t2+245t.(3)当S= 485时,∵485>12×3×6∴点P在AB上当S= 485时,- 35t2+245t= 485∴t=4∴PD= 48-6×45= 245,AD=16-2×4=8AD= 82-(245)2= 325∴OD=8- 325= 85∴P(85,245)M1(285,245),M2(- 125,245),M3(125,- 245)点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.。
部编人教版八年级数学下册难点突破专题

部编人教版八年级数学下册难点突破微专题(含解答)目录1、难点突破微专题一:勾股定理与旋转问题2、难点突破微专题二:一次函数方案设计3、难点突破微专题三:一次函数与定点、定值、定直线4、难点突破微专题四:一次函数与方程、不等式5、难点突破微专题五:一次函数与几何结合6、难点突破微专题六:借助勾股定理求最值7、难点突破微专题七:勾股定理与分类讨论8、难点突破微专题八:中点问题9、部编人教版八年级数学下册难点突破微专题九:四边形中的综合运用部编人教版八年级数学下册难点突破微专题一勾股定理与旋转问题【方法技巧】将图形旋转后得到直角三角形,再考虑用勾股定理难点突破一等边三角形为背景→旋转︒601.如图,点P为等边三角形△ABC内的一点,且PC=3,PB=4,PA=5(1)画出将△BPC绕点B逆时针方向旋转︒60后的图形;(2)求∠BPC的度数难点突破二等腰直角三角形为背景→旋转︒902.如图,在等腰直角△ABC中,∠ACB=︒45,90,点D,E在AB上,且∠DCE=︒BE=2,AD=3(1)将△BCE绕点C逆时针旋转︒90后,在图中画出旋转后的图形;(2)求DE的长难点突破三︒60(补形)→构成共顶点的两个等边三角形3.如图,在△ABC中,∠ABC=︒30,AB=6,BC=8,△ACD是等边三角形,求BD的长。
难点突破四旋转︒90(补形)→构成共顶点的两个等腰直角三角形4.如图,AB=AC,∠CAB=︒90,∠ADC=︒45,AD=4,CD=3,求BD的长。
参考答案1. 解(1)如图所示,△BQA 为△BPC 绕点B 逆时针方向旋转︒60后的图形; (2)如图,连PQ由旋转性质,△BQA ≌△BPC ,△BPQ 为等边三角形 ∴AQ =3 ,QB =4,∠BPC =∠AQB ∠BQP =︒60 又PA =5∴△PQA 为直角三角形 ∴∠AQC =︒90∴∠BPC =∠AQB =∠AQC+∠BQP =︒150134513904522901.222======中和在又===,==,==由旋转后全等性,有:)连(后的图形。
人教版八年级数学下学期期末重难点知识专题06一网打尽动点及折叠类型题目1(解析版).doc

【本文档由书林工作坊整理发布,谢谢你的下载和关注!】1专题06 一网打尽动点及折叠类型题目1动点类、折叠类题目是初中学生头疼的问题,也是教师教学过程中最烦心的问题,本专题将八年级下册所遇到的动点问题、折叠问题进行分类,并选取一些有代表性的题目供大家研讨,帮助学生们理清一些思路,掌握做题方法.(1)折叠类题目:借助圆规、直尺作出图形,利用勾股定理、方程等手段求解;(2)动点类题目:其中的等腰三角形、直角三角形、平行四边形等存在性问题要分类讨论,并作出图形;用时间、速度表示线段的长要准确;根据图形列出方程求解.题1. 一次函数与平行四边形存在性问题综合 (解题核心点:基本图形的运用)在平面直角坐标系xoy 中,A (1,2)、B (-1,1)、C (3,m ),D 点是直线y =x 上的一个动点,是否存在实数m 使得以A 、B 、C 、D 为顶点的四边形是平行四边形.若存在,求出m 值,若不存在说明理由. 【答案】见解析. 【解析】解:存在. 设D 点坐标为(n ,n )①当四边形ACBD 是平行四边形时, 可得:x A + x B = x C + x D ,y A + y B = y C + y D 即1+(-1)=3+n ,2+1=m +n , 解得:n =-3,m =6;②当四边形ABCD 是平行四边形时, 可得:x A + x C = x B + x D ,y A + y C = y B + y D【本文档由书林工作坊整理发布,谢谢你的下载和关注!】2即1+3=(-1)+n ,2+m =1+n , 解得:n =5,m =4;③当四边形ABDC 是平行四边形时, 可得:x A + x D = x B + x C ,y A + y D = y B + y C 即1+n =(-1)+3,2+n =1+m , 解得:n =1,m =2;综上所述,m 的值为6、4、2. 题2. 一次函数与最短路径综合(解题核心点:待定系数法、勾股定理及转化思想)如图2-1所示,直线l 1 :y =-3x +3与x 轴交于点D ,直线l 2经过A (4,0)、B (3,-1.5)两点,直线l 1 与直线l 2交于点C .(1)求直线l 2的解析式和点C 的坐标;(2)在y 轴上是否存在一点P ,使得四边形PDBC 的周长最小?若存在,请求出点P 的坐标,若不存在,请说明理由.图2-1【答案】见解析.【解析】解:(1)设直线l 2的解析式为y =kx +b , 将A (4,0)、B (3,-1.5)代入,得:40332k b k b +=⎧⎪⎨+=-⎪⎩,【本文档由书林工作坊整理发布,谢谢你的下载和关注!】3解得:326k b ⎧=⎪⎨⎪=-⎩即直线l 2的解析式为y =32x -6. 联立y =32x -6,y =-3x +3,解得: 23x y =⎧⎨=-⎩,即点C 的坐标为(2,-3) (2)在y =-3x +3中,当y =0时,x =1,即D (1,0), 由勾股定理,得BD =52,BC,因为四边形PDBC 的周长等于PD +DB +BC +CP , 所以当PD +CP 最小时,四边形PDBC 的周长最小,作点D 关于y 轴的对称点D ’(-1,0),连接D ’C 交y 轴于点P ,如图2-2所示, 此时即为所求P 点位置,图2-2设直线B ’P 的解析式为y =mx +n , 将(-1,0),(3,-1.5)代入,得:【本文档由书林工作坊整理发布,谢谢你的下载和关注!】40332k b k b -+=⎧⎪⎨+=-⎪⎩,解得:3838k b ⎧=-⎪⎪⎨⎪=-⎪⎩所以P 点坐标为(0,38-). 题3. 一次函数与全等三角形综合如图3-1所示,在直角坐标系中,点A 的坐标是(0.3),点C 是x 轴上的一个动点,点C 在x 轴上移动时,始终保持△ACP 是等边三角形.当点C 移动到点O 时,得到等边三角形AOB (此时点P 与点B 重合).(1)点C 在移动的过程中,当等边三角形ACP 的顶点P 在第三象限时(如图),求证:△AOC ≌△ABP ;由此你发现什么结论?(2)求点C 在x 轴上移动时,点P 所在函数图象的解析式.【答案】见解析. 【解析】解:(1)证明:∵△AOB 与△ACP 都是等边三角形, ∴AO =AB ,AC =AP ,∠CAP =∠OAB =60°, ∴∠CAP +∠PAO =∠OAB +∠PAO , 即∠CAO =∠PAB , 在△AOC 与△ABP 中,【本文档由书林工作坊整理发布,谢谢你的下载和关注!】5AO AB CAO PAB AC AP =⎧⎪=⎨⎪=⎩∠∠ ∴△AOC ≌△ABP ∴∠COA =∠PBA =90°,∴点P 在过点B 且与AB 垂直的直线上或PB ⊥AB 或∠ABP =90°. 故结论是:点P 在过点B 且与AB 垂直的直线上或PB ⊥AB 或∠ABP =90°; (2)解:由(1)知点P 在过点B 且与AB 垂直的直线上. ∵△AOB 是等边三角形,A (0,3), ∴B32). 当点C 移动到点P 在y 轴上时,得P (0,﹣3). 设点P 所在的直线方程为:y =kx +b (k ≠0). 将点B 、P 的坐标分别代入,得:3=223k b b ⎧+⎪⎨⎪=-⎩,解得:3k b ⎧⎪⎨=-⎪⎩, 故所求的函数解析式为:y﹣3. 题4. 一次函数与等腰三角形存在性综合如图4-1所示,在平面直角坐标系中,矩形ABCD 的顶点A 、B 、C 的坐标分别为(0,5)、(0,2)、(4,2),直线l 的解析式为y =kx +5-4k (k >0).(1)当直线l 经过点B 时,求一次函数的解析式; (2)通过计算说明:不论k 为何值,直线l 总经过点D ;(3)直线l 与y 轴交于点M ,点N 是线段DM 上的一点,且△NBD 为等腰三角形,试探究:当函数y =kx +5-4k 为正比例函数时,点N 的个数有______个.【本文档由书林工作坊整理发布,谢谢你的下载和关注!】6图4-1【答案】见解析. 【解析】解:(1)将(0,2)代入y =kx +5-4k 中,得:k =34, 即当直线l 经过点B 时,一次函数的解析式为y =34x +2; (2)由题意可得:点D 坐标为(4,5) 把x =4代入y =kx +5-4k , 得y =5,∴不论k 为何值,直线l 总经过点D ; (3)2;理由如下:y =kx +5-4k 为正比例函数时,可得5-4k =0, 即k =54,函数解析式为y =54x , 如图4-2所示,图4-2N 点在PD 的垂直平分线上时,符合要求;以D 为圆心以PD 长为半径画弧与MD 的交点N 符合要求;以P 为圆心,以PD 长为半径画弧与线段DM 交点为D ,不符合要求,即共2个N 点.题5. 已知C 坐标为(2,0),P 坐标为(x ,y ),直线y =-x +4与x 轴、y 轴分别交于A 、B 两点.若点P (a ,b )在直线y =-x +4上.(1)求出A 、B 坐标,并求出△AOB 的面积;【本文档由书林工作坊整理发布,谢谢你的下载和关注!】7(2)若点P 在第一象限内,连接PC ,OP ,△OPC 的面积为S ,请找出S 与a 之间的函数关系式,并求出a 的取值范围;(3)当△OPC 的面积等于2时,求P 点坐标.(4)点P 在移动的过程中,若BC =BP ,求出满足条件的点P 坐标.(直接写出答案)图5-1【答案】见解析. 【解析】解:(1)在y =-x +4中,x =0时,y =4;y =0时,x =4, 即A (4,0),B (0,4),OA =OB =4 △AOB 的面积为8;(2)∵P 在直线y =-x +4上,所以P 坐标为(a ,-a +4),OC =2, ∵P 在第一象限,∴-a +4>0, ∴S =12×OC ×(-a +4)=-a +4, 其中,0<a <4; (3)S =2时,①-a +4=2,解得a =2, 即P 点坐标为(2,2); ②-a +4=-2,解得a =6, 即P 点坐标为(6, -2);综上所述,P 点坐标为(2,2)或(6, -2);(4)以点B 为圆心,以BC 长为半径画弧,交直线AB 于点P 1,P 2,即为所求,【本文档由书林工作坊整理发布,谢谢你的下载和关注!】8过点P 1作P 1H ⊥y 轴于H ,如图5-2所示,图5-2由勾股定理,得:BC =BP 1= ∵OA =OB ,∴∠OAB =∠OBA =45°, ∴∠BP 1H =45° ∴HP 1BP 1, 即P 1,4),同理得:P 2,).题6. 如图6-1所示,在平面直角坐标系中,直线l 1:y =kx +b 与直线l 2:y =x 交于点A (2,a ),与y 轴交于点B (0,6),与x 轴交于点C .(1)求直线l 1的函数表达式; (2)求△AOC 的面积;(3)在平面直角坐标系中有一动点P (5,m ),使得AOP AOC S S △△,请求出点P 的坐标;【本文档由书林工作坊整理发布,谢谢你的下载和关注!】9图6-1【答案】见解析. 【解析】解:(1)∵y =kx +b 与直线y =x 交于点A (2,a ), ∴a =2,即A (2,2),将(2,2),(0,6)代入y =kx +b 得:226k b b +=⎧⎨=⎩,解得:26k b =-⎧⎨=⎩即直线l 1的函数表达式为y =-2x +6; (2)在y =-2x +6中,当y =0时,x =3, 所以C (3,0), △AOC 的面积为1232⨯⨯=3; (3)∵AOP AOC S S =△△,∴当两三角形等底等高时面积相等, 平移直线OA ,如6-2所示,图6-2求得直线CD 的解析式为y =x -3,当x =5时,y =2,即P 点坐标为(5,2) 同理,得另一条直线的解析式为y =x +3,当x =5时,y =8,即P 点坐标为(5,8). 综上所述,点P 的坐标为(5,2)、(5,8). 题7. 平行四边形及三角形存在性问题综合 (解题核心:勾股定理、一次函数的性质应用)【本文档由书林工作坊整理发布,谢谢你的下载和关注!】10如图7-1所示,已知点A 从点(1,0)出发,以1个单位每秒的速度沿x 轴正方形运动,以O 、A 为顶点作菱形OABC ,使得点B 、C 在第一象限,且∠AOC =60°.同时点G 从点D (8,0)出发,以2个单位长度每秒的速度沿x 轴向负方向运动,以D 、G 为顶点在x 轴的上方作正方形DEFG .若点P 的坐标为(0,3),设点A 的运动时间为t (s ),求: (1)点B 的坐标(用含t 的代数式表示);(2)当点A 在运动的过程中,当t 为何值时,点O 、B 、E 在同一直线上;(3)在点A 的运动过程中,是否存在t 值,使得△OCP 为等腰三角形,若存在,求出t 值;若不存在,说明理由.图7-1图7-2【答案】见解析. 【解析】解:(1)如图7-2所示,过B 作BH ⊥x 轴于H , ∵OA =AB =t +1,OABC 是菱形 ∴∠BAH =∠AOC =60°, ∴∠ABH =30°, ∴AH =12AB =12(t +1),由勾股定理得:BHt +1),∴点B 的坐标为(()312t +)1t +);【本文档由书林工作坊整理发布,谢谢你的下载和关注!】11(2)由题意得:E 点坐标为(8,2t ),设直线OE 的解析式为y =kx ,将E 点坐标代入,得: 2t =8k ,即k =4t , 直线OE 解析式为y =4t x 若O 、B 、E 三点共线,则B 点在直线OE 上,将B 点坐标代入得:)1t +=4t ×()312t + 解得:t =-1(舍)或t=3, 即当t为3时,点O 、B 、E 在同一直线上.图7-3(3)过C 作CM ⊥x 轴于M ,如图4-2所示,则C 点坐标为(()112t +,)12t +),OC =t +1,OP =3, 在图7-3中,若△OCP 是等腰三角形,①当OC =OP 时,即t +1=3,解得t =2;②当OP =PC 时,∠PCO =∠POC =30°,∴OC= ,即:t,解得:t1;【本文档由书林工作坊整理发布,谢谢你的下载和关注!】12③当OC =PC 时,此时,C 在线段OP 的垂直平分线上,即P 点纵坐标为32, 32)1t +,解得:t1; 综上所述,当t 为2或1-1时,△OCP 为等腰三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题动点与特殊三角形存在性问题大视野
【例题精讲】
题型一、等腰三角形存在性问题
例1. 【2019·黄石期中】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2cm,E、F分别是AB、AC 的中点,动点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时动点Q从点B出发,沿BF方向匀速运动,速度为2cm/s,连接PQ,设运动时间为ts(0<t<1),则当t=______时,△PQF为等腰三角形.
例2. 【2019·广州市番禺区期末】已知:如图,在Rt△ABC中,△C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
例3. 【2019·乐亭县期末】如图,矩形OABC的顶点A,C分别在坐标轴上,B(8,7),D(5,0),点P 是边AB或边BC上的一点,连接OP,DP,当△ODP为等腰三角形时,点P的坐标为______.
题型二、直角三角形存在性问题
例1. 【2019·厦门六中月考】如图,在RtΔABC中,△B=90°,AC=60,△A=60°.点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,设点D、E运动的时间是t秒(0<t≤15).过点D作DF△BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,ΔDEF为直角三角形?请说明理由.
题型三、等腰直角三角形存在性问题
例1. 【2019·株洲市期末】(1)操作思考:如图1,在平面直角坐标系中,等腰Rt△ACB的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点(1,2)处.则△OA的长为______;△点B的坐标为______.(直接写结果)
(2)感悟应用:如图2,在平面直角坐标系中,将等腰Rt△ACB如图放置,直角顶点C(-1,0),点A(0,4),试求直线AB的函数表达式.
(3)拓展研究:如图3,在直角坐标系中,点B(4,3),过点B作BA△y轴,垂足为点A,作BC△x轴,垂足为点C,P是线段BC上的一个动点,点Q是直线y=2x-6上一动点.问是否存在以点P为直角顶点的等腰Rt△APQ,若存在,请求出此时P的坐标,若不存在,请说明理由.
【刻意练习】
1. 【2019·大连市期末】如图,直线x=t与直线y=x和直线y=
1
2
-x+2分别交于点D、E(E在D的上方).
(1)直线y=x和直线y=
1
2
-x+2交于点Q,点Q的坐标为______;
(2)求线段DE的长(用含t的代数式表示);
(3)点P是y轴上一动点,且△PDE为等腰直角三角形,求t的值及点P的坐标.
2. 【2019·兴城市期末】如图,在平面直角坐标系中,一次函数y =kx +b 的图象经过点A (-2,6),且与x 轴交于点B ,与正比例函数y =3x 的图象相交于点C ,点C 的横坐标是1.
(1)求此一次函数的解析式;
(2)请直接写出不等式(k -3)x +b >0的解集;
(3)设一次函数y =kx +b 的图象与y 轴交于点M ,点N 在坐标轴上,当△CMN 是直角三角形时,请直接写出所有符合条件的点N 的坐标.
3. 【2019·泉州市晋江区期中】如图,在平面直角坐标系中,A (a ,0),B (0,b ),且a 、b 满足(a ﹣2)
2+0.
(1)求直线AB 的解析式;
(2)若点M 为直线y =mx 上一点,且△ABM 是等腰直角三角形,求m 值;
(3)过A 点的直线y =kx ﹣2k 交y 轴于负半轴于P ,N 点的横坐标为﹣1,过N 点的直线y =2k x ﹣2
k 交AP 于点M ,试证明PM PN AM
-的值为定值.
4. 【2019·厦门大学附中期末】如图(1),Rt △AOB 中,△A =90°,△AOB =60°,OB =,△AOB 的平分
线OC交AB于C,过O点作与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
(1)求OC、BC的长;
(2)当t=1时,求△CPQ的面积;
(3)当P在OC上,Q在ON上运动时,如图(2),设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.
5. 【2019·潮州市期末】如图,在△ABC中,△A=120°,AB=AC=4,点P、Q同时从点B出发,以相同的速度分别沿折线B→A→C,射线BC运动,连接PQ. 当点P到达点C时,点P、Q同时停止运动. 设BQ=x,△BPQ和△ABC重叠部分的面积为S.
(1)求BC的长;
(2)求S关于x的函数关系式,并写出x的取值范围;
(3)请直接写出△PCQ为等腰三角形时,x的值.
6. 【2019·南宁市期末】如图,在四边形ABCD中,AD△BC,△B=90°,AD=8cm,BC=10cm,AB=6cm,点
Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向点C运动,P、Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s).
(1)直接写出:QD=,PC=;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当t为何值时,△DPQ是等腰三角形?
7. 【2019·涟源市期末】如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,动点P从点B 出发,以每秒1个单位的速度沿着边BA向终点A运动,连接EP,设点P的运动时间为t秒,则当t为何值时,△P AE为等腰三角形.
8. 【2019·重庆外国语月考】如图,在Rt△ABC中,△ACB=90°,△A=30°,AB=12,点F是AB的中点,
过点F作FD△AB交AC于点D.若△AFD以每秒2个单位长度的速度沿射线FB向右移动,得到△A1F1D1,当F1与点B重合时停止移动.设移动时间为t秒,如果D1,B,F构成的△D1BF为等腰三角形,求出t值.
9. 【2019·平潭期中】如图,在平面直角坐标系中,A(0,8),B(4,0),AB的垂直平分线交y轴与点D,连接BD,M(a,1)为第一象限内的点.
(1)求点D坐标;
(2)当S△DBC=S△DBM时,求a的值;
(3)点E为y轴上的一个动点,当△CDE为等腰三角形时,直接写出点E的坐标.。
