信号与噪声_第二章精讲
信号与噪声分析
第2章信号与噪声分析知识点及层次1. 确知信号时－频域分析(1) 现代通信系统周期信号的傅氏级数表示和非周期信号的傅氏积分。
(2) 几个简单且常用的傅氏变换对及其互易性。
(3) 信号与系统特征－卷积相关－维钠－辛钦定理。
2. 随机过程统计特征(1) 二维随机变量统计特征。
(2) 广义平稳特征、自相关函数与功率谱特点。
(3) 高斯过程的统计特征。
3. 高斯型白噪声统计特征(1) 理想白噪声及限带高斯白噪声特征。
(2) 窄带高斯白噪声主要统计特征。
以上三个层次是一个层层深入的数学系统，最终旨在解决信号、系统及噪声性能分析，是全书各章的基本理论基础，也是系统分析的最主要的数学方法。
2.1信号与系统表示法2.1.1通信系统常用信号类型通信系统所指的信号在不加声明时，一般指随时间变化的信号。
通常主要涉及以下几种不同类型的信号：1.周期与非周期信号周期信号满足下列条件：全部时域(2-1) ——的周期，是满足（2-1）式条件的最小时段。
因此，该也可表示为：(2-2) ——是在一个周期内的波形（形状）。
若对于某一信号，不存在能满足式（2-1）的任何大小的值，则不为周期信号（如随机信号）。
从确知信号的角度出发，非周期信号一般多为有限持续时间的特定时间波形。
2．确知和随机信号确知信号的特征是：无论是过去、现在和未来的任何时间，其取值总是唯一确定的。
如一个正弦波形，当幅度、角频和初相均为确定值时，它就属于确知信号，因此它是一个完全确定的时间函数。
随机信号是指其全部或一个参量具有随机性的时间信号，亦即信号的某一个或更多参量具有不确定取值，因此在它未发生之前或未对它具体测量之前，这种取值是不可预测的。
如上述正弦波中某一参量（比如相位）在其可能取值范围内没有固定值的情况，可将其表示为：(2-3) 其中和为确定值，可能是在（0，2π）内的随机取值。
3．能量与功率信号在我们常用的电子通信系统中，信号以电压或电流（变化）值表示，它在电阻上的瞬时功率为：或(2-4) 功率正比于信号幅度的平方。
第2信号与噪声
（2）平稳随机过程
（补充）随机过程的统计特性 n 分布函数和概率密度函数
n 了解随机过程X(t)的一维分布函数F(x1,t)的定义；二维分布函数F(x1, x2,t1,t2)的定义。
n 了解随机过程X(t)的一维概率密度函数p(x1,t)的定义；二维概率密度函数 p(x1, x2,t1,t2)的定义。
H( )kejt0
() t0
(补充)信号带宽的常用定义
3dB带宽
n 3dB带宽：指的是比峰值功率小3dB（就是峰值的50％）的频 谱范围的带宽；
n 6dB带宽同上，6dB对应的是峰值功率的25％。
n 当计算A的功率相比于B大或小多少个dB时，可按公式10lgA／B计算。例 如：A功率比B功率大一倍，那么10lgA／B＝10lg2＝3dB，也就是说，A 的功率比B的功率大3dB。
n 复指数形式（通信中广泛应用，是傅里叶变换的基础）
周期信号的频谱特点： 频谱（幅度谱）是离散的，脉冲周期越长，谱线间
【例】幅度隔为越A，小宽。度为τ，周期为T的脉冲序列，用指数傅立叶级
数展开。
（2）非周期信号的傅里叶变换
非周期信号可以看成是周期T为无穷大的信号。
【例】求图示脉冲的频谱
解:
f(t) / 2
n 用数学式表示
r(t)k(ftt0)
R()kF ()ejt0 F ( )H ( )k( F)ejt0
H()kejt0
n 信号通过线性系统不产生波形失真, 要求系统应具备以下两个 条件: (1 ) 系统的幅频特性应该是一个不随频率变化的常数。 (2) 系统的相频特性应与频率成直线关系。
无失真传输系统
信号分类（续）
n 能量信号和功率信号
n 功率：电压u(t)或电流i(t)在电阻R上的瞬时功率。
信号与噪声
4
语音信号：空气压力随时间变化的函数
语 音 信 号 “ 你 好” 的 波 形
0
0.1
0.2
0.3
0.4
5
静止的单色图象： 亮度随空间位置变化的信号f(x,y)。
6
2.信号的分类
确定信号与随机信号
确定信号是指能够以确定的时间函数表示的信号， 在其定义域内任意时刻都有确定的函数值。 例如电路中的正弦信号和各种形状的周期信号等。 随机信号也称为不确定信号，不是时间的确定函数。 只能用概率统计方法来描述，其取值具有不可预知 的不确定性，则称此类信号为随机信号。随机信号 也是工程中的一类应用广泛的信号。 例如：在通信传输中引入的各种噪声，海面上海 浪的起伏等。
29
4)冲激信号的极限模型
f (t ) 1 2
g (t ) 1
t
t
(t ) lim f (t ) lim g (t ) lim h (t )
0 0 0
30
冲激信号的性质 (1)抽样（筛选）特性
f (t ) (t t0 )dt f (t0 )
s s
25
f (t ) e [u(t ) u(t t0 )]
f(t)
t
t
26
4.奇异信号
单位冲激信号
自然界有这样的现象，发生在很短的瞬间，其他时刻没有动作。 如电学中的雷击电闪、力学中的瞬间作用的冲击力等。为此，引 入冲激信号。
s s
27
4.奇异信号
设冲激信号有一个总的冲激强度，它在整个时间域上的积分等 于该强度，而在除冲激点之外的其他点的函数取值为0。
第二章4 信号与噪声傅立叶变换
+∞ −∞
∫f
2
(t )dt ≠ +∞
−
则称f (t )为能量信号
18
2、功率信号 、
若E =
+∞
−∞
∫f
2
(t )dt = +∞
T 2
1 但S = lim T →∞ T
∫f
T 2
2
(t )dt ≠ +∞
−
则称f (t )为功率信号.
19
傅立叶变换性质一览表
1. 线性特性 2. 对称互易特性 3. 展缩特性 4. 时移特性 5. 频移特性 6. 时域卷积特性 7. 频域卷积特性 8. 时域微分特性 积分特性 9. 频域微分特性
= F (ω − ω 0 )
5
利用欧拉公式：通过乘以余弦信号（正弦信号）， 利用欧拉公式：通过乘以余弦信号（正弦信号）， 频谱搬移的目的 可以达到频谱搬移的目的。 可以达到频谱搬移的目的。
F [ f (t ) cos ω 0t ] = 1 F [ f (t )e jω 0t ] + 1 F [ f (t )e - jω 0t ] 2 2 1 1 = F (ω − ω 0 ) + F (ω + ω 0 ) 2 2 信号f(t)与余弦信号cosω0 t相乘后，其频谱是 将原来信号频谱向左右搬移ω0，幅度减半。
δ(t)
F(ω)
1
t
F(ω)
ω
f (t)
t
ω
13
F (t ) ← 2πf (−ω ) →
F (ω )
f (t )
A
Eτ
−
τ
2
0
τ
2
t
−4π
−2π
第2章随机信号与噪声
●随机过程：尽管随机信号和随机噪声是不可预测的、随机 的，但它们具有一定的统计规律。从统计学的观点看，均可 表示为随机过程。
随机过程是一类随时间作随机变化的过程，它不能用确切的时
间函数描述。
统计学中的有关随机过程的理论可以运用到随机信号和噪声分
析中来。
2021/5/12
通信原理
3
பைடு நூலகம்
第2章 随机信号与噪声分析
2021/5/12
通信原理
5
第2章 随机信号与噪声分析
x1 (t)
角度1：对应不同随机试验结
果的时间过程的集合。
x2 (t)
角度2：随机过程是随机变量
概念的延伸。
xn (t)
讨论：
t1
t2
t
图 2- 1 n图 图 图 图 图 图 图 图 图
●在任一给定时刻t1上，每一个样本函数xi (t)都有一个确定的
●全部随机函数的集合－－随 机过程：
X(t) ={x1(t), x2(t), …, xn(t)} ●每一条曲线xi(t)都是随机过 程的一个实现/样本－－为确 定的时间函数。
角度1：对应不同随机试验结果的时间过程的集合。 角度2：随机过程是随机变量概念的延伸。
●在某一特定时刻t1观察各台接收机的输出噪声值x(t1) ，发现 他们的值是不同的－－ 是一个随机量（随机变量）。
过程。
意义： ●具有各态历经性平稳随机过程－－十分有趣，非常有用。 ●通信系统中所遇到的信号与噪声，大多数可视为平稳、具 有各态历经性的随机过程。
2021/5/12
通信原理
21
第2章 随机信号与噪声分析
2.3.2 平稳随机过程的各态历经性
●问题的提出 随机过程的数字特征（均值、相关函数）是对随机过程的 所有样本函数的统计平均，但在实际中常常很难测得大量 的样本。 问题：能否从一次试验而得到的一个样本函数x(t)来决定平 稳过程的数字特征呢?
信号检测与估计 第二章 匹配滤波
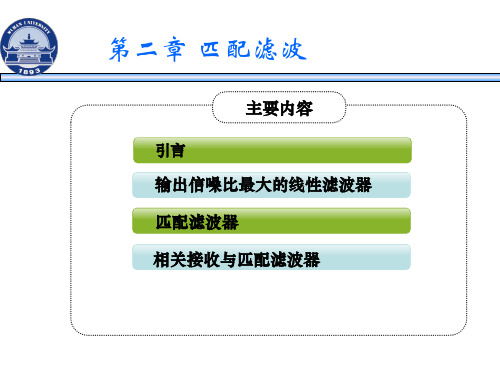
代表一个雷达回波信号,α及τ 是未知的参量或随机变量
S 1 ( ) a S ( ) e
j ( t1 )
j
caS ( )e
aH ( )e
j t1 ( t0 )
t1与to在输入信号结束后可以任选，如果取t1 = to+τ
H 1 ( ) a H ( )
2 j ( t t0 )
j t
d d
j arg H ( ) arg S ( ) t
e
d
arg H ( )
补偿了输入信号的
arg S ( )
§2.3
匹配滤波器
滤波器内部和外部产生的随机噪声(可等效为系统输入端 的噪声), 其功率谱宽度往往大于系统的通频带。
H ( ) Gn ( ) d
2
S ( )
2
Gn ( )d来自A ( ) H ） G n ( ) e （
j t 0
cB ( ) c
*
S ( )
*
G n ( )
H ） c （
S ( )
*
G n ( )
e
j t 0
输出波形
最大输出信噪比
*
G n ( )
e
j t 0
arg H ( ) arg S ( ) t 0
第一项与信号相频特性反相 第二项与频率成线性关系
s0 (t ) 1 2 1 2 1 2
H ）（）e （ S H ）（） （ S e S ( ) Gn ( )
取t0=(L-1)T+τ，令
H 1 ） cS1 ( )e （
信号与噪声_第二章
13
二、噪声的分类和噪声源 核电子学中的噪声主要有三类：
散粒噪声 (Shot noise)
探测器漏电流的噪声、场效应管的栅极漏电流的噪声。
热噪声(Thermal noise) 场效应管的沟道噪声、电阻元件的热噪声。 低频噪声(Flicker noise) 场效应管闪烁噪声。
14
散粒噪声
“周期信号都可表示为谐波关系的正弦信号的 加权和”——傅里叶的第一个主要论点
“非周期信号都可用正弦信号的加权积分表示
” ——傅里叶的第二个主要论点
19
傅里叶变换分析的直观说明
：把一个信号的波形分解为许多不同频率正弦波之和。
1
1.299
2
f ( t) 5 0 5
1
1 t
h( t)
4
2
0
2
在信号的产生、传输和测量过程中,探测器和电子学的噪声会叠加
在有用信号上,从而降低测量精度，甚至某些有用的微弱信号会被 噪声所淹没。
通常用信噪比S/N(信号与噪声均方值的比值)来表示系统的噪声指
标。信噪比越高，噪音引起的测量误差越小。
6
噪声的时间平均值为零。但是只要有噪声存在，其 平均功率就不为零，因此通常采用均方值（噪声电压的 平方值按时间求平均） Vn2 作为噪声大小的衡量尺度：
8
噪声的表示方法
通常用信噪比S/N(信号与噪声均方值的比值)来表
示系统的噪声指标。信噪比越高，噪音引起的测量 误差越小 考虑一个常见的探测器与放大器组成的测量系统。 在系统的输出端测得电压信号幅度Vo和噪声均方根 值Vno
辐射源
能量E
探测器 等效 噪声 能量 ENE 等效噪声 电荷ENC 输入信号 电压Vi 等效噪声 电压ENV 放大器 （放大倍数A）
第二章(4-1)噪声
2 I n,D 2 gm Zi 2
则
2 In =
( g m RL ) 2 Z i
2
不考虑 负载噪声
2 In =
相关的 Vn2 和 I n2 是相关的
2.3 噪声系数 2.3.1 噪声系数定义
F= SNRi P / Ni = i SNRo Po / N o
S I = 2qI 0
Vn2,rbb′ = 4kTrbb′ B
2.2.3 场效应管的噪声
1. 沟道电阻热噪声 —— S I = 4kTλg d 0 2. 噪声等效电路 I n , D = 4kTλg d 0 B 3. 闪烁噪声 ——
1 f
噪声 SV =
K 1 WLC OX f
2.2.4 电抗元件的噪声
2 n f1
f2
I n2 : 白噪声 S ( f ) 是常数 I n2 = ∫ S I ( f )d f = S I ∫ df = S I ( f 2 − f1 ) （3）等效噪声带宽 噪声通过线性系统 噪声通过线性系统
f1 f1
f2
f2
输入功率谱密度 输入功率谱密度 系统传递函数 系统传递函数
电抗元件的噪声来源于它的损耗电阻——热噪声 热噪声 电抗元件的噪声来源于它的损耗电阻
2.2. 两端口网络的等效输入噪声源 .2.5 .2. 串联噪声电压源 串联噪声电压源 Vn2 噪声 并联噪声 噪声电流源 2 并联噪声电流源 I n
等效
求法： 求法：
Vn2
2 In
输入端短路， 输入端短路，将有噪网络的输出噪声功率等效到输入端的值 短路 输入端开路， 输入端开路，将有噪网络的输出噪声功率等效到输入端的值 开路
第二章_噪声与统计分析 PPT
Ro ( ) Rh ( ) Ri ( )
第2次作业
1，写出单边功率谱密度为a的白噪声经过下图所示
电路后，功率谱密度函数（so(ω)）。
电路1
电路2
2，参考教材，描述平稳随机过程、各态遍历随机过 程、能量信号、功率信号的概念。
R( ) lim 1
T /2
v(t)v(t )dt
?
T T T / 2
2.5 应用实例
噪声可以看成是强度Q各不相同的冲击信号组成的随 机冲击序列。即
i(t) Qk (t tk ) k
2.5 应用实例
研究方法
i(t) Q (t kT) i(t) Q (t tk )
vk
lim 1 T T
T /2
T / 2 vk (t)dt
vk2
lim
T
1 T
T /2 T / 2
vk2
(t
)dt
均方值
2.2 统计分析的基本概念
平稳随机过程与各态遍历随机过程
平稳随机过程：集合平均不随时间变化，是一个常 数，即各个时刻的集合平均值是相同的。
设有N个强度为Q、周期为T的冲激序列，相位各不相同，且 N=nT。将这N个序列迭加起来，当T∞时，N∞，其集合 就趋近于上述随机冲激序列。
2.5 应用实例
由上述分析可得，等强度随机冲击序列的功率谱密 度函数可表示为：
S() n 2Q2 ( f ) nQ2
s() 2n 2Q2 () nQ2 /
2.2 统计分析的基本概念
噪声的特性（二）
独立无关的噪声之间，有如下特性
v1 v2 v3 v1 v2 v3
信号与噪声
T/2
−∞
1 T/2 2 f ( t )dt T ∫−T / 2
1 T/2 2 1 P = lim { ∫ f ( t )dt } = − T / 2 2π T T →∞
功率谱密度 W ( ω ) = lim
T →∞
∫ lim
−∞ T →∞ 2
∞
FT ( ω ) dω T
2
FT ( ω ) T
瓦特/赫兹
k = −∞
∫
T0 / 2
−T0 / 2
f ( t )e jkω0t * k
=
k = −∞ ∞
∑C
∞
2 k
由采样性质∫ f ( t )δ ( t − t0 ) = f ( t0 )
−∞
∴∫
−∞
k =−∞ ∞
∑ Ck δ ( ω − kω 0 )dω =
2 ∞ 2 −∞ k = −∞
k =−∞
∑C
2 k
e j 2 kπτ / T0
§2.2 确定信号通过线性系统
一.卷积定理
1.时域：
δ (t)
f(t)
∞ −∞
线性系统
h (t) y(t)
Y(ω)=H(ω)F(ω)
y( t ) = ∫ f ( τ )h( t − τ )dτ = ∫ h( τ ) f ( t − τ )dτ
−∞ ∞
双边功率谱密度 单边功率谱密度
定义在（-∞，+∞） 定义在（0，+∞）
例：试求功率信号为周期性信号时的功率谱密度 解：取截短周期 T=NT0
∞
用f ( t ) =
P = lim
k = −∞
∑C e
k
jkω0t
代入
《信号与噪声》课件
03
信号处理技术
滤波器的工作原理
滤波器分类
根据不同的分类标准，滤波器可 以分为多种类型，如低通滤波器 、高通滤波器、带通滤波器和带
阻滤波器等。
工作原理
滤波器通过选择性地让某些频率的 信号通过，而阻止其他频率的信号 ，实现对信号的筛选和处理。
应用场景
滤波器在信号处理中广泛应用于消 除噪声、提取特定频率分量以及频 谱分析等场景。
环境噪声的降低方法
建筑隔音
通过合理设计建筑结构、 使用隔音材料等手段降低 室内外噪声传播。
声源控制
对产生噪声的设备进行改 造或更换低噪声设备，从 源头上降低噪声产生。
声屏障
在噪声传播途径上设置声 屏障，如隔音墙、隔音林 等，吸收或反射噪声。
ቤተ መጻሕፍቲ ባይዱ器学习在噪声抑制中的应用
深度学习
利用深度神经网络对噪声数据进行学习，提取出 纯净信号，如自编码器等。
迁移学习
将训练好的模型应用于新场景，快速适应新环境 的噪声特性。
无监督学习
利用无标签数据进行噪声识别和分类，进一步优 化噪声抑制效果。
05
信号与噪声的应用场景
通信系统中的信号与噪声
信号
在通信系统中，信号是传递信息 的电波或电磁波。例如，手机通 话、电视广播和互联网数据传输 都依赖于信号的传递。
噪声
决能力。
培养创新思维和团队协作精神
03
鼓励学生发挥创新思维，培养团队协作精神，为未来的学习和
工作打下坚实的基础。
02
信号与噪声的基本概念
信号的定义与特性
信号的定义
信号是传递信息的一种方式，它包含了所要传达的消息或数据。
信号的特性
信号通常具有确定性、可重复性和可测量性。确定性是指信号在特定的条件下可 以重复出现，并且具有稳定的特性；可重复性是指信号可以在相同的条件下重复 产生；可测量性是指信号可以通过一定的手段进行测量和评估。
第二章信号与噪声分析
R (t ) = ∫ 12
∞ −∞
f1(t ) f2 (t +τ )dτ
18
卷积计算
f1(τ) 1
f2(τ) 1 τ
相关计算
a τ
0 f2(-τ) 1
a
0
f2(τ)
1 折叠 τ f2(t-τ)
-a
0 1 t t-a 0 t
0
a f2(t+τ)
τ
位移 左移 右移 t τ
1
-t 0
a-t f1(τ)*f2(t+τ)
第二章： 第二章：信号与噪声分析
2.1 信号的分类 2.2 确知信号的分析 2.3 随机变量的统计特征 2.4 随机过程的一般表述 2.5 平稳随机过程 2.6 高斯随机过程 2.7 随机过程通过系统的分析 2.8 窄带高斯噪声
1
2.1信号的分类 信号的分类
2.1.1 确知信号与随机信号 确知信号是指能够以确定的时间函数表示的信号，它 确知信号是指能够以确定的时间函数表示的信号， 是指能够以确定的时间函数表示的信号 在定义域内任意时刻都有确定的函数值。 在定义域内任意时刻都有确定的函数值。 例如：电路中的正弦信号和各种形状的周期信号等。 例如：电路中的正弦信号和各种形状的周期信号等。 随机信号是指在事件发生之前无法预知信号的取值 是指在事件发生之前无法预知信号的取值， 随机信号是指在事件发生之前无法预知信号的取值， 即写不出明确的数学表达式， 即写不出明确的数学表达式，通常只知道它取某一数值 的概率，这种具有随机性的信号称为随机信号。 的概率，这种具有随机性的信号称为随机信号。
（是
cn jϕn F− n = e = Fn* 2
Fn
的共轭） 的共轭）。
7
信号与噪声
信号与噪声作者：（美）西尔弗经济预测中不可避免地会存在偏见如果你想进行经济预测，最好的选择就是查看平均预测或群体预测，而不是求助于某个经济学家。
我对“调查”的研究显示，群体预测总是比个体预测更准确，在预测GDP增长、失业率和通货膨胀这三个方面，群体预测比个体预测的准确率分别高出20%、10%和30%。
通过研究许多领域的预测结果，人们发现几乎所有的群体预测都优于个体预测。
然而，虽说群体预测优于个体预测这一观念已成为重要的经验性规律，可是当预测与事实有很大的出入时，这一观念有时就会成为蹩脚的借口。
群体预测是由个体预测组成的，如果个体预测的质量提高了，群体预测的质量也会提高。
另外，在现实生活中，经济群体预测的质量也很差劲儿，所以还有很大的提升空间。
大多数经济学家作预测时，会在一定程度上依赖自己的判断，而不是依据统计模型输出的信息进行预测。
考虑到数据是那么杂乱，这种做法或许是有益的。
波士顿联储前副总裁斯蒂芬?K?麦克内斯曾经进行过一项研究，他发现根据统计学预测方法对人为的判断进行调整会使预测的准确率提高约15%。
20世纪七八十年代计算机开始广泛使用时，人们普遍认为统计模型能够“解决”经济预测问题。
但是，改进的技术无法掩盖对经济领域理论认识的缺乏，只会让经济学家更加快速、更加煞费苦心地将噪声误认为是信号。
看似前景不错的预测模型在某些方面一败涂地，最后惨遭淘汰。
在其他领域，比如那一时期的地震预测，也会遭遇这样的状况。
援引某个人为判断也会带来潜在的偏见。
人们在进行预测时，会倾向于使预测满足自己的经济动机或政治信仰。
人们或许太过自负，即使事实和环境要求他做出改变，他也不愿对自己的预测进行修正。
哈祖斯告诉我：“我认为人们绝对有这样的倾向，急切地希望事情能按照自己希望的方式发展下去。
”是否有经济学家更擅长把握这种权衡的度？预测出上一次经济衰退的经济学家是不是也可以预测出下一次经济衰退？这个问题有一个非常有趣的答案。
通信原理课件——信号与噪声
*
(t)e
j
2n T
t
dt
因此
P FnFn* | Fn |2
(2.23)
n
n
这就是帕什瓦尔功率定理。 它表明: 一个周期信号的归
一化平均功率值等于信号的所有谐波分量的平方之和，
即总功率等于各谐波单独贡献出的功率之和。
对于一个有界的、待续时间有限的信号，信号的能量为有限值， 全部时间的平均功率为零，这类信号叫做能量信号。
解：在一个周期内，f(t)可表示为
A
f
(t)
0
/ 2 t / 2
其它
利用式（2.6），并令ω0=2π/T，有：
12
j2 T
n
t
F T Ae dt n
2
A S (n / 2)
A e jn0t
jn T 0
2
2
2A
n T 0
sin(n 0
/ 2)
Ta
0
2.1.2 傅立叶变换
前面介绍了用傅里叶级数表示一个周期信号的方法，那么对 于非周期性信号，可不可以用傅里叶级数表示呢？
(2.7) (2.8)
Fn
1 T
T 2
T 2
fT (t )e jn0t dt
(2.9)
式中Fn为频率nw0分量的振幅，是nw0的函数，是离散的，当T增大时， 基频w0变小，频谱变密，而当T向于无穷大时，Fn变成w的连续函数。
令： 这样Fn成为wn的函数Fn(wn),令：
n0 n
于是：
TFn (n) F(n )
若
f1(t) F1(), f2 (t) F2 ()
则
f1(t) * f2 (t) F1()F2 ()
通信原理-第2章 信道与噪声
p( y1/ x1 ) p ( y 1 / x2 ) P( y j / xi ) ... p( y1/ xl )
p( y 2 / x1 ) p ( y 2 / x2 ) ... p( y 2 / xl )
... p( yM / x1 ) ... p( y M / x2 ) ... ... ... p( y M / xl )
11/66
（5）依据乘性噪声对信号的影响是否随时间变化而 将信道分为恒参信道和随参信道。
v i (t)
H( , t )
n(t)
v 0 (t)
(a)变参信道
v i (t)
H( )
n(t)
v 0 (t)
(b)恒参信道
12/66
（6）对于恒参信道而言，信道传输函数 H (, t ) 可以简 化为： H ( ) H ( ) e j ( )（传输函数和时间无关） 恒参信道的输出表达式为：
10/66
一、调制信道模型
（1）研究信道主要是研究输入信号和输出信道之间
的关系。
（2）影响输入输出关系的因素归结为两点：一是乘 性干扰（乘性噪声）；二是加性噪声。 （3）乘性噪声是信道设备或器件特性不理想产生的， 随信号的消失而消失。
（4）加性噪声是外界干扰叠加在信道上的，不因传
输信号的有无而始终存在。
信道的幅－频失真是一种线性失真，可以 用一个线性网络进行补偿。若此线性网络的频 率特性与信道的幅－频特性之和，在信号频谱 占用频带内，为一条水平直线，则此补偿网络 就能够完全抵消信道产生的幅－频失真。信道 的相－频失真也是一种线性失真，所以也可以 用一个线性网络进行补偿。
二. 随参信道对信号传输的影响
信号与噪声分析
信号与噪声分析确知信号分析1、周期信号的傅里叶级数任何一个周期为T 的周期信号)(t f ，只要满足狄里赫利条件，则可展开为傅里叶级数0()jn tnn f t F eω∞=-∞=∑ （2-1）式中，⎰--=2/2/0)(1T T t jn n dt e t f T F ω (0,1, 2.3,,n =±±±)；000a c F ==; 2nj n n c F e ϕ-=(称为复振幅)；*2nj n n n c F e F ϕ-==（是n F 的共轭）。
一般地，n F 是一个复数，由n F 确定周期信号)(t f 的第n 次谐波分量的幅度，它与频率之间的关系图形称为信号的幅度频谱。
由于它不连续，仅存在于0ω的整数倍处，故这种频谱是离散谱。
许多情况下，利用信号的频谱进行分析比较直观方便。
2、非周期信号的傅里叶变换ωωπωd e F t f t j ⎰∞∞-=)(21)( （2-2）⎰∞∞--=dt et f F tj ωω)()( （2-3）式（2-2）和式（2-3）分别称为傅里叶正变换和傅里叶反变换，两式称为)(t f 傅里叶变换对，表示为)()(ωF t f ⇔ 信号的傅里叶变换具有一些重要的特性，灵活运用这些特性可较快地求出许多复杂信号的频谱密度函数，或从谱密度函数中求出原信号，因此掌握这些特性是非常有益的。
其中较为重要且经常用到的一些性质和傅里叶变换对见附录二。
3、卷积与相关函数 （1）、卷积设有函数)(1t f 和)(2t f ，称积分⎰∞∞--τττd t f f )()(21为)(1t f 和)(2t f 的卷积，常用)()(21t f t f *表示，即121221()()()()()()f t f t f f t d f f t d ττττττ∞-∞∞-∞*=-=-⎰⎰（2-4）时域卷积定理：令)()(11ωF t f ⇔，)()(22ωF t f ⇔，则有)()()()(2121ωωF F t f t f ⇔* （2-5） 频域卷积定理：令)()(11ωF t f ⇔，)()(22ωF t f ⇔，则有[])()(21)()(2121ωωπF F t f t f *⇔（2-6） （2）、相关函数信号之间的相关程度，通常采用相关函数来表征，它是衡量信号之间关联或相似程度的一个函数。
第2章信号与噪声分析
第 2 章信号与噪声分析 2.1 通信常用信号和系统响应 2.2 信号频谱分析概述 2.3 随机变量的统计特性 2.4 随机过程返回主目录通信过程是有用信号通过通信系统的过程，且在通信系统各点常常伴随有噪声的加入及此加入噪声在系统中的传输。
由此看来，分析与研究通信系统，总离不开对信号和噪声的分析。
实际的信号通常是随机的，加之通信系统中毡榇嬖诘脑肷 际撬婊 模 远运婊 藕诺姆治鍪欠浅Ｖ匾 摹?从统计数学的观点看，随机信号和噪声统称为随机过程。
因此，统计数学中有关随机过程的理论可以运用到随机信号和噪声的分析中来。
本章将在先修课程的基础上，首先介绍通信系统常用信号并对确知信号的分析作必要的复习巩固，然后在复习概率论基本概念的基础上，讨论随机信号和噪声的数学模型——随机过程。
2.1 通信常用信号和系统响应 2.1.1常用信号由语音、图像、数码等形成的电信号，其形式可以是多种多样的，从不同的角度进行分类可以得出各种不同的名称。
但是从信号数学分析的角度来说，通常采用下面的几种分类。
⑴数字信号与模拟信号⑵确知信号与随机信号⑶周期信号与非周期信号⑷能量信号与功率信号在通信过程中，信号的变换和传输是由系统完成的。
系统是指包括有若干元件或若干部件的设备。
系统有大有小，大到由很多部件组成的完整系统，小到由具体几个电路组成的部件。
信号在系统中的变换和传输可用图2.1表示，图中假设输入信号为x(t)，通过系统后得到的输出响应为y(t)。
从数学的观点来看，和之间存在着如下的函数关系：y(t)=f[x(t)] 图2.1 系统示意图 2.1.2系统响应⑴线性系统与非线性系统一个系统如果是线性的，那么叠加原理一定适用。
对于线性系统而言，一个激励的存在并不影响另一个激励的响应。
⑵时不变与时变系统时不变系统也称恒参系统，时变系统也称变参（随参）系统。
2.2信号频谱分析概述我们知道，信号可以分为确知信号和随机信号。
对于确知信号，频谱分析是研究它的有效工具；对于随机信号，则要用统计的方法来分析。
第二章5信号与噪声傅立叶变换
p(x)x12e(x2 m x 2x)2
( x )
mx为均值，σx2为方差
16
综上所述，散粒噪声、渡越时间噪声和热噪声，和宇宙噪声， 服从高斯分布，在一般的工作频率范围内，属于平坦的功率谱 密度。常常近似认为为高斯白噪声。
17
信号通过线性系统的传输
信号作用于系统产生响应举例：汽车系统&照相机系统
脚压力
汽车
汽车制动
3
1.3 系统的描述与分类 信号通过线性系统的传输
光信号
照相机
像片
f(t)
系统
r(t)
4
1.3 系统的描述与分类 信号通过线性系统的传输
线性系统
叠加性：几个分量分别输入和同时输入， 输出相同
齐次性：输入增加K倍，输出放大相同倍数
若
f1(t)
r 1
(t)
,
f (t) r (t)
2
2
则 k f( t ) k f( t ) k r ( t) k r ( t)
11
22
1 1
2 2
5
信号通过线性系统的传输
f ( t )表示为分量和
f(t) f()(t )d f(t)(t)
f(t)lim[f()](t) 0
2 倍(3db)之
11
噪声
指通信系统意图传输的信号以外的有害干扰信号。
把周期性的、有规则的有害信号叫做干扰； 其它有害的随机干扰叫噪声；
下图显示了一个无噪声的正弦信号及其存在噪声的情况。
12
噪声
噪声分类：
乘性噪声和加性噪声。
乘性噪声是指噪声在信号出现时存在， 加性噪声是指噪声无论信号是否出现，在任何时间均存在。
《信号与噪声》PPT课件
一、根本组成
§4. 核电子学测量系统概述
§4. 核电子学测量系统概述
二． 核电子学常用的信号处理系统 １． 前置放大器 初步放大〔以降低输出信号在传递过程中受噪 声和干扰影响〕 ２． 主放大器 放大〔便于测量，信号成形〕，有其他功能 〔滤波形式，基线恢复，堆积拒绝等〕 ３． 甄别〔幅度，时间〕 ４． 模数变换 模数变换(幅度－数字变换，时间－数字变换) ５． 数据获取分析，处理 计数分类统计，谱数据得到〔计算机应用〕
Pv2Sdfsd
0
sS/ 0 S,R
0
0
组成傅氏变换对。
§3. 核电子学中的信号与噪声分析根底
白噪声——白谱
S R
噪声频带比欲 测电路的频带 大得多时，即 可近似认为是 白噪声。
图1.3.11有限宽的白噪声谱密度与自相关函数
§3. 核电子学中的信号与噪声分析根底
〔2〕核辐射随机信号
§2. 核电子学中的噪声
2.热噪声
导体或电阻中载流子的热运动，与外加电压和平均 电流无关，主要与温度有关。
图1.2.3
d2i4kTd/R f
场效应管多子在沟道中 作热运动产生的沟道热 噪声电压如1.2.12式
3.低频噪声 一种随频率降低而增大的噪声
d2fvAf/fdf
场效应管的低频噪声〔闪 烁噪声〕电压如1.2.14式
第二章1信号与噪声课件
9
2.信号的分类
▪ 时间连续信号与时间离散信号
根据数学上连续与离散的概念区分连续信号与离散 信号。 为时间的连续函数时，称为“连续信号” 。 在时间上离散时，称为“离散信号”。
▪ 模拟信号与数字信号
取值是连续的或取无穷多个值，称为模拟信号。 在时间上和取值上都离散，称为数字信号。
15
2.信号的分类
▪ 普通信号与奇异信号 若信号本身有不连续点，其导数或高阶导数出现奇 异值，而且不能以普通函数的概念来定义，则称此 类信号为奇异信号，反之，则称为普通信号。
16
3.普通信号
▪ 正弦信号
正弦信号和余弦信号二者仅在相位上相差 ，经常统 称为正弦信号，其表达式一般写作 f (t) K sin(t )
▪ 单位斜变信号是理想信号，是不可实现的。现实中常见的充电 过程可以理想化地表示为截顶的单位斜变信号
s s
22
4.奇异信号
▪ 单位阶跃信号
单位阶跃信号u(t)的函数表达式为 ▪ 其波形为：
单位阶跃信号
延时的单位阶跃信号
▪ 单位阶跃函数的物理背景是，在t=0时刻对某一路电 路接入单位电源，并且无限持续下去。(开关开合过 程)
E f 2 (t) dt
▪ 能量信号 信号能量为有限值，全部时间的平均功率为0的
信号。
▪ 功率信号 具有无限的能量，但它的平均功率为有限值的周期
信号。
周期信号的归一化平均功率（简称功率）－周期信号在单位电
阻上所消耗功率的平均值。其瞬时功率等于| f ( t )|2，在周期T
内的平均功率为
P
t
特点：
(1) Sa函数是偶函数 (2) 过零区间宽度 (3) Sa函数过零位置
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
S ( ) / , 0 s ( ) 0, 0
S(w)称为噪声的功率谱密度函数，它是数学频率域内的噪声在某频率 分量内产生的平均功率，单位为[瓦/赫兹], s(w)称为单边噪声功率谱 密度函数，是物理频率域内，相对于角频率的功率谱密度函数，单位 为[瓦/（弧度/秒）]。
输出
叠加
VO
VnO
Vo S 输出信噪比表示为: N Vno
9
辐射源
能量E 探测器 等效 噪声 能量 ENE
输入信号 电压Vi
等效噪声 电压ENV
放大器 （放大倍数A）
输出 叠加
VO
VnO
等效噪声 电荷ENC
•为便于在输入端与被测的物理量进行比较，一般噪声也由输出端折算到 输入端。设放大器放大倍数为A，输入信号可以表示为 Vi Vo ，则等 A 效到输入端的等效噪声电压（ENV）为:
3
五、输出信号的数学模拟
ii (t ) Qi . (t ti ) 冲击序列I（ t）= i i
Qi ：ti时刻发生的第i个冲击电荷量
4
§2 核电子学中的噪声
一、噪声对核测量的影响 噪声引起的谱线展宽：电子学噪声会造成电路中一些重要节点 的电平随机涨落，而叠加在信号上，从而造成信号幅度的随机 涨落，加宽了能谱曲线。电子学噪声平均值为0，概率分布服 从高斯分布，它对能谱线展宽的方差贡献为sn 。
第一章核电子系统中的 信号与噪声
§1.核辐射探测器及其输出信号
! ! !
§2.核电子学中的噪声
§3 核电子学中的信号与噪声分析基础 §4 核电子学测量系统概述
1
! ! !
输出信号的数学模拟
当信号延迟时间远小于时间常数RC时，信号以脉冲形式出现， 当电荷收集时间较短时，可认为是一种持续时间极短的电流脉冲
•电流是由电子或其他载流子的流动形成的。在电子器件或探 测器中，由于载流子的产生和消失的随机涨落，形成电流或电
压的瞬时波动。这种瞬时波动就是散粒噪声。
存在于少数载流子导电器件中 （例如：探测器漏电流的噪声、场效应管的栅极漏电流的噪声等）
时域：随机分布的电流脉冲序列（平均值为0）
频域：白噪声( fh < 10 9 Hz ) 设器件的平均电流为
1 T 2 V lim V (t )dt T T 0 n
2 n
由于噪声电压是随机地叠加在信号电压上，它会使原来 幅度确定的信号，在平均值作上下起伏。因而被测量的 分辨率变坏。
7
从频域上分析，噪声的平均功率可以也分解为各频率分量之和 （S(w）对频段的积分）。即
P v S df s d
单个电流冲击脉冲： i (t ) lim Q /
0
2
五、输出信号的数学模拟
数学上引入单位冲击函数
(t t0 )
1 lim t 0 t t 0 0 0 t t 0 ;t t 0
电流冲击脉冲i(t)=Q*δ(t-t0)
I 。
s s Ie
单边噪声功率谱密度函数 只与平均电流有关,与频率无关.
其中 e 为电子电荷量
在d 或 df 内平均功率为：
8
噪声的表示方法
通常用信噪比S/N(信号与噪声均方值的比值)来表
示系统的噪声指标。信噪比越高，噪音引起的测量 误差越小 考虑一个常见的探测器与放大器组成的测量系统。 在系统的输出端测得电压信号幅度Vo和噪声均方根 值Vno
辐射源
能量E
探测器 等效 噪声 能量 ENE 等效噪声 电荷ENC 输入信号 电压Vi 等效噪声 电压ENV 放大器 （放大倍数A）
实际测量： 峰位确定粒子能量； 能谱线的宽窄是衡量探测器系 统和电子学系统对相邻很近谱 线的分辨能力。
5
噪声
噪声与我们通常所说的空间电磁波感应、工频交流电网以及电源
纹波等外界干扰不同。这些干扰是外部的，可以通过屏蔽、隔离 、滤波、稳压等各种措施加以消除或改善。噪声则是由所采用的 器件本身产生的，原则上是只能设法减小但不能完全消除。
Vo Q ACQ Vno Vno
其中
ACQ
Vo
Q
为电荷电压的变换增益
等效噪声电荷：
Vno Q ( ENC ) ACQ
11
等效噪声电荷数和等效噪声能量：
等效噪声电荷数:
( ENC ) ( ENN ) e 等效噪声能量：
Q Vno ( ENE) ( ENN ) w w e Vo 由噪声造成的半高全宽为
(N )
FWHM NE
2s N
2.36( ENE)
N0
FWHM FWTM
12
N
噪声的相加
如果探测器固有的能量分辨率半高全宽为 FWHM DE
，则由于噪声的叠加，系统的能量分辨性能变坏， 总的半高全宽 FWHM E 表达为:
2 ( FWHM ) E ( FWHM ) 2 ( FWHM ) NE DE
13
二、噪声的分类和噪声源 核电子学中的噪声主要有三类：
散粒噪声 (Shot noise)
探测器漏电流Thermal noise) 场效应管的沟道噪声、电阻元件的热噪声。 低频噪声(Flicker noise) 场效应管闪烁噪声。
14
散粒噪声
在信号的产生、传输和测量过程中,探测器和电子学的噪声会叠加
在有用信号上,从而降低测量精度，甚至某些有用的微弱信号会被 噪声所淹没。
通常用信噪比S/N(信号与噪声均方值的比值)来表示系统的噪声指
标。信噪比越高，噪音引起的测量误差越小。
6
噪声的时间平均值为零。但是只要有噪声存在，其 平均功率就不为零，因此通常采用均方值（噪声电压的 平方值按时间求平均） Vn2 作为噪声大小的衡量尺度：
Vno Vno Vi ( ENV ) A Vo Vi
10
辐射源
能量E 探测器 等效 噪声 能量 ENE
输入信号 电压Vi
等效噪声 电压ENV
放大器 （放大倍数A）
输出 叠加
VO
VnO
等效噪声 电荷ENC
•为了判断能谱测量系统对电荷量、能量的分辨程度，也 可将系统的输出噪声折算到输入端，给出噪声所对应的 等效噪声电荷或等效噪声能量。