noip普及组复赛模拟试题22(答案)
NOIP2011普及组复赛试题

1.数字反转(reverse.cpp/c/pas)【问题描述】给定一个整数,请将该数各个位上数字反转得到一个新数。
新数也应满足整数的常见形式,即除非给定的原数为零,否则反转后得到的新数的最高位数字不应为零(参见样例2)。
【输入】输入文件名为reverse.in。
输入共1行,一个整数N。
【输出】输出文件名为reverse.out。
输出共1行,一个整数,表示反转后的新数。
【输入输出样例1】reverse.in reverse.out 123 321【输入输出样例2】Reverse.in reverse.out -380 -83【数据范围】-1,000,000,000≤N≤1,000,000,000。
2.统计单词数(stat.cpp/c/pas)【问题描述】一般的文本编辑器都有查找单词的功能,该功能可以快速定位特定单词在文章中的位置,有的还能统计出特定单词在文章中出现的次数。
现在,请你编程实现这一功能,具体要求是:给定一个单词,请你输出它在给定的文章中出现的次数和第一次出现的位置。
注意:匹配单词时,不区分大小写,但要求完全匹配,即给定单词必须与文章中的某一独立单词在不区分大小写的情况下完全相同(参见样例1),如果给定单词仅是文章中某一单词的一部分则不算匹配(参见样例2)。
【输入】输入文件名为stat.in,2行。
第1行为一个字符串,其中只含字母,表示给定单词;第2行为一个字符串,其中只可能包含字母和空格,表示给定的文章。
【输出】输出文件名为stat.out。
只有一行,如果在文章中找到给定单词则输出两个整数,两个整数之间用一个空格隔开,分别是单词在文章中出现的次数和第一次出现的位置(即在文章中第一次出现时,单词首字母在文章中的位置,位置从0开始);如果单词在文章中没有出现,则直接输出一个整数-1。
【输入输出样例1】stat.in stat.out2 0Toto be or not to be is a question【输入输出样例1说明】输出结果表示给定的单词To在文章中出现两次,第一次出现的位置为0。
NOIP普及组初赛历年试题及答案选择题篇

NOIP普及组初赛历年试题及答案选择题篇单项选择题:每次共20题,每题1.5分,共计30分。
每题有且仅有一个正确选项。
注:答案在文末一、计算机基础(每年8-10题,占选择题的一半,找份材料翻几遍就可拿分了)NOIP2011-3. 一片容量为8G的SD卡能储存大约()张大小为2MB的数码照片。
A.1600B.2000C.4000D.16000NOIP2011-4. 摩尔定律(Moore'slaw)是由英特尔创始人之一戈登·摩尔(GordonMoor)提出来的。
根据摩尔定律,在过去几十年一级在可预测的未来纪念,单块集成电路的集成度大约每()个月翻一番。
A.1B.6C.18D.36NOIP2011-6.寄存器是()的重要组成部分。
A.硬盘B.高速缓存C.内存D.中央处理器(CPU)NOIP2011-10. 有人认为,在个人电脑送修前,将文件放入回收站中就是已经将其删除了。
这种想法是()。
A.正确的,将文件放入回收站以为着彻底删除、无法恢复B.不正确的,只有将回收站清空后,才意味着彻底删除、无法恢复C.不正确的,即使回收站清空,文件只是被标记为删除,仍可能通过回复软件找回D.不正确的,只要在硬盘上出现过的文件,永远不可能被彻底删除NOIP2011-14. 生物特征识别,是利用人体本身的生物特征进行身份认证的一种技术。
目前,指纹识别、虹膜识别、人脸识别等技术已广泛应用于政府、银行、安全防卫等领域。
以下不属于生物特征识别技术及其应用的是()。
NOIP2011-16. 关于汇编语言,下列说法错误的是()。
A.是一种与具体硬件相关的程序设计语言B.在编写复杂程序时,相对于高级语言而言代码量较大,且不易调试C.可以直接访问寄存器、内存单元、以及I/O端口D.随着高级语言的诞生,如今已完全被淘汰,不再使用NOIP2011-18. 1956年()授予肖克利、巴丁和布拉顿,以表彰他们对半导体的研究和晶体管效应的发现。
noip普及组复赛入门测试(答案+测试数据)

一、新龟兔赛跑(文件名xgtsp.pas)新龟兔赛跑比赛即将举行,此次龟兔赛跑比赛的规则与以往有所不同,不再考察兔子和乌龟谁在最短的时间内跑完规定的路程,而是考察谁在规定时间内跑的路程更长,且兔子和乌龟跑步都是匀速的。
由于兔子的坏习惯,它总喜欢把比赛的总时间T小时中的K小时拿来睡觉。
现在给你比赛的总时间T、兔子的睡觉时间K、兔子的速度U、乌龟的速度V,需要你求出该次比赛谁最后获胜。
输入第一行为一个整数X,表示有X组输入数据。
每组数据只有一行,包括4个数T、K、U、V (1 ≤ T≤ 300,0 ≤ K ≤ T,1 ≤ U ≤ 100,1 ≤ V ≤ 100)。
对于每组数据,输出只有一个数,如果兔子获胜则输出-1,如果乌龟获胜则输出1,如果同时到达则输出0。
允许输入一组数后立即输出对应的结果。
样例输入:21 12 16 2 6 3样例输出:1-1varv,u,t,k,n,i:integer;beginreadln(n);for i:=1 to n do beginreadln(t,k,u,v);if v*t>U*(t-k) then writeln(1);if v*t<U*(t-k) then writeln(-1);if v*t=U*(t-k) then writeln(0);end;end.1、输入:26 2 6 28 6 8 2输出:-12、输入:2300 280 60 20120 0 12 13输出:113、输入:3100 20 50 30100 50 45 25100 80 27 17输出:-1114、输入:3150 77 29 23127 11 22 13139 22 13 7输出:1-1-1二、小球路程(文件名:XQLC.PAS )已知小球从100米高度自由下落,落地后反弹起,又落地,又弹起,……。
每次弹起的高度都是上一次高度的一半。
求小球第N次反弹起的高度和球在整个过程所经过的路程(包括下落和反弹),用键盘输入N,输出反弹高度和经过路程,结果保留两位小数。
NOIP普及组初赛历年试题及答案求解题篇

NOIP普及组初赛历年试题及答案求解题篇问题求解:每次共2题,每空5分,共计10分。
每题全部答对得 5 分,没有部分分。
注:答案在文末在NOIP初赛问题求解中,经常会遇到排列组合问题。
这一类问题不仅内容抽象,解法灵活,而且解题过程极易出现“重复”和“遗漏”的错误,这些错误甚至不容易检查出来,所以解题时要注意不断积累经验,总结解题规律。
解答排列组合问题,首先必须认真审题,明确是属于排列问题还是组合问题,或者属于排列与组合的混合问题,其次要抓住问题的本质特征,灵活运用基本原理和公式进行分析解答。
同时还要注意讲究一些策略和技巧,比如采用分类、分步、捆绑等方法,也可以借助表格、方程等工具,使一些看似复杂的问题迎刃而解。
NOIP2011-1. 每份考卷都有一个8位二进制序列号。
当且仅当一个序列号含有偶数个1时,它才是有效的。
例如,0000000、01010011都是有效的序列号,而11111110不是。
那么,有效的序列号共有______个。
NOIP2011-2. 定义字符串的基本操作为: 删除一个字符、插入一个字符和将一个字符修改成另外一个字符这三种操作。
将字符串A变成字符串B的最少操作步数,称为字符串A到字符串B的编辑距离。
字符串“ ABCDEFG ”到字符串“BADECG ”的编辑距离为_______。
NOIP2012-1. 如果平面上任取n 个整点(横纵坐标都是整数) ,其中一定存在两个点,它们连线的中点也是整点,那么n至少是_____。
NOIP2012-2. 在NOI期间,主办单位为了欢迎来自全国各地的选手,举行了盛大的晚宴。
在第十八桌,有5名大陆选手和5名港澳选手共同进膳。
为了增进交流,他们决定相隔就坐,即每个大陆选手左右相邻的都是港澳选手、每个港澳选手左右相邻的都是大陆选手。
那么,这一桌共有_____种不同的就坐方案。
注意:如果在两个方案中,每个选手左边相邻的选手均相同,则视为同一个方案。
NOIP2013-1. 7 个同学围坐一圈,要选2 个不相邻的作为代表,有_____种不同的选法。
NOIP2012普及组复赛试题及解答

全国信息学奥林匹克联赛(NOIP2012)复赛 试题及解答
普及组
start--; do{ start++; start%=m; //start是刚进入第i+1层时的房间号 if (a[i][start][0]==1) //此房间有楼梯 { k--; } } while (k!=0); //k!=0表示尚未找到牌号所指示的房间 } fprintf(outputfp,"%d\n",temp); } fclose(inputfp); fclose(outputfp); return 0; }
第 3 页 共 10页
全国信息学奥林匹克联赛(NOIP2012)复赛 试题及解答
普及组
2.寻宝
(treasure.cpp/c/pas) 传说很遥远的藏宝楼顶层藏着诱人的宝藏。 小明历尽千辛万苦终于找到传说中的这个藏 宝楼,藏宝楼的门 口竖着一个木板,上面写有几个大字:寻宝说明书。说明书的内容如下: 藏宝楼共有 N+1 层, 最上面一层是顶层, 顶层有一个房间里面藏着宝藏。 除了顶层外,藏宝楼另有 N 层, 每层 M 个房间, 这 M 个房间围成一圈并按逆时针方向依次编号为 0, …, M-1。其中一些房间有通往上一层的 楼梯,每层楼的楼梯设计可能不同。每个房间里有一个 指示牌,指示牌上有一个数字 x,表示从这个房间开始 按逆时针方向选择第 x 个有楼梯的房 间(假定该房间的编号为 k) ,从该房间上楼,上楼后到达上一层的 k 号 房间。比如当前房 间的指示牌上写着 2, 则按逆时针方向开始尝试, 找到第 2 个有楼梯的房间, 从该房间上楼。 如果当前房间本身就有楼梯通向上层,该房间作为第一个有楼梯的房间。 寻宝说明书的最后用红色大号字体写着: “寻宝须知:帮助你找到每层上楼房间的指示 牌上的数字(即每 层第一个进入的房间内指示牌上的数字)总和为打开宝箱的密钥” 。 请帮助小明算出这个打开宝箱的密钥。 【输入】 输入文件为 treasure.in 第一行 2 个整数 N 和 M,之间用一个空格隔开。N 表示除了顶层外藏宝楼共 N 层楼, M 表示除顶层外每层楼有 M 个房间。 接下来 N*M 行,每行两个整数,之间用一个空格隔开,每行描述一个房间内的情况, 其中第(i-1)*M+j 行表示第 i 层 j-1 号房间的情况(i=1, 2, …, N;j=1, 2, … ,M) 。第一个整数 表示该房间是否有楼梯通往上一层 (0 表示没有,1 表示有) ,第二个整数表示指示牌上的数 字。注意,从 j 号房间的楼梯爬到上一层到达的房间 一定也是 j 号房间。 最后一行,一个整数,表示小明从藏宝楼底层的几号房间进入开始寻宝(注:房间编号 从 0 开始) 。 【输出】 输出文件名为 treasure.out。 输出只有一行,一个整数,表示打开宝箱的密钥,这个数可能会很大,请输 出对 20123 取模的结果即可。 【输入输出样例】 treasure.in 2 3 1 2 0 3 1 4 0 1 1 5 1 2 1
NOIP普及组初赛历年试题及标准答案选择题篇

NOIP普及组初赛历年试题及答案选择题篇————————————————————————————————作者:————————————————————————————————日期:NOIP普及组初赛历年试题及答案选择题篇单项选择题:每次共20题,每题1.5分,共计30分。
每题有且仅有一个正确选项。
注:答案在文末一、计算机基础(每年8-10题,占选择题的一半,找份材料翻几遍就可拿分了)NOIP2011-3. 一片容量为8G的SD卡能储存大约( )张大小为2MB的数码照片。
A.1600B.2000C.4000D.16000NOIP2011-4. 摩尔定律(Moore'slaw)是由英特尔创始人之一戈登·摩尔(GordonMoor)提出来的。
根据摩尔定律,在过去几十年一级在可预测的未来纪念,单块集成电路的集成度大约每( )个月翻一番。
A.1B.6C.18D.36NOIP2011-6.寄存器是( )的重要组成部分。
A.硬盘B.高速缓存C.内存D.中央处理器(CPU)NOIP2011-10. 有人认为,在个人电脑送修前,将文件放入回收站中就是已经将其删除了。
这种想法是( )。
A .正确的,将文件放入回收站以为着彻底删除、无法恢复B.不正确的,只有将回收站清空后,才意味着彻底删除、无法恢复C.不正确的,即使回收站清空,文件只是被标记为删除,仍可能通过回复软件找回D.不正确的,只要在硬盘上出现过的文件,永远不可能被彻底删除NOIP2011-14. 生物特征识别,是利用人体本身的生物特征进行身份认证的一种技术。
目前,指纹识别、虹膜识别、人脸识别等技术已广泛应用于政府、银行、安全防卫等领域。
以下不属于生物特征识别技术及其应用的是( )。
NOIP2011-16. 关于汇编语言,下列说法错误的是( )。
A.是一种与具体硬件相关的程序设计语言B.在编写复杂程序时,相对于高级语言而言代码量较大,且不易调试C.可以直接访问寄存器、内存单元、以及I/O端口D.随着高级语言的诞生,如今已完全被淘汰,不再使用NOIP2011-18. 1956年( )授予肖克利、巴丁和布拉顿,以表彰他们对半导体的研究和晶体管效应的发现。
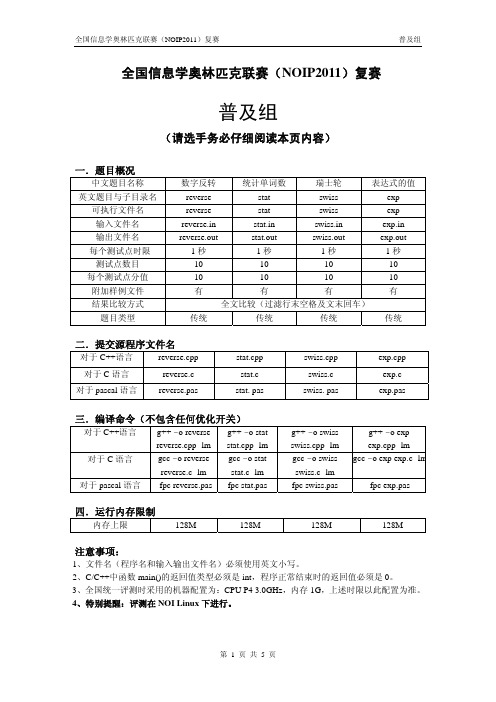
NOIP2011普及组复赛试题
1 ≤ 单词长度 ≤ 10。 1 ≤ 文章长度 ≤ 1,000,000。
3.瑞士轮
(swiss.cpp/c/pas) 【背景】
在双人对决的竞技性比赛,如乒乓球、羽毛球、国际象棋中,最常见的赛制是淘汰赛和 循环赛。前者的特点是比赛场数少,每场都紧张刺激,但偶然性较高。后者的特点是较为公 平,偶然性较低,但比赛过程往往十分冗长。
选手、R 轮比赛,以及我们关心的名次 Q。 第二行是 2*N 个非负整数 s1, s2, …, s2N,每两个数之间用一个空格隔开,其中 si 表示编
号为 i 的选手的初始分数。 第三行是 2*N 个正整数 w1, w2, …, w2N,每两个数之间用一个空格隔开,其中 wi 表示编
号为 i 的选手的实力值。
(’、’)’是左右括号,’+’、’*’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序
给出了给定表达式中除去变量外的运算符和括号。 【输出】
输出文件 exp.out 共 1 行。包含一个整数,即所有的方案数。注意:这个数可能会很大, 请输出方案数对 10007 取模后的结果。
【输入输出样例 1】 exp.in 4 +(*)
三.编译命令(不包含任何优化开关)
对于 C++语言 g++ -o reverse g++ -o stat
reverse.cpp -lm stat.cpp -lm
对于 C 语言
gcc -o reverse gcc -o stat
reverse.c -lm
stat.c -lm
对于 pascal 语言 fpc reverse.pas fpc stat.pas
①—④ ②—③
学科竞赛-NOIP2017_普及组复赛试题

NOIP2017_普及组复赛试题CCF全国信息学奥林匹克联赛(NOIP2017)复赛普及组(请选手务必仔细阅读本页内容)注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存4G,上述时限以此配置为准。
4、只提供Linux格式附加样例文件。
5、提交的程序代码文件的放置位置请参照各省的具体要求。
6、特别提醒:评测在当前最新公布的NOI Linux下进行,各语言的编译器版本以其为准。
1. 成绩(score.cpp/c/pas)【问题描述】牛牛最近学习了C++入门课程,这门课程的总成绩计算方法是:总成绩=作业成绩×20%+小测成绩×30%+期末考试成绩×50%牛牛想知道,这门课程自己最终能得到多少分。
【输入格式】输入文件名为score.in。
输入文件只有1行,包含三个非负整数A、B、C,分别表示牛牛的作业成绩、小测成绩和期末考试成绩。
相邻两个数之间用一个空格隔开,三项成绩满分都是100分。
【输出格式】输出文件名为score.out。
输出文件只有1行,包含一个整数,即牛牛这门课程的总成绩,满分也是100分。
见选手目录下的score/score1.in和score/score1.ans。
【输入输出样例1说明】牛牛的作业成绩是100分,小测成绩是100分,期末考试成绩是80分,总成绩是100×20%+100×30%+80×50%=20+30+40=90。
【输入输出样例2说明】牛牛的作业成绩是60分,小测成绩是90分,期末考试成绩是80分,总成绩是60×20%+90×30%+80×50%=12+27+40=79。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
军方截获的信息由n(n<=30000)个数字组成,因为是敌国的高端秘密,所以一时不能破获。
最原始的想法就是对这n个数进行小到大排序,每个数都对应一个序号,然后对第i个是什么数感兴趣,现在要求编程完成。
【输入格式】第一行n,接着是n个截获的数字,接着一行是数字k,接着是k行要输出数的序号。
【输出格式】k行序号对应的数字。
【输入样例】Secret.in5121 1 126 123 73243【输出样例】Secret.out7123121program secret;const max=30000;var n,i,x,k:longint;a:array[1..max] of longint;procedure sort(l,r:longint);var i,j,t,mid:longint;begini:=l;j:=r;mid:=a[(l+r)div 2];repeatwhile a[i]<mid do inc(i);while a[j]>mid do dec(j);if j>=i thenbegint:=a[i];a[i]:=a[j];a[j]:=t;inc(i);dec(j)end;until i>j;if l<j then sort(l,j);if i<r then sort(i,r);end;assign(input,'secret.in');assign(output,'secret.out');reset(input);rewrite(output);readln(n);for i:=1 to n do read(a[i]);sort(1,n);readln(k);for i:=1 to k dobeginreadln(x);writeln(a[x]);end;close(input);close(output);end.输入1512 10 36 127 126 123 75 89 101 999 777 654 456 890 134624391014 输出127536127134890输入248 18 12 24 434 10 36 127 126 123 75 89 101 999 777 654 456 890 134 555 221 108 888 65685431920141710 输出2412654656134456108有一只坏的里程表:它总是跳过数字3和数字8。
也就是说,当前显示已走过两公里时,如果车子再向前走一公里,那么将显示4公里,而不是三公里(数字3跳过了)。
再比如,当前是15229公里,车子再向前走一公里,显示的是15240公里,而不是15230公里。
数字8也同样跳过现在,给你里程表上显示的数字,请你告诉我车子真正走了多少公里。
输入:15输出:12program yx;const alph='01245679';var n,m,w,g,t:longint;st:string;beginassign(input,'yx.in');assign(output,'yx.out');reset(input);rewrite(output);readln(n);m:=0;t:=1;while n<>0 dobeging:=n mod 10;n:=n div 10;str(g,st);w:=pos(st,alph)-1;m:=m+t*w;t:=t*8;end;writeln(m);close(input);close(output);end.输入27 输出22 输入4567 输出1838 输入44565677 输出7231862硬币游戏DescriptionFarmer John的奶牛喜欢玩硬币游戏,因此FJ发明了一种称为“Xoinc”的两人硬币游戏。
初始时,一个有N(5 <= N <= 2,000)枚硬币的堆栈放在地上,从堆顶数起的第I 枚硬币的币值为C_i (1 <= C_i <= 100,000)。
开始玩游戏时,第一个玩家可以从堆顶拿走一枚或两枚硬币。
如果第一个玩家只拿走堆顶的一枚硬币,那么第二个玩家可以拿走随后的一枚或两枚硬币。
如果第一个玩家拿走两枚硬币,则第二个玩家可以拿走1,2,3,或4枚硬币。
在每一轮中,当前的玩家至少拿走一枚硬币,至多拿走对手上一次所拿硬币数量的两倍。
当没有硬币可拿时,游戏结束。
两个玩家都希望拿到最多钱数的硬币。
请问,当游戏结束时,第一个玩家最多能拿多少钱呢?Input第1行:1个整数N第2..N+1行:第i+1行包含1个整数C_iOutput第1行:1个整数表示第1个玩家能拿走的最大钱数。
Sample Input513172Sample Output9Hint样例说明:第1个玩家先取走第1枚,第2个玩家取第2枚;第1个取走第3,4两枚,第2个玩家取走最后1枚。
SourceUSACO NOV09 SILVER********************************************************************* **************本题是求最优解,常用的方法有DP、贪心、搜索。
对N=2000的数据规模,搜索显然是会超时的。
每步都取最优的贪心明显不对,样例就是反例。
根据题设条件,发现问题状态和两个因素有关:当前剩下的硬币数量和对手上一次拿走的硬币数量。
对于当前状态,要得到最优解,需要枚举自己能拿走的硬币数量x。
一旦这次自己拿走了x枚硬币(自然可以算出本次所拿的总钱数),就交由对手走,状态就转移成剩下total-x枚硬币(total是“上上”次取走硬币后,剩下的总硬币枚数),上一次拿走x枚硬币。
对手也会拿走最多钱数的硬币。
这里有个关键的地方要想通:在交给对方走之后,自己还能在以后的游戏中拿走多少钱数的硬币?答案是:剩下total-x枚的总钱数减去对手拿走的总钱数(这个值恰好是剩下total-x枚硬币,上一次拿走x枚硬币所表示的最优解)令DP[c][p] 表示剩下c 枚硬币,上次对手拿走p枚硬币的最优解。
SUM[i][j]表示从第i枚到第j枚硬币的钱数之和。
DP[c][p] = max{SUM[c-i+1][c] + (SUM[1][c-i] - DP[c-i][i])} 1 <=i <= min(2*p, c) SUM[c-i+1][c]表示本次自己拿走第i枚的钱数和SUM[1][c-i] - DP[c-i][i]表示在剩下的局面中自己还能拿的钱数和上式化简得:DP[c][p] = max{SUM[1][c] - DP[c-i][i]}边界状态:DP[0][*] = 0 (剩下0枚硬币,当然只能拿走0了)目标状态:ans = DP[N][1]可以先将SUM预处理出来。
但是整个DP仍然有N^2个状态,每次转移是O(N),所以整个时间为O(N^3)。
要通过全部数据,需要进一步优化才行。
分析后发现,在按上述方程计算两个相邻状态DP[c][p] 和DP[c][p+1]时做了很多重复:DP[c][p] = max{SUM[1][c] - DP[c-i][i]} 1 <=i<=min(2*p, c)DP[c][p+1] = max{SUM[1][c] - DP[c-i][i]} 1 <=i<=min(2*(p+1), c)= max{DP[c][p], SUM[1][c] - DP[c-(2*p+1)][2*p+1],SUM[1][c] - DP[c-(2*p+2)][2*p+2]}这样就把转移时间降为O(1),整个时间降为O(N^2)了。
当然,在处理2*p+1 > c 和2*p+2 > c 要特别小心,否则就要造成数组访问出界的错误。
program P1075;constmaxn=2000;varf:array[0..maxn,0..maxn] of longint;sum:array[0..maxn+1] of longint;n,ans:longint;procedure gf_init;var i:longint;beginreadln(n);for i:=n downto 1 do readln(sum[i]);for i:=1 to n do inc(sum[i],sum[i-1]);end;function max(x,y:longint):longint;beginif x>y then exit(x) else exit(y);end;//f[i,j]表示剩下的i枚硬币~上一次取的个数是j个的最优值procedure gf_work;var i,j:longint;beginfor i:=1 to n do f[0,i]:=0;for i:=1 to n dofor j:=1 to n dobeginf[i,j]:=f[i,j-1];if i-(2*j-1)>=0 thenf[i,j]:=max(f[i,j],sum[i]-f[i-(2*j-1),2*j-1]);if i-(2*j)>=0 thenf[i,j]:=max(f[i,j],sum[i]-f[i-(2*j),2*j]); end;end;procedure gf_print;beginwriteln(f[n,1]);end;begingf_init;gf_work;gf_print;end.输入12358451218161091512 输出59输入201000020000150002300045000900005000015000600006500055000340004200045000800007600079000850002700039000 输出503000宝物筛选(Treasure.pas/c/cpp)【题目描述】终于,破解了千年的难题。
小FF找到了王室的宝物室,里面堆满了无数价值连城的宝物……这下小FF可发财了,嘎嘎。
但是这里的宝物实在是太多了,小FF 的采集车似乎装不下那么多宝物。
看来小FF只能含泪舍弃其中的一部分宝物了……小FF对洞穴里的宝物进行了整理,他发现每样宝物都有一件或者多件,他粗略的估算了下每样宝物的价值,之后开始了宝物筛选工作:小FF有一个最大载重为W的采集车,洞穴里总共有n种宝物,每种宝物的价值为v[i],重量为w[i],每种宝物有m[i]件。
小FF希望在采集车不超载的前提下,选择一些宝物装进采集车,使得它们的价值和最大。
【输入格式】第一行为一个整数N和W,分别表示宝物种数和采集车的最大载重。
