中考数学24题 几何证明
2023年数学中考试题精选:几何综合证明(一)

1.(2023.营口24题)在平行四边形ABCD中,∠ADB=90°,点E在CD 上,点G在AB上,点F在BD的延长线上,连接EF,DG, ∠FED=∠ADG,ADBD =DG EF=k.(1)如图1,当k=1时,请用等式表示线段AG与线段DF的数量关系________;(2)如图2,当k=√(3)时,写出线段AD,DE和DF之间的数量关系,并说明理由;(3)在(2)的条件下,当点G是AB的中点时,连接BE,求tan∠EBF的值2.(2023.本溪铁岭辽阳25题)在Rt△ABC中,∠ACB=90°,CA=CB,点O为AB的中点,点D在直线AB上(不与点A,B重合),连接CD,线段CD绕点C逆时针旋转90°,得到线段CE,过点B作直线l⊥BC,过点E作EF⊥l,垂足为点F,直线EF交直线OC于点G.(1)如图1,当点D与点O重合时,请直接写出线段AD与线段EF 的数量关系;(2)如图2,当点D在线段AB上时,求证:CG+BD=√2BC;(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3时,请直接写出S1S2的值.3.(2023.大连25题)综合与实践问题情境:数学活动课上,王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质。
已知AB=AC,∠A>90°,点E为AC上一动点,将△ABE以BE为对称轴翻折,同学们经过思考后进行如下探究:独立思考:小明:“当点D落在BC上时,∠EDC=2∠ACB.”小红:“若点E为AC中点,给出AC与DC的长,就可求出BE的长.”补足探究:奋进小组的同学们经过探究后提出问题1,请你回答:问题1:在等腰△ABC中,AB=AC,∠A>90°,△BDE由△ABE翻折得到.(1)如图1,当点D落在BC上时,求证:∠EDC=2∠ACB;(2)如图2,若点E为AC中点,AC=4,CD=3,求BE的长.问题解决:小明经过探究发现:若将问题1中的等腰三角形换成∠A<90°的等腰三角形,可以问题进一步拓展.问题2:如图3,在等腰△ABC中,∠A<90°,AB=AC=BD=4,2∠D=∠ABD.若CD=1,则求BC的长.4.(2023.牡丹江26题)平行四边形ABCD中,AE⊥BC,垂足为E,连接DE,将ED绕点E逆时针旋转90°,得到EF,连接BF.(1)当点E在线段BC上,∠ABC=45°时,如图1,求证:AE+EC=BF;(2)当点E在线段BC延长线上,∠ABC=45°时,如图2,当点E在线段CB延长线上,∠ABC=135°时,如图3,请猜想并直接写出线段AE,EC,BF的数量关系;(3)在(1)、(2)的条件下,若BE=3,DE=5,则CE=______.5.(2023.贵州省25题)如图1,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B,点P在CB上.(1)【动手操作】如图2,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为______度;(2)【问题探究】根据(1)所画图形,探究线段PA与PE的数量关系,并说明理由;(3)【拓展延伸】如图3,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD将于点E,探究线段BA,BP,BE之间的数量关系,并说明理由.6.(2023.沈阳24题)如图1.在平行四边形纸片中,AB=10,AD=6,∠DAB=60°,点E为BC边上的一点(点E不与点C重合),连接AE,将平行四边形ABCD纸片沿AE所在直线折叠,点C,D的对应点分别为C`,D`,射线C`E与射线AD将于点F.(1)求证:AF=EF;(2)如图2,当EF⊥AF时,DF的长为______;(3)如图3,当CE=2时,过点F作FM⊥AE,垂足为点M,延长FM 交C`D`于点N,连接AN,EN,求△ANE的面积。
2019届中考数学复习《几何证明与计算》专题训练含答案
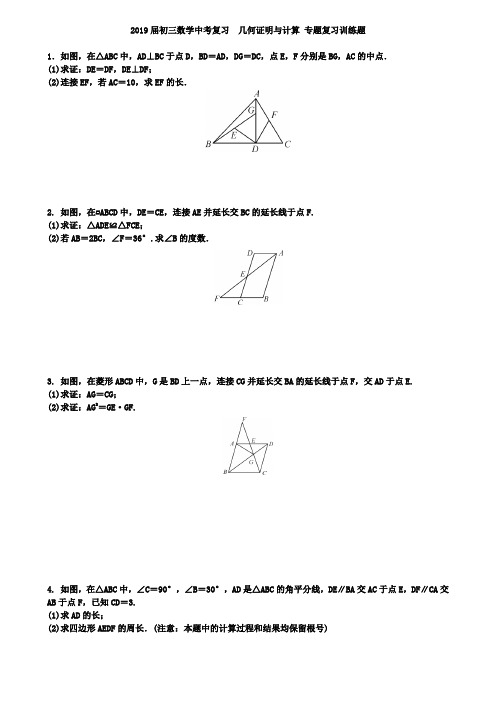
2019届初三数学中考复习几何证明与计算专题复习训练题1.如图,在△ABC中,AD⊥BC于点D,BD=AD,DG=DC,点E,F分别是BG,AC的中点.(1)求证:DE=DF,DE⊥DF;(2)连接EF,若AC=10,求EF的长.2. 如图,在▱ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.(1)求证:△ADE≌△FCE;(2)若AB=2BC,∠F=36°.求∠B的度数.3. 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:AG=CG;(2)求证:AG2=GE·GF.4. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.(1)求AD的长;(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)5. 如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.6. 如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于点H,交CD于点G.(1)求证:BG=DE;(2)若点G为CD的中点,求HGGF的值.7. 如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.8. 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.(1)求证:△ACD∽△BFD;(2)当tan∠ABD=1,AC=3时,求BF的长.9. 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:AG=CG;(2)求证:AG2=GE·GF.10. 如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF,延长DB交EF于点N.(1)求证:AD=AF;(2)求证:BD=EF;(3)试判断四边形ABNE的形状,并说明理由.11. 在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.(1)如图①,若AB=32,BC=5,求AC的长;(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.12. 如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.(1)求证:△ABM∽△EFA;(2)若AB=12,BM=5,求DE的长.参考答案:1. 解:(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°.在△BDG和△ADC中,⎩⎪⎨⎪⎧BD =AD ,∠BDG =∠ADC DG =DC ,,∴△BDG ≌△ADC. ∴BG =AC ,∠BGD =∠C.∵∠ADB=∠ADC=90°, E ,F 分别是BG ,AC 的中点,∴DE =12BG =EG ,DF =12AC =AF.∴DE=DF ,∠EDG =∠EGD,∠FDA =∠FAD.∴∠EDG+∠FDA=90°,∴DE ⊥DF.(2)∵AC=10,∴DE =DF =5,由勾股定理,得EF =DE 2+DF 2=5 2. 2. 解:(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC.∴∠D=∠ECF.在△ADE 和△FCE 中,⎩⎪⎨⎪⎧∠D=∠ECF,DE =CE ,∠AED =∠FEC,∴△ADE ≌△FCE(ASA).(2)∵△ADE≌△FCE,∴AD=FC.∵AD=BC ,AB =2BC ,∴AB=FB.∴∠BAF=∠F=36°.∴∠B=180°-2×36°=108°. 3. 证明:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB.又GD 为公共边,∴△ADG ≌△CDG(SAS),∴AG =CG. (2)∵△ADG≌△CDG,∴∠EAG =∠DCG.∵AB∥CD,∴∠DCG =∠F.∴∠EAG=∠F.∵∠AGE=∠AGE,∴△AGE ∽△FGA.∴AG FG =EG AG.∴AG 2=GE·GF. 4. 解:(1)∵∠C=90°,∠B =30°,∴∠CAB =60°.∵AD 平分∠CAB ,∴∠CAD =12∠CAB=30°.在Rt △ACD 中,∵∠ACD =90°,∠CAD =30°,∴AD =2CD =6. (2)∵DE∥BA 交AC 于点E ,DF ∥CA 交AB 于点F , ∴四边形AEDF 是平行四边形,∠EAD =∠ADF=∠DAF. ∴AF=DF.∴四边形AEDF 是菱形.∴AE=DE =DF =AF. 在Rt △CED 中,∵DE ∥AB ,∴∠CDE =∠B=30°. ∴DE =CDcos30°=2 3.∴四边形AEDF 的周长为8 3.5. 解:(1)证明:∵四边形ABCD 是菱形,∴∠B =∠D,AB =BC =DC =AD.∵点E ,O ,F 分别为AB ,AC ,AD 的中点,∴AE =BE =DF =AF ,OF =12DC ,OE =12BC ,OE ∥BC.在△BCE 和△DCF 中,⎩⎪⎨⎪⎧BE =DF ,∠B =∠D,BC =DC ,∴△BCE ≌△DCF(SAS). (2)当AB⊥BC 时,四边形AEOF 是正方形, 理由如下:由(1)得AE =OE =OF =AF ,∴四边形AEOF 是菱形.∵AB⊥BC,OE∥BC,∴OE⊥AB.∴∠AEO=90°.∴四边形AEOF 是正方形.6. 解:(1)证明:∵BF⊥DE,∴∠GFD =90°.∵∠BCG =90°,∠BGC =∠DGF,∴∠CBG =∠CDE. 在△BCG 与△DCE 中.⎩⎪⎨⎪⎧∠CBG=∠CDE,BC =CD ,∠BCG =∠DCE,∴△BCG ≌△DCE(ASA),∴BG =DE.(2)设CG =x ,∵G 为CD 的中点,∴GD =CG =x , 由(1)可知△BCG≌△DCE(ASA),∴CG =CE =x.由勾股定理可知DE =BG =5x ,∵sin ∠CDE =CE DE =GFGD ,∴GF=55x.∵AB∥CG,∴△ABH ∽△CGH.∴AB CG =BH GH =21. ∴BH=253x ,GH =53x.∴HG GF =53.7. 解:(1)结论:AG 2=GE 2+GF 2.理由:连接CG.∵四边形ABCD 是正方形,∴点A ,C 关于对角线BD 对称. ∵点G 在BD 上,∴GA=GC.∵GE⊥DC 于点E ,GF⊥BC 于点F , ∴∠GEC=∠ECF=∠CFG=90°.∴四边形EGFC 是矩形.∴CF=GE.在Rt △GFC 中,∵CG 2=GF 2+CF 2,∴AG 2=GF 2+GE 2.(2)过点B 作BN⊥AG 于点N ,在BN 上取一点M ,使得AM =BM.设AN =x.∵∠AGF=105°,∠FBG =∠FGB=∠ABG=45°, ∴∠AGB =60°,∠GBN =30°,∠ABM =∠MAB=15°.∴∠AMN =30°.∴AM =BM =2x ,MN =3x.在Rt △ABN 中,∵AB 2=AN 2+BN 2,∴1=x 2+(2x +3x)2,解得x =6-24,∴BN =6+24.∴BG=BN cos30°=32+66. 8. 解:(1)∵AD⊥BC,BE ⊥AC ,∴∠BDF =∠ADC=∠BEC=90°,∴∠C +∠DBF=90°,∠C +∠DAC=90°,∴∠DBF =∠DAC,∴△ACD ∽△BFD(2)∵tan ∠ABD =1,∠ADB =90°,∴AD BD =1,∵△ACD ∽△BFD ,∴AC BF =ADBD=1,∴BF =AC =39. 解:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB,可证△ADG≌△CDG(SAS),∴AG =CG(2)∵△ADG≌△CDG,∴∠EAG =∠DCG,∵AB ∥CD ,∴∠DCG =∠F,∴∠EAG =∠F,∵∠AGE =∠AGE,∴△AGE ∽△FGA ,∴AG FG =EG AG,∴AG 2=GE·GF10. 解:(1)∵AB=AC ,∠BAC =90°,∴∠ABC =∠ACB =45°,∴∠ABF =135°,∵∠BCD =90°,∴∠ACD =∠ACB+∠BCD=135°,∴∠ABF =∠ACD,∵CB =CD ,CB =BF ,∴BF =CD ,可证△ABF≌△ACD(SAS),∴AD =AF(2)由(1)知AF =AD ,△ABF ≌△ACD ,∴∠FAB =∠DAC,∵∠BAC =90°,∴∠EAB =∠BAC=90°,∴∠EAF =∠BAD,可证△AEF≌△ABD(SAS),∴BD =EF(3)四边形ABNE 是正方形.理由如下:∵CD=CB ,∠BCD =90°,∴∠CBD =45°,又∵∠ABC=45°,∴∠ABD =∠ABC+∠CBD=90°,由(2)知∠EAB=90°,△AEF ≌△ABD ,∴∠AEF =∠ABD=90°,∴四边形ABNE 是矩形,又∵AE=AB ,∴四边形ABNE 是正方形 11. 解:(1)∵∠ABM=45°,AM ⊥BM ,∴AM =BM =ABcos45°=32×22=3. 则CM =BC -BM =5-3=2,∴AC =AM 2+CM 2=22+32=13.(2)证明:延长EF 到点G ,使得FG =EF ,连接BG.∵DM =MC ,∠BMD =∠AMC ,BM =AM ,∴△BMD≌△AMC(SAS).∴AC =BD.又CE =AC ,∴BD =CE.∵BF =FC ,∠BFG =∠EFC ,FG =FE ,∴△BFG≌△CFE.∴BG=CE ,∠G=∠E.∴BD=CE =BG ,∴∠BDG=∠G=∠E. 12. 解:(1)证明:∵四边形ABCD 是正方形, ∴AB=AD ,∠B=90°,AD∥BC.∴∠AMB=∠EA F.又∵EF⊥AM,∴∠AFE=90°.∴∠B=∠AFE.∴△ABM∽△EFA. (2)∵∠B=90°,AB =AD =12,BM =5,∴AM =122+52=13.∵F 是AM 的中点,∴AF =12AM =6.5.∵△ABM∽△EFA,∴BM AF =AM AE ,即56.5=13AE.∴AE =16.9,∴DE =AE -AD =4.9.2019-2020学年数学中考模拟试卷一、选择题1.已知二次函数y =ax 2+bx+c (a≠0),过(1,y 1)、(2,y 2).下列结论:①若y 1>0时,则a+b+c >0; ②若a =2b 时,则y 1<y 2;③若y 1<0,y 2>0,且a+b <0,则a >0.其中正确的结论个数为( ) A .0个B .1个C .2个D .3个2.已知直线a ∥b ,将一块含45o角的直角三角板(∠C=90o)按如图所示的位置摆放,若∠1=55o,则∠2 的度数为( )A .85oB .70oC .80oD .75o3.如图,⊙O 与BC 相切于点B ,弦AB ∥OC ,若∠C =40°,则∠AOB 的度数是( )A.60B.70°C.80°D.90°4.如图,点P(-a,2a)是反比例函数与的一个交点,图中阴影部分的面积为5π,则反比例函数的解析是为( )A. B. C. D.5.如图,等边三角形ABC ,B 点在坐标原点,C 点的坐标为(4,0),则点A 的坐标为( )A .(2,3)B .(2,)C .(,2)D .(2,6.如图,在平面直角坐标系中,四边形OABC 是菱形,点C 的坐标为(4,0),60AOC ∠=︒,垂直于x 轴的直线l 从y 轴出发,沿x 轴正方向以每秒1个单位长度的速度向右平移,设直线l 与菱形OABC 的两边分别交于点M ,N(点M 在点N 的上方),若OMN ∆的面积为S ,直线l 的运动时间为t 秒(04)t ≤≤,则能大致反映S 与t 的函数关系的图象是( )A. B.C. D.7.如果a+b =12,那么a b a b b a+--22的值是( ) A .12B .14C .2D .48.《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十.问甲乙持钱各几何?”其大意是:今有甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱;如果乙得到甲所有钱的三分之二,那么乙也共有.问甲、乙两人各带了多少钱?设甲带钱为,乙带钱为,根据题意,可列方程组为( )A.B.C.D.9.如图,在矩形ABCD 中,AB=8,BC=6,点E 在边AB 上,点F 在边CD 上,点G ,H 在对角线AC 上,若四边形GEHF 是菱形,则AE 的长是( )A.5B.254C. D.10.正比例函数y =kx(k≠0)的图象上一点A 到x 轴的距离与到y 轴的距离之比为2 : 3,且y 随x 的增大而减小,则k 的值是 ( ) A .23B .32C .32-D .23-11.如图,在四边形ABCD 中,AC 与BD 相交于点O ,∠BAD =90°,BO =DO ,那么添加下列一个条件后,仍不能判定四边形ABCD 是矩形的是( )A .∠ABC =90°B .∠BCD =90°C .AB =CD D .AB ∥CD12.如图,在矩形ABCD 中,6AB =,4BC =,动点E 从点A 出发,沿A B C →→的路线运动,当点E 到达点C 时停止运动,过点E 作FE AE ⊥,交CD 于点F ,设点E 运动的路程为x ,FC y =.则y 关于x 的图象大致为( )A .B .C .D .二、填空题13.如图,将边长为3的正方形纸片ABCD 对折,使AB 与DC 重合,折痕为EF ,展平后,再将点B 折到边CD 上,使边AB 经过点E ,折痕为GH ,点B 的对应点为M ,点A 的对应点为N ,那么折痕GH 的长为_____.14.计算:①232n m ⎛⎫= ⎪⎝⎭_____;②b a a b a b -=-- _____. 15.如图是23名射击运动员的一次测试成绩的频数分布折线图,则射击成绩的中位数_____。
中考数学复习专题24全等三角形试题(A卷,含解析)

全等三角形一、选择题 1. (新疆建设兵团,4,5分)如图,在△ABC 和△DEF 中,∠B =∠DEF ,AB =DE ,添加下列一个条件后,仍然不能证明△ABC ≌△DEF ,这个条件是( )A .∠A =∠DB .BC =EF C .∠ACB =∠FD .AC =DF【答案】D【逐步提示】本题考查了全等三角形的判定方法,解题的关键是熟练掌握全等三角形常见判定方法.注意到题目中给出一组角相等,一组边相等,分别结合四个选项,找到不符号常见判定方法的那个选项.【详细解答】解:选项A 可采用“ASA ”来判定三角形全等,选项B 可采用“SAS ”来判定三角形全等,选项C 可采用“AAS ”来判定三角形全等,选项D 为两边和其中一边的对角不能判定三角形全等,故选择D . 【解后反思】此类问题容易出错的地方是由SSA 就判定三角形全等,从而错选D 选项.三角形全等的判定方法有:SAS ,ASA ,AAS ,SSS ,HL (直角三角形). 【关键词】 三角形全等的判定;(浙江金华,6,3分)如图,已知=ABC BAD ∠∠,添加下列条件还不能判定△ABC ≌△BAD 的是( )A. AC=BDB.∠CAB =∠DBAC.∠C =∠DD.BC=AD 【答案】A【逐步提示】将题目中的条件表示到图形中,再结合图形条件判断已有哪些条件,然后根据三角形全等的判定方法确定正确的选项.【解析】题目中已给出一角相等,图形中有一条公共边,即已有一边及一角对应相等,再需要一边或一角相等即可,A 选项与两已知条件构成SSA 不能确定两个三角形全等;B 选项与两已知条件构成ASA 能确定两个三角形全等;C 选项与两已知条件构成AAS 能确定两个三角形全等;D 选项与两已知条件构成SAS 能确定两个三角形全等,故选择A.【解后反思】对于添加条件从而判断两个全等三角形全等类问题的解题策略:首先理解题目中已存在的条件(包括已知条件及图形条件),再根据三角形全等的五种判定方法[(1)三边对应相等的两个三角形全等SSS ;(2)两边和它们的夹角对应相等的两个三角形全等SAS ;(3)两角和它们的夹边对应相等的两个三角形全等ASA ;(4)两个角和其中一角的对边对应相等的两个三角形全等AAS ;(5)斜边和一条直角边对应相等的两个直角三角形全等HL]进行综合评判,从而确定需要添加的条件. 【关键词】三角形全等的识别 2.3. ( 四川省广安市,8,3分)下列说法: ①三角形的三条高一定都在三角形内;AB(第6题图)DC②有一个角是直角的四边形是矩形;③有一组邻边相等的平行四边形是菱形;④两边及一角对应相等的两个三角形全等;⑤一组对边平行,另一组对边相等的四边形是平行四边形.其中正确的个数有()A.1个 B.2个 C.3个 D.4个【答案】A【逐步提示】本题考查了三角形的中线、高线、角平分线的概念,矩形的判定,菱形的判定,全等三角形的判定,平行四边形的判定等,解题的关键是掌握这些概念、定理等.因为直角三角形与钝角三角形的三条高不都在三角形内,故①错;至少有三个角是直角的四边形是才是矩形,故②错;③是菱形的定义,正确;满足④的条件时有可能形成“边边角”的情况,故错误;等腰梯形满足“一组对边平行,另一组对边相等”,但它不是平行四边形,故⑤错误.【详细解答】解:只有③正确,故选择A.【解后反思】要理解三角形“三线”的概念,掌握三角形、平行四边形、矩形、菱形的判定方法,这是正确解题的基础.能画图举反例,以排除不符合条件情形,也是解这类题的基本功,要多思考,勤积累.类似的问题还有:判断下列说法是否正确:(1)一组对边相等且一组对角相等的四边形是平行四边形.解:错误.如图1,作△ABC,使AB=AC,在BC上取一点D(D点不与B、C重合且BD≠CD),连接AD.再以A为顶点,AD为一边,作∠EAD,使∠EAD=∠ADC,且AE=DC,连接DE.由上述画图方法,可知△ADC≌△DAE(SAS).所以DE=AC=AB,∠AED=∠C=∠B.即四边形ABCD有一组对边相等(DE=AB)、一组对角相等(∠AED=∠B),但却不是平行四边形(另一组对边AE 和BD不平行也不相等).(2)一组对边相等,且一条对角线平分另一条对角线的四边形是平行四边形.解:错误.如图2,画两条相交直线,交点为O,在其中一条直线上截取OA=OC,分别过A、C两点向另一条直线作垂线,垂足分别为E、F.在线段OF上取一点D(D点不与O、F重合),连接CD.再在线段OE的延长线上取一点B,使EB=FD,连接AB.由上述画图方法,易知△COF≌△AOE(AAS),则CF=AE,由“SAS”可判定△CFD≌△AEB,则CD=AB.连接AD、BC,则四边形ABCD满足条件,却不是平行四边形.(3)一组对角相等,且连接这一组对角的顶点的对角线被另一条对角线平分的四边形是平行四边形.解:错误.如图,画一个“筝形”ABCD,其中AB=AD,BC=DC且AO≠OC,则该“筝形”满足条件,但它不是平行四边形.【关键词】 中线、高线、角平分线;矩形的判定;菱形的判定;全等三角形的判定;平行四边形的判定二、填空题1. ( 山东省枣庄市,17,4分)如图,在△ABC 中,∠C =90°,AC =BC 2ABC 绕点A 顺时针方向旋转60°到△A ´B ´C ´的位置,连接C ´B ,则C ´B = .31【逐步提示】本题考查了旋转、全等三角形、解直角三角形,解题的关键是通过旋转的性质及角度得出△ABB ´为等边三角形.连接BB ´,延长BC ´交AB ´于点H ,根据旋转的性质,对应点到旋转中心的距离相等,可知△ABB ´为等边三角形,然后再证明△ABC ´≌△B ´BC ´,再利用等腰三角形三线合一,证明BH ⊥AB ´,然后分别求HC ´与BH 即可求C ´B .【详细解答】解:连接BB ´,延长BC ´交AB ´于点H ,∵∠C =90°,AC =BC 2,∴AB 22AC BC +2,由题意可知:AB ´=AB =2,且∠BAB ´=60°,∴△ABB ´为等边三角形,∴BB ´=AB ,∠ABB ´=60°,又∵BC ´=BC ´,B´C ´=AC ´,∴△ABC ´≌△B ´B C ´,∴∠ABC ´=∠B ´ BC ´=30°,∴BH ⊥AB ´,且AH =12AB ´=1,∴BH 22AB AH -3AC ´B ´=90°,AH =B ´H ,∴C ´H =12AB ´=1,∴ C ´B =BH -C ´H 31 ,故答案为31 .【解后反思】本题考查了旋转的知识,解这类题通常抓住变换前后的全等图形中对应边、对应角相等.当旋转角为60°时,可以得到等边三角形;当旋转角为45°时,可以得到等腰直角三角形. 【关键词】三角形全等的识别 ;全等三角形的性质;等腰三角形的性质;勾股定理;C ´ABHCB ´ABCB ´C ´2. ( 四川省成都市,12,4分)如图,△ABC ≌△A ´B ´C ´,其中∠A =36°,∠C ´=24°,∠B = .【答案】120°.【逐步提示】本题考查了三角形全等的性质及三角形内角和定理,解题的关键是掌握有关的性质.先根据全等三角形对应角相等求出∠C ,再利用三角形内角和定理可求出∠B .【详细解答】解:∵△ABC ≌△A ´B ´C ´,∴∠C =∠C ´=24°,∴ ∠B =180°―∠A ―∠C =180°―36°―24°=120° ,故答案为 120° .【解后反思】全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等. 【关键词】三角形的内角和;全等三角形的性质三、解答题1. ( 山东省枣庄市,24,10分)如图,把△EFP 放置在菱形ABCD 中,使得顶点E ,F ,P 分别在线段AB ,AD ,AC 上,EP =FP =6,EF =3,∠BAD =60°,AB >63⑴求∠EPF 的大小;⑵若AP =10,求AE +AF ;⑶若△EFP 的三个顶点E ,F ,P 分别在线段AB ,AD ,AC 上运动,请直接写出AP 长的最大值和最小值.【逐步提示】本题考查了菱形的性质、等腰三角形三线合一性及全等三角形等知识,解题的关键是熟练掌握图形的性质和判定,善于转化.⑴过点P 作PG ⊥EF 于G .根据等腰三角形三线合一性,得∠EPF =2∠FPG ,再解Rt △PFG ,利用特殊角三角函数值求∠FPG 的大小,即可得∠EPF ;⑵作PM ⊥AB 于M ,PN ⊥AD 于N .根据菱形的对角线平分对角的性质,可证明△PME ≌ △PNF ,得ME =NF ,再利用三角函数求出AM =AN ,通过线段和差得到AE +AF 与AM 、AN 的关系,即可求值;⑶当E 、F 分别与A 、B 重合时,AP 取最小值,当EF ⊥AC 时,AP 取最大值. 【详细解答】解:⑴如图,过点P 作PG ⊥EF 于G . ∵PE =PF =6,PG ⊥EF ,∴FG =EG =12 EF =33FPG =∠EPG =12∠EPF . 在Rt △FPG 中,sin ∠FPG =FG PF333.∴∠FPG =60°,∴∠EPF =2∠FPG =120°.AC BCA ´B ´ABDCFPE⑵作PM ⊥AB 于M ,PN ⊥AD 于N .∵AC 为菱形ABCD 的对角线,∴∠DAC =∠BAC ,AM =AN ,PM =PN . 在Rt △PME 和Rt △PNF 中,PM =PN ,PE =PF , ∴Rt △PME ≌Rt △PNF .∴ME =NF . 又AP =10,∠PAM =12∠DAB =30°, ∴AM =AN =AP ·cos30°=10×3=53. ∴AE +AF =(AM +ME )+(AN -NF )=AM +AN =103.⑶如图,当△EFP 的三个顶E ,F ,P 分别在线段AB ,AD ,AC 上运动时,点P 在P 1,P 2之间运动,易知P 1O =P 2O =3,AO =9,∴AP 的最大值为12,AP 的最小值为6.【解后反思】运动型问题一般是图形在运动中产生函数关系问题或探究几何图形的变化规律问题,这类问题可细分为点动型、线动型、形动型.解答这类问题时,要求对几何元素的运动过程有一个完整、清晰的认识,不管点动、线动还是形动,要善于借助动态思维的观点来分析,不被“动”所迷惑,从特殊情形入手,变中求不变,动中求静,抓住静的瞬间,以静制动,把动态的问题转化为静态的问题来解决,从而找到“动”与“静”的联系,揭示问题的本质,发现运动中的各个变量之间互相依存的函数关系,从而找到解决问题的突破口,也就找到了解决这类问题的途径.【关键词】全等三角形的性质 ;三角形全等的识别;等腰三角形的性质;特殊角三角函数值的运用;动点题型2. (重庆A ,19,7分)如图,点A ,B ,C ,D 在同一条直线上,CE //DF ,EC =BD ,AC =FD . 求证:AE =FB .【逐步提示】由CE //DF ,可知∠ACE =∠D . 利用“SAS ”可以判定△ACE ≌△FDB ,即可判定AE =FB . 【详细解答】证明:∵CE //DF ,∴∠ACE =∠D . 在△ACE 和△FDB 中,OABDCFP 1EP 2M ABDCFPE N G∵EC=BD,∠ACE=∠D,AC=FD,∴△ACE≌△FDB(SAS).∴AE=FB.【解后反思】利用三角形全等是证明两条线段或两个角相等的重要方法. 证明两个三角形全等必须有一组对应边相等的条件,判定两个三角形全等的方法主要有“SAS”、“ASA”、“AAS”和“SSS”,对于直角三角形,还有“HL”,结合全等三角形的判定方法,可寻找所需要的条件. 当题目中出现平行线时,可根据平行线的性质得到相等的角,还要注意公共线段、公共角、重合线段、重合角在得到相等线段和相等角的作用.【关键词】全等三角形的识别;全等三角形的性质(重庆B,19,7分)如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.【逐步提示】根据两直线平行,内错角相等可得∠BAC=∠ECD,再利用“边角边”证明△ABC≌△CED,然后根据全等三角形对应角相等即可证明∠B=∠E.【详细解答】证明:∵AB∥CD,∴∠BAC=∠ECD,在△ABC和△CED中,,,,AB CEBAC ECDAC CD=⎧⎪∠=∠⎨⎪=⎩∴△ABC≌△CED(SAS),∴∠B=∠E.【解后反思】利用三角形全等是证明两个角或两条线段相等的重要方法. 证明两个三角形全等必须有一组对应边相等的条件,判定两个三角形全等的方法主要有“SAS”、“ASA”、“AAS”和“SSS”,对于直角三角形,还有“HL”,结合全等三角形的判定方法,可寻找所需要的条件. 当题目中出现平行线时,可根据平行线的性质得到相等的角,还要注意公共线段、公共角、重合线段、重合角在得到相等线段和相等角的作用.【关键词】全等三角形的识别;全等三角形的性质3.(重庆B,25,12分)已知△ABC是等腰直角三角形,∠BAC=90°,CD=12BC,DE⊥CE,DE=CE,连接AE,点M 是AE的中点.(1)如图1,若点D在BC边上,连接CM,当AB=4时,求CM的长;(2)如图2,若点D在△ABC的内部,连接BD,点N是BD中点,连接MN,NE,求证MN⊥AE;(3)如图3,将图2中的△CDE绕点C逆时针旋转,使∠BCD=30°,连接BD,点N是BD中点,连接MN,探索MNAC 的值并直接写出结果.EMCBA图1D图2NMEDCBAENMCBA图3D【逐步提示】(1)先证明△ACE是直角三角形,根据CM=12AE,求出AE即可解决问题.(2)如图,延长EN至点F,使NF=EN,连接BF,连接AF.先证明△NBF≌△NDE,可得BF=DE=CE,∠FBN=∠NDE.根据题意可得∠ACE=∠ACB+∠DCE-∠DCB=90°-∠DCB,只要证出∠ABF=90°-∠DCB.即可证明∠ACE=∠ABF,又AB=AC,利用“SAS”可证出△ABF≌△ACE,进而可得∠FAB=∠EAC,所以有∠FAE=∠FAB+∠BAE=∠EAC+∠BAE=∠BAC=90°,又MN是△EAF的中位线.根据三角形的中位线的性质可得MN∥AF,从而∠NME=∠FAE=90°,可证MN⊥AF.(3)如图5,连接DM并延长到点G,使MG=MD,连接AG、BG,延长AG、EC交于点F.可得△AMG≌△EMD,∴AG=DE=EC,∠GAM=∠DEM,∴AG∥DE,∴∠F=∠DEC=90°,∵∠FAC+∠ACF=90°,∠BCD+∠ACF=90°,∴∠FAC=∠BCD=30°∴∠BAG=∠ACE=120°,在△ABG和△CAE中,,,,AB ACBAG ACEAG EC=⎧⎪∠=∠⎨⎪=⎩∴△ABG≌△CAE,∴BG=AE,∵BN=ND,DM=MG,∴MN是△DBG的中位线,∴BG=AE=2MN,设BC=2a,则CD=a,DE=EC=22a,AC=2a,CF=22a,AF=62a,EF=2a,∴AE=22142AF EF+=a,∴MN=144a,∴147442aMNAC a==.【详细解答】(1)解:∵△ABC是等腰直角三角形,∠BAC=90°,AB=4,∴AC=AB=4,BC=42,∠ACB=∠ABC=45°.∵CD=12BC,∴CD=22∵DE⊥CE,DE=CE,∴△CDE是等腰直角三角形,∴∠DCE=∠CDE=45°,∴CE=CD·sin45°=2.∵∠ACE=∠DCE+∠ACB=45°+45°=90°,∴在Rt△ACE中,AE2225AC CE+=∵点M是AE中点,∴CM=12AE5(2)证明:如图4,延长EN至点F,使NF=EN,连接BF,连接AF.∵点N是BD的中点,∴BN=DN.∵∠BNF=∠DNE,∴△NBF≌△NDE.∴BF=DE,∠FBN=∠NDE,∵DE=CE,∴BF=CE.∵∠ACE=∠ACB+∠DCE-∠DCB,∴∠ACE=45°+45°-∠DCB=90°-∠DCB.在△BCD中,∵∠DBC+∠BDC+∠DCB=180°,∠BDC=∠NDE+∠CDE,又∵∠CDE=45°,∴∠DBC+∠NDE=135°-∠DCB.∵∠ABF=∠DBC+∠FBN-∠ABC,∠FBN=∠NDE,∴∠ABF=∠DBC+∠NDE-∠ABC=135°-∠DCB-45°=90°-∠DCB.∴∠ABF=∠ACE.∵AB=AC,∴△ABF≌△ACE.∴∠FAB=∠EAC∵∠BAC=∠BAE+∠EAC=90°,∴∠FAB+∠BAE=90°,即∠FAE=90°.∵点M是AE中点,NF=NE,∴MN是△EAF的中位线.∴MN∥AF.∴∠NME=∠FAE=90°.∴MN⊥AF.(3)解:7 MNAC.【解后反思】本题综合考查全等三角形的判定和性质、勾股定理、三角形的中位线等知识,解题的关键是添加辅助线,构造全等三角形.在几何问题的求解或证明中,全等三角形起着很重要的作用,应该充分利用已知条件和图形找出图中的全等三角形,根据全等三角形对应边、对应角分别相等的性质可实现等边、等角的代换,而当要证明的两线段之间或两角之间没有直接联系时,往往需要通过等量代换适当转换来求解..【关键词】三角形全等的识别;全等三角形的性质;勾股定理;三角形中位线定理4.5.(四川泸州,18,6分)如图,C是线段AB的中点,CD=BE, CD∥BE.求证:∠D=∠E.【逐步提示】要证明两个不同三角形中的两个角相等,可以证明这两个角所在的两个三角形全等,从而选择合适的判定方法证明两个三角形全等.【详细解答】证明:∵C 是线段AB 的中点,∴AC=CB ,∵CD ∥BE ,∴∠ACD=∠CBE ,在△ACD 和△CBE 中,AC CB ACD CBE CD BE =⎧⎪∠=∠⎨⎪=⎩∴△ACD ≌△CBE, ∴∠D=∠E.【解后反思】证明两个三角形全等,一般情况下是已知两个条件去找第三个全等条件,有以下几种情况:(1)已知两边.⎧⎨⎩找第三边;找两边的夹角;(2)已知两角⎧⎨⎩找其中任意一角的对边找两角的夹边;(3)已知一边及其邻角⎧⎨⎩找任意一角找夹该已知角的边;(4)已知一边及其对角,找余下的任一角. 【关键词】三角形全等的判定方法5. ( 四川南充,19,8分)已知ΔABN 和ΔACM 位置如图所示,AB =AC ,AD =AE ,∠1=∠2. (1)求证:BD =CE ; (2)求证:∠M =∠N .21O ED MAN【逐步提示】本题考查了全等三角形的判定与性质;解题的关键是证明三角形全等.(1)由SAS 证明△ABD≌△ACE,得出对应边相等即可(2)证出∠BAN=∠CAM,由全等三角形的性质得出∠B=∠C,由AAS 证明△ACM≌△ABN,得出对应角相等即可. 【详细解答】解:(1)证明:在△ABD 和△ACE 中,12AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD≌△ACE(SAS ), ∴BD=CE;(2)证明:∵∠1=∠2, ∴∠1+∠DAE=∠2+∠DAE, 即∠BAN=∠CAM,由(1)得:△ABD≌△ACE, ∴∠B=∠C,在△ACM 和△ABN 中,C BAC ABCAM BAN∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ACM≌△ABN(ASA),∴∠M=∠N.已知条件寻找的条件选择的判定方法两角夹边或一角对边ASA或AAS一角及其对边任一角AAS一角及其邻边角的另一边或边的另一邻角或边的对角SA S或ASA或AAS 两边夹角或另一边或直角SAS或SSS或HL 【关键词】全等三角形的性质;三角形全等的识别6(四川省宜宾市,18,6分)如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD【逐步提示】已知∠CAB=∠DBA,可得AO=BO,因而可证明△BOC≌△AOD,结论成立. 【详细解答】证明:∠CAB=∠DBA,所以AO=BO在△BOC和△AOD 中∠CBD=∠DAC(已知)OB=OA(已证)∠CBD=∠DAC(已证)△BOC≌△AOD(ASA)所以BC=AD【解后反思】除了上面的证明方法外,也可以证明△BAC≌△ABD(ASA)【关键词】全等三角形的性质与判定;等腰三角形的性质与判定。
中考复习初中数学几何证明 试题(含答案)
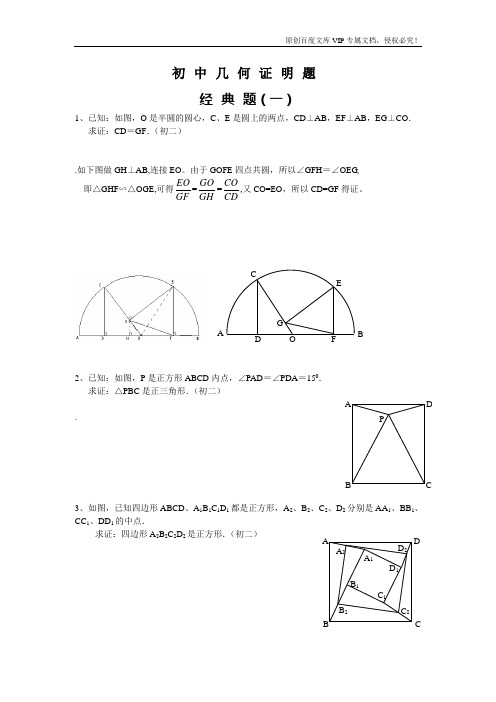
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.BF求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值. A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
(完整word)重点高中自招必备九年级专题24平面几何的定值问题

专题24平面几何的定值问题【阅读与思考】所谓定值问题,是指按照一定条件构成的几何图形,当某些几何元素按一定的规律在确定的范围内变化时,与它有关的元素的量保持不变(或几何元素间的某些几何性质或位置关系不变).几何定值问题的基本特点是:题设条件中都包含着变动元素和固定元素,变动元素是指可变化运动的元素,固定元素也就是“不变量”,有的是明显的,有的是隐含的,在运动变化中始终没有发生变化的元素,也就是我们要探求的定值.解答定值问题的一般步骤是:1.探求定值;2.给出证明.【例题与求解】—^ PA + PC .【例1】如图,已知P为正方形ABCD的外接圆的劣弧AD上任意一点.求证:一后一为定值.PB解题思路:线段的和差倍分考虑截长补短,利用圆的基本性质,证明三角形全等.【例2】如图,AB为。
O的一固定直径,它把。
O分成上、下两个半圆,自上半圆上一点C作弦CD±AB,Z OCD的平分线交。
O于点P,当点C在上半圆(不包括A,B两点)上移动时,点P()A.到CD的距离保持不变B.位置不变C.等分DBD.随C点的移动而移动(济南市中考试题)解题思路:添出圆中相关辅助线,运用圆的基本性质,用排除法得出结论.【例3】如图,定长的弦ST在一个以AB为直径的半圆上滑动,M是ST的中点,P是S对AB作垂线的垂足.求证:不管ST滑到什么位置,Z SPM是一定角.(加拿大数学奥林匹克试题)解题思路:不管ST滑到什么位置,Z SOT的度数是定值.从探寻Z SPM与Z SOT的关系入手.【例4】如图,扇形OAB的半径OA=3,圆心角/AOB=90°.点C是箫上异于A, B的动点,过点C作CD±OA于点D,作CE±OB于点E.连接DE,点G, H在线段DE上,且DG=GH=HE.(1)求证:四边形OGCH是平行四边形;(2)当点C在箫上运动时,在CD, CG, DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3 CH2是定值. (广州市中考试题)解题思路:延长OG交CD于N,利用题中的三等分点、平行四边形和三角形中位线的性质,实现把线段ON转化成线段CH的倍分关系,再以及△ OND为基础,通过勾股定理,使问题得以解决.【例5】如图1,在平面直角坐标系xOy中,点M在x轴的正半轴上,。
北京市中考数学24题解法说明

5.教学中多总结归纳基本图形,分类整合出 一些基本模型和基本题型。
谢谢大家!
A
D E
B
C
图3
(3)解法六、七:辅助圆及方程思想和转化思想 的运用。
A
A
D
E
B
C
图3
D E
B
C
图3
综上所述,讲与解几何综合题要:
1.具有平移、轴对称、旋转、相似等变换观念。
2.注意运用转化与化归思想、方程与函数思想、 数形结合思想、分类与整合思想。
3.渗透联系与变化、特殊与一般、螺旋式上 升等哲学观点。
北京市中考数学 第24题解法说明
(1)由等腰三角形ABC已知顶角求出底角∠ABC, 减去60度,得∠ABD.
(2)解法一至三:综合题的结合分析思想——条 件与条件结合,条件与结论结合,结论与结论结 合。(哲学的联系的观点)
A
① 由同一端点的两条线段旋转60
度,结合要证的等边三角形ABE,
联想△BCE和△BDA旋转全等。
D
②利用轴对称图形寻找全等条件,
两种变换结合分析。(综合分析法)
B
E 图2 C
要重视中垂线、三线合一的教学要求
(2)解法四:割补法证明全等,是把一般化为特 殊的思想。
D
E
B
F
C
G 图2
(2)解法五、六:辅助圆的思想。辅助图形与辅 助未知数(元)类比。
A D
E
B
C
A D
G
E
B
F
C
(3)解法一至五:由线段等导角等,由角等或角 的和差倍分列方程。注意转化思想的运用。
中考数学几何证明与计算专练

几何证明与计算专练1、如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;(2)求证:BG2﹣GE2=EA2.2、等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N(如图1)。
(1)求证:AM=AN;(2)设BP=x。
①若,BM=38,求x的值;②记四边形ADPE与△ABC重叠部分的面积为S,求S与x之间的函数关系式以及S的最小值;③连接DE,分别与边AB、AC交于点G、H(如图2),当x取何值时,∠BAD=150?并判断此时以DG、GH、HE这三条线段为边构成的三角形是什么特殊三角形,请说明理由。
3、在正方形ABCD 中,对角线AC ,BD 交于点O ,点P 在线段BC 上(不含点B ),∠BPE =12∠ACB ,PE 交BO 于点E ,过点B 作BF ⊥PE ,垂足为F ,交AC 于点G .(1)当点P 与点C 重合时(如图①),求证:△BOG ≌△POE ; (2)通过观察、测量、猜想:BFPE,并结合图②证明你的猜想;(3)把正方形ABCD 改为菱形,其他条件不变(如图③),若∠ACB =α,求BFPE的值.(用含α的式子表示)4、如图,在正方形ABCD 中,E 是BC 上的一点,连结AE ,作BF ⊥AE ,垂足为H ,交CD 于F ,作CG ∥AE ,交BF 于G .(1)求证CG =BH ;(2)FC 2=BF·GF ;(3)22AB FC =GBGF .(图①)(图③)(图②)BEF G OBDACPP5、已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.(1)如图1,求证:PC=AN;(2)如图2,点E 是MN上一点,连接EP并延长交BC于点K,点D是AB上一点,连接DK,∠DKE=∠ABC,EF⊥PM 于点H,交BC延长线于点F,若NP=2,PC=3,CK:CF=2:3,求DQ的长.7、在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;(2)设∠BAC=α,∠BCE=β.①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.8、如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接AA1,射线AA1分别交射线PB、射线B1B于点E、F.(1)如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP 始终存在关系(填“相似”或“全等”),并说明理由;(2)如图2,设∠ABP=β.当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;(3)如图3,当α=60°时,点E、F与点B重合.已知AB=4,设DP=x,△A1BB1的面积为S,求S关于x的函数关系式.9、如图(1),在直角△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=nEA(m,n为实数).试探究线段EF与EG的数量关系.(1)如图(2),当m=1,n=1时,EF与EG的数量关系是.(2)如图(3),当m=1,n为任意实数时,EF与EG的数量关系是.(3)如图(1),当m,n均为任意实数时,EF与EG的数量关系是.(写出关系式,不必证明)10、已知菱形ABCD的边长为1.∠ADC=60°,等边△AEF两边分别交边DC、CB于点E、F.(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为等边△AEF 的外心;(2)若点E、F始终分别在边DC、CB上移动.记等边△AEF的外心为点P.①猜想验证:如图2.猜想△AEF的外心P落在哪一直线上,并加以证明;②拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,试判断1DM+1DN是否为定值.若是,请求出该定值;若不是.请说明理由.11、已知:在△ABC中,BC=2AC,∠DBC=∠ACB,BD=BC,CD交线段AB于点E.(1)如图l,当∠ACB=90°时,则线段DE、CE之间的数量关系为;(2)如图2,当∠ACB=120°时,求证:DE=3CE;(3)如图3,在(2)的条件下,点F是BC边的中点,连接DF,DF与AB交于G,△DKG和△DBG关于直线DG对称(点B的对称点是点K,延长DK交AB于点H.若BH=10,求CE的长.12、如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90o,且EF交正方形外角的平分线CF于点F (1)证明:∠BA E=∠FEC;(2)证明:△AG E≌△ECF;(3)求△AEF的面积.13、(1)如图1,在正方形ABCD 中,M 是BC 边(不含端点B 、C )上任意一点,P 是BC 延长线上一点,N 是∠DCP 的平分线上一点.若∠AMN=90°,求证:AM=MN .(下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明)证明:在边AB 上截取AE=MC ,连ME .正方形ABCD 中,∠B=∠BCD=90°,AB=BC . ∴∠NMC=180°—∠AMN —∠AMB=180°—∠B —∠AMB=∠MAB=∠MAE . (下面请你完成余下的证明过程)(2)若将(1)中的“正方形ABCD ”改为“正三角形ABC ”(如图2),N 是∠ACP 的平分线上一点,则当∠AMN=60°时,结论AM=MN 是否还成立?请说明理由.(3)若将(1)中的“正方形ABCD ”改为“正n 边形ABCD ……X ”,请你作出猜想:当∠AMN= °时,结论AM=MN 仍然成立.(直接写出答案,不需要证明)14、Rt△ABC 与Rt△FED 是两块全等的含30o 、60o角的三角板,按如图(一)所示拼在一起,CB 与DE 重合.(1)求证:四边形ABFC 为平行四边形;(2)取BC 中点O ,将△ABC 绕点O 顺时钟方向旋转到如图(二)中△C B A '''位置,直线C B ''与AB 、CF 分别相交于P 、Q 两点,猜想OQ 、OP 长度的大小关系,并证明你的猜想. (3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB 为菱形(不要求证明).图(二)图(一)FFB(D)M N P D C E B A 图1 M NP C B A图215、在Rt ABC △中,902BAC AB AC ∠=== ,,点D 在BC 所在的直线上运动,作45ADE ∠=(A D E ,,按逆时针方向).(1)如图1,若点D 在线段BC 上运动,DE 交AC 于E . ①求证:ABD DCE △∽△;②当ADE △是等腰三角形时,求AE 的长. (2)①如图2,若点D 在BC 的延长线上运动,DE 的反向延长线与AC 的延长线相交于点E ',是否存在点D ,使ADE '△是等腰三角形?若存在,写出所有点D 的位置;若不存在,请简要说明理由;②如图3,若点D 在BC 的反向延长线上运动,是否存在点D ,使ADE △是等腰三角形?若存在,写出所有点D 的位置;若不存在,请简要说明理由.45 CDB A E E 'C ABD E 第28题图2 第28题图3 45 45 A B D C E 第28题图1。
中考数学几何证明题--(专题练习 答案详解)

中考数学24题专题练习1、如图,等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,连接BE,CE(1)求证:BE=CE;(2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD.2、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G 为CH的中点.(1)若HE=HG,求证:△EBH≌△GFC;(2)若CD=4,BH=1,求AD的长.3、如图,梯形ABCD中,AB∥CD,AD=DC=BC,∠DAB=60°,E是对角线AC延长线上一点,F是AD延长线上的一点,且EB⊥AB,EF⊥AF.(1)当CE=1时,求△BCE的面积;(2)求证:BD=EF+CE.4、如图.在平行四边形ABCD中,O为对角线的交点,点E为线段BC延长线上的一点,且.过点E EF∥CA,交CD于点F,连接OF.(1)求证:OF∥BC;(2)如果梯形OBEF是等腰梯形,判断四边形ABCD的形状,并给出证明.5、如图,梯形ABCD中,AD∥BC,∠ABC=90°,BF⊥CD于F,延长BF交AD的延长线于E,延长CD交BA的延长线于G,且DG=DE,AB=,CF=6.(1)求线段CD的长;(2)H在边BF上,且∠HDF=∠E,连接CH,求证:∠BCH=45°﹣∠EBC.6、如图,直角梯形ABCD中,AD∥BC,∠B=90°,∠D=45°.(1)若AB=6cm,,求梯形ABCD的面积;(2)若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点,且满足EF=GH,∠EFH=∠FHG,求证:HD=BE+BF.7、已知:如图,ABCD中,对角线AC,BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.(1)求证:AE=ED;(2)若AB=BC,求∠CAF的度数.8、已知:如图,在正方形ABCD中,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F.(1)求证:∠DAE=∠DCE;(2)当CG=CE时,试判断CF与EG之间有怎样的数量关系?并证明你的结论.9、如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.(1)求证:DP平分∠ADC;(2)若∠AEB=75°,AB=2,求△DFP的面积.10、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD=BC,E为CD的中点,交BC的延长线于F;(1)证明:EF=EA;(2)过D作DG⊥BC于G,连接EG,试证明:EG⊥AF.11、如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60度.以AD 为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.(1)求证:EB=EF;(2)延长FE交BC于点G,点G恰好是BC的中点,若AB=6,求BC的长.12、如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.(1)求证:AE=GF;(2)设AE=1,求四边形DEGF的面积.13、已知,如图在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC,连AG.(1)求证:FC=BE;(2)若AD=DC=2,求AG的长.14、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.(1)求证:AD=BE;(2)试判断△ABF的形状,并说明理由.15、(2011•潼南县)如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.(1)求证:AD=AE;(2)若AD=8,DC=4,求AB的长.16、如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.(1)求证:AE⊥BD;(2)若AD=4,BC=14,求EF的长.17、如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.(1)求证:CD=BE;(2)若AD=3,DC=4,求AE.18、如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=1,BC=4,求DC的长.19、已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且.(1)求证:BF=EF﹣ED;(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.20、如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.(1)若EF⊥AF,AF=4,AB=6,求AE的长.(2)若点F是CD的中点,求证:CE=BE﹣AD.21、如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.(1)求证:DH=(AD+BC);(2)若AC=6,求梯形ABCD的面积.22、已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE,BD.(1)求证:△AGE≌△DAB;(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.23、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.(1)试说明梯形ABCD是等腰梯形;(2)若AD=1,BC=3,DC=,试判断△DCF的形状;(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.24、如图,在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD=DC,E、F分别在AD、DC的延长线上,且DE=CF.AF交BE于P.(1)证明:△ABE≌△DAF;(2)求∠BPF的度数.25、如图,在梯形ABCD中,AD∥BC,AB=AD=DC,BD⊥DC,将BC延长至点F,使CF=CD.(1)求∠ABC的度数;(2)如果BC=8,求△DBF的面积?26、如图,梯形ABCD中,AD∥BC,AB=DC=10cm,AC交BD于G,且∠AGD=60°,E、F分别为CG、AB的中点.(1)求证:△AGD为正三角形;(2)求EF的长度.27、已知,如图,AD∥BC,∠ABC=90°,AB=BC,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F.(1)若∠BEC=75°,FC=3,求梯形ABCD的周长.(2)求证:ED=BE+FC.28、(2005•镇江)已知:如图,梯形ABCD中,AD∥BC,E是AB的中点,直线CE交DA的延长线于点F.(1)求证:△BCE≌△AFE;(2)若AB⊥BC且BC=4,AB=6,求EF的长.29、已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF 的延长线交DC于点E.求证:(1)△BFC≌△DFC;(2)AD=DE;(3)若△DEF的周长为6,AD=2,BC=5,求梯形ABCD的面积.30、如图,梯形ABCD中,AD∥BC.∠C=90°,且AB=AD.连接BD,过A点作BD的垂线,交BC于E.(1)求证:四边形ABED是菱形;(2)如果EC=3cm,CD=4cm,求梯形ABCD的面积.参考答案1、如图,等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,连接BE,CE(1)求证:BE=CE;(2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD.证明:(1)已知等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,∴AB=DC,∠BAE=∠CDE,AE=DE,∴△BAE≌△CDE,∴BE=CE;(2)延长CD和BE的延长线交于H,∵BF⊥CD,∠HEC=90°,∴∠EBF+∠H=∠ECH+∠H=90°∴∠EBF=∠ECH,又∠BEC=∠CEH=90°,BE=CE(已证),∴△BEG≌△CEH,∴EG=EH,BG=CH=DH+CD,∵△BAE≌△CDE(已证),∴∠AEB=∠GED,∠HED=∠AEB,∴∠GED=∠HED,又EG=EH(已证),ED=ED,∴△GED≌△HED,∴DG=DH,∴BG=DG+CD.2、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G 为CH的中点.(1)若HE=HG,求证:△EBH≌△GFC;(2)若CD=4,BH=1,求AD的长.(1)证明:∵HE=HG,∴∠HEG=∠HGE,∵∠HGE=∠FGC,∠BEH=∠HEG,∴∠BEH=∠FGC,∵G是HC的中点,∴HG=GC,∴HE=GC,∵∠HBE=∠CFG=90°.∴△EBH≌△GFC;(2)解:∵ED平分∠AEF,∠A=∠DFE=90°,∴AD=DF,∵DF=DC﹣FC,∵△EBH≌△GFC,∴FC=BH=1,∴AD=4﹣1=3.3、如图,梯形ABCD中,AB∥CD,AD=DC=BC,∠DAB=60°,E是对角线AC延长线上一点,F是AD延长线上的一点,且EB⊥AB,EF⊥AF.(1)当CE=1时,求△BCE的面积;(2)求证:BD=EF+CE.(2)过E点作EM⊥DB于点M,四边形FDME是矩形,FE=DM,∠BME=∠BCE=90°,∠BEC=∠MBE=60°,△BME≌△ECB,BM=CE,继而可证明BD=DM+BM=EF+CE.(1)解:∵AD=CD,∴∠DAC=∠DCA,∵DC∥AB,∴∠DCA=∠CAB,∴,∵DC∥AB,AD=BC,∴∠DAB=∠CBA=60°,∴∠ACB=180°﹣(∠CAB+∠CBA)=90°,∴∠BCE=180°﹣∠ACB=90°,∵BE⊥AB,∴∠ABE=90°,∴∠CBE=∠ABE﹣∠ABC=30°,在Rt△BCE中,BE=2CE=2,,∴…(5分)(2)证明:过E点作EM⊥DB于点M,∴四边形FDME是矩形,∴FE=DM,∵∠BME=∠BCE=90°,∠BEC=∠MBE=60°,∴△BME≌△ECB,∴BM=CE,∴BD=DM+BM=EF+CE…(10分)4、如图.在平行四边形ABCD中,O为对角线的交点,点E为线段BC延长线上的一点,且.过点E作EF∥CA,交CD于点F,连接OF.(1)求证:OF∥BC;(2)如果梯形OBEF是等腰梯形,判断四边形ABCD的形状,并给出证明.解答:(1)证明:延长EF交AD于G(如图),在平行四边形ABCD中,AD∥BC,AD=BC,∵EF∥CA,EG∥CA,∴四边形ACEG是平行四边形,∴AG=CE,又∵,AD=BC,∴,∴∠ADC=∠ECF,在△CEF和△DGF中,∵∠CFE=∠DFG,∠ADC=∠ECF,CE=DG,∴△CEF≌△DGF(AAS),∴CF=DF,∵四边形ABCD是平行四边形,∴OB=OD,∴OF∥BE.(2)解:如果梯形OBEF是等腰梯形,那么四边形ABCD是矩形.证明:∵OF∥CE,EF∥CO,∴四边形OCEF是平行四边形,∴EF=OC,又∵梯形OBEF是等腰梯形,∴BO=EF,∴OB=OC,∵四边形ABCD是平行四边形,∴AC=2OC,BD=2BO.∴AC=BD,∴平行四边形ABCD是矩形.5、如图,梯形ABCD中,AD∥BC,∠ABC=90°,BF⊥CD于F,延长BF交AD的延长线于E,延长CD交BA的延长线于G,且DG=DE,AB=,CF=6.(1)求线段CD的长;(2)H在边BF上,且∠HDF=∠E,连接CH,求证:∠BCH=45°﹣∠EBC.(1)解:连接BD,由∠ABC=90°,AD∥BC得∠GAD=90°,又∵BF⊥CD,∴∠DFE=90°又∵DG=DE,∠GDA=∠EDF,∴△GAD≌△EFD,∴DA=DF,又∵BD=BD,∴Rt△BAD≌Rt△BFD(HL),∴BF=BA=,∠ADB=∠BDF又∵CF=6,∴BC=,又∵AD∥BC,∴∠ADB=∠CBD,∴∠BDF=∠CBD,∴CD=CB=8.(2)证明:∵AD∥BC,∴∠E=∠CBF,∴∠HDF=∠CBF ,由(1)得,∠ADB=∠CBD ,∴∠HDB=∠HBD ,∴HD=HB ,由(1)得CD=CB ,CBD CDBCBD HDF CDB CBH∴∠=∠∴∠-∠=∠-∠∠∠∴即BDH=HBDHB=HD∴△CDH ≌△CBH ,∴∠DCH=∠BCH ,∴∠BCH=∠BCD==.6、如图,直角梯形ABCD 中,AD ∥BC ,∠B=90°,∠D=45°.(1)若AB=6cm ,,求梯形ABCD 的面积;(2)若E 、F 、G 、H 分别是梯形ABCD 的边AB 、BC 、CD 、DA 上一点,且满足EF=GH ,∠EFH=∠FHG ,求证:HD=BE+BF .解:(1)连AC ,过C 作CM ⊥AD 于M ,如图,在Rt △ABC 中,AB=6,sin ∠ACB==,∴AC=10,∴BC=8,在Rt △CDM 中,∠D=45°,∴DM=CM=AB=6,∴AD=6+8=14,∴梯形ABCD 的面积=•(8+14)•6=66(cm 2);(2)证明:过G 作GN ⊥AD ,如图,∵∠D=45°,∴△DNG 为等腰直角三角形,∴DN=GN ,又∵AD ∥BC ,∴∠BFH=∠FHN ,而∠EFH=∠FHG ,∴∠BFE=∠GHN ,∵EF=GH ,∴Rt △BEF ≌Rt △NGH ,∴BE=GN ,BF=HN ,∴DA=AN+DN=AN+DG=BF+BE .7、已知:如图,▱ABCD 中,对角线AC ,BD 相交于点O ,延长CD 至F ,使DF=CD ,连接BF 交AD 于点E .(1)求证:AE=ED;(2)若AB=BC,求∠CAF的度数.(1)证明:如图.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∵DF=CD,∴AB∥DF.∵DF=CD,∴AB=DF.∴四边形ABDF是平行四边形,∴AE=DE.(2)解:∵四边形ABCD是平行四边形,且AB=BC,∴四边形ABCD是菱形.∴AC⊥BD.∴∠COD=90°.∵四边形ABDF是平行四边形,∴AF∥BD.∴∠CAF=∠COD=90°.8、已知:如图,在正方形ABCD中,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F.(1)求证:∠DAE=∠DCE;(2)当CG=CE时,试判断CF与EG之间有怎样的数量关系?并证明你的结论.(1)证明:在△DAE和△DCE中,∠ADE=∠CDE(正方形的对角线平分对角),ED=DE(公共边),AE=CE(正方形的四条边长相等),∴△DAE≌△DCE (SAS),∴∠DAE=∠DCE(全等三角形的对应角相等);(2)解:如图,由(1)知,△DAE≌△DCE,∴AE=EC,∴∠EAC=∠ECA(等边对等角);又∵CG=CE(已知),∴∠G=∠CEG(等边对等角);而∠CEG=2∠EAC(外角定理),∠ECB=2∠CEG(外角定理),∴4∠EAC﹣∠ECA=∠ACB=45°,∴∠G=∠CEG=30°;过点C作CH⊥AG于点H,∴∠FCH=30°,∴在直角△ECH中,EH=CH,EG=2CH,在直角△FCH中,CH=CF,∴EG=2×CF=3CF.9、如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.(1)求证:DP平分∠ADC;(2)若∠AEB=75°,AB=2,求△DFP的面积.(1)证明:连接PC.∵ABCD是正方形,∴∠ABE=∠ADF=90°,AB=AD.∵BE=DF,∴△ABE≌△ADF.(SAS)∴∠BAE=∠DAF,AE=AF.∴∠EAF=∠BAD=90°.∵P是EF的中点,∴PA=EF,PC=EF,∴PA=PC.又AD=CD,PD公共,∴△PAD≌△PCD,(SSS)∴∠ADP=∠CDP,即DP平分∠ADC;(2)作PH⊥CF于H点.∵P是EF的中点,∴PH=EC.设EC=x.由(1)知△EAF是等腰直角三角形,∴∠AEF=45°,∴∠FEC=180°﹣45°﹣75°=60°,∴EF=2x,FC=x,BE=2﹣x.在Rt△ABE中,22+(2﹣x)2=(x)2解得x1=﹣2﹣2(舍去),x2=﹣2+2.∴PH=﹣1+,FD=(﹣2+2)﹣2=﹣2+4.∴S△DPF=(﹣2+4)×=3﹣5.10、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD=BC,E为CD的中点,交BC的延长线于F;(1)证明:EF=EA;(2)过D作DG⊥BC于G,连接EG,试证明:EG⊥AF.(1)证明:∵AD∥BC,∴∠DAE=∠F,∠ADE=∠FCE.∵E为CD的中点,∴ED=EC.∴△ADE≌△FCE.∴EF=EA.(5分)(2)解:连接GA,∵AD∥BC,∠ABC=90°,∴∠DAB=90°.∵DG⊥BC,∴四边形ABGD是矩形.∴BG=AD,GA=BD.∵BD=BC,∴GA=BC.由(1)得△ADE≌△FCE,∴AD=FC.∴GF=GC+FC=GC+AD=GC+BG=BC=GA.∵由(1)得EF=EA,∴EG⊥AF.(5分)11、如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60度.以AD 为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.(1)求证:EB=EF;(2)延长FE交BC于点G,点G恰好是BC的中点,若AB=6,求BC的长.(1)证明:∵△ADF为等边三角形,∴AF=AD,∠FAD=60°(1分)∵∠DAB=90°,∠EAD=15°,AD=AB(2分)∴∠FAE=∠BAE=75°,AB=AF,(3分)∵AE为公共边∴△FAE≌△BAE(4分)∴EF=EB(5分)(2)解:如图,连接EC.(6分)∵在等边三角形△ADF中,∴FD=FA,∵∠EAD=∠EDA=15°,∴ED=EA,∴EF是AD的垂直平分线,则∠EFA=∠EFD=30°.(7分)由(1)△FAE≌△BAE知∠EBA=∠EFA=30°.∵∠FAE=∠BAE=75°,∴∠BEA=∠BAE=∠FEA=75°,∴BE=BA=6.∵∠FEA+∠BEA+∠GEB=180°,∴∠GEB=30°,∵∠ABC=60°,∴∠GBE=30°∴GE=GB.(8分)∵点G是BC的中点,∴EG=CG∵∠CGE=∠GEB+∠GBE=60°,∴△CEG为等边三角形,∴∠CEG=60°,∴∠CEB=∠CEG+∠GEB=90°(9分)∴在Rt△CEB中,BC=2CE,BC2=CE2+BE2∴CE=,∴BC=(10分);解法二:过C作CQ⊥AB于Q,∵CQ=AB=AD=6,∵∠ABC=60°,∴BC=6÷=4.12、如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.(1)求证:AE=GF;(2)设AE=1,求四边形DEGF的面积.(1)证明:∵AB=DC,∴梯形ABCD为等腰梯形.∵∠C=60°,∴∠BAD=∠ADC=120°,又∵AB=AD,∴∠ABD=∠ADB=30°.∴∠DBC=∠ADB=30°.∴∠BDC=90°.(1分)由已知AE⊥BD,∴AE∥DC.(2分)又∵AE为等腰三角形ABD的高,∴E是BD的中点,∵F是DC的中点,∴EF∥BC.∴EF∥AD.∴四边形AEFD是平行四边形.(3分)∴AE=DF(4分)∵F是DC的中点,DG是梯形ABCD的高,∴GF=DF,(5分)∴AE=GF.(6分)(2)解:在Rt△AED中,∠ADB=30°,∵AE=1,∴AD=2.在Rt△DGC中∠C=60°,并且DC=AD=2,∴DG=.(8分)由(1)知:在平行四边形AEFD中EF=AD=2,又∵DG⊥BC,∴DG⊥EF,∴四边形DEGF的面积=EF•DG=.(10分)13、已知,如图在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC,连AG.(1)求证:FC=BE;(2)若AD=DC=2,求AG的长.解答:(1)证明:∵∠ABC=90°,DE⊥AC于点F,∴∠ABC=∠AFE.∵AC=AE,∠EAF=∠CAB,∴△ABC≌△AFE,∴AB=AF.∴AE﹣AB=AC﹣AF,即FC=BE;(2)解:∵AD=DC=2,DF⊥AC,∴AF=AC=AE.∴AG=CG,∴∠E=30°.∵∠EAD=90°,∴∠ADE=60°,∴∠FAD=∠E=30°,∴FC=,∵AD∥BC,∴∠ACG=∠FAD=30°,∴CG=2,∴AG=2.14、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.(1)求证:AD=BE;(2)试判断△ABF的形状,并说明理由.(1)证明:∵AD∥BC,∴∠BAD+∠ABC=180°,∵∠ABC=90°,∴∠BAD=∠ABC=90°,∵DE⊥EC,∴∠AED+∠BEC=90°∵∠AED+∠ADE=90°,∴∠BEC=∠ADE,∵∠DAE=∠EBC,AE=BC,∴△EAD≌△EBC,∴AD=BE.(2)答:△ABF是等腰直角三角形.理由是:延长AF交BC的延长线于M,∵AD∥BM,∴∠DAF=∠M,∵∠AFD=∠CFM,DF=FC,∴△ADF≌△MFC,∴AD=CM,∵AD=BE,∴BE=CM,∵AE=BC,∴AB=BM,∴△ABM是等腰直角三角形,∵△ADF≌△MFC,∴AF=FM,∴∠ABC=90°,∴BF⊥AM,BF=AM=AF,∴△AFB是等腰直角三角形.15、(2011•潼南县)如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.(1)求证:AD=AE;(2)若AD=8,DC=4,求AB的长.解答:(1)证明:连接AC,∵AB∥CD,∴∠ACD=∠BAC,∵AB=BC,∴∠ACB=∠BAC,∴∠ACD=∠ACB,∵AD⊥DC,AE⊥BC,∴∠D=∠AEC=90°,∵AC=AC,∴,∴△ADC≌△AEC,(AAS)∴AD=AE;(2)解:由(1)知:AD=AE,DC=EC,设AB=x,则BE=x﹣4,AE=8,在Rt△ABE中∠AEB=90°,由勾股定理得:82+(x﹣4)2=x2,解得:x=10,∴AB=10.说明:依据此评分标准,其它方法如:过点C作CF⊥AB用来证明和计算均可得分.16、如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.(1)求证:AE⊥BD;(2)若AD=4,BC=14,求EF的长.(1)证明:∵AD∥CB,∴∠ADB=∠CBD,又BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠ABD,∴AB=AD,∴△ABD是等腰三角形,已知E是BD的中点,∴AE⊥BD.(2)解:延长AE交BC于G,∵BD平分∠ABC,∴∠ABE=∠GBE,又∵AE⊥BD(已证),∴∠AEB=∠GEB,BE=BE,∴△ABE≌△GBE,∴AE=GE,BG=AB=AD,又F是AC的中点(已知),所以由三角形中位线定理得:EF=CG=(BC﹣BG)=(BC﹣AD)=×(14﹣4)=5.答:EF的长为5.17、如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.(1)求证:CD=BE;(2)若AD=3,DC=4,求AE.(1)证明:∵AD∥BC,∴∠DAC=∠BCE,而BE⊥AC,∴∠D=∠BEC=90°,AC=BC,∴△BCE≌△CAD.∴CD=BE.(2)解:在Rt△ADC中,根据勾股定理得AC==5,∵△BCE≌△CAD,∴CE=AD=3.∴AE=AC﹣CE=2.18、如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=1,BC=4,求DC的长.解:如图,过点D作DF∥AB,分别交AC,BC于点E,F.(1分)∵AB⊥AC,∴∠AED=∠BAC=90度.∵AD∥BC,∴∠DAE=180°﹣∠B﹣∠BAC=45度.在Rt△ABC中,∠BAC=90°,∠B=45°,BC=4,∴AC=BC•sin45°=4×=2(2分)在Rt△ADE中,∠AED=90°,∠DAE=45°,AD=1,∴DE=AE=.∴CE=AC﹣AE=.(4分)在Rt△DEC中,∠CED=90°,∴DC==.(5分)19、已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且.(1)求证:BF=EF﹣ED;(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.证明:∵FC=F′C,EC=EC,∠ECF'=∠BCF+∠DCE=∠ECF,∴△FCE≌△F′CE,∴EF′=EF=DF′+ED,∴BF=EF﹣ED;(2)解:∵AB=BC,∠B=80°,∴∠ACB=50°,由(1)得∠FEC=∠DEC=70°,∴∠ECB=70°,而∠B=∠BCD=80°,∴∠DCE=10°,∴∠BCF=30°,∴∠ACF=∠BCA﹣∠BCF=20°.20、如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.(1)若EF⊥AF,AF=4,AB=6,求AE的长.(2)若点F是CD的中点,求证:CE=BE﹣AD.解:(1)作EM⊥AB,交AB于点M.∵AE=BE,EM⊥AB,∴AM=BM=×6=3;∵∠AME=∠MAF=∠AFE=90°,∴四边形AMEF是矩形,∴EF=AM=3;在Rt△AFE中,AE==5;(2)延长AF、BC交于点N.∵AD∥EN,∴∠DAF=∠N;∵∠AFD=∠NFC,DF=FC,∴△ADF≌△NCF(AAS),∴AD=CN;∵∠B+∠N=90°,∠BAE+∠EAN=90°,又AE=BE,∠B=∠BAE,∴∠N=∠EAN,AE=EN,∴BE=EN=EC+CN=EC+AD,∴CE=BE﹣AD..21、如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.(1)求证:DH=(AD+BC);(2)若AC=6,求梯形ABCD的面积.解:(1)证明:过D作DE∥AC交BC延长线于E,(1分)∵AD∥BC,∴四边形ACED为平行四边形.(2分)∴CE=AD,DE=AC.∵四边形ABCD为等腰梯形,∴BD=AC=DE.∵AC⊥BD,∴DE⊥BD.∴△DBE为等腰直角三角形.(4分)∵DH⊥BC,∴DH=BE=(CE+BC)=(AD+BC).(5分)(2)∵AD=CE,∴.(7分)∵△DBE为等腰直角三角形BD=DE=6,∴.∴梯形ABCD的面积为18.(8分)注:此题解题方法并不唯一.22、已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE,BD.(1)求证:△AGE≌△DAB;(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.(1)证明:∵△ABC是等边三角形,DG∥BC,∴∠AGD=∠ABC=60°,∠ADG=∠ACB=60°,且∠BAC=60°,∴△AGD是等边三角形,AG=GD=AD,∠AGD=60°.∵DE=DC,∴GE=GD+DE=AD+DC=AC=AB,∵∠AGD=∠BAD,AG=AD,∴△AGE≌△DAB;(2)解:由(1)知AE=BD,∠ABD=∠AEG.∵EF∥DB,DG∥BC,∴四边形BFED是平行四边形.∴EF=BD,∴EF=AE.∵∠DBC=∠DEF,∴∠ABD+∠DBC=∠AEG+∠DEF,即∠AEF=∠ABC=60°.∴△AFE是等边三角形,∠AFE=60°.23、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.(1)试说明梯形ABCD是等腰梯形;(2)若AD=1,BC=3,DC=,试判断△DCF的形状;(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.解:(1)证明:∵EF=EC,∴∠EFC=∠ECF,∵EF∥AB,∴∠B=∠EFC,∴∠B=∠ECF,∴梯形ABCD是等腰梯形;(2)△DCF是等腰直角三角形,证明:∵DE=EC,EF=EC,∴EF=CD,∴△CDF是直角三角形(如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形),∵梯形ABCD是等腰梯形,∴CF=(BC﹣AD)=1,∵DC=,∴由勾股定理得:DF=1,∴△DCF是等腰直角三角形;(3)共四种情况:∵DF⊥BC,∴当PF=CF时,△PCD是等腰三角形,即PF=1,∴PB=1;当P与F重合时,△PCD是等腰三角形,∴PB=2;当PC=CD=(P在点C的左侧)时,△PCD是等腰三角形,∴PB=3﹣;当PC=CD=(P在点C的右侧)时,△PCD是等腰三角形,∴PB=3+.故共四种情况:PB=1,PB=2,PB=3﹣,PB=3+.(每个1分)24、如图,在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD=DC,E、F分别在AD、DC的延长线上,且DE=CF.AF交BE于P.(1)证明:△ABE≌△DAF;(2)求∠BPF的度数.解答:(1)证明:∵在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,∴AB=CD,∵AD=DC,∴BA=AD,∠BAE=∠ADF=120°,∵DE=CF,∴AE=DF,在△BAE和△ADF中,,∴△ABE≌△DAF(SAS).(2)解:∵由(1)△BAE≌△ADF,∴∠ABE=∠DAF.∴∠BPF=∠ABE+∠BAP=∠BAE.而AD∥BC,∠C=∠ABC=60°,∴∠BPF=120°.25、如图,在梯形ABCD中,AD∥BC,AB=AD=DC,BD⊥DC,将BC延长至点F,使CF=CD.(1)求∠ABC的度数;(2)如果BC=8,求△DBF的面积?解答:解:(1)∵AD∥BC,∴∠ADB=∠DBC,∵AB=AD,∴∠ADB=∠ABD,∴∠DBC=∠ABD,∵在梯形ABCD中AB=DC,∴∠ABC=∠DCB=2∠DBC,∵BD⊥DC,∴∠DBC+2∠DBC=90°∴∠DBC=30°∴∠ABC=60°(2)过点D作DH⊥BC,垂足为H,∵∠DBC=30°,BC=8,∴DC=4,∵CF=CD∴CF=4,∴BF=12,∵∠F+∠FDC=∠DCB=60°,∠F=∠FDC∴∠F=30°,∵∠DBC=30°,∴∠F=∠DBC,∴DB=DF,∴,在直角三角形DBH中,∴,∴,∴,即△DBF的面积为.26、如图,梯形ABCD中,AD∥BC,AB=DC=10cm,AC交BD于G,且∠AGD=60°,E、F分别为CG、AB的中点.(1)求证:△AGD为正三角形;(2)求EF的长度.(1)证明:连接BE,∵梯形ABCD中,AB=DC,∴AC=BD,可证△ABC≌△DCB,∴∠GCB=∠GBC,又∵∠BGC=∠AGD=60°∴△AGD为等边三角形,(2)解:∵BE为△BCG的中线,∴BE⊥AC,在Rt△ABE中,EF为斜边AB上的中线,∴EF=AB=5cm.27、已知,如图,AD∥BC,∠ABC=90°,AB=BC,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F.(1)若∠BEC=75°,FC=3,求梯形ABCD的周长.(2)求证:ED=BE+FC.解:(1)∵∠BEC=75°,∠ABC=90°,∴∠ECB=15°,∵∠ECD=45°,∴∠DCF=60°,在Rt△DFC中:∠DCF=60°,FC=3,∴DF=3,DC=6,由题得,四边形ABFD是矩形,∴AB=DF=3,∵AB=BC,∴BC=3,∴BF=BC﹣FC=3﹣3,∴AD=DF=3﹣3,∴C梯形ABCD=3×2+6+3﹣3=9+3,答:梯形ABCD的周长是9+3.(2)过点C作CM垂直AD的延长线于M,再延长DM到N,使MN=BE,∴CN=CE,可证∠NCD=∠DCE,∵CD=CD,∴△DEC≌△DNC,∴ED=EN,∴ED=BE+FC.28、(2005•镇江)已知:如图,梯形ABCD中,AD∥BC,E是AB的中点,直线CE交DA的延长线于点F.(1)求证:△BCE≌△AFE;(2)若AB⊥BC且BC=4,AB=6,求EF的长.(1)证明:∵AD∥BC,E是AB的中点,∴AE=BE,∠B=∠EAF,∠BCE=∠F.∴△BCE≌△AFE(AAS).(2)解:∵AD∥BC,∴∠DAB=∠ABC=90°.∵AE=BE,∠AEF=∠BEC,∴△BCE≌△AFE.∴AF=BC=4.∵EF2=AF2+AE2=9+16=25,∴EF=5.29、已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF 的延长线交DC于点E.求证:(1)△BFC≌△DFC;(2)AD=DE;(3)若△DEF的周长为6,AD=2,BC=5,求梯形ABCD的面积.(1)∵DC=BC,∠1=∠2,CF=CF,∴△DCF≌△BCF.(2)延长DF交BC于G,∵AD∥BG,AB∥DG,∴四边形ABGD为平行四边形.∴AD=BG.∵△DFC≌△BFC,∴∠EDF=∠GBF,DF=BF.又∵∠3=∠4,∴△DFE≌△BFG.∴DE=BG,EF=GF.∴AD=DE.(3)∵EF=GF,DF=BF,∴EF+BF=GF+DF,即:BE=DG.∵DG=AB,∴BE=AB.∵C△DFE=DF+FE+DE=6,∴BF+FE+DE=6,即:EB+DE=6.∴AB+AD=6.又∵AD=2,∴AB=4.∴DG=AB=4.∵BG=AD=2,∴GC=BC﹣BG=5﹣2=3.又∵DC=BC=5,在△DGC中∵42+32=52∴DG2+GC2=DC2∴∠DGC=90°.∴S梯形ABCD=(AD+BC)•DG=(2+5)×4=14.30、如图,梯形ABCD中,AD∥BC.∠C=90°,且AB=AD.连接BD,过A点作BD的垂线,交BC于E.(1)求证:四边形ABED是菱形;(2)如果EC=3cm,CD=4cm,求梯形ABCD的面积.解答:解:(1)证明:∵AD∥BC,DE2=CD2+CE2=42+32=25,∴∠OAD=∠OEB,∴DE=5又∵AB=AD,AO⊥BD,∴AD=BE=5,∴OB=OD,∴S梯形ABCD=.又∵∠AOD=∠EOB,∴△ADO≌△EBO(AAS),∴AD=EB,又∵AD∥BE,∴四边形ABCD是平行四边形,又∵AB=AD∴四边形ABCD是菱形.(2)∵四边形ABCD是菱形,∴AD=DE=BE,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆中考数学第24题专题训练【典题1】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G为CH的中点,且∠BEH=∠HEG.(1)若HE=HG,求证:△EBH≌△GFC;(2)若CD=4,BH=1,求AD的长.(1)证明:∵HE=HG,∴∠HEG=∠HGE,∵∠HGE=∠FGC,∠BEH=∠HEG,∴∠BEH=∠FGC,∵G是HC的中点,∴HG=GC,∴HE=GC,∵∠HBE=∠CFG=90°.∴△EBH≌△GFC;(2)解:过点H作HI⊥EG于I,∵G为CH的中点,∴HG=GC,∵EF⊥DC,HI⊥EF,∴∠HIG=∠GFC=90°,∠FGC=∠HGI,∴△GIH≌△GFC,∵△EBH≌△EIH(AAS),∴FC=HI=BH=1,∴AD=4-1=3.【典题2】已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向形外作等边△ABD和等边△ACE.(1)如图1,连接线段BE、CD.求证:BE=CD;(2)如图2,连接DE交AB于点F.求证:F为DE中点.证明:(1)∵△ABD和△ACE是等边三角形,∴AB=AD,AC=AE,∠DAB=∠EAC=60°,∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,在△DAC和△BAE中,AC=AE ∠DAC=∠BAE AD=AB ,∴△DAC≌△BAE(SAS),∴DC=BE;(2)如图,作DG∥AE,交AB于点G,由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,∴∠DGF=∠FAE=90°,又∵∠ACB=90°,∠CAB=30°,∴∠ABC=60°,又∵△ABD为等边三角形,∠DBG=60°,DB=AB,∴∠DBG=∠ABC=60°,在△DGB和△ACB中,∠DGB=∠ACB ∠DBG=∠ABC DB=AB ,∴△DGB≌△ACB(AAS),∴DG=AC,又∵△AEC为等边三角形,∴AE=AC,∴DG=AE,在△DGF和△EAF中,∠DGF=∠EAF ∠DFG=∠EFA DG=EA ,∴△DGF≌△EAF(AAS),∴DF=EF,即F为DE中点.【典题3】如图,在梯形ABCD中,AD∥BC,∠C=90°,E为CD的中点,EF∥AB交BC于点F (1)求证:BF=AD+CF;(2)当AD=1,BC=7,且BE平分∠ABC时,求EF的长.(1)证明:如图(1),延长AD交FE的延长线于N∵∠NDE=∠FCE=90°∠DEN=∠FECDE=EC∴△NDE≌△FCE∴DN=CF∵AB∥FN,AN∥BF∴四边形ABFN是平行四边形∴BF=AD+DN=AD+FC(2)解:∵AB∥EF,∴∠ABN=∠EFC,即∠1+∠2=∠3,又∵∠2+∠BEF=∠3,∴∠1=∠BEF,∴BF=EF,∵∠1=∠2,∴∠BEF=∠2,∴EF=BF,又∵ BC+AD=7+1∴ BF+CF+AD=8而由(1)知CF+AD=BF∴ BF+BF=8∴2BF=8,∴BF=4,∴BF=EF=4【典题4】在等腰梯形ABCD中,AD∥BC,AB=AD=CD,∠ABC=60°,延长AD到E,使DE=AD,延长DC到F,使DC=CF,连接BE、BF和EF.⑴求证:△ABE≌△CFB;⑵如果AD=6,tan∠EBC的值.解:(1)证明:连结CE,在△BAE与△FCB中,∵ BA=FC,∠A=∠BCF,, AE=BC,∴△BAE≌△FCB;(2)延长BC交EF于点G,作AH⊥BG于H,作AM⊥BG,∵△BAE≌△FCB,∴∠AEB=∠FBG,BE=BF,∴△BEF为等腰三角形,又∵AE∥BC,∴∠AEB=∠EBG,∴∠EBG=∠FBG,∴BG⊥EF,∵∠AMG=∠EGM=∠AEG=90°,∴四边形AMGE为矩形,∴AM=EG,在Rt△ABM中,AB DECFAM=AB •sin60°=6× 23 =33 ,∴EG=AM=33,BG=BM+MG=6×2+6×cos60°=15,∴tan ∠EBC=531533==BGEG 【典题5】已知:AC 是矩形ABCD 的对角线,延长CB 至E ,使CE=CA ,F 是AE 的中点,连接DF 、CF 分别交AB 于G 、H 点(1)求证:FG=FH ;(2)若∠E=60°,且AE=8时,求梯形AECD 的面积.(1)证明:连接BF∵ABCD 为矩形∴AB ⊥BC AB ⊥AD AD=BC∴△ABE 为直角三角形∵F 是AE 的中点∴AF=BF=BE∴∠FAB=∠FBA∴∠DAF=∠CBF∵ AD=BC, ∠DAF=∠CBF ,AF=BF ,∴△DAF ≌△CBF∴∠ADF=∠BCF∴∠FDC=∠FCD∴∠FGH=∠FHG∴FG=FH ;(2)解:∵AC=CE ∠E=60° ∴△ACE 为等边三角形∴CE=AE=8∵AB ⊥BC∴BC=BE=CE21=4∴根据勾股定理AB=34∴梯形AECD 的面积=21×(AD+CE)×CD=21×(4+8)×34=324【典题6】如图,直角梯形ABCD 中,AD ∥BC ,∠BCD=90°,且CD=2AD ,tan ∠ABC=2,过点D 作DE ∥AB ,交∠BCD 的平分线于点E ,连接BE .(1)求证:BC=CD ;(2)将△BCE 绕点C ,顺时针旋转90°得到△DCG ,连接EG .求证:CD 垂直平分EG ;(3)延长BE 交CD 于点P .求证:P 是CD 的中点.证明:(1)延长DE 交BC 于F ,∵AD ∥BC ,AB ∥DF ,∴AD=BF ,∠ABC=∠DFC .在Rt △DCF 中,∵tan ∠DFC=tan ∠ABC=2, ∴CF CD=2,即CD=2CF ,∵CD=2AD=2BF ,∴BF=CF ,∴BC=BF+CF=21CD+21CD=CD .即BC=CD .(2)∵CE 平分∠BCD ,∴∠BCE=∠DCE ,由(1)知BC=CD ,∵CE=CE ,∴△BCE ≌△DCE ,∴BE=DE ,由图形旋转的性质知CE=CG ,BE=DG ,∴DE=DG ,∴C ,D 都在EG 的垂直平分线上,∴CD 垂直平分EG .(3)连接BD ,由(2)知BE=DE ,∴∠1=∠2.∵AB ∥DE ,∴∠3=∠2.∴∠1=∠3.∵AD ∥BC ,∴∠4=∠DBC .由(1)知BC=CD ,∴∠DBC=∠BDC ,∴∠4=∠BDP .又∵BD=BD ,∴△BAD ≌△BPD(ASA)∴DP=AD .∵AD=21CD ,∴DP=21CD .∴P 是CD 的中点.【典题7】如图,直角梯形ABCD 中,∠DAB=90°,AB ∥CD ,AB=AD ,∠ABC=60度.以AD 为边在直角梯形ABCD 外作等边三角形ADF ,点E 是直角梯形ABCD 内一点,且∠EAD=∠EDA=15°,连接EB 、EF .(1)求证:EB=EF ;(2)延长FE 交BC 于点G ,点G 恰好是BC 的中点,若AB=6,求BC 的长.(1)证明:∵△ADF 为等边三角形,∴AF=AD ,∠FAD=60°∵∠DAB=90°,∠EAD=15°,AD=AB∴∠FAE=∠BAE=75°,AB=AF ,∵AE 为公共边∴△FAE ≌△BAE∴EF=EB(2)过C 作CQ ⊥AB 于Q ,∵CQ=AB=AD=6,∵∠ABC=60°,∴BC=6÷ 23 =34.【典题8】已知,矩形ABCD 中,延长BC 至E ,使BE=BD ,F 为DE 的中点,连结AF 、CF.求证:(1)∠ADF=∠BCF ;(2) AF ⊥CF.证明:(1)在矩形ABCD 中,∵∠ADC=∠BCD=90°,∴∠DCE=90°,在Rt △DCE 中,∵F 为DE 中点,∴DF=CF ,∴∠FDC=∠DCF ,∴∠ADC+∠CDF=∠BCD+∠DCF ,即∠ADF=∠BCF ;(2)连接BF ,∵BE=BD ,F 为DE 的中点,∴BF ⊥DE ,∴∠BFD=90°,即∠BFA+∠AFD=90°,在△AFD 和△BFC 中 AD=BC ∠ADF=∠BCF CF=DF ,∴△ADF ≌△BCF ,∴∠AFD=∠BFC ,∵∠AFD+∠BFA=90°,∴∠BFC+∠BFA=90°,即∠AFC=90°,∴AF ⊥FC .【典题9】如图,在直角梯形ABCD 中,AD ⊥DC ,AB ∥DC ,AB=BC ,AD与BC 延长线交于点F ,G 是DC 延长线上一点,AG ⊥BC 于E .(1)求证:CF=CG ;(2)连接DE ,若BE=4CE ,CD=2,求DE 的长.解答:(1)证明:连接AC ,∵DC ∥AB ,AB=BC ,∴∠1=∠CAB ,∠CAB=∠2,∴∠1=∠2;∵∠ADC=∠AEC=90°,AC=AC ,∴△ADC ≌△AEC ,∴CD=CE ;∵∠FDC=∠GEC=90°,∠3=∠4,∴△FDC ≌△GEC ,∴CF=CG .(2)解:由(1)知,CE=CD=2,∴BE=4CE=8,∴AB=BC=CE+BE=10,∴在Rt △ABE 中,AE= AB 2-BE 2 =6,∴在Rt △ACE 中,AC= AE 2+CE 2 =102由(1)知,△ADC ≌△AEC ,∴CD=CE ,AD=AE ,∴C 、A 分别是DE 垂直平分线上的点,∴DE ⊥AC ,DE=2EH ;(8分)在Rt △AEC 中,S △AEC =21 AE •CE=21AC •EH , ∴EH=AC CEAE ⋅ =10226⨯ =5103∴DE=2EH=2×5103=5106【典题10】如图,在正方形ABCD 中,E 、F 分别为BC 、AB 上两点,且BE=BF ,过点B 作AE 的垂线交AC 于点G ,过点G 作CF 的垂线交BC 于点H 延长线段AE 、GH 交于点M .(1)求证:∠BFC=∠BEA ;(2)求证:AM=BG+GM .证明:(1)在正方形ABCD 中,AB=BC ,∠ABC=90°,在△ABE 和△CBF 中,AB=BC ∠ABC=∠ABC BE=BF ,∴△ABE ≌△CBF (SAS ),∴∠BFC=∠BEA ;(2)连接DG ,在△ABG 和△ADG 中,AB=AD ∠DAC=∠BAC=45° AG=AG ,∴△ABG ≌△ADG (SAS ),∴BG=DG ,∠2=∠3,∵BG ⊥AE ,∴∠BAE+∠2=90°,∵∠BAD=∠BAE+∠4=90°,∴∠2=∠3=∠4,∵GM⊥CF,∴∠BCF+∠1=90°,又∠BCF+∠BFC=90°,∴∠1=∠BFC=∠2,∴∠1=∠3,在△ADG中,∠DGC=∠3+45°,∴∠DGC也是△CGH的外角,∴D、G、M三点共线,∵∠3=∠4(已证),∴AM=DM,∵DM=DG+GM=BG+GM,∴AM=BG+GM.【典题11】直角梯形ABCD中,AB∥CD,∠C=90°,AB=BC,M为BC边上一点.(1)若∠DMC=45°,求证:AD=AM.(2)若∠DAM=45°,AB=7,CD=4,求BM的值.(1)证明:作AF⊥CD交延长线于点F.∵∠DMC=45°,∠C=90°∴CM=CD,又∵∠B=∠C=∠AFD=90°,AB=BC,∴四边形ABCF为正方形,∴BC=CF,∴BM=DF,在Rt△ABM和Rt△AFD中,AB=AF,∠B=∠AFD=90°,BM=DF,∴△ABM≌△AFD,∴AD=AM.(2)解:把Rt△ABM绕点A顺时针旋转90°,使AB与AE重合,得Rt△AFN.∵∠DAM=45°,∴∠BAM+∠DAF=45°,由旋转知∠BAM=∠NAF,∴∠DAF+∠NAF=45°,即∠DAM=∠DAN,由旋转知AM=AN,∴△ADM≌△ADN,∴DM=DN,设BM=x,∵AB=BC=CF=7,∴CM=7-x又∵CD=4,∴DF=3,BM=FN=x,∴MD=DN=3+x,在Rt △CDM 中,(7-x )2+42=(3+x )2, 解得:x=514∴BM 的值为514.答:BM 的值为514.【典题12】如图,AC 是正方形ABCD 的对角线,点O 是AC 的中点,点Q 是AB 上一点,连接CQ ,DP ⊥CQ 于点E ,交BC 于点P ,连接OP ,OQ ;求证:(1)△BCQ ≌△CDP ;(2)OP=OQ .证明:∵四边形ABCD 是正方形,∴∠B=∠PCD=90°,BC=CD ,∴∠2+∠3=90°,又∵DP ⊥CQ ,∴∠2+∠1=90°,∴∠1=∠3,在△BCQ 和△CDP 中,∠B=∠PCD BC=CD ∠1=∠3 .∴△BCQ ≌△CDP .(2)连接OB .由(1):△BCQ ≌△CDP 可知:BQ=PC ,∵四边形ABCD 是正方形,∴∠ABC=90°,AB=BC ,而点O 是AC 中点, ∴BO=21AC=CO ,∠4=21∠ABC=45°=∠PCO ,在△BCQ 和△CDP 中, BQ=CP ∠4=∠PCO BO=CO∴△BOQ ≌△COP ,∴OQ=OP .。
