房室模型的综述
经典房室模型理论
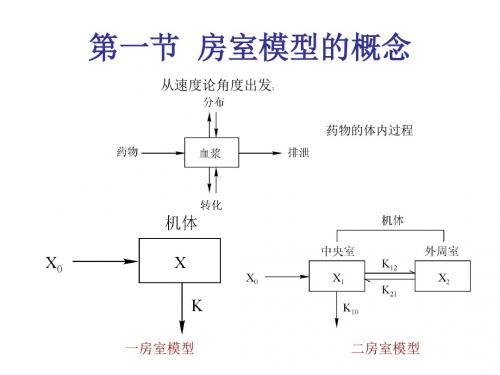
三. 房室模型的判别与选择
2 ˆ • 1.残差平方和法 Re= (Ci Ci ) i 1 n
ˆ 为拟合浓度,Re→0最好 Ci为实测浓度,C i
• 2.拟合度法: r2→1 最好
• 3.AIC法:AIC=NlnRe + 2P •
关于房室模型拟合中的权重问题
• 1 Wi=1
• 2
• 3
Wi=1/Ci
Wi=1/Ci2
四 药动学参数的生理及临床意义
60.00 50.00 40.00 30.00 20.00 10.00 0.00 0.00 2.00 4.00 6.00 8.00 10.00 12.00 14.00
• 1 tmax 与 Cmax • 二者是反映药物吸收快慢的两个重要指 标,常被用于制剂的质量评价,药物经 血管外给药吸收后的血药浓度最大值称 药峰浓度(Cmax),达到Cmax所需时 间为浓度达峰时间tmax。
x x Le
kt
k0 kt (1 e ) k
(iv项) (inf. 项) 当t→∞时,x→x2,e-kt→0
即为负荷剂量的计算方法。
k0 x2 k
四、血管外给药的动力学
体内药量变化为:
k x dx k a x a kx sx 0 k a x a kx x a a dt sk
,
(二)静脉滴注给药的药动学参数 计算
1.达稳态后停止滴注 经整理得
C
k0 kV(s k )
k 0 kt e t′为滴注后时间 kV k k logC log 0 t kV 2.303 经线性回归,由斜率得k值,由截距得V值。 拉氏逆变换 C
k a Fx0 x kat kt C (e e ) V V (k a k )
房室模型的划分依据和动力学特征

房室模型的划分依据和动力学特征示例文章篇一:《房室模型的划分依据和动力学特征》嘿,你知道吗?在我们探索身体里那些奇妙的变化呀,有个特别有趣又超级有用的东西叫房室模型呢。
我就先说说啥是房室模型吧。
你可以把我们的身体想象成一个大城堡,这个城堡里呢,有不同的房间。
每个房间就像是一个房室。
房室模型就是科学家们想出来的一种办法,用来描述药物在我们身体这个大城堡里是怎么跑来跑去的。
那房室模型的划分依据是啥呢?这就好比我们要把城堡里的房间分类。
有些房间可能挨得特别近,药物在它们之间跑得就特别快,就像在同一个小院子里的屋子似的。
比如说,我们的血液就像城堡里的一条大河,那些和血液关系特别紧密的地方,药物一进去就能快速到达,这就可能被划分成一个房室。
像我们的心脏、血管这些地方,药物一下子就能在里面扩散开,那它们就可能被看作是一个房室。
还有啊,如果有一些组织器官,它们对药物的吸收啊、分布啊的速度差不多,那它们也能被划到同一个房室里。
就像城堡里的一些功能相似的小角落,它们对待客人(药物)的态度很相似,那就把它们归为一类啦。
这就好比厨房和餐厅,总是有很多东西在它们之间来来去去,速度也差不多,就可以算是一种类型的房室。
再讲讲房室模型的动力学特征吧。
这就像在城堡里,每个房间都有自己独特的规则来迎接和送走客人。
比如说一房室模型,药物进入身体这个城堡后,就像一个小探险家在一个大房间里跑来跑去。
这个小探险家(药物)在这个大房间(一房室)里的运动速度是有一定规律的。
它可能会均匀地分散在这个房室里,就像你把一把沙子撒在一个大盒子里,慢慢地沙子就会均匀分布一样。
这个时候呢,药物的浓度变化是按照一定的数学公式来的。
如果用一个简单的比喻,就像是一个小水滴在一个平静的小池塘里,慢慢地扩散开来,它的扩散速度是有规律可循的。
二房室模型就更有趣了。
就像城堡里有两个不同的区域,一个可能是中心区域,一个是边缘区域。
药物先进入中心区域,这个中心区域就像是城堡里的大厅,药物在大厅里一下子就能散开,浓度变化比较快。
房室模型

1
~ 由上式, 再由较小的 ti 及算出的 c1 (ti ),同样的方法估计出 和B.
2.确定k12, k21,k13
因为 t 时, c1 (t ), c2 (t ) 0, 药物全部排除 , 所以 D0 k13V1 c1 (t )dt, 结合 (6)式就可以得到
参数估计
我们以快速静脉注射的给药方式为例估计参数.先估计 (6)式中的α,β,A,B,再确定k12, k21,k13. 1.计算α,β,A,B 不妨设α<β,则当t充分大,解近似为
c1 (t ) Ae t 或ln c1 (t ) ln A t.对于充分大的它及 ti 测得的c1 (ti ), 用最小二乘法就可估计 , ln A和A. 出
0
D0 k13V1 (
A
B
).
D0 又c1 (0) A B, 结合上式就可以得到 V1
( A B ) k13 . B A
再由 3)式就可得到 21 ( k
k13
, k12 k13 k21.
t充分大?
实际情形:停止滴注后?
3.口服或肌肉注射
这种给药方式相当于在药物进入中心室之前有一个将药物吸 收进入血液的过程,可以简化为有一个给药室.药物由吸收室进 入中心室的转移速率系数为k01,因此
x0 (t ) k x0 , x0 (0) D0 . 其解为 (t ) D0e x
f 0 (t ) 0, c1 (0) D0 , c 2 (0) 0 V1 (5)
在初始条件(5)下,我们可以求得微分方程(2)的解为
房室模型[汇总]
![房室模型[汇总]](https://img.taocdn.com/s3/m/4669a0fc80c758f5f61fb7360b4c2e3f57272582.png)
§3 房室模型[问题的提出]药物进入机体后,在随血液输运到各个器官和组织的过程中,不断地被吸收、分布、代谢,最终排出体外.药物在血液中的浓度,即单位体积血液(毫升)中药物含量(毫克或微克),称血药浓度,随时间和空间(机体的各部分)而变化.血药浓度的大小直接影响到药物的疗效,浓度太低不能达到预期的效果,浓度太高又可能导致药物中毒、副作用太强或造成浪费.因此研究药物在体内吸收、分布和排除的动态过程,及这些过程与药理反应间的定量关系,对于新药研制、剂量确定、给药方案设计等药理学和临床医学的发展都具有重要的指导意义和实用价值.这个学科分支称药物动力学.建立房室模型(Compannlent Model)是药物动力学研究上述动态过程的基本步骤之一.所谓房室是指机体的一部分,药物在一个房室内呈均匀分布,即血药浓度是常数,而在不同房室之间则按照一定规律进行药物的转移.一个机体分为几个房室,要看不同药物的吸收、分布、排除过程的具体情况,以及研究对象所要求的精度而定.本节只讨论二室模型,即将机体分为血液较丰富的中心室(包括心、肺、肾等器官)和血液较贫乏的周边室(四肢、肌肉组织等).药物的动态过程在每个房室内是一致的,转移只在两个房室之间以及某个房室与体外之间进行.二室模型的建立和求解方法可以推广到多室模型.显然,将一个机体划分为若干房室是人们为了研究目的所做的简化.值得庆幸的是,这种简化在一定条下已由临床试验证明是正确的,为医学界和药理学界所接受.[模型的假设] 1.机体分为中心室( 室)和周边室( 室),两个室的容积(即血液体积或药物分布容积)在过程中保持不变;2.药物从一室向另一室的转移速率,及向体外的排除速率,与该室的血药浓度成正比;3.只有中心室与体外有药物交换,即药物从体外进人中心室,最后又从中心室排出体外.与转移和排除的数量相比药物的吸收可以忽略.在这些假设下的一种二室模型示意图如下,)(),(t x t c i i 和i V 分别表示第i 室)2,1(=i 的血药浓度、药量和容积,12k 和21k 是两室之间药物转移速率系数,13k 是药物从I 室向体外排除的速率系数.)(0t f 是给药速率,由给药方式和剂量确定.这种速率系数为常数的房室模型称乳突状模型.[模型的建立] 根据假设条件和上图可以写出两个房室中药量)(),(21t x t x 满足的微分方程.)(1t x 的变化率由I 室向Ⅱ室的转移12k -1x ,I 室向体外的排除113x k -,Ⅱ室向I 室的转移是221x k ,及给药)(0t f 组成;)(2t x 的变化率由I 室向Ⅱ室的转移112x k 及Ⅱ室向I 室的转移221,x k -组成.于是有)(t x i 与血药浓度)(t c i 、房室容积i V 之间显然有关系式(2)代人(1)式可得这是线性常系数非齐次方程,它的解由齐次方程的通解和非齐次方程的特解组成.其对应齐次方程的通解为:其中βα,由确定.为了得到非齐次方程的特解从而解出(3),需要设定给药速率)(0t f 和初始条件.我们考察下面几种常见的给药方式.1.快速静脉注射这种注射可简化为在0=t 的瞬时将剂量0D 的药物输入中心室,血药浓度立即上升为10/V D ,于是)(0t f 和初始条件为方程(3)在条件(6)下的解为其中βα,由(5)确定.可以看出当∞→t 时0)(,0)(21→→t c t c .2.恒速静脉滴注 当静脉滴注的速率为常数是0k 时,)(0t f 和初始条件为方程(3)在条件(9)下的解可表示为其中常数11,B A 由初始条件0)0()0(21==c c 确定. 当t 充分大时)(),(21t c t c 将趋向于(10)式右端第3项表示的常值.实际上,若T t =后停止滴注,那么)(),(21t c t c 在T t >以后将按指数规律衰减并趋于零.3.口服或肌肉注射这种给药方式相当于在药物输入中心室之前先有一个将药物吸收人血掖的过程,可以简化为有一个吸收室,如图16.)(0t x 为吸收室的药量,药物由吸收室进人中心室的转移速率系数为01k ,于是)(0t x 满足0D 是给药量.而药物进人中心室的速率为将方程(11)的解代人(12)式得在这种情况下方程(3)的解)(1t c 的一般形式为(设βα,01≠k ).其中系数A ,B ,,E 正由初始条件0)0()0(21==c c 确定.从以上的讨论可以看出,中心室的血药浓度)(1t c 取决于转移速率系数132112,,k k k ,房室容积21,V V 以及输入参数00,k D 等因素,而房室模型的用途恰是通过对)(1t c 的量测,确定对于药理学和临床医学最为重要的参数,如转移速率系数,特别是从中心室向体外排除的速率系数13k .下面介绍在快速静脉注射给药方式下估计诸参数的方法.[参数估计] 在0=t 瞬时快速注射剂量为0D 的药物以后,在一系列时刻),2,1(n i t i ,⋯=从中心室采取血样并获得血药浓度)(1t c ,根据这些数据利用 (7),(5)式估计参数132112,,k k k 的过程可分两步:先计算(7)式中的B A ,,,βα再确定132112,,k k k .1.计算B A ,,,βα 不妨设βα<,于是当t 充分大时(7)式近似为或对于适当大的i t 和相应的)(1t c ,用最小二乘法不难估计出α,1nA 和A .然后计算再利用(7)式得对于较小的i t 和由(17)式算出的)(1i t c ,仍用最小二乘法即可得到β和B .2.确定132112,,k k k因为∞→t 时0)(),(21→t c t c ,进人中心室的药物全部被排除,所以将(7)代人(19)式可得又因为联合(20),(21)式解出再利用(5)式即可确定这就完成了根据中心室血药浓度的量测数据,估计转移和排除速率系数的过程.[ 评注] 建立房室模型的目的是研究体内血药浓度的变化过程,确定诸如转移和排除速率系数等参数,为制订给药方案和剂量大小提供数量依据.建模过程是将机理分析和测试分析相结合,先由机理分析确定方程形式,再由测试数据估计参数.选用几个房室建模是一个重要问题,可以先选择一室模型,其计算非常简单.不满意时再采用二室或多室模型,甚至非线性房室模型.常见的一种非线性模型(以一室为例)是12111.)(c k c k t c +-=,当1c 较小时它近似于线性模型;称为一级排除过程,而当1c 较大时)(1.t c 近似于常数,称为零级排除过程,所以它表示了一种混合型的排除过程.。
房室模型及其划分的依据

房室模型及其划分的依据
《房室模型及其划分的依据》
房室模型是描述心脏结构和功能的一种常用方法,它通过将心脏分为房室两个腔进行建模,以便更好地了解心脏的运作原理。
房室模型的划分依据主要有以下几个方面。
1. 解剖学划分:
心脏是由四个腔室组成,包括左右心房和左右心室。
心脏的左心室和右心室分别负责将氧合血液和非氧合血液泵送到全身。
心脏的左心房和右心房则接受相应腔室的血液,将其注入相应腔室,维持心血管循环的正常运转。
2. 功能学划分:
心脏的左边和右边在解剖结构上有所不同,也反映在其功能上。
左心室是心脏最大的腔室,主要承担将氧合血液泵送到全身的功能,所以它的肌肉更加强壮,收缩更有力。
右心室则较小,将经肺循环氧合后的血液泵送到肺部。
3. 血液流动的方向:
心脏内部的血液流动方向也成为划分的依据之一。
血液在心脏内外来回流动,其中两个心房接受血液,两个心室将血液泵出。
心房和心室之间通过房室瓣膜相隔开来,控制血液流动的方向。
4. 协同收缩和舒张:
心脏的房室周期性地进行收缩和舒张,以维持正常的心血管功能。
一次收缩和舒张过程称为一个心搏。
房室模型的划分也可以根据心脏收缩的节律和协同进行,从而更好地理解心脏的工作原理。
综上所述,《房室模型及其划分的依据》主要根据心脏的解剖学结构、功能学特点、血液流动方向以及协同收缩和舒张等方面进行了划分,这种模型的建立有助于我们更好地了解心脏的工作原理,并在临床上应用于心血管疾病的诊断和治疗。
4房室模型

(三)静脉注射加静脉滴注给药的动力学
由前式可知CssV=k/k0,故负荷剂量可按下式计算
• (四). 血管外途径给药动力学 • 1.模型的建立及其动力学特征
一房室模型血管外给药后的血药浓度-时间曲线
• 血管外给药的动力学特性: • (1).血药浓度-时间曲线为一条双指数曲 线,这条双指数曲线可以看成是由两条具 有相同截距的直线相减而成C=Ie-kt-Ie-kat, 其中
第四章 房室模型
• 药物动力学研究的主要目标就是揭示药物 在体内的动态变化规律性。药物在体内经 历吸收(absorption)、分布 (distribution)、代谢(metabolism) 和排泄(excretion)过程的处置(如图41所示),自始至终都处于动态变化之中, 且药物的体内处置过程较为复杂,受到体 内外诸多因素的影响。
我们可以根据体液的分布情况,由药物的分布容积 可以粗略地推测其在体内的大致分布情况
• 如一个药物的Vd为3~5升左右,那么这个药物可 能主要分布于血液并与血浆蛋白大量结合,如双 香豆素、苯妥英钠和保泰松等;如一个药物的Vd 为10~20升左右,则说明这个药物主要分布于血 浆和细胞外液,这类药物往往不易通过细胞膜, 因此无法进入细胞内液,如溴化物和碘化物等; 如一个药物的分布容积为40升,则这个药物可以 分布于血浆和细胞内、外液,表明其在体内的分 布较广,如安替比林;有些药物的Vd非常大,可 以达到100升以上,这一体积已远远地超过了体 液的总容积,这类药物在体内往往有特异性的组 织分布,如硫喷妥钠具有较高的脂溶性,可以大 量地分布于脂肪组织,而I131可以大量地浓集于甲 状腺,因而其分布容积也很大。由此可见我们可 以通过分布容积来了解药物在体内的分布情况。
药物的体内处置过程
房室模型名词解释

房室模型是心脏解剖和心脏电活动的一种简化模型,用于描述心脏内部的结构和电流传导路径。
在房室模型中,心脏被分为两个主要部分:心房和心室。
心房是上部的心腔,其收缩将血液推向心室。
心室是下部的心腔,其主要功能是将血液泵送到全身各个器官。
房室之间有一个称为房室结(AV结)的区域,它位于心房底部和心室之间,起到连接和传导信号的作用。
房室模型还包括其他重要的结构,例如窦房结(SA结)、希氏束和浦肯野纤维等。
窦房结是心脏的起搏点,控制心脏的节律。
希氏束和浦肯野纤维是心室内部的电流传导通路,负责将来自心房的电信号传递到心室肌肉,引发心室收缩。
通过房室模型,可以更好地理解心脏的结构和电活动,为诊断和治疗心脏疾病提供参考和指导。
请注意,房室模型只是心脏解剖和电活动的简化描述,并不能完全涵盖所有细节和复杂性。
在实际的医学和生理学研究中,对心脏功能和电活动的理解还需要更加详细和深入的模型和方法。
第2讲 房室模型

用MatLab 软件编制程序如下:
19
function f=fun1(t,x); r1 =1; r2 =0.5; r3 =0.6; lambda1 =0.1; lambda2 =0.02; lambda3=0.06; mu=0.1; f=[ x(1)*(r1 - lambda1*x(2)); x(2)*(- r2 + lambda2*x(1) - mu*x(3)); x(3)*(- r3 + lambda3*x(2)) ]; [t, x] = ode45 ('fun1', [0, 20], [100, 40, 6]); subplot(1,2,1) plot(t,x(:,1),'- ',t,x(:,2),'- .',t,x(:,3),':') legend('x1(t)','x2(t)','x3(t)') grid subplot(1,2,2) plot3(x(:,1),x(:,2),x(:,3)) grid
由较大的 ti , c1 (ti ) 用最小二乘法定A,
t t ~ c1 (t ) c1 (t ) Ae Be
由较小的
~ ti , c1 (ti )用最小二乘法定B,
10
再估计参数: k12 , k21, k13
t , c1 , c2 0
D0 k13V1 0 c1 (t )dt
dx1 x1 ( r1 1 x2 ) dt
比例系数λ1 反映哺乳动物掠取植物的能力。
(1)
14
哺乳动物离开植物无法生存, 设它独自存在时死亡率 为r2, 即 x2(t) = -r2 x2, 而植物的存在又为哺乳动物提供了 食物, 植物的存在相当于使哺乳动物的死亡率降低, 且促使 哺乳动物增长, 设这种作用与植物的数量成正比, 则有:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
房室模型的综述1前言神经系统可能是我们体内最复杂和最重要的系统。
它负责传递有关肌肉运动和感官输入的信息,使我们能够与周围的世界互动并感知它们。
神经系统主要由称为神经元的大量互连细胞网络组成。
因此,对神经元的研究具有重要意义,因为了解神经元本身的性质有助于理解它们如何在更大的网络中协同工作。
1.1神经元解剖学神经元可以分解为三个主要部分;躯体,树突和轴突。
体细胞是神经元的主体,具有容纳细胞核的半透性细胞膜。
树枝状结构形成一个巨大的树状结构,从躯体延伸出来。
树突负责接收来自其他神经元的突触输入(神经递质)。
神经元的轴突是长轴状结构,终止于轴突末端。
轴突末端负责释放由其他神经元的树突所接收的神经递质。
神经元图如图1所示。
树突和轴突末端的大分支结构允许每个神经元与数千个其他神经元连接,形成大规模的通信网。
神经元通过突触进行通信,突触由轴突终端中的电脉冲触发。
轴突末端的电脉冲释放神经递质,该神经递质与另一神经元的树突上的受体位点结合。
树突上的兴奋性神经递质的累积可以引起动作电位,这是跨细胞膜的电压的大的尖峰。
该电脉冲可以沿树突移动到轴突终端,其中可以定位其他突触,允许信息在网络上传播。
1.2数学方法为了捕获沿单个神经元的电脉冲传播的基本动态,可以使用数学方程。
然而,神经元的复杂生理结构产生难以分析的方程式。
跨越神经元细胞膜的潜在差异取决于空间和时间,因此生理上准确的神经元模型将受部分差异方程(PDE)控制。
PDE难以通过分析和数值分析。
为了克服这种困难,神经元可以通过称为区室化的过程离散化(图2)。
当神经元被划分时,它被分解成称为隔室的不连续区段。
图1:神经元图。
神经元的三个主要部分是体细胞,树突和轴突。
单个隔室没有空间依赖性,因此它们的电压仅取决于时间,这使得它们可以由普通的二元方程(ODE)控制。
通常,对ODE系统的分析比PDE系统的分析容易得多。
区室化过程允许使用空间独立的隔室对神经元进行建模。
模型具有的隔室越多,其生理学上就越现实。
然而,大隔室模型可能极难分析,因此可能难以揭示导致特定神经元动力学的潜在机制。
因此,分析具有少量隔室的模型更为实际。
神经元的典型数学模型仅由单个隔室组成,这意味着轴突,体细胞和树突在仅具有单个电压的孤立隔室中组合在一起。
在这种情况下,神经元的一些重要特征被忽略。
例如,在动作电位期间,电脉冲沿树突的长度传播到体细胞,然后可能传播到轴突终端。
这不能在单室模型中发生,因为树突,体细胞和轴突是由没有空间依赖性的均匀电压建模的。
本报告的重点是分析具有两个隔室的神经元模型。
一个隔间将模拟躯体,而另一个隔间将是树突的非常基本的模型。
我们的模型将结合真实神经元的一些基本特征,包括从一个隔室到另一个隔室的电位转移,其模拟从树突到躯体的电位传播。
通过改变体细胞室上树突状隔室的影响,我们希望确定和分析树突状隔室对神经元整体动力学的影响。
这是我们将使用分叉分析解决的问题。
图2:神经元的离散化。
从左到右;一个完整的神经元,一个八室神经元,一个四室神经元,一个单室神经元。
每个隔间都有一个独特的电压。
完整的神经元模型是最复杂的,而单个神经元模型是最简单的。
1.3动力系统理论大多数动力系统,包括神经元系统,都无法通过分析解决。
因此,必须使用替代方法来提取有关系统动态的信息。
通常,这些方法涉及检查解决方案的定性结构。
这些方法中最基本的是线性稳定性分析,其中方程是关于已知稳态平衡解的线性化并且计算特征值。
特征值决定了平衡解的类型和稳定性,从而描述了局部系统动力学。
但是,如果系统依赖于某些参数,通常很重要的是要知道这些平衡解决方案如何在一个或多个参数的变化下发展。
这是分叉分析特别有用的地方。
分叉分析允许在参数变化下跟踪已知解决方案,从而在广泛的参数范围内提供关于系统动态的信息。
然而,更重要的是,分叉分析可以检测出现新解决方案或现有解决方案被破坏的关键参数值。
与临界参数值一致的点称为分叉点。
了解分叉点的位置非常重要,因为它标志着从一种动力学状态向另一种动力学状态的转变。
分岔的确切类型和发生的动态转换的性质可取决于许多因素,例如,关于稳态解的线性化的零实部特征值的数量,或正规形状系数的值。
稳态解与周期解之间的碰撞称为全局分岔。
这是因为对稳态解的局部分析将不会揭示附近周期解的存在。
出于这些原因,确定系统的全局动态需要更多的工作。
分岔理论中一些最有力的工具是中心流形和正规形式定理,它们可以用来证明分岔点某些邻域中特定类型解的存在性和稳定性。
通过在分叉点处应用这些定理,可以将完整的动力系统简化为具有相同定性动力学的更简单的系统。
该系统称为拓扑正规形式。
对于接近分叉点的参数值,完整方程组的动力学与正常形式的动力学相同。
因此,正规形式的解决方案结构在质量上与整个系统类似,并且正常形式可用于推断关于整个系统的动态的信息。
然而,重要的一点是,两个定理都不能用于确定正常形式和完整系统具有定性相似动态的邻域的大小。
1.4概述在本报告中,我们分析了神经元的两室模型。
特别地,我们感兴趣的是第二隔室如何模拟树突,影响神经元的整体动力学。
为此,我们将使用分析和数值分岔理论的各个方面。
2两房室模型神经元的数值计算具有丰富的结果,其基础是Hodgkin-Huxley 的离子通道模型和Rall 的神经元被动电缆模型。
神经元电缆模型的离散描述就是房室模型。
房室模型将空间上连续的单个神经元分成离散的多个房室,房室之间相互连接后整体描述神经元的时空变化。
1991年Traub 构造了一个由19个房室组成的海马CA3锥体神经元模型[5],Pinsky 和Rinzel 在Traub 的基础上提出了由两个房室构成的简化的CA3锥体神经元模型,从此,各类神经元的房室模型文献大量出现,实验结果分析结合房室模型讨论逐渐成为研究神经元电学特性的主要方法。
在此,先给出本论文中所要用到的房室数学模型:)()(111++--+-=k k k k k k k k m v v r M v v r dtdv C 其中,k v 是第k 个房室的膜电压,此房室可以用来表示胞体、树突或轴突,单位是mV;k r 、1r +k 分别表示第k 个房室与第1-k 及第1k +个房室的耦合电导;m C 表示膜电容,其值为12cm /F μ;k M 是房室之间的连接强度,在胞体处k M =8,在其它各房室处k M =2。
神经元的数学建模是使用物理原理和使用精确确定的实验数据的经验方法的分析推导的有趣组合。
通过将这些方法应用于每个隔室,可以导出一个普通的不同方程系统,该系统模拟该隔室中的电压。
出于我们的目的,我们只考虑具有两个隔室的神经元;体细胞室和树突室。
在本节中,我们推导出控制跨越体细胞的潜在差异和跨细胞膜的离子的方程式。
此外,我们讨论如何建模树突并呈现报告中使用的特定神经元方程。
2.1胞体电位与体内许多其他细胞一样,神经元的体细胞由浸入离子溶液中的半透性细胞膜组成。
内部和外部(细胞内和细胞外)体细胞离子浓度的差异将导致离子跨越细胞膜,从而产生可测量的潜在差异和电性(参见图3)。
由于细胞膜具有分离电荷的能力,因此可以将其建模为电容器。
整个体细胞的潜在差异是内部和外部潜力之间的差异。
e i V V V -=s (1)当电子平衡时,将达到平衡电位。
事实上,任意离子A 的平衡势可以使用能斯特方程来计算,)][][ln(ie A A A nF RT E =(2)其中R 是通用气体常数,T 是绝对温度,n 是离子的电荷,F 是法拉第常数,e A ,i ][分别是内部和外部离子浓度。
当体细胞不处于静电平衡时,离子穿过膜的运动产生电流,细胞膜充当电阻器。
像电池膜一样的电容器和电阻器可以将其建模为简单的电子电路(图4)。
利用完善的电磁学定律,我们可以推导出一个能够模拟整个体细胞的潜在差异的不等方程。
如上所述,细胞膜的作用类似于电容器,因此我们假设跨细胞膜的电压S V 满足等式Q CV S =(3)图3:内部浓度i A 与离子的外部浓度e A 之间的差异导致离子在细胞膜上使用,从而产生潜在的差异。
为了便于说明,我们使用了任意离子A .图4:使用电容器和电阻器将电池膜建模为电路。
电阻器代表对膜上使用的所有离子的总电阻.其中C 是膜的电容,Q 是电荷,S V 是上面定义的躯体的潜在差异。
我们确定了这种表达方式,并且认识到每单位时间的电荷变化是最新的,有I dtdQ C≡=dt dV S (4)假设离子过程产生的电流与体电位具有线性关系。
因此,电流-电压关系采用众所周知的形式IR V =,其中R 是电阻。
就任意离子A 而言,由电极产生的电流是)(g A s A A E V I -= (5)其中A E 是使用能斯特方程(2)计算的平衡势AA R 1g ≡ 是离子特异性膜电导。
膜电导率是膜电阻的倒数。
离子扩散产生的总电流量将表示为ion I ,其中)(g i i s iion E V I -=∑ (6)其中总和超过所有离子。
在大多数神经元模型中,ion I 包含泄漏项)(g L L s E V -=,它表示小的时间独立电流,它们共同作用以使体细胞电位达到平衡电位。
现在我们已经拥有了控制电路各个元件的必要方程式,我们可以推导出一个控制整个电路的方程,理想情况是膜电位。
Kirchho®定律指出,进入结的电流总和必须等于离开结的电流之和,因此细胞膜的状态方程是0dtdV ion S =+I C (7)在实验和理论分析中,通常将外部电流注入到体细胞中以刺激离子扩散。
在这种情况下,膜电位的等式采用这种形式app ion S dtdV I I C =+(8)其中app I 是施加的电流。
2.2电压相关电导在对穿过细胞膜的单一物种离子产生的电流进行建模时,我们假设电流建模方程采用的形式)(g A s A A E V I -= A g 是膜的电导。
然而,由于膜电导的生物学解释,单独该方程是不现实的。
通过穿过开放的通道或门,离开细胞膜。
因此,细胞膜的电导与打开多少通道并且可用于离子移动有关。
通道的状态以及膜的电导通常取决于体细胞电位差。
为了模拟通道的状态,采用统计方法并将膜电导写为A A A p g g = ,10≤≤A P (9)其中A g 是最大电导,好像每个通道都是开放的,A P 是与开放通道相关的电压依赖概率。
概率A P 通常是激活变量a 和失活变量b 的单项式,其采用形式y x A b P a =(10)指数x 和y 是整数,通常选择这些整数以获得最佳实验数据。
统计上,激活变量是任何通道打开的概率,而失活变量是任何通道关闭的概率。
因此,如果我们能够准确地模拟(in)激活变量的方程,我们就可以准确地描述膜电导和离子扩散产生的电流。
模拟(in)激活变量演变的方程基于这样的前提,新道以与闭合信道的概率成比例的速率打开,反之亦然。
