对数平均值的几何解释与探究(岳峻)
对数均值不等式的证明方法

对数均值不等式的证明方法对数均值不等式(AM-GM不等式)是数学中常用的一种不等式,它是初等数学和高等数学中必学的知识点之一。
本文将介绍针对对数均值不等式的证明方法。
一、对数均值不等式的表述对数均值不等式又称为算术平均数和几何平均数不等式,它的数学表述为:对于任意非负实数$x_1, x_2, \ldots, x_n$,有:$$\sqrt[n]{x_1 \cdot x_2 \cdots x_n} \le \frac{x_1 + x_2 + \cdots + x_n}{n} $$其中,$n$为非负整数。
二、直接证明法对数均值不等式的证明方法有多种,其中一种是直接证明法。
这种方法通过将不等式两边进行变换和分析,从而得到等价的形式,最终得证。
首先,根据不等式的左侧,我们可以将$x_1, x_2, \ldots, x_n$的乘积写成指数的形式:$$x_1 \cdot x_2 \cdots x_n = e^{\ln(x_1 \cdot x_2 \cdots x_n)}$$然后,利用指数函数的性质,我们知道:$$e^{\ln(x_1 \cdot x_2 \cdots x_n)} = e^{\ln x_1 + \ln x_2 + \cdots + \lnx_n}$$接下来,我们可以应用算术平均数和指数函数的关系,即:$$\frac{\ln x_1 + \ln x_2 + \cdots + \ln x_n}{n} \ge \ln\left(\frac{x_1 +x_2 + \cdots + x_n}{n}\right)$$再次利用指数函数的性质,我们有:$$e^{\frac{\ln x_1 + \ln x_2 + \cdots + \ln x_n}{n}} \gee^{\ln\left(\frac{x_1 + x_2 + \cdots + x_n}{n}\right)}$$化简后得:$$\sqrt[n]{x_1 \cdot x_2 \cdots x_n} \le \frac{x_1 + x_2 + \cdots + x_n}{n}因此,我们通过直接证明法证明了对数均值不等式。
房山区房山高中数学对数与对数函数教学提纲

诚西郊市崇武区沿街学校"房山区房山
中学高中数学3.2.1对数与对数函
数〔1〕教学提纲必修1"
一、知识要点
〔1〕理解对数的概念;对数与指数的关系;
〔2〕掌握对数式与指数式的互相转化.
二、探究研究
〔对数的起源〕
1.对数的概念一般地,假设b a N =(),那么数b 叫做以a 为底N 的对数,记作读作
其中,a 叫做N 叫做
考虑:为什么对数的定义中要求底数0>a ,且1≠a ;
是否是所有的实数都有对数呢?
2、两个重要对数:
常用对数:自然对数:
lg 100=lg 0.01=
lg 10000=lg 0.0001=
3、对数式与指数式的互化
指数式对数式
4、对数的性质
〔1〕负数和零没有对数;
〔2〕1的对数是零:log 1a =;
〔3〕底数的对数是1:log a a=;
a=;〔4〕对数恒等式:log a N
a=.〔5〕对数恒等式:log N
a
三、典型例题
例1将以下指数式写成对数式:
〔1〕45=625〔2〕62-=641〔3〕a 3=27(4)m )(31=3 例2将以下对数式写成指数式:
〔1〕416log 2
1-=;〔2〕2log 128=7;
〔3〕lg0.01=-2;〔4〕ln10=03
例3.求以下各式的值
2log 2=2log 1=2log 16=
21log 2=5log 25=2log 161
=
4.0log 1=9log 81=
5.2log 625=7log 343=3log 243=
五、小结。
对数平均不等式的证明及应用

2( a - b )
a
① L ( a, b ) ≤
⇔ lna - lnb>
⇔ ln >
b
2
a+b
a
2
-1
a
b
( ※ ). 令 x = > 1,则 ※ 式 等 价 于 lnx >
a
b
+1
b
2( x - 1 )
2( x - 1 )
. 构造函数 f ( x )= lnx ( x > 1 ),f '( x )=
所
a+b
以 L ( a,b ) ≥ ab 成立 . 因此, ab ≤ L ( a,b ) ≤
成立 .
2
二、对数平均不等式在高考解题中的应用
f ( x1 ) - f ( x2 )
对数平均不等式能有效解决含有
型
x1 - x2
不等式问题和极值点偏移问题 . 下面以近几年高考数学
试题为例,
给出对数平均不等式的应用 .
,要证
< a - 2,只需证
-2 +
x1 - x2
x1 - x2
a( lnx 1 - lnx 2 )
lnx 1 - lnx 2
明
< a,只需证明
< 1. 由对数平
x1 - x2
x1 - x2
lnx 1 - lnx 2
1
均不等式可知:
<
,又因为 x 1 x 2 = 1,所
x1 - x2
x1 x2
证明:
(Ⅱ)f '( x ) =
以
lnx 1 - lnx 2
f ( x1 ) - f ( x2 )
利用对数平均不等式巧解一类数学压轴题

利用对数平均不等式巧解一类数学压轴题作者:行凯歌
来源:《新高考·高一数学》2018年第05期
基本不等式是高中数学中的重要内容,它往往和函数、导数、最值等聯系紧密,对学生的逻辑思维能力要求很高,倍受高考命题者的青睐.几何平均、算术平均是我们熟知的两个概念,对数平均虽然在教材中未提及,但是却在高考压轴题和各地模拟题中频频m现,因此,同学们要高度重视.如果以函数思想为指导,把一类双变量齐次函数问题转化为一元函数问题,再用导数为T具就能有效解决,而这个转化的思想就蕴含在对数平均不等式的证明之中.
一、知识介绍——对数平均不等式及证明
二、推广变形——对数平均不等式的常见变形形式
总之,与“对数平均”有关的证明题,常以压轴题的最后一问出现,综合性强,难度较高.同学们在解题时应简化思路与计算,领悟构造函数法在高考数学证明题中的无穷魅力,。
对数应用在调研中的应用

对数应用在调研中的应用一、前言对数是数学中的一个重要概念,它在各个领域都有着广泛的应用。
在调研中,对数也是一个非常有用的工具。
本文将从理论和实践两个方面探讨对数在调研中的应用。
二、理论探讨1. 对数的定义和性质对数是指以某个固定底数为基准,求出一个数在该底下的指数。
例如,以10为底的对数就是常见的“以10为底的对数”,记作log10,简称log。
对于任意正实数a和b(a≠1),有以下性质:(1)loga 1=0;(2)loga a=1;(3)loga (mn)=loga m+loga n;(4)loga (m/n)=loga m-loga n;(5)loga mn=n loga m。
其中,性质(3)、(4)、(5)被称为对数运算法则,它们是我们使用对数进行计算的基础。
2. 对数在数据处理中的应用在调研中,我们经常需要处理大量数据。
如果直接使用原始数据进行计算和分析,往往会遇到数据范围过大或过小、精度不足等问题。
这时候,我们可以使用对数进行数据转换,使得数据范围更加合理,精度更高。
例如,我们需要计算某个城市的人口增长率。
假设该城市现有人口为100万,去年有90万,前年有80万。
直接计算增长率会得到10%和12.5%的结果,但这并不能反映出实际情况。
如果使用对数进行数据转换,则可以得到更加准确的结果。
具体方法如下:(1)将原始数据取对数,即log10 100=6、log10 90=5.95、log10 80=5.9;(2)计算增长率的对数差值:(6-5.95)/5.95≈0.0084、(5.95-5.9)/5.9≈0.0084;(3)将对数差值转换为增长率:exp(0.0084)-1≈0.0084×100%=0.84%。
通过使用对数进行数据转换,我们得到了更加准确的人口增长率结果。
三、实践应用1. 对数在调查问卷中的应用在调查问卷设计中,我们经常需要使用“量表题”来评估被试者的态度或行为倾向。
太和中学(岳峻)

的应用
例4 (2015广州三模)记函数 H x 的图象为曲线 C. 设 A(x1, y1 ), B (x2 , y2 ) 为曲线 C 上的不同两点。如果在曲线 C 上存在点 M (x0 , y0 ), 使得: x + x2 (1) x0 = 1 . 2 (2)曲线 C 在点 M 处的切线平行于直线 AB,则称函数 H x 存在“中 值相依切线”. 1 2 f x ln x ax a 1 x a R, a 0 是否存在“中值 试问函数 相依切线”,请说明理由。 2 解析:假设函数 f x 存在“中值相依切线”, 则 kAB f x0 , 即 ln x ln x 1 x x 2 2 1 a x2 x1 a 1 a 2 1 a 1, x2 x1 2 x2 x1 2 化简可得: ln x2 ln x1 x x x x 2 , 由 2 1 2 1 知假设不成立。 ln x2 ln x1 2 x2 x1 x2 x1
三、不等式链的证明
证法2:设 b a 0, a b ,则不等式等价于 骣 骣 b 鼢 b b 珑 1鼢 ln > 2 - 1 (a + b)(ln b - ln a) > 2(b - a) ? 珑 鼢 珑 桫 桫 a a a 设函数 h(x) = (a + x)(ln x - ln a)- 2(x - a)(x > a), 则 x ln x ln a 1 x a a h x ln x ln a 1 , x x
由于 b a 0时,b >
五、不等式链的应用
1
b> b- a > a ( a > 0) ln b - ln a
对数平均数不等式链的几何证明及变式探究
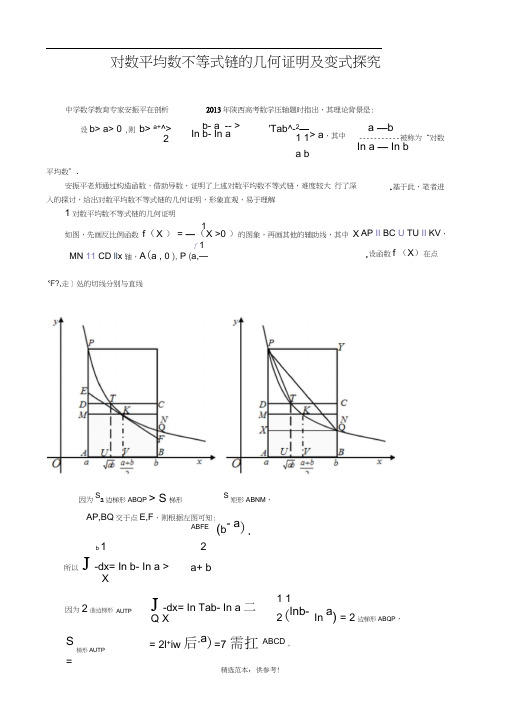
对数平均数不等式链的几何证明及变式探究2013年陕西高考数学压轴题时指出,其理论背景是:平均数”.安振平老师通过构造函数,借助导数,证明了上述对数平均数不等式链,难度较大行了深入的探讨,给出对数平均数不等式链的几何证明,形象直观,易于理解1对数平均数不等式链的几何证明1如图,先画反比例函数f(X )= —(X >0 )的图象,再画其他的辅助线,其中Xf1MN 11 CD ll x 轴,A(a , 0 ), P (a,—AP,BQ交于点E,F,则根据左图可知:ABFEb 1 2所以J -dx= In b- In a >X因为2曲边梯形AUTPJ -dx= In Tab- In a 二Q X1 12(lnb-In a) = 2边梯形ABQP,S梯形AUTP= 2l+iw后-a)=7 需扛ABCD,设b> a> 0 ,则b> a+^>2b- a -- >In b- In a 'Tab^-2—1 1a b> a,其中a —b----------- 被称为“对数In a — In b 中学数学教育专家安振平在剖析.基于此,笔者进AP II BC U TU II KV,.设函数f (X)在点(b- a).a+ bS矩形ABNM,因为S a边梯形ABQP > S梯形K F?,走〕处的切线分别与直线b - a 而根据右图可知:S 曲边梯形AU TPv S 梯形AUT P ,所以Inb- I nav —.J ab综上,结合重要不等式可知:X — X求证:In X 2 T 门%<^^^.VX 1X2知 X 2 > X 1 > 0,求证:1一互 < I n X2T n % <X 21(b- a )v4vInb- b' ' a+ bInavb-a屁<1骣 2?吿+1 j b- a )v1(b-a),即 b>U b- a >2 In b- In aT ab > 2------- > 1 1 —+ - a ba (b> a> 0).2对数平均数不等式链的变式探究 近年来,以对数平均数不等式链为落点的压轴试题层出不穷,如年新课标I 、 2014年陕西卷、2014福建预赛、2014年绵阳一、三诊、2015合肥最后一卷等等,因此关注对数平均数不等式链的变式探究是十分必要的 . 2010年湖北卷、 2012年天津、2013 为了行文叙述的方便,将对数平均数不等式链中的不等式 ,记为①式;将 In b- In a b- a ---- > In b- In a J Ob ,记为②式;将b> ln b- b- a ---- > In a,记为③式 变式探究1:取a = X i ,b = X 2,则由①知:X 1 +x 2 2X 2-X 1 >In X 2 Tn x 1于是,可编制如下试题:已知X 2 >X i >0, 求证:lnx 2-lnx .>2(X2—X1)X 1 +X 2变式探究2 :取a=x ,,b=X 2,则由②知:X 2 -X 1 In X 2 Tn x 1>7x1x r .于是,可编制如下试题:已知另外,根据S 矩形ABQX < S 曲边梯形ABQP <S弟形ABQP< S 矩形ABYP ,可得:[(b- a ) v Inb- Inav + - j (b- b 2?® b ■ a)<^(b- aa ).X 2 AX j >0, 变式探究 3:取a =捲山=X 2,则由③知:2>—-—.于是,可编制如下试题:已In X 2 Tnx 1 丄 + 丄X 1 X 2X 2> X 2-X 12 2X 2-X 12X 1X 2变式探究4:取 a =X 1 +1,b =X 2 +1,则由①知:(X1+1)+(X2+1)A 区+“^为十.于是,可 " In (X 2 +1) -1 n (捲 +1)编制如下试题: 对任意X i , X 2 € ( —h ),且 X i 工 X 2 , X 2 — Xi X i +X 2求证:In (X 2 +1)-Ind j +1) V —厂 +1.变式探究 5:取a=X i +1,b =X 2 +1,则由②知:朋:肌时丙.于是,可编制如下试题: 对任意X i , X 2 匸(—1, ,且 X i H X 2 , X 2 - X1求证: -------- -- ------- > J X 1X ^ X <l- X ^1 . In (X2+1)—I n (X 1 +1) J变式探究 6:取 a +1,b =X 2 +1,则由③知:一(X2+1) —(X1+1)2 X <H 1 > -------------------------- > ------------ ---In (X2+1)—I n^ +1) 1 + 1人+1 X2+1是,可编制如下试题:对任意 X 1,X 2 忘(一1,母),且 X 1 H X 2,求证: X 2 —X1 2(X 1+1)(X 2+1)X2 +1 > ---------- = --- : -------- > In (X 2 +1)—I 门(为 +1) 为 +X 2 +2变式探究 7:取a =为-1,b =X 2 -1,则由①知: (x 1 1)rx 2-1)于是, In (X 2—1) —I n (X 1 —1) 编制如下试题: 对任意 X 1, X 2 € (1,邑),且 X 1 HX 2,求证: .4—1. In (X 2 -1) —I 门(为-1) 2 变式探究 =X 1 -1,b =X 2 —1,则由②知:(X 2 -"-(花 一1) In (X 2 -1) jnd j T ) > J (X 1 -1)(X 2 -1).于是, 编制如下试题: 对任意 X 1,X 2 巳1,+^),且 X 1 KX 2,求证: X 2 — X1 In (X 2 T )Tn (为 T ) > J X ,X2 - % - X 2 +1 .变式探究 9:取 a = X 1—1,b = X 2-1,则由③知:X 2_1 A (X 2 -“-(捲-1)In (X 2 -1) —In (X 1 -1) +为 一1 X 2 -1可编制如下试题:对任意 X 1,X ^(1^),且X 1 H X 2, 求证: X 2 十化-1)“-1)In ( X 2 -1) Tn ( X i-1) >2(X 1-1)(X 2-1) X j + X 2 -2X1 变式探究 10:取a=e X1,b=e'严,则由①知:— +e X 22A 兰三.于是,可编制如下试题:对任意X 2 -X 1总之,对数平均数不等式链的运用是近几年数学竞赛、 名校模拟数学试题、高考数学真题的理论背景,正如陕西师范大学罗增儒教授所言:我们可以通过有限的典型考题的学习,去领悟那种解无限道题的数学 机智.这里的领悟解题的数学机智从某种意义上说就是对问题本质的理解,而对问题本质的发现还在于我 们对问题信息的审视和挖掘 .水有源,题有根,茫茫题海,寻觅其根源,领悟其通性通法,方是提升数学 思维素养的有效途径.【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和 关注,我们将会做得更好】X j , X 2 壬 R ,且 X 2 >x 1,求证: X 2 X 1 X 2e -e 1~> X 1X2e^e "2变式探究11:取a =e Xl ,b XX 1= e X2,则由②知:eeX2.于是,可编制如下试题:对任意X i ,X 2 迂 R ,且 X 2 >X i ,求证: (X 2-X i 丫尹2变式探究12 :取a = e x , b X 2 -X i<(e J”eX2e X2-e "1> -------------------X 2 — X12> 一2一 .于是,可编制如下试题:对 丄+―1X ie eX 22eXi恢e X 2 _e X 1任意 X2 R ,且 X ^X1,求证:e X2>K 〉E-X 22e X11-严 1 e* + e X^ X 2 -X-i V。
几何平均数

几何平均数的计算
6
1、几何平均数的计算
(1)简单几何平均法
N
G n X 1 X 2 X n n
(2)加权几何平均法
Xi
i 1
G X X X
f f1 1 f2 2
fn n
i 1
n
f
X
i 1
N
fi i
几何平均数的计算
7
(3)几何平均数计算应注意的问题 1、变量数列中任何一个变量值不能为0,一个为0,则几何平均 数为0。 2、用环比指数计算的几何平均易受最初水平和最末水平的影响 。 3、几何平均法主要用于动态平均数的计算。 (4)几何平均数的特点 1、几何平均数受极端值的影响较算术平均数小。 2、如果变量值有负值,计算出的几何平均数就会成为负数或 虚数。 3、它仅适用于具有等比或近似等比关系的数据。 4、几何平均数的对数是各变量值对数的算术平均数。
因为:
a b 2 ab
时, a b
即
ab 2
ab 2
.
ab
ab
显然,当且仅当
概念及定义
5
ab 为a, b的算术平均数; 1 我们称 2
ab为a, b的几何平均数.
(2)几何平均数:几何平均数(geometric mean)是 指n个观察值连乘积的n次方根。 根据资料的条件不同,几何平均数有加权和不加 权之分。 设一组数据为X1,X2,…,Xn,且均大于0,则 几何平均数Xg为: X g n X 1 X 2 X 3 X n
析中有广泛的应用,是编制和检查计划的重要依据。还可
以用于一个国家或地区不同阶段发展状况的比较,以及同
一时期不同国家或地区发展状况的比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、不等式链的证明
评注:涉及两个变量的不等式的证明,其解题策略耐人 寻味: 证法1是先将不等式逆推分析,进行等价转化,使得其 中的两个变量的特征、规律更明朗,然后将两个变量的比值 (或和、或差、或积)替换为新的一元变量,便于构造出新 的一元函数,再通过对新的一元函数求导,判断其单调性、 确定极值(或最值),达到解决问题的目的,可归结为 “化归-换元-构造-求导”; 证法2将地位均衡的两个变量之一作为主元,另外的一 个变量视为常量来处理,构造出一元函数,可归结为 “化归-主元-构造-求导”.
高考压轴题与对数平均值
一、对数平均值的概念
中学数学教育专家安振平在剖析2013年 陕西高考数学时指出,其压轴题的理论背景 是: 设 a, b 0, 则
ab a b ab 2 ln a ln b
其中
,
a b ln a ln b
被称之为对数平均值.
一、对数平均值的概念
对数平均值在现行高中教材没有出现, 但其蕴含着高等数学的背景,近几年的高考 压轴题中,频频出现。 安振平老师构造函数,借助于导数证明 了对数平均数的有关不等式,难度较大,为 此,本人作了一些探讨,以期对2016年的复 习迎考有所启发。
三、不等式链的证明
设函数 f x 1 x ln x 2 x 1 x 1 , 则
证法1:设 b a 0, a b ,则不等式等价于 骣 骣 b 鼢 b b 珑 1鼢 ln > 2 - 1 (a + b)(ln b - ln a) > 2(b - a) ? 珑 鼢 珑 桫 桫 a a a
ab
四、对数平均值的几何解释
(3)又 S矩形ABQX < S曲边梯形ABQP < S梯形ABQP , < S矩形ABYP , 1 1骣 1 1÷ 1 ç + ÷ (b - a) < (b - a),L ③ 所以 b (b - a) < ln b - ln a < 2 ç ÷ ç 桫 a b a
综上可知:
ab 2 , f x 在点 K 处 2 ab
的切线分别与 AP, BQ交于 E , F,
四、形ABFE = 1 2 dx = ln b ln a > (b - a ),L ① 所以 ò x a+ b 1 (2) S = ò dx = ln ab - ln a
令 u x x ln x ln a 1 x a x a , 则
u x ln x 1 ln a 1 ln x ln a 0,
所以 u x 在 a, 单调递增,u x u a 0, 所以 h x 0, h x 在 a, 单调递增,h x h a 0, 故待证不等式成立。
f x ln x
x 1 x ln x x 1 2 , x x
令 g x x ln x x 1 x 1 , 则 g x ln x 0,
所以 g x 在 1, 单调递增,g x g 1 0,
三、不等式链的证明
证法2:设 b a 0, a b ,则不等式等价于 骣 骣 b 鼢 b b 珑 1鼢 ln > 2 - 1 (a + b)(ln b - ln a) > 2(b - a) ? 珑 鼢 珑 桫 桫 a a a 设函数 h(x) = (a + x)(ln x - ln a)- 2(x - a)(x > a), 则 x ln x ln a 1 x a a h x ln x ln a 1 , x x
b a
ab 曲边梯形AUTP a
S矩形ABNM,
x
=
1 1 (ln b - ln a) = S曲边梯形ABQP 2 2
1 ÷ ab - a ÷ ÷ ab
1骣 1 S梯形AUTP = ç + ç 2ç 桫 a
=
(
)
1 b- a ? 2 ab
1 S梯形ABCD 2
S曲边梯形AUTP < S梯形AUTP , 如图可知: b- a 所以 ln b - ln a < ,L ②
二、对数平均值的不等式链
设 b a 0, a b,则
a+ b b- a b> > > 2 ln b - ln a
ab >
2 1 1 + a b
>a
三、不等式链的证明
a+ b b- a > 下面以 为例加以证明。 2 ln b - ln a
思路1:由于 a , b 为两个独立的变量,如果能 够变形为一个整体,那么就可以构造两个变量的 比值(或差值)通过换元转化为一元变量,再利 用导数这个工具证明此不等式.
四、对数平均值的几何解释 1
反比例函数 f x
x
x 0 的图象,
如图所示,作 AP
BC TU KV ,
1 MN CD x轴,则 A a,0 , P a, , a
1 ,作 1 B b,0 , Q b, , T ab , ab b
2(b - a) 1 b- a 1 骣 1 1÷ 1 ç < ln b - ln a < < ç + ÷ (b - a) < (b - a) < (b - a) ÷ ç 桫 b a+ b a ab 2 a b
即 b>
a+ b b- a > > 2 ln b - ln a
ab >
2 1 1 + a b
所以 f x 0, f
x
在 1, 单调递增, f x f 1 0,
故待证不等式成立。
三、不等式链的证明
思路2:因为要证的不等式中含有两个变量,地位均衡. 如果我们辩证的看到它们,将其中某一个变量作为主元,另 外的一个变量视作为常量来处理,那么往往问题就可破解.
