Matlab程序设计大作业(终审稿)
MATLAB大作业

1.设计一个程序,要求用户用键盘输入10次,输入内容可以是数字、英文、汉字、或者
其他文字或者符号。
如果输入的是数字,则把存入一个数字数组当中;如果输入的是英文的字符,则存入一个英文字符数组当中;如果是其他字符,则存入一个字符串数组中。
当10次内容都输入完毕后,先输出英文数组中的内容,然后输出字符串数组中的内容。
如果数字数组中元素数量大于3个,则由数字数组中的数字组成一个a0 X n+a1X n-1+………an=f(X),其中a0…an是数组中第一到最后一个元素,n为元素的个数,并且画出这个函数在区间[0,20]之间的曲线。
如果数字数组中的元素数量小于等于3个,则由数字数组中的数字组成一个a0 X n+a1Y n-1+anZ=0的方程,并且画出这个函数在[0,10]之间的曲线。
具体要求:
(1)画出程序的结构图
(2)画出程序的流程图
(3)每一行或者每一小段都需要标注
(4)附上完整的程序
2.按如下条件,设计一个完整的程序。
(1)有一片草原,草原上有人、狼、羊、鸡和蝗虫生活;
(2)被吃过的草,三年之后可以修复;
(3)一个人一年吃一只羊,10个人一年杀一只狼,一个人一年吃一只鸡;
(4)一头狼一年吃一只羊,一头狼三年成活一个幼崽;
(5)一只羊一年吃掉100平方米的草原;
(6)一只鸡一年吃掉1000只蝗虫;
(7)一只蝗虫一年吃掉一平方米的草原。
按如上条件,模拟出草原及其上述的生物从现在起500年间的状态。
具体要求:
(1)写出具体的解题思路
(2)列出详细的变量表,写出每一个变量的含义
(3)写出完整的程序,最好有图。
matlab大作业实验报告,《Matlab程序设计》期末实验报告-大作业2015.doc

matlab⼤作业实验报告,《Matlab程序设计》期末实验报告-⼤作业2015.doc《MATLAB程序设计》实验报告学院: 学号: 姓名:⼀、题⽬:1、(10分)已知矩阵,⽤Matlab代码实现以下要求:(1)将矩阵赋给变量A,并在屏幕上显⽰A;(2)将A按列进列逆序重排,重排后的矩阵赋给变量B,并在屏幕上显⽰B;(3)⽤reshape命令将A重排为⼀个2⾏6列矩阵并赋给变量C;(4)将A重排为⼀个列向量,将其赋给变量D,求D的平均值,在屏幕上显⽰D和它的平均值;(5)⽤命令查看变量A的维数,并显⽰运⾏结果。
2、(10分)写代码实现以下要求:构造菜单项‘Plot’,菜单项Plot有两个⼦菜单项Plot sin(选择此项后执⾏画出曲线,线型为虚线,线条颜⾊为红⾊)和Plot cos(选择此项后执⾏画出曲线 ,线型为实线,线条宽度为2)。
3、(20分)已知,实现下列操作:(1)在同⼀个图形窗⼝,同⼀坐标系下⽤不同的颜⾊和线型绘制三条曲线,并添加图例来区分三条曲线(5分)。
(2)⽤subplot命令,以⼦图的⽅式绘制三条曲线,图形排列⽅式为三⾏⼀列(5分)。
(3) 分别⽤直⽅图(bar)、棒状图(stem)和填充图(fill)绘制三条曲线,以⼦图⽅式绘制,排列⽅式为3⾏3列,共9幅⼦图(10分)。
4、(10分)⽤surf命令绘制曲⾯图形,⽤shading interp命令进⾏插值着⾊处理并添加垂直颜⾊棒。
5、(15分)⾃2011年9⽉1⽇起,我国实⾏新的个⼈所得税征收办法,起征点为3500元,请⽤If-else if-else-end结构实现⼈⼯输⼊⽉收⼊后能计算出个⼈所得税的缴纳额并显⽰⽉收⼊10000元时应缴纳的税款。
级数应纳税所得额x(元)税率备注1x<=15003%x指⽉收⼊扣除起征点3500元之后的余额;215008000045%同上6. (10分)⽤while-end循环结构计算级数和的值,输⼊n值,能计算出f的值,并显⽰结果。
最后的matlab大作业

课程:《控制系统MATLAB仿真》课程作业与总结院系:智能工程学院专业:工业机器人技术班级:机器人181学生姓名:李飞学号:1802262135指导教师:陈浩然2019年 6月3日一、简述MATLAB/Simulink的特点1. MATLAB的特点(1)便利的开发环境。
MATLAB提供了一组具有GUI的工具,包括MATLAB主窗口、文件编辑器、帮助文档等。
(2)强大的数学计算能力。
MATLAB可进行包括基本函数、复杂算法、高级矩阵运算等非常强大的数学计算功能,特别适合矩阵代数领域的应用。
更别说,其他许多高性能数值计算的高级算法与极其丰富的库函数。
(3)强大的图形功能。
MATLAB提供了丰富的绘图函数命令,并且具有较强的编辑图形界面的能力,对于图形的编辑和设置完全可以在可视化环境下进行。
(4)强大的工具箱。
MATLAB工具箱分为功能性工具箱和学科性工具箱两类。
功能性工具箱:主要用于扩充符号计算功能、图示建模仿真功能、文字处理功能以及与硬件实时交互功能。
学科性工具箱:由相关专业领域内的专家编写,专业性强。
2. Simulink 的特点(1)建模方式直观。
Simulink是一种图形化的仿真工具,利用其可视化的建模方式,可迅速地建立动态系统的框图模型。
(2)模块可定制。
Simulink允许自定义模块的使用,可以对模块的图标、对话框等进行自定义编辑。
Simulink也允许将C、FORTRAN、Ada代码直接移植到Simulink模型当中。
(3)复杂系统的层次性。
Simulink利用子系统模块,使得庞杂的系统模型构建变得简单易行。
整个系统可以按照自上而下或自下而上的方式进行分层构建,子系统的嵌套使用不受限制。
(4)仿真分析的交互性。
Simulink提供示波器等观察器,用于对动画或图形的显示。
仿真过程中,利用这些观察器可以监视仿真结果。
这种交互式特性能让开发者快速进行算法评估以及参数优化。
二、简述自己课堂收获通过学习MATLAB,我发现原来代码也是可以有趣的,只有自己想学习一门课程才可以学好,这几周的学习使我对这门课程有了大致的认识和一些很简单的操作,认真严谨的学习态度是学好这门功课必不可少的因素,虽然只是选修课,但不能因是选修就不重视,人生当中有许多需要学习的地方,活到老学到老的精神值得我们发扬传承,对待每一件事情,只有认真负责的态度,你才可以做好学好它,不要小看每一件事物,因为它可能会改变你的一生。
MATLAB大作业
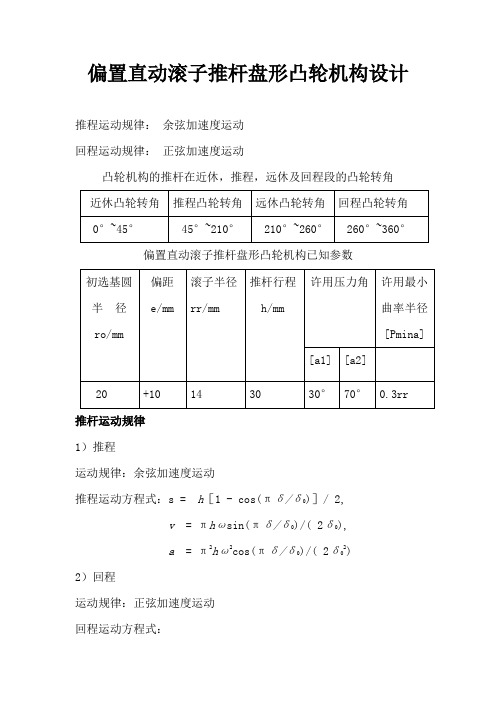
偏置直动滚子推杆盘形凸轮机构设计推程运动规律:余弦加速度运动回程运动规律:正弦加速度运动凸轮机构的推杆在近休,推程,远休及回程段的凸轮转角偏置直动滚子推杆盘形凸轮机构已知参数推杆运动规律1)推程运动规律:余弦加速度运动推程运动方程式:s = h[1 - cos(πδ/δ0)]/ 2,v= πhωsin(πδ/δ0)/( 2δ0),a= π2hω2cos(πδ/δ0)/( 2δ02)2)回程运动规律:正弦加速度运动回程运动方程式:s = h [1-(δ/δ0’)+sin(2πδ/δ0’)/(2π) v = hω [cos(2πδ/δ0’-1)]/δ0’a = -2πhω2sin(2πδ/δ0’)/(δ0’2)滚子中心坐标:x=(s+s0)sinδ+ecosδy=(s+s0)cosδ-ecosδ其中s0=r02−e2实际轮廓曲线坐标:x′=x−r r cosθy′=y−r r sinθ其中sinθdxdδ(dδ)2+(dδ)2cosθ=−dydδ(dδ)2+(dδ)2计算压力角:α=tan−1dsdδ−er02−e2+s计算曲率半径:ρ=dxdδ2+dydδ2 3dδ∙2dδ2−dδ∙2dδ2计算程序符号的表示含义:r0 初选基圆半径x 理论轮廓曲线的x坐标y 理论轮廓曲线的y坐标X 实际轮廓曲线的x坐标Y 实际轮廓曲线的x坐标p 曲率半径s 推杆位移rr 滚子半径 a 压力角paamin 许用最小曲率半径pamin 实际曲率半径的最小值a1max 回程前压力角的最大值a2max 回程后压力角的最大值e 偏距h 推杆行程a1 推程许用压力角a2 回程程许用压力角dar0 每次修正r0所加的长度N 计算点数k1 近休角k2 推程角k3 远休角k4 回程角kamin 实际曲率半径最小值所对应的角度k1max 回程前压力角的最大值所对应的角度k2max 回程后压力角的最大值所对应的角度子程序1计算最大压力角:function [amax,kmax]=yalijiao1(a,N1,b)amax=0;kmax=0;amax=max(a);for i=1:N1if a(i)==amaxkmax=i*b;endendend子程序2计算最小曲率半径:function [pamin,kamin]=qulv(p,b,N)pamin=0;kamin=0;for i=1:N-1p(i)=abs(p(i));endpamin=min(p);for i=1:N-1pamin=min(p)if p(i)==paminkamin=i*b;endendend子程序3计算回程前的压力角及修正r0:function [A,r0]=haha(r0,rr,e,h,a1,dar0,N,k1,k2,k3,k4)N1=(k1+k2)/360*N;eta=pi/180;%化为弧度while(1)s0=(r0^2-e^2)^(1/2);syms k s dk ds d2k d2sn1=k1/360*N;k11=linspace(0,k1,n1);s1=k11./k11.*0;x1=e.*cos(k11.*pi/180)+(s0+s1).*sin(k11.*pi/180);y1=(s0+s1).*cos(k11.*pi/180)-e.*sin(k11.*pi/180);n2=k2/360*N;k22=linspace(k1,k1+k2,n2);s2=(h/2).*(1-cos(pi.*(k22-k1)/k2));x2=e.*cos(k22.*pi/180)+(s0+s2).*sin(k22.*pi/180);y2=(s0+s2).*cos(k22.*pi/180)-e.*sin(k22.*pi/180);x=[x1,x2];y=[y1,y2];k=[k11,k22];s=[s1,s2];dx=diff(x)./diff(k);dk=k(1:end-1);dy=diff(y)./diff(k);dk=k(1:end-1);ds=diff(s)./diff(k);dk=k(1:end-1);ds(N1)=0;for i=1:N1f(i)=(ds(i)-e)/(sqrt(r0^2-e^2)+s(i));a(i)=atan(f(i));%计算a压力角A(i)=abs(a(i))/eta;if A(i)>a1r0=r0+dar0;break;endendif i==N1break;endendend子程序4计算回程后的压力角及修正r0:function [A,r0]=hahaha(r0,rr,e,h,a2,dar0,N,k1,k2,k3,k4) N2=(k3+k4)/360*N;b=360/N;eta=pi/180;%化为弧度while(1)s0=(r0^2-e^2)^(1/2);syms k s dk ds d2k d2sn3=k3/360*N;k33=linspace(k1+k2,k1+k2+k3,n3);s3=k33./k33.*h;x3=e*cos(k33*pi/180)+(s0+h).*sin(k33*pi/180);y3=(s0+h).*cos(k33*pi/180)-e*sin(k33*pi/180);n4=k4/360*N;k44=linspace(k1+k2+k3,k1+k2+k3+k4,n4+1);s4=h.*(1-(k44-k1-k2-k3)./k4+sin(2*pi.*(k44-k1-k2-k3)./k4)/(2*pi));x4=e.*cos(k44*pi/180)+(s0+s4).*sin(k44*pi/180);y4=(s0+s4).*cos(k44*pi/180)-e*sin(k44*pi/180);x=[x3,x4];y=[y3,y4];k=[k33,k44];s=[s3,s4];dx=diff(x)./diff(k);dk=k(1:end-1);dy=diff(y)./diff(k);dk=k(1:end-1);ds=diff(s)./diff(k);dk=k(1:end-1);ds(N2)=0;for i=1:N2f(i)=(ds(i)-e)/(sqrt(r0^2-e^2)+s(i));a(i)=atan(f(i));%计算a压力角A(i)=abs(a(i))/eta;if A(i)>a2r0=r0+dar0;break;endendif i==N2break;endendend子程序5计算曲率半径,并修正r0,计算理论轮廓曲线坐标和实际轮廓曲线的坐标及曲率半径,拖杆位移:function [x,y,X,Y,p,s,r0]=qulvvv(r0,rr,e,h,paamin,dar0,N,k1,k2,k3,k4)eta=pi/180;%化为弧度i=1;while(1)s0=(r0^2-e^2)^(1/2);syms k s dk ds d2k d2sn1=k1/360*N;k11=linspace(0,k1,n1);s1=k11./k11.*0;x1=e.*cos(k11.*pi/180)+(s0+s1).*sin(k11.*pi/180);y1=(s0+s1).*cos(k11.*pi/180)-e.*sin(k11.*pi/180);n2=k2/360*N;k22=linspace(k1,k1+k2,n2);s2=(h/2).*(1-cos(pi.*(k22-k1)/k2));x2=e.*cos(k22.*pi/180)+(s0+s2).*sin(k22.*pi/180);y2=(s0+s2).*cos(k22.*pi/180)-e.*sin(k22.*pi/180);n3=k3/360*N;k33=linspace(k1+k2,k1+k2+k3,n3);s3=k33./k33.*h;x3=e*cos(k33*pi/180)+(s0+h).*sin(k33*pi/180);y3=(s0+h).*cos(k33*pi/180)-e*sin(k33*pi/180);n4=k4/360*N;k44=linspace(k1+k2+k3,k1+k2+k3+k4,n4);s4=h.*(1-(k44-k1-k2-k3)./k4+sin(2*pi.*(k44-k1-k2-k3)./k4)/(2*pi));x4=e.*cos(k44*pi/180)+(s0+s4).*sin(k44*pi/180);y4=(s0+s4).*cos(k44*pi/180)-e*sin(k44*pi/180);x=[x1,x2,x3,x4];y=[y1,y2,y3,y4];k=[k11,k22,k33,k44];s=[s1,s2,s3,s4];dx=diff(x)./diff(k);dk=k(1:end-1);dy=diff(y)./diff(k);dk=k(1:end-1);ds=diff(s)./diff(k);dk=k(1:end-1);d2x=diff(dx)./diff(dk);d2y=diff(dy)./diff(dk);d2y(N)=0;dy(N)=0;dx(N)=0;d2x(N)=0;while(1)p(i)=(dx(i)^2+dy(i)^2)^(3/2)/(dx(i)*d2y(i)-dy(i)*d2x(i));%计算曲率半径pp(i)=abs(p(i))if pp(i)-rr<paaminr0=r0+dar0;i=1;break;elsefor ii=1:Nsino(ii)=dx(ii)/(dx(ii)^2+dy(ii)^2)^0.5;coso(ii)=(-1)*dy(ii)/(dx(ii)^2+dy(ii)^2)^0.5;X(ii)=x(ii)-rr*coso(ii); %定义实际轮廓线的X座标Y(ii)=y(ii)-rr*sino(ii); %定义实际轮廓线的Y座endendi=i+1;if i==Nbreak;endendif i==Nbreak;endendend主程序function[r0,x,y,X,Y,p,s,a,pamin,kamin,a1max,k1max,a2max,k2max]=zuizhong(r0,rr,e,h,a1,a2,paamin,dar0 ,N,k1,k2,k3,k4)N1=(k1+k2)/360*N;N2=(k3+k4)/360*N;b=360/N;eta=pi/180;%化为弧度a11=0;a22=0;s=0;pamin=0;kamin=0;a1max=0;k1max=0;a2max=0; k2max=0;while(1)while(1)[a11,r0]=haha(r0,rr,e,h,a1,dar0,N,k1,k2,k3,k4);%计算符合推程许可压力角的修正的r0r1=r0;[a22,r0]=hahaha(r0,rr,e,h,a2,dar0,N,k1,k2,k3,k4);%计算符合回程许可压力角的修正的r0r2=r0;if r0~=r1break;else[x,y,X,Y,p,s,r0]=qulvvv(r0,rr,e,h,paamin,dar0,N,k1,k2,k3,k4);%计算满足最小许可曲率半径条件的修正的r0,计算实际轮廓曲线坐标和理论轮廓曲线坐标,及曲率半径r3=r0;if r0~=r2break;endendif r0==r3break;endendif r0==r3break;endend[paminkamin]=qulv(p,b,N);[a1max k1max]=yalijiao1(a11,N1,b);[a2max k2max]=yalijiao1(a22,N2,b);a=[a11 a22];figure(1);plot(x,y);hold on;t=linspace(0,2*pi,N);x=r0*cos(t);y=r0*sin(t);plot(0,0,'*',x,y,X,Y);title('凸轮的理论轮廓曲线');axis([-70,70,-70,70]);axis square;end只需输入[r0,x,y,X,Y,p,s,a,pamin,kamin,a1max,k1max,a2max,k2max]=zuizhong(20,14,10,30,40,70,4.2,1,72 ,45,165,50,100)即可得到所需图形和数据。
MATLAB大作业

基于M A T L A B识别图片中的文字知识点:图像识别图像处理计算机视觉实验目的:以MATLAB为工具,识别图片中的文字。
问题描述:交通是一个十分重要的问题,红绿灯上的摄像头可以辨别车主的身份。
现在,我们是否能够用matlab设计一个图像识别的系统,通过车牌号的来识别相应的数字。
问题分析及模型建立:第一步:确定车牌号的区域对于一张图像在matlab中,在处理图像元素时用(x,y,z)三坐标的形式表达的灰度集时,其中,x和y是空间坐标,z是f 在坐标(x,y)处的值,就可以表达图像在该坐标轴上的点。
再将,将f(x,y)的数值简单地显示为一个矩阵,就可以定量地表达了一幅数值图像。
矩阵中的每个元素称为像素。
所以,如果我们想要截取一段车牌号的图像,我们就可以扫描图像每一个点的像素。
然后我们进行恢复处理,算子边缘检测,腐蚀,闭操作,删除小对象得到我们就可以利用RGB的值找到白色区域的边界,然后我们利用边界,截取我们的原图像就可以得到我们所需要的车牌号的区域了。
第二步:进行文字的分割在进行分割之前,就需要将我们所获得的车牌号的区域的图像进行进一步的处理,突出我们需要的文字部分。
灰度处理彩色的图片占用的空间比较大,处理会花费很长的时间,先将图片进行灰度处理二值化再将图片二值化,将图片的256个灰度级强制减少到只有{0,255}2个灰度级,更加方便了后续的文字识别识别。
均值滤波均值滤波是对是对图像进行局部平均, 以平均值来代表该像素点的灰度值。
矩形滤波器对这个二维矢量的每一个分量进行独立的平滑处理。
获得一张比较干净清晰的图像。
腐蚀和膨胀腐蚀可以分割独立的图像元素,膨胀用于连接相邻的元素,更加利于图像的分割进行完图像的预处理,就可以开始图像的切割了首先进行边缘的切割,处理完后的图像为黑底白字。
其中黑色为0,白色1为。
这样我们就可以从四个边缘进行扫描,若行或者列像素之和0的话,就为背景,这样就可以继续向内推移,直到和不为0的位置为止。
Matlab期末大作业

华南农业大学《控制系统仿真与计算机辅助设计》基于Matlab /Simulink的风力发电机仿真施茂良200830460226陶杰2008304602272012年1月2日题目:用simulink 搭建风力发电机部分的仿真图,使其工作模式满足式(2-4),使用的发电机是永磁同步电机,具体背景材料附后。
风力发电机的控制思路如下:我们需要依据风的速度控制电机的转速使得风能的利用率最高,而电机的转速通过改变永磁同步电机的定子端电压ud 和uq 来实现,具体方程为(3-28)。
最终通过PWM 的导通关断时间来改变端电压,如材料图 2所示。
具体要求:1. 根据公式(2-5)画出类似 图2.3 的曲线。
且当β=0时,画出为获得最大的风能利用率,叶尖速λ和风速v 之间的曲线关系。
风力机用来捕获风能,将叶片迎风扫掠面积内的一部分空气的动能转换为有用的机械能,它决定了整个风力发电系统装置有效功率的输出。
风力机的输入功率是3231122V P A v R v ρρπ==式中,ρ为空气密度;A 为风力机叶片扫掠面积;R 为叶片半径。
v 为风速。
风力机的输出功率为3012p P A v C ρ=式中,pC 为风能利用系数,其值小于1。
风力机输出转矩为;其中λ为叶尖速比 风能利用系数pC 为风力机将风能转换为机械能的效率,它与风速、叶片转速,叶片直径和桨叶节距角均有关系,是叶尖速比λ和桨叶节距角β的函数。
叶尖速比λ是风能叶尖速与风速之比,即R v ωλ=式中,ω为风力机叶片旋转角速度。
根据上文可知,功率与风速具有一定的关系,它们可以用下面的函数来表示213116(,)0.5176(0.45)0.0068110.0350.081i p i iC e λβλβλλλλββ-⎧=--+⎪⎪⎨⎪=-⎪++⎩根据公式(2-5)在simulink 中的建模如图所示:Matlab 波形曲线图其中(β = 0 ,2,5,8,12,15 )代入公式2-5的曲线 蓝色曲线为β=0时风能利用系数p C 与β和λ之间的曲线据根λ=RW/v; 叶尖速λ和转速v 的关系,绘制如下图:2.搭建一个模块,使其产生自然风(5-26),并封装起来,画出一具体的 然风的曲线自然风是非常随机的一种物理现象,其产生机理非常复杂,对其建模也殊为不易。
matlab程序设计作业

Matlab程序设计作业姓名:学号:专业:《MATLAB程序设计》作业1、考虑如下x-y 一组实验数据:x=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]y=[1.2, 3, 4, 4, 5, 4.7, 5, 5.2, 6, 7.2]分别绘出plot的原始数据、一次拟合曲线和三次拟合曲线,给出MATLAB代码和运行结果。
12345678910原始曲线1234567891022.533.544.555.566.57一次拟合12345678910三次拟合x=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10];y=[1.2, 3, 4, 4, 5, 4.7, 5, 5.2, 6, 7.2];figure;plot(x,y)p1=polyfit(x,y,1);y1=polyval(p1,x);figure;plot(x,y1)p2=polyfit(x,y,3);y2=polyval(p2,x);figure;plot(x,y2)2、在[0,3π]区间,绘制y=sin(x)曲线(要求消去负半波,即(π,2π)区间内的函数值置零),求出曲线y的平均值,以及y的最大值及其最大值的位置。
给出执行代码和运行结果。
x=0:pi/1000:3*pi;y=sin(x);y1=(y>=0).*y; %消去负半波figure(1);plot(x,y1,'b');a=mean(y1) %求出y1的平均值b=max(y1) %求出y1的最大值b,以及最大值在矩阵中的位置;d=x(find(y1==b))>> ex1a =0.4243b =1d =1.5708 7.8540>>1234567891000.10.20.30.40.50.60.70.80.913、给出函数z=x^2+y^2的三维曲面的绘制结果和MATLAB 代码,x=-3:0.1:3; y=-4:0.1:4;[x,y]=meshgrid(x,y); z=x.^2+y.^2; mesh(x,y,z);4、将一幅彩色图像文件转换为灰度图像,存储并显示转换后的灰度图像,给出运行结果和执行代码。
MATLAB大作业

MATLAB大作业一、作业说明MATLAB,即matrix laboratory,作为强大的数学处理软件,在化学化工领域中也有着极为广泛的应用。
而作为化工专业的学生,我认为本课学习MATLAB最直接和有效的意义在于,学生能够利用MATLAB处理实验数据和图形。
而对于MATLAB本身数学逻辑与语言的理解和掌握相信在之前所上交的“高斯消元法”和“二分法改进”两次小作业中得到体现。
因此,本次大作业我选择利用MATLAB处理化工原理实验中已经做过的离心泵实验来进行数据处理和图形制作。
其中实验原始数据皆由本人进行化工原理实验时所记录,水的密度和粘度表由文献查得。
二、编程思路整个M文件的目标是,利用现有的实验做得数据,进行实验数据的处理以及图形绘制,主要分为三个步骤完成:第一部分利用插值和拟合求实验温度下水的密度和粘度值;第二部分利用公式和矩阵变换计算离心泵的扬程He和轴功率Pzhou;第三部分作图:离心泵的扬程和轴功率随流量变化的曲线(双y轴)。
具体思路已在主程序文件中进行注释。
三、MATLAB主程序clearclose allformat compact,format shortecho off% 处理化工原理实验数据及图形制作% 第一部分求水的密度和粘度%已知条件:(1)实验温度为23.1℃% (2)网上查得15℃-30℃下水的密度和粘度表,记录为excel表% (3)此部分数据存放在原始数据表的sheet1和sheet2中%%主要方法:(1)MATLAB数据读入% (2)矩阵初等变换% (3)函数拟合% (4)函数插值%[num1]=xlsread('原始数据表');%读取excel表格中sheet1的数据x0=[num1(:,1)];%x0x表示温度值,sheet1的第1列y0=[num1(:,2)];%y0表示密度值,sheet1的第2列x1=x0';%进行转置,将列向量转换为相应的行向量y=y0';%进行转置,将列向量转换为相应的行向量%下面开始拟合密度随温度的变化函数n = length(y);ss = '';for k = 1:n;yy = num2str(y(k));ss = strcat(ss,['+''(' yy ')''*''x''^' num2str(n+1-k)]);%将数值转换为字符串格式,在MATLAB内将密度与温度的关系拟合为n次多项式endpause,ss%输出密度随温度变化函数式%%进行图像表示%x轴为温度,y轴为密度,表示在figure窗口的上半部分pause,subplot(2,1,1),line(x1,y,'linewidth',2),title('T-density'),xlabel('温度T/℃'),ylabel('密度/(kg?m^-3)')axis([15,30,995,1000])pause, x2=23.1,y1=interp1(x1,y,x2,'spline');%读取excel表格中sheet2的数据,接下来步骤与密度处理方法相同[num2]=xlsread('原始数据表',2);t0=[num2(:,1)];z0=[num2(:,2)];t1=t0';z=z0';n = length(z);rr= '';for k = 1:n;zz = num2str(z(k));rr = strcat(rr,['+''(' zz ')''*''t''^' num2str(n+1-k)]);endpause,rr%x轴为温度,y轴为粘度,表示在figure窗口的下半部分pause,subplot(2,1,2),line(t1,z,'linewidth',2),title('T-viscosity'), xlabel('温度T/℃'),ylabel('粘度/(Pa?s)')axis([15,30,0.0008 0.0012])pause,t2=23.1,z1=interp1(t1,z,t2,'spline');y1,z1%显示实验温度下流体的密度与粘度值,y1为密度,z1为粘度pause,close all%关闭图像窗口pause,clc% 第二部分计算离心泵的扬程He和轴功率Pzhou%%已知条件:(1)所需数据存放在原始数据表的sheet3中% (2)从左至右分别为“入口压强、出口压强、入口速度、出口速度、流量、电机功率”% (3)计算公式:He=pout-pin+0.2+(uout.^2-uin.^2)./(9.81*2);% Pzhou=P.*0.9;%%主要方法:(1)MATLAB数据读入% (2)矩阵初等运算与变换% (3)利用MATLAB进行实验数据处理%读取excel表格中sheet3的数据%“pin、pout、uin、uout、qv、P、He、Pzhou”分别表示为%“入口压强、出口压强、入口速度、出口速度、流量、电机功率、扬程和轴功率”[num3]=xlsread('原始数据表',3);pout0=[num3(:,2)];pin0=[num3(:,1)];uout0=[num3(:,4)];uin0=[num3(:,3)];qv0=[num3(:,5)];pout=pout0';pin=pin0';uout=uout0';uin=uin0';qv=qv0';He=pout-pin+0.2+(uout.^2-uin.^2)./(9.81*2);P0=[num3(:,6)];P=P0';Pzhou=P.*0.9;pause,clc%输出计算结果pause,HePzhouclose allpause,clcpause,%第三部分作图:离心泵的扬程和轴功率随流量变化的曲线(双y轴)%%pause,s1=He;s2=Pzhou;x5=qv;yWidth = 60;%设置两个y轴的间隔(像素)axesPosition = [110 40 200 200];%设置图像生成位置x5Limit = [min(x5) max(x5)];%设定自变量范围x5Offset=-yWidth*diff(x5Limit)/axesPosition(3);%建立图像,设置双变量与双坐标轴h1 = axes('Units','pixels','Position',axesPosition,...'Color','w','XColor','k','YColor','r',...'XLim',x5Limit,'YLim',[10 22],'NextPlot','add');h2 = axes('Units','pixels','Position',axesPosition+yWidth.*[-1 0 1 0],...'Color','none','XColor','k','YColor','m',...'XLim',x5Limit+[x5Offset 0],'YLim',[0.3 0.7],...'XTick',[],'XTickLabel',[],'NextPlot','add');xlabel(h1,'qv');ylabel(h2,'Pzhou');%给坐标轴命名pause,plot(h2,x5,s2,'*m');pause,plot(h1,x5,s1,'^r');四、工作日志density_viscosity(密度_粘度)clearclose allformat compact,format shortecho offss =+(999.126)*x^31+(999.05)*x^30+(998.97)*x^29+(998.888)*x^28+(998.802)* x^27+(998.714)*x^26+(998.623)*x^25+(998.53)*x^24+(998.433)*x^23+(998. 334)*x^22+(998.232)*x^21+(998.128)*x^20+(998.021)*x^19+(997.911)*x^18 +(997.799)*x^17+(997.685)*x^16+(997.567)*x^15+(997.448)*x^14+(997.327 )*x^13+(997.201)*x^12+(997.074)*x^11+(996.944)*x^10+(996.813)*x^9+(99 6.679)*x^8+(996.542)*x^7+(996.403)*x^6+(996.262)*x^5+(996.119)*x^4+(9 95.974)*x^3+(995.826)*x^2+(995.676)*x^1x2 =23.1000rr =+(0.0011404)*t^16+(0.0011111)*t^15+(0.0010828)*t^14+(0.0010559)*t^13+ (0.0010299)*t^12+(0.001005)*t^11+(0.000981)*t^10+(0.0009579)*t^9+(0.0009358)*t^8+(0.0009142)*t^7+(0.0008937)*t^6+(0.0008737)*t^5+(0.000854 5)*t^4+(0.000836)*t^3+(0.000818)*t^2+(0.0008007)*t^1t2 =23.1000y1 =997.5432z1 =9.3361e-04He =Columns 1 through 1021.7000 20.9069 19.9348 19.1688 18.7950 18.3412 17.9656 17.1311 16.2075 15.6581Columns 11 through 1415.1075 14.2847 13.4611 12.6543Pzhou =Columns 1 through 100.3240 0.3600 0.4050 0.4500 0.4770 0.5040 0.5310 0.5670 0.5940 0.6120Columns 11 through 140.6300 0.6390 0.6570 0.6750diary off五、附录附录1. 温度在15-30℃时,水的密度表附录2. 温度在15-30℃时,水的粘度表附录3. 离心泵实验原始数据记录表附录4. 生成图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M a t l a b程序设计大作
业
公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]
Matlab程序设计
课程大作业
题目名称:_________________________________ 班级:_________________________________
姓名:_________________________________
学号:_________________________________
课程教师:温海骏
学期: 2015-2016学年第2学期
完成时间:
MATLAB优化应用
§1 线性规划模型
一、线性规划问题:
问题1:生产计划问题
假设某厂计划生产甲、乙两种产品,现库存主要材料有A类3600公斤,B类2000公斤,C类3000公斤。
每件甲产品需用材料A类9公斤,B类4公斤,C类3公斤。
每件乙产品,需用材料A类4公斤,B类5公斤,C类10公斤。
甲单位产品的利润70元,乙单位产品的利润120元。
问如何安排生产,才能使该厂所获的利润最大。
问题2:投资问题
某公司有一批资金用于4个工程项目的投资,其投资各项目时所得的净收益(投入资金百分比)如下表:工程项目收益表
由于某种原因,决定用于项目A的投资不大于其他各项投资之和而用于项目B和C的投资要大于项目D的投资。
试确定该公司收益最大的投资分配方案。
问题3:运输问题
有A 、B 、C 三个食品加工厂,负责供给甲、乙、丙、丁四个市场。
三个厂每天生产食品箱数上限如下表:
四个市场每天的需求量如下表:
从各厂运到各市场的运输费(元/每箱)由下表给出:
求在基本满足供需平衡的约束条件下使总运输费用最小。
§2 多目标规划模型
多目标规划定义为在一组约束下,多个不同的目标函数进行优化设计。
数学模型:
12min ()()
().()0,1,2,
,m j f x f x f x st g x j k
⎡⎤⎣⎦
≤=
其中x=(x 1 ,x 2 , … ,x n )为一个n 维向量;f i (x)为目标函数,i=1,
2, … ,m; g j (x)为系统约束, j=1, 2, … ,k 。
当目标函数处于冲突状态时,不存在最优解使所有目标函数同时达到最优。
于是我们寻求有效解(又称非劣解或非支配解或帕累托解) 定义:若 x *(x *∈Ω)的邻域内不存在Δx ,使得(x *+Δx ∈Ω),且
()(),1,2,,()(), i i j j F x x F x i m
F x x F x j
***
*
+∆≤=+∆≥某些
则称 x *为有效解。
多目标规划问题的几种常用解法: (1) 主要目标法
其基本思想是:在多目标问题中,根据问题的实际情况,确定一个目标为主要目标,而把其余目标作为次要目标,并且根据经验,选取一定的界限值。
这样就可以把次要目标作为约束来处理,于是就将原来的多目标问题转化为一个在新的约束下的单目标最优化问题。
(2) 线性加权和法
其基本思想是:按照多目标f i (x) (i=1, 2, … ,m)的重要程度,分别乘以一组权系数λj (j=1, 2, … ,m)然后相加作为目标函数而构成单目标规划问题。
即1
min ()m
j j j f f x λ==∑,其中 1
01m
j j j λλ=>=∑且
问题1:某钢铁厂准备用5000万用于A 、B 两个项目的技术改造投资。
设x 1、x 2分别表示分配给项目A 、B 的投资。
据专家预估计,投资项目A 、B 的年收益分别为70%和66%。
同时,投资后总的风险损失将随着
总投资和单项投资的增加而增加,已知总的风险损失为++(x 1+x 2)2
,问应如何分配资金才能使期望的收益最大,同时使风险损失为最小。
(3) 极大极小法
其基本思想是:对于极小化的多目标规划,让其中最大的目标函数值尽可能地小为此,对每个 x ∈R ,我们先求诸目标函数值f i (x)的最大值,然后再求这些最大值中的最小值。
即构造单目标规划:
{}
1min max ()j j m
f f x ≤≤=
(4) 目标达到法
对于多目标规划:
12min ()()
().()0,1,2,
,m j f x f x f x st g x j n
⎡⎤⎣⎦
≤=
先设计与目标函数相应的一组目标值理想化向量
()12,,
,m f
f f *
**,
再设γ为一松弛因子标量。
设()12,,,m w w w 为权值系数向量。
于是多目标规划问题化为:
,min (),1,2,,()0,1,2,
,x j j F x weight f j m
g x j k
γ
γ
γ*-•≤=≤=
问题2:某 化工厂拟生产两种新产品A 和B ,其生产设备费用分别为2万元/吨和5万元/吨。
这两种产品均将造成环境污染,设由公害所造成的损失可折算为A 为4万元 /吨,B 为1万元/吨。
由于条件限制,工厂
生产产品A 和B 的最大生产能力各为每月5吨和6吨,而市场需要这两种产品的总量每月不少于7吨。
试问工厂如何安排生产计划,在满足市场需要的前提下,使设备投资和公害损失均达最小。
该工厂决策认为,这两个目标中环境污染应优先考虑,设备投资的目标值为20万元,公害损失的目标为12万元。
问题3:某工厂生产两种产品甲和乙,已知生产甲产品100公斤需6个工时,生产乙产品100公斤需8个工时。
假定每日可用的工时数为48工时。
这两种产品每100公斤均可获利500元。
乙产品较受欢迎,且若有个老顾客要求每日供应他乙种产品500公斤,问应如何安排生产计划 §3 最大最小化模型
问题1 求解下列最大最小值问题:
123422112121222312
2241212minmax (),(),(),() ()321235
()547
()6()491220
f x f x f x f x f x x x x f x x x x f x x x f x x x x x ⎡⎤⎣⎦
=+-+=-+=+=+-+其中
例2:选址问题
设某城市有某种物品的10个需求点,第i 个需求点P i 的坐标为(a i ,b i ),道路网与坐标轴平行,彼此正交。
现打算建一个该物品的供应中心,且由于受到城市某些条件的限制,该供应中心只能设在x 界于[5,8],y 界于[5,8]的范围之内。
问该中心应建在何处为好
P点的坐标为:。
