编译原理之有限自动机
编译原理 实验1 有穷自动机的构造与实现

}
char digitprocess(char buffer, FILE* fp)
{
int i=-1;
while((IsDigit(buffer)))
{
digittp[++i]=buffer;
buffer=fgetc(fp);
}
digittp[i+1]=\0';
return(buffer);
buffer=fgetc(fp);
}
alphatp[i+1]='\0';
return(buffer);
}
int main(int argc, char* argv[])
{
FILE *fp;//文件指针,指向要分析的源程序
char cbuffer;//保存最新读入的字符
if((fp=fopen(sourceFile,"r"))==NULL)//判断源文件是否存在
}
int main(int argc, char* argv[])
{
FILE *fp;//文件指针,指向要分析的源程序
char cbuffer;//保存最新读入的字符
if((fp=fopen(sourceFile,"r"))==NULL)//判断源文件是否存在
printf("文件%s不存在", sourceFile);
(2)无符号整型数,要求长度不超过20。
四、实验结果
1.识别标识符(以字母开始由字母和数字构成的字符串,要求长度不超过10)。
#include <stdio.h>
#include <string.h>
【编译原理】词法分析:正则表达式与有限自动机基础

【编译原理】词法分析:正则表达式与有限⾃动机基础引⾔: 编译语⾔设计的精髓在于⾃动化过程,即如果要设计⼀门编程语⾔,那么⼀定要设计⼀个⾃动化系统,能够⾃⾏读⼊分析程序员写⼊的程序,将其翻译为机器能够识别的指令等信息。
当然⾼级语⾔的编译不是⼀蹴⽽就的,⽽是通过若⼲步的分解、规约、转换、优化,最后得到⽬标程序。
具体的编译步骤如下: 源程序就是我们写⼊的⾼级语⾔,编译的第⼀步叫做“词法分析”。
词法分析的本质,就是要拆解出语句的每⼀个单词,然后对这个单词的类型进⾏辨识。
⾸先拿中⽂来举例。
⽐如有⼀句话是“我喜欢你”,那么⾸先我们要把这句话拆成“我”、“喜欢”、“你”,然后再逐个分析他们的类型,得到“我”->主语;“喜欢”->谓语;“你”->宾语。
这样我们就把这句话每个单词都分析出来了,也就完成了中⽂的“词法分析”。
那么回到编程语⾔,它的词法分析就是将字符序列转换为单词(Token)序列的过程。
翻译成俗话,就是把我们写的⼤⽚语⾔⽂本分解为⼀个⼀个单词,再输出每个单词的类型。
举⼀个例⼦:int p = 3 + a; 这个语句⾮常简单,即定义⼀个变量p,它的初值为变量a与3的加和。
那么接下来我们要对这个语句进⾏词法分析,⾸先我们要把这段⽂本拆解成单词,拆出来就是'int'、'p'、'='、'3'、'+'、'a'、';'。
对这些单词再进⾏类型的辨识,那么就得到以下结果:语素语⾔类型int关键字p标识符=运算符3数字+运算符a标识符 这样我们就把这段⽂本中的每个单词的类型都分析出来了。
乍⼀看⾮常简单对不对,对于⼈类⽽⾔你只需要⽤⾁眼就可以轻松观察出来每个单词的类型,但对于计算机⽽⾔,它可没有⼈类那样的智能。
如果想要计算机能够识别并分析语素的类型,那就需要我们⼈类来为它构造⼀个⾃动化输⼊和分析的系统。
编译原理与技术 词法分析 (2)(2)
2024/7/1
《编译原理与技术》讲义
20
正规式与有限自动机
✓ R= R1 | R2
Si
S0 Sj
(3)
fi
f0
fj
引入新的终态f0和 (fi,)=f0和(fj,)=f0
2024/7/1
《编译原理与技术》讲义
21
正规式与有限自动机
✓ R= R1 ·R2
(1)
Si
fi
Sj
fj
R1对应的 NFA,Si为初 态,fi为终态
…
2024/7/1
《编译原理与技术》讲义
5
有限自动机的表示
e.g.7 NFA Mn =(, S, S0,F,),其中:
= { 0,1 } , S = {S0, S1 , S2 , S3 , S4 },F={S2 , S4}
(S0,0)= {S0, S3 } (S0,1)= {S0, S1 }
(S1,0)= ∅
有限自动机
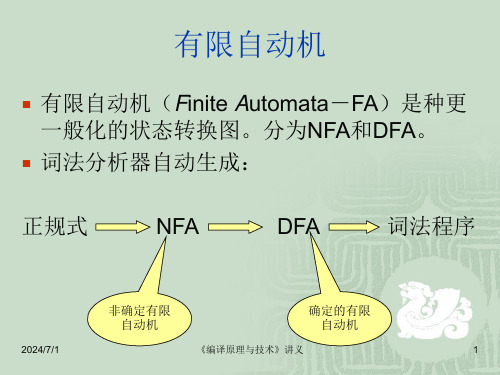
有限自动机(Finite Automata-FA)是种更 一般化的状态转换图。分为NFA和DFA。
词法分析器自动生成:
正规式
NFA
DFA
词法程序
非确定有限 自动机
确定的有限 自动机
2024/7/1
《编译原理与技术》讲义
1
非确定有限自动机-NFA
NFA Mn 是一个五元组 Mn =(, S, S0,F,), 其中:
2024/7/1
《编译原理与技术》讲义
15
比较 DFA 和 NFA(2)
DFA
NFA
容易实现-当输入串结束 由于面临同样输入符号存 时(或不存在相应状态转 在多重状态转换或存在转 换)时,若当前状态为终 换的选择,实现较为复杂。 态即为接受“已读入”的串, 一般地,NFA接受串如果
编译原理第三章 自动机基础(1)

接受空串的 FA的典型特征!
Ⅱ.第二条通路:FA2
+ ① => ①
∴ L(FA1)={ abnc| n≥0 }
b + ① => ④
bb + ① => ④ => ④
…
因而
∴ L(FA2)={ bn| n≥0 }
∴ L(FA)={abnc, bn| n≥0}
3.2.3 有限自动机的两种表现形式
【例3.6】有限自动机 :FA=( Q,∑,S,F, ) 其中: Q={1,2,3,4},∑={a,b,c}, S={1,2}, F={3,4}
9.
={abn|n≥0}
10.7. L((a|b)*)= (L(a|b))*={a,b}*
11. 即:由a,b组成的所有符号串(包括空串)集合。
➢基本图形库
=+>
.=+>
=.+ℓ>
=+ℓ>
A
P: E T
F
T | E +T | E -T F | T *F | T /F i|( E )
=>*, =>+ , =>.* , =>.+ , =>l* , =>l+ , =>.l+ ,=>.l*
如 右图有限自动机:
则 L(FA)的 识别过程如下所
+- ①
a b
b ②
c
b
③-
示:
④-
※ L(FA)的生成(或识别)过程示例:
Ⅰ.第一条通路:FA1 ac
+ ① => ② => ③
+- ①
编译原理第三章_有穷自动机

例 过河问题 分析(续)
初始状态:MWGC-φ;终止状态:φ-MWGC。 g
MWGC-φ
WC-MG
问题:
6
例 过河问题 状态转换图
起始 g
MWGC-φ g
g φ-MWGC
g
7
WC-MG
m
m MWC-G
w
w
c
C-MWG
c W-MGC
g
g
MGC-W c
MG-WC
w
m
c G-MWC
m
gg MWG-C
+dd. ddd;
输入符号串
数字 数字
SB
.
数字
+
A
H
-.
数字
.G
接收:若扫描完输入串, 且在一个终止状态上结 束。
数字 阻塞:若扫描结束但未 停止在终止状态上;或 者为能扫描完输入串 (如遇不合法符号)。
不完全描述:某些状态 对于某些输入符号不存 在转换。
练习:+34.567 .123 3.4.5
w
有穷自动机(FA)
数字系统:可以从一个状态移动到另一个状态;每次 状态转换,都上由当前状态及一组输入符号确定的;可以 输出某些离散的值集。
FA:一个状态集合;状态间的转换规则;通过读头来 扫描的一个输入符号串。
读头:从左到右扫描符号串。移动(扫描)是由状态 转换规则来决定的。
8
读头
一个FA的例子
(3)运行: 串f(,Q,且t1tt21)∈= Σf(,f(Qt1,t2t1∈), Σt2*),其中Q∈K, t1t2为输入字符
17
例3
题:试证abba可为例1的DFA M所识别(所接受)。
编译原理第三版复习

图 3-8
句型(S,(a))的语法树
3.9 考虑文法 G[S]: S→(T) | a+S | a T→T,S | S 消除文法的左递归及提取公共左因子, 然后对每个非终结符写出不带回溯的 递归子程序。 【解答】 消除文法 G[S]的左递归: S→(T) | a+S | a T→ST′ T′→,ST′| ε 提取公共左因子: S→(T) | aS′ S′→+S | ε T→ST′ T′→,ST′| ε
S 1 2 a 1 1 b 2 2
图 2-18
习题 2.7 的最简 DFA
图 2-19
正规式(a | b)*b 对应的 NFA
图 2-20
图 2-19 确定化后的状态转换矩阵
比较图 2-20 与图 2-17,重新命名后的转换矩阵是完全一样的,也即正规式(a | b)*b 可以同样得到化简后的 DFA 如图 2-18 所示。因此,两个自动机完全一样, 即两个正规文法等价。 (2) 对图 2-18,令 A 对应状态 1,B 对应状态 2,则相应的正规文法 G[A] 为 G[A]:A→aA | bB | b B→aA | bB | b G[A]可进一步化简为 G[S]:S→aS | bS | b(非终结符 B 对应的产生式与 A 对 应的产生式相同,故两非终结符等价,即可合并为一个产生式)。 3.2 令文法 G[N]为 G[N]: N→D | ND D→0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 (1) G[N]的语言 L(G)是什么? (2) 给出句子 0127、34 和 568 的最左推导和最右推导。 【解答】 (1) G[N]的语言 L(G[N])是非负整数。 (2) 最左推导:
图 2-5
正规式(ab)*a 对应的 NFA
程序设计语言编译原理(第三版)第3章

程序设计语言编译原理(第三版)第3章第3章词法分析任务:从左至右逐个字符地对源程序进行扫描,产生一个个的单词符号,把作为字符串的源程序改造成为单词符号串。
§3.1§3.2§3.3§3.4对于词法分析器的要求词法分析器的设计正规表达式与有限自动机词法分析器的自动产生(LE某)—略1§3.1对于词法分析器的要求一.功能和输出形式二.接口设计§3.1对于词法分析器的要求一.功能和输出形式1.功能:输入源程序,输出单词符号2.单词符号的分类(1)关键字:由程序语言定义的具有固定意义的标识符,也称为保留字或基本字。
例如:Pacal语言中begin(2)标识符:用来表示各种名字。
endifwhile等。
如变量名、数组名、过程名等。
(3)常数:整型、实型、布尔型、文字型等例:100(5)界符:,;3.14159()true等ample(4)运算符:+、-、某、/3§3.1对于词法分析器的要求3.输出的单词符号形式二元式:(单词种别,单词符号的属性值)通常用“整数编码”“单词符号的特征或特性”单词符号的编码:标识符:一般统归为一种常数:常按整型、实型、布尔型等分类关键字:全体视为一种/一字一种运算符:一符一种界符:一符一种4§3.1对于词法分析器的要求例:考虑下述C++代码段:while(i>=j)i--;经词法分析器处理后,它将被转换为如下的单词符号序列:<while,-><(,-><id,指向i的符号表项的指针><>=,-><id,指向j的符号表项的指针><),-><id,指向i的符号表项的指针><--,-><;,->§3.1对于词法分析器的要求二.接口设计1.词法分析器作为独立的一遍词法分析字符流(源程序)单词序列(输出在一个中间文件上)2.词法分析器作为一个独立的子程序,但并不一定作为独立的一遍语法分析器单词(至少一个)调用(取下一个单词)词法分析器优点:使整个编译程序的结构更简洁、清晰和条理化.6§3.2词法分析器的设计一.输入和预处理二.单词符号的识别三.状态转换图及其实现§3.2词法分析器的设计一.输入、预处理1.预处理:剔掉空白符、跳格符、回车符、换行符、注解部分等.原因:编辑性字符除了出现在文字常数中之外,在别处的任何出现都无意义.#注解部分不是程序的必要组成部分,它的作用仅在于改善程序的易读性和易理解性.8§3.2词法分析器的设计2.预处理子程序:每当词法分析器调用时,就处理出一串确定长度(如120个字符)的输入字符,并将其装进词法分析器所确定的扫描缓冲区中。
编译原理作业集-第三章-修订版

第三章词法分析本章要点1•词法分析器设计,2.正规表达式与有限自动机,3•词法分析器自动生成。
本章目标:1•理解对词法分析器的任务,掌握词法分析器的设计;2.掌握正规表达式与有限自动机;3•掌握词法分析器的自动产生。
本章重点:1. 词法分析器的作用和接口,用高级语言编写词法分析器等内容,它们与词法分析器的实现有关。
应重点掌握词法分析器的任务与设计,状态转换图等内容。
2 •掌握下面涉及的一些概念,它们之间转换的技巧、方法或算法。
(1)非形式描述的语言正规式(2)正规式NFA (非确定的有限自动机)(3)NFADFA (确定的有限自动机)(4)DFA最简DFA本章难点(1)非形式描述的语言正规式(2)正规式NFA (非确定的有限自动机)(3)NFADFA (确定的有限自动机)(4)DFA最简DFA作业题、单项选择题(按照组卷方案,至少15道) 1•程序语言下面的单词符号中,一般不需要超前搜索a.关键字b.标识符c.常数d.算符和界符2. 在状态转换图的实现中,一般对应一个循环语句a.不含回路的分叉结点b.含回路的状态结点c.终态结点d.都不是3. 用了表示字母,d表示数字,={1,d},则定义标识符的正则表达式可以是:。
(a)ld* (b)ll* (c)l(l | d) * (d)ll* | d*4. 正规表达式(e |ajb表示的集合是(a){ , ab, ba, aa, bb} (b){ab , ba, aa, bb}(c){a , b, ab, aa, ba, bb} (d){,込b, aa, bb, ab, ba}5. 有限状态自动机可用五元组( V T , Q , & q o , Q f)来描述,设有一有限状态自动机M的定义如下:V T={0 , 1}, Q={q 0 , q1 , q2}, Q f={q 2}, 3 的定义为:氷 q o , 0) =q1 3 (q1, 0) =q23(q2 , 1) =q2 3 (q2 , 0) =q2M所对应的状态转换图为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b
4
5
2.3 有 限 自 动 机
A = {0, 1, 2, 4, 7} B = {1, 2, 3, 4, 6, 7, 8}
状态 A
输入符号 ab B
a
2
3
开始
0
1
a
b
6
7
8
9
b
4
5
2.3 有 限 自 动 机
A = {0, 1, 2, 4, 7} B = {1, 2, 3, 4, 6, 7, 8}
识别器:是一个程序,取串x作为输入,当 x是语言的句子时,它回答“是”,否则回 答“不是”。 状态转换图(有限自动机)识别器 确定/不确定有限自动机——时空权衡问题
确定有限自动机:快,空间大
2.3 有 限 自 动 机
2.3.1 不确定的有限自动机(简称NFA)
一个数学模型,它包括: 状态集合S;
缺点:1、输入字 符包括
NFA能到达的所有状态:s1, s2, …, sk,则 DFA到达状态{s1, s2, …, sk}
2.3 有 限 自 动 机
输入符号
状态 a
b
a
2
3
开始
0
1
a
b
6
7
8
9
b
4
5
2.3 有 限 自 动 机
A = {0, 1, 2, 4, 7}
状态 A
输入符号 ab
a
2
3
开始
0
1
a
b
6
7
8
9
输入符号 ab BC BD
a
2
3
开始
2.2 词法记号的描述与识别
无符号数的转换图
num digit+ (.digit+)? (E (+ | )? digit+)?
E
digit
digit
digit digit
开始
12
digit
13
.
digit
14
15
E
+/ digit
16
17
18
other
other
other
*
19
return( install_num( ) )
2.2 词法记号的描述与识别
标识符和保留字的转换图
id letter (letter | digit )* letter或digit
开始
9
letter
10
other
*
11 return(install_id( ))
1、检查保留字表,如果在表中发现该词法单元则返回 相应的记号并退出,否则转向2 2、该词法单元是标识符,在符号表中查找,若找到该 词法单元则返回该条目的指针并退出,否则执行3 3、在符号表中建立一个新的条目,把该词法单元填入, 并返回此新条目的指针
温故知新
源程序 字符流
集 字母合
顺 序 词法 模 组 单元 式 合
词法 记号
状态 转换 图
非形式 形式化
化描述 描述 名
字
?
正规式
字母表
和
计算机 实现
LUM
组 合
串
集 合
连接 指数
语言
连接 LM 闭包 L* 正闭包 L+
词法记号的识别
词法记号的识别
等同于对字符串的匹配过程
这个匹配过程可以基于有限状态机来完成
状态
A B C
输入符号 ab BC B
a
2
3
开始
0
1
a
b
6
7
8
9Leabharlann b452.3 有 限 自 动 机
A = {0, 1, 2, 4, 7} B = {1, 2, 3, 4, 6, 7, 8} C = {1, 2, 4, 5, 6, 7} D = {1, 2, 4, 5, 6, 7, 9}
状态
A B C
• 唯一的初态 s S;
• 终态集合F S;
b
优点:1、输入字 符不包括
2、一个状态对于 某个字符,只可能 存在唯一条输出边
b
识别语言
(a|b)*ab 的DFA
开始
a
0
b
1
2
a a
2.3 有 限 自 动 机
2.3.3 NFA到DFA的变换
子集构造法 DFA的一个状态是NFA的一个状态集合 读了输入a1 a2 … an后,
• 关系算符的转换图
=
2 return(relop, LE)
1
>
3 return(relop, NE)
<
开始 0
=
other
* return(relop, LT) 4
5 return(relop, EQ)
>
=
7 return(relop, GE)
6
other 8 * return(relop, GT)
A = {0, 1, 2, 4, 7} B = {1, 2, 3, 4, 6, 7, 8} C = {1, 2, 4, 5, 6, 7}
状态
A B C
输入符号 ab BC
a
2
3
开始
0
1
a
b
6
7
8
9
b
4
5
2.3 有 限 自 动 机
A = {0, 1, 2, 4, 7} B = {1, 2, 3, 4, 6, 7, 8} C = {1, 2, 4, 5, 6, 7}
输入符号集合;
2、一个状态对于 某个字符,可能有
转换函数move : S ({}) P(S); 多条输出边
状态s0是开始状态;
F S是接受状态集合。
a
识别语言 (a|b)*ab
开始 0
a
1b
2
的NFA
b
2.3
• NFA的转换表
状态
有限自动机 优点:快速定位 缺点:字母表过大 或大部分转换状态 为空集时浪费空间 输入符号
简单的正则式d->a
a
0
1
正则式d->ab
a
b
0
1
2
正则式d->a|b
a
0
1
b
正规式d->a*
a 0
自动机的定义
正规式d->a?
字符a出现一次或者0次
a
0
1
练习
正规式d->a(a|b)*
请画出它的状态转换图
a
a
0
1
b
2.2 词法记号的描述与识别
2.2.4 转换图 relop < | < = | = | < > | > | > =
a
b
0
{0, 1}
{0}
1
{2}
2
识别语言
(a|b)*ab 的NFA
a
开始
a
0
1b
2
b
2.3 有 限 自 动 机
例 识别aa*|bb*的NFA
a
a
1
2
开始
0
b
b
3
4
2.3 有 限 自 动 机
2.3.2 确定的有限自动机(简称DFA)
一个数学模型,包括:
• 状态集合S;
• 输入字母表;
• 转换函数move : S S;
状态
A B
输入符号 ab B
a
2
3
开始
0
1
a
b
6
7
8
9
b
4
5
2.3 有 限 自 动 机
A = {0, 1, 2, 4, 7} B = {1, 2, 3, 4, 6, 7, 8} C = {1, 2, 4, 5, 6, 7}
状态
A B
输入符号 ab BC
a
2
3
开始
0
1
a
b
6
7
8
9
b
4
5
2.3 有 限 自 动 机
2.2 词法记号的描述与识别
空白的转换图
delim blank | tab | newline ws delim+
开始
delim
delim
other
*
20
21
22
2.3 有 限 自 动 机
? 正规式
状态转换图
有限自动机
计算机 实现
等价
不确定有 限自动机
确定有限 自动机
2.3 有 限 自 动 机
