人教版八年级上册:第十二章小结与复习ppt课件
合集下载
人教版 初中数学八年级上册第十二章12.2全等三角形性质与判定小结与复习 (共23张PPT)

•
17、儿童是中心,教育的措施便围绕 他们而 组织起 来。2021/8/102021/8/102021/8/102021/8/10
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四
必做题 1.如图,∠BAC=90°,AB=AC,过点A作直线DE,
且作CE⊥ED,BD⊥ED,若CE=2,BD=6,求DE长
选做题 2.如图,△ABC中,AD⊥BC, CE⊥AB,垂足分别为D,E,AD,CE 交于点H,添加下列条件能使 △AEH≌△CEB的有( ) ①AE=EC;②AH=BC;③EH=BE; ④∠EAH=∠B. A.①②④ B.①②③ C.②③④ D.①③④
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成 。2021/8/102021/8/102021/8/102021/8/108/10/2021
•
14、谁要是自己还没有发展培养和教 育好, 他就不 能发展 培养和 教育别 人。2021年8月 10日星 期二2021/8/102021/8/102021/8/10
• 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
人教版数学八年级上册 第十二章 小结与复习

(可以简写成“边角边”或“SAS”).
用符号语言表示为:
在△ABC 与△DEF 中, AC = DF,
A
D
∠C =∠F, BC = EF,
CF
B
E
∴△ABC≌△DEF (SAS).
3. 有两角和它们夹边分别相等的两个三角形全等
(可以简写成“角边角”或“ASA”).
用符号语言表示为:
在△ABC 和△DEF 中, ∠A =∠D ,
E
A 1
N P
2
B
FC
证明:过点 P 作 PE⊥BA,PF⊥BC,垂足分别为 E,F.
又∵∠1 =∠2,∴ PE = PF,∠PEA =∠PFC = 90°.
∵∠PCB + ∠BAP = 180°,∠BAP +∠EAP = 180°,
∴∠EAP = ∠FCP.
在△APE 和△CPF 中,
∠PEA =∠PFC = 90°,
第十二章 全等三角形
小结与复习
知识结构图
对应边相等,对应角相等
三角形
性质 全等三角形 判定
应用 角的平分线
知识回顾 一、全等三角形的定义和性质
能够完全重合的两个图形叫全等形,能够完全重 合的两个三角形叫全等三角形.
把两个全等的三角形重合到一起,重合的顶点叫做 对应顶点,重合的边叫做对应边,重合的角叫做对应角.
内就在三角形外;
④三角形的一条中线把该三角形分成面积相等的两部分.
A.①② B.②③
C.③④ D.②④
考点三 全等三角形的性质与判定的综合应用
例3 如图,在△ABC 中,AD 平分∠BAC,CE⊥AD 于
点 G,交 AB 于点 E,EF∥BC 交 AC 于点 F.
人教版八年级上册数学第十二章小结与复习课件ppt

为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
Hale Waihona Puke 为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
Hale Waihona Puke 为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
人教版版八年级上册 第十二章 12.3 角平分线复习课件(共20张PPT)

八年级上习题—— 角平分线复习
相关概念 ——单元复习
根本图形 方法链接
——阶段复习
开展思维 ——期末复习
请写出关于角平分线的联想——
关于角平分线的联想—— 角:角相等
线:垂线段相等
形:+垂直角平分线 +平行 角是轴对称图形
等腰△
等腰△
构造翻折式 全等△
随堂练习
如图,BG,CG是△ABC的外角的平分
根本图形
对称美
E
D
F
B
A
与角平分线有关的根本图形和常用小结论
与角平分线有关的根本图形和常用小结论
4.面积法: S A B C 1 2B C A H 1 2 A B B C C A P D
A
E
P
F
B
C DH
...
作业:
1.校本作业 2.分层作业 联想与中点有关的根本图形 归纳与中点有关的常用方法、结论
B
A
知三推二,其他组合方式
根本图形与结论
E
D AB∥DE
BF平分∠ABE
F EF平分∠BED
B
A
AB∥DE
BF平分∠ABE
BE=AB+DE
F是AD中点 BE=AB+DE
F是AD中点 EF平分∠BED
联积 想累 助丰 力富 思联 维想
随堂检测
小结: 1.几何复习三层次:概念定理、根本图形与
常用结论、思维建构 2.综合题思维建构:破题一句一思、二句一思、 多句一思、关联性思考与图形结论联想 3. 角平分线的根本图形和常用结论,不同联想 得不同的解题思路,常归纳积累不断充实
多句一思,关联性思考
B
C
不同联想, 得不同解题思路
相关概念 ——单元复习
根本图形 方法链接
——阶段复习
开展思维 ——期末复习
请写出关于角平分线的联想——
关于角平分线的联想—— 角:角相等
线:垂线段相等
形:+垂直角平分线 +平行 角是轴对称图形
等腰△
等腰△
构造翻折式 全等△
随堂练习
如图,BG,CG是△ABC的外角的平分
根本图形
对称美
E
D
F
B
A
与角平分线有关的根本图形和常用小结论
与角平分线有关的根本图形和常用小结论
4.面积法: S A B C 1 2B C A H 1 2 A B B C C A P D
A
E
P
F
B
C DH
...
作业:
1.校本作业 2.分层作业 联想与中点有关的根本图形 归纳与中点有关的常用方法、结论
B
A
知三推二,其他组合方式
根本图形与结论
E
D AB∥DE
BF平分∠ABE
F EF平分∠BED
B
A
AB∥DE
BF平分∠ABE
BE=AB+DE
F是AD中点 BE=AB+DE
F是AD中点 EF平分∠BED
联积 想累 助丰 力富 思联 维想
随堂检测
小结: 1.几何复习三层次:概念定理、根本图形与
常用结论、思维建构 2.综合题思维建构:破题一句一思、二句一思、 多句一思、关联性思考与图形结论联想 3. 角平分线的根本图形和常用结论,不同联想 得不同的解题思路,常归纳积累不断充实
多句一思,关联性思考
B
C
不同联想, 得不同解题思路
人教版八年级上数学第12章 全等三角形的复习 课件 (共21张PPT)

EB =CD
B
C
D
全等三角形的复习
学习目标: 1.了解全等三角形的概念,掌握全等三角形
的性质,判定. 2.在图形变换中,熟练把握全等三角形
重点,难点:利用全等三角形解决实际问题.
一、自主复习: 回顾知识,构建知识网络,并完成下列各题:
1.如图1:△ABC ≌△DEF,可得到的相等
的线段有
,
相等的角有
A
D
E
BCBiblioteka 四、拓展提升: 5. 在等边△ABC的顶点A,C处各有一只蜗牛, 它们同时出发,分别以相同的速度由A向B和由C
向A爬行。其中一只爬到终点时另一只也停止运
动,经t分钟后它们分别爬到D,E处,(1)请问
DC和BE相等吗?(2)若蜗牛A和蜗牛C分别爬
到了AB和CA的延长线上的D,E处,其它条件不
A AC=DE,∠A=∠D(ASA)
B ∠ A=∠ D ∠B =∠F(AAA)
C AC=DE BC=EF(SAS) D AB=DF∠A=∠D(AAS)
A
D
C
BE
F
A 1个 B 2个 C 3个 D 4个
4. 如图,在△ABC中,∠C=90° ,D、
E 分 别 为 AC 、 AB 上 的 点 , 且
AD=BD,AE=BC,DE=DC. 判 断 DE 与
AB的位置关系并说明理由。
A
E D
B
C
4. 如图,在△ABC中,∠C=90° ,D、
E 分 别 为 AC 、 AB 上 的 点 , 且
AD=BD,AE=BC,DE=DC. 判 断 DE 与
AB的位置关系并说明理由。
A
E B
人教版初中八年级数学上册第12章_全等三角形小结与复习ppt课件

仅做学习交流,谢谢!
巩固
14.如图,△ABC的∠B的平分线BD与
∠C的外角的平分线CE相交于点P。
求证:点P到三边AB、BC、CA的距离
相等。
A
E
D
P
B
C
几何语言
在△ABC与△DEF中 ∠A= ∠D
AB=DE
A
D
B
C
E
F
∠B= ∠E ∴△ABC≌△DEF(ASA)
三角形全等判定方法4
两角和它们其中一角的对边对应相等的两个三角形全等. (简写为“角角边”或“AAS”)
几何语言
在△ABC与△DEF中
A
D
∠A= ∠D ∠B= ∠E
B
C
E
F
BC= EF
∴△ABC≌△DEF(AAS)
Байду номын сангаас
• 三角形全等的判定1: 三边对应相等的两个三角形全等, 简写为“边边边”或“SSS”。
在△ABC和△ DEF中 AB=DE BC=EF CA=FD
∴ △ABC ≌△ DEF(SSS)
边side 角angle
A
B
C
D
E
F
我们利用前面的结论,还可以得到作一个角等于已知角的方法。
例3:已知∠AOB 求作:∠A′O′B′=∠AOB
找全等形
1.如图,AB∥CD, BC∥AD, AE∥CF,则图中全等
三角形有( )
A 3对
B 4对
D
C
C 5对
E
D 6对
A
F B
找全等形
2.如图,AD平分∠BAC,AB=AC, 连结BD、CD并
延长交AC、AB于E、F,则图中全等三角形有( )
巩固
14.如图,△ABC的∠B的平分线BD与
∠C的外角的平分线CE相交于点P。
求证:点P到三边AB、BC、CA的距离
相等。
A
E
D
P
B
C
几何语言
在△ABC与△DEF中 ∠A= ∠D
AB=DE
A
D
B
C
E
F
∠B= ∠E ∴△ABC≌△DEF(ASA)
三角形全等判定方法4
两角和它们其中一角的对边对应相等的两个三角形全等. (简写为“角角边”或“AAS”)
几何语言
在△ABC与△DEF中
A
D
∠A= ∠D ∠B= ∠E
B
C
E
F
BC= EF
∴△ABC≌△DEF(AAS)
Байду номын сангаас
• 三角形全等的判定1: 三边对应相等的两个三角形全等, 简写为“边边边”或“SSS”。
在△ABC和△ DEF中 AB=DE BC=EF CA=FD
∴ △ABC ≌△ DEF(SSS)
边side 角angle
A
B
C
D
E
F
我们利用前面的结论,还可以得到作一个角等于已知角的方法。
例3:已知∠AOB 求作:∠A′O′B′=∠AOB
找全等形
1.如图,AB∥CD, BC∥AD, AE∥CF,则图中全等
三角形有( )
A 3对
B 4对
D
C
C 5对
E
D 6对
A
F B
找全等形
2.如图,AD平分∠BAC,AB=AC, 连结BD、CD并
延长交AC、AB于E、F,则图中全等三角形有( )
人教版八年级数学上册第12章 全等三角形 小结与复习

∠A =∠D,∠B =∠E,∠C =∠F
( 全等三角形的对应角相等).
二、三角形全等的判定方法
1. 三边分别相等的两个三角形全等 (可以简写为
“边边边”或“SSS”).
A
用符号语言表示为:
在△ABC 和△ DEF 中,
AB = DE, BC = EF,
B
C
D
CA = FD,
∴△ABC≌△DEF (SSS).
∠PEA =∠PFC = 90°,
∠EAP =∠FCP,
PE = PF, ∴△APE≌△CPF (AAS). ∴ AP = CP.
E
A 1
N P
2
B
FC
证法2 思路分析:由角是轴对称图形,其对称轴是角
平分线所在的直线,所以可想到构造轴对称图形. 方法
是在 BC 上截取 BD = BA,连接 PD (如图).
1 2
N P
FC
∴∠EAP =∠FCP =∠PCB. ∵∠BAP +∠EAP = 180°, ∴∠PCB +∠BAP = 180°.
E
N
A 1 2
B
P FC
想一想:本题如果不给图,条件不变,请问∠PCB 与∠PAB 有怎样的数量关系呢?
性质
全等 三角形
判定
作用 角的平分线 的性质定理 角的平分线 的判定定理
构造角平分线模型.
1 2
N P
B
FC
证明:过点 P 作 PE⊥BA,PF⊥BC,垂足分别为 E,F.
又∵∠1 =∠2,∴ PE = PF,∠PEA =∠PFC = 90°.
∵∠PCB + ∠BAP = 180°,∠BAP +∠EAP = 180°,
八年级数学上册 第十二章全等三角形小结与复习课件2_6-10
∵∠ACB=∠ECD,CB=CD,
∠ABC=∠EDC, ∴△EDC≌△ABC(ASA).
CD
∴DE=BA.
E
答:测出DE的长就是A、B之间的距离.
花瓶里的纸花与笔筒中毛笔同时被主人摆放在案桌上。之后,蚂蚁逢人便说:“当你遇到无法逾越的障碍时,不妨换一种方式。玛茨亚很机灵,不过还是被吓了一跳。 电影在线观看 /tv/29.html 它倒还能挺直身子走路。
AD=AD, AB=AC,
∴ Rt△ADB ≌ Rt△ADC(HL). ∴BD=CD.
A
B
D
C
方法总结
利用全等三角形可以测量一些不易测量的距离和长度,还可对某些 因素作出判断,一般采用以下步骤: (1)先明确实际问题;
(2)根据实际抽象出几何图形;
(3)经过分析,找出证明途径; (4)书写证明过程.
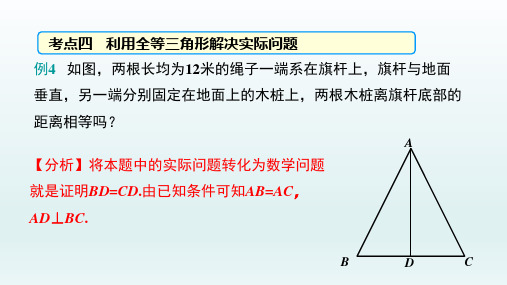
考点四 利用全等三角形解决实际问题 例4 如图,两根长均为12米的绳子一端系在旗杆上,旗杆与地面 垂直,另一端分别固定在地面上的木桩上,两根木桩离旗杆底部的 距离相等吗?
A
【分析】将本题中的实际问题转化为数学问题
就是证明BD=CD.由已知条件可知AB=AC,
AD⊥BC.
B
D
C
解:相等,理由如下:
∵AD⊥BC, ∴∠ADB=∠ADC=90°. 在Rt△ADB和Rt△ADC中,
针对训练
5.如图,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离不 能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间 的距离吗?
解:要测量A、B间的距离,可用如下方法:
D=BC,
再作出BF的垂线DE,使A、C、E在一条直
线上,
“现在我再来匀一匀。,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
针对训练
4.如图,OB⊥AB,OC⊥AC,垂足为B,C,OB=OC,
∠BAO =∠CAO吗?为什么?
解: ∠BAO=∠CAO,
B
理由:∵ OB⊥AB,OC⊥AC,
∴ ∠B=∠C=90°. A
O
在Rt△ABO和Rt△ACO中,
OB=OC,AO=AO,
C
∴ Rt△ABO≌Rt△ACO ,(HL)
∴ ∠BAO=∠CAO.
针对训练
1.如图所示,△ABD≌△ACD,∠BAC=90°. (1)求∠B; (2)判断AD与BC的位置关系,并说明理由.
解:(1)∵△ABD≌△ACD, ∴∠B=∠C, 又∵∠BAC=90°, ∴∠B=∠C=45°; (2)AD⊥BC. 理由:∵△ABD≌△ACD, ∴∠BDA=∠CDA, ∵∠BDA+∠CDA=180°, ∴∠BDA=∠CDA=90°, ∴AD⊥BC.
A D
B
CE
F
性质:
全等三角形的对应边相等,对应角相等.
A
D
B
CE
F
应用格式:如图:∵△ABC≌△DEF,
∴AB=DE,BC=EF,AC=DF (全等三角形的对应边相等 ), ∠A=∠D,∠B=∠E,∠C=∠F ( 全等三角形的对应角相等).
二、三角形全等的判定方法 1.两边和它们的夹角对应相等的两个三角形全
CF
AB=DE,(已知 ) B
E
∠B=∠E,(已知 )
∴ △ABC≌△DEF.(ASA)
3.三边对应相等的两个三角形全等(可以简写为“
边边边”或“SSS”).
A
用符号语言表达为:
在△ABC和△ DEF中,
AB=DE,
B
C
BC=EF,
D
CA=FD,
∴ △ABC ≌△ DEF.(SSS)
E
F
4.有两角和其中一个角的对边对应相等的两个三
等 (可以简写成“边角边”或“SAS”).
用符号语言表达为:
在△ABC与△DEF中
A
D
AC=DF,
∠C=∠F,
CF
BC=EF,
B
E
∴△ABC≌△DEF.(SAS)
2.有两角和它们夹边对应相等的两个三角形 全等(可以简写成“角边角”或“ASA”).
用符号语言表达为:
A
D
在△ABC和△DEF中,
∠A=∠D ,(已知 )
∴ ∠DEG = ∠ DCG. ∵EF//BC, ∴ ∠FEC= ∠ECD, ∴ ∠DEG = ∠ FEC.
E B
A
G
F
D
C
方法总结
利用全等三角形证明角相等,首先要找到两个角 所在的两个三角形,看它们全等的条件够不够;有时 会用到等角转换,等角转换的途径很多,如:余角, 补角的性质、平行线的性质等,必要时要想到添加辅 助线.
第十二章
八年级数学上(RJ) 教学课件
全等三角形
小结与复习
要点梳理
考点讲练
课堂小结
课后作业
要点梳理
一、全等三角形的性质 能够完全重合的两个图形叫全等图形,能够完全重 合的两个三角形叫全等三角形.
把两个全等的三角形重合到一起,重合的顶点叫做对 应顶点,重合的边叫做对应边,重合的角叫做对应角.
其中点A和 点D,点B和 点E ,点C和_ 点F _是对应顶点. AB和 DE ,BC和 EF ,AC和 DF 是对应边. ∠A和 ∠D ,∠B和 ∠E , ∠C和 ∠F 是对应角.
考点二 全等三角形的判定
例2 已知,∠ABC=∠DCB,∠ACB= ∠DBC, 求证:△ABC≌△DCB.
【分析】运用“两角和它们的夹边对应相等两个三角 形全等”进行判定.
证明:在△ABC和△DCB中,
A
D
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知), B
C
∴△ABC≌△DCB(ASA ).
C
B
O
A
D
考点三 全等三角形的性质与判定的综合应用
例3 如图,在△ABC中,AD平分∠BAC,CE⊥AD于点
G,交AB于点E,EF∥BC交AC于点F,
A
求证:∠DEC=∠FEC.
【分析】欲证∠DEC=∠FEC
E
G
F
B
由平行线的性质转化为证明
D
C
∠DEC=∠DCE
只需要证明△DEG ≌ △DCG.
证明: ∵CE⊥AD, ∴ ∠AGE=∠AGC=90 °.
角形全等(可以简写成“角角边”或“AAS”).
5.斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”或“HL”.
注意:①对应相等.
A
②“HL”仅适用直角三角形,
③书写格式应为:
C
B
∵在Rt△ ABC 和Rt△ DEF中, D AB =DE,
AC=DF,
E
F
∴Rt△ABC≌Rt△DEF (HL)
解:(1)∵△ACE≌△DBF, ∴AC=BD,则AB=DC, ∵BC=2,∴2AB+2=8, ∴AB=3,∴AC=3+2=5; (2)∵△ACE≌△DBF, ∴∠ECA=∠FBD, ∴CE∥BF.
方法总结
两个全等三角形的长边与长边,短边与短边分 别是对应边,大角与大角,小角与小角分别是对应 角.有对顶角的,两个对顶角一定为一对对应角.有 公共边的,公共边一定是对应边.有公共角的,公共 角一定是对应角.
针对训练
2.已知△ABC和△DEF,下列条件中,不能保证△ABC
和△DEF全等的是( D )
A.AB=DE,AC=DF,BC=EF
B. ∠A= ∠ D, ∠ B= ∠ E,AC=DF
C.AB=DE,AC=DF, ∠A= ∠D D.AB=DE,BC=EF, ∠ C= ∠ F
3.如图所示,AB与CD相交于点O, ∠A=∠B, OA=OB 添加条件 ∠C=∠D 或∠AOC=∠,BOD 所以 △AOC≌△BOD 理由是 AAS 或ASA .
A
∵AD平分∠BAC,∴ ∠EAG=∠CAG,.
在△AGE和△AGC中,
∠AGE=∠AGC, AG=AG, ∠EAG=∠CAG,
E B
∴ △AGE ≌ △AGC(ASA),
∴ GE =△DGE和△DGC中,
EG=CG, ∠ EGD= ∠ CGD=90 °, DG=DG.
∴ △DGE ≌ △DGC(SAS).
三、 角平分线的性质与判定 角的平分线的性质 角的平分线的判定
图形
C
P
已知 条件
结论
OP平分∠AOB PD⊥OA于D PE⊥OB于E
PD=PE
C P
PD=PE PD⊥OA于D PE⊥OB于E OP平分∠AOB
考点讲练
考点一 全等三角形的性质 例1 如图,已知△ACE≌△DBF.CE=BF,AE=DF, AD=8,BC=2. (1)求AC的长度; (2)试说明CE∥BF.
