文科立体几何知识点方法总结高三复习
高中数学(文科)立体几何知识点总结

l立体几何知识点整理(文科)l // ml //m m直线和平面的三种位置关系:一.αl1. 线面平行方法二:用面面平行实现。
l//l //αl符号表示:2. 线面相交βl lαAα方法三:用平面法向量实现。
符号表示:n 为平若面线在面内3. 的一个法向量,lnn l ll //且。
,则lαα符号表示:二.平行关系:线线平行:1.方法一:用线面平行实现。
3. 面面平行:l mβl //l方法一:用线线平行实现。
l'l // ml m'αl // l 'm m // m'm//且相交l , m且相交l ' , m'方法二:用面面平行实现。
//l βl // mlγm mα方法二:用线面平行实现。
方法三:用线面垂直实现。
l //l, m l // m //m //若。
,则l l , m且相交mβ方法四:用向量方法:m l l // m。
若向量和向量共线且l、m不重合,则α2.线面平行:方法一:用线线平行实现。
1/11lC A方法三:用向量方法:Bαl m l m ,则的数量积为和向量若向量0。
三.垂直关系:夹角问题。
三.线面垂直:1.异面直线所成的角:一)(方法一:用线线垂直实现。
(0 ,90 ]范围:(1)ACl ABl 求法:(2)P n lABAC A方法一:定义法。
AθO AC, ABα:平移,使它们相交,找到夹角。
步骤1方法二:用面面垂直实现。
)常用到余弦定理步骤2:解三角形求出角。
(余弦定理:βl lm a c222cab l m, l mcosθ2ab bα)计算结果可能是其补角(面面垂直:2.方法二:向量法。
转化为向量方法一:用线面垂直实现。
C的夹角βl lθl:)(计算结果可能是其补角BA AB ACαcos AB AC方法二:计算所成二面角为直角。
线面角)(二线线垂直:3.上任取一点(1) 定义:直线l ,作(交点除外)P方法一:用线面垂直实现。
高中文科立体几何基础知识点
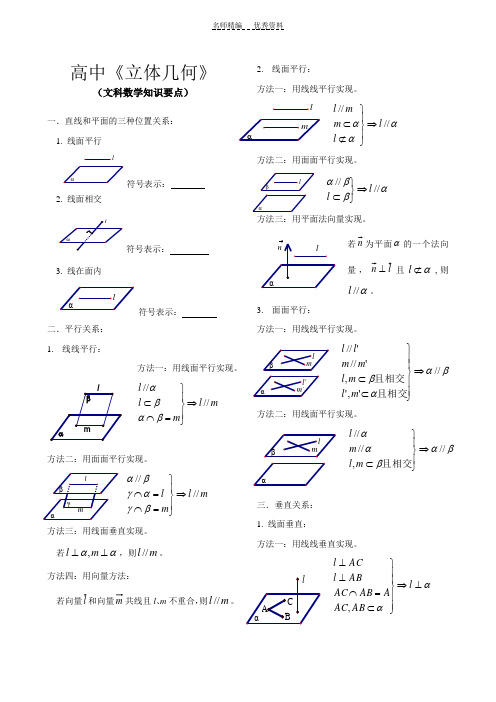
高中《立体几何》(文科数学知识要点)一.直线和平面的三种位置关系:1. 线面平行l符号表示:2. 线面相交符号表示:3. 线在面内符号表示:二.平行关系:1.线线平行:方法一:用线面平行实现。
mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα方法二:用面面平行实现。
mlml////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα方法三:用线面垂直实现。
若αα⊥⊥ml,,则ml//。
方法四:用向量方法:若向量和向量共线且l、m不重合,则ml//。
2.线面平行:方法一:用线线平行实现。
ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂方法二:用面面平行实现。
αββα////ll⇒⎭⎬⎫⊂方法三:用平面法向量实现。
若n为平面α的一个法向量,ln⊥且α⊄l,则α//l。
3.面面平行:方法一:用线线平行实现。
βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll方法二:用线面平行实现。
βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三.垂直关系:1. 线面垂直:方法一:用线线垂直实现。
αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥lABACAABACABlACl,mlα方法二:用面面垂直实现。
αββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥l l m l m ,2. 面面垂直:方法一:用线面垂直实现。
βαβα⊥⇒⎭⎬⎫⊂⊥l l方法二:计算所成二面角为直角。
3. 线线垂直:方法一:用线面垂直实现。
m l m l ⊥⇒⎭⎬⎫⊂⊥αα方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭三.夹角问题。
(一) 异面直线所成的角: (1) 范围:]90,0(︒︒ (2)求法:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理) 余弦定理:abcb a 2cos 222-+=θ(计算结果可能是其补角) (二) 线面角(1)定义:直线l 上任取一点P (交点除外),作PO ⊥α于O,连结AO ,则AO 为斜线PA 在面α内的射影,PAO ∠(图中θ)为直线l 与面α所成的角。
高中文科数学立体几何知识点

立体几何知识点(文科)一.平行关系1. 线线平行:方法一:用线面平行实现。
m l m l l ////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα方法二:用面面平行实现。
m l m l ////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα 方法三:用线面垂直实现。
若αα⊥⊥m l,,则m l //。
方法四:用向量方法:若向量l 和向量m 共线且l 、m 不重合,则m l //。
2。
线面平行:方法一:用线线平行实现。
ααα////l l m m l ⇒⎪⎭⎪⎬⎫⊄⊂ 方法二:用面面平行实现。
αββα////l l ⇒⎭⎬⎫⊂方法三:用平面法向量实现。
若n为平面α的一个法向量,l n ⊥且α⊄l ,则α//l 。
3。
面面平行:方法一:用线线平行实现。
βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交m l m l m m l l方法二:用线面平行实现.βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交m l m l 二.垂直关系: 2. 线面垂直:方法一:用线线垂直实现。
αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥l AB AC A AB AC AB l ACl ,方法二:用面面垂直实现。
αββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥l l m l m , 2。
面面垂直:方法一:用线面垂直实现。
βαβα⊥⇒⎭⎬⎫⊂⊥l l方法二:计算所成二面角为直角。
3. 线线垂直:方法一:用线面垂直实现.m l m l ⊥⇒⎭⎬⎫⊂⊥αα方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭三 夹角问题。
(一) 异面直线所成的角:(1) 范围:]90,0(︒︒(2)求法:方法一:定义法。
l步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理)余弦定理:abcb a 2cos 222-+=θ(计算结果可能是其补角)(二) 线面角(1)定义:直线l 上任取一点P (交点除外),作PO ⊥α于O ,连结AO ,则AO 为斜线PA 在面α内的射影,PAO ∠(图中θ)为直线l 与面α所成的角。
高中文科数学立体几何知识点

高考立体几何中直线、平面之间的地点关系知识点总结(文科)一.平行问题(一)线线平行:方法一:常用初中方法( 1 中位线定理; 2 平行四边形定理;3 三角形中对应边成比率;4 同位角、内错角、同旁内角)方法二: 1 线面平行线线平行ll //l l // m mm方法三: 2 面面平行线线平行lβ//γml l // mαm方法四: 3 线面垂直线线平行若 l, m,则 l // m 。
方法五:用向量方法:若向量 l 和向量 m 共线且l、m不重合,则l // m。
(二)线面平行:方法一: 4 线线平行线面平行ll // m mm l //αl方法二: 5 面面平行线面平行lβ//l //αl方法三:法向量n l若 n 为平面的一个法向量,n l且 l, 则l //。
α(三)面面平行: 6 方法一:线线平行面面平行l // l 'lm // m'βm //l , m且订交l'l ', m'且订交αm'方法二: 7 线面平行面面平行l //, m //βlml , m//l m Aα方法三: 8 线面垂直面面平行面l// 面面面l方法三:用向量实现。
平面、的法向量分别是m、 nm // n 面 // 面二.垂直问题:(一)线线垂直方法一:常用初中的方法( 1 勾股定理的逆定理; 2 三线合一;3 直径所对的圆周角为直角;4 菱形的对角线相互垂直。
)方法二: 9 线面垂直线线垂l直mαll mm方法三:三垂线定理及其逆定理。
PPO A Ol OA l PAαll l方法四:直线 l、 m上的向量分别是l 、 m ml m l mα(二)线面垂直:10 方法一:线线垂直线面垂直l AC ll ABlAC AB A CAAC ,ABBα方法二: 11 面面垂直线面垂直βlmm ll m, lα方法三:平面的法向量是 nn// l平面l(面)面面垂直:方法一: 12 线面垂直面面垂直βlllα方法二:平面、的法向量分别是 m、 n n m面面三、夹角问题:异面直线所成的角:( 一) 范围:(0 ,90 ]增补:空间向量在立体几何问题中的应用1 A(x, y, z) , x叫横坐标, y 叫纵坐标,z 叫竖坐标。
2021年文科立体几何知识点方法总结高三复习

立体几何知识点整顿(文科)一.直线和平面三种位置关系:1. 线面平行l符号表达:2. 线面相交符号表达:3. 线在面内符号表达:二.平行关系:1.线线平行:办法一:用线面平行实现。
mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα办法二:用面面平行实现。
mlml////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα办法三:用线面垂直实现。
若αα⊥⊥ml,,则ml//。
办法四:用向量办法:若向量l和向量m共线且l、m不重叠,则ml//。
2.线面平行:办法一:用线线平行实现。
ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂办法二:用面面平行实现。
αββα////ll⇒⎭⎬⎫⊂办法三:用平面法向量实现。
若为平面α一种法向量,⊥且α⊄l,则α//l。
3.面面平行:办法一:用线线平行实现。
βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll办法二:用线面平行实现。
βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三.垂直关系:1. 线面垂直:办法一:用线线垂直实现。
lαα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥l AB AC A AB AC AB l ACl ,办法二:用面面垂直实现。
αββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥l l m l m ,2. 面面垂直:办法一:用线面垂直实现。
βαβα⊥⇒⎭⎬⎫⊂⊥l l办法二:计算所成二面角为直角。
3. 线线垂直:办法一:用线面垂直实现。
m l m l ⊥⇒⎭⎬⎫⊂⊥αα办法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭办法三:用向量办法:若向量和向量数量积为0,则m l ⊥。
三.夹角问题。
(一) 异面直线所成角: (1) 范畴:]90,0(︒︒ (2)求法: 办法一:定义法。
环节1:平移,使它们相交,找到夹角。
环节2:解三角形求出角。
(惯用到余弦定理) 余弦定理:cos =θ(计算成果也许是其补角) 办法二:向量法。
文科立体几何知识点、方法总结材料高三复习
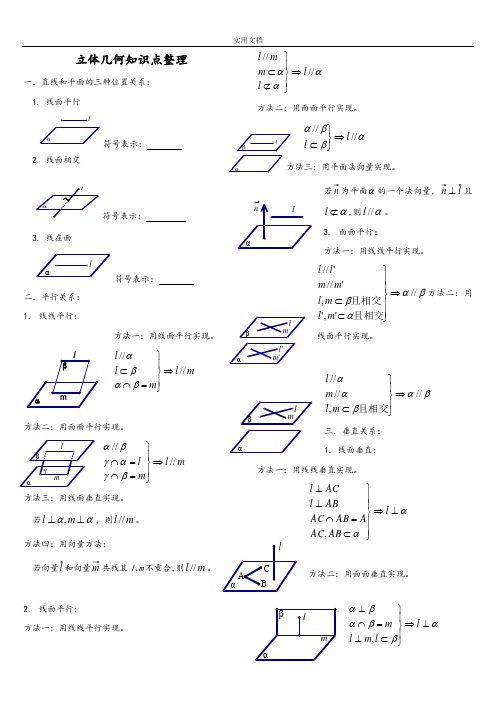
立体几何知识点整理一.直线和平面的三种位置关系:1. 线面平行l符号表示:2. 线面相交符号表示:3. 线在面符号表示:二.平行关系:1.线线平行:方法一:用线面平行实现。
mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα方法二:用面面平行实现。
mlml////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα方法三:用线面垂直实现。
若αα⊥⊥ml,,则ml//。
方法四:用向量方法:若向量和向量共线且l、m不重合,则ml//。
2.线面平行:方法一:用线线平行实现。
ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂方法二:用面面平行实现。
αββα////ll⇒⎭⎬⎫⊂方法三:用平面法向量实现。
若为平面α的一个法向量,⊥且α⊄l,则α//l。
3.面面平行:方法一:用线线平行实现。
βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll方法二:用线面平行实现。
βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三.垂直关系:1. 线面垂直:方法一:用线线垂直实现。
αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥lABACAABACABlACl,方法二:用面面垂直实现。
αββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥llmlm,2. 面面垂直:方法一:用线面垂直实现。
βαβα⊥⇒⎭⎬⎫⊂⊥l l方法二:计算所成二面角为直角。
3. 线线垂直:方法一:用线面垂直实现。
m l m l ⊥⇒⎭⎬⎫⊂⊥αα方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭方法三:用向量方法:若向量和向量的数量积为0,则m l ⊥。
三.夹角问题。
(一)异面直线所成的角:(1) 围:]90,0(︒︒ (2)求法: 方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理) 余弦定理:abc b a 2cos 222-+=θ(计算结果可能是其补角)方法二:向量法。
转化为向量的夹角 (计算结果可能是其补角):=θcos(二)线面角(1)定义:直线l 上任取一点P (交点除外),作PO ⊥α于O,连结AO ,则AO 为斜线PA 在面α的射影,PAO ∠(图中θ)为直线l 与面α所成的角。
文科立体几何知识点、方法总结高三复习 (1)

立体几何知识点整理一.直线和平面的三种位置关系:1. 线面平行l符号表示:2. 线面相交符号表示:3. 线在面内符号表示:二.平行关系:1.线线平行:方法一:用线面平行实现。
mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα方法二:用面面平行实现。
mlml////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα方法三:用线面垂直实现。
若αα⊥⊥ml,,则ml//。
方法四:用向量方法:若向量和向量共线且l、m不重合,则ml//。
2.线面平行:方法一:用线线平行实现。
ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂方法二:用面面平行实现。
αββα////ll⇒⎭⎬⎫⊂方法三:用平面法向量实现。
若n为平面α的一个法向量,ln⊥且α⊄l,则α//l。
3.面面平行:方法一:用线线平行实现。
βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll方法二:用线面平行实现。
βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三.垂直关系:1. 线面垂直:方法一:用线线垂直实现。
αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥lABACAABACABlACl,方法二:用面面垂直实现。
αββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥llmlm,2. 面面垂直:方法一:用线面垂直实现。
βαβα⊥⇒⎭⎬⎫⊂⊥l l方法二:计算所成二面角为直角。
3. 线线垂直:方法一:用线面垂直实现。
m l m l ⊥⇒⎭⎬⎫⊂⊥αα方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭方法三:用向量方法:若向量和向量的数量积为0,则m l ⊥。
三.夹角问题。
(一) 异面直线所成的角: (1) 范围:]90,0(︒︒ (2)求法: 方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理) 余弦定理:abcb a 2cos 222-+=θ(计算结果可能是其补角)方法二:向量法。
高中文科数学立体几何知识点总结材料

高中文科数学立体几何知识点总结材料立体几何知识点整理(文科)l 若向量 l 和向量 m 共线且 l 、m一. 直线和平面的三种地点关系:αm 不重合,则 l // m 。
1. 线面平行l2. 线面平行:α 符号表示:方法一:用线线平行实现。
lβ2. 线面订交α l // m m l //llAα符号表示:方法二:用面面平行实现。
3. 线在面内nl//ll //αlα符号表示:二. 平行关系:1. 线线平行:方法三:用平面法向量实现。
方法一:用线面平行实现。
若 n 为平面的一个法向量,n l 且 l,则ll //l // 。
ll // mmm方法二:用面面平行实现。
lβ//3. 面面平行:γl l // mαmm方法一:用线线平行实现。
方法三:用线面垂直实现。
l // l 'm // m'//若 l, m,则 l // m 。
l , m 且订交l ', m'且订交lβml' αm'高中文科数学立体几何知识点总结材料2. 面面垂直:方法一:用线面垂直实现。
C方法二:用线面平行实现。
βll //m ////l αl , m且订交mβllθAB方法二:计算所成二面角为直角。
α3. 线线垂直:方法一:用线面垂直实现。
lC AαBlllmmmα方法二:三垂线定理及其逆定理。
PPOlOAl PA三.垂直关系:A Ol1. 线面垂直:αl方法一:用线线垂直实现。
l AC 方法三:用向量方法:lAB若向量 l 和向量 m 的数目积为0 ,则 lm 。
AC lAB A AC,AB三. 夹角问题。
(一 )异面直线所成的角:方法二:用面面垂直实现。
(1) 范围: (0 ,90 ](2) 求法:Pβlnmlmlm, lα方法一:定义法。
αAθO步骤 1 :平移,使它们订交,找到夹角。
步骤 2 :解三角形求出角。
(常用到余弦定理 )余弦定理:aca 2b 2c 2θbcos2ab(计算结果可能是其补角 )方法二:向量法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何知识点整理方法二:用面面平行实现。
•直线和平面的三种位置关系:// ll //1.线面平行方法三:用平面法向量实现。
若n 为平面的一个法向量,n2.线面相交则丨〃3.面面平行:符号表示:方法一:用线线平行实现。
l //l' m// m' l, m 且相交 l',m' 且相交方法用线面平行实现。
二•平行关系: 1.线线平行: l // 方法一:用线面平行实现。
l //l 〃m mm//且相交•垂直关系:1.线面垂直://方法二:用面面平行实现。
『二'刁7〃 a m 丰 方法三:用线面垂直实现。
l l //m m 方法一:用线线垂直实现。
l AC l AB lAC AB A AC, AB方法二:用面面垂直实现。
若 I ,m ,则 l // m 。
方法四:用向量方法: 若向量l 和向量m 共线且I 、m 不重合,则l//m 。
m ll m,l2.面面垂直:2.线面平行: 方法一:用线线平行实现。
l//m ml //方法一:用线面垂 直实现。
(1)定义:直线l上任取一点P (交点除外),作PO 于O,连结AO ,则AO为斜线PA在面内的射影,PAO (图中)为直线I与面所成的角。
方法二:计算所成二面角为直角。
3.线线垂直:方法一:用线面垂直实现。
方法二:三垂线定理及其逆定理。
方法三:用向量方法: POl OAll PA⑵范围:[0 ,90 ]当0时,l 或丨〃当90时,l(3)求法:方法一:定义法。
步骤1:作出线面角,并证明。
步骤2:解三角形,求出线面角。
若向量l和向量m的数量积为0,则l m。
三•夹角问题。
(一)异面直线所成的角:(1)范围:(0,90] (三)二面角及其平面角(1)定义:在棱I上取一点P,两个半平面内分别作I的垂线(射线)m、n,则射线m和n的夹角为二面角一l —的平面角。
(2)求法:方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理)余弦定理:2 2 2a b ccos2ab b ⑵范围:[0,180] (3)求法:方法一:定义法。
(计算结果可能是其补角)方法二:向量法。
转化为向量的夹角(计算结果可能是其补角):AB ACcos —: ------ rAB AC 步骤1:作出二面角的平面角(三垂线定理),并证明。
步骤2:解三角形,求出二面角的平面角。
方法二:截面法。
步骤1:如图,若平面POA同时垂直于平面和,则交线(射线)AP和AO的夹角就是二面角。
步骤2:解三角形,求出二面角。
(二)线面角和等面积法;换点法)2 .线面距、面面距均可转化为点面距。
3 .异面直线之间的距离方法一:转化为线面距离。
如图,AD是异面直线m和n的公垂线段,m//m', 则异面直线m和n之间的距离为:步骤1:过点P作PO 于0,线段PO即为所求。
步骤2:计算线段P0的长度。
(直接解三角形;等体积法高考题典例考点1点到平面的距离例1如图,正三棱柱ABC ABQ的所有棱长都为2 , D为CG中点.(I)求证:AB丄平面ABD ;(D )求二面角 A A1D B的大小;(川)求点C到平面ABD的距离.解答过程(I)取BC中点0,连结AO . Q A ABC为正三角形,A0丄BC . Q正三棱柱ABC AB1C1中,平面ABC丄平面BCGB1, AO丄平面BCGB .连结BQ,在正方形BBCQ中,O, D分别为BC, CG的中点,BO丄BD ,步骤一:计算ir uuLTuucos n i n2步骤二:判断与IT UUq n2的关系,可能相等或者互补。
如图,m和n为两条异面直线,n 且m〃则异面直线m和n之间的距离可转化为直线m与平面之间的距离。
方法二:直接计算公垂线段的长度。
方法三:公式法。
四•距离问题。
1 .点面距。
方法一:几何法。
d c2a2b22ab cos方法三:坐标法)。
AB i 丄BD .在正方形 ABBiA 中,AB ’丄A ,B , AB ’丄平面ABD •(^)设AB I 与AB 交于点G ,在平面 ABD3中,作GF 丄AD 于F ,连结AF ,由(I )得AB 丄平面A BD . AF 丄A D ,/AFG 为二面角 A AD B的平面角.在厶AA D 中 ,由等面 sin Z AFG 竺 2 卫•4所以二面角AF 4.5法可求得AF 土卫,又Q AG - AB 12 , 521A DB 的大小为 arcsi m)△ ABD 中,4BD AD .5, A B 2 2,S A A BD6 , S △ BCD在正三棱柱中, A 到平面BCGB 的距离为 3 .设点C到平面 A l BD 的距离为 d .由 V A BCDV C A BD ,得 BCD g 31S ^ A B°gd , d 二•点 C 到平33S A A BD2面ABD 的距离为』2 .考点2 异面直线的距离2例2已知三棱锥S ABC ,底面是边长为4.. 2的正三角形,棱 SC 的长为2,且垂直于底面.E 、D 分别 为BC 、AB 的中点,求CD 与SE 间的距离.解答过程:如图所示,取 BD 的中点F ,连结EF , SF , CF ,EF 为 BCD 的中位线, EF // CD, CD //面 SEF , CD到平面SEF 的距离即为两异面直线间的距离 •又 线面之间的距 离可转化为线 CD 上一点C 到平面SEF的距离,设其为h ,由题意知,BC 4:2,D 、E 、F 分别是AB 、 BC 、BD 的中点,CD 2 6, EF -CD . 6, DF . 2, SC 2 2V S 1 1CEF——EF DF SC1 -6 2 2 2.33 23 23在Rt SCE中,SESC2CE 22 3在Rt SCF SFSC 2 CF 24 24 230又 EF 6, S SEF 3由于V C SEFVS CEF3S SEF1 h ,即一3 h32一3 3故CD 与SE 间的距离为2 -312 ;6即BD 到平面GB i D i 的距离等于 ——3解析二 BD //平面GB i D i ,BD 上任意一点到平面 GB i D i 的距离皆为所求,以下求点 B 平面GB i D i 的距离.设点B 到平面GB i D i 的距离为h ,将它视为三棱锥 B GB i D i 的高,则V B GB i D i V D i GBB i,由于 SGB i Di即BD 到平面GB i D i 的距离等于 小结:当直线与平面平行时,直线上的每一点到平面的距离都相等,选准恰当的点,转化为点面距离•本例解析一是根据选出的点直接作出距离;解析二是等体积法求出点面距考点4异面直线所成的角考点3 直线到平面的距离例3 .如图,在棱长为 2的正方体 AG 中,G 是AA 的中点,求 BD 到平面GB 1D 1的距离.思路启迪:把线面距离转化为点面距离,再用点到平面距离的方法求解解答过程:解析一 BD //平面GB i D i ,BD 上任意一点到平面 GB i D i 的距离皆为所求,以下求点0平面GB i D 1的距离,B i D i A iC i , B iD iA 1A ,B i D i 平面 AACG ,又 B 1D 1平面GB 1D 1平面A i ACC iGB i D i ,两个平面的交线是 O i G ,作OH 0i G 于H ,则有 0H 平面GB D i ,即0H 是0点到平面GB i D i 的距离.在 O i OG 中,S O -OG1 O i O AO2 OQGAA_-OH O i G- .3 OH 2 22, OH &3V D i GBB i都是线面距离•所以求线面距离关键是例4如图,在Rt A AOB 中,OAB 芒,斜边 AB 4 . Rt △ AOC 可以通过Rt △ AOB 以直线 AO 为轴旋转6得到,且二面角B AO C 的直二面角.D 是AB 的中点.(I) 求证:平面COD 平面AOB ; (II) 求异面直线 AO 与CD 所成角的大小. 解答过程:(I )由题意,CO AO , BO AO ,BOC 是二面角B AO C 是直二面角, CO BO ,又 Q AOI BO O , CO 平面 AOB ,又CO 平面COD . 平面COD 平面AOB .(II )作DE OB ,垂足为E ,连结CE (如图),则DE // AO ,小结: 求异面直线所成的角常常先作出所成角的平面图形,作法有:①平移法:在异面直线中的一条直 线上选择“特殊点”,作另一条直线的平行线,如解析一,或利用中位线,如解析二;②补形法:把空间图形补成熟悉的几何体, 其目的在于容易发现两条异面直线间的关系, 如解析三•一般来说,平移法是最常 用的,应作为求异面直线所成的角的首选方法•同时要特别注意异面直线所成的角的范围:0_,2考点5直线和平面所成的角例5.四棱锥S ABCD 中,底面ABCD 为平行四边形,侧面SBC 底面ABCD .已知/ ABC 45°, AB BC 2 2, SA SB 3 .(I)证明SA BC ; (n)求直线SD 与平面SAB 所成角的大小. 解答过程:(I)作SO 丄BC ,垂足为O ,连结AO ,由侧面SBC 丄ABCD ,得SO 丄底面ABCD .因为SA SB ,所以AO BO ,又Z ABC 45° ,故△ AOB 为等腰直角三角形,AO 丄BO ,由三垂线定理,得 SA 丄BC .(n)由(I)知 SA 丄BC ,依题设AD // BC ,在 Rt A COE 中,CO BO 2 , OE 1BO 〔,2CECO 2 OE 2又 DE 1AO 3 .在 Rt △CDE 中,tanCDECE5 315 . 2DE 3异面直线AO 与CD 所成角的大小为arcta n 153ADE.z -DB yCDE 是异面直线AO 与CD 所成的角. AB故 SA 丄 AD ,由 AD BC 2、2 , SA 、3 , AO ,2,得 SO 1 , SD J1 . △ SAB 的面积 S 1 ABg SA 2 1 AB .2 • 连结 DB ,得△ DAB 的面积 S 2 丄ABgAD sin135° 2 2 设D 到平面SAB 的距离为h ,由于V SAB V S ABD 设SD 与平面SAB 所成角为,则si n 所以,直线SD 与平面SBC 所成的我为 h _2 SD 11.V22 arcs in11,得丄 hgS - SOgS 2,解得 h 2 . 3 322 11小结:求直线与平面所成的角时,应注意的问题是( 1 )先判断直线和平面的位置关系; (2)当直线和平 面斜交时,常用以下步骤:①构造一一作出斜线与射影所成的角,②证明一一论证作出的角为所求的角, ③计算一一常用解三角形的方法求角,④结论一一点明直线和平面所成的角的值 考点6 二面角 例6 .如图,已知直二面角 PQ , A PQ , B , C , CA BAP 45°,直线CA 和平面 所成的角为30o . (I )证明BC 丄PQB AC Q过程指引:(1)在平面 内过点C 作CO 丄PQ 于点O ,连结OB .因为 丄 ,I PQ ,所以CO 丄,又因为CA CB ,所以 OA OB .而 BAO 45°,所以 ABO 45°, AOB 90°,从而 BO 丄 PQ ,又 CO 丄 PQ ,所以 PQ 丄平面OBC . 因为BC 平面OBC , 故PQ 丄BC .(II ) 由(1)知,BO 丄PQ ,又 丄 ,1 PQ ,BO所以BO 丄 .过点O 作OH 丄AC 于点H ,连结BH(II )求二面角 P 的大小.,由三垂线定理知, BH 丄AC .故QBHO 是二面角B AC P 的平面角.由(I )知,CO 丄,所以 CAO 是CA 和平面 所成的角,贝U CAO 30°,不妨设AC 2,贝V AO 、3 , OH AOsin 30°3•2在Rt A OAB 中, ABO BAO 45°,所以BO AO 、、3 ,于是在Rt△BOH 中,tan BHO 2 .故二面角B AC P的大小为arctan2 .OH 船T小结:本题是一个无棱二面角的求解问题•解法一是确定二面角的棱,进而找出二面角的平面角•无棱二面角棱的确定有以下三种途径:①由二面角两个面内的两条相交直线确定棱,②由二面角两个平面内的两条平行直线找出棱,③补形构造几何体发现棱;解法二则是利用平面向量计算的方法,这也是解决无棱二面角的一种常用方法,即当二面角的平面角不易作出时,可由平面向量计算的方法求出二面角的大小考点7利用空间向量求空间距离和角例7 .如图,已知ABCD A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,且AE FC1 1 .(1)求证:E, B, F, D1四点共面;2垂足为(2)若点G 在BC 上, BG ,点M 在BB1 上, GM 丄BF ,3H,求证:EM丄平面BCC1B1;(3)用表示截面EBFD1和侧面BCC1B1所成的锐二面角的大小,求tan过程指引:(1)如图,在DD1上取点N,使DN 1,连结EN , CN ,则AE DN 1 , CF ND12.因为AE // DN , ND1 // CF,所以四边形ADNE , CFD1N都为平行四边形.从而EN /AD , FD1// CN .又因为AD /BC,所以EN /BC,故四边形BCNE是平行四边形,由此推知CN // BE,从而FD1// BE •因此,E, B, F, D1四点共面.(2)如图,GM 丄BF,又BM 丄BC,所以/ BGM / CFB ,BC 2 3BM BGgtan/ BGM BGgtan/CFB BGg 1.因为AE //BM ,所以ABME 为平行四边形,从而 AB // EM •又AB 丄平面BCG Bi ,所以EM 丄平面BCC i B •是所求的二面角的平面角,即 / EHM因为 /MBH / CFB ,所以 MH BM gsin / MBHBMg 「BC 2 i pip 亠,tan 列用•JBC 2 CF 2 拧 22 寸13MH(3)如图,连结EH •因为MH 丄BF , EM 丄BF ,所以BF 丄平面EMH ,得EH 丄BF • 是 / EHMBM gsin / CFB。
