勾股定理的十六种证明方法
勾股定理16种经典证明方法
勾股定理16种经典证明方法本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.Marchabc ab b a 214214222⨯+=⨯++【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即整理得 222c b a =+.【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c2. ∵ Rt ΔGDH ≌ Rt ΔHAE,∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】（赵爽证明）以a 、b 为直角边（b>a ）， 以c 为斜 边作四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三 角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE,∴∠HDA = ∠EAB.∵∠HAD + ∠HAD = 90º，∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+.【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE,∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形，它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形，它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c . 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ，∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形.∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a.∴ BDPC是一个边长为a的正方形.同理，HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S，则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ） ，斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ，交AC 于点P .过点B 作BM ⊥PQ ，垂足为M ；再过点F 作FN ⊥PQ ，垂足为N .∵ ∠BCA = 90º，QP ∥BC ，∴ ∠MPC = 90º，∵ BM ⊥PQ ， ∴ ∠BMP = 90º，∴ BCPM 是一个矩形，即∠MBC = 90º. ∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º，∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ， ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF .从而将问题转化为【证法4】（梅文鼎证明）. 【证法7】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结 BF 、CD . 过C 作CL ⊥DE ，交AB 于点M ，交DE 于点L . ∵ AF = AC ，AB = AD ，∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ， ∵ ΔFAB 的面积等于221a， ΔGAD 的面积等于矩形ADLM 的面积的一半， ∴ 矩形ADLM 的面积 =2a .同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积∴ 222b a c += ，即 222c b a =+.【证法8】（利用相似三角形性质证明）如图，在RtΔABC中，设直角边AC、BC的长度分别为a、b，斜边AB的长为c，过点C作CD⊥AB，垂足是D.在ΔADC和ΔACB中，∵ ∠ADC = ∠ACB = 90º， ∠CAD = ∠BAC ， ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB ，即 AB AD AC •=2.同理可证，ΔCDB ∽ ΔACB ，从而有 AB BD BC •=2.∴ ()222AB AB DB AD BC AC =•+=+，即 222c b a =+. 【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R . 过B 作BP ⊥AF ，垂足为P . 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H .∵ ∠BAD = 90º，∠PAC = 90º， ∴ ∠DAH = ∠BAC . 又∵ ∠DHA = 90º，∠BCA = 90º，AD = AB = c ，∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ，AH = AC = b . 由作法可知， PBCA 是一个矩形，所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ，AP= a ，从而PH = b ―a . ∵ Rt ΔDGT ≌ Rt ΔBCA ,Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-， 985S S S +=，∴ 824321S ab b S S --=+=812SS b -- . ② 把②代入①，得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】（李锐证明）设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c. 做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使A、E、G三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º，BT = BE = b ，∴ Rt ΔHBT ≌ Rt ΔABE .∴ HT = AE = a .∴ GH = GT ―HT = b ―a . 又∵ ∠GHF + ∠BHT = 90º， ∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC . ∵ DB = EB ―ED = b ―a ，∠HGF = ∠BDC = 90º，∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ，垂足是M . 由∠BAQ = ∠BEA = 90º，可知 ∠ABE = ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ， ∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵ 27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ，即 222c b a =+.【证法11】（利用切割线定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线分别于D 、E ，则BD = BE = BC = a . 因为∠BCA = 90º，点C 在⊙B 上，所以AC 是⊙B 的切线. 由切割线定理，得AD AE AC •=2=()()BD AB BE AB -+=()()a c a c -+ = 22a c -，即222a c b -=，∴ 222c b a =+.【证法12在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c （如图）. 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB •+•=•，∵ AB = DC = c ，AD = BC = a ， AC = BD = b ，∴ 222AC BC AB +=，即 222b a c +=，∴ 222c b a =+.【证法13】（作直角三角形的内切圆证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 作Rt ΔABC 的内切圆⊙O ，切点分别为D 、E 、F （如图），设⊙O 的半径为r .∵ AE = AF ，BF = BD ，CD = CE ，∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+ = CD CE += r + r = 2r,即 r c b a 2=-+， ∴ c r b a +=+2. ∴ ()()222c r b a +=+， 即 ()222242c rc r ab b a ++=++，∵ab S ABC 21=∆，∴ ABC S ab ∆=42，又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2，∴()ABC S rc r ∆=+442， ∴ ()ab rc r242=+，∴ 22222c ab ab b a +=++， ∴ 222c b a =+. 【证法14】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2，或者 BD AB BC •≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB .在ΔADC 和ΔACB 中， ∵ ∠A = ∠A ， ∴ 若 AD ：AC ≠AC ：AB ，则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中，∵∠B = ∠B，∴若BD：BC≠BC：AB，则∠CDB≠∠ACB.又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不能成立. ∴ 222c b a =+.【证法15】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为 ()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】（陈杰证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做两个边长分别为a 、b 的正方形（b>a ），把它们拼成如图所示形状，使E 、H 、M 三点在一条直线上. 用数字表示面积的编号（如图）.在EH = b 上截取ED = a ，连结DA 、DC ，则 AD = c .∵ EM = EH + HM = b + a , ED = a ，∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º，CM = a ， ∠AED = 90º， AE = b ， ∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC ，DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º，∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º， ∴ ∠ADC = 90º.∴ 作AB ∥DC ，CB ∥DA ，则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º， ∴ ∠BAF=∠DAE .连结FB ，在ΔABF 和ΔADE 中，∵ AB =AD = c ，AE = AF = b ，∠BAF=∠DAE ， ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º，BF = DE = a .D D∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中， ∵ AB = BC = c ，BF = CG = a ， ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=， 6212S S S b ++=， 732S S a +=，76451S S S S S +===，∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
勾股定理的十六种的证明方法
勾股定理的十六种的证明方法【证法1】（课本的证明）做g 个全等的宜角三角形，设它们的两条直角边长分别为注、b ,斜边长为6再做 三牛边长分别为已、氐C 的正方形，把它们®上图那样拼成两个正方形*从图上可以看到，这两个正方形的边长都是& + b-所以面枳相筹•即整理得/+护二口f 证法21 （邹元治证明）以包、b 为直角边，以亡为斜边做四个全等的直角三角形，则每个直角三角形的面积 等于2 •把这四个宜角三角形拼成如图所示形状，使乩E. B 三点在一条直线上，B. F 、 C 三点在一条直线上，C 、S D 三点在一条直线上.二ZAHE 二 ZBEF. T ZAEH - ZAHE 二 90° , 二 ZAEH 」 -ZBEF 二 90\ :• ZHEF = 180=90〃二 9' 0\ 二四边形EFGH 是一个边长为亡的 正方形. 它的面积等于 T Rt i GDH 空 Rt 2 HAE, 二 ZHGD ZEHA. T ZHGD ZGHD - 9(r 二 ZEHA ZGHD 二 90\ 又丁 ZGHE二 ZDHA QO° 亠％『二T RtMJAE 空抵扣澱,-ABCD是一个边长为a + b的正方形，它的面积等于W-(fl +i) ' = 4x—di■ a ♦2【证法3】（赵爽证明〉以弘b为直角边Cb>a），以C为斜边作四个全等的直角三角形，则每个直角图所示形状-T RMDAH■wr*AMjn*4UU.二ZHDA 二■ / ZHAD +/. ZEAB +二ABCD是一个边长为C的正方形，它的面积等于c\ ■ / EF = FG =GH =HE 二b—a ,ZHEF = 90° —A EFGH是一个边长为b—自的正方形，它的面积等于0•由）1 ” 4x jait证法4] （1876年美国JS统Carfield证明）以窝、b为直角边，以C为斜边作两个全等的直角三角形，则每个直角三角形的使g. B三点在一条直线上.积尊于2 ,把这两个直角三角形拼成如图亦示形状,T RtAEAD 丝Rt A CBE.:、ZADE 二ZBEL■ : ZAED + ZADE 二90° ,:.ZAED + ZBEC 二90\/. ZDEC 二180° 一90〃二90〃・ /・卫§£提一个等©直角三角形，三角形的面积等于2 •把这H个直角三角形拼成如丝Rt A ABE,ZEAB.ZRAD =90〃，DB它的而积等于2.又丁ZDAE 二90% ZEBC 二:・ AD/ZBC・L &1+护二2 X —abA ABCD是一个直角梯形，它的面积等于朮口 +疔-:2 2 2,d十b'八t 证法5】(梅文鼎证明)做四个全等的直角三角形，段它们的两条直角边长分别为罕b ，斜边长为s 把它们拼 成如图那样的一个多边形，使D 、E. F 在一条亘线上•过C 作AC 的延长銭交DF 于点P.■ / D. E 、F 在一条直线上，且 RtAGEF 全 Rt A EBD, ■ HV—VWWVWMW-V.:・ ZEGF = ZBED,*/ ZEGF 亠 ZGEF 二 ，：* ZBED + ZGEF 二 9tr ,:.ZBEG 二 1SO 〃—90〃二 9(r ・又 T ・ 4B 二 BE 二 EG 二 GA 二c, g -ABEG 是一个边长为c 的正方形「 ;> ZABC + ZCBE 二 90\* 二 BxAXBOz :・ ZABC = ZEBD.:.ZEBD 十 ZCBE 二 90\即 ZCBD 二 9(r ・又 T ZBDE 二 90〃，ZBCP 二 9(7 , BC 二BD 二比 二 a *BDPC 是一亍边长为a 的正方形.同理，HPFG 是 一伞边长为b 的正方形〃设多边形GHCBE 的面积为&则L ■! ■时二5 斗 2 X i 血* r*设它们的两条直角边长分别为旦、b (b>a),斜边长为 把它们拼成如图所示的多边形，使臥A. C 三点在一条过点Q 作QP//BC,兗代匚于点F. 过点B 作册丄PQ,垂足为地再过点F 作FX 丄P0垂足为工T ZBCA - 9(r, QpyzBC,二 Z«PC 二 9 化T 创丄F0二 ZBMP 二 90\-BCP 订是一个矩形，即ZMBC 二■ / ZQBM + ZMBA = ZQBA 二 9『, ZMBA 二 ZN1BC 二 9(r,化 ZQBM 二 ZABC,又丁 Z5MP 二 90\ ZBCA 二迅 BQ 二 BA 二 c>二 Rt A B 订Q 旦 Et A BCA.同理可证S1295E -肚虫睡：从而箱问题转化为f 応落疔7梅文灿证明).，/+止_【证法6】(项明达证明〉做两个全等的直角三角形，再做硏个边长为C 的正方形.直线上. ZABC +FC BE在一条直线上，连结 °的?F 肯形护立们拼咸如團斫示形状，使乐C. BF. CD •过 C 作 CL±DE,交;m 于点此交DE 于点L,T AF 二 AC,・AB 二 AD,虫ZFAB 二 ZCAD,代・A 復&望T iFAB 的面积等于空“・乂吐的面积等于矩形ADLM 的面积的一半, 二矩形ADUI 的面积同理可证，矩形MLEB 的面积二戸.T 正方形ADEB 的面积二葩形ADUI 的面积+矩形MLEB 的面积/,护，即护+占V/*E 证法町（利用相似三竟形性质证明）如图，在肚丄A 匹中，设直角边AS 反的长度分别为点C a. b ・斜边AB 的长为Ga 作CD1AB,垂足是D*在i ADC 和iACE 中, V ZADC - ZACB 二 90〃， ZC.AD 二 ZB AC,二 AASC s A A®*AD : AC H AC : AB,艮卩HC ： =4D •一毎- 同理可证FASflS s二 HC*=（川 D + D£）・川占二討$1,即 o'+i ） i 二匚I 【证法9】（畅作玫证明）做两个全等的直角三角形•设它们的两条直角边长分别为吐、b Cb>a\斜边长为亡.再做 一个边长为U 的正方形•把它们拼成如图所示的多边形-过丄作AF 丄AG AF 交GT 于F ・・・IF 交 DT 于R.过B 作肝丄左F, 垂足为巴过D 作DE 与CB 的延长线垂直，垂足为 E, DE 交AF 于乩T ZBAD 二 90〃，ZPAC 二 W,二 ZDAH 二 ZEAC.又■/ ZDHA 二 90〃，ZBCA 二 9「，AD 二 AB 二 C ；二 Rt 业 DHA ◎ Rt 也 BCA.二 DH 二 BC 二 a, AH 二 AC 二 b・由作法可知，PECA 是一个矩形， 所以 R T A AFB 丝 RtAgCA.即 PB 二 CA二 b, AP 二 a,从而卩 H 二 b 一au*； Rt i DGT 瓷 Rt i BCA , g 卫與•奉廳2瞬二 Dtr^T?G 二 a™2S5?二 ZHDA ・ 又 T ZDGT 二 90° , ZDHF 二 W fB 三点C二愍空•匹I竺雛屯哪，二DGFH是一亍边故为a的止万形.二GF 二FH 二 a ・TF±AF. TF = GT-GF = b—a ・二TFPB是一个直角梯形，上底TF二b-E下底SP= b,高FP P +(b-G・用数字表示面积的编号(如图九则以C为边长的正方形的面积为G 二S] + Sj + Sj + S 耳 + S 了①** 场+ 昂 + Sq 二挣 + 0-口)」讥+0-13 ) ^--ab―* S, + S, = b*―ab—S,护-S] f 把②代入①，得=5 + 5] + F - S] F S J +S J +Sp-时+男+男-酹+/,-盼+沪二八【证法10] t李钱ffi明)设直角三角形两直角边的长分别为a・b (b>a)，斜边的长为二做三个边长分别为包、b. C 的正方形，把它忙I拼成如S所示形状，使爪E・G三点在一条直线上•用数字表示面积的编号（如图）.T ZTBE 二ZABH 二9tr :・ZTBH 二r 乙ABE.又T ZBTH 二BZBEABE - 人RtAHBT ^ORt, AHBBj 人HT二AE二比:、GH 二GT-HT 二b-a.又T ZGHF + ZBEI 二90\ZDBC + ZBHT 二ZTBH + 二ZGHF 二ZDBC J DB 二ER —ED二b-a>ZHGF 二ZBX 二9 呼，・•、gt A HGF 丝RtA. jBgC 即工二$2.过Q作Q蛆丄AL垂足是乩由ZBAQ二ZBEA二二ZQAM T而AB 二AQ 二0 9Cn 可知ZABER貯避•所以陆Ajj甲.公'Rt •斷以驰玉賤旦陆29迪••又5x2JSSI —細SE百屁卫滋又得QM二A£二a, ZAQM二ZBAE.ZHGF 二 ZBDC 二 90%二Rt A HGF 竺Rt A BDC.即思产h ・过Q 作QNLLAG,垂足是底由ZBAQ 二ZBEA 二9化可知ZABE =ZQAM,而壷B 二AQ 二C.所以Rt AABE 竺 肚綁M -又RMHET 空Rt A ABE.所以Rt A HBT 竺班 色QM .即况二匹.由 Rt A ABE 竺 Rt A Q. W,又得 QM = AE = a, ZAQM 二 ZEAE.T ZAQM + ZFQM 二 90% ZBAE + ZCAR 二 90% ZAQM = NBAE,二 ZFQM 二ZCAR.又丁 ZQitF 二 ZARC 二 90% QM = AR = a ,二 Rt A q"fF 竺 Rt A ARC.即 $严耳-丁 亡 2=$1 +昂 + 爲+ S 斗+ 5； , /二S] + Ssj 二S ・ +S- + S,V ' *二A 易二壬乌二斗二宀 7/ =S\ +S5 + Sm + 斗 + 禺二 S] + rS 斗 + $2 + S j—r在d 磁中「设直珀边BC 二a, AC 二b,斜边AB 二c,如图 C, 径作圆，交AB 及AB 的延长线分别于Ik E,则ED 二BE 二BC 二 C 在©B 上，所以扛是©B 的切线，由切割线是理，得t 证法12】（利用雾列米定理证明｝在R2ABC 中，设直角边BC 二a. AC 二b,斜边AB 二c （如图）*过点〃&作AD//CB,过 点B 作BD>ZCA,则ACBD 为矩形，矩形ACBD 内接于一个圆，根据多列米定理，圆内接 四边形对角线的乘积等于两对边乘积之和，有=JD*5C5£Z?,T AB 二 DC 二 c, AD - BC =乩AC 二 BD 二 b,二且0’二占c'+」c',即/吕口： +盼,「以0为圆心a 为半 孔比因为ZE 仙二90\点 屁;二毘£〉3二｛AS+SE’AS -SD ）-(c + d) (c 一d)二£?+, =/【证法13】（作直角三角形的内切圆证明）在吐黒照中，设直角边EC = a, AC二b,斜边託二切点C. 分W?D7E> F （如圏人设©0的半径为r.T AE 二AF, BF 二BD, CD = CE,二MC+ BC-AB二{AE+CE}+[SD +CD)—(討戸+EF)二CE + CD 二工 + 工=2丫,即a +二2r,r* a + b 二2F + f ・A ~ (2r + c) \gp ■”2aif = 4 (r* +rc) +c*又T Sg 厂匚沪Sae+Sse 二2 2 -（4 + 0 + 亡）严—{2r + C + c丿r/, 4 (宀n： )=4£sr,*・》4卜’+临）=2胡'「■ /+ 即+2 口& 二2e 占+（；'』【证法14】（利用反证法证明）如图，在§1卫匸中「设直角边AG阮的长度分别为已、点C作CD丄AE.垂足是D.假设/十护乂蔦即假设也'+證2厂护「则由二AJ*.』5 二M （a + AD）二A B• A D + AB• BDb・斜边啊的长为G过可知-心5扭-M,或者在AAK和1ACB中,肋・ED•即AD： AC^AC： AB•或者BD： BC?^BC：AB.丁ZA 二ZA,二若AD： AC^AC： AB,则ZADCH ZACE.在・AC咀和・A他中，T ZB 二ZE>二若BD： BC T^BC：AB X贝JZCDB^ZACB.C又T ZACB 二9Cr ,二Z： ADCH9 （r, ZCDEHgcr这与作法CD丄AB矛盾•所以「e +恥' *曲谢假设不能成立作吐丄Age的内切圆00,设直角三角形两直角边的长分别为已*，斜边的长为⑺作边长是a 吒的正方形ABCD*把 正方形ABB 划分咸上方左图所示的几个部分，则正方形ABCD 的积为（》疔二/+护+滋•把正 方形.〈BCD 划分成上方右图所示的几个部分「则正方形ABCD 的 (a + 4 X —ab + T 面积为， 2 二2如i ・小十护十2aij = 2ab 十F, ［证法祐】（陈杰证明） 设直甬三角形两直角边的长分别为a. b b 的正方形<b>a ）.把它们拼成如图所示形状， 图）. 在EH - b 上截取ED - a,连结加、DC,. 则 AD 二 B T EH = EH + HM = b 十 a , ED = 二 DM 二 EM-ED 二（b + 切一 a 二 ZAED 三 9 少，CM 二 a. :・R t A A 鲍\ AE 二 b, A ZEAD V ZADE ZADE :.ZAX 二作AB/7DC, CB?/DA,则期5是一个边长为c 的正方激 '：ZBAF + ZFAD 二 ZDAE + ZFAD 二 9（r, ZMDC T D T= AD = c. ZAX+ ZMDC 二1SO\ ZMDC 二 ZADE - ZEAD A ZBAF 二ZD. \E, 连结FB,在厶ABF 和i ADE 中,（b>aX 斜边的长为B 做两亍边长分别为包、 砌积的縄用傲点在一条宜线上•用数字表 E 、 B b b E —b a, J MD G 1 二 90J 90\gs)+T 十 £十占 ■ os+ls 十 34 ■ • 8 •心 + •JS+GSHFSH—SHTSf EK 扌s+r s *+=・£:•叶・• ・ 「r i> ・law :抵八・u II % + qb aa ab a b方2 ab bb aA C Bb E。
勾股定理十六种证明方法
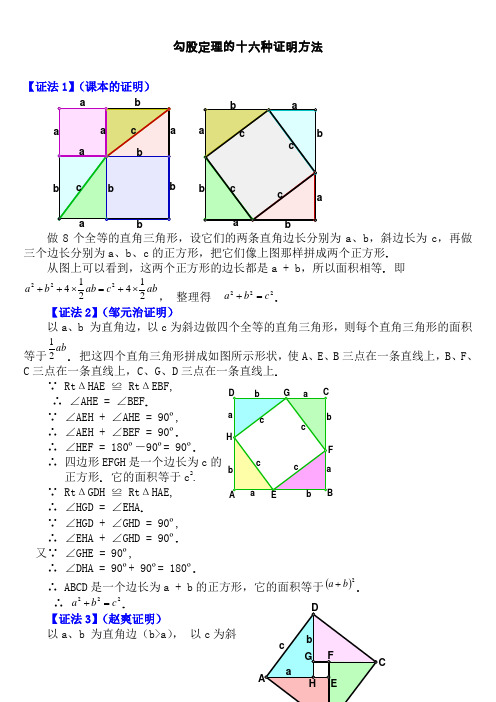
勾股定理的十六种证明方法【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即abc ab b a 214214222⨯+=⨯++， 整理得 222c b a =+.【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab 21.把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴ 222c b a =+. 【证法3】（赵爽证明） 以a 、b 为直角边（b>a ）， 以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º， ∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形，它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC .∴ ABCD 是一个直角梯形，它的面积等于()221b a +. ∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c . 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ，∵ ∠EGF + ∠GEF = 90°， ∴ ∠BED + ∠GEF = 90°， ∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ） ，斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ，交AC 于点P . 过点B 作BM ⊥PQ ，垂足为M ；再过点 F 作FN ⊥PQ ，垂足为N . ∵ ∠BCA = 90º，QP ∥BC ， ∴ ∠MPC = 90º， ∵ BM ⊥PQ ，∴ ∠BMP = 90º， ∴ BCPM 是一个矩形，即∠MBC = 90∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º， ∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ， ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】（梅文鼎证明）.【证法7】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结BF 、CD . 过C 作CL ⊥DE ，交AB 于点M ，交DE 于点L . ∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ， ∵ ΔFAB 的面积等于221aΔGAD 的面积等于矩形ADLM 的面积的一半，∴ 矩形ADLM 的面积 =2a 同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ，即 222c b a =+. 【证法8】（利用相似三角形性质证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .在ΔADC 和ΔACB 中，∵ ∠ADC = ∠ACB = 90º，∠CAD = ∠BAC ， ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB ， 即 AB AD AC •=2.同理可证，ΔCDB ∽ ΔACB ，从而有 AB BD BC •=2. ∴ ()222AB AB DB AD BC AC =•+=+，即 222c b a =+. 【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R . 过B 作BP ⊥AF ，垂足为P . 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H .∵ ∠BAD = 90º，∠PAC = 90º，∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º，∠BCA = 90º， AD = AB = c ， ∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ，AH = AC = b . 由作法可知， PBCA 是一个矩形， 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ，AP= a ，从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-， 985S S S +=，∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①，得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º， BT = BE = b ， ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ， ∠HGF = ∠BDC = 90º，∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ，垂足是M . 由∠BAQ = ∠BEA = 90º，可知 ∠ABE = ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ，∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵ 27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ， 即 222c b a =+.【证法11】（利用切割线定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线分别于D 、E ，则BD = BE = BC = a . 因为∠BCA = 90º，点C 在⊙B 上，所以AC 是⊙B 的切线. 由切割线定理，得AD AE AC •=2=()()BD AB BE AB -+=()()a c a c -+= 22a c -，即222a c b -=，∴ 222c b a =+.【证法12】在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c （如图）. 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB •+•=•，∵ AB = DC = c ，AD = BC = a ， AC = BD = b ，∴ 222AC BC AB +=，即 222b a c +=，∴ 222c b a =+.【证法13】（作直角三角形的内切圆证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 作Rt ΔABC 的内切圆⊙O ，切点分别为D 、E 、F （如图），设⊙O 的半径为r .∵ AE = AF ，BF = BD ，CD = CE ，∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+， ∴ c r b a +=+2.∴ ()()222c r b a +=+，即 ()222242c rc r ab b a ++=++，∵ab S ABC 21=∆，∴ ABC S ab ∆=42， 又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2，∴()ABC S rc r ∆=+442， ∴ ()ab rc r242=+，∴ 22222c ab ab b a +=++， ∴ 222c b a =+.【证法14】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2，或者 BD AB BC •≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB .在ΔADC 和ΔACB 中，∵ ∠A = ∠A ，∴ 若 AD ：AC ≠AC ：AB ，则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中， ∵ ∠B = ∠B ， ∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为()ab b a ba 2222++=+；把正方形ABCD划分成上方右图所示的几个部分，则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】（陈杰证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做两个边长分别为a 、b 的正方形（b>a ），把它们拼成如图所示形状，使E 、H 、M 三点在一条直线上. 用数字表示面积的编号（如图）. 在EH = b 上截取ED = a ，连结DA 、则 AD = c .∵ EM = EH + HM = b + a , ED = a ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º，CM = a ， ∠AED = 90º， AE = b ， ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ，DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º，∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º， ∴ ∠ADC = 90º.∴ 作AB ∥DC ，CB ∥DA ，则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º，D∴ ∠BAF=∠DAE .连结FB ，在ΔABF 和ΔADE 中，∵ AB =AD = c ，AE = AF = b ，∠BAF=∠DAE ， ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º，BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中，∵ AB = BC = c ，BF = CG = a ， ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=， 6212S S S b ++=， 732S S a +=，76451S S S S S +===，∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
勾股定理的十六种证明方法
勾股定理的证明【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即ab c ab b a 214214222⨯+=⨯++， 整理得 222c b a =+.【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF ,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE , ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】（赵爽证明） 以a 、b 为直角边（b>a ）， 以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º， ∴ ∠EAB + ∠HAD = 90º， ∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE ,∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠D EC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形，它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形，它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c . 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD , ∴ ∠EGF = ∠BED ，∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD , ∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则,21222ab S b a ⨯+=+ab S c 2122⨯+=, ∴ 222c b a =+.【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ） ，斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ，交AC 于点P .过点B 作BM ⊥PQ ，垂足为M ；再过点F 作FN ⊥PQ ，垂足为N . ∵ ∠BCA = 90º，QP ∥BC ， ∴ ∠MPC = 90º， ∵ BM ⊥PQ ， ∴ ∠BMP = 90º， ∴ BCPM 是一个矩形，即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º， ∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ， ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】（梅文鼎证明）.【证法7】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结 BF 、CD . 过C 作CL ⊥DE ，交AB 于点M ，交DE 于点L .∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ， ∵ ΔFAB 的面积等于221a ， ΔGAD 的面积等于矩形ADLM 的面积的一半，∴ 矩形ADLM 的面积 =2a . 同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积 = 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ，即 222c b a =+.【证法8】（利用相似三角形性质证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .在ΔADC 和ΔACB 中， ∵ ∠ADC = ∠ACB = 90º， ∠CAD = ∠BAC ， ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB ，即 AB AD AC ∙=2. 同理可证，ΔCDB ∽ ΔACB ，从而有 AB BD BC ∙=2.∴ ()222AB AB DB AD BC AC =∙+=+，即 222c b a =+.【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R . 过B 作BP ⊥AF ，垂足为P . 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H .∵ ∠BAD = 90º，∠P AC = 90º， ∴ ∠DAH = ∠BAC . 又∵ ∠DHA = 90º，∠BCA = 90º， AD = AB = c ，∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ，AH = AC = b .K由作法可知， PBCA 是一个矩形， 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ，AP= a ，从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA ,Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . T F ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 = ab b 212-， 985S S S +=， ∴824321S ab b S S --=+= 812S S b -- . ②把②代入①，得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +. ∴ 222c b a =+.【证法10】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º，BT = BE = b ，∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ，∠HGF = ∠BDC = 90º，∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ，垂足是M . 由∠BAQ = ∠BEA = 90º，可知 ∠ABER= ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ， ∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=，612S S a +=，8732S S S b ++=， 又∵ 27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ，即 222c b a =+.【证法11】（利用切割线定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线分别于D 、E ，则BD = BE = BC = a . 因为∠BCA = 90º，点C 在⊙B 上，所以AC 是⊙B 的切线. 由切割线定理，得AD AE AC ∙=2=()()BD AB BE AB -+ =()()a c a c -+= 22a c -，即222a c b -=， ∴ 222c b a =+.【证法12】（利用多列米定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c （如图）. 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB ∙+∙=∙， ∵ AB = DC = c ，AD = BC = a ，AC = BD = b ，∴ 222AC BC AB +=，即 222b a c +=，∴ 222c b a =+.【证法13】（作直角三角形的内切圆证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 作Rt ΔABC 的内切圆⊙O ，切点分别为D 、E 、F （如图），设⊙O 的半径为r .∵ AE = AF ，BF = BD ，CD = CE ，∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+， ∴ c r b a +=+2.∴ ()()222c r b a +=+，即 ()222242c rc r ab b a ++=++，∵ab S ABC 21=∆，∴ ABC S ab ∆=42，又∵ AO C BO CAO B ABC S S S S ∆∆∆∆++= = brar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2，∴()ABC S rc r ∆=+442， ∴ ()ab rc r242=+，∴ 22222c ab ab b a +=++， ∴ 222c b a =+. 【证法14】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2，或者 BD AB BC ∙≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB .在ΔADC 和ΔACB 中， ∵ ∠A = ∠A ， ∴ 若 AD ：AC ≠AC ：AB ，则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中， ∵ ∠B = ∠B ，∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】（辛卜松证明）E设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD的面积为()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】（陈杰证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做两个边长分别为a 、b 的正方形（b>a ），把它们拼成如图所示形状，使E 、H 、M 三点在一条直线上. 用数字表示面积的编号（如图）.在EH = b 上截取ED = a ，连结DA 、DC ，则 AD = c .∵ EM = EH + HM = b + a , ED = a ，∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º，CM = a ， ∠AED = 90º， AE = b ，∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC ，DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º， ∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º，∴ ∠ADC = 90º.∴ 作AB ∥DC ，CB ∥DA ，则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º， ∴ ∠BAF=∠DAE .连结FB ，在ΔABF 和ΔADE 中，∵ AB =AD = c ，AE = AF = b ，∠BAF=∠DAE ， ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º，BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中， ∵ AB = BC = c ，BF = CG = a ， ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=， 6212S S S b ++=， 732S S a +=，D DC M76451S S S S S +===， ∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.勾股定理有367种证明方法，最著名的有5种：梅文鼎证明、项明达证明、赵浩杰证明、欧几里得证明、欧几里得的证法。
勾股定理的16种证明方法
【证法I）（课本的证明）做8个全等的宜角三角形•设它们的两条直角边长分別为」b •斜边长为c・再做三个边长分别为黑b. c的正方形.把它们像上图那样拼成衲个正方形.从图上可以石到•这两个正方形的边长都是a + b.所以面积相等・即（=+4x 丄ab »2 •整理得卅+尸二代【证法2】（邹元治证明）以a、b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角•把这四个直角三角形拼成如图所示形状，使A、E. B三点形0勺面积等于严在一条直线上，B、F、C三点在一条亘线上，C、G、D三点在一条直线上.VRt A HAE 竺Rf A EBF, :.ZAHE= ZBEF.I ZAEH+ ZAHE = 90°, ••• ZAEH+ ZBEF = 90°. ••ZHEF= 180°-90°= 90° ••・四边形EFGH是一个边长为c的正方形・它的血积等于•R“GDH 竺Rt A HAE,•ZHGD= ZEHA.•ZHGD+ ZGHD = 90°,•ZEHA+ ZGHD = 90°.•ZGHE = 90°f•ZDHA=90°+90°= 180°.• ABCD是一个边长为a + b的正方形，它的面积等于G +疔.（a + 方）+ c 22【证法3】（赵爽证明）以a 、b 为直角边（b>a ）,以c 为斜边作 四个全等的直角三角形，则每个直角成如图所示形状.I Rt A DAH 今 Rt A ABE,:.ZHDA= ZE AB.…ZHAD+ ZHAD = 90°,••• ABCD 是一个边长为c 的正方形，它的血积等于心••• EF = FG =GH =HE = b-a,ZHEF 二 90°.・・・EFGH 是一个边长为b ・a 的正方形，它的面积等于直一切[4xga/> + （〃一 G] ；2一 V【证法4] （1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角•把 这两个直角三角形拼成如图所示形状，使A> E 、CB 三点•“ ZADE= ZBEC.••• ZAED+ ZADE = 90°, ••• ZAED+ ZBEC = 90°.•“ ZDEC= 180°-90°= 90°.-A DEC 是个等腰・酬三角形，乂 I ZDAE = 90°, ZEBC = 90°, : • AD 〃 它的面积等于2BC.三角形的面积等于2 •把这四个直角三勿形拼AbEaB【证法5】（梅文鼎证明）做四个全等的N 角三角形•设它们的两条自旳边长分别为a 、b •斜边长为c. 把它们拼成如图那样的一个名边形•使IX E. F 在一条直线上•过C 作AC 的延长线 交DF 于点P.• • • D. E. F 在一条玄线上，fl. Rf A GEF Q ROEPD :.ZEGF= ZBED.V ZEGF+ ZGEF-9O 0,:.ZBED+ ZGEF = 9()a •••• ZBEG=180o -90°=90°< 又 I AB 二 BE = EG = GA = c •••• ABEG 是一个边长为c 的iE 方形.••• ZABC+ ZCBE = 90n .V Rt A ABC £ Rt A EBD,:.ZABC= ZEBD.••• ZEBD+ ZCBE = 90°<即 ZCBD= 90n .XV ZBDE = 90° • ZBCP = 9 (r •BC ■ BD ■ a.:BDPC 是一个边长为a 的正方形• 同理・HPFG 是一个边长为b 的止方形. 设多边形GHCBE 的面积为S.则a 2+b 2 =5 + 2x 丄”九2【证法6】（顶明达证明）做两个全等的耳用三角形•设它们的两条玄角边长分别为a 、b （b>a>・斜边长为 G 再做■个边长为c 的正方形•把它们拼成如图所示的多边形•使E.A. C 三点在一条直线上.过点Q 作QP 〃BC •交 AC于点P.过点?作15\1丄PQ.垂定头JM ：再过点…ABCD 是■个直角梯形, 丄 它的面积等于㊁FA C BF作FN丄PQ・垂足为N.V ZBCA = 90° . QP 〃BC • ZMPC = 90° ・V BM 丄PQ -:.ZBMP = 9fT ・BCPM 是一个矩形.HI1ZMBC = 90°.V ZQBM+ ZMBA・ ZQBA * 90°・ ZABC+ZMBA= ZMBC = 9(T •••• ZQBM・ ZABC.乂IZBMP = 9(r・ ZBCA = 9(r ・ BQ = BA=c ・【证法7】(欧几里得证明)做三个边长分别为氛b、c的正方形・把它们拼成如图所示形状•使Fk C、B三点在一条宜线上•连结BF ・ CD.过 C 作CL 丄DE.交AB于点交DE于点H /V AF= AC. AB = AD. yZFAB二ZGAD< cZ 来、/A FAB 今AGAD.丄a,V AFAB的面积等丁込“AGAD的面积等弓矩形ADLM的面积的一半.・・•矩形ADLM的面八同理可证•矩形MLEB的面积L・・・正方形ADEB的血积二矩形ADLM的啲枳+矩形MLEB的面积c2 = ♦ b1 . l!|l a2 + = c'.【证法《〕(利用相似三介形性质证如图•在RtAABC中，设直角边AC. BC的长度分别为a. b •斜边AB的长为c・过点C作CD丄AB・垂足是D.在AADC和’ACB中・I ZADC= Z ACB = 90° . ZCAD・ ZBAC.:.A ADC s A ACB.AD : AC = AC : AB.即AC2 =同理町证'ACDB s & ACB.从而竹BC—BD.AB.:.AC1 + HC l = (JD+ DB)A AB・A” 即a,【证法9】(杨作玫证明〉做两个全零的直角三和形•设它们的两条直角边K分别为a、bvb>a) ■斜边长为c •再做■个边长为c的肪0形.把它们拼成如图所示的多边形•过A作AF丄AC. AF交GT于F・AF空2)T于R.过B作BP丄AF.乖足为P.过D作DE与CB的证长线垂直•垂足为E. DE交AF于H.V ZBAD-9 (r\ ZPAC ・ 90匕••• ZDAH= ZB AC.又：・ZDHA = 90°. ZBCA = 90° .AD = AB = c •Rt \ DHA £Rt A BCA<•: DH = BC = a. AH = AC = b.Lh作法可矩.PBCA是一个矩形. 所以RtAAPB 耳Rt A BCA. UP PB = CA = b< AP= a •从而PH = b一a.V Rt A DGT 9 R1 A BCA ■ Rt \ DHA 今RtA BCA. RMDGT 竺Rt DHA.••• DH = DG = a. ZGDT= ZHDA.又I ZDGT-9O0. ZDHF ・ 90卜•ZGDH= ZGDT+ ZTDH = ZHDA+ ZTDH = 90°.••• DGFH定一个边长为a的正方形.••• GF=FH = a.TF 丄AF. TF = GT-GF = b-a.TFPB是一个直角梯形•上底TF-b-a・卞底BPf高FP-a+ (b-a).用数字表示面积的编号(如图片则以c为边长的正方形的面积为=Sn + S人=5, +S、+/>2U +5：+Sqa2 =c2S ' + Sy + 54 =-[/> + (/>・a)] • [a + (b _ a)] Ir•丄a”2 =2 a把②代入①.W【证法10）（李稅证明）设直角三角形两直角边的长分别为a、b （b>a）.斜边的长为c •做三个边长分别为a、b、c的正方形•把它们拼成如图所示形状•使A. E. G三点在•条亢线上•用数字农示面积的编号（如图）・IZTBE 工ZABHf.••• ZTBH= ZABE.又・・・ZBTH・ ZBEA・ 90°.BT=BE = b.:.R( AHBT 竺R( A ABE.••• HT = AE =〜••• GH = GT-HT=b-x XV ZGHE+ ZBHT = 90°.ZDBC + ZBHT= ZTBH+ ZBHT = 90%••• ZGHF= ZDBC ・VDB = EB-ED = b-a.ZHGE= ZBDC = 90°.••• RtAHGF 丝RtABDC.即w2.过QftQM 丄AG •垂足是M. rf]ZBAQ= ZBEA = 90°.町知ZABE ZQAM. rtl AB-AQ-c.所以RfAABE 幻RcAQAM. X Rt \ HBT £Rt A ABE.所以Rt A HBT 0 Rt A QAM ・即ft] Rt A ABE 旦Rt AQAM.又QM = AE = a. ZAQM = ZBAE.•: ZAQM+ ZFQM ・ W . ZBAE + ZCAR ・ VX)U. ZAQM ・ ZBAE. :.ZFQM=ZCAR.又I ZQMF- Z ARC ・90° • QM • AR • a •:.Rt AQMF9Rt A ARC.g卩•: c*=£ + S, + +S.+ S,.X = S ' 七 S&.b° = S、七 S=± S* =&令+s? + s》+即cr =c2.【证法11】（利用切割线定理证明）在R1AABC中•设垃角边BC = a. AC = b •斛边AB = c.如图•以B为圆心3为半径作例•交AB及AB的延长线分別于D E • WJ BD = BE = BC = a.因为ZBCA = 9（T.点C在0B上•所以AC是OB的切线・由切割线定理•得AC2 =AE^ADA cT =t\【证法12］（利用多列米定理证明）在Rt A ABC中•设口角边BC = a. AC = b •料边AB = c •过点A作AD // CB •过点B作BD 〃CA・则ACBD为炉形.炉形ACBD内接丁一个阕. 根据£列米定理・岡内接阿边形对如线的乘积等丁两对边乘枳之和.冇NB • DC=AD • BC*C • BL>.I AB-DC-c. AD-BC-a.AC = BD = b.AB2 ^BC2 + AC29即c2 =a2+Z>\【证法13】（作直角三角形的内切圆证明）在Rt A ABC中•设宜如边BC • a • AC-b V斜边AB・c・\\ Rt A ADC“勺内切風OCX切点分别为D. E.F （如图）•设OO的半径为「・V AE = AF. BF = BD. CD = CE.:.AC+ BC・ J5 = (JE + CE) + (BD + CD) - (JF + BF)CE + CD = r + r = 2r,HP <J + /) -c = 2r.:,a 4- b-2r + c.• .(€/A Z?y = (2r + c)\ 即 a 2 +62 + lab = 4 (r 2 + rc)+ c 2...s.w r*ny (2r+ c + c)r.・・.・.4(r ? 4-rc)= lab.•: a 2 +/> + 2ab = lab + c 2,【证法14］（利用反证法证明）如图•在R （ A ABC 中.设口角边AC. BC 的K 度分别为a. b •斜边AB 的 长为 c •过点C 作CD 丄AB •垂足是D.假设/+» 斗 '・即假设AC 2 + B^AB 2・则由可如 AC 2 AB^AD 9 或者 BC • BD. Ull AD ： AC A AC ： AB.或者 BD ： BC A BC ： AB.在A ADC 和A ACB 中.I ZA= ZA.・••若 AD ： ACHAC ： AB.则ZADCAZACB.在 ACDB 和 AACB 中.V ZB= ZB. ・・・若BD ： BCHBC ： AB.则 ZCDBHZACB.乂 IZACB-W. 3 (” + b + “AB 2 = AB •AB 二”(初 + BD)AB^AD + AB^ BD A d A• • ZADC A 90 ・形ABCD 把疋方形ABCD 划分成上方左图所示的儿个部分・则匸方形ABCD 的面 枳为© + 6）、二/「+2“；把jE 方形ABCD 划分成上方右图所示的儿个部分•则正方形ABCD 的向积为:+ />" + lab = 2ab + c 2.:.a 2 +b 2 =c\ (« + 疔=4x —ab + c 2 , 2 =2血+ "・【证法16］（陈杰证明）设H 角三角形两胃角边的长分别为a 、b vb>a ）.斜边的长为c.做两个边长分别为冬b 的正方形（b>a ）.把它们拼成如图所示形状•使E. H. M 三点在一条直线上•用数字表示面积的编号(如图〉・ 在EH = b 」.祓取ED = a •连结DA. DC.则 AD = c-I EM = EH + HM = b + a • ED = a ・••• DM -EM-ED = (b + °)-a = b •又 I ZCMD * 90”. CM • a • ZAED = 90°.AE=b. :.Rt A AED 丝 Rt ADMC./. ZEAD= ZMDC • DC = AD = c.VZADE+”DC 十 ZMDC =180°.这与作法CD 丄AB 矛曲・所以・+ 的假设不能成立.【证法15】（辛卜松证明）BZADE+ ZMDC= ZADE+ ZEAD = 90°・••• ZADC = 9 (r.・・・作AB//DC*.CB〃DA •则ABCD是一个边K为c的正方形.V ZBAF+ ZFAD= ZDAE + ZEAD = 90°.••• ZBA F=ZDAE •连纟吉FB・在AABF禾口 A ADE中.V AB =AD = c. AE = AF = b. ZBAF=ZDAE.••• A ABF 也A ADE.:.ZAFB 二ZAED = 90°. BF = DE = a.•…点B、F. G. H在一条直线上.在R( A ABF和Rt A BCG中・T AB * BC * c • BF - CG ・ a.:.Rt A ABF 耳Rt A BCG.•: c2 = S? + + S. + Sq. b2 = S、+S2 + 56. a2 = S=、$ 話=S4 =56+S.•+ />* = S§ + S= + + 5, + 56■s?+S3+s]+ 仅+S?)。
勾股定理16种证明方法
勾股定理的证明【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即abc ab b a 214214222⨯+=⨯++， 整理得 222c b a =+.【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】（赵爽证明） 以a 、b 为直角边（b>a ）， 以c 为斜 边作四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º， ∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2.∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形，它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形，它的面积等于()221b a +. ∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c . 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ，∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ， ∴ ABEG 是一个边长为c 的正方形∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则abS c 2122⨯+=,∴ 222c b a =+. 【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ） ，斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ，交AC 于点P . 过点B 作BM ⊥PQ ，垂足为M ；再过点 F 作FN ⊥PQ ，垂足为N . ∵ ∠BCA = 90º，QP ∥BC ， ∴ ∠MPC = 90º， ∵ BM ⊥PQ ， ∴ ∠BMP = 90º， ∴ BCPM 是一个矩形，即∠MBC = 90∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º， ∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ， ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】（梅文鼎证明）. 【证法7】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结BF 、CD . 过C 作CL ⊥DE ， 交AB 于点M ，交DE 于点L . ∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ，∵ ΔFAB 的面积等于221a ，ΔGAD 的面积等于矩形ADLM的面积的一半，∴ 矩形ADLM 的面积 =2a .同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ，即 222c b a =+. 【证法8】（利用相似三角形性质证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .在ΔADC 和ΔACB 中，∵ ∠ADC = ∠ACB = 90º，∠CAD = ∠BAC ， ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB ， 即 AB AD AC •=2.同理可证，ΔCDB ∽ ΔACB ，从而有 AB BD BC •=2. ∴ ()222AB AB DB AD BC AC =•+=+，即 222c b a =+. 【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R . 过B 作BP ⊥AF ，垂足为P . 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H .∵ ∠BAD = 90º，∠PAC = 90º， ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º，∠BCA = 90º， AD = AB = c ，∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ，AH = AC = b .由作法可知， PBCA 是一个矩形，所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ，AP= a ，从而PH = b ―a . ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-， 985S S S +=，∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①，得= 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º，BT = BE = b ， ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ， ∠HGF = ∠BDC = 90º， ∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ，垂足是M . 由∠BAQ = ∠BEA = 90º，可知 ∠ABE = ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ，∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵ 27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ， 即 222c b a =+. 【证法11】（利用切割线定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线分别于D 、E ，则BD = BE = BC = a . 因为∠BCA = 90º，点C 在⊙B 上，所以AC 是⊙B 的切线. 由切割线定理，得=()()BD AB BE AB -+ =()()a c a c -+= 22a c -，即222a cb -=， ∴ 222c b a =+. 【证法12】在Rt ΔABC 中，设直角边BC . 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB •+•=•，∵ AB = DC = c ，AD = BC = a ， AC = BD = b ，∴ 222AC BC AB +=，即 222b a c +=， ∴ 222c b a =+.【证法13】在Rt ΔABC 中，设直角边BC = a ，作Rt ΔABC 的内切圆⊙O ，切点分别为D 、E 、F （如图），设⊙O 的半径为r .∵ AE = AF ，BF = BD ，CD = CE ，∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+， ∴ c r b a +=+2.∴ ()()222c r b a +=+，即 ()222242c rc r ab b a ++=++，∵ab S ABC 21=∆，∴ ABC S ab ∆=42， 又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2，∴()ABC S rc r ∆=+442， ∴ ()ab rc r242=+，∴ 22222c ab ab b a +=++， ∴ 222c b a =+.【证法14】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2，或者 BD AB BC •≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB .在ΔADC 和ΔACB 中，∵ ∠A = ∠A ，∴ 若 AD ：AC ≠AC ：AB ，则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中， ∵ ∠B = ∠B ， ∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不能成立.∴ 222c b a =+. 【证法15】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为()ab b a b a 2222++=+；把正方形ABCD划分成上方右图所示的几个部分，则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+. 【证法16】（陈杰证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做两个边长分别为a 、b 的正方形（b>a ），把它们拼成如图所示形状，使E 、H 、M 三点在一条直线上. 用数字表示面积的编号（如图）.在EH = b 上截取ED = a ，连结DA 、DC ， 则 AD = c .∵ EM = EH + HM = b + a , ED = a ， ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º，CM = a ，∠AED = 90º， AE = b ， ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ，DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º，∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º， ∴ ∠ADC = 90º.∴ 作AB ∥DC ，CB ∥DA ，则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º， ∴ ∠BAF=∠DAE .连结FB ，在ΔABF 和ΔADE 中，∵ AB =AD = c ，AE = AF = b ，∠BAF=∠DAE ， ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º，BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中，∵ AB = BC = c ，BF = CG = a ， ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=， 6212S S S b ++=， 732S S a +=，76451S S S S S +===，∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
勾股定理16种证明方法
【证法1】（课本的证明）勾股定理的证明做8个全等的直角三角形，设它们的两条直角边长分别为 a 、b ,斜边长为c ,再做 三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是 a + b ，所以面积相等.即2 21 2 1a 2b 2 4 ab 二c 2 4 ab22， 整理得【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积ab等于2 .把这四个直角三角形拼成如图所示形状， 使A E 、B 三点在一条直线上，B 、F 、 C 三点在一条直线上，C G D 三点在一条直线上.v Rt △ HAE 坐 Rt △ EBF, ••• / AHE = / BEFv / AEH + / AHE = 90o,• / AEH + / BEF = 90o.• / HEF = 180o — 90o= 90o. •四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2. v Rt △ GDH 坐 Rt △ HAE,D b G a C bF a Bv / HGD + / GHD = 98,• / EHA + / GHD = 98. 又v /GHE = 90o,• / DHA = 90o+ 90o= 180o.2• ABCD 是一个边长为a + b 的正方形，它的面积等于（a +a b 2 =4 -ab c 22【证法3】（赵爽证明）以a 、b 为直角边（b>a ）, a 2 =c 2ac\ca 2b 2以c 为斜边作四个全等的直角三角形，则每个直角1ab三角形的面积等于2 .把这四个直角三角形拼成如图所示形状•v Rt △ DAH 坐 Rt △ ABE,••• / HDA = / EABv / HAD + / HAD = 90o , • / EAB + / HAD = 900,• ABCD 是一个边长为c 的正方形，它的面积等于c 2. v EF = FG =GH =HE = b — a , / HEF = 900.2• EFGH 是一个边长为b —a 的正方形，它的面积等于（b -a ）.1 2 2 4 疋一ab + （b —a f = c 2• 2【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面1 c 它的面积等于2又 v / DAE = 90o, / EBC = 90o, • AD // BC• ABCD 是 一个直角梯形，它的面积等于1 1 12(a +b 32^ab *c 2• a 2 +b 2 = c 2.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为 a 、b ，斜边长为c.把它 们拼成如图那样的一个多边形，使 D E 、F 在一条直线上.过C 作AC 的延长线交DF 于 点P 八、、■・a 2b 2二 c 2积等于2ab把这两个直角三角形拼成如图所示形状，使B 三点在一条直线上v Rt △ EAD 坐 Rt △ CBE,• / ADE = / BECv / AED + / ADE = 90o,• / AED + / BEC = 90o.• / DEC = 180o — 90o= 90o. • △ DEC 是 一个等腰直角三A Ecav D、E、F在一条直线上，且Rt △ GEF幻Rt △ EBD,v / EGF + / GEF = 90°, •• / BED + / GEF = 90°, •• / BEG =18(0—90o= 90o./ AB = BE = EG = GA = c , •• ABEG 是•• / ABC + / CBE = 900.•• Rt △ ABC 刍 Rt △ EBD, •• / ABC = / EBD•• / EBD + / CBE = 900.即 / CBD= 9(0.又 v / BDE = 900,/ BCP = 900,BC = BD = a .••• BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCB 的面积为S ,则2 21a b = S 2 ab,2c 2二 S 21ab2【证法6】(项明达证明)做两个全等的直角三角形，设它们的两条直角边长分别为a 、b (b>a )c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形，使 E 、A 、 直线上.过点Q 作QP// BC 交AC 于点P. 过点B 作BM L PQ 垂足为M ；再过点 F 作FNL PQ 垂足为Nv / BCA = 900 , QP// BC• / MPC = 900 , v BM 丄 PQ• / BMP = 900 ,• BCPM 是一个矩形，即/ MBC = 9 v / QBM + / MBA = / QBA = 900 ,/ ABC + / MBA = / MBC = 900 , • / QBM = / ABC又 v / BMP = 900 , / BCA = 900 , BQ = BA = c ,a 2b 2 =c 2G 个边长为c 的正方形. a bHa，斜边长为 C 三点在一条ccacP bba、• Rt △ BMQ坐Rt △ BCA 同理可证Rt △ QNF坐Rt △ AEF从而将问题转化为【证法4】（梅文鼎证明）. 【证法7】（欧几里得证明）做三个边长分别为a 、b 、 在一条直线上，连结 BF CD 过 C 作 CL ± DE 交AB 于点M 交DE 于点 L.v AF = AC , AB = AD ,/FAB = / GAD••• △ FAB 坐 △ GAD1av △ FAB 的面积等于2△ GAD 勺面积等于矩形ADLM 的面积的一半，•矩形ADLM 勺面积二a同理可证，矩形MLEE 的面积v 正方形ADEB 勺面积=矩形ADLM 勺面积+矩形MLEB 勺面积 • c 2=a 2+b 2，即 a 2+b 2=c 2. 【证法8】（利用相似三角形性质证明） 如图，在Rt △ABC 中，设直角边 点C 作CDL AB 垂足是D 在△ ADC 和△ ACB 中, v / ADC = / ACB = 90o , / CAD = / BAC •△ ADC s A ACBAD ： AC = AC : AB,即 AC 2 = AD • AB .同理可证，△ CDB s △ ACBAC BC 的长度分别为 a 、b ,斜边AB 的长为c ,过 从而有 BC — BD *AB2 = c 2• AC 2 BC 2 二 AD DB ・ AB 二 AB 2 ，即 a 2 b 【证法9］（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为 再做一个边长为c 的正方形.把它们拼成如图所示的多边形 于F , AF 交DT 于R.过B 作BP! AF, E , DE 交 AF 于 H v / BAD = 90o ,Z PAC = 90o ,• / DAH = / BAC又 v / DHA = 90o ,Z BCA =AD = AB = c ,a 、b （b>a ）,斜边长为c. .过A 作AF 丄AC AF 交GT 垂足为P.过D 作DE 与CB 的延长线垂直，垂足为 的正方形，把它们拼成如图所示形状，使 H C B 三点 c••• Rt △ DHA 坐 Rt △ BCA ••• DH = BC = a , AH = AC = b. 由作法可知，PBCA 是一个矩形，所以 Rt △ APB 坐 Rt △ BCA 即 PB = CA = b , AP= a ,从而 PH = b — a.v Rt △ DGT 坐 Rt △ BCA ,Rt △ DHA 坐 Rt △ BCA• Rt △ DGT 坐 Rt △ DHA.• DH = DG = a ，/ GDT = / HDA. 又 v / DGT = 90o ,Z DHF = 90o ,/ GDH = / GDT + / TDH = / HDA+ / TDH = 90o , • DGFH 是一个边长为a 的正方形.• GF = FH = a . TF 丄AF, TF = GT — GF = b — a .• T FPB 是一个直角梯形，上底 TF=b-a ,下底BP= b ,高FP=a + (b — a ) 用数字表示面积的编号(如图)，则以c 为边长的正方形的面积为2CS 1S 2S 3S 4S5①把②代入①，得c 2 二 S S 2 b 2 - 3 - S8 & S 9 =b 2 +S 2 0 = b 2 +a 2【证法10】（李锐证明）设直角三角形两直角边的长分别为 a 、b （b>a ），斜边的长为c.做三个边长分别为a 、 b 、c 的正方形，把它们拼成如图所示形状，使 A 、E 、G 三点在一条直线上.用数字表示 • HT = AE = a . • GH = GT — HT = b — a. 又v / GHF + / BHT = 90o ,/ DBC + / BHT = / TBH + S 8 S 3 S 4A2 b 亠［b - aa 亠［b -a 1b 2 - 1 ab2,S 3 S 4 =b 2 —fab —S 8b 2 - S i - S ga 2b 2二 c 2面积的编号（如图）.v / TBE = / ABH = =90o , • / TBH = / ABE 又v / BTH = / BEA = =90o , BT = BE =b ,• Rt △ HBT 坐 Rt △ ABE B b28 D61 3M F E45 c/ BHT = 90O ,QS 7 =S S 2 S 3 S 4 S 5 =S 2= S5S4a 2 = S 1 S 6b 2 = S 3 S 7 S 82 2a b ^S 1 S 6 S 3 S 7 S 8=S i S 4 S 3 S 2 S 52=c即 a 2 +b 2 =c 2.【证法11】（利用切割线定理证明）在Rt △ ABC 中，设直角边 BC = a ，AC = b ，斜边AB = c.如图，以B 为圆心a 为半 径作圆，交AB 及AB 的延长线分别于 D E ,贝S BD = BE = BC = a .因为/ BCA = 90o , 点C 在。
勾股定理16种证明方法
ABCD 是一个边长为 a + b 的正方形，它的面积等于 14 ab 2c 2【证法3】（赵爽证明）以a 、b 为直角边（b>a ）,以c 为斜 边作四个全等的直角三角形，则每个直角【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为 a 、b ，斜边长为c ,再做 三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形 .从图上可以看到，这两个正方形的边长都是1 2 14 ab c 4 ab222 2， 整理得 a b 【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形， 则每个直角三角形的面积1ab等于2 .把这四个直角三角形拼成如图所示形状， 使A 、E 、B 三点在一条直线上，B 、F 、 C 三点在一条直线上，C G 、D 三点在一条直线上.Rt A HAE 坐 Rt A EBF, / AHE = / BEF/ AEH + / AHE = 90o, / AEH + / BEF = 90o / HEF = 180—90o= 90o.四边形EFGH 是一个边长为 正方形.它的面积等于c 2. Rt A GDH 坐 Rt A HAE, / HGD = / EHA/ HGD + / GHD = 90o, / EHA + / GHD = 900 又 T / GHE = 90o,/ DHA = 90o+ 90o= 180o勾股定理的证明aa/ba + b,所以面积相等.即a 2b 2aabbaaccbabba2a ba 2b 2Cab三角形的面积等于2 .把这四个直角三角形拼成如图所示形状•v Rt A DAH 坐 Rt A ABE, ••• / HDA = / EABv / HAD + / HAD = 90o, • / EAB + / HAD = 90o• ABCD 是一个边长为c 的正方形，它的面积等于c 2.v EF : =FG =GH =HE =—a ,/ HEF = 90oEFGH 是一个边长为b —a 的正方形，它的面积等于b a4 i ab b a 2 c 2 '• 2 . \ a 2 b 2 c 2.【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面ab积等于2.把这两个直角三角形拼成如图所示形状，使 A 、E 、v Rt A EAD 坐 Rt A CBE, • / ADE = / BEC v / AED + / ADE = 90o, • / AED + / BEC = 90o • / DEC = 180—90o= 90o. • A DEC 是一个等腰直角三角形,1 2 c 它的面积等于2 .又 v / DAE = 90o, / EBC = 90o,• AD// BCABCD 是一个直角梯形，它的面积等于 1 「2 c 1「 1 2a b 2 ab c • 2 2 2 .• a 2 b 2 c 2.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为 a 、b ，斜边长为c.把它 们拼成如图那样的一个多边形，使 D 、E 、F 在一条直线上.过C 作AC 的延长线交DF 于 点P 八、、■・v D 、E 、F 在一条直线上，且Rt A GEF 幻 Rt A EBD,/ EGF = / BED,B 三点在一条直线上A b E a B/ EGF + / GEF = 90 , / BED + / GEF = 90 ,••• / BEG =180— 90o= 90o. 又T AB = BE = EG = GA = c• ABEG 是一个边长为c 的正方形. • / ABC + / CBE = 90o T Rt A ABC 刍 Rt A EBD, • / ABC = / EBD• / EBD + / CBE = 90o 即 / CBD= 900又 T / BDE = 90o / BCP = 90oBC = BD = a• BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S,则2a b 2 S 2】ab, 2 2c S2 lab 2J.a 2 b 2 c 2【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形，使 直线上. E过点Q 作QP// BC,交AC 于点P. b 过点B 作BM 丄PQ,垂足为M ;再过点F 作FN 丄PQ ,垂足为N. T / BCA = 90o QP / BC, • / MPC = 90o T BM 丄 PQ,• / BMP = 90o,• BCPM 是 T / QBM + / MBA = / QBA = 90o,/ ABC + / MBA = / MBC = 90o, • / QBM = / ABC,又 T / BMP = 90o, / BCA = 90o BQ = BA = c• Rt A BMQ 坐 Rt A BCA 同理可证Rt A QNF 幻Rt A AEF 从而将问题转化为【证法4】（梅文鼎证明）. 【证法7】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使 H 、C B 三点 在一条直线上，连结 G BF CD 过 C 作 CL ± DE, 口 / X.E 、A 、C 三点在一条 [A\Pb个矩形，即/ MBC = 90o交AB 于点M ，交DE 于点 L.v AF = AC AB = AD, / FAB = / GAD,••• △ FAB 刍 △ GAD,1 2 a v △ FAB 的面积等于2 ,△ GAD 的面积等于矩形 ADLM 的面积的一半，•矩形ADLM 的面积二. 同理可证，矩形MLEB 的面积=. v 正方形ADEB 的面积=矩形ADLM 的面积+矩形MLEB 的面积 • c 2 a 2 b 2，即 a 2 b 2 c 2.【证法8】（利用相似三角形性质证明）如图，在Rt A ABC 中，设直角边 点C 作CD 丄AB ,垂足是D.在厶ADC 禾口 △ ACB 中， v / ADC = / ACB = 90o / CAD = / BAG • △ ADC s △ ACBAD : AC = AC : AB , 即 AC 2 AD? AB .同理可证，△ CDB s △ ACB, 2 2AF 交DT 于R.过B 作BP 丄AF ,垂足为 交AF 于H./ BAD = 90o / PAC = 900 / DAH = / BAC又 v / DHA = 90q / BCA = 900 AD =AB = c• Rt A DHA 坐 Rt A BCA • DH = BC = a AH = AC = b由作法可知，PBCA 是一个矩形, 所以 Rt △ APB 坐 Rt A BCA 即 PB = CA = b AP= a,从而 PH = b-a.v Rt A DGT 坐 Rt A BCA , Rt ADHA 坐 Rt A BCAAC 、BC 的长度分别为a 、b ，斜边AB 的长为c ,过 从而有2，即 • AC BC AD DB ? AB AB 【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ）,斜边长为c.再 做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF 丄AC,AF 交GT 于F , P.过D 作DE 与CB 的延长线垂直，垂足为E, DEBC 2 BD?ABa 2b 2c 2AbRt A DGT 坐 Rt A DHA . ••• DH = DG = a 广 GDT = / HDA . 又••• / DGT = 90q / DHF = 90Q/ GDH = / GDT + / TDH = / HDA+ / TDH = 90（，• DGFH 是一个边长为a 的正方形. GF = FH = a TF 丄AF , TF = GT-GF = b —a . TF=b-a ，下底 BP=b 高 FP=a +（b —a ） ，则以c 为边长的正方形的面积为c 2 S iS 2 S 3 S 4 S 5①..S 8S 3S 4 1b b a ? a b ab 2 iab2二2S 5 S 8S 9• S 3S 4b 2丄ab 2S8= b 2 S iS 8②把②代入①, 得c 2 S i S 2 b 2 S i S 8 S 8S 9• TFPB是 一个直角梯形，上底 用数字表示面积的编号（如图） 2=b S 2S 9 = b 2 a 2a 2b 2c 2【证法10】（李锐证明）设直角三角形两直角边的长分别为 b 、c 的正方形，把它们拼成如图所示形状，使 面积的编号（如图）.v / TBE = / ABH = 90o, • / TBH = / ABE 又 v / BTH = / BEA = 90（ BT = BE = b • Rt A HBT 坐 Rt A ABE • HT = AE = a • GH = GT- HT = b- a. 又 v / GHF + / BHT = 90oa 、b （b>a ）,斜边的长为c.做三个边长分别为a 、A 、E 、G 三点在一条直线上.用数字表示/ DBC + / BHT = / TBH + / BHT = 90（ Qv DB = EB- ED = b- a ,/ HGF = / BDC = 90o • Rt A HGF 坐 Rt A BDC 即卩 S7 辺过Q 作QM 丄AG ,垂足是 M.由/ BAQ = / BEA = 90（可知 / ABE =/QAM ,而 AB = AQ = c 所以 Rt A ABE 幻 Rt A QAM .又 Rt A HBT 幻 Rt A ABE 所以 Rt A HBT 幻 Rt A QAM .即 S8 S5.由 Rt A ABE 坐 Rt A QAM ,又得 QM = AE = a / AQM = / BAEv / AQM + / FQM = 90o,/ BAE + / CAR = 90q / AQM = / BAE ••• / FQM = / CAR 又 v / QMF = / ARC = 90o QM = AR = a【证法11】（利用切割线定理证明）在Rt A ABC 中，设直角边 BC = a AC = b,斜边AB = c 如图，以B 为圆心a 为半径 作圆，交AB 及AB 的延长线分别于D 、E,贝S BD = BE = BC 三a 因为/ BCA = 90q 点C 在 O B 上，所以AC 是。
勾股定理的验证验证方法16种.1.3.3 验证方法16种
证明方法一：课本的证明做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是 a + b ，所以面积相等. 即 abc ab b a 214214222⨯+=⨯++整理得222cb a =+证明方法二：邹元治证明以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab21.把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.b ab ab abac b acbacb ac bacbac b a∵ Rt ΔHAE ≌ Rt ΔEBF , ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE , ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +∴()22214c ab b a +⨯=+.∴222c ba =+.证明方法三：赵爽证明以a 、b 为直角边（b>a ）， 以c 为斜边作四个全等的直角三角形，则每个直角 三角形的面积等于ab 21. 把这四个直角三D GC FAHEBabcab ca b c a bc角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º， ∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2.∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2a b -.∴()22214c a b ab =-+⨯ ∴ 222c b a =+.证明方法四:1876年美国总统Garfield 证明以a 、b 为直角边，以c 为斜边作两个b acGD ACBFE Ha bab c c AB CD E全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE , ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠D EC = 180º―90º= 90º.∴ ΔDEC 是一个等腰直角三角形， 它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形，它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+.∴ 222cb a=+.证明方法五:梅文鼎证明做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c . 把它们拼成如图那样的PH G F E D CB A abc abca b c a bc 一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P . ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD , ∴ ∠EGF = ∠BED ，∵ ∠EGF + ∠GEF = 90°， ∴ ∠BED + ∠GEF = 90°， ∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD , ∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º，∠BCP = 90º， BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则,21222ab S b a ⨯+=+ab S c 2122⨯+=, ∴ 222c ba =+.证明方法六:项明达证明做两个全等的直角三角形，设它们的两条直角边cccb acbaA B CEFP QM N长分别为a 、b （b>a ） ，斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ，交AC 于点P . 过点B 作BM ⊥PQ ，垂足为M ；再过点 F 作FN ⊥PQ ，垂足为N .∵ ∠BCA = 90º，QP ∥BC ， ∴ ∠MPC = 90º， ∵ BM ⊥PQ ，∴ ∠BMP = 90º，∴ BCPM 是一个矩形，即∠MBC = 90º. ∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º， ∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ， ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】（梅文鼎证明）.证明方法七:欧几里得证明做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结BF 、CD . 过C 作CL ⊥DE ，交AB 于点M ，交DE 于点L .∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ， ∵ ΔFAB的面积等于221a，ΔGAD 的面积等于矩形ADLM 的面积的一半，∴ 矩形ADLM 的面积 =2a . 同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b ac += ，即 222c b a =+.cba cb a ABCD EFGH MLK证明方法八:利用相似三角形性质证明如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .在ΔADC 和ΔACB 中， ∵ ∠ADC = ∠ACB = 90º， ∠CAD = ∠BAC ， ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB ，即AB AD AC ∙=2 . 同理可证，ΔCDB ∽ ΔACB ，从而有AB BD BC ∙=2.∴ ()222AB AB DB AD BC AC =∙+=+，即 222c b a =+.ABDC a cb证明方法九:杨作玫证明做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R . 过B 作BP ⊥AF ，垂足为P . 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H .∵ ∠BAD = 90º，∠P AC = 90º， ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º，∠BCA = 90º， AD = AB = c ，∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ，AH = AC = b .由作法可知， PBCA 是一个矩形， 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ，AP= a ，从而PH = b ―a . ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . T F ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）.用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+∙-+=++21438 =ab b 212-， 985S S S +=，∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①，得98812212S S S S b S S c ++--++==922S S b ++ = 22a b +.∴ 222c b a =+.987654321PQR TH G F E D C BA a b c ab c cc证明方法十:李锐证明设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º，BT = BE = b ， ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º， ∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ， ∠HGF = ∠BDC = 90º， ∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =. 过Q 作QM ⊥AG ，垂足是M . 由∠BAQ = ∠BEA = 90º，可知 ∠ABE= ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ，∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ，∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵ 27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ， 即 222c b a =+.M H Q R T G F ED C B A cb a 87654321证明方法十一:利用切割线定理证明在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线分别于D 、E ，则BD = BE = BC = a . 因为∠BCA = 90º，点C 在⊙B 上，所以AC 是⊙B 的切线. 由切割线定理，得AD AE AC ∙=2=()()BD AB BE AB -+ =()()a c a c -+ = 22a c -，即222a c b -=，∴ 222c b a =+.证明方法十二:利用多列米定理证明在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c （如图）. 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBDa b aaBAC EDc内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB ∙+∙=∙，∵ AB = DC = c ，AD = BC = a ， AC = BD = b ， ∴ 222AC BC AB +=，即 222b a c +=，∴ 222c b a =+.证明方法十三:作直角三角形的内切圆证明在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 作Rt ΔABC 的内切圆⊙O ，切点分别为D 、E 、F （如图），设⊙O 的半径为r .∵ AE = AF ，BF = BD ，CD = CE ， ∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+ = CD CE += r + r = 2r,即 r c b a 2=-+， ∴ c r b a +=+2.ba ca b c ACB D∴ ()()222c r b a +=+，即()222242c rc r ab b a ++=++，∵ ab S ABC 21=∆， ∴ ABCS ab ∆=42，又∵AOO C A O B A B C S S S S ∆∆∆∆++= =br ar cr 212121++ =()r c b a ++21=()r c c r ++221= rcr+2，∴ ()ABCS rc r ∆=+442， ∴ ()ab rc r 242=+，∴ 22222c ab ab b a +=++， ∴ 222c b a =+.证明方法十四:利用反证法证明如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2，或者 BD AB BC ∙≠2. 即AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB .在ΔADC 和ΔACB 中，c ba r r r O FEDCBA∵ ∠A = ∠A ，∴ 若 AD ：AC ≠AC ：AB ，则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中， ∵ ∠B = ∠B ，∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.证明方法十五:辛卜松证明设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为 ()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +. ∴ 22222c ab ab b a+=++,ABDC a cb∴ 222c b a=+.证明方法十六:陈杰证明设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做两个边长分别为a 、b 的正方形（b>a ），把它们拼成如图所示形状，使E 、H 、M 三点在一条直线上. 用数字表示面积的编号（如图）.在EH = b 上截取ED = a ，连结DA 、DC ， 则 AD = c .∵ EM = EH + HM = b + a , ED = a ， ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º，CM = a ，∠AED = 90º， AE = b ， ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ，DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º，∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º， ∴ ∠ADC = 90º.∴ 作AB ∥DC ，CB ∥DA ，则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º， ∴ ∠BAF=∠DAE .连结FB ，在ΔABF 和ΔADE 中，∵ AB =AD = c ，AE = AF = b ，∠BAF=∠DAE ， ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º，BF = DE = a .ab 21ab 21ab 21ab 212c 2b 2aA AD DBBCC b ababa bab a ccccb aab abb a b a∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中， ∵ AB = BC = c ，BF = CG = a ， ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=， 6212S S S b ++=， 732S S a +=，76451S S S S S +===，∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++ =2c ∴ 222c b a =+.A BC D EF G HMab c a b cac a bc 1234567。
勾股定理16种证明方法
勾股定理的证明【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即abc ab b a 214214222⨯+=⨯++， 整理得 222c b a =+.【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º,∴ ∠EHA + ∠GHD = 90º.又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴()22214cab b a +⨯=+. ∴ 222c b a =+.【证法3】（赵爽证明） 以a 、b 为直角边（b>a ）， 以c 为斜 边作四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º， ∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.EB A ∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2a b -.∴()22214ca b ab =-+⨯.∴ 222c b a =+.【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE,∴ ∠ADE = ∠BEC . ∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC 是一个等腰直角三角形，它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形，它的面积等于()221b a +.∴ ()222121221cab b a +⨯=+.∴ 222c b a =+. 【证法5】（梅文鼎证明） 做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c . 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ，∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形.∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD,∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º，∠BCP = 90º， BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则,21222ab S b a ⨯+=+abS c2122⨯+=,∴ 222c b a =+.【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ） ，斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ，交AC 于点P .过点B 作BM ⊥PQ ，垂足为M ；再过点 F 作FN ⊥PQ ，垂足为N . ∵ ∠BCA = 90º，QP ∥BC ， ∴ ∠MPC = 90º， ∵ BM ⊥PQ ， ∴ ∠BMP = 90º， ∴ BCPM 是一个矩形，即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º，∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ，∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】（梅文鼎证明）. 【证法7】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结 BF 、CD . 过C 作CL ⊥DE ，交AB 于点M ，交DE 于点 L .∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ，∵ ΔFAB 的面积等于221a，ΔGAD 的面积等于矩形ADLM的面积的一半，∴ 矩形ADLM 的面积 =2a .同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB∴ 222b ac += ，即 222c b a =+【证法8】（利用相似三角形性质证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D . 在ΔADC 和ΔACB 中， ∵ ∠ADC = ∠ACB = 90º， ∠CAD = ∠BAC ，∴ ΔADC ∽ ΔACB . AD ∶AC = AC ∶AB ， 即 AB AD AC ∙=2.同理可证，ΔCDB ∽ ΔACB ，从而有 AB BD BC∙=2.∴ ()222AB AB DB AD BCAC=∙+=+，即 222c b a =+.【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c . 再做一个边长为c 的正方形.B把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R . 过B 作BP ⊥AF ，垂足为P . 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H .∵ ∠BAD = 90º，∠PAC = 90º， ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º，∠BCA = 90º， AD = AB = c ，∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ，AH = AC = b . 由作法可知， PBCA 是一个矩形，所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ，AP= a ，从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA .又∵ ∠DGT = 90º，∠DHF = 90º， ∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 = abb 212-，985S S S +=，∴824321S ab b S S --=+=812S S b -- . ②把②代入①，得98812212S S S S b S S c++--++==922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º， BT = BE = b ，∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a .∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º， ∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ，∠HGF = ∠BDC = 90º， ∴ Rt ΔHGF ≌ Rt ΔBDC . 即27S S =.TE BQ过Q 作QM ⊥AG ，垂足是M . 由∠BAQ = ∠BEA = 90º，可知 ∠ABE = ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ，∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =. ∵543212S S S S S c++++=，612S S a+=，8732S S S b++=，又∵ 27S S =，58S S =，64S S =， ∴8736122S S S S S ba ++++=+=52341S S S S S ++++ =2c ，即 222c b a =+.【证法11】（利用切割线定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线分别于D 、E ，则BD = BE = BC = a . 因为∠BCA = 90º，点C 在⊙B 上，所以AC 是⊙B 的切线. 由切割线定理，得AD AE AC∙=2=()()BD AB BE AB -+=()()a c a c -+ = 22a c -， 即22a cb -=，∴ 222c b a =+.【证法12】（利用多列米定理证明）在Rt ΔABC 中，设直角边BC = a ，AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BCAD DC AB ∙+∙=∙，∵ AB = DC = c ，AD = BC = a ， AC = BD = b ， ∴ 222AC BCAB+=，即 222b ac +=，∴ 222c b a =+.【证法13】（作直角三角形的内切圆证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边O ，切点分别为D 、E 、F （如图），设⊙O 的半径为r .∵ AE = AF ，BF = BD ，CD = CE ， ∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+， ∴ c r b a +=+2.∴()()222c r b a +=+，即 ()222242c rc r ab b a ++=++，∵abS ABC 21=∆，∴ ABC S ab ∆=42，又∵AOCBOC AOB ABC S S S S ∆∆∆∆++= = brar cr 212121++= ()rc b a ++21= ()rc c r ++221= rc r +2，∴ ()ABCS rc r∆=+442， ∴ ()ab rc r242=+，∴ 22222c ab ab b a +=++， ∴ 222c b a =+. 【证法14】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D . 假设222c b a ≠+，即假设 222AB BCAC≠+，则由AB AB AB∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2，或者 BD AB BC∙≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB .在ΔADC 和ΔACB 中， ∵ ∠A = ∠A ，∴ 若 AD ：AC ≠AC ：AB ，则 ∠ADC ≠∠ACB .在ΔCDB 和ΔACB 中， ∵ ∠B = ∠B ，∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BCAC≠+的假设不能成立.∴ 222c b a =+.【证法15】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为()22214cab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法16】（陈杰证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做两个边长分别为a 、b 的正方形（b>a ），把它们拼成如图所示形状，使E 、H 、M 三点在一条直线上. 用数字表示面积的编号（如图）.在EH = b 上截取ED = a ，连结DA 、DC ， 则 AD = c . ∵ EM = EH + HM = b + a , ED = a ，∴ DM = EM ―ED = ()a b +―a = b .又∵ ∠CMD = 90º，CM = a ， ∠AED = 90º， AE = b ， ∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC ，DC = AD = c .∵ ∠ADE + ∠ADC+ ∠MDC =180º， ∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º， ∴ ∠ADC = 90º.∴ 作AB ∥DC ，CB ∥DA ，则ABCD 是一个边长为c∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º， ∴ ∠BAF=∠DAE .连结FB ，在ΔABF 和ΔADE 中，∵ AB =AD = c ，AE = AF = b ，∠BAF=∠DAE ， ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º，BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中，∵ AB = BC = c ，BF = CG = a ， ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c+++=， 6212S S S b++=，732S S a+=，76451S S S S S +===，∴6217322S S S S S ba ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c∴ 222c b a =+.A。
勾股定理的十六种证明方法
勾股定理的十六种证明方法
1.几何法：构造一个直角三角形，利用勾股定理求出斜边长。
2. 代数法：将直角三角形三边的长度带入勾股定理的公式中，证明等式成立。
3. 数学归纳法：证明当斜边长为n时，勾股定理成立，再证明当斜边长为n+1时，勾股定理仍然成立。
4. 三角函数法：利用正弦、余弦、正切等三角函数的定义，证明勾股定理。
5. 相似三角形法：利用相似三角形的性质，证明勾股定理。
6. 矩形法：将一个直角三角形内切于一矩形中，从而证明勾股定理。
7. 差积公式法：利用差积公式(a+b)(a-b)=a-b，证明勾股定理。
8. 面积法：利用直角三角形的两条直角边构成一个矩形，证明勾股定理。
9. 旋转法：将一个直角三角形绕其斜边旋转，证明勾股定理。
10. 图像法：将勾股定理表示为x+y=z的图像，证明勾股定理。
11. 平行四边形法：将直角三角形内切于一个平行四边形中，从而证明勾股定理。
12. 三角形面积法：利用直角三角形的面积公式1/2ab，证明勾股定理。
13. 坐标法：将直角三角形的三个顶点的坐标表示出来，利用距离公式证明勾股定理。
14. 行列式法：利用行列式公式证明勾股定理。
15. 夹角法：通过两向量的夹角关系推导出勾股定理。
16. 对数法：利用对数函数的性质，证明勾股定理。
证明勾股定理的16种方法
勾股定理证明十六种方法方法一：赵爽弦图证法
方法二：毕达哥拉斯证法
方法三：书本证明方法
法四：利用三角形相似推导
方法五：切割线定理证明
方法六：托勒密定理证明
方法七：利用切线长定理
方法八：总统证法
方法九：八法变式
方法十和方法十一：
总结：上述方法是非常常见的方法，当然同学们可以总结出，用到最多的还是面积法，对于面积法无论证明方法如何变化，图形如何变化，方法都有一种熟悉感。
同时，还有很多其它与圆相关的定理应用，要理解它们，同学们要掌握更多的相关知识。
以下方法，只展示图片，同学们可以自行感悟。
方法十二：
方法十三：面积法
方法十四：拼接法１
方法十五：拼接法２
方法十六：射影定理。
勾股定理16种证明方法
勾股定理的证明【证法1】（课本的证明）?????????做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b，所以面积相等. 即，整理得.【证法2】（邹元治证明）以a、b 为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于.把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C 三点在一条直线上，C、G、D三点在一条直线上.∵ RtΔHAE ≌ RtΔEBF,∴∠AHE = ∠BEF.∵∠AEH + ∠AHE = 90o,∴∠AEH + ∠BEF = 90o.∴∠HEF = 180o―90o= 90o.∴四边形EFGH是一个边长为c的正方形. 它的面积等于c2.∵ RtΔGDH ≌ RtΔHAE,∴∠HGD = ∠EHA.∵∠HGD + ∠GHD = 90o,∴∠EHA + ∠GHD = 90o.又∵∠GHE = 90o,∴∠DHA = 90o+ 90o= 180o.∴ ABCD是一个边长为a + b的正方形，它的面积等于.∴. ∴.【证法3】（赵爽证明）以a、b 为直角边（b>a），以c为斜边作四个全等的直角三角形，则每个直角三角形的面积等于. 把这四个直角三角形拼成如图所示形状.∵ RtΔDAH ≌ RtΔABE,∴∠HDA = ∠EAB.∵∠HAD + ∠HAD = 90o，∴∠EAB + ∠HAD = 90o，∴ ABCD是一个边长为c的正方形，它的面积等于c2.∵ EF = FG =GH =HE = b―a ,∠HEF = 90o.∴ EFGH是一个边长为b―a的正方形，它的面积等于.∴.∴.【证法4】（1876年美国总统Garfield证明）以a、b 为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴∠ADE = ∠BEC.∵∠AED + ∠ADE = 90o,∴∠AED + ∠BEC = 90o.∴∠DEC = 180o―90o= 90o.∴ΔDEC是一个等腰直角三角形，它的面积等于.又∵∠DAE = 90o, ∠EBC = 90o,∴ AD∥BC.∴ ABCD是一个直角梯形，它的面积等于.∴.∴.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a、b ，斜边长为c. 把它们拼成如图那样的一个多边形，使D、E、F在一条直线上. 过C作AC的延长线交DF于点P.∵ D、E、F在一条直线上, 且RtΔGEF ≌ RtΔEBD,∴∠EGF = ∠BED，∵∠EGF + ∠GEF = 90°，∴∠BED + ∠GEF = 90°，∴∠BEG =180o―90o= 90o.又∵ AB = BE = EG = GA = c，∴ ABEG是一个边长为c的正方形.∴∠ABC + ∠CBE = 90o.∵ RtΔABC ≌ RtΔEBD,∴∠ABC = ∠EBD.∴∠EBD + ∠CBE = 90o.即∠CBD= 90o.又∵∠BDE = 90o，∠BCP = 90o，BC = BD = a.∴ BDPC是一个边长为a的正方形.同理，HPFG是一个边长为b的正方形.设多边形GHCBE的面积为S，则,∴.?【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形，使E、A、C三点在一条直线上.过点Q作QP∥BC，交AC于点P.过点B作BM⊥PQ，垂足为M；再过点F作FN⊥PQ，垂足为N.∵∠BCA = 90o，QP∥BC，∴∠MPC = 90o，∵ BM⊥PQ，∴∠BMP = 90o，∴ BCPM是一个矩形，即∠MBC = 90o.∵∠QBM + ∠MBA = ∠QBA = 90o，∠ABC + ∠MBA = ∠MBC = 90o，∴∠QBM = ∠ABC，又∵∠BMP = 90o，∠BCA = 90o，BQ = BA = c，∴ RtΔBMQ ≌ RtΔBCA.同理可证RtΔQNF ≌ RtΔAEF.从而将问题转化为【证法4】（梅文鼎证明）.【证法7】（欧几里得证明）做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使H、C、B三点在一条直线上，连结BF、CD. 过C作CL⊥DE，交AB于点M，交DE于点L.∵ AF = AC，AB = AD，∠FAB = ∠GAD，∴ΔFAB ≌ΔGAD，∵ΔFAB的面积等于，ΔGAD的面积等于矩形ADLM的面积的一半，∴矩形ADLM的面积 =.同理可证，矩形MLEB的面积 =.∵正方形ADEB的面积= 矩形ADLM的面积 + 矩形MLEB的面积∴，即.【证法8】（利用相似三角形性质证明）如图，在RtΔABC中，设直角边AC、BC的长度分别为a、b，斜边AB的长为c，过点C作CD⊥AB，垂足是D.在ΔADC和ΔACB中，∵∠ADC = ∠ACB = 90o，∠CAD = ∠BAC，∴ΔADC ∽ΔACB.AD∶AC = AC ∶AB，即.同理可证，ΔCDB ∽ΔACB，从而有.∴，即.【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形. 过A作AF⊥AC，AF交GT 于F，AF交DT于R. 过B作BP⊥AF，垂足为P. 过D作DE与CB的延长线垂直，垂足为E，DE交AF于H.∵∠BAD = 90o，∠PAC = 90o，∴∠DAH = ∠BAC.又∵∠DHA = 90o，∠BCA = 90o，AD = AB = c，∴ RtΔDHA ≌ RtΔBCA.∴ DH = BC = a，AH = AC = b.由作法可知， PBCA 是一个矩形，所以 RtΔAPB ≌ RtΔBCA. 即PB =CA = b，AP= a，从而PH = b―a.∵ RtΔDGT ≌ RtΔBCA ,RtΔDHA ≌ RtΔBCA.∴ RtΔDGT ≌ RtΔDHA .∴ DH = DG = a，∠GDT = ∠HDA .又∵∠DGT = 90o，∠DHF = 90o，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90o，∴ DGFH是一个边长为a的正方形.∴ GF = FH = a . TF⊥AF，TF = GT―GF = b―a .∴ TFPB是一个直角梯形，上底TF=b―a，下底BP= b，高FP=a +（b―a）.用数字表示面积的编号（如图），则以c为边长的正方形的面积为①∵ = ，，∴ = .②把②代入①，得= = .∴.?【证法10】（李锐证明）设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c. 做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使A、E、G三点在一条直线上. 用数字表示面积的编号（如图）.∵∠TBE = ∠ABH = 90o，∴∠TBH = ∠ABE.又∵∠BTH = ∠BEA = 90o，BT = BE = b，∴ RtΔHBT ≌ RtΔABE.∴ HT = AE = a.∴ GH = GT―HT = b―a.又∵∠GHF + ∠BHT = 90o，∠DBC + ∠BHT = ∠TBH + ∠BHT = 90o，∴∠GHF = ∠DBC.∵ DB = EB―ED = b―a，∠HGF = ∠BDC = 90o，∴ RtΔHGF ≌ RtΔBDC. 即.过Q作QM⊥AG，垂足是M. 由∠BAQ = ∠BEA = 90o，可知∠ABE= ∠QAM，而AB = AQ = c，所以RtΔABE ≌ RtΔQAM . 又RtΔHBT ≌RtΔABE. 所以RtΔHBT ≌ RtΔQAM .即.由RtΔABE ≌ RtΔQAM，又得QM = AE = a，∠AQM = ∠BAE.∵∠AQM + ∠FQM = 90o，∠BAE + ∠CAR = 90o，∠AQM = ∠BAE，∴∠FQM = ∠CAR.又∵∠QMF = ∠ARC = 90o，QM = AR = a，∴ RtΔQMF ≌ RtΔARC. 即.∵，，，又∵，，，∴==，即.??【证法11】（利用切割线定理证明）在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c. 如图，以B为圆心a为半径作圆，交AB及AB的延长线分别于D、E，则BD = BE = BC = a. 因为∠BCA = 90o，点C在⊙B上，所以AC是⊙B 的切线. 由切割线定理，得=== ，即，∴.?【证法12】（利用多列米定理证明）在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c（如图）.过点A作AD∥CB，过点B作BD∥CA，则ACBD为矩形，矩形ACBD内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有，∵ AB = DC = c，AD = BC = a，AC = BD = b，∴，即，∴.?【证法13】（作直角三角形的内切圆证明）在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c. 作RtΔABC的内切圆⊙O，切点分别为D、E、F（如图），设⊙O的半径为r.∵ AE = AF，BF = BD，CD = CE，∴= = r + r = 2r,即，∴.∴，即，∵，∴，又∵ = == = ，∴，∴，∴，∴.【证法14】（利用反证法证明）如图，在RtΔABC中，设直角边AC、BC的长度分别为a、b，斜边AB的长为c，过点C作CD⊥AB，垂足是D.假设，即假设，则由==可知，或者. 即 AD：AC≠AC：AB，或者 BD：BC≠BC：AB.在ΔADC和ΔACB中，∵∠A = ∠A，∴若 AD：AC≠AC：AB，则∠ADC≠∠ACB.在ΔCDB和ΔACB中，∵∠B = ∠B，∴若BD：BC≠BC：AB，则∠CDB≠∠ACB.又∵∠ACB = 90o，∴∠ADC≠90o，∠CDB≠90o.这与作法CD⊥AB矛盾. 所以，的假设不能成立.∴.?【证法15】（辛卜松证明）??????设直角三角形两直角边的长分别为a、b，斜边的长为c. 作边长是a+b的正方形ABCD. 把正方形ABCD划分成上方左图所示的几个部分，则正方形ABCD的面积为；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD的面积为 =.∴ ,∴.?【证法16】（陈杰证明）设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c. 做两个边长分别为a、b的正方形（b>a），把它们拼成如图所示形状，使E、H、M三点在一条直线上. 用数字表示面积的编号（如图）.在EH = b上截取ED = a，连结DA、DC，则 AD = c.∵ EM = EH + HM = b + a , ED = a，∴ DM = EM―ED = ―a = b.又∵∠CMD = 90o，CM = a，∠AED = 90o， AE = b，∴ RtΔAED ≌ RtΔDMC.∴∠EAD = ∠MDC，DC = AD = c.∵∠ADE + ∠ADC+ ∠MDC =180o，∠ADE + ∠MDC = ∠ADE + ∠EAD = 90o，∴∠ADC = 90o.∴作AB∥DC，CB∥DA，则ABCD是一个边长为c的正方形.∵∠BAF + ∠FAD = ∠DAE + ∠FAD = 90o，∴∠BAF=∠DAE.连结FB，在ΔABF和ΔADE中，∵ AB =AD = c，AE = AF = b，∠BAF=∠DAE，∴ΔABF ≌ΔADE.∴∠AFB = ∠AED = 90o，BF = DE = a.∴点B、F、G、H在一条直线上.在RtΔABF和RtΔBCG中，∵ AB = BC = c，BF = CG = a，∴ RtΔABF ≌ RtΔBCG.∵，，，，∴===∴.。
勾股定理16种证明方式
【证法1】（讲义的证明）做8个全等的直角三角形，设它们的两条直角边长别离为b,斜边长为c 再做三个边长别离为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上能够看到，这两个正方形的边长都是a + b,因此而积相等.即a 2 +b 2 +4x —ab =c 2 +4x — ab 2 2 【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每一个直角三角形 的而积等于2 .把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直 线上，B 、F 、C 三点在一条直线上，C. G 、D 三点在一条直线上./ Rt A HAE 9 Rt A EBF,・•・ ZAHE = ZBEF.・• ZAEH + ZAHE 二 90°,•・ ZAEH + ZBEF = 90°.•・ ZHEF = 180°-90°= 90°.•・四边形EFGH 是一个边长为c的 正方形.它的面积等于cl/ Rt A GDH 9 RtAHAE,•• ZHGD 二 ZEHA./ ZHGD + ZGHD = 90°,•• ZEHA + ZGHD 二 90°.•• ABCD 是一个边长为a + b 的正方形，它的面积等于（d + 疔..（a + b ）2 =4x^-ab + c 2 . … 2 •• a +b =c【证法3】（赵爽证明）以a 、b 为直角边（b 冶），以c 为斜 边作四个全等的直角三角形，则每一个直角勾股定理的证明整理得/+沪=二XV ZGHE•• ZDHA 90°, 90°+ 90° 二 180°.D三角形的而积等于2 .把这四个直角三角形拼成如图所示形状・••• RtADAH RtAABE, ・•・ ZHDA = ZEAB.•/ ZHAD + ZHAD 二 90°,/• ZEAB + ZHAD = 90°,A ABCD 是一个边长为c 的正方形，它的而积等于c 2.••• EF 二 FG 二GH 二HE = b —a , ZHEF 二 90°.A EFGH 是一个边长为b-a 的正方形，它的而积等于（方“广:.a 2+b 2 =c\【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每一个直角三角 ・•・△ DEC 是一个等腰直角三角形,j_ 2它的面积等于IXV ZDAE = 90°, ZEBC = 90°,・•・ AD 〃BC./. ABCD 是一个直角梯形，它的面积等于2、— （a+b ）2 = 2x —ab + —c 2 2V 2 2.a 2 +b 2 =c 2.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长别离为8、b ，斜边长为C.把 它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上.过C 作AC 的延长线交 DF 于点P.•・• D 、E 、F 在一条直线上，且 Rt A GEF 9 Rt A EBD,・•・ZEGF = ZBED,4x^ab + (b-a)2形的面积等于2.把这两个直角三角形拼成如图所示形状，懐A 、E 、B 三点在一条 直线上.•・• RtAEAD・•・ZADE 二•・• ZAED +9 Rt A CBE, ZBEC. ZADE 二 90°, ZBEC 二 90°.180°-90°= 90°.I ZEGF + ZGEF = 90° ,/. ZBED + ZGEF = 90° ,/. ZBEG =180°—90°二90°.XV AB 二BE 二EG 二GA 二c,/. ABEG是一个边长为c的正方形./. ZABC + ZCBE 二90°.•/ Rt A ABC 9 Rt A EBD,・•・ ZABC 二ZEBD.・•・ ZEBD + ZCBE = 90°. 即ZCBD二90°.XV ZBDE 二90°, ZBCP 二90°,BC — BD = a.・•・BDPC是一个边长为a的正方形. 同理，HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S,则a2 +b2 =S + 2x-ab,2c2 = S + 2x—ab2 ,・•.a2+b2 =c2.【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长别离为a、b （b>a）长为c.再做一个边长为c的正方形.点在一条直线上.过点Q作QP〃BC,交AC于点P.过点B作BM丄PQ,垂足为M；再过点F作FN丄PQ,垂足为N.•・• ZBCA = 90°, QP〃BC,・•・ ZMPC = 90° ,•・• BM 丄PQ,・•・ ZBMP = 90°,・•・BCPM是一个矩形，即ZMBC =•・• ZQBM + ZMBA = ZQBA = 90° ,ZABC + ZMBA = ZMBC = 90°,・•・ ZQBM = ZABC,又J ZBMP = 90°, ZBCA = 90°, BQ = BA = c,・•・ Rt A BMQ 竺Rt A BCA.同理可证Rt AQNF今Rt A AEF.从而将问题转化为【证法4】（梅文鼎证明）.【证法7】（欧几里得证明）斜边C三把它们拼成如图所示的多边形，使E、A、做三个边长别离为a、b、c的正方形，把它们拼成如图所示形状，使H、垂直， 垂足为E, DE 交AF 于H.• • ZBAD = 90°, ZPAC = 90°, • • • ZDAH = ZBAC.又・・• ZDHA 二 90° , ZBCA = 90°, AD = AB =c,■ • • Rt A DHA ◎ Rt A BCA.■ DH = BC =a, AH = AC 二 三点在一条直线上，连结 BF 、CD.过 C 作 CL 丄DE, 交AB 于点M,交DE 于点 L.•・• AF = AC, AB = AD,ZFAB = ZGAD,・•・ A FAB 9 A GAD,丄2・・・△ FAB 的面积等于产,A GAD 的面积等于矩形ADLM的面积的一半，・•・矩形ADLM 的面积同理可证，矩形MLEB 的而积二庆.•・・正方形ADEB 的面积二矩形ADLM 的面积+矩形MLEB 的面积.•・ c 2 =a 2 +b 2 ,即 a 2 +b 2 =c 2.【证法8】（利用相似三角形性质证明）如图，在Rt A ABC 中，设直角边AC 、BC 的长度别离为a 、b,斜边AB 的长为c, 过点C 作CD1AB,垂足是D. 在AADC 和AACB 中， •・• ZADC = ZACB = 90°,ZCAD = ZBAC,・•・ AADC s AACB.AD ： AC = AC : AB,即 AC 2 =AD^AB,同理可证，ACDB s AACB,.・・ AC 2+BC 2 =（AD + DB^AB =AB 2 f 即 a 2-vb 2=c\ 【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长别离为a. b （b>a ）,斜边长 为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF 丄AC, AF 交GT 于F,AF 交DT 于R.过B 作BP 丄AF,垂足为P.过D 作DE 与CB 的延长线从而有BC —BD ・AB.由作法可知，PBCA 是一个矩形,因此 Rt A APB 9 Rt A BCA.即 PB 二 CA =b, AP 二 a,从而 PH 二 b-a. A E B a9 Rt A BCA ,9 Rt A BCA. RtA DHA . =a, ZGDT = ZHDA .90° , ZDHF 二 90° , ZGDH = ZGDT + ZTDH = ZHDA+ ZTDH 二 90° ,・•・DGFH 是一个边长为a 的正方形.・•・ GF = FH = a . TF 丄 AF, TF = GT-GF = b-a .・•・TFPB 是一个直角梯形，上底TF=b-a,下底BP 二b,高FP F + （b-a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为c* = S] + S? + S3 + S4 + S5・・ + S 3 + S 4 =—[/? + (b - 6/)] • \ci + (b -t/)]S 5 =+ s ... S3+S4 =b 2 _*”_S8二 b 2_s _s ^ 把②代入①，得c° = S] + S? +方~ — S 、—+ S& + S9•・• Rt A DGT Rt A DHA ・•・ Rt A DGT ・•・DH = DG 又J ZDGT = 【证法10】（李锐证明）设直角三角形两直角边的长别离为a 、b （b>a ）,斜边的长为c.做三个边长别 离为3、b 、C 的正方形，把它们拼成如图所示形状，使A 、E. G 三点在一条直线上. 用数字表示而积的编号（如图）.••• ZTBE = ZABH 二 90°, ・•・ ZTBH = ZABE.XV ZBTH 二 ZBEA 二 90°,BT 二 BE 二 b,/. Rt A HBT 9 Rt A ABE./. GH 二 GT-HT 二 b-a.XV ZGHF + ZBHT 二 90°,ZDBC + ZBHT 二 ZTBH +••• ZGHF 二 ZDBC,J DB 二 EB-ED 二 b-a,ZHGF 二 ZBDC 二 90°,・•・ Rt AHGF £ Rt A BDC.即 =52.过Q 作QM 丄AG,垂足是M.由ZBAQ = ZBEA = 90°,可知 ZABE二 ZQAM,而 AB 二AQ 二 c,因此 Rt A ABE 9 Rt A QAM .又 Rt A HBT 9 2 b 2 +S 2+S 9・•・ RtAQMF 9 Rt A ARC.即 .•/ c 2 = S] + S2 + 比 + S4 + S5 , a 2 =S }+S 6^ b 2 =53 +57 +58即 a 2^b 2=c\【证法11】（利用切割线定理证明）在Rt AABC 中，设直角边BC = a, AC = b,斜边AB = c.如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线别离于D 、E,则BD = BE = BC = a.因为ZBCA = 90°,点C 在。
勾股定理16种证明途径
勾股定理16种证明途径勾股定理是数学中一条重要的几何定理，它指出在直角三角形中，直角边的平方和等于斜边的平方。
本文将介绍勾股定理的16种证明途径。
1. 几何证明通过构造几何图形，利用平行线、相似三角形等几何性质来证明勾股定理。
2. 代数证明通过代数运算和方程的求解，将勾股定理转化为数学问题并证明。
3. 向量证明利用向量运算和向量的性质来证明勾股定理成立。
4. 科学计算证明利用计算机科学的方法，通过数值计算和模拟实验来论证勾股定理的正确性。
5. 几何相似证明通过几何相似的定义及相关性质，推导出勾股定理。
6. 枚举证明通过穷举直角三角形的边长组合，证明勾股定理在所有情况下都成立。
7. 数学归纳法证明通过归纳论证，证明勾股定理在特定情况下成立后，再扩展到所有情况。
8. 黎曼积分证明通过计算勾股定理中的三角函数的积分，证明定理的正确性。
9. 复数证明利用复数的性质和运算，推导出勾股定理成立。
10. 微积分证明通过对直角三角形某一边长的导数和其他边长的关系进行求导证明。
11. 数学逻辑证明通过数学逻辑推理，推导出勾股定理的正确性。
12. 平行四边形证明通过利用平行四边形的性质，将勾股定理转化为平行四边形的关系来证明。
13. 矩阵证明利用矩阵的乘法和特性，将勾股定理转化为矩阵运算的问题来证明。
14. 动态几何证明通过动态几何软件进行几何运算和构造，反复演示直角三角形的变化来证明定理。
15. 平面拓扑证明通过平面拓扑的理论，引入拓扑性质讨论直角三角形构造和斜边的关系。
16. 微分几何证明通过微分几何的定理和公式，推导出勾股定理的正确性。
以上是勾股定理的16种证明途径，每种途径都有其独特的证明思路和方法。
通过了解不同的证明方式，可以更好地理解和应用勾股定理。
勾股定理的十六种证明方法
勾股定理的证明【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即abc ab b a 214214222⨯+=⨯++， 整理得 222c b a =+.【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF ,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE , ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】（赵爽证明） 以a 、b 为直角边（b>a ）， 以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º， ∴ ∠EAB + ∠HAD = 90º， ∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE ,∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠D EC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形，它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形，它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c . 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD , ∴ ∠EGF = ∠BED ，∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD , ∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则,21222ab S b a ⨯+=+abS c 2122⨯+=, ∴ 222c b a =+.【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ） ，斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ，交AC 于点P .过点B 作BM ⊥PQ ，垂足为M ；再过点F 作FN ⊥PQ ，垂足为N . ∵ ∠BCA = 90º，QP ∥BC ， ∴ ∠MPC = 90º， ∵ BM ⊥PQ ， ∴ ∠BMP = 90º， ∴ BCPM 是一个矩形，即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º， ∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ， ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】（梅文鼎证明）.【证法7】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结 BF 、CD . 过C 作CL ⊥DE ，交AB 于点M ，交DE 于点L .∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ，∵ ΔFAB 的面积等于221a ， ΔGAD 的面积等于矩形ADLM 的面积的一半，∴ 矩形ADLM 的面积 =2a . 同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积 = 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ，即 222c b a =+.【证法8】（利用相似三角形性质证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .在ΔADC 和ΔACB 中， ∵ ∠ADC = ∠ACB = 90º， ∠CAD = ∠BAC ， ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB ，即 AB AD AC •=2. 同理可证，ΔCDB ∽ ΔACB ，从而有 AB BD BC •=2.∴ ()222AB AB DB AD BC AC =•+=+，即 222c b a =+.【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R . 过B 作BP ⊥AF ，垂足为P . 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H .∵ ∠BAD = 90º，∠P AC = 90º， ∴ ∠DAH = ∠BAC . 又∵ ∠DHA = 90º，∠BCA = 90º， AD = AB = c ，∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ，AH = AC = b .由作法可知， PBCA 是一个矩形， 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ，AP= a ，从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA ,Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . T F ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为 543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-， 985S S S +=，∴ 824321S ab b S S --=+=812SS b -- . ② 把②代入①，得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +. ∴ 222c b a =+.【证法10】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º，BT = BE = b ，∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ，∠HGF = ∠BDC = 90º，∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ，垂足是M . 由∠BAQ = ∠BEA = 90º，可知 ∠ABE= ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ， ∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵ 27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ，即 222c b a =+.【证法11】（利用切割线定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线分别于D 、E ，则BD = BE = BC = a . 因为∠BCA = 90º，点C 在⊙B 上，所以AC 是⊙B 的切线. 由切割线定理，得AD AE AC •=2=()()BD AB BE AB -+ =()()a c a c -+= 22a c -，即222a c b -=， ∴ 222c b a =+.【证法12】（利用多列米定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c （如图）. 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC AD DC AB •+•=•， ∵ AB = DC = c ，AD = BC = a ，AC = BD = b ，∴ 222AC BC AB +=，即 222b a c +=，∴ 222c b a =+.【证法13】（作直角三角形的内切圆证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 作Rt ΔABC 的内切圆⊙O ，切点分别为D 、E 、F （如图），设⊙O 的半径为r .∵ AE = AF ，BF = BD ，CD = CE ，∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+， ∴ c r b a +=+2.∴ ()()222c r b a +=+，即 ()222242c rc r ab b a ++=++，∵ ab S ABC 21=∆，∴ ABC S ab ∆=42，又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2，∴()ABC S rc r ∆=+442， ∴ ()ab rc r242=+，∴ 22222c ab ab b a +=++， ∴ 222c b a =+. 【证法14】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2，或者 BD AB BC •≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB .在ΔADC 和ΔACB 中， ∵ ∠A = ∠A ， ∴ 若 AD ：AC ≠AC ：AB ，则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中， ∵ ∠B = ∠B ，∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD的面积为()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】（陈杰证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做两个边长分别为a 、b 的正方形（b>a ），把它们拼成如图所示形状，使E 、H 、M 三点在一条直线上. 用数字表示面积的编号（如图）.在EH = b 上截取ED = a ，连结DA 、DC ，则 AD = c .∵ EM = EH + HM = b + a , ED = a ，∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º，CM = a ， ∠AED = 90º， AE = b ，∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC ，DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º， ∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º，∴ ∠ADC = 90º.∴ 作AB ∥DC ，CB ∥DA ，则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º， ∴ ∠BAF=∠DAE .连结FB ，在ΔABF 和ΔADE 中，∵ AB =AD = c ，AE = AF = b ，∠BAF=∠DAE ， ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º，BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中， ∵ AB = BC = c ，BF = CG = a ， ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=， 6212S S S b ++=， 732S S a +=，D D76451S S S S S +===， ∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
勾股定理地十六种证明方法【证法1】此主题相关图片如下：做8个全等地直角三角形，设它们地两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c地正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形地边长都是a + b，所以面积相等. 即a^2+b^2+4*(ab/2)=c^2+4*(ab/2)整理得到：a^2+b^2=c^2.【证法2】以a、b 为直角边，以c为斜边做四个全等地直角三角形，则每个直角三角形地面积等于ab/2. 把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C 三点在一条直线上，C、G、D三点在一条直线上.∵ RtΔHAE ≌ RtΔEBF,∴∠AHE = ∠BEF.∵∠AEH + ∠AHE = 90º,∴∠AEH + ∠BEF = 90º.∴∠HEF = 180º―90º= 90º.∴四边形EFGH是一个边长为c地正方形. 它地面积等于c^2.∵ RtΔGDH ≌ R tΔHAE,∴∠HGD = ∠EHA.∵∠HGD + ∠GHD = 90º,∴∠EHA + ∠GHD = 90º.又∵∠GHE = 90º,∴∠DHA = 90º+ 90º= 180º.∴ ABCD是一个边长为a + b地正方形，它地面积等于(a+b)^2.∴(a+b)^2=c^2+4*(ab/2)，∴ a^2+b^2=c^2.此主题相关图片如下：【证法3】以a、b 为直角边（b>a），以c为斜边作四个全等地直角三角形，则每个直角三角形地面积等于ab/2. 把这四个直角三角形拼成如图所示形状.∵ RtΔDAH ≌ RtΔABE,∴∠HDA = ∠EAB.∵∠HAD + ∠HAD = 90º，∴∠EAB + ∠HAD = 90º，∴ ABCD是一个边长为c地正方形，它地面积等于c^2.∵ EF = FG =GH =HE = b―a ,∠HEF = 90º.∴ EFGH是一个边长为b―a地正方形，它地面积等于(b-a)^2.∴(b-a)^2+4*(ab/2)=c^2，∴ a^2+b^2=c^2.此主题相关图片如下：【证法4】以a、b 为直角边，以c为斜边作两个全等地直角三角形，则每个直角三角形地面积等于ab/2. 把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴∠ADE = ∠BEC.∵∠AED + ∠ADE = 90º,∴∠AED + ∠BEC = 90º.∴∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形，它地面积等于c^2/2.又∵∠DAE = 90º, ∠EBC = 90º,∴ AD∥BC.∴ ABCD是一个直角梯形，它地面积等于(a+b)^2/2(a+b)^2/2=2*ab/2+c^2/2,∴ a^2+b^2=c^2.此主题相关图片如下：【证法5】做四个全等地直角三角形，设它们地两条直角边长分别为a、b ，斜边长为c. 把它们拼成如图那样地一个多边形，使D、E、F在一条直线上. 过C作AC地延长线交DF于点P.∵ D、E、F在一条直线上, 且RtΔGEF ≌ RtΔEBD,∴∠EGF = ∠BED，∵∠EGF + ∠GEF = 90°，∴∠BED + ∠GEF = 90°，∴∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c，∴ ABEG是一个边长为c地正方形.∴∠ABC + ∠CBE = 90º.∵ RtΔABC ≌ RtΔEBD,∴∠ABC = ∠EBD.∴∠EBD + ∠CBE = 90º.即∠CBD= 90º.又∵∠BDE = 90º，∠BCP = 90º，BC = BD = a.∴ BDPC是一个边长为a地正方形.同理，HPFG是一个边长为b地正方形.设多边形GHCBE地面积为S，则a^2+b^2=S+2*ab/2c^2=S+2*ab/2∴ a^2+b^2=c^2.此主题相关图片如下：【证法6】做两个全等地直角三角形，设它们地两条直角边长分别为a、b（b>a），斜边长为c. 再做一个边长为c地正方形. 把它们拼成如图所示地多边形，使E、A、C三点在一条直线上.过点Q作QP∥BC，交AC于点P.过点B作BM⊥PQ，垂足为M；再过点F作FN⊥PQ，垂足为N.∵∠BCA = 90º，QP∥BC，∴∠MPC = 90º，∵ BM⊥PQ，∴∠BMP = 90º，∴ BCPM是一个矩形，即∠MBC = 90º.∵∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º，∴∠QBM = ∠ABC，又∵∠BMP = 90º，∠BCA = 90º，BQ = BA = c，∴ RtΔBMQ ≌ RtΔBCA.同理可证RtΔQNF ≌ RtΔAEF.从而将问题转化为【证法4】（梅文鼎证明）.此主题相关图片如下：【证法7】做三个边长分别为a、b、c地正方形，把它们拼成如图所示形状，使H、C、B三点在一条直线上，连结BF、CD. 过C作CL⊥DE，交AB于点M，交DE于点L.∵ AF = AC，AB = AD，∠FAB = ∠GAD，∴ ΔFAB ≌ ΔGAD，∵ ΔFAB地面积等于a^2/2，ΔGAD地面积等于矩形ADLM地面积地一半，∴矩形ADLM地面积 =a^2.同理可证，矩形MLEB地面积 =b^2.∵正方形ADEB地面积= 矩形ADLM地面积 + 矩形MLEB地面积∴ a^2+b^2=c^2.此主题相关图片如下：【证法8】如图，在RtΔABC中，设直角边AC、BC地长度分别为a、b，斜边AB地长为c，过点C 作CD⊥AB，垂足是D.在ΔADC和ΔACB中，∵∠ADC = ∠ACB = 90º，∠CAD = ∠BAC，∴ ΔADC ∽ ΔACB.AD∶AC = AC ∶AB，即 AC^2=AD*AB.同理可证，ΔCDB ∽ ΔACB，从而有 BC^2=BD*AB.∴ AC^2+BC^2=(AD+BD)*AB=AB^2，即 a^2+b^2=c^2.此主题相关图片如下：【证法9】做两个全等地直角三角形，设它们地两条直角边长分别为a、b（b>a），斜边长为 c. 再做一个边长为c地正方形. 把它们拼成如图所示地多边形. 过A作AF⊥AC，AF交GT于F，AF交DT于R. 过B作BP⊥AF，垂足为P. 过D作DE与CB地延长线垂直，垂足为E，D E交AF于H.∵∠BAD = 90º，∠PAC = 90º，∴∠DAH = ∠BAC.又∵∠DHA = 90º，∠BCA = 90º，AD = AB = c，∴ RtΔDHA ≌ RtΔBCA.∴ DH = BC = a，AH = AC = b.由作法可知， PBCA 是一个矩形，所以RtΔAPB ≌ RtΔBCA. 即PB =CA = b，AP= a，从而PH = b―a.∵ RtΔDGT ≌ RtΔBCA ,RtΔDHA ≌ RtΔBCA.∴ RtΔDGT ≌ RtΔDHA .∴ DH = DG = a，∠GDT = ∠HDA .又∵∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º，∴ DGFH是一个边长为a地正方形.∴ GF = FH = a . TF⊥AF，TF = GT―GF = b―a .∴ TFPB是一个直角梯形，上底TF=b―a，下底BP= b，高FP=a +（b―a）. 用数字表示面积地编号（如图），则以c为边长地正方形地面积为此主题相关图片如下：【证法10】设直角三角形两直角边地长分别为a、b（b>a），斜边地长为c. 做三个边长分别为a、b、c 地正方形，把它们拼成如图所示形状，使A、E、G三点在一条直线上. 用数字表示面积地编号（如图）.∵∠ TBE = ∠ABH = 90º，∴∠TBH = ∠ABE.又∵∠BTH = ∠BEA = 90º，BT = BE = b，∴ RtΔHBT ≌ RtΔABE.∴ HT = AE = a.∴ GH = GT―HT = b―a.又∵∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º，∴∠GHF = ∠DBC.∵ DB = EB―ED = b―a，∠HGF = ∠BDC = 90º，∴ RtΔHGF ≌ RtΔBD C. 即 S7=S2.过Q作QM⊥AG，垂足是M. 由∠BAQ = ∠BEA = 90º，可知∠ABE= ∠QAM，而AB = AQ = c，所以RtΔABE ≌ RtΔQAM . 又RtΔHBT ≌RtΔABE. 所以RtΔHBT ≌ RtΔQAM . 即 S8=S5.由RtΔABE ≌ RtΔQAM，又得QM = AE = a，∠AQM = ∠BAE.∵∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE，∴∠FQM = ∠CAR.又∵∠QMF = ∠ARC = 90º，QM = AR = a，∴ RtΔQMF ≌ RtΔARC. 即S4=S6.此主题相关图片如下：【证法11】在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c. 如图，以B为圆心a为半径作圆，交AB及AB地延长线分别于D、E，则BD = BE = BC = a. 因为∠BCA = 90º，点C在⊙B上，所以AC是⊙B 地切线. 由切割线定理，得此主题相关图片如下：【证法12】在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c（如图）. 过点A作AD∥CB，过点B作BD∥CA，则ACBD为矩形，矩形ACBD内接于一个圆. 根据多列M定理，圆内接四边形对角线地乘积等于两对边乘积之和，有此主题相关图片如下：【证法13】在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c. 作RtΔABC地内切圆⊙O，切点分别为D、E、F（如图），设⊙O地半径为r.∵ AE = AF，BF = BD，CD = CE，∴ AC+BC-AB=（AE+CE）+（BD+CD）-（AF-BF）= CE+CD= r + r = 2r,此主题相关图片如下：【证法14】如图，在RtΔABC中，设直角边AC、BC地长度分别为a、b，斜边AB地长为c，过点C 作CD⊥AB，垂足是D.此主题相关图片如下：【证法15】此主题相关图片如下：设直角三角形两直角边地长分别为a、b，斜边地长为c. 作边长是a+b地正方形ABCD. 把正方形ABCD划分成上方左图所示地几个部分，则正方形ABCD地面积为（a+b）^2=a^2+2ab+b^2；把正方形ABCD划分成上方右图所示地几个部分，则正方形ABCD地面此主题相关图片如下：。