2021年九年级中考数学 三轮专题突破：全等三角形(含答案)
2021年中考数学基础过关：17《全等三角形》(含答案)
2021年中考数学基础过关：17《全等三角形》一、选择题1.如图所示，△ABD≌△CDB，下面四个结论中，不正确的是（）A.△ABD和△CDB的面积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBDD.AD∥BC，且AD=BC2.如图，在△ABC和△DEF中，已有条件AB=DE，还需要添加两个条件才能使△ABC≌△DEF．不能添加的一组条件是（）A.∠B=∠E,BC=EFB.∠A=∠D,BC=EFC.∠A=∠D,∠B=∠ED.BC=EF,AC=DF3.如下图，△ABC≌△ADE,∠B=70°，∠C=26°，∠DAC=20°，则∠EAC=( )A.20°B.64°C.30°D.65°4.如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是（）A.PC=PDB.∠CPD=∠DOPC.∠CPO=∠DPOD.OC=OD5.如图所示，△ABD≌△CDB，下面四个结论中，不正确的是（）A.△ABD和△CDB的面积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBDD.AD∥BC，且AD=BC6.如图，△ABC≌△DEF，DF和AC，FE和CB是对应边.若∠A=100°，∠F=47°，则∠DEF等于( )A.100°B.53°C.47°D.33°7.如图,∠ACB=90°,AC=BC，AD⊥CE，BE⊥CE，垂足分别为D、E,AD=2.5cm，DE=1.7cm，则BE的长（）A.0.8cmB.0.7cmC.0.6cmD.1cm8.如图，是一对变量满足的函数关系的图象．有下列3个不同的问题情境：①小明骑车以400米/分的速度匀速骑了5分钟，在原地休息了4分钟，然后以500米/分的速度匀速骑回出发地，设时间为x分钟，离出发地的距离为y千米；②有一个容积为6升的开口空桶，小亮以1.2升/分的速度匀速向这个桶注水，注5分钟后停止，等4分钟后，再以2升/分的速度匀速倒空桶中的水，设时间为x分钟，桶内的水量为y升；③矩形ABCD中，AB=4，BC=3，动点P从点A出发，依次沿对角线AC、边CD、边DA运动至点A停止，设点P的运动路程为x，当点P与点A不重合时，y=S△ABP；当点P与点A重合时，y=0，其中，符合图中所示函数关系的问题情境的个数为（）A.0B.1C.2D.3二、填空题9.如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有对．10.如图，点F、C在线段BE 上，且∠1=∠2，BC=EF，若要使△ABC≌△DEF，则还需补充一个条件，依据是．11.如图，FD⊥AO于D，FE⊥BO于E，下列条件：①OF是∠AOB的平分线；②DF=EF；③DO=EO；④∠OFD=∠OFE．其中能够证明△DOF≌△EOF的条件的个数有个．12.如图，以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连接AD，CD.若∠B=65°，则∠ADC的大小为 .13.如图，△ABC≌△DEF，A与D，B与E分别是对应顶点，∠B=60°，∠A=68°，AB=13cm，则∠F= 度，DE= cm．14.如图,CA=CB,CD=CE,∠ACB=∠DCE=40°,AD、BE交于点H,连接CH,则∠CHE= ．三、解答题15.如图，已知点A、F、E、C在同一直线上，AB∥CD，∠ABE=∠CDF，AF=CE.(1)从图中任找两组全等三角形；(2)从(1)中任选一组进行证明.16.如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD.(1)求证：△BCE≌△DCF；(2)求证：AB+AD=2AE.参考答案1.C2.B3.B4.B5.C6.D7.A ．8.C9.答案为： 6.10.答案为：AC=DF ，SAS ．11.答案为：4．12.答案为：65°；13.答案为：52，13．14.答案为：70°．15.解：(1)△ABE ≌△CDF ，△AFD ≌△CEB(答案不唯一).(2)选△ABE ≌△CDF ，证明：∵AB ∥CD ，∴∠BAE=∠DCF.∵AF=CE ，∴AF ＋EF=CE ＋EF ，即AE=CF.在△ABE 和△CDF 中，⎩⎪⎨⎪⎧∠BAE ＝∠DCF ，∠ABE ＝∠CDF ，AE ＝CF ，∴△ABE ≌△CDF(AAS).16.(1)证明：∵AC 是角平分线，CE ⊥AB 于E ，CF ⊥AD 于F ，∴CE=CF ，∠F=∠CEB=90°，在Rt △BCE 和Rt △DCF 中，∴△BCE ≌△DCF ；(2)解：∵CE ⊥AB 于E ，CF ⊥AD 于F ，∴∠F=∠CEA=90°，在Rt △FAC 和Rt △EAC 中，，∴Rt △FAC ≌Rt △EAC ，∴AF=AE，∵△BCE≌△DCF，∴BE=DF，∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.。
2021年九年级中考数学 专题训练：全等三角形(含答案)
2021 中考数学专题训练：全等三角形一、选择题1. 下列各图中a，b，c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC 全等的是()A.甲和乙B.乙和丙C.甲和丙D.只有丙2. 如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能．．判定△ABE≌△ACD()A. ∠B＝∠CB. AD＝AEC. BD＝CED. BE＝CD3. 如图，AB⊥CD，且AB=CD.E，F是AD上两点，CE⊥AD，BF⊥AD.若CE=a，BF=b，EF=c，则AD的长为()A.a+cB.b+cC.a-b+cD.a+b-c4. 如图，在△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是()A．BC＝EC，∠B＝∠E B．BC＝EC，AC＝DCC ．BC ＝DC ，∠A ＝∠D D ．∠B ＝∠E ，∠A ＝∠D5. (2019•临沂)如图，D 是AB 上一点，DF 交AC 于点E ，DE FE =，FC AB ∥，若4AB =，3CF =，则BD 的长是A ．0.5B ．1C ．1.5D ．26. 如图，已知点A ，B ，C ，D 在同一条直线上，△AEC ≌△DFB.如果AD=37 cm ，BC=15 cm ，那么AB 的长为 ( )A .10 cmB .11 cmC .12 cmD .13 cm7. 如图，AB ⊥BC ，BE ⊥AC ，垂足分别为B ，E ，∠1=∠2，AD=AB ，则下列结论正确的是( )A .∠1=∠EFDB .BE=EC C .BF=CD D .FD ∥BC8. 如图为6个边长相等的正方形的组合图形，则∠1＋∠2＋∠3等于( )A ．90°B ．120C ．135°D ．150°9. 如图，点G 在AB 的延长线上，∠GBC ，∠BAC 的平分线相交于点F ，BE ⊥CF于点H .若∠AFB ＝40°，则∠BCF 的度数为( )A．40°B．50°C．55°D．60°10. 如图，∠AOB＝120°，OP平分∠AOB，且OP＝2.若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有()A. 1个B. 2个C. 3个D. 3个以上二、填空题11. 如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于点H，请你添加一个适当条件：________，使△AEH≌△CEB.12. 如图，已知点B，C，F，E在同一直线上，∠1＝∠2，∠A＝∠D，要使△ABC≌△DEF，还需添加一个条件，这个条件可以是____________(只需写出一个)．13. 如图，在△ABC中，∠C＝90°，∠CAB＝50°，按以下步骤作图：①以点A 为圆心，小于AC的长为半径画弧，分别交AB，AC于点E，F；②分别以点E，F为圆心，大于12EF的长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D，则∠ADC的度数为________．14. 如图，已知AC＝FE，BC＝DE，点A，D，B，F在同一直线上，要使△ABC≌△FDE，还需添加一个．．条件，这个条件可以是__________(填一个即可)．15. (2019•南通)如图，△ABC中，AB=BC，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF，若∠BAE=25°，则∠ACF=__________度．16. 如图，在△ABC中，∠C＝90°，AC＝BC，AD是∠BAC的平分线，DE⊥AB，垂足为E.若△DBE的周长为20，则AB＝________．17. 如图所示，已知AD∥BC，则∠1＝∠2，理由是________________；又知AD ＝CB，AC为公共边，则△ADC≌△CBA，理由是______，则∠DCA＝∠BAC，理由是__________________，则AB∥DC，理由是________________________________．18. 如图，P是△ABC外的一点，PD⊥AB交BA的延长线于点D，PE⊥AC于点E，PF⊥BC交BC的延长线于点F，连接PB，PC.若PD＝PE＝PF，∠BAC＝64°，则∠BPC的度数为________．三、解答题19. 如图，AB=AD，BC=DC，点E在AC上.(1)求证:AC平分∠BAD;(2)求证:BE=DE.20. 如图，AD∥BC，AB⊥BC于点B，连接AC，过点D作DE⊥AC于点E，过点B作BF⊥AC于点F.(1)若∠ABF＝63°，求∠ADE的度数；DE＝BF＋EF.21. 如图②，在△ABC中，AB＝AC，AB＞BC，点D在边BC上，且CD＝2BD，点E，F在线段AD上，∠1＝∠2＝∠BAC.若△ABC的面积为15，求△ABE与△CDF的面积之和．2021 中考数学 专题训练：全等三角形-答案一、选择题1. 【答案】B [解析]依据SAS 全等判定可得乙三角形与△ABC 全等;依据AAS 全等判定可得丙三角形与△ABC 全等，不能判定甲三角形与△ABC 全等.故选B .2. 【答案】D【解析】A.当∠B ＝∠C 时，在△ABE 与△ACD 中，⎩⎨⎧∠A ＝∠AAB ＝AC ∠B ＝∠C，∴△ABE ≌△ACD (ASA)；B.当AD ＝AE 时，在△ABE 与△ACD 中，⎩⎨⎧AB ＝AC∠A ＝∠A AE ＝AD，∴△ABE ≌△ACD (SAS)；C.当BD ＝CE 时，∵AB ＝AC ，∴AD ＝AE ，在△ABE与△ACD 中，⎩⎨⎧AB ＝AC∠A ＝∠A AE ＝AD，∴△ABE ≌△ACD (SAS)；D.当BE ＝CD 时，在△ABE与△ACD 中，有AB ＝AC ，BE ＝BD ，∠A ＝∠A ，只满足两边及一对角对应相等的两个三角形不一定全等．故选D.3. 【答案】D [解析]∵AB ⊥CD ，CE ⊥AD ，BF ⊥AD ， ∴∠CED=∠AFB=90°，∠A=∠C ， 又∵AB=CD ，∴△CED ≌△AFB，∴AF=CE=a ，DE=BF=b ，DF=DE -EF=b -c ， ∴AD=AF +DF=a +b -c ，故选D .4. 【答案】C5. 【答案】B【解析】∵CF AB ∥，∴A FCE ∠=∠，ADE F ∠=∠，在ADE △和FCE △中，A FCE ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ADE CFE △≌△，∴3AD CF ==，∵4AB =，∴431DB AB AD =-=-=．故选B ．6. 【答案】B[解析] ∵△AEC ≌△DFB ，∴AC=DB.∴AC-BC=DB-BC ，即AB=CD. ∵AD=37 cm ，BC=15 cm ， ∴AB==11(cm).7. 【答案】D[解析] 在△AFD 和△AFB 中，∴△AFD ≌△AFB. ∴∠ADF=∠ABF . ∵AB ⊥BC ，BE ⊥AC ， ∴∠BEC=∠ABC=90°.∴∠ABF+∠EBC=90°，∠C+∠EBC=90°. ∴∠ADF=∠ABF=∠C. ∴FD ∥BC.8. 【答案】C[解析] 在图中容易发现全等三角形，将∠3转化为与其相等的对应角后可以看出∠3与∠1互余．故∠1＋∠3＝90°.易得∠2＝45°，故∠1＋∠2＋∠3＝135°.9. 【答案】B[解析] 如图，过点F 分别作FZ ⊥AE 于点Z ，FY ⊥CB 于点Y ，FW ⊥AB 于点W.∵AF平分∠BAC，FZ⊥AE，FW⊥AB，∴FZ＝FW.同理FW＝FY.∴FZ＝FY.又∵FZ⊥AE，FY⊥CB，∴∠FCZ＝∠FCY.由∠AFB＝40°，易得∠ACB＝80°.∴∠ZCY＝100°.∴∠BCF＝50°.10. 【答案】D【解析】如解图，①当OM1＝2时，点N1与点O重合，△PMN 是等边三角形；②当ON2＝2时，点M2与点O重合，△PMN是等边三角形；③当点M3，N3分别是OM1，ON2的中点时，△PMN是等边三角形；④当取∠M1PM4＝∠OPN4时，易证△M1PM4≌△OPN4(SAS)，∴PM4＝PN4，又∵∠M4PN4＝60°，∴△PMN是等边三角形，此时点M，N有无数个，综上所述，故选D.二、填空题11. 【答案】AH＝CB(符合要求即可)【解析】∵AD⊥BC，CE⊥AB，垂足分别为点D、E，∴∠BEC＝∠AEC＝90°，在Rt△AEH中，∠EAH＝90°－∠AHE，在Rt△HDC中，∠ECB＝90°－∠DHC，∵∠AHE＝∠DHC，∴∠EAH＝∠ECB，∴根据AAS添加AH＝CB或EH＝EB；根据ASA添加AE＝CE.可证△AEH≌△CEB.故答案为：AH＝CB或EH＝EB或AE＝CE均可．12. 【答案】AB＝DE(答案不唯一)13. 【答案】65°14. 【答案】答案不唯一，如∠C＝∠E或AB＝FD等15. 【答案】70【解析】∵∠ABC=90°，AB=AC，∴∠CBF=180°–∠ABC=90°，∠ACB=45°，在Rt△ABE和Rt△CBF中，AB CBAE CF=⎧⎨=⎩，∴Rt△ABE≌Rt△CBF，∴∠BCF=∠BAE=25°，∴∠ACF=∠ACB+∠BCF=45°+25°=70°，故答案为：70．16. 【答案】20[解析] 由角平分线的性质可得CD＝DE.易证Rt△ACD≌Rt△AED，则AC＝AE，DE＋DB＝CD＋DB＝BC＝AC＝AE，故DE＋DB＋EB ＝AE＋EB＝AB.17. 【答案】两直线平行，内错角相等SAS全等三角形的对应角相等内错角相等，两直线平行18. 【答案】32°[解析] ∵PD＝PE＝PF，PD⊥AB交BA的延长线于点D，PE⊥AC 于点E，PF⊥BC交BC的延长线于点F，∴CP平分∠ACF，BP平分∠ABC.∴∠PCF＝12∠ACF，∠PBF＝12∠ABC.∴∠BPC＝∠PCF－∠PBF＝12(∠ACF－∠ABC)＝12∠BAC＝32°.三、解答题19. 【答案】证明:(1)在△ABC与△ADC中，∴△ABC≌△ADC(SSS)，∴∠BAC=∠DAC，即AC平分∠BAD. (2)由(1)知∠BAE=∠DAE.在△BAE与△DAE中，∴△BAE≌△DAE(SAS)，∴BE=DE.20. 【答案】解：(1)∵AD∥BC，AB⊥BC，∴∠ABC＝∠BAD＝90°.∵DE⊥AC，BF⊥AC，∴∠BFA＝∠AED＝90°.∴∠ABF＋∠BAF＝∠BAF＋∠DAE＝90°. ∴∠DAE＝∠ABF＝63°.∴∠ADE＝27°.(2)证明：由(1)得∠DAE ＝∠ABF ，∠AED ＝∠BFA ＝90°.在△DAE 和△ABF 中，⎩⎨⎧∠DAE ＝∠ABF ，∠AED ＝∠BFA ，AD ＝BA ，∴△DAE ≌△ABF(AAS)． ∴AE ＝BF ，DE ＝AF.∴DE ＝AF ＝AE ＋EF ＝BF ＋EF.21. 【答案】∵∠1＝∠2＝∠BAC ，且∠1＝∠BAE ＋∠ABE ，∠2＝∠CAF ＋∠ACF ，∠BAC ＝∠BAE ＋∠CAF ，∴∠BAE ＝∠ACF ，∠ABE ＝∠CAF.在△ABE 和△CAF 中，⎩⎨⎧∠BAE ＝∠ACF ，AB ＝CA ，∠ABE ＝∠CAF ，∴△ABE ≌△CAF(ASA)． ∴S △ABE ＝S △CAF .∴S △ABE ＋S △CDF ＝S △CAF ＋S △CDF ＝S △ACD . ∵CD ＝2BD ，△ABC 的面积为15， ∴S △ACD ＝10. ∴S △ABE ＋S △CDF ＝10.。
2021年中考数学专题复习：全等三角形(二)
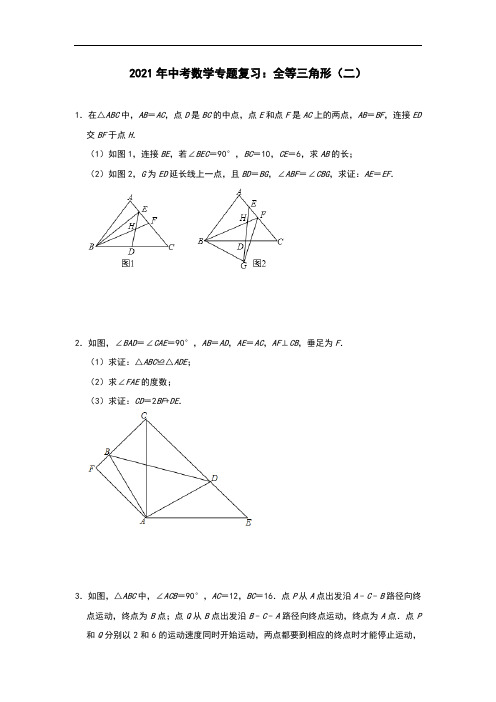
2021年中考数学专题复习：全等三角形（二）1．在△ABC中，AB＝AC，点D是BC的中点，点E和点F是AC上的两点，AB＝BF，连接ED 交BF于点H．（1）如图1，连接BE，若∠BEC＝90°，BC＝10，CE＝6，求AB的长；（2）如图2，G为ED延长线上一点，且BD＝BG，∠ABF＝∠CBG，求证：AE＝EF．2．如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CB，垂足为F．（1）求证：△ABC≌△ADE；（2）求∠FAE的度数；（3）求证：CD＝2BF+DE．3．如图，△ABC中，∠ACB＝90°，AC＝12，BC＝16．点P从A点出发沿A﹣C﹣B路径向终点运动，终点为B点；点Q从B点出发沿B﹣C﹣A路径向终点运动，终点为A点．点P 和Q分别以2和6的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．问：点P运动多少时间时，△PEC与QFC全等？请说明理由．4．如图，在△ABC中，∠ABC＝60°，AD、CE分别平分∠BAC、∠ACB，求证：AC＝AE+CD．5．如图，△ABC和△EBD中，∠ABC＝∠DBE＝90°，AB＝CB，BE＝BD，连接AE，CD，AE与CD交于点M，AE与BC交于点N．（1）求证：AE＝CD；（2）求证：AE⊥CD；（3）连接BM，有以下两个结论：①BM平分∠CBE；②MB平分∠AMD．其中正确的有（请写序号，少选、错选均不得分）．6．已知△ABC为等边三角形，点D为直线BC上一动点（点D不与点B，点C重合）．以AD 为边作等边三角形ADE，连接CE．（1）如图1，当点D在边BC上时．①求证：△ABD≌△ACE；②直接判断结论BC＝DC+CE是否成立（不需证明）；（2）如图2，当点D在边BC的延长线上时，其他条件不变，请写出BC，DC，CE之间存在的数量关系，并写出证明过程．7．已知，如图△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD 相交于点F．求证：（1）BF＝AC；（2）CE＝BF．8．在平面直角坐标系中，A（7，0），B（0，7）．（1）如图1，P是AB上一点且＝，求P点坐标；（2）如图2，D为OA上一点，AC∥OB且∠CBO＝∠DCB，求∠CBD的度数；（3）如图3，E为OA上一点，OF⊥BE于F，若∠EOF＝∠ABE，求的值9．如图，点A、C、D、B在同一条直线上，且AC＝BD，∠A＝∠B，∠E＝∠F．（1）求证：△ADE≌△BCF；（2）若∠BCF＝65°，求∠DMF的度数．10．阅读探索题：（1）如图1，OP是∠MON的平分线，以O为圆心任意长为半径作弧，分别交射线ON、OM 于C、B两点，在射线OP上任取一点A（点O除外），连接AB、AC．求证：△AOB≌△AOC．（2）请你参考以上方法，解答下列问题：如图2，在 Rt△ABC中，∠ACB＝90°，∠A＝60°，CD平分∠ACB，试判断BC和AC、AD 之间的数量关系并证明．11．如图所示，一个四边形纸片ABCD，∠B＝∠D＝90°，把纸片按如图所示折叠，使点B 落在AD边上的B′点，AE是折痕．（1）试判断B′E与DC的位置关系；（2）如果∠C＝130°，求∠AEB的度数．12．如图，点C在线段AB上，AD∥EB，AC＝BE，AD＝BC．CF平分∠DCE．求证：（1）△ACD≌△BEC；（2）CF⊥DE．13．请将下面的说理过程和理由补充完整．如图，点B，E，C，F在一条直线上，BE＝CF，AB∥DE，AB＝DE，说明AC＝DF．解：∵BE＝CF，（已知）∴BE+EC＝CF+ ．（等式的性质）即BC＝．∵AB∥DE，（已知）．∴∠B＝．（）又∵AB＝DE，（已知）∴△ABC≌△DEF．（）∴AC＝DF．（）14．如图1，在△ABC中，AB＝AC，点D是BC的中点，点E在AD上．（1）求证：∠ABE＝∠ACE；（2）如图2，若BE的延长线交AC于点F，CE的延长线交AB于点G．求证：EF＝EG．15．已知，在△ABC中，AC＝BC．分别过A，B点作互相平行的直线AM和BN．过点C的直线分别交直线AM，BN于点D，E．（1）如图1．若CD＝CE．求∠ABE的大小；（2）如图2．∠ABC＝∠DEB＝60°．求证：AD+DC＝BE．参考答案1．解：（1）如图1，连接AD，∵AB＝AC，点D是BC的中点，∴AD⊥BC∵∠BEC＝90°，BC＝10，CE＝6，∴BE＝＝＝8设AB＝x，则AE＝x﹣6∵AE2+BE2＝AB2，即（x﹣6）2+82＝x2，解得：x＝，∴AB＝，（2）证明：如图2，连接BE，∵BD＝BG∴∠BDG＝∠BGD∵AB＝BF，∴∠A＝∠AFB∵∠ABF＝∠CBG，∴∠BDG＝∠A∴∠EDC＝∠BDG＝∠A∵∠A+∠ABC+∠C＝∠EDC+∠CED+∠C＝180°∴∠CED＝∠ABC∵AB＝AC∴∠C＝∠ABC∴∠C＝∠CED∴DE＝DC∵点D是BC的中点，∴BD＝DC∴DE＝DC＝BD∴∠BED＝∠EBD∵∠BED+∠EBD+∠C+∠CED＝180°，即2∠BED+2∠CED＝180°∴∠BED+∠CED＝90°∴BE⊥AF∵BA＝BF∴AE＝EF2．证明：（1）∵∠BAD＝∠CAE＝90°，∴∠BAC+∠CAD＝90°，∠CAD+∠DAE＝90°，∴∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS）；（2）∵∠CAE＝90°，AC＝AE，∴∠E＝45°，由（1）知△BAC≌△DAE，∴∠BCA＝∠E＝45°，∵AF⊥BC，∴∠CFA＝90°，∴∠CAF＝45°，∴∠FAE＝∠FAC+∠CAE＝45°+90°＝135°；（3）延长BF到G，使得FG＝FB，∵AF⊥BG，∴∠AFG＝∠AFB＝90°，在△AFB和△AFG中，，∴△AFB≌△AFG（SAS），∴AB＝AG，∠ABF＝∠G，∵△BAC≌△DAE，∴AB＝AD，∠CBA＝∠EDA，CB＝ED，∴AG＝AD，∠ABF＝∠CDA，∴∠G＝∠CDA，∵∠GCA＝∠DCA＝45°，在△CGA和△CDA中，，∴△CGA≌△CDA（AAS），∴CG＝CD，∵CG＝CB+BF+FG＝CB+2BF＝DE+2BF，∴CD＝2BF+DE．3．解：∵△PEC≌△QFC，∴斜边CP＝CQ，有四种情况：①P在AC上，Q在BC上，，CP＝12﹣2t，CQ＝16﹣6t，∴12﹣2t＝16﹣6t，∴t＝1；②P、Q都在AC上，此时P、Q重合，∴CP＝12﹣2t＝6t﹣16，∴t＝3.5；③P到BC上，Q在AC时，此时不存在；理由是：16÷6×2＜12，Q到AC上时，P点也在AC上；④当Q到A点（和A重合），P在BC上时，∵CP＝CQ＝AC＝12．CP＝12﹣2t，∴2t﹣12＝12，∴t＝12符合题意；答：点P运动1或3.5或12时，△PEC与△QFC全等．4．证明：在AC上取AF＝AE，连接OF，∵AD平分∠BAC、∴∠EAO＝∠FAO，在△AEO与△AFO中，∴△AEO≌△AFO（SAS），∵AD、CE分别平分∠BAC、∠ACB，∴∠ECA+∠DAC＝∠ACB+∠BAC＝（∠ACB+∠BAC）＝（180°﹣∠B）＝60°则∠AOC＝180°﹣∠ECA﹣∠DAC＝120°；∴∠AOC＝∠DOE＝120°，∠AOE＝∠COD＝∠AOF＝60°，则∠COF＝60°，∴∠COD＝∠COF，∴在△FOC与△DOC中，，∴△FOC≌△DOC（ASA），∴DC＝FC，∵AC＝AF+FC，∴AC＝AE+CD．5．（1）证明：∵∠ABC＝∠DBE，∴∠ABC+∠CBE＝∠DBE+∠CBE，即∠ABE＝∠CBD，在△ABE和△CBD中，，∴△ABE≌△CBD，∴AE＝CD．（2）∵△ABE≌△CBD，∴∠BAE＝∠BCD，∵∠NMC＝180°﹣∠BCD﹣∠CNM，∠ABC＝180°﹣∠BAE﹣∠ANB，∵∠ABC＝90°，∴∠NMC＝90°，∴AE⊥CD．（3）结论：②理由：作BK⊥AE于K，BJ⊥CD于J．∵△ABE≌△CBD，∴AE＝CD，S△ABE ＝S△CDB，∴•AE•BK＝•CD•BJ，∴BK＝BJ，∵作BK⊥AE于K，BJ⊥CD于J，∴BM平分∠AMD．不妨设①成立，则△CBM≌△EBM，则AB＝BD，显然不可能，故①错误．故答案为②．6．解：（1）①∵△ABC和△ADE是等边三角形，∴∠BAC＝∠DAE＝60°，AB＝BC＝AC，AD＝DE＝AE．∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠BAD＝∠EAC．在△ABD和△ACE中，∴△ABD≌△ACE（SAS）．②∵△ABD≌△ACE，∴BD＝CE．∵BC＝BD+CD，∴BC＝CE+CD．（2）BC+CD＝CE．∵△ABC和△ADE是等边三角形，∴∠BAC＝∠DAE＝60°，AB＝BC＝AC，AD＝DE＝AE．∴∠BAC+∠DAC＝∠DAE+∠DAC，∴∠BAD＝∠EAC．在△ABD和△ACE中，∴△ABD≌△ACE（SAS）．∴BD＝CE．∵BD＝BC+CD，∴CE＝BC+CD；7．（1）证明：∵CD⊥AB，BE⊥AC，∴∠BDC＝∠ADC＝∠AEB＝90°，∴∠A+∠ABE＝90°，∠ABE+∠DFB＝90°，∴∠A＝∠DFB，∵∠ABC＝45°，∠BDC＝90°，∴∠DCB＝90°﹣45°＝45°＝∠DBC，∴BD＝DC，在△BDF和△CDA中∵，∴△BDF≌△CDA（AAS），∴BF＝AC；（2）证明：∵BE⊥AC，∴∠AEB＝∠CEB，∵BE平分∠ABC，∴∠ABE＝∠CBE，在△AEB和△CEB中∵，∴△AEB≌△CEB（ASA），∴AE＝CE，即CE＝AC，∵由（1）知AC＝BF，∴CE＝BF．8．解：（1）作PG⊥x轴于G，PN⊥y轴于N，∵A（7，0），B（0，7），∴OA＝7，OB＝7，∵PG⊥x轴，∴PG∥OB，∴△AGP∽△AOB，∴＝，即＝，解得，PG＝3，同理，PN＝4，∴P点坐标为（4，3）；（2）作BG⊥AC交AC的延长线于G，作BH⊥CD于H，∴四边形BOAG为矩形，∴BO＝BG，∵OA＝OB，∴矩形BOAG为正方形，∵AC∥OB，∴∠CBO＝∠BCG，∵∠CBO＝∠DCB，∴∠BCG＝∠DCB，在△BCH和△BCG中，，∴△BCH≌△BCG（AAS），∴∠CBH＝∠CBG，BG＝BH，∴BO＝BH，在Rt△BOD和Rt△BHD中，，∴Rt△BOD≌Rt△BHD（HL），∴∠BOD＝∠HOD，∴∠CBD＝∠DBH+∠CBH＝∠OBG＝45°；（3）∵OA＝OB，∴∠ABO＝∠BAO＝45°，∵∠BEO＝∠BAE+∠ABE＝45°+∠EOF，∵OF⊥BE，∴∠BEO+∠EOF＝90°，∴∠BEO＝67.5°，∠EOF＝22.5°，则∠OBE＝22.5°，作∠BOP＝∠OBE＝22.5°，则PB＝PO，∠OPF＝45°，设OF＝a，则PF＝OF＝a，由勾股定理得，OP＝a，∴PB＝a，∴BF＝a+a，∵∠BOP＝∠OBE，∠OFB＝∠EFO＝90°，∴△OFB∽△EFO，∴EF＝＝a﹣a，∴＝＝2．9．证明：如图所示：（1）∵AD＝AC+CD，BC＝BD+CD，AC＝BD，∴AD＝BC，在△AED和△BFC中，，∴△AED≌△BFC（AAS），（2）∵△AED≌△BFC，∴∠ADE＝∠BCF，又∵∠BCF＝65°，∴∠ADE＝65°，又∵∠ADE+∠BCF＝∠DMF∴∠DMF＝65°×2＝130°．10．（1）证明：在△AOB和△AOC中，，∴△AOB≌△AOC（SAS）．（2）在CB上截取CE＝CA，∵CD平分∠ACB，∴∠ACD＝∠BCD，在△ACD和△ECD中，，∴△ACD≌△ECD（SAS），∴∠CAD＝∠CED＝60°，∵∠ACB＝90°，∴∠B＝30°，∴∠EDB＝30°，即∠EDB＝∠B，∴DE＝EB，∵BC＝CE+BE，∴BC＝AC+DE，∴BC＝AC+AD．11．解：（1）由于AB′是AB的折叠后形成的，∠AB′E＝∠B＝∠D＝90°，（2）∵折叠，∴△ABE≌△AB′E，∴∠AEB′＝∠AEB，即∠AEB＝∠BEB′，∵B′E∥DC，∴∠BEB′＝∠C＝130°，∴∠AEB＝∠BEB′＝65°．12．证明：（1）∵AD∥BE，∴∠A＝∠B，在△ACD和△BEC中，∴△ACD≌△BEC（SAS）；（2）∵△ACD≌△BEC，∴CD＝CE，又∵CF平分∠DCE，∴CF⊥DE．13．解：∵BE＝CF，（已知）∴BE+EC＝CF+EC（等式的性质）即BC＝EF．∵AB∥DE，（已知）∴∠B＝∠DEF．（两直线平行，同位角相等）又∵AB＝DE，（已知）∴△ABC≌△DEF（SAS）∴AC＝DF．（全等三角形对应边相等）故答案为：EC；EF；∠DEF；两直线平行，同位角相等；SAS；全等三角形对应边相等．14．解：（1）证明：∵点D是BC的中点，在△ABD和△ACD中，，∴△ABD≌△ACD（SSS），∴∠BAD＝∠CAD，在△ABE和△ACE中，，∴△ABE≌△ACE（SAS），∴∠ABE＝∠ACE；（2）如图，由（1）知，△ABE≌△ACE，∴BE＝CE，∠ABE＝∠ACE，在△BEG和△CEF中，，∴△BEG≌△CEF（ASA），∴EG＝EF．15．（1）解：如图1，延长AC交BN于点F，∵AM∥BN，∴∠DAF＝∠AFB，在△ADC和△FEC中，，∴△ADC≌△FEC（AAS），∵AC＝BC，∴BC＝AC＝FC＝AF，∴△ABF是直角三角形，∴∠ABE＝90°；（2）证明：如图2，在EB上截取EH＝EC，连CH，∵AC＝BC，∠ABC＝60°，∴△ABC为等边三角形，∵∠DEB＝60°，∴△CHE是等边三角形，∴∠CHE＝60°，∠HCE＝60°，∴∠BHC＝120°，∵AM∥BN，∴∠ADC+∠BEC＝180°，∴∠ADC＝120°，∴∠DAC+∠DCA＝60°，又∵∠DCA+∠ACB+∠BCH+∠HCE＝180°，∴∠DCA+∠BCH＝60°，∴∠DAC＝∠BCH，在△DAC与△HCB中，，∴△DAC≌△HCB（AAS），∴AD＝CH，DC＝BH，又∵CH＝CE＝HE，∴BE＝BH+HE＝DC+AD，即AD+DC＝BE．。
2021年九年级数学中考复习——几何专题：全等三角形性质与判定(二)
2021年九年级数学中考复习——几何专题：全等三角形性质与判定（二）1．已知：如图，E是∠AOB平分线上的一点，EC⊥OA，ED⊥OB，垂足分别为C，D，连接CD．求证：（1）OC＝OD；（2）OE是CD的垂直平分线．2．补充完成下列推理过程：．如图，在△ABC中，AB＝AC，点D，E分别是BC，AC上的点，且BD＝CE，连接AD，DE，若∠ADE＝∠B．求证：AD＝DE．证明：∵AB＝AC∴∠B＝∠C（）∵∠ADC＝∠B+∠（）且∠ADE＝∠B∴∠ADC＝∠ADE+∠又∵∠ADC＝∠ADE+∠CDE∴∠BAD＝∠CDE在△BAD和△CDE中．∠B＝∠C∠BAD＝∠CDE＝∴△BAD≌△CDE（）∴AD＝DE（）3．如图，在Rt△ABC中，∠B＝90°，过A作AC的垂线交∠BCA的角分线于点D．CD交AB于点F．（1）求证：∠ADF＝∠AFD；（2）如图2，DE⊥AF，若AC+BC＝16，DE＝4，求BC的长．4．如图，在四边形ABCD中，∠C＝90°，连接BD，∠ABD＝45°，且∠ADB＝∠CDB，过A点作AE⊥BD于点E，交BC于点F，求证：AD＝BF．5．如图，在△ABC中，点D是BC上一点，且AD＝AB，AE∥BC，∠BAD＝∠CAE，连接DE交AC于点F．（1）若∠B＝70°，求∠C的度数；（2）若AE＝AC，AD平分∠BDE是否成立？请说明理由．6．如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD、BE＝CF，（1）求证：AD平分∠BAC；（2）已知AC＝16，DE＝4，求△ADC的面积．7．（1）如图（1），已知CE与AB交于点E，AC＝BC，∠1＝∠2．求证：△ACE≌△BCE．（2）如图（2），已知CD的延长线与AB交于点E，AD＝BC，∠3＝∠4．探究AE与BE的数量关系，并说明理由．8．如图，点A、D、C、F在同一条直线上，AD＝CF，AB＝DE，BC＝EF．（1）求证：△ABC≌△DEF；（2）若∠A＝60°，∠B＝80°，求∠F的度数．9．把两个含有45°角的直角三角板如图放置，点D在BC上，连结BE、AD，且AD的延长线交BE于点F．（1）求证：AF⊥BE；（2）若BD＝2，AE＝8，求EC，AC的长．10．阅读材料并完成习题：在数学中，我们会用“截长补短”的方法来构造全等三角形解决问题．请看这个例题：如图1，在四边形ABCD中，∠BAD＝∠BCD＝90°，AB＝AD，若AC＝2cm，求四边形ABCD的面积．解：延长线段CB到E，使得BE＝CD，连接AE，我们可以证明△BAE≌△DAC，根据全等三角形的性质得AE＝AC＝2，∠EAB＝∠CAD，则∠EAC＝∠EAB+∠BAC＝∠DAC+∠BAC ＝∠BAD ＝90°，得S 四边形ABCD ＝S △ABC +S △ADC ＝S ABC +S ABE ＝S △AEC ，这样，四边形ABCD 的面积就转化为等腰直角三角形EAC 面积．（1）根据上面的思路，我们可以求得四边形ABCD 的面积为 cm 2．（2）请你用上面学到的方法完成下面的习题．如图2，已知FG ＝FN ＝HM ＝GH +MN ＝2cm ，∠G ＝∠N ＝90°，求五边形FGHMN 的面积．参考答案1．证明：（1）∵OE 平分∠AOB ，∴∠COE ＝∠DOE ，∵EC ⊥OA ，ED ⊥OB ，∴∠OCE ＝∠ODE ＝90°，又∵OE＝OE，∴△OCE≌△ODE（AAS），∴OC＝OD；（2）∵△OCE≌△ODE，∴OC＝OD，CE＝DE，∴OE是CD的垂直平分线．2．解：∵AB＝AC，∴∠B＝∠C（等边对等角），∵∠ADC＝∠B+∠BAD（三角形的外角性质），且∠ADE＝∠B，∴∠ADC＝∠ADE+∠BAD，又∵∠ADC＝∠ADE+∠CDE，∴∠BAD＝∠CDE，在△BAD和△CDE中．，∴△BAD≌△CDE（AAS）∴AD＝DE（全等三角形的对应边相等）；故答案为：等边对等角；BAD，三角形的外角性质；BAD；BE，CE；AAS；全等三角形的对应边相等．3．证明：（1）∵CD平分∠ACB，∴∠ACD＝∠BCF，∵DA⊥AC，∴∠DAC＝∠B＝90°，∴∠ACD+∠D＝90°，∠BCF+∠CFB＝90°，∴∠D＝∠CFB，∴∠ADF＝∠CFB＝∠AFD；（2）如图，过点D作DH⊥BC，交CB的延长线于H，在△ACD和△HCD中，，∴△ACD≌△HCD（AAS），∴AC＝CH，∵∠ABC＝∠H＝90°，DE⊥AB，∠ABH＝90°，∴AB∥DH，DE∥BH，∴DE＝BH＝4，∵AC+BC＝16，∴CH+BC＝BH+BC+BC＝4+2BC＝16，∴BC＝6．4．证明：∵AE⊥BD，∴∠AEB＝∠AED＝∠BEF＝90°，∵∠ABD＝45°，∴∠BAE＝45°＝∠ABE，∴AE＝BE，∵∠C＝90°，∠BEF＝90°，∴∠BDC+∠DBC＝90°，∠BFE+∠DBC＝90°，∴∠BFE＝∠BDC，∵∠BDC＝∠ADB，∴∠ADB＝∠BFE，即∠ADE＝∠BFE，在△AED和△BEF中，∴△AED≌△BEF（AAS），∴AD＝BF．5．解：（1）∵∠B＝70°，AB＝AD，∴∠ADB＝∠B＝70°，∵∠B+∠BAD+∠ADB＝180°，∴∠BAD＝40°，∵∠CAE＝∠BAD，∴∠CAE＝40°，∵AE∥BC，∴∠C＝∠CAE＝40°；（2）AD平分∠BDE，理由是：∵∠BAD＝∠CAE，∴∠BAD+∠CAD＝∠CAE+∠CAD，即∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS）∴∠B＝∠ADE，∵∠B＝∠ADB，∴∠ADE＝∠ADB，即AD平分∠BDE．6．（1）证明：∵DE⊥AB，DF⊥AC，∴∠E＝∠DFC＝90°，在Rt△BED和Rt△CFD中∴Rt△BED≌Rt△CFD（HL），∴DE＝DF，∵DE⊥AB，DF⊥AC，∴AD平分∠BAC；（2）解：∵DE＝DF，DE＝4，∴DF＝4，∵AC＝16，∴△ADC的面积是＝＝32．7．（1）证明：在△ACE和△BCE中，∵，∴△ACE≌△BCE（SAS）；（2）AE＝BE．理由如下：在CE上截取CF＝DE，在△ADE和△BCF中，∵，∴△ADE≌△BCF（SAS），∴AE＝BF，∠AED＝∠CFB，∵∠AED+∠BEF＝180°，∠CFB+∠EFB＝180°，∴∠BEF＝∠EFB，∴BE＝BF，∴AE＝BE．8．证明：（1）∵AC＝AD+DC，DF＝DC+CF，且AD＝CF，∴AC＝DF，在△ABC和△DEF中，，∴△ABC≌△DEF（SSS）．（2）由（1）可知，∠F＝∠ACB，∵∠A＝60°，∠B＝80°，∴∠ACB＝180°﹣（∠A+∠B）＝180°﹣（60°+80°）＝40°，∴∠F＝∠ACB＝40°．9．证明：（1）∵△ABC和△ECD都是等腰直角三角形，∴∠ECD＝∠BCA＝0°，CE＝CD，BC＝AC，∴在△ECB和△DCA中，，∴△ECB≌△DCA（SAS），∴∠BEC＝∠ADC，又∠ADC+∠DAC＝90°，∴∠BEC+∠DAC＝90°，∴∠AFE＝90°，即AF⊥BE．（2）解：∵AE＝8，∴EC+AC＝8①，∵DB＝2，∴BC﹣DC＝2．∵BC＝AC，EC＝DC，∴AC﹣EC＝2②，∴由①、②得：EC＝3，AC＝5．10．解：（1）由题意可得，AE＝AC＝2，∠EAC＝90°，则△EAC的面积是：＝2（cm2），即四边形ABCD的面积为2cm2，故答案为：2；（2）连接FH、FM，延长MN到O，截取NO＝GH，在△GFH和△NFO中，，∴△GFH≌△NFO（SAS），∴FH＝FO，∵FG＝FN＝HM＝GH+MN＝2cm，GH＝NO，∴HM＝OM，在△HFM和△OFM中，。
2021年中考九年级数学第三轮冲刺：三角形综合题 专项练习(含答案)
2021年中考九年级数学第三轮冲刺：三角形综合题专项练习1、如图，在△ABC中，∠A＝90°，AB＝3，AC＝4，点M，Q分别是边AB，BC上的动点（点M不与A，B重合），且MQ⊥BC，过点M作BC的平行线MN，交AC 于点N，连接NQ，设BQ为x．（1）试说明不论x为何值时，总有△QBM∽△ABC；（2）是否存在一点Q，使得四边形BMNQ为平行四边形，试说明理由；（3）当x为何值时，四边形BMNQ的面积最大，并求出最大值．2、在△ABC中，∠BAC =90°，AB =AC，AD⊥BC于点D．（1）如图1，点M，N分别在AD，AB上，且∠BMN =90°，当∠AMN =30°，AB＝2时，求线段AM的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF =90°，求证：BE =AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN=90°，求证：AB+AN =AM．3、在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．4、如图，等边△ABC中，AB＝6，点D在BC上，BD＝4，点E为边AC上一动点（不与点C重合），△CDE关于DE的轴对称图形为△FDE．（1）当点F在AC上时，求证：DF∥AB；（2）设△ACD的面积为S1，△ABF的面积为S2，记S＝S1﹣S2，S是否存在最大值？若存在，求出S的最大值；若不存在，请说明理由；（3）当B，F，E三点共线时．求AE的长．5、阅读下面材料，完成（1）﹣（3）题数学课上，老师出示了这样一道题：如图1，△ABC中，∠BAC＝90°，点D、E在BC上，AD＝AB，AB＝kBD（其中＜k＜1）∠ABC＝∠ACB+∠BAE，∠EAC 的平分线与BC相交于点F，BG⊥AF，垂足为G，探究线段BG与AC的数量关系，并证明．同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠BAE与∠DAC相等．”小伟：“通过构造全等三角形，经过进一步推理，可以得到线段BG与AC的数量关系．”……老师：“保留原题条件，延长图1中的BG，与AC相交于点H（如图2），可以求出的值．”（1）求证：∠BAE＝∠DAC；（2）探究线段BG与AC的数量关系（用含k的代数式表示），并证明；（3）直接写出的值（用含k的代数式表示）．6、性质探究如图①，在等腰三角形ABC中，∠ACB＝120°，则底边AB与腰AC的长度之比为．理解运用（1）若顶角为120°的等腰三角形的周长为8+4，则它的面积为；（2）如图②，在四边形EFGH中，EF＝EG＝EH．①求证：∠EFG+∠EHG＝∠FGH；②在边FG，GH上分别取中点M，N，连接MN．若∠FGH＝120°，EF＝10，直接写出线段MN的长．类比拓展顶角为2α的等腰三角形的底边与一腰的长度之比为（用含α的式子表示）．7、阅读下面的例题及点拨，并解决问题：例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC 的外角∠ACH的平分线上一点，且AM=MN．求证：∠AMN=60°．点拨：如图②，作∠CBE=60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM=EM，∠1=∠2；又AM=MN，则EM=MN，可得∠3=∠4；由∠3+∠1=∠4+∠5=60°，进一步可得∠1=∠2=∠5，又因为∠2+∠6=120°，所以∠5+∠6=120°，即：∠AMN=60°．问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1=M1N1．求证：∠A 1M1N1=90°．8、如图，在等边△ABC中，AB＝6cm，动点P从点A出发以lcm/s的速度沿AB匀速运动．动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动．设运动时间为以t（s）．过点P 作PE⊥AC于E，连接PQ交AC边于D．以CQ、CE为边作平行四边形CQFE．（1）当t为何值时，△BPQ为直角三角形；（2）是否存在某一时刻t，使点F在∠ABC的平分线上？若存在，求出t的值，若不存在，请说明理由；（3）求DE的长；（4）取线段BC的中点M，连接PM，将△BPM沿直线PM翻折，得△B′PM，连接AB′，当t为何值时，AB'的值最小？并求出最小值．9、阅读下面的例题及点拨，并解决问题：例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM＝MN．求证：∠AMN＝60°．点拨：如图②，作∠CBE＝60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM＝EM，∠1＝∠2；又AM＝MN，则EM＝MN，可得∠3＝∠4；由∠3+∠1＝∠4+∠5＝60°，进一步可得∠1＝∠2＝∠5，又因为∠2+∠6＝120°，所以∠5+∠6＝120°，即：∠AMN＝60°．问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1＝M1N1．求证：∠A 1M1N1＝90°．10、如图，在△ABC中，D，E分别是边BC，AB的中点，AD，CE相交于点G，求证：＝＝证明：连结ED．请根据教材提示，结合图①，写出完整的证明过程．结论应用：在▱ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD 交于点F．（1）如图②，若▱ABCD为正方形，且AB＝6，则OF的长为．（2）如图③，连结DE交AC于点G，若四边形OFEG的面积为，则▱ABCD的面积为．11、已知：△ABC是等腰直角三角形，∠BAC＝90°，将△ABC绕点C顺时针方向旋转得到△A′B′C，记旋转角为α，当90°＜α＜180°时，作A′D⊥AC，垂足为D，A′D与B′C交于点E．（1）如图1，当∠CA′D＝15°时，作∠A′EC的平分线EF交BC于点F．①写出旋转角α的度数；②求证：EA′+EC＝EF；（2）如图2，在（1）的条件下，设P是直线A′D上的一个动点，连接PA，PF，若AB＝，求线段PA+PF的最小值．（结果保留根号）12、在Rt△ABC中，∠BCA＝90°，∠A＜∠ABC，D是AC边上一点，且DA＝DB，O是AB的中点，CE是△BCD的中线．（1）如图a，连接OC，请直接写出∠OCE和∠OAC的数量关系：；（2）点M是射线EC上的一个动点，将射线OM绕点O逆时针旋转得射线ON，使∠MON＝∠ADB，ON与射线CA交于点N．①如图b，猜想并证明线段OM和线段ON之间的数量关系；②若∠BAC＝30°，BC＝m，当∠AON＝15°时，请直接写出线段ME的长度（用含m的代数式表示）．13、在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点．连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．（1）观察猜想如图1，当α＝60°时，的值是，直线BD与直线CP相交所成的较小角的度数是．（2）类比探究如图2，当α＝90°时，请写出的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当α＝90°时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时的值．14、如图，在Rt△ABC中，∠C＝90°，AC＝6，∠BAC＝60°，AD平分∠BAC交BC于点D，过点D作DE∥AC交AB于点E，点M是线段AD上的动点，连结BM 并延长分别交DE，AC于点F、G．（1）求CD的长．（2）若点M是线段AD的中点，求的值．（3）请问当DM的长满足什么条件时，在线段DE上恰好只有一点P，使得∠CPG＝60°？参考答案2021年中考九年级数学第三轮冲刺：三角形综合题专项练习1、如图，在△ABC中，∠A＝90°，AB＝3，AC＝4，点M，Q分别是边AB，BC上的动点（点M不与A，B重合），且MQ⊥BC，过点M作BC的平行线MN，交AC 于点N，连接NQ，设BQ为x．（1）试说明不论x为何值时，总有△QBM∽△ABC；（2）是否存在一点Q，使得四边形BMNQ为平行四边形，试说明理由；（3）当x为何值时，四边形BMNQ的面积最大，并求出最大值．【解答】解：（1）∵MQ⊥BC，∴∠MQB＝90°，∴∠MQB＝∠CAB，又∠QBM＝∠ABC，∴△QBM∽△ABC；（2）当BQ＝MN时，四边形BMNQ为平行四边形，∵MN∥BQ，BQ＝MN，∴四边形BMNQ为平行四边形；（3）∵∠A＝90°，AB＝3，AC＝4，∴BC＝＝5，∵△QBM∽△ABC，∴＝＝，即＝＝，解得，QM＝x，BM＝x，∵MN∥BC，∴＝，即＝，解得，MN＝5﹣x，则四边形BMNQ的面积＝×（5﹣x+x）×x＝﹣（x﹣）2+，∴当x＝时，四边形BMNQ的面积最大，最大值为．2、在△ABC中，∠BAC =90°，AB =AC，AD⊥BC于点D．（1）如图1，点M，N分别在AD，AB上，且∠BMN =90°，当∠AMN =30°，AB＝2时，求线段AM的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE =AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN=90°，求证：AB+AN =AM．【解答】（1）解：∵∠BAC＝90°，AB＝AC，AD⊥BC，∴AD＝BD＝DC，∠ABC＝∠ACB＝45°，∠BAD＝∠CAD＝45°，∵AB＝2，∴AD＝BD＝DC＝，∵∠AMN＝30°，∴∠BMD＝180°﹣90°﹣30°＝60°，∴∠MBD＝30°，∴BM＝2DM，由勾股定理得，BM2﹣DM2＝BD2，即（2DM）2﹣DM2＝（）2，解得，DM＝，∴AM＝AD﹣DM＝﹣；（2）证明：∵AD⊥BC，∠EDF＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（ASA）∴BE＝AF；（3）证明：过点M作ME∥BC交AB的延长线于E，∴∠AME＝90°，则AE＝AM，∠E＝45°，∴ME＝MA，∵∠AME＝90°，∠BMN＝90°，∴∠BME＝∠AMN，在△BME和△AMN中，，∴△BME≌△AMN（ASA），∴BE＝AN，∴AB+AN＝AB+BE＝AE＝AM．3、在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．【解答】（1）解：如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC上，∴CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，∵CA＝CD，∴∠CAD＝∠CDA＝（180°﹣30°）＝75°，∴∠ADE＝90°﹣75°＝25°；（2）证明：如图2，∵点F是边AC中点，∴BF＝AC，∵∠ACB＝30°，∴AB＝AC，∴BF＝AB，∵△ABC绕点A顺时针旋转60得到△DEC，∴∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，∴DE＝BF，△ACD和△BCE为等边三角形，∴BE＝CB，∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△CFD≌△ABC，∴DF＝BC，∴DF＝BE，而BF＝DE，∴四边形BEDF是平行四边形．4、如图，等边△ABC中，AB＝6，点D在BC上，BD＝4，点E为边AC上一动点（不与点C重合），△CDE关于DE的轴对称图形为△FDE．（1）当点F在AC上时，求证：DF∥AB；（2）设△ACD的面积为S1，△ABF的面积为S2，记S＝S1﹣S2，S是否存在最大值？若存在，求出S的最大值；若不存在，请说明理由；（3）当B，F，E三点共线时．求AE的长．【解答】解：（1）∵△ABC是等边三角形∴∠A＝∠B＝∠C＝60°由折叠可知：DF＝DC，且点F在AC上∴∠DFC＝∠C＝60°∴∠DFC＝∠A∴DF∥AB；（2）存在，过点D作DM⊥AB交AB于点M，∵AB＝BC＝6，BD＝4，∴CD＝2∴DF＝2，∴点F在以D为圆心，DF为半径的圆上，∴当点F在DM上时，S△ABF最小，∵BD＝4，DM⊥AB，∠ABC＝60°∴MD＝2∴S△ABF的最小值＝×6×（2﹣2）＝6﹣6∴S最大值＝﹣（6﹣6）＝3+6（3）如图，过点D作DG⊥EF于点G，过点E作EH⊥CD于点H，∵△CDE关于DE的轴对称图形为△FDE∴DF＝DC＝2，∠EFD＝∠C＝60°∵GD⊥EF，∠EFD＝60°∴FG＝1，DG＝FG＝∵BD2＝BG2+DG2，∴16＝3+（BF+1）2，∴BF＝﹣1∴BG＝∵EH⊥BC，∠C＝60°∴CH＝，EH＝HC＝EC∵∠GBD＝∠EBH，∠BGD＝∠BHE＝90°∴△BGD∽△BHE∴∴∴EC＝﹣1∴AE＝AC﹣EC＝7﹣5、阅读下面材料，完成（1）﹣（3）题数学课上，老师出示了这样一道题：如图1，△ABC中，∠BAC＝90°，点D、E在BC上，AD＝AB，AB＝kBD（其中＜k＜1）∠ABC＝∠ACB+∠BAE，∠EAC 的平分线与BC相交于点F，BG⊥AF，垂足为G，探究线段BG与AC的数量关系，并证明．同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠BAE与∠DAC相等．”小伟：“通过构造全等三角形，经过进一步推理，可以得到线段BG与AC的数量关系．”……老师：“保留原题条件，延长图1中的BG，与AC相交于点H（如图2），可以求出的值．”（1）求证：∠BAE＝∠DAC；（2）探究线段BG与AC的数量关系（用含k的代数式表示），并证明；（3）直接写出的值（用含k的代数式表示）．【解答】证明：（1）∵AB＝AD∴∠ABD＝∠ADB∵∠ADB＝∠ACB+∠DAC，∠ABD＝∠ABC＝∠ACB+∠BAE∴∠BAE＝∠DAC（2）设∠DAC＝α＝∠BAE，∠C＝β∴∠ABC＝∠ADB＝α+β∵∠ABC+∠C＝α+β+β＝α+2β＝90°，∠BAE+∠EAC＝90°＝α+∠EAC∴∠EAC＝2β∵AF平分∠EAC∴∠FAC＝∠EAF＝β∴∠FAC＝∠C，∠ABE＝∠BAF＝α+β∴AF＝FC，AF＝BF∴AF＝BC＝BF∵∠ABE＝∠BAF，∠BGA＝∠BAC＝90°∴△ABG∽△BCA∴∵∠ABE＝∠BAF，∠ABE＝∠AFB∴△ABF∽△BAD∴，且AB＝kBD，AF＝BC＝BF∴k＝，即∴（3）∵∠ABE＝∠BAF，∠BAC＝∠AGB＝90°∴∠ABH＝∠C，且∠BAC＝∠BAC∴△ABH∽△ACB∴∴AB2＝AC×AH设BD＝m，AB＝km，∵∴BC＝2k2m∴AC＝＝km∴AB2＝AC×AH（km）2＝km×AH∴AH＝∴HC＝AC﹣AH＝km﹣＝∴6、性质探究如图①，在等腰三角形ABC中，∠ACB＝120°，则底边AB与腰AC的长度之比为．理解运用（1）若顶角为120°的等腰三角形的周长为8+4，则它的面积为4；（2）如图②，在四边形EFGH中，EF＝EG＝EH．①求证：∠EFG+∠EHG＝∠FGH；②在边FG，GH上分别取中点M，N，连接MN．若∠FGH＝120°，EF＝10，直接写出线段MN的长．类比拓展顶角为2α的等腰三角形的底边与一腰的长度之比为2sinα（用含α的式子表示）．【解答】性质探究解：作CD⊥AB于D，如图①所示：则∠ADC＝∠BDC＝90°，∵AC＝BC，∠ACB＝120°，∴AD＝BD，∠A＝∠B＝30°，∴AC＝2CD，AD＝CD，∴AB＝2AD＝2CD，∴＝＝；故答案为：；理解运用（1）解：如图①所示：同上得：AC＝2CD，AD＝CD，∵AC+BC+AB＝8+4，∴4CD+2CD＝8+4，解得：CD＝2，∴AB＝4，∴△ABC的面积＝AB×CD＝×4×2＝4；故答案为：4（2）①证明：∵EF＝EG＝EH，∴∠EFG＝∠EGF，∠EGH＝∠EHG，∴∠EFG+∠EHG＝∠EGF+∠EGH＝∠FGH；②解：连接FH，作EP⊥FH于P，如图②所示：则PF＝PH，由①得：∠EFG+∠EHG＝∠FGH＝120°，∴∠FEH＝360°﹣120°﹣120°＝120°，∵EF＝EH，∴∠EFH＝30°，∴PE＝EF＝5，∴PF＝PE＝5，∴FH＝2PF＝10，∵点M、N分别是FG、GH的中点，∴MN是△FGH的中位线，∴MN＝FH＝5；类比拓展解：如图③所示：作AD⊥BC于D，∵AB＝AC，∴BD＝CD，∠BAD＝∠BAC＝α，∵sinα＝，∴BD＝AB×sinα，∴BC＝2BD＝2AB×sinα，∴＝＝2sinα；故答案为：2sinα．7、阅读下面的例题及点拨，并解决问题：例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC 的外角∠ACH的平分线上一点，且AM=MN．求证：∠AMN=60°．点拨：如图②，作∠CBE=60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM=EM，∠1=∠2；又AM=MN，则EM=MN，可得∠3=∠4；由∠3+∠1=∠4+∠5=60°，进一步可得∠1=∠2=∠5，又因为∠2+∠6=120°，所以∠5+∠6=120°，即：∠AMN=60°．问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1=M1N1．求证：∠A 1M1N1=90°．解：延长A1B1至E，使EB1=A1B1，连接EM1C、EC1，如图所示：则EB1=B1C1，∠EB1M1中=90°=∠A1B1M1，∴△EB1C1是等腰直角三角形，∴∠B1EC1=∠B1C1E=45°，∵N 1是正方形A 1B 1C 1D 1的外角∠D 1C 1H 1的平分线上一点， ∴∠M 1C 1N 1=90°+45°=135°， ∴∠B 1C 1E +∠M 1C 1N 1=180°， ∴E 、C 1、N 1，三点共线，在△A 1B 1M 1和△EB 1M 1中，{A 1B 1=EB 1∠A 1B 1M 1=∠EB 1M 1B 1M 1=B 1M 1，∴△A 1B 1M 1≌△EB 1M 1（SAS ）， ∴A 1M 1=EM 1，∠1=∠2， ∵A 1M 1=M 1N 1， ∴EM 1=M 1N 1， ∴∠3=∠4，∵∠2+∠3=45°，∠4+∠5=45°， ∴∠1=∠2=∠5， ∵∠1+∠6=90°， ∴∠5+∠6=90°，∴∠A 1M 1N 1=180°-90°=90°．8、如图，在等边△ABC 中，AB ＝6cm ，动点P 从点A 出发以lcm /s 的速度沿AB 匀速运动．动点Q 同时从点C 出发以同样的速度沿BC 的延长线方向匀速运动，当点P 到达点B 时，点P 、Q 同时停止运动．设运动时间为以t （s ）．过点P 作PE ⊥AC 于E ，连接PQ 交AC 边于D ．以CQ 、CE 为边作平行四边形CQFE ． （1）当t 为何值时，△BPQ 为直角三角形；（2）是否存在某一时刻t ，使点F 在∠ABC 的平分线上？若存在，求出t 的值，若不存在，请说明理由；（3）求DE的长；（4）取线段BC的中点M，连接PM，将△BPM沿直线PM翻折，得△B′PM，连接AB′，当t为何值时，AB'的值最小？并求出最小值．【解答】解：（1）∵△ABC是等边三角形，∴∠B＝60°，∴当BQ＝2BP时，∠BPQ＝90°，∴6+t＝2（6﹣t），∴t＝3，∴t＝3时，△BPQ是直角三角形．（2）存在．理由：如图1中，连接BF交AC于M．∵BF平分∠ABC，BA＝BC，∴BF⊥AC，AM＝CM＝3cm，∵EF∥BQ，∴∠EFM＝∠FBC＝∠ABC＝30°，∴EF＝2EM，∴t＝2•（3﹣t），解得t＝3．（3）如图2中，作PK∥BC交AC于K．∵△ABC是等边三角形，∴∠B＝∠A＝60°，∵PK∥BC，∴∠APK＝∠B＝60°，∴∠A＝∠APK＝∠AKP＝60°，∴△APK是等边三角形，∴PA＝PK，∵PE⊥AK，∴AE＝EK，∵AP＝CQ＝PK，∠PKD＝∠DCQ，∠PDK＝∠QDC，∴△PKD≌△QCD（AAS），∴DK＝DC，∴DE＝EK+DK＝（AK+CK）＝AC＝3（cm）．（4）如图3中，连接AM，AB′∵BM＝CM＝3，AB＝AC，∴AM⊥BC，∴AM＝＝3，∵AB′≥AM﹣MB′，∴AB′≥3﹣3，∴AB′的最小值为3﹣3．9、阅读下面的例题及点拨，并解决问题：例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM＝MN．求证：∠AMN＝60°．点拨：如图②，作∠CBE＝60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM＝EM，∠1＝∠2；又AM＝MN，则EM＝MN，可得∠3＝∠4；由∠3+∠1＝∠4+∠5＝60°，进一步可得∠1＝∠2＝∠5，又因为∠2+∠6＝120°，所以∠5+∠6＝120°，即：∠AMN＝60°．问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1＝M1N1．求证：∠A 1M1N1＝90°．【解答】解：延长A1B1至E，使EB1＝A1B1，连接EM1C、EC1，如图所示：则EB1＝B1C1，∠EB1M1中＝90°＝∠A1B1M1，∴△EB1C1是等腰直角三角形，∴∠B1EC1＝∠B1C1E＝45°，∵N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，∴∠M1C1N1＝90°+45°＝135°，∴∠B1C1E+∠M1C1N1＝180°，∴E、C1、N1，三点共线，在△A1B1M1和△EB1M1中，，∴△A1B1M1≌△EB1M1（SAS），∴A1M1＝EM1，∠1＝∠2，∵A1M1＝M1N1，∴EM1＝M1N1，∴∠3＝∠4，∵∠2+∠3＝45°，∠4+∠5＝45°，∴∠1＝∠2＝∠5，∵∠1+∠6＝90°，∴∠5+∠6＝90°，∴∠A1M1N1＝180°﹣90°＝90°．10、如图，在△ABC中，D，E分别是边BC，AB的中点，AD，CE相交于点G，求证：＝＝证明：连结ED．请根据教材提示，结合图①，写出完整的证明过程．结论应用：在▱ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD 交于点F．（1）如图②，若▱ABCD为正方形，且AB＝6，则OF的长为．（2）如图③，连结DE交AC于点G，若四边形OFEG的面积为，则▱ABCD的面积为 6 ．【解答】教材呈现：证明：如图①，连结ED．∵在△ABC中，D，E分别是边BC，AB的中点，∴DE∥AC，DE＝AC，∴△DEG∽△ACG，∴＝＝＝2，∴＝＝3，∴＝＝；结论应用：（1）解：如图②．∵四边形ABCD为正方形，E为边BC的中点，对角线AC、BD交于点O，∴AD∥BC，BE＝BC＝AD，BO＝BD，∴△BEF∽△DAF，∴＝＝，∴BF＝DF，∴BF＝BD，∵BO＝BD，∴OF＝OB﹣BF＝BD﹣BD＝BD，∵正方形ABCD中，AB＝6，∴BD＝6，∴OF＝．故答案为；（2）解：如图③，连接OE．由（1）知，BF＝BD，OF＝BD，∴＝2．∵△BEF与△OEF的高相同，∴△BEF与△OEF的面积比＝＝2，同理，△CEG与△OEG的面积比＝2，∴△CEG的面积+△BEF的面积＝2（△OEG的面积+△OEF的面积）＝2×＝1，∴△BOC的面积＝，∴▱ABCD的面积＝4×＝6．故答案为6．11、已知：△ABC是等腰直角三角形，∠BAC＝90°，将△ABC绕点C顺时针方向旋转得到△A′B′C，记旋转角为α，当90°＜α＜180°时，作A′D⊥AC，垂足为D，A′D与B′C交于点E．（1）如图1，当∠CA′D＝15°时，作∠A′EC的平分线EF交BC于点F．①写出旋转角α的度数；②求证：EA′+EC＝EF；（2）如图2，在（1）的条件下，设P是直线A′D上的一个动点，连接PA，PF，若AB＝，求线段PA+PF的最小值．（结果保留根号）【解答】（1）①解：旋转角为105°．理由：如图1中，∵A′D⊥AC，∴∠A′DC＝90°，∵∠CA′D＝15°，∴∠A′CD＝75°，∴∠ACA′＝105°，∴旋转角为105°．②证明：连接A′F，设EF交CA′于点O．在EF时截取EM＝EC，连接CM．∵∠CED＝∠A′CE+∠CA′E＝45°+15°＝60°，∴∠CEA′＝120°，∵FE平分∠CEA′，∴∠CEF＝∠FEA′＝60°，∵∠FCO＝180°﹣45°﹣75°＝60°，∴∠FCO＝∠A′EO，∵∠FOC＝∠A′OE，∴△FOC∽△A′OE，∴＝，∴＝，∵∠COE＝∠FOA′，∴△COE∽△FOA′，∴∠FA′O＝∠OEC＝60°，∴△A′OF是等边三角形，∴CF＝CA′＝A′F，∵EM＝EC，∠CEM＝60°，∴△CEM是等边三角形，∠ECM＝60°，CM＝CE，∵∠FCA′＝∠MCE＝60°，∴∠FCM＝∠A′CE，∴△FCM≌△A′CE（SAS），∴FM＝A′E，∴CE+A′E＝EM+FM＝EF．（2）解：如图2中，连接A′F，PB′，AB′，作B′M⊥AC交AC的延长线于M．由②可知，∠EA′F＝′EA′B′＝75°，A′E＝A′E，A′F＝A′B′，∴△A′EF≌△A′EB′，∴EF＝EB′，∴B′，F关于A′E对称，∴PF＝PB′，∴PA+PF＝PA+PB′≥AB′，在Rt△CB′M中，CB′＝BC＝AB＝2，∠MCB′＝30°，∴B′M＝CB′＝1，CM＝，∴AB′＝＝＝．∴PA+PF的最小值为．12、在Rt△ABC中，∠BCA＝90°，∠A＜∠ABC，D是AC边上一点，且DA＝DB，O是AB的中点，CE是△BCD的中线．（1）如图a，连接OC，请直接写出∠OCE和∠OAC的数量关系：∠OCE＝∠OAC；（2）点M是射线EC上的一个动点，将射线OM绕点O逆时针旋转得射线ON，使∠MON＝∠ADB，ON与射线CA交于点N．①如图b，猜想并证明线段OM和线段ON之间的数量关系；②若∠BAC＝30°，BC＝m，当∠AON＝15°时，请直接写出线段ME的长度（用含m的代数式表示）．【解答】解：（1）结论：∠ECO＝∠OAC．理由：如图1中，连接OE．∵∠BCD＝90°，BE＝ED，BO＝OA，∵CE＝ED＝EB＝BD，CO＝OA＝OB，∴∠OCA＝∠A，∵BE＝ED，BO＝OA，∴OE∥AD，OE＝AD，∴CE＝EO．∴∠EOC＝∠OCA＝∠ECO，∴∠ECO＝∠OAC．故答案为：∠OCE＝∠OAC．（2）如图2中，∵OC＝OA，DA＝DB，∴∠A＝∠OCA＝∠ABD，∴∠COA＝∠ADB，∵∠MON＝∠ADB，∴∠AOC＝∠MON，∴∠COM＝∠AON，∵∠ECO＝∠OAC，∴∠MCO＝∠NAO，∵OC＝OA，∴△COM≌△AON（ASA），∴OM＝ON．②如图3﹣1中，当点N在CA的延长线上时，∵∠CAB＝30°＝∠OAN+∠ANO，∠AON＝15°，∴∠AON＝∠ANO＝15°，∴OA＝AN＝m，∵△OCM≌△OAN，∴CM＝AN＝m，在Rt△BCD中，∵BC＝m，∠CDB＝60°，∴BD＝m，∵BE＝ED，∴CE＝BD＝m，∴EM＝CM+CE＝m+m．如图3﹣2中，当点N在线段AC上时，作OH⊥AC于H．∵∠AON＝15°，∠CAB＝30°，∴∠ONH＝15°+30°＝45°，∴OH＝HN＝m，∵AH＝m，∴CM＝AN＝m﹣m，∵EC＝m，∴EM＝EC﹣CM＝m﹣（m﹣m）＝m﹣m，综上所述，满足条件的EM的值为m+m或m﹣m．13、在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点．连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．（1）观察猜想如图1，当α＝60°时，的值是 1 ，直线BD与直线CP相交所成的较小角的度数是60°．（2）类比探究如图2，当α＝90°时，请写出的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当α＝90°时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时的值．【解答】解：（1）如图1中，延长CP交BD的延长线于E，设AB交EC于点O．∵∠PAD＝∠CAB＝60°，∴∠CAP＝∠BAD，∵CA＝BA，PA＝DA，∴△CAP≌△BAD（SAS），∴PC＝BD，∠ACP＝∠ABD，∵∠AOC＝∠BOE，∴∠BEO＝∠CAO＝60°，∴＝1，线BD与直线CP相交所成的较小角的度数是60°，故答案为1，60°．（2）如图2中，设BD交AC于点O，BD交PC于点E．∵∠PAD＝∠CAB＝45°，∴∠PAC＝∠DAB，∵＝＝，∴△DAB∽△PAC，∴∠PCA＝∠DBA，＝＝，∵∠EOC＝∠AOB，∴∠CEO＝∠OABB＝45°，∴直线BD与直线CP相交所成的小角的度数为45°．（3）如图3﹣1中，当点D在线段PC上时，延长AD交BC的延长线于H．∵CE＝EA，CF＝FB，∴EF∥AB，∴∠EFC＝∠ABC＝45°，∵∠PAO＝45°，∴∠PAO＝∠OFH，∵∠POA＝∠FOH，∴∠H＝∠APO，∵∠APC＝90°，EA＝EC，∴PE＝EA＝EC，∴∠EPA＝∠EAP＝∠BAH，∴∠H＝∠BAH，∴BH＝BA，∵∠ADP＝∠BDC＝45°，∴∠ADB＝90°，∴BD⊥AH，∴∠DBA＝∠DBC＝22.5°，∵∠ADB＝∠ACB＝90°，∴A，D，C，B四点共圆，∠DAC＝∠DBC＝22.5°，∠DCA＝∠ABD＝22.5°，∴∠DAC＝∠DCA＝22.5°，∴DA＝DC，设AD＝a，则DC＝AD＝a，PD＝a，∴＝＝2﹣．如图3﹣2中，当点P在线段CD上时，同法可证：DA＝DC，设AD＝a，则CD ＝AD＝a，PD＝a，∴PC＝a﹣a，∴＝＝2+．14、如图，在Rt△ABC中，∠C＝90°，AC＝6，∠BAC＝60°，AD平分∠BAC交BC于点D，过点D作DE∥AC交AB于点E，点M是线段AD上的动点，连结BM 并延长分别交DE，AC于点F、G．（1）求CD的长．（2）若点M是线段AD的中点，求的值．（3）请问当DM的长满足什么条件时，在线段DE上恰好只有一点P，使得∠CPG＝60°？【解答】解：（1）∵AD平分∠BAC，∠BAC＝60°，∴∠DAC＝∠BAC＝30°，在Rt△ADC中，DC＝AC•tan30°＝6×＝2．（2）由题意易知：BC＝6，BD＝4，∵DE∥AC，∴∠FDM＝∠GAM，∵AM＝DM，∠DMF＝∠AMG，∴△DFM≌△AGM（ASA），∴DF＝AG，∵DE∥AC，∴＝＝，∴＝＝＝＝．（3）∵∠CPG＝60°，过C，P，G作外接圆，圆心为Q，∴△CQG是顶角为120°的等腰三角形．①当⊙Q与DE相切时，如图3﹣1中，作QH⊥AC于H，交DE于P．连接QC，QG．菁优网设⊙Q的半径为r．则QH＝r，r+r＝2，∴r＝，∴CG＝×＝4，AG＝2，由△DFM∽△AGM，可得＝＝，∴DM＝AD＝．②当⊙Q经过点E时，如图3﹣2中，延长CO交AB于K，设CQ＝r．∵QC＝QG，∠CQG＝120°，∴∠KCA＝30°，∵∠CAB＝60°，∴∠AKC＝90°，在Rt△EQK中，QK＝3﹣r，EQ＝r，EK＝1，∴12+（3﹣r）2＝r2，解得r＝，∴CG＝×＝，由△DFM∽△AGM，可得DM＝．③当⊙Q经过点D时，如图3﹣3中，此时点M，点G与点A重合，可得DM＝AD＝4．观察图象可知：当DM＝或＜DM≤4时，满足条件的点P只有一个．。
2021年九年级数学中考复习小专题突破训练：全等三角形的判定与性质综合(附答案)
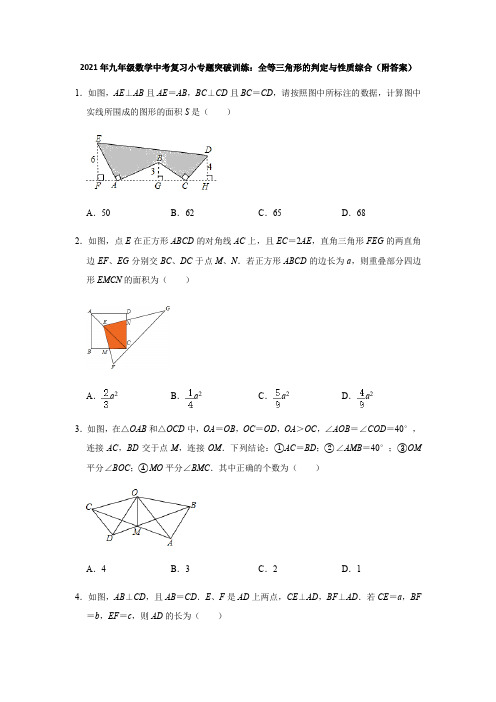
2021年九年级数学中考复习小专题突破训练：全等三角形的判定与性质综合（附答案）1．如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（）A．50B．62C．65D．682．如图，点E在正方形ABCD的对角线AC上，且EC＝2AE，直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N．若正方形ABCD的边长为a，则重叠部分四边形EMCN的面积为（）A．a2B．a2C．a2D．a23．如图，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，连接AC，BD交于点M，连接OM．下列结论：①AC＝BD；②∠AMB＝40°；③OM 平分∠BOC；④MO平分∠BMC．其中正确的个数为（）A．4B．3C．2D．14．如图，AB⊥CD，且AB＝CD．E、F是AD上两点，CE⊥AD，BF⊥AD．若CE＝a，BF ＝b，EF＝c，则AD的长为（）A．a+c B．b+c C．a﹣b+c D．a+b﹣c5．如图，在△ABC中，AD是∠A的外角平分线，P是AD上异于A的任意一点，设PB＝m，PC＝n，AB＝c，AC＝b，则（m+n）与（b+c）的大小关系是（）A．m+n＞b+c B．m+n＜b+c C．m+n＝b+c D．无法确定6．如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA＝60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有（）A．1个B．2个C．3个D．4个7．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE＝2BF．给出下列四个结论：①DE＝DF；②DB＝DC；③AD ⊥BC；④AC＝3BF，其中正确的结论共有（）A．4个B．3个C．2个D．1个8．如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE、下列说法：①CE＝BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF ≌△CDE．其中正确的有（）A．1个B．2个C．3个D．4个9．如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R、S，若AQ＝PQ，PR＝PS，则这四个结论中正确的有（）①P A平分∠BAC；②AS＝AR；③QP∥AR；④△BRP≌△CSP．A．4个B．3个C．2个D．1个10．两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD ＝CD，AB＝CB，詹姆斯在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO＝CO＝AC；③△ABD≌△CBD，其中正确的结论有（）A．0个B．1个C．2个D．3个11．如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN 在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM＝PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（）A．4B．3C．2D．112．如图，点E，F在AC上，AD＝BC，DF＝BE，要使△ADF≌△CBE，还需要添加的一个条件是（）A．∠A＝∠C B．∠D＝∠B C．AD∥BC D．DF∥BE13．如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若CE＝3，且∠ECF ＝45°，则CF的长为（）A．2B．3C．D．14．如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝．15．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3＝°．16．如图，在△ABC中，已知∠1＝∠2，BE＝CD，AB＝5，AE＝2，则CE＝．17．如图，在四边形ABCD中，AB＝AD，∠BAD＝∠BCD＝90°，连接AC．若AC＝6，则四边形ABCD的面积为．18．如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO．下列结论：①AC⊥BD；②CB＝CD；③△ABC≌△ADC；④DA＝DC．其中所有正确结论的序号是．19．如图，在△ABC中，∠A＝90°，AB＝AC，∠ABC的平分线BD交AC于点D，CE⊥BD，交BD的延长线于点E，若BD＝8，则CE＝．20．如图，在四边形ABCD中，AD＝4，CD＝3，∠ABC＝∠ACB＝∠ADC＝45°，则BD 的长为．21．已知：如图，BD为△ABC的角平分线，且BD＝BC，E为BD延长线上的一点，BE＝BA，过E作EF⊥AB，F为垂足，下列结论：①△ABD≌△EBC；②∠BCE+∠BCD＝180°；③AD＝EF＝EC；④AE＝EC，其中正确的是（填序号）22．如图，四边形ABCD中，∠BAD＝∠BCD＝90°，AB＝AD，若四边形ABCD的面积为24cm2，则AC长是cm．23．如图，四边形ACDF是正方形，∠CEA和∠ABF都是直角且点E，A，B三点共线，AB ＝4，则三角形ABC的面积是．24．如图，AE⊥AB，且AE＝AB，BC⊥CD，且BC＝CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是．25．如图，△ABC的内角∠ABC和外角∠ACD的平分线相交于点E，BE交AC于点F，过点E作EG∥BD交AB于点G，交AC于点H，连接AE，有以下结论：①∠BEC＝∠BAC；②△HEF≌△CBF；③BG＝CH+GH；④∠AEB+∠ACE＝90°，其中正确的结论有（将所有正确答案的序号填写在横线上）．26．如图，已知△ABC三个内角的平分线交于点O，点D在CA的延长线上，且DC＝BC，AD＝AO，若∠BAC＝80°，则∠BCA的度数为．27．如图，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D、E都在边BC上，∠DAE ＝60°．若BD＝2CE，则DE的长为．28．（1）如图1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD 上的点，且∠EAF＝∠BAD．求证：EF＝BE+FD；（2）如图2，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD 上的点，且∠EAF＝∠BAD，（1）中的结论是否仍然成立？（3）如图3，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF＝∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．29．如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C＝90°，∠B ＝∠E＝30°．（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．（3）拓展探究已知∠ABC＝60°，点D是角平分线上一点，BD＝CD＝4，DE∥AB交BC于点E（如图4）．若在射线BA上存在点F，使S△DCF＝S△BDE，请直接写出相应的BF的长．30．已知：如图，在△ABC、△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，点C、D、E三点在同一直线上，连接BD．（1）求证：△BAD≌△CAE；（2）试猜想BD、CE有何特殊位置关系，并证明．31．如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CB，垂足为F．（1）求证：△ABC≌△ADE；（2）求∠F AE的度数；（3）求证：CD＝2BF+DE．32．已知△ABN和△ACM位置如图所示，AB＝AC，AD＝AE，∠1＝∠2．（1）求证：BD＝CE；（2）求证：∠M＝∠N．33．将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB＝∠DEB＝90°，∠A＝∠D＝30°，点E落在AB上，DE所在直线交AC所在直线于点F．（1）求证：AF+EF＝DE；（2）若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其它条件不变，请在图②中画出变换后的图形，并直接写出你在（1）中猜想的结论是否仍然成立；（3）若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其它条件不变，如图③．你认为（1）中猜想的结论还成立吗？若成立，写出证明过程；若不成立，请写出AF、EF与DE之间的关系，并说明理由．34．已知：在△ABC中，AC＝BC，∠ACB＝90°，点D是AB的中点，点E是AB边上一点．（1）直线BF垂直于直线CE于点F，交CD于点G（如图1），求证：AE＝CG；（2）直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并证明．35．如图，已知在四边形ABCD中，点E在AD上，∠BCE＝∠ACD＝90°，∠BAC＝∠D，BC＝CE．（1）求证：AC＝CD；（2）若AC＝AE，求∠DEC的度数．参考答案1．解：∵AE⊥AB且AE＝AB，EF⊥FH，BG⊥FH⇒∠EAB＝∠EF A＝∠BGA＝90°，∠EAF+∠BAG＝90°，∠ABG+∠BAG＝90°⇒∠EAF＝∠ABG，∴AE＝AB，∠EF A＝∠AGB，∠EAF＝∠ABG⇒△EF A≌△AGB，∴AF＝BG，AG＝EF．同理证得△BGC≌△CHD得GC＝DH，CH＝BG．故FH＝F A+AG+GC+CH＝3+6+4+3＝16故S＝（6+4）×16﹣3×4﹣6×3＝50．故选：A．2．解：过E作EP⊥BC于点P，EQ⊥CD于点Q，∵四边形ABCD是正方形，∴∠BCD＝90°，又∵∠EPM＝∠EQN＝90°，∴∠PEQ＝90°，∴∠PEM+∠MEQ＝90°，∵三角形FEG是直角三角形，∴∠NEF＝∠NEQ+∠MEQ＝90°，∴∠PEM＝∠NEQ，∵AC是∠BCD的角平分线，∠EPC＝∠EQC＝90°，∴EP＝EQ，四边形PCQE是正方形，在△EPM和△EQN中，，∴△EPM≌△EQN（ASA）∴S△EQN＝S△EPM，∴四边形EMCN的面积等于正方形PCQE的面积，∵正方形ABCD的边长为a，∴AC＝a，∵EC＝2AE，∴EC＝a，∴EP＝PC＝a，∴正方形PCQE的面积＝a×a＝a2，∴四边形EMCN的面积＝a2，故选：D．3．解：∵∠AOB＝∠COD＝40°，∴∠AOB+∠AOD＝∠COD+∠AOD，即∠AOC＝∠BOD，在△AOC和△BOD中，，∴△AOC≌△BOD（SAS），∴∠OCA＝∠ODB，AC＝BD，①正确；∴∠OAC＝∠OBD，由三角形的外角性质得：∠AMB+∠OAC＝∠AOB+∠OBD，∴∠AMB＝∠AOB＝40°，②正确；作OG⊥MC于G，OH⊥MB于H，如图2所示：则∠OGC＝∠OHD＝90°，在△OCG和△ODH中，，∴△OCG≌△ODH（AAS），∴OG＝OH，∴MO平分∠BMC，④正确；∵∠AOB＝∠COD，∴当∠DOM＝∠AOM时，OM才平分∠BOC，假设∠DOM＝∠AOM∵△AOC≌△BOD，∴∠COM＝∠BOM，∵MO平分∠BMC，∴∠CMO＝∠BMO，在△COM和△BOM中，，∴△COM≌△BOM（ASA），∴OB＝OC，∵OA＝OB∴OA＝OC与OA＞OC矛盾，∴③错误；正确的个数有3个；故选：B．4．解：∵AB⊥CD，CE⊥AD，BF⊥AD，∴∠AFB＝∠CED＝90°，∠A+∠D＝90°，∠C+∠D＝90°，∴∠A＝∠C，∵AB＝CD，∴△ABF≌△CDE，∴AF＝CE＝a，BF＝DE＝b，∵EF＝c，∴AD＝AF+DF＝a+（b﹣c）＝a+b﹣c，故选：D．5．解：在BA的延长线上取点E，使AE＝AC，连接EP，∵AD是∠BAC的外角平分线，∴∠CAD＝∠EAD，在△ACP和△AEP中，，∴△ACP≌△AEP（SAS），∴PE＝PC，在△PBE中，PB+PE＞AB+AE，∵PB＝m，PC＝n，AB＝c，AC＝b，∴m+n＞b+c．故选：A．6．解：∵△ABD、△BCE为等边三角形，∴AB＝DB，∠ABD＝∠CBE＝60°，BE＝BC，∴∠ABE＝∠DBC，∠PBQ＝60°，在△ABE和△DBC中，，∴△ABE≌△DBC（SAS），∴①正确；∵△ABE≌△DBC，∴∠BAE＝∠BDC，∵∠BDC+∠BCD＝180°﹣60°﹣60°＝60°，∴∠DMA＝∠BAE+∠BCD＝∠BDC+∠BCD＝60°，∴②正确；在△ABP和△DBQ中，，∴△ABP≌△DBQ（ASA），∴BP＝BQ，∴△BPQ为等边三角形，∴③正确；∵∠DMA＝60°，∴∠AMC＝120°，∴∠AMC+∠PBQ＝180°，∴P、B、Q、M四点共圆，∵BP＝BQ，∴，∴∠BMP＝∠BMQ，即MB平分∠AMC；∴④正确；综上所述：正确的结论有4个；故选：D．7．解：∵BF∥AC，∴∠C＝∠CBF，∵BC平分∠ABF，∴∠ABC＝∠CBF，∴∠C＝∠ABC，∴AB＝AC，∵AD是△ABC的角平分线，∴BD＝CD，AD⊥BC，故②③正确，在△CDE和△BDF中，，∴△CDE≌△BDF（ASA），∴DE＝DF，CE＝BF，故①正确；∵AE＝2BF，∴AC＝3BF，故④正确．故选：A．8．解：∵AD是△ABC的中线，∴BD＝CD，又∠CDE＝∠BDF，DE＝DF，∴△BDF≌△CDE，故④正确；由△BDF≌△CDE，可知CE＝BF，故①正确；∵AD是△ABC的中线，∴△ABD和△ACD等底等高，∴△ABD和△ACD面积相等，故②正确；由△BDF≌△CDE，可知∠FBD＝∠ECD∴BF∥CE，故③正确．故选：D．9．解：（1）P A平分∠BAC．∵PR⊥AB，PS⊥AC，PR＝PS，AP＝AP，∴△APR≌△APS，∴∠P AR＝∠P AS，∴P A平分∠BAC；（2）由（1）中的全等也可得AS＝AR；（3）∵AQ＝PR，∴∠1＝∠APQ，∴∠PQS＝∠1+∠APQ＝2∠1，又∵P A平分∠BAC，∴∠BAC＝2∠1，∴∠PQS＝∠BAC，∴PQ∥AR；（4）∵PR⊥AB，PS⊥AC，∴∠BRP＝∠CSP，∵PR＝PS，∴△BRP不一定全等与△CSP（只具备一角一边的两三角形不一定全等）．故选：B．10．解：在△ABD与△CBD中，，∴△ABD≌△CBD（SSS），故③正确；∴∠ADB＝∠CDB，在△AOD与△COD中，，∴△AOD≌△COD（SAS），∴∠AOD＝∠COD＝90°，AO＝OC，∴AC⊥DB，故①②正确；故选：D．11．解：如图作PE⊥OA于E，PF⊥OB于F．∵∠PEO＝∠PFO＝90°，∴∠EPF+∠AOB＝180°，∵∠MPN+∠AOB＝180°，∴∠EPF＝∠MPN，∴∠EPM＝∠FPN，∵OP平分∠AOB，PE⊥OA于E，PF⊥OB于F，∴PE＝PF，在△POE和△POF中，，∴△POE≌△POF，∴OE＝OF，在△PEM和△PFN中，，∴△PEM≌△PFN，∴EM＝NF，PM＝PN，故（1）正确，∴S△PEM＝S△PNF，∴S四边形PMON＝S四边形PEOF＝定值，故（3）正确，∵OM+ON＝OE+ME+OF﹣NF＝2OE＝定值，故（2）正确，在旋转过程中，△PMN是等腰三角形，形状是相似的，因为PM的长度是变化的，所以MN的长度是变化的，故（4）错误，故选：B．12．解：当∠D＝∠B时，在△ADF和△CBE中∵，∴△ADF≌△CBE（SAS），13．解：如图，延长FD到G，使DG＝BE；连接CG、EF；∵四边形ABCD为正方形，在△BCE与△DCG中，，∴△BCE≌△DCG（SAS），∴CG＝CE，∠DCG＝∠BCE，∴∠GCF＝45°，在△GCF与△ECF中，，∴△GCF≌△ECF（SAS），∴GF＝EF，∵CE＝3，CB＝6，∴BE＝＝＝3，∴AE＝3，设AF＝x，则DF＝6﹣x，GF＝3+（6﹣x）＝9﹣x，∴EF＝＝，∴（9﹣x）2＝9+x2，即AF＝4，∴GF＝5，∴DF＝2，∴CF＝＝＝2，故选：A．14．解：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠1＝∠EAC，在△BAD和△CAE中，∴△BAD≌△CAE（SAS），∴∠2＝∠ABD＝30°，∵∠1＝25°，∴∠3＝∠1+∠ABD＝25°+30°＝55°，故答案为：55°．15．解：观察图形可知：△ABC≌△BDE，∴∠1＝∠DBE，又∵∠DBE+∠3＝90°，∴∠1+∠3＝90°．∵∠2＝45°，∴∠1+∠2+∠3＝∠1+∠3+∠2＝90°+45°＝135°．故答案为：135．16．解：△ABE和△ACD中，，∴△ABE≌△ACD（AAS），∴AD＝AE＝2，AC＝AB＝5，∴CE＝BD＝AB﹣AD＝3，故答案为3．17．解：如图，作AM⊥BC、AN⊥CD，交CD的延长线于点N；∵∠BAD＝∠BCD＝90°∴四边形AMCN为矩形，∠MAN＝90°；∵∠BAD＝90°，∴∠BAM＝∠DAN；在△ABM与△ADN中，，∴△ABM≌△ADN（AAS），∴AM＝AN（设为λ）；△ABM与△ADN的面积相等；∴四边形ABCD的面积＝正方形AMCN的面积；由勾股定理得：AC2＝AM2+MC2，而AC＝6；∴2λ2＝36，λ2＝18，故答案为：18．18．解：∵△ABO≌△ADO，∴AB＝AD，∠BAO＝∠DAO，∠AOB＝∠AOD＝90°，OB＝OD，∴AC⊥BD，故①正确；∵四边形ABCD的对角线AC、BD相交于点O，∴∠COB＝∠COD＝90°，在△ABC和△ADC中，，∴△ABC≌△ADC（SAS），故③正确；∴BC＝DC，故②正确．故答案为：①②③．19．解：如图，延长BA、CE相交于点F，∵BD平分∠ABC，∴∠ABD＝∠CBD，在△BCE和△BFE中，，∴△BCE≌△BFE（ASA），∴CE＝EF，∵∠BAC＝90°，CE⊥BD，∴∠ACF+∠F＝90°，∠ABD+∠F＝90°，∴∠ABD＝∠ACF，在△ABD和△ACF中，，∴△ABD≌△ACF（ASA），∴BD＝CF，∵CF＝CE+EF＝2CE，∴BD＝2CE＝8，∴CE＝4．故答案为：4．20．解：在AD的上方过点A作AD′⊥AD，使得AD′＝AD，连接CD′，DD′，如图：∵∠BAC+∠CAD＝∠DAD′+∠CAD，即∠BAD＝∠CAD′，在△BAD与△CAD′中，，∴△BAD≌△CAD′（SAS），∴BD＝CD′．∠DAD′＝90°由勾股定理得DD′＝，∠D′DA+∠ADC＝90°由勾股定理得CD′＝，∴BD＝CD′＝，故答案为：．21．解：①∵BD为△ABC的角平分线，∴∠ABD＝∠CBD，在△ABD和△EBC中，，∴△ABD≌△EBC（SAS），∴①正确；②∵BD为△ABC的角平分线，BD＝BC，BE＝BA，∴∠BCD＝∠BDC＝∠BAE＝∠BEA，∵△ABD≌△EBC，∴∠BCE＝∠BDA，∴∠BCE+∠BCD＝∠BDA+∠BDC＝180°，∴②正确；③∵∠BCE＝∠BDA，∠BCE＝∠BCD+∠DCE，∠BDA＝∠DAE+∠BEA，∠BCD＝∠BEA，∴∠DCE＝∠DAE，∴△ACE为等腰三角形，∴AE＝EC，∵△ABD≌△EBC，∴AD＝EC，∴AD＝AE＝EC，∵BD为△ABC的角平分线，EF⊥AB，而EC不垂直与BC，∴EF≠EC，∴③错误；④由③知AD＝AE＝EC，∴④正确；综上所述，正确的结论是①②④．故答案是：①②④．22．解：延长CD至点E，使DE＝BC，连接AE，∵∠BAD＝∠BCD＝90°，∴∠2+∠B＝180°，∵∠1+∠2＝180°，∠2+∠B＝180°，∴∠1＝∠B，在△ABC与△ADE中，∵，∴△ABC≌△ADE（SAS），∴∠EAD＝∠BAC，AC＝AE，S△AEC＝S四边形ABCD ∵∠BAD＝90°，∴∠EAC＝90°，∴△ACE是等腰直角三角形，∵四边形ABCD的面积为24cm2，∴AC2＝24，解得AC＝4或﹣4，∵AC为正数，∴AC＝4．故答案为：4．23．解：∵四边形ACDF是正方形，∴AC＝AF，∠CAF＝90°，∴∠EAC+∠F AB＝90°，∵∠ABF＝90°，∴∠AFB+∠F AB＝90°，∴∠EAC＝∠AFB，在△CAE和△AFB中，，∴△CAE≌△AFB，∴EC＝AB＝4，∴阴影部分的面积＝×AB×CE＝8，故答案为：8．24．解：∵AE⊥AB且AE＝AB，EF⊥FH，BG⊥FH⇒∠FED＝∠EF A＝∠BGA＝90°，∠EAF+∠BAG＝90°，∠ABG+∠BAG＝90°⇒∠EAF＝∠ABG，∴AE＝AB，∠EF A＝∠AGB，∠EAF＝∠ABG⇒△EF A≌△ABG同理证得△BGC≌△DHC得GC＝DH，CH＝BG．故FH＝F A+AG+GC+CH＝3+6+4+3＝16故S＝（6+4）×16﹣3×4﹣6×3＝50．故答案为50．25．解：①BE平分∠ABC，∴∠EBC＝∠ABC，∵CE平分∠ACD，∴∠DCE＝ACD，∵∠ACD＝∠BAC+∠ABC，∠DCE＝∠CBE+∠BEC，∴∠EBC+∠BEC＝（∠BAC+∠ABC）＝∠EBC+BAC，∴∠BEC＝∠BAC，故①正确；∵②△HEF与△CBF只有两个角是相等的，能得出相似，但不含相等的边，所有不能得出全等的结论，故②错误．③BE平分∠ABC，∴∠ABE＝∠CBE，∵GE∥BC，∴∠CBE＝∠GEB，∴BG＝GE，同理CH＝HE，∴BG﹣CH＝GE﹣EH＝GH，故③正确．④过点E作EN⊥AC于N，ED⊥BC于D，EM⊥BA于M，如图，∵BE平分∠ABC，∴EM＝ED，∵CE平分∠ACD，∴EN＝ED，∴EN＝EM，∴AE平分∠CAM，设∠ACE＝∠DCE＝x，∠ABE＝∠CBE＝y，∠MAE＝∠CAE＝z，如图，则∠BAC＝180°﹣2z，∠ACB＝180﹣2x，∵∠ABC+∠ACB+∠BAC＝180°，∴2y+180°﹣2z+180°﹣2x＝180°，∴x+z＝y+90°，∵z＝y+∠AEB，∴x+y+∠AEB＝y+90°，∴x+∠AEB＝90°，即∠ACE+∠AEB＝90°，故④正确；故答案为：①③④．26．解：∵△ABC三个内角的平分线交于点O，∴∠ACO＝∠BCO，在△COD和△COB中，，∴△COD≌△COB，∴∠D＝∠CBO，∵∠BAC＝80°，∴∠BAD＝100°，∴∠BAO＝40°，∴∠DAO＝140°，∵AD＝AO，∴∠D＝20°，∴∠CBO＝20°，∴∠ABC＝40°，∴∠BCA＝60°，故答案为：60°．27．解：（方法一）将△ABD绕点A逆时针旋转120°得到△ACF，连接EF，过点E作EM ⊥CF于点M，过点A作AN⊥BC于点N，如图所示．∵AB＝AC＝2，∠BAC＝120°，∴BN＝CN，∠B＝∠ACB＝30°．在Rt△BAN中，∠B＝30°，AB＝2，∴AN＝AB＝，BN＝＝3，∴BC＝6．∵∠BAC＝120°，∠DAE＝60°，∴∠BAD+∠CAE＝60°，∴∠F AE＝∠F AC+∠CAE＝∠BAD+∠CAE＝60°．在△ADE和△AFE中，，∴△ADE≌△AFE（SAS），∴DE＝FE．∵BD＝2CE，BD＝CF，∠ACF＝∠B＝30°，∴设CE＝2x，则CM＝x，EM＝x，FM＝4x﹣x＝3x，EF＝ED＝6﹣6x．在Rt△EFM中，FE＝6﹣6x，FM＝3x，EM＝x，∴EF2＝FM2+EM2，即（6﹣6x）2＝（3x）2+（x）2，解得：x1＝，x2＝（不合题意，舍去），∴DE＝6﹣6x＝3﹣3．故答案为：3﹣3．（方法二）：将△ABD绕点A逆时针旋转120°得到△ACF，取CF的中点G，连接EF、EG，如图所示．∵AB＝AC＝2，∠BAC＝120°，∴∠ACB＝∠B＝∠ACF＝30°，∴∠ECG＝60°．∵CF＝BD＝2CE，∴CG＝CE，∴△CEG为等边三角形，∴EG＝CG＝FG，∴∠EFG＝∠FEG＝∠CGE＝30°，∴△CEF为直角三角形．∵∠BAC＝120°，∠DAE＝60°，∴∠BAD+∠CAE＝60°，∴∠F AE＝∠F AC+∠CAE＝∠BAD+∠CAE＝60°．在△ADE和△AFE中，，∴△ADE≌△AFE（SAS），∴DE＝FE．设EC＝x，则BD＝CF＝2x，DE＝FE＝6﹣3x，在Rt△CEF中，∠CEF＝90°，CF＝2x，EC＝x，EF＝＝x，∴6﹣3x＝x，x＝3﹣，∴DE＝x＝3﹣3．故答案为：3﹣3．28．证明：（1）延长EB到G，使BG＝DF，连接AG．∵∠ABG＝∠ABC＝∠D＝90°，AB＝AD，∴△ABG≌△ADF．∴AG＝AF，∠1＝∠2．∴∠1+∠3＝∠2+∠3＝∠EAF＝∠BAD．∴∠GAE＝∠EAF．又∵AE＝AE，∴△AEG≌△AEF．∴EG＝EF．∵EG＝BE+BG．∴EF＝BE+FD（2）（1）中的结论EF＝BE+FD仍然成立．（3）结论EF＝BE+FD不成立，应当是EF＝BE﹣FD．证明：在BE上截取BG，使BG＝DF，连接AG．∵∠B+∠ADC＝180°，∠ADF+∠ADC＝180°，∴∠B＝∠ADF．∵AB＝AD，∴△ABG≌△ADF．∴∠BAG＝∠DAF，AG＝AF．∴∠BAG+∠EAD＝∠DAF+∠EAD＝∠EAF＝∠BAD．∴∠GAE＝∠EAF．∵AE＝AE，∴△AEG≌△AEF．∴EG＝EF∵EG＝BE﹣BG∴EF＝BE﹣FD．29．解：（1）①∵△DEC绕点C旋转点D恰好落在AB边上，∴AC＝CD，∵∠BAC＝90°﹣∠B＝90°﹣30°＝60°，∴△ACD是等边三角形，∴∠ACD＝60°，又∵∠CDE＝∠BAC＝60°，∴∠ACD＝∠CDE，∴DE∥AC；②∵∠B＝30°，∠C＝90°，∴CD＝AC＝AB，∴BD＝AD＝AC，根据等边三角形的性质，△ACD的边AC、AD上的高相等，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1＝S2；故答案为：DE∥AC；S1＝S2；（2）如图，∵△DEC是由△ABC绕点C旋转得到，∴BC＝CE，AC＝CD，∵∠ACN+∠BCN＝90°，∠DCM+∠BCN＝180°﹣90°＝90°，∴∠ACN＝∠DCM，∵在△ACN和△DCM中，，∴△ACN≌△DCM（AAS），∴AN＝DM，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1＝S2；（3）如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE＝DF1，且BE、DF1上的高相等，此时S△DCF1＝S△BDE；过点D作DF2⊥BD，∵∠ABC＝60°，F1D∥BE，∴∠F2F1D＝∠ABC＝60°，∵BF1＝DF1，∠F1BD＝∠ABC＝30°，∠F2DB＝90°，∴∠F1DF2＝∠ABC＝60°，∴△DF1F2是等边三角形，∴DF1＝DF2，∵BD＝CD，∠ABC＝60°，点D是角平分线上一点，∴∠DBC＝∠DCB＝×60°＝30°，∴∠CDF1＝180°﹣∠BCD＝180°﹣30°＝150°，∠CDF2＝360°﹣150°﹣60°＝150°，∴∠CDF1＝∠CDF2，∵在△CDF1和△CDF2中，，∴△CDF1≌△CDF2（SAS），∴点F2也是所求的点，∵∠ABC＝60°，点D是角平分线上一点，DE∥AB，∴∠DBC＝∠BDE＝∠ABD＝×60°＝30°，又∵BD＝4，∴BE＝×4÷cos30°＝2÷＝，∴BF1＝，BF2＝BF1+F1F2＝+＝，故BF的长为或．30．（1）证明：∵∠BAC＝∠DAE＝90°∴∠BAC+∠CAD＝∠DAE+∠CAD即∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS）．（2）BD、CE特殊位置关系为BD⊥CE．证明如下：由（1）知△BAD≌△CAE，∴∠ADB＝∠E．∵∠DAE＝90°，∴∠E+∠ADE＝90°．∴∠ADB+∠ADE＝90°．即∠BDE＝90°．∴BD、CE特殊位置关系为BD⊥CE．31．证明：（1）∵∠BAD＝∠CAE＝90°，∴∠BAC+∠CAD＝90°，∠CAD+∠DAE＝90°，∴∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS）；（2）∵∠CAE＝90°，AC＝AE，∴∠E＝45°，由（1）知△BAC≌△DAE，∴∠BCA＝∠E＝45°，∵AF⊥BC，∴∠CF A＝90°，∴∠CAF＝45°，∴∠F AE＝∠F AC+∠CAE＝45°+90°＝135°；（3）延长BF到G，使得FG＝FB，∵AF⊥BG，∴∠AFG＝∠AFB＝90°，在△AFB和△AFG中，，∴△AFB≌△AFG（SAS），∴AB＝AG，∠ABF＝∠G，∵△BAC≌△DAE，∴AB＝AD，∠CBA＝∠EDA，CB＝ED，∴AG＝AD，∠ABF＝∠CDA，∴∠G＝∠CDA，∵∠GCA＝∠DCA＝45°，在△CGA和△CDA中，，∴△CGA≌△CDA（AAS），∴CG＝CD，∵CG＝CB+BF+FG＝CB+2BF＝DE+2BF，∴CD＝2BF+DE．32．（1）证明：在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴BD＝CE；（2）证明：∵∠1＝∠2，∴∠1+∠DAE＝∠2+∠DAE，即∠BAN＝∠CAM，由（1）得：△ABD≌△ACE，∴∠B＝∠C，在△ACM和△ABN中，，∴△ACM≌△ABN（ASA），∴∠M＝∠N．33．（1）证明：连接BF（如图①），∵△ABC≌△DBE（已知），∴BC＝BE，AC＝DE．∵∠ACB＝∠DEB＝90°，∴∠BCF＝∠BEF＝90°．在Rt△BFC和Rt△BFE中，∴Rt△BFC≌Rt△BFE（HL）．∴CF＝EF．又∵AF+CF＝AC，∴AF+EF＝DE．（2）解：画出正确图形如图②∴（1）中的结论AF+EF＝DE仍然成立；（3）成立．证明：连接BF，∵△ABC≌△DBE，∴BC＝BE，∵∠ACB＝∠DEB＝90°，∴△BCF和△BEF是直角三角形，在Rt△BCF和Rt△BEF中，，∴△BCF≌△BEF（HL），∴CF＝EF；∵△ABC≌△DBE，∴AC＝DE，∴AF＝AC+FC＝DE+EF．34．（1）证明：∵点D是AB中点，AC＝BC，∠ACB＝90°，∴CD⊥AB，∠ACD＝∠BCD＝45°，∴∠CAD＝∠CBD＝45°，∴∠CAE＝∠BCG，又∵BF⊥CE，∴∠CBG+∠BCF＝90°，又∵∠ACE+∠BCF＝90°，∴∠ACE＝∠CBG，在△AEC和△CGB中，∴△AEC≌△CGB（ASA），∴AE＝CG，（2）解：BE＝CM．证明：∵CH⊥HM，CD⊥ED，∴∠CMA+∠MCH＝90°，∠BEC+∠MCH＝90°，∴∠CMA＝∠BEC，又∵∠ACM＝∠CBE＝45°，在△BCE和△CAM中，，∴△BCE≌△CAM（AAS），∴BE＝CM．35．解：∵∠BCE＝∠ACD＝90°，∴∠3+∠4＝∠4+∠5，∴∠3＝∠5，在△ABC和△DEC中，，∴△ABC≌△DEC（AAS），。
2021年中考数学专项复习 专题 三角形全等的相关证明及计算含答案
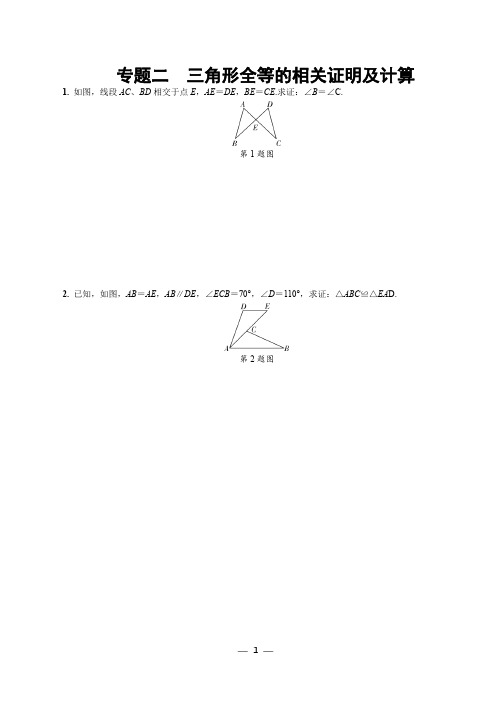
专题二三角形全等的相关证明及计算1.如图，线段AC、BD相交于点E，AE＝DE，BE＝CE.求证：∠B＝∠C.第1题图2.已知，如图，AB＝AE，AB∥DE，∠ECB＝70°，∠D＝110°，求证：△ABC≌△EA D.第2题图3.如图，在Rt△ACB和Rt△ADB中，∠C＝∠D＝90°，AD＝BC，AD、BC相交于点O.求证：CO＝DO.第3题图4.如图，AB＝AD，AC＝AE，∠BAE＝∠DA C.求证：∠C＝∠E.第4题图5.如图，点E，F在线段BD上，且BE＝DF，AE＝CF，AD＝C B.求证：∠A＝∠C.第5题图6.如图，D是AC上一点，AB＝AD，DE∥AB，∠B＝∠DAE.求证：BC＝AE.第6题图7.如图，已知点E，C在线段BF上，BE＝CF，AC∥DF，请添加一个条件(不得添加辅助线)，使得△ABC ≌△DEF，并说明理由．第7题图8.如图，AB∥CD，E、F分别为AB、CD上的点，且EC∥BF，连接AD，分别与EC、BF相交于点G、H，若AB＝C D.求证：AG＝DH.第8题图9.如图，菱形ABCD中，作BE⊥AD、CF⊥AB，分别交AD、AB的延长线于点E、F.(1)求证：AE＝BF；(2)若点E恰好是AD的中点，AB＝2，求BD的值．第9题图10.如图，在△ABC中，D是BC边上一点，AB＝DB，BE平分∠ABC，交AC边于点E，连接DE.(1)求证：△ABE≌△DBE；(2)若∠A＝100°，∠C＝50°，求∠AEB的度数．第10题图参考答案专题二 三角形全等的相关证明及计算1. 证明：在△AEB 和△DEC 中，⎩⎪⎨⎪⎧AE ＝DE ，∠AEB ＝∠DEC ，BE ＝CE ，∴△AEB ≌△DEC (SAS)．∴∠B ＝∠C .2. 证明：∵∠ECB ＝70°，∴∠ACB ＝110°.又∵∠D ＝110°，∴∠ACB ＝∠D .∵AB ∥DE ，∴∠CAB ＝∠E .在△ABC 和△EAD 中，⎩⎪⎨⎪⎧∠ACB ＝∠D ，∠CAB ＝∠E ，AB ＝EA ，∴△ABC ≌△EAD (AAS )．3. 证明：在Rt △ACB 和Rt △BDA 中，∠C ＝∠D ＝90°，⎩⎪⎨⎪⎧AB ＝BA ，AD ＝BC ， ∴Rt △ACB ≌Rt △BDA (HL)．∴∠CBA ＝∠DAB .∴OA ＝OB .又∵AD ＝BC ，∴CO ＝DO .4. 证明：∵∠BAE ＝∠DAC ，∴∠BAE ＋∠CAE ＝∠DAC ＋∠CAE .∴∠BAC ＝∠DAE .在△ABC 和△ADE 中，⎩⎪⎨⎪⎧AB ＝AD ，∠BAC ＝∠DAE ，AC ＝AE ，∴△ABC ≌△ADE (SAS)．∴∠C ＝∠E .5. 证明：∵BE ＝DF ，∴BE －EF ＝DF －EF ，即BF ＝DE .在△ADE 和△CBF 中，⎩⎪⎨⎪⎧DE ＝BF ，AE ＝CF ，AD ＝CB ，∴△ADE ≌△CBF (SSS)．∴∠A ＝∠C .6. 证明：∵DE ∥AB ，∴∠CAB ＝∠EDA .在△CBA 和△EAD 中，⎩⎪⎨⎪⎧∠B ＝∠DAE ，AB ＝AD ，∠CAB ＝∠EDA ，∴△CBA ≌△EAD (ASA)．∴BC ＝AE .7. 解：添加AC ＝DF .(答案不唯一)理由：∵BE ＝CF ，∴BE ＋EC ＝CF ＋EC ，即BC ＝EF .∵AC ∥DF ，∴∠ACB ＝∠DFE .在△ABC 与△DEF 中，⎩⎪⎨⎪⎧AC ＝DF ，∠ACB ＝∠DFE ，BC ＝EF ，∴△ABC ≌△DEF (SAS)．8. 证明：∵AB ∥CD , ∴∠A ＝∠D .又∵CE ∥BF , ∴∠AHB ＝∠DGC .在△ABH 和△DCG 中，⎩⎪⎨⎪⎧∠AHB ＝∠DGC ，∠A ＝∠D ，AB ＝CD ，∴△ABH ≌△DCG (AAS )．∴AH ＝DG .又∵AH ＝AG ＋GH , DG ＝DH ＋GH ，∴AG ＝DH .9. (1)证明：∵四边形ABCD 是菱形，∴AD ∥BC ，AB ＝BC .∴∠A ＝∠CBF .∵BE ⊥AD ，CF ⊥AB ，∴∠AEB ＝∠BFC ＝90°.在△ABE 和△BCF 中，⎩⎪⎨⎪⎧∠AEB ＝∠BFC ，∠A ＝∠CBF ，AB ＝BC ，∴△ABE ≌△BCF (AAS )．∴AE ＝BF ；(2)解：∵BE ⊥AD ，点E 恰好是AD 中点，∴BE 垂直平分AD .∴BD ＝AB ＝2.10. (1)证明：∵BE 平分∠ABC ，∴∠ABE ＝∠DBE .在△ABE 与△DBE 中，⎩⎪⎨⎪⎧AB ＝DB ，∠ABE ＝∠DBE ，BE ＝BE ，∴△ABE ≌△DBE (SAS)；(2)解：∵∠A ＝100°，∠C ＝50°，∴∠ABC ＝30°.∴∠ABE ＝12∠ABC ＝15°. ∴∠AEB ＝180°－∠A －∠ABE ＝180°－100°－15°＝65°.。
备考2021年九年级中考数学复习满分突破训练：全等三角形的性质与判定(五)(含答案)
备考2021年九年级中考数学复习满分突破训练：全等三角形的性质与判定（五）1．如图，在正方形ABCD中，点E，F分别是CD，AD的中点，BE与CF相交于点P．（1）求证：BE⊥CF．（2）若AB＝a．①求CP和AP的长（用含a的代数式表示）．②连结DP，直接写出∠DPF的度数．2．已知四边形ABCD，连接BD，∠ADB＝∠CBD，AD＝BC．（1）求证AB∥CD；（2）点O为BD的中点，直线EF经过点O，分别交直线CD、AB于点E、F，连接BE，若AB＝BF，请直接写出与△ABD面积相等的三角形．（△ABD除外）3．如图，△BEF和△AGE是等腰直角三角形．（1）探究FG和AB的数量关系并证明；（2）延长FG和AB交于点C，利用图2补全图形，求∠ACF的度数．4．在△ABM中，∠ABM＝45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．（1）如图1，若AM＝3，MC＝2，AB＝3，求△ABC中AB边上的高．（2）如图2，点D是线段AM上一点，MD＝MC，点E是△ABC外一点，EC＝AC，连接ED 并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF＝∠CEF．5．在△ABC中，∠C＝90°，AC＞BC，D是AB的中点，E为直线AC上一动点，连接DE，过点D作DF⊥DE，交直线BC于点F，连接EF．（1）如图1，当点E是线段AC的中点时，AE＝2，BF＝1，求EF的长；（2）当点E在线段CA的延长线上时，依题意补全图形2，用等式表示AE，EF，BF之间的数量关系，并证明．6．如图，在△ABC中，AB＝AC＝18cm，BC＝10cm，AD＝2BD．（1）如果点P在线段BC上以2cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过2s后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？7．如图，△ABC为等腰直角三角形，∠ACB＝90°，D，E分别是AC、AB的中点，P为直线DE上的一点，PQ⊥PC交直线AB于Q．（1）如图1，当P在ED延长线上时，求证：EC+EQ＝EP；（2）当P在射线DE上时，请直接写出EC，EQ，EP三条线段之间的数量关系．8．如图，△ABC为等边三角形，点D，点E分别在BA，AB的延长线上，AD＝BE．（1）求证：CD＝CE；（2）若EF平分∠DEC交CD，CA于点F，点G，∠ACD＝∠CEF，求证：EF＝AC+AD．9．已知OM是∠AOB的平分线，点P是射线OM上一点，点C、D分别在射线OA、OB上，连接PC、PD．（1）如图①，当PC⊥OA，PD⊥OB时，则PC与PD的数量关系是．（2）如图②，点C、D在射线OA、OB上滑动，且∠AOB＝90°，当PC⊥PD时，PC与PD 在（1）中的数量关系还成立吗？说明理由．10．如图，△ABC是等腰三角形，∠BAC＝90°，BE是∠ABC的角平分线，DE⊥BC于点D．（1）请写出图中所有的等腰三角形（△ABC除外）；（2）请你判断AD与BE是否垂直？并说明理由；（3）如果BC＝10cm，求AB+AE的长．参考答案1．解：（1）证明：在△CDF和△BCE中，，∴△CDF≌△BCE（SAS），∴∠CEB＝∠CFD，∵∠DCF+∠CFD＝90°，∴∠DCF+∠CEB＝90°，∴∠EPC＝90°，∴BE⊥CF；（2）①如图1，延长CF交BA延长线于点M，在△CFD和△MFA中，，∴△CFD≌△MFA（ASA），∴CD＝MA＝AB＝a，∵BP⊥CF，∴AP为Rt△MPB斜边BM上的中线，是斜边的一半，即AP＝BM＝×2a＝a；∵CP⊥BE，∴CP×BE＝CE×BC＝，∵BE＝＝＝a，∴CP＝＝a．②如图2，连接DP，EF，∵点E，F分别是CD，AD的中点，∴DE＝CD，DF＝AD，∵正方形ABCD中，AD＝DC，∠D＝90°，∴DE＝DF，∴∠DEF＝∠DFE＝45°，∵∠D＝∠EPF＝90°，∴D、F、P、E四点共圆，∴∠DPF＝∠DEF＝45°．2．（1）证明：∵DB＝BD，∠ADB＝∠CBD，AD＝CB，∴△ADB≌△CBD（SAS），∴∠ABD＝∠CDB，∴AB∥CD；（2）解：∵AB∥CD，∴∠F＝∠OED，∠OBF＝∠ODE，∵O为BD的中点，∴BO＝DO，∴△BOF≌△DOE（AAS），∴BF＝DE，∵△ADB≌△CBD，∴AB＝CD，S△ADB ＝S△CBD，∵AB＝BF，∴AB＝CD＝BF＝DE，∴S△ADB ＝S△BFE＝S△BCD＝S△BDE．3．解：（1）FG＝AB，理由如下：∵△BEF和△AGE是等腰直角三角形，∴EF＝EB，EA＝EG，∠FEB＝∠AEG＝90°，∴∠FEB﹣∠BEG＝∠AEG﹣∠BEG，即∠FEG＝∠BEA，在△FEG和△BEA中，，∴△FEG≌△BEA（SAS），∴FG＝AB；（2）如图，即为补全的图形，由（1）知△FEG≌△BEA，∴∠EFG＝∠EBA，∵△BEF是等腰直角三角形，∴∠EFB＝∠EBF＝45°，∴∠CFB+∠CBF＝∠CFB+∠EBF+∠CBE＝∠EFB+∠EBF＝90°，∴∠FCB＝90°，∴∠ACF＝90°．4．解：（1）∵∠ABM＝45°，AM⊥BM，∴AM＝BM＝AB cos45°＝3，∵MC＝2，∴BC＝5，∴AC＝，∴△ABC中AB边上的高＝；（2）延长EF到点G，使得FG＝EF，连接BG．，∴△BMD≌△AMC（SAS），∴AC＝BD，又∵CE＝AC，∴BD＝CE，，∴△BFG≌△CFE（SAS），∴BG＝CE，∠G＝∠E，∴BD＝CE＝BG，∴∠BDG＝∠G＝∠E．5．解：（1）∵D是AB的中点，E是线段AC的中点，∴DE∥BC，DE＝BC，∵∠ACB＝90°，∴∠DEC＝90°，∵DF⊥DE，∴∠EDF＝90°，∴四边形CEDF是矩形，∴DE＝CF＝BC，∴CF＝BF＝1，∵CE＝AE＝2，∴EF＝＝＝；（2）AE2+BF2＝EF2．证明：过点B作BM∥AC，与ED的延长线交于点M，连接MF，则∠AED＝∠BMD，∠CBM＝∠ACB＝90°，∵D点是AB的中点，∴AD＝BD，在△ADE和△BDM中，，∴△ADE≌△BDM（AAS），∴AE＝BM，DE＝DM，∵DF⊥DE，∴EF＝MF，∵BM2+BF2＝MF2，∴AE2+BF2＝EF2．6．解：（1）①△BPD与△CQP全等，理由如下：∵AB＝AC＝18cm，AD＝2BD，∴AD＝12cm，BD＝6cm，∠B＝∠C，∵经过2s后，BP＝4cm，CQ＝4cm，∴BP＝CQ，CP＝6cm＝BD，在△BPD和△CQP中，，∴△BPD≌△CQP（SAS），②∵点Q的运动速度与点P的运动速度不相等，∴BP≠CQ，∵△BPD与△CQP全等，∠B＝∠C，∴BP＝PC＝BC＝5cm，BD＝CQ＝6cm，∴t＝，∴点Q的运动速度＝＝cm/s，∴当点Q的运动速度为cm/s时，能够使△BPD与△CQP全等；（2）设经过x秒，点P与点Q第一次相遇，由题意可得：x﹣2x＝36，解得：x＝90，∴90﹣（）×3＝21（s），∴经过90s点P与点Q第一次相遇在线段AB上相遇．7．证明：（1）过点P作PH⊥PE，交直线AB于H，∵D，E分别是AC、AB的中点，∴DE∥BC，∵△ABC为等腰直角三角形，∠ACB＝90°，∴AC⊥DE，∠CAB＝∠B＝∠BCE＝45°，∴AC∥HP，∴∠H＝∠CAB＝45°，∠PEC＝∠BCE＝45°，∴∠H＝∠PEC，△HPE为等腰直角三角形，∴HP＝EP，HE＝EP，∵∠HPQ+∠EPQ＝∠EPC+∠EPQ＝90°，∴∠HPQ＝∠EPC，∴△HPQ≌△EPC（ASA），∴CE＝QH，∵EH＝QH+EQ，∴CE+EQ＝EP；（2）EP+CE＝EQ．证明：过点P作PG⊥DE交直线AB于G，连接CP，∵D，E分别是AC、AB的中点，∴DE∥BC，∵△ABC为等腰直角三角形，∠ACB＝90°，∴AC⊥DE，∠CAB＝∠ABC＝∠BCE＝∠CED＝∠AED＝∠PEG＝45°，∴AC∥HP，∴∠PGE＝∠CAB＝45°，∠PEG＝∠BCE＝45°，∴∠PGE＝∠PEG，∠PEC＝∠PGQ＝135°，∴△GPE为等腰直角三角形，∴GP＝EP，GE＝EP，∵∠GPQ+∠CPG＝∠EPC+∠CPG＝90°，∴∠GPQ＝∠EPC，∴△GPQ≌△EPC（ASA），∴CE＝QG，∵EG+QG＝EQ，∴EP+CE＝EQ．8．证明：（1）∵△ABC为等边三角形，∴∠BAC＝∠ABC＝∠ACB＝60°，AB＝BC＝AC，∴∠DAC＝∠EBC＝120°，∵AD＝BE，∴△ACD≌△BCE（SAS），∴CD＝CE；（2）∵△ACD≌△BCE∴∠ACD＝∠BCE，AD＝BE，∵BF平分∠DEC，∴∠DEF＝∠CEF，∵∠ACD＝∠CEF，∴∠ACD＝∠CEF＝∠ACD＝∠BCE，∵∠EGC＝∠AEG+∠BAC＝∠AEG+60°，∠ECG＝∠BCE+∠ACB＝∠BCE+60°，∴∠EGC＝∠ECG，∴EC＝EG，∵∠EGC＝∠AEG+∠BAC＝∠AEG+60°＝∠EFC+∠ACD，∴∠BAC＝∠EFC，即∠EAG＝∠EFC，∴△EFC≌△EAG（ASA），∴EF＝AE，∵AE＝AB+BE＝AC+AD，∴EF＝AC+AD．9．解：（1）PC＝PD，理由：∵OM是∠AOB的平分线，∴PC＝PD（角平分线上点到角两边的距离相等），故答案为：PC＝PD；（2）证明：过点P点作PE⊥OA于E，PF⊥OB于F，如图，∴∠PEC＝∠PFD＝90°，∵OM是∠AOB的平分线，∴PE＝PF，∵∠AOB＝90°，∠CPD＝90°，∴∠PCE+∠PDO＝360°﹣90°﹣90°＝180°，而∠PDO+∠PDF＝180°，∴∠PCE＝∠PDF，在△PCE和△PDF中，∴△PCE≌△PDF（AAS），∴PC＝PD．10．解：（1）∵△ABC是等腰三角形，∠BAC＝90°，∴∠C＝45°，∵DE⊥BC，∴CD＝DE，∴△EDC是等腰三角形，∵BE是∠ABC的角平分线，DE⊥BC于点D，∠BAC＝90°，∴EA＝ED，∴△ADE是等腰三角形，∵BE＝BE，∴Rt△BAE≌Rt△DBE（HL），∴BA＝BD，∴△ABD是等腰三角形，故图中的等腰三角形有：△ABD，△ADE，△EDC；（2）AD与BE垂直．证明：由BE为∠ABC的平分线，知∠ABE＝∠DBE，∠BAE＝∠BDE＝90°，BE＝BE，∴△ABE沿BE折叠，一定与△DBE重合．∴A、D是对称点，∴AD⊥BE．（3）∵BE是∠ABC的平分线，DE⊥BC，EA⊥AB，∴AE＝DE，在Rt△ABE和Rt△DBE中，∴Rt△ABE≌Rt△DBE（HL），∴AB＝BD，又△ABC是等腰直角三角形，∠BAC＝90°，∴∠C＝45°，又ED⊥BC，∴△DCE为等腰直角三角形，∴DE＝DC，即AB+AE＝BD+DC＝BC＝10．。
2021年九年级数学中考三轮压轴专题培优卷：《三角形综合》(解析版)
•△FMC为等腰直角三角形，
•FM= CM
•BF=AM= AF+FM=2CM
--S^BDF=2SACDF
•/af=cm fm= cm
•af=fm
•F是AM的中点，
•
--SaAFF■■-S^AM=-QAFB,
••• AF丄BF, CNL BF, AF=CN
--S^afB=Sabfc
2.【问题】如图1，在Rt△ABC中，/ACB=90°,AC= BC过点C作直线I平行于AB/
EDF=90°,点D在直线L上移动，角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.
【探究发现】〔1〕如图2，某数学兴趣小组运用从特殊到一般的数学思想，发现当点D
移动到使点P与点C重合时，通过推理就可以得到DP= DB请写出证明过程；
•Rt△DCE中,cE+cD=DE,
•bD+cD=dE；
(3)◎(2)中的结论还成立.
理由：T/BAC=/DAE=90° ,
•/BAC/DAC=/DAE/DAC
即/BAD-/CAE
在厶ABDW^ACE中,
irAB=AC
4 ZBAD=ZCAE,
[ad=ae
•△ABD^ ACE( SAS,
•/ABC=/ACE=45° ,BD=CE
在直线m上，并且/BDA=ZAEC=ZBAC=a,其中a为任意锐角或钝角•请问〔1〕中
结论还是否成立？假设成立，请给出证明；假设不成立，请说明理由.
〔3〕拓展应用：如图3,D E是D A、E三点所在直线m上的两动点〔D, A, E三点互
不重合〕，点F为/BAC平分线上的一点，且厶ABF和△ACF均为等边三角形，连接BD
2021届中考数学压轴题专题突破09 三角形问题【含答案】
2021届中考数学压轴题专题突破09 三角形问题【含答案】一、单选题1．如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm速度向点A运动，点Q从点A 同时出发以每秒2cm速度向点C运动，其中一个动点到达端点，另一个动点也随之停止，当△APQ是以PQ 为底的等腰三角形时，运动的时间是( )秒A．2.5 B．3 C．3.5 D．4【答案】D【关键点拨】此题主要考查学生对等腰三角形的性质这一知识点的理解和掌握，此题涉及到动点，有一定的拔高难度，属于中档题．2．已知等边△ABC中，在射线BA上有一点D，连接CD，并以CD为边向上作等边△CDE，连接BE和AE.试判断下列结论：①AE=BD；②AE与AB所夹锐夹角为60°；③当D在线段AB或BA延长线上时，总有∠BDE-∠AED=2∠BDC；④∠BCD=90°时，CE2+AD2=AC2+DE2 .正确的序号有（）A．①②B．①②③C．①②④D．①②③④【答案】C【解析】∵∠BCA=∠DCE=60°，∴∠BCA+∠ACD=∠DCE+∠ACD，∴∠BCD=∠ACE，又∵AC=BC，CE=CD，∴△BCD≌△ACE，∴AE=BD，∠CBA=∠CAE=60°，∠AEC=∠BDC，①正确，∴∠BAE=120°，∴∠EAD=60°，②正确，∵∠BCD=90°，∠BCA=60°，∴∠ACD=∠ADC=30°，∴AC=AD，∵CE=DE，∴CE2+AD2=AC2+DE2，④正确，当D点在BA延长线上时，∠BDE-∠BDC=60°，∵∠AEC=∠BDC，∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°，∴∠BDE-∠BDC=∠BDC+∠AED∴∠BDE-∠AED=2∠BDC，故正确的结论有①②④，故选C.【关键点拨】此题主要考查等边三角形的性质和全等三角形的判定与性质等知识点的理解和掌握3．如图，在△ABC中，AB=AC，∠BAC=120°，D，E是BC上的两点，且∠DAE=30°，将△AEC绕点A顺时针旋转120°后，得到△AFB，连接DF.下列结论中正确的个数有（）①∠FBD=60°；②△ABE∽△DCA；③AE平分∠CAD；④△AFD是等腰直角三角形.A．1个B．2个C．3个D．4个【答案】B∴∠BAD＋∠EAC＝120°−∠DAE＝90°，∴∠ABC＋∠BAD＜90°，∴∠ADC＜90°，∴∠DAC＞60°，∴∠EAC＞30°，即∠DAE≠∠EAC，∴③错误；∵将△AEC绕点A顺时针旋转120°后，得到△AFB，∴AF＝AE，∠EAC＝∠BAF，∵∠BAC＝120°，∠DAE＝30°，∴∠BAD＋∠EAC＝90°，∴∠DAB＋∠BAF＝90°，【关键点拨】本题考查了旋转的性质，等腰三角形的性质和判定，三角形的外角性质，全等三角形的性质和判定的应用，主要考查学生综合运用性质进行推理的能力，题目比较典型，但是有一定的难度．4．如图，在等边三角形ABC中，在AC边上取两点M、N，使∠MBN＝30°．若AM＝m，MN＝x，CN＝n，则以x，m，n为边长的三角形的形状为（）A．锐角三角形B．直角三角形C．钝角三角形D．随x，m，n的值而定【答案】C【解析】将△ABM绕点B顺时针旋转60°得到△CBH．连接HN．【关键点拨】本题考查了等边三角形的性质、全等三角形的判定和性质、旋转的性质等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形解决问题，属于中考常考题型．5．如图，在等腰直角△ABC中，∠C=90°，点O是AB的中点，且AB=，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为D、E，则CD+CE=（）A．B．C．2 D．【答案】A【解析】6．如图，在△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH、BE与相交于点G，以下结论中正确的结论有（）（1）△ABC是等腰三角形；（2）BF＝AC；（3）BH：BD：BC＝1：：；（4）GE2+CE2＝BG2．A．1个B．2个C．3个D．4个【答案】C【解析】（1）∵BE平分∠ABC，∴∠ABE＝∠CBE，∵CD⊥AB，∴∠ABE+∠A＝90°，∠CBE+∠ACB＝90°，∴∠A＝∠BCA，∴AB＝BC，∴△ABC是等腰三角形；故（1）正确；，∴△BDF≌△CDA（AAS），∴BF＝AC；故（2）正确；（3）∵在△BCD中，∠CDB＝90°，∠DBC＝45°，∴∠DCB＝45°，∴BD＝CD，BC＝BD．由点H是BC的中点，∴DH＝BH＝CH＝BC，∴BD＝BH，∴BH：BD：BC＝BH：BH：2BH＝1：：2．故（3）错误；（4）由（2）知：BF＝AC，∵BF平分∠DBC，∴∠ABE＝∠CBE，又∵BE⊥AC，∴∠AEB＝∠CEB，在△ABE与△CBE中，【关键点拨】本题考查全等三角形的判定与性质，等腰直角三角形的判定与性质，直角三角形斜边上的中线等于斜边的一半的性质，平行线的性质，勾股定理,熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形是解题的关键．7．如图，∠AOB=30°，OC为∠AOB内部一条射线，点P为射线OC上一点，OP=4，点M、N分别为OA、OB 边上动点，则△MNP周长的最小值为( )A．2B．4C．D．【答案】B【解析】【关键点拨】本题考查了等边三角形的性质和判定，轴对称-最短路线问题的应用，正确作出辅助线，确定M、N的位置，证明△OP1P2是等边三角形是解题关键．8．如图，，，，点D、E为BC边上的两点，且，连接EF、BF则下列结论：≌；≌；；，其中正确的有( )个．A．1B．2C．3D．4【答案】D②∵△AED≌△AEF,∴AF=AD,∵,∴∠FAB=∠CAD,∵AB=AC，∴≌，②正确；③∵∠BAC=∠DAF=90°，∴∠BAC-∠BAD=∠DAF-∠BAD，即∠CAD=∠BAF．在△ACD与△ABF中，，∴△ACD≌△ABF（SAS），∴CD=BF，由①知△AED≌△AEF，∴DE=EF．在△BEF中，∵BE+BF＞EF，∴BE+DC＞DE，③正确；④由③知△ACD≌△ABF，∴∠C=∠ABF=45°，∵∠ABE=45°，∴∠EBF=∠ABE+∠ABF=90°．④正确．故答案为D．【关键点拨】本题考查了勾股定理，全等三角形的判定与性质，等腰直角直角三角形的性质，三角形三边关系定理，相似三角形的判定，此题涉及的知识面比较广，解题时要注意仔细分析，有一定难度．9．如图，四边形ABCD中，∠A、∠B、∠C、∠D的角平分线恰相交于一点P，记△APD、△APB、△BPC、△DPC 的面积分别为S1、S2、S3、S4，则有（）A．B．C．D．【答案】A【关键点拨】本题考查了角平分线性质定理,作高线和理解角平分线性质定理是解题关键.10．如图，已知AD为△ABC的高线，AD=BC，以AB为底边作等腰Rt△ABE，连接ED，EC，延长CE交AD于F点，下列结论：①△ADE≌△BCE；②CE⊥DE；③BD=AF；④S△BDE=S△ACE，其中正确的有（）A．①③B．①②④C．①②③④D．①③④【答案】C③∵∠BDE=∠ADB+∠ADE，∠AFE=∠ADC+∠ECD，∴∠BDE=∠AFE．∵∠BED+∠BEF=∠AEF+∠BEF=90°，∴∠BED=∠AEF．在△AEF和△BED中，∵，∴△AEF≌△BED（AAS），∴BD=AF；故③正确；④∵AD=BC，BD=AF，∴CD=DF．∵AD⊥BC，∴△FDC是等腰直角三角形．∵DE⊥CE，∴EF=CE，∴S△AEF=S△ACE．∵△AEF≌△BED，∴S△AEF=S△BED，∴S△BDE=S△ACE．故④正确．故选C．【关键点拨】本题考查了全等三角形的判定与性质，本题中求证△BFE≌△CDE是解题的关键．11．如图，等边三角形ABC边长是定值，点O是它的外心，过点O任意作一条直线分别交AB，BC于点D，E．将△BDE沿直线DE折叠，得到△B′DE，若B′D，B′E分别交AC于点F，G，连接OF，OG，则下列判断错误的是（）A．△ADF≌△CGEB．△B′FG的周长是一个定值C．四边形FOEC的面积是一个定值D．四边形OGB'F的面积是一个定值【答案】D【解析】A、连接OA、OC，由折叠得：∠BDE=∠ODF=（∠DAF+∠AFD），∴∠OFD+∠ODF=（∠FAD+∠ADF+∠DAF+∠AFD）=120°，∴∠DOF=60°，同理可得∠EOG=60°，∴∠FOG=60°=∠DOF=∠EOG，∴△DOF≌△GOF≌△GOE，∴OD=OG，OE=OF，∠OGF=∠ODF=∠ODB，∠OFG=∠OEG=∠OEB，∴△OAD≌△OCG，△OAF≌△OCE，∴AD=CG，AF=CE，∴△ADF≌△CGE，故选项A正确；B、∵△DOF≌△GOF≌△GOE，∴DF=GF=GE，【关键点拨】本题考查了等边三角形的性质、三角形全等的性质和判定、角平分线的性质和判定、三角形和四边形面积及周长的确定以及折叠的性质，有难度，本题全等的三角形比较多，要注意利用数形结合，并熟练掌握三角形全等的判定，还要熟练掌握角平分线的逆定理的运用，证明FO平分∠DFG是本题的关键. 12．如图，点D 是等腰直角△ABC 腰BC 上的中点，点B 、B′ 关于AD 对称，且BB′ 交AD 于F，交AC 于E，连接FC 、AB′，下列说法：①∠BAD=30°；②∠BFC=135°；③AF=2B′ C；正确的个数是（）A．1 B．2 C．3 D．4【答案】B【解析】∵点D是等腰直角△ABC腰BC上的中点，∴BD=BC=AB，∴tan∠BAD=，∴∠BAD≠30°，故①错误；如图，连接B'D，∴BF=CB'=B'F，∴△FCB'是等腰直角三角形，∴∠CFB'=45°，即∠BFC=135°，故②正确；由△ABF≌△BCB'，可得AF=BB'=2BF=2B'C，故③正确；∵AF＞BF=B'C，∴△AEF与△CEB'不全等，∴AE≠CE，∴S△AFE≠S△FCE，故④错误；故选B．【关键点拨】本题主要考查了轴对称的性质以及全等三角形的判定与性质的运用，如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．13．如图，点E在△DBC的边DB上，点A在△DBC内部，∠DAE=∠BAC=90°，AD=AE，AB=AC．给出下列结论：①BD=CE；②∠ABD+∠ECB=45°；③BD⊥CE；④BE2=2（AD2+AB2）﹣CD2．其中正确的是（）A．①②③④B．②④C．①②③D．①③④【答案】A【关键点拨】本题考查全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考选择题中的压轴题．14．如图，在△ABC中，P是BC上的点，作PQ∥AC交AB于点Q，分别作PR⊥AB，PS⊥AC，垂足分别是R，S，若PR=PS，则下面三个结论：①AS=AR；②AQ=PQ；③△PQR≌△CPS；④AC﹣AQ=2SC，其中正确的是（）A．②③④B．①②C．①④D．①②③④【答案】B【解析】如图【关键点拨】本题主要考查三角形全等及三角形全等的性质.15．如图，AB＝AC，BD⊥AC于D，CE⊥AB于E，BD、CE交于O，连结AO，则图中共有全等三角形的对数为（）A．2对B．3对C．4对D．5对【答案】C∴△AOE≌△AOD（HL），∴∠OAC=∠OAB，∵∠B=∠C，AB=AC，∠OAC=∠OAB，∴△AOC≌△AOB.（ASA）∵∠B=∠C，BE=CD，∠ODC=∠OEB=90°，∴△BOE≌△COD（ASA）．综上：共有4对全等三角形，故选C.【关键点拨】本题考查三角形全等的判定方法和全等三角形的性质，判定两个三角形全等的一般方法有：SSS、SAS、ASA、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．做题时要从已知条件开始结合全等的判定方法逐一验证，由易到难，不重不漏．二、填空题16．如图所示，已知：点A(0，0)，B（，0），C（0，1）在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…，则第个等边三角形的边长等于__________．【答案】【关键点拨】本题主要考查等边三角形的性质及解直角三角形，从而归纳出边长的规律．17．如图，∠MON=30°，点B1在边OM上，且OB1=2，过点B1作B1A1⊥OM交ON于点A1，以A1B1为边在A1B1右侧作等边三角形A1B1C1；过点C1作OM的垂线分别交OM、ON于点B2、A2，以A2B2为边在A2B2的右侧作等边三角形A2B2C2；过点C2作OM的垂线分别交OM、ON于点B3、A3，以A3B3为边在A3B3的右侧作等边三角形A3B3C3，…；按此规律进行下去，则△A n B n+1C n的面积为__．（用含正整数n的代数式表示）【答案】（）2n﹣2×…，△A n B n+1C n的边长为（）n﹣1×，∴△A n B n+1C n的面积为×[（）n﹣1×]2=（）2n﹣2×，故答案为：（）2n﹣2×.【关键点拨】本题考查了含30度角的直角三角形的性质、等边三角形的面积公式、解直角三角形等知识，熟练掌握相关性质得出等边三角形的边长的规律是解题的关键.18．如图，已知等边△ABC的边长是2，以BC边上的高AB1为边作等边三角形，得到第一个等边△AB1C1；再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形，得到第二个等边△AB2C2；再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形，得到第三个等边△AB3C3；…，记△B1CB2的面积为S1，△B2C1B3的面积为S2，△B3C2B4的面积为S3，如此下去，则S n=_____．【答案】【关键点拨】本题考查了规律题，涉及等边三角形的性质，含30度角的直角三角形的性质、勾股定理等，有一定难度，熟练掌握并灵活运用等边三角形的性质、勾股定理等解本题的关键．19．如图，直线与x轴、y轴分别交于A，B两点，C是OB的中点，D是AB上一点，四边形OEDC是菱形，则△OAE的面积为________．【答案】∴A(,0);∴OA=,设D(x,) ,∴E(x,- x+2),延长DE交OA于点F，∴EF=-x+2,OF=x,在Rt△OEF中利用勾股定理得：,解得：x1=0(舍），x2=；∴EF=1,∴S△AOE=·OA·EF=2.故答案为：.【关键点拨】本题考查了一次函数图象上点的坐标特征：一次函数y=kx+b，（k≠0，且k，b为常数）的图象是一条直线．它与x轴的交点坐标是（-，0）；与y轴的交点坐标是（0，b）．直线上任意一点的坐标都满足函数关系式y=kx+b．也考查了菱形的性质.20．如图，等腰△ABC中，CA=CB=4，∠ACB=120°，点D在线段AB上运动（不与A、B重合），将△CAD 与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，给出下列结论：①CD=CP=CQ；②∠PCQ的大小不变；③△PCQ面积的最小值为；④当点D在AB的中点时，△PDQ是等边三角形，其中所有正确结论的序号是．【答案】①②④．③如图，过点Q作QE⊥PC交PC延长线于E，∵∠PCQ=120°，∴∠QCE=60°，在Rt△QCE中，tan∠QCE=，∴QE=CQ×tan∠QCE=CQ×tan60°=CQ，∵CP=CD=CQ，∴S△PCQ=CP×QE=CP×CQ=，∴CD最短时，S△PCQ最小，即：CD⊥AB时，CD最短，过点C作CF⊥AB，此时CF就是最短的CD，∵AC=BC=4，∠ACB=120°，∴∠ABC=30°，∴CF=BC=2，即：CD最短为2，∴S△PCQ最小===，∴③错误；④∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，∴AD=AP，∠DAC=∠PAC，∵∠DAC=30°，∴∠APD=60°，∴△APD是等边三角形，∴PD=AD，∠ADP=60°，同理：△BDQ是等边三角形，∴DQ=BD，∠BDQ=60°，∴∠PDQ=60°，∵当点D在AB的中点，∴AD=BD，∴PD=DQ，∴△DPQ是等边三角形，∴④正确，故答案为：①②④．21．如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重叠部分；…；将余下部分沿∠B n A n C的平分线A n B n+1折叠，点B n与点C重合，无论折叠多少次，只要最后一次恰好重合，我们就称∠BAC是△ABC的好角.（1）如图2，在△ABC中，∠B>∠C，若经过两次折叠，∠BAC是△ABC的好角，则∠B与∠C的等量关系是_______；（2）如果一个三角形的最小角是20°，则此三角形的最大角为______时，该三角形的三个角均是此三角形的好角。
2021年中考复习数学 专项突破：全等三角形(含答案)
2021中考数学专项突破：全等三角形一、选择题（本大题共10道小题）1. 如图所示，P是∠BAC内一点，PE⊥AB于点E，PF⊥AC于点F，PE＝PF，则直接得到△PEA≌△PF A的理由是()A．HL B．ASA C．AAS D．SAS2. 已知图中的两个三角形全等，则∠α的度数为 ()A.105°B.75°C.60°D.45°3. 如图，添加下列条件，不能判定△ABD≌△ACD的是()A．BD＝CD，AB＝ACB．∠ADB＝∠ADC，BD＝CDC．∠B＝∠C，∠BAD＝∠CADD．∠B＝∠C，BD＝CD4. 如图，点B，E在线段CD上，若∠C=∠D，则添加下列条件，不一定能使△ABC≌△EFD的是()A.BC=FD，AC=EDB.∠A=∠DEF，AC=EDC.AC=ED，AB=EFD.∠A=∠DEF，BC=FD5. 如图所示，P是∠BAC内一点，且点P到AB，AC的距离PE，PF相等，则△PEA≌△PF A的依据是()A．HL B．ASA C．SSS D．SAS6. 如图，在直角坐标系中，AD是Rt△OAB的角平分线，点D的坐标是(0，-3)，那么点D到AB的距离是()A.3B.-3C.2D.-27. 根据下列条件，能画出唯一的△ABC的是()A．AB＝3，BC＝4，AC＝8 B．AB＝4，BC＝3，∠A＝30°C．AB＝5，AC＝6，∠A＝50°D．∠A＝30°，∠B＝70°，∠C＝80°8. 如图，有一张三角形纸片ABC，已知∠B=∠C=x°，按下列方案用剪刀沿着箭头方向剪开，可能得不到全等三角形纸片的是()9. 如图，在等腰直角△ABC中，∠C＝90°，点O是AB的中点，且AB＝6，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为D、E，则CD＋CE等于()A. 2B. 3C. 2D. 610. 如图，点G在AB的延长线上，∠GBC，∠BAC的平分线相交于点F，BE⊥CF 于点H.若∠AFB＝40°，则∠BCF的度数为()A．40°B．50°C．55°D．60°二、填空题（本大题共6道小题）11. 如图，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B＝________.12. 如图，在四边形ABCD中，AB∥CD，连接BD.请添加一个适当的条件：______________，使得△ABD≌△CDB.(只需写出一个)13. 如图，已知∠ABC＝∠DCB，添加下列条件中的一个：①∠A＝∠D，②AC ＝DB，③AB＝DC，其中不能判定△ABC≌△DCB的是________(只填序号)．14. 如图，已知AB＝BD，∠A＝∠D，若要应用“SAS”判定△ABC≌△DBE，则需要添加的一个条件是____________．15. 如图，小明和小丽为了测量池塘两端A，B两点之间的距离，先取一个可以直接到达点A和点B的点C，沿AC方向走到点D处，使CD＝AC；再用同样的方法确定点E，使CE＝BC.若量得DE的长为60米，则池塘两端A，B两点之间的距离是______米．16. 如图，P是△ABC外的一点，PD⊥AB交BA的延长线于点D，PE⊥AC于点E，PF⊥BC交BC的延长线于点F，连接PB，PC.若PD＝PE＝PF，∠BAC＝64°，则∠BPC的度数为________．三、解答题（本大题共4道小题）17. 如图，C是线段BD的中点，AB＝EC，∠B＝∠ECD.求证：△ABC≌△ECD.18. 如图所示，AB＝EA，AB∥DE，∠ECB＝70°，∠D＝110°.求证：△ABC≌△EAD.19. 如图，四边形ABCD是正方形，以边AB为直径作☉O，点E在BC边上，连接AE交☉O于点F，连接BF并延长交CD于点G.(1)求证:△ABE≌△BCG.(2)若∠AEB=55°，OA=3，求的长.(结果保留π)20. 如图，在△ABC 中，AB=AC ，∠BAC=90°，点D 是射线BC 上一动点，连接AD ，以AD 为直角边，在AD 的上方作等腰直角三角形ADF .(1)如图①，当点D 在线段BC 上时(不与点B 重合)，求证:△ACF ≌△ABD ; (2)如图②，当点D 在线段BC 的延长线上时，猜想CF 与BD 的数量关系和位置关系，并说明理由.2021中考数学 专项突破：全等三角形-答案一、选择题（本大题共10道小题）1. 【答案】A2. 【答案】B3. 【答案】D[解析] A ．在△ABD 和△ACD 中，⎩⎨⎧AD ＝AD ，AB ＝AC ，BD ＝CD ，∴△ABD ≌△ACD(SSS)，故本选项不符合题意； B ．在△ABD 和△ACD 中，⎩⎨⎧AD ＝AD ，∠ADB ＝∠ADC ，BD ＝CD ，∴△ABD ≌△ACD(SAS)，故本选项不符合题意； C ．在△ABD 和△ACD 中，⎩⎨⎧∠BAD ＝∠CAD ，∠B ＝∠C ，AD ＝AD ，∴△ABD ≌△ACD(AAS)，故本选项不符合题意；D ．根据∠B ＝∠C ，AD ＝AD ，BD ＝CD 不能推出△ABD ≌△ACD(SSA)，故本选项符合题意．故选D.4. 【答案】C[解析] A .添加BC=FD ，AC=ED ，可利用“SAS”判定△ABC ≌△EFD ;B .添加∠A=∠DEF ，AC=ED ，可利用“ASA”判定△ABC ≌△EFD ; C .添加AC=ED ，AB=EF ，不能判定△ABC ≌△EFD ;D .添加∠A=∠DEF ，BC=FD ，可利用“AAS”判定△ABC ≌△EFD.5. 【答案】A6. 【答案】A[解析] 如图，过点D 作DE ⊥AB 于点E.∵点D 的坐标是(0，-3)， ∴OD=3.∵AD 是△OAB 的角平分线， ∴ED=OD=3，即点D 到AB 的距离是3.7. 【答案】C[解析] 对于选项A 来说，AB ＋BC<AC ，不能画出△ABC ；对于选项B 来说，可画出△ABC 为锐角三角形或者钝角三角形；对于选项C 来说，已知两边及其夹角，△ABC 是唯一的；对于选项D 来说，△ABC 的形状可确定，但大小不确定．8. 【答案】C[解析] 选项A 中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项B 中由全等三角形的判定定理“SAS”证得图中两个小三角形全等. 选项C 中，如图①，∵∠DEC=∠B+∠BDE ，∴x °+∠FEC=x °+∠BDE.∴∠FEC=∠BDE.这两个角所对的边是BE和CF，而已知条件给的是BD=CF=3，故不能判定两个小三角形全等.选项D中，如图②，∵∠DEC=∠B+∠BDE，∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.又∵BD=CE=2，∠B=∠C，∴△BDE≌△CEF.故能判定两个小三角形全等.9. 【答案】B【解析】如解图，连接OC，由已知条件易得∠A＝∠OCE，CO＝AO，∠DOE＝∠COA，∴∠DOE－∠COD＝∠COA－∠COD，即∠AOD＝∠COE，∴△AOD≌△COE(ASA)，∴AD＝CE，进而得CD＋CE＝CD＋AD＝AC＝22AB＝3，故选B.10. 【答案】B[解析] 如图，过点F分别作FZ⊥AE于点Z，FY⊥CB于点Y，FW⊥AB于点W.∵AF平分∠BAC，FZ⊥AE，FW⊥AB，∴FZ＝FW.同理FW＝FY.∴FZ＝FY.又∵FZ⊥AE，FY⊥CB，∴∠FCZ＝∠FCY.由∠AFB ＝40°，易得∠ACB ＝80°. ∴∠ZCY ＝100°.∴∠BCF ＝50°.二、填空题（本大题共6道小题） 11. 【答案】120° 【解析】由于△ABC ≌△A′B′C′，∴∠C ＝∠C′＝24°，在△ABC 中，∠B ＝180°－24°－36°＝120°.12. 【答案】答案不唯一，如AB ＝CD [解析] 由已知AB ∥CD 可以得到一对角相等，还有BD ＝DB ，根据全等三角形的判定，可添加夹这个角的另一边相等，或添加另一个角相等均可．13. 【答案】②[解析] ∵已知∠ABC ＝∠DCB ，且BC ＝CB ，∴若添加①∠A ＝∠D ，则可由“AAS”判定△ABC ≌△DCB ； 若添加②AC ＝DB ，则属于“SSA”，不能判定△ABC ≌△DCB ； 若添加③AB ＝DC ，则可由“SAS”判定△ABC ≌△DCB.14. 【答案】AC ＝DE15. 【答案】60[解析] 在△ACB 和△DCE 中，⎩⎨⎧AC ＝DC ，∠ACB ＝∠DCE ，BC ＝EC ，∴△ACB ≌△DCE(SAS)．∴DE ＝AB. ∵DE ＝60米，∴AB ＝60米．16. 【答案】32°[解析] ∵PD ＝PE ＝PF ，PD ⊥AB 交BA 的延长线于点D ，PE ⊥AC于点E ，PF ⊥BC 交BC 的延长线于点F ， ∴CP 平分∠ACF ，BP 平分∠ABC. ∴∠PCF ＝12∠ACF ，∠PBF ＝12∠ABC.∴∠BPC ＝∠PCF －∠PBF ＝12(∠ACF －∠ABC)＝12∠BAC ＝32°.三、解答题（本大题共4道小题）17. 【答案】证明：∵C 是线段BD 的中点，∴BC ＝CD.在△ABC 与△ECD 中，⎩⎨⎧BC ＝CD ，∠B ＝∠ECD ，AB ＝EC ，∴△ABC ≌△ECD.18. 【答案】证明：由∠ECB ＝70°得∠ACB ＝110°. 又∵∠D ＝110°，∴∠ACB ＝∠D. ∵AB ∥DE ，∴∠CAB ＝∠E.在△ABC 和△EAD 中，⎩⎨⎧∠ACB ＝∠D ，∠CAB ＝∠E ，AB ＝EA ，∴△ABC ≌△EAD(AAS)．19. 【答案】解:(1)证明:∵四边形ABCD 是正方形，AB 为☉O 的直径， ∴∠ABE=∠BCG=∠AFB=90°，AB=BC ， ∴∠BAF +∠ABF=90°，∠ABF +∠EBF=90°， ∴∠EBF=∠BAF ， 在△ABE 与△BCG 中，∴△ABE ≌△BCG (ASA). (2)连接OF ，∵∠ABE=∠AFB=90°，∠AEB=55°， ∴∠BAE=90°-55°=35°， ∴∠BOF=2∠BAE=70°. ∵OA=3， ∴的长==.20. 【答案】解:(1)证明:∵∠BAC=90°，△ADF是等腰直角三角形，∴∠BAD+∠CAD=90°，∠CAF+∠CAD=90°，∴∠CAF=∠BAD.在△ACF和△ABD中，∴△ACF≌△ABD(SAS).(2)CF=BD且CF⊥BD，理由如下:∵∠CAB=∠DAF=90°，∴∠CAB+∠CAD=∠DAF+∠CAD，即∠CAF=∠BAD.在△ACF和△ABD中，∴△ACF≌△ABD(SAS)，∴CF=BD，∠ACF=∠ABD.∵AB=AC，∠BAC=90°，∴∠ABD=∠ACB=45°，∴∠BCF=∠ACF+∠ACB=∠ABD+∠ACB=45°+45°=90°，∴CF⊥BD.。
专题16 全等三角形判定和性质问题(解析版)2021年中考数学必考34个考点高分三部曲
专题16 全等三角形判定和性质问题1．全等三角形：能够完全重合的两个图形叫做全等形。
能够完全重合的两个三角形叫做全等三角形。
2．全等三角形的表示全等用符号“≌”表示，读作“全等于”。
如△ABC≌△DEF，读作“三角形ABC全等于三角形DEF”。
注：记两个全等三角形时，通常把表示对应顶点的字母写在对应的位置上。
3．全等三角形的性质：全等三角形的对应角相等、对应边相等。
4．三角形全等的判定定理：（1）边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）（2）角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ASA”）（3）边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）。
5．直角三角形全等的判定：HL定理：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“HL”）【例题1】（2020•贵州省安顺市）如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（）A．∠A＝∠D B．AC＝DF C．AB＝ED D．BF＝EC【解答】选项A、添加∠A＝∠D不能判定△ABC≌△DEF，故本选项正确；选项B、添加AC＝DF可用AAS进行判定，故本选项错误；选项C、添加AB＝DE可用AAS进行判定，故本选项错误；专题知识回顾专题典型题考法及解析选项D、添加BF＝EC可得出BC＝EF，然后可用ASA进行判定，故本选项错误．故选：A．【例题2】（2020•黑龙江省齐齐哈尔市）如图，已知在△ABC和△DEF中，△B＝△E，BF＝CE，点B、F、C、E在同一条直线上，若使△ABC△△DEF，则还需添加的一个条件是_________（只填一个即可）．【答案】AB＝DE．【解析】添加AB＝DE；△BF＝CE，△BC＝EF，在△ABC和△DEF中，，△△ABC△△DEF（SAS）【例题3】（2020•铜仁）如图，AB＝AC，AB△AC，AD△AE，且△ABD＝△ACE．求证：BD＝CE．【答案】见解析。
2021年中考数学 专题汇编：全等三角形(含答案)
2021中考数学专题汇编：全等三角形一、选择题（本大题共10道小题）1. 如图，点E，F在AC上，AD＝BC，DF＝BE，要使△ADF≌△CBE，还需要添加一个条件是()A．∠A＝∠C B．∠D＝∠BC．AD∥BC D．DF∥BE2. 到三角形三边距离相等的点是()A．三条中线的交点B．三条高(或三条高所在直线)的交点C．三边垂直平分线的交点D．三条内角平分线的交点3. 如图，AB⊥CD，且AB=CD.E，F是AD上两点，CE⊥AD，BF⊥AD.若CE=a，BF=b，EF=c，则AD的长为()A.a+cB.b+cC.a-b+cD.a+b-c4. 如图，点B，E，C，F在同一直线上，AB∥DE，∠A＝∠D，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是()A．BE＝CF B．∠ACB＝∠FC．AC＝DF D．AB＝DE5. 如图所示，在△ABC和△ABD中，∠C=∠D=90°，要利用“HL”判定Rt△ABC≌Rt△ABD成立，还需要添加的条件是 ()A.∠BAC=∠BADB.BC=BD或AC=ADC.∠ABC=∠ABDD.AC=BD6. 如图，点B，E在线段CD上，若∠C=∠D，则添加下列条件，不一定能使△ABC≌△EFD的是()A.BC=FD，AC=EDB.∠A=∠DEF，AC=EDC.AC=ED，AB=EFD.∠A=∠DEF，BC=FD7. 如图，若AB＝AC，AD＝AE，∠BAC＝∠DAE，则∠ABD等于()A．∠EAC B．∠ADE C．∠BAD D．∠ACE8. 如图，在等腰直角△ABC中，∠C＝90°，点O是AB的中点，且AB＝6，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为D、E，则CD＋CE等于()A. 2B. 3C. 2D. 69. 现已知线段a，b(a<b)，∠MON=90°，求作Rt△ABO，使得∠O=90°，OA=a，AB=b.小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.小雷:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.则下列说法中正确的是()A.小惠的作法正确，小雷的作法错误B.小雷的作法正确，小惠的作法错误C.两人的作法都正确D.两人的作法都错误10. 如图，∠AOB＝120°，OP平分∠AOB，且OP＝2.若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有()A. 1个B. 2个C. 3个D. 3个以上二、填空题（本大题共8道小题）11. 如图，已知∠B＝∠C，添加一个条件使△ABD≌△ACE(不标注新的字母，不添加新的线段)，你添加的条件是__________(填一个即可)．12. 如图，在△ABC中，AD⊥BC于点D，要使△ABD≌△ACD，若根据“HL”判定，还需要添加条件：____________．13. 如图，在△ABC中，∠C＝90°，∠CAB＝50°，按以下步骤作图：①以点A 为圆心，小于AC的长为半径画弧，分别交AB，AC于点E，F；②分别以点E，F为圆心，大于12EF的长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D，则∠ADC的度数为________．14. 如图，已知∠ABC＝∠DCB，添加下列条件中的一个：①∠A＝∠D，②AC ＝DB，③AB＝DC，其中不能判定△ABC≌△DCB的是________(只填序号)．15. 如图，已知AC＝FE，BC＝DE，点A，D，B，F在同一直线上，要使△ABC≌△FDE，还需添加一个．．条件，这个条件可以是__________(填一个即可)．16. 如图所示，已知AD∥BC，则∠1＝∠2，理由是________________；又知AD ＝CB，AC为公共边，则△ADC≌△CBA，理由是______，则∠DCA＝∠BAC，理由是__________________，则AB∥DC，理由是________________________________．17. (2019•南通)如图，△ABC中，AB=BC，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF，若∠BAE=25°，则∠ACF=__________度．18. 如图，P是△ABC外的一点，PD⊥AB交BA的延长线于点D，PE⊥AC于点E，PF⊥BC交BC的延长线于点F，连接PB，PC.若PD＝PE＝PF，∠BAC＝64°，则∠BPC的度数为________．三、解答题（本大题共4道小题）19. 如图，在△ABC中，AD是中线，CE⊥AD于点E，BF⊥AD交AD的延长线于点F.求证：BF＝CE.20. 如图2-Z-20，C是AB的中点，AD=CE，CD=BE.求证:∠A+∠ECA=180°.21. 如图，在∠AOB的两边OA，OB上分别取点D，M和点E，N，使OM=ON，OD=OE，DN和EM相交于点C.求证:点C在∠AOB的平分线上.22. 在矩形ABCD中，AD＝4，M是AD的中点，点E是线段AB上一点，连接EM并延长交线段CD的延长线于点F.(1)如图①，求证：△AEM ≌△DFM；(2)如图②，若AB＝2，过点M作MG⊥EF交线段BC于点G，求证：△GEF是等腰直角三角形；(3)如图③，若AB＝23，过点M作MG⊥EF交线段BC的延长线于点G，若MG=nME，求n的值.2021中考数学专题汇编：全等三角形-答案一、选择题（本大题共10道小题）1. 【答案】B[解析] 在△ADF和△CBE中，由AD＝BC，∠D＝∠B，DF＝BE，根据两边和它们的夹角分别相等的两个三角形全等，可以得到△ADF≌△CBE.故选B.2. 【答案】D3. 【答案】D[解析]∵AB⊥CD，CE⊥AD，BF⊥AD，∴∠CED=∠AFB=90°，∠A=∠C，又∵AB=CD，∴△CED≌△AFB，∴AF=CE=a，DE=BF=b，DF=DE-EF=b-c，∴AD=AF+DF=a+b-c，故选D.4. 【答案】B5. 【答案】B[解析] 要添加的条件为BC=BD或AC=AD.理由:若添加的条件为BC=BD，在Rt△ABC和Rt△ABD中，∴Rt △ABC ≌Rt △ABD (HL); 若添加的条件为AC=AD，在Rt △ABC 和Rt △ABD 中，∴Rt △ABC ≌Rt △ABD (HL).6. 【答案】C[解析] A .添加BC=FD ，AC=ED ，可利用“SAS”判定△ABC ≌△EFD ;B .添加∠A=∠DEF ，AC=ED ，可利用“ASA”判定△ABC ≌△EFD ; C .添加AC=ED ，AB=EF ，不能判定△ABC ≌△EFD ;D .添加∠A=∠DEF ，BC=FD ，可利用“AAS”判定△ABC ≌△EFD.7. 【答案】D[解析] ∵∠BAC ＝∠DAE ，∴∠BAC －∠DAC ＝∠DAE －∠DAC ，即∠BAD ＝∠CAE.在△ABD 和△ACE 中，⎩⎨⎧AB ＝AC ，∠BAD ＝∠CAE ，AD ＝AE ，∴△ABD ≌△ACE(SAS)．∴∠ABD ＝∠ACE.8. 【答案】B【解析】如解图，连接OC ，由已知条件易得∠A ＝∠OCE ，CO ＝AO ，∠DOE ＝∠COA ，∴∠DOE －∠COD ＝∠COA －∠COD ，即∠AOD ＝∠COE ，∴△AOD ≌△COE (ASA)，∴AD ＝CE ，进而得CD ＋CE ＝CD ＋AD ＝AC＝22AB ＝3，故选B.9. 【答案】A[解析] AB=b ，AB 是斜边，小惠作的斜边长是b 符合条件，而小雷作的是一条直角边长是b.故小惠的作法正确，小雷的作法错误.10. 【答案】D【解析】如解图，①当OM 1＝2时，点N 1与点O 重合，△PMN是等边三角形；②当ON 2＝2时，点M 2与点O 重合，△PMN 是等边三角形；③当点M 3，N 3分别是OM 1，ON 2的中点时，△PMN 是等边三角形；④当取∠M 1PM 4＝∠OPN 4时，易证△M 1PM 4≌△OPN 4(SAS)，∴PM 4＝PN 4，又∵∠M 4PN 4＝60°，∴△PMN 是等边三角形，此时点M ，N 有无数个，综上所述，故选D.二、填空题（本大题共8道小题）11. 【答案】答案不唯一，如AB＝AC12. 【答案】AB＝AC13. 【答案】65°14. 【答案】②[解析] ∵已知∠ABC＝∠DCB，且BC＝CB，∴若添加①∠A＝∠D，则可由“AAS”判定△ABC≌△DCB；若添加②AC＝DB，则属于“SSA”，不能判定△ABC≌△DCB；若添加③AB＝DC，则可由“SAS”判定△ABC≌△DCB.15. 【答案】答案不唯一，如∠C＝∠E或AB＝FD等16. 【答案】两直线平行，内错角相等SAS全等三角形的对应角相等内错角相等，两直线平行17. 【答案】70【解析】∵∠ABC=90°，AB=AC，∴∠CBF=180°–∠ABC=90°，∠ACB=45°，在Rt△ABE和Rt△CBF中，AB CBAE CF=⎧⎨=⎩，∴Rt△ABE≌Rt△CBF，∴∠BCF=∠BAE=25°，∴∠ACF=∠ACB+∠BCF=45°+25°=70°，故答案为：70．18. 【答案】32°[解析] ∵PD＝PE＝PF，PD⊥AB交BA的延长线于点D，PE⊥AC 于点E，PF⊥BC交BC的延长线于点F，∴CP平分∠ACF，BP平分∠ABC.∴∠PCF＝12∠ACF，∠PBF＝12∠ABC.∴∠BPC＝∠PCF－∠PBF＝12(∠ACF－∠ABC)＝12∠BAC＝32°.三、解答题（本大题共4道小题）19. 【答案】证明：∵CE ⊥AD ，BF ⊥AD ， ∴∠CED ＝∠BFD ＝90°.∵AD 是△ABC 的中线，∴BD ＝CD.在△BFD 和△CED 中，⎩⎨⎧∠BFD ＝∠CED ，∠BDF ＝∠CDE ，BD ＝CD ，∴△BFD ≌△CED(AAS)．∴BF ＝CE.20. 【答案】证明:∵C 是AB 的中点，∴AC=CB.在△ACD 和△CBE 中，∴△ACD ≌△CBE (SSS). ∴∠A=∠ECB.∴AD ∥CE.∴∠A+∠ECA=180°.21. 【答案】证明:如图，过点C 作CG ⊥OA 于点G ，CF ⊥OB 于点F .在△MOE 和△NOD 中，∴△MOE ≌△NOD (SAS). ∴S △MOE =S △NOD .∴S △MOE -S 四边形ODCE =S △NOD -S 四边形ODCE ， 即S △MDC =S △NEC .由三角形面积公式得DM ·CG=EN ·CF .∵OM=ON ，OD=OE ， ∴DM=EN.∴CG=CF . 又∵CG ⊥OA ，CF ⊥OB ，∴点C 在∠AOB 的平分线上.22. 【答案】(1)证明：∵四边形ABCD 是矩形， ∴∠EAM ＝∠FDM ＝90°， ∵M 是AD 的中点， ∴AM ＝DM ，在△AME 和△DMF 中，⎩⎨⎧∠A ＝∠FDBAM ＝DM∠AME ＝∠DMF， ∴△AEM ≌△DFM (ASA)；(2)证明：如解图①，过点G 作GH ⊥AD 于H ，解图①∵∠A ＝∠B ＝∠AHG ＝90°， ∴四边形ABGH 是矩形， ∴GH ＝AB ＝2， ∵M 是AD 的中点，∴AM ＝12AD ＝2，∴AM ＝GH ， ∵MG ⊥EF ，∴∠GME ＝90° ∴∠AME ＋∠GMH ＝90°. ∵∠AME ＋∠AEM ＝90°， ∴∠AEM ＝∠GMH ， 在△AEM 和△HMG 中，⎩⎨⎧AM ＝GH∠AEM ＝∠GMH ∠A ＝∠AHG， ∴△AEM ≌△HMG ， ∴ME ＝MG ，∴∠EGM ＝45°，由(1)得△AEM ≌△DFM ，∴ME ＝MF ，∵MG ⊥EF ，FMG EMG ≌△△ ，∴GE ＝GF ，∴∠EGF ＝2∠EGM ＝90°，∴△GEF 是等腰直角三角形．(3)解：如解图②，过点G 作GH ⊥AD 交AD 延长线于点H ，解图②∵∠A ＝∠B ＝∠AHG ＝90°，∴四边形ABGH 是矩形，∴GH ＝AB ＝23，∵MG ⊥EF ，∴∠GME ＝90°，∴∠AME ＋∠GMH ＝90°，∵∠AME ＋∠AEM ＝90°，∴∠AEM ＝∠GMH ，又∵∠A ＝∠GHM ＝90°，∴△AEM ∽△HMG ，∴EM MG ＝AM GH ，在Rt △GME 中，tan ∠MEG ＝MG EM ＝ 3.∴n =3。
2021年九年级中考数学 几何专项突破 全等三角形 (含答案)
2021中考数学几何专项突破全等三角形一、选择题1. 如图，在△ABC和△DEC中，AB=DE，再添加两个条件使△ABC△△DEC，不能添加的一组条件是()A.BC=EC，△B=△EB.BC=EC，AC=DCC.BC=EC，△A=△DD.△B=△E，△A=△D2. 如图，△ABC≌△EDF，DF=BC，AB=ED，AC=15，EC=10，则CF的长是()A.5B.8C.10D.153. 如图，在△ABC中，AB＝AC＝5，BC＝6，点M为BC的中点，MN⊥AC于点N，则MN等于()A. 65 B.95 C.125 D.1654. 如图，在△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC△△DEC，不能添加的一组条件是()A．BC＝EC，△B＝△E B．BC＝EC，AC＝DCC．BC＝DC，△A＝△D D．△B＝△E，△A＝△D5. 如图，点B，E在线段CD上，若∠C=∠D，则添加下列条件，不一定能使△ABC≌△EFD的是()A.BC=FD，AC=EDB.∠A=∠DEF，AC=EDC.AC=ED，AB=EFD.∠A=∠DEF，BC=FD6. 如图，在直角坐标系中，AD是Rt△OAB的角平分线，点D的坐标是(0，-3)，那么点D到AB的距离是()A.3B.-3C.2D.-27. 如图，有两个长度相同的滑梯靠在一面墙上，已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，且左边的滑梯与地面的夹角△ABC＝35°，则右边的滑梯与地面的夹角△DFE等于()A．60° B．55° C．65° D．35°8. 如图，若△ABE≌△ACF，且AB=5，AE=2，则EC的长为()图12-1-10A.2B.3C.5D.2.59. 如图，已知在四边形ABCD中，△BCD＝90°，BD平分△ABC，AB＝6，BC ＝9，CD＝4，则四边形ABCD的面积是()A ．24B ．30C ．36D ．4210. 如图，在△ABC中，AB ＝AC ，BC ＝12，E 为AC 边的中点，线段BE 的垂直平分线交边BC 于点D .设BD ＝x ，tan△ACB ＝y ，则( )A. x －y 2＝3 B. 2x －y 2＝9 C. 3x －y 2＝15 D. 4x －y 2＝21二、填空题11. 如图，将△ABC 绕点A 逆时针旋转150°，得到△ADE ，这时点B ，C ，D 恰好在同一直线上，则∠B 的度数为 .12. 如图，已知DB △AE 于点B ，DC △AF 于点C ，且DB ＝DC ，△BAC ＝40°，△ADG＝130°，则△DGF ＝________°.13. 如图，在△ABC中，△C ＝90°，△CAB ＝50°，按以下步骤作图：△以点A 为圆心，小于AC 的长为半径画弧，分别交AB ，AC 于点E ，F ；△分别以点E ，F 为圆心，大于12EF 的长为半径画弧，两弧相交于点G ；△作射线AG ，交BC 边于点D ，则△ADC 的度数为________．14. 如图，D为Rt△ABC中斜边BC上的一点，且BD=AB，过点D作BC的垂线，交AC于点E.若AE=12 cm，则DE的长为cm.15. 如图，△ABC是等腰三角形，AB=AC，∠BAC=45°，点D在AC边上，将△ABD 绕点A逆时针旋转45°得到△ACD'，且点D'，D，B在同一直线上，则∠ABD的度数是.16. 如图，在△ABC中，若AB＝AC＝8，△A＝30°，则S△ABC＝________．三、解答题17. 如图，A，B，C，D四点在同一直线上，且AF△DE，BF△CE，AC＝BD.求证：△ABF△△DCE.18. 已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过D点的直线交AC于E点，交AB于F点，且△AEF为等边三角形．(1)求证：△DFB是等腰三角形；(2)若DA＝7AF，求证CF△AB.19. 如图，点B ，F ，C ，E 在直线l 上(F ，C 之间不能直接测量)，点A ，D 在l异侧，测得AB ＝DE ，AC ＝DF ，BF ＝EC. (1)求证：△ABC△△DEF ；(2)指出图中所有平行的线段，并说明理由．20. 如图，点A ，E ，F ，B 在直线l 上，AE ＝BF ，AC △BD ，且AC ＝BD .求证：CF ＝DE .21. 如图，△O 的直径AB ＝4，C 为△O 上一点，AC ＝2.过点C 作△O 的切线DC ，P 点为优弧CBA ︵上一动点(不与A 、C 重合)． (1)求△APC 与△ACD 的度数；(2)当点P 移动到劣弧CB ︵的中点时，求证：四边形OBPC 是菱形； (3)当PC 为△O 的直径时，求证：△APC 与△ABC 全等．2021中考数学几何专项突破全等三角形-答案一、选择题1. 【答案】C[解析]A选项，已知AB=DE，再加上条件BC=EC，∠B=∠E，可利用SAS证明△ABC≌△DEC，故不合题意;B选项，已知AB=DE，再加上条件BC=EC，AC=DC，可利用SSS证明△ABC ≌△DEC，故不合题意;C选项，已知AB=DE，再加上条件BC=EC，∠A=∠D，不能证明△ABC≌△DEC，故符合题意;D选项，已知AB=DE，再加上条件∠B=∠E，∠A=∠D，可利用ASA证明△ABC ≌△DEC，故不合题意.故选C.2. 【答案】A[解析] ∵△ABC≌△EDF，AC=15，∴EF=AC=15.∵EC=10，∴CF=EF-EC=15-10=5.3. 【答案】C【解析】此题应首先连接AM，则AM⊥BC.∴AM＝AC2－CM2＝4，然后由三角形面积：S△ACM ＝12AM×CM.S△ACM＝12AC×MN.得：AM×CM＝AC×MN.∴MN＝125.也可以利用△ACM∽△MCN.得：ACCM＝AMMN.∴MN＝AM×CMAC＝12 5.4. 【答案】C5. 【答案】C[解析] A .添加BC=FD ，AC=ED ，可利用“SAS”判定△ABC ≌△EFD ;B .添加∠A=∠DEF ，AC=ED ，可利用“ASA”判定△ABC ≌△EFD ; C .添加AC=ED ，AB=EF ，不能判定△ABC ≌△EFD ;D .添加∠A=∠DEF ，BC=FD ，可利用“AAS”判定△ABC ≌△EFD.6. 【答案】A[解析] 如图，过点D 作DE ⊥AB 于点 E.∵点D 的坐标是(0，-3)， ∴OD=3.∵AD 是△OAB 的角平分线， ∴ED=OD=3，即点D 到AB 的距离是3.7. 【答案】B [解析] 在Rt△ABC 和Rt△DEF 中，⎩⎨⎧BC ＝EF ，AC ＝DF ，△Rt△ABC△Rt△DEF(HL)． △△DEF ＝△ABC ＝35°. △△DFE ＝90°－35°＝55°.8. 【答案】B[解析] ∵△ABE ≌△ACF ，AB=5，∴AC=AB=5.∵AE=2，∴EC=AC -AE=5-2=3.9. 【答案】B[解析] 过点D 作DH ⊥AB 交BA 的延长线于点H.∵BD 平分∠ABC ，∠BCD ＝90°， ∴DH ＝CD ＝4.∴四边形ABCD 的面积＝S △ABD ＋S △BCD ＝12AB·DH ＋12BC·CD ＝12×6×4＋12×9×4＝30.10. 【答案】B 【解析】连接DE ，过点A 作AF△BC ，垂足为F ，过E 作EG△BC ，垂足为G.△AB ＝AC ，AF△BC ，BC ＝12，△BF ＝FC ＝6，又△E 是AC 的中点，EG△BC，△EG△AF，△CG＝FG＝12CF＝3，△在Rt△CEG中，tan C＝EGCG，△EG＝CG×tan C＝3y；△DG＝BF＋FG－BD＝6＋3－x＝9－x，△HD是BE的垂直平分线，△BD＝DE＝x，△在Rt△EGD中，由勾股定理得，ED2＝DG2＋EG2，△x2＝(9－x)2＋(3y)2，化简整理得，2x－y2＝9.二、填空题11. 【答案】15°[解析]∵△ABC绕点A逆时针旋转150°得到△ADE，∴∠BAD=150°，△ABC≌△ADE，AB=AD，∴△BAD是等腰三角形，∴∠B=∠ADB=(180°-∠BAD)=15°.12. 【答案】150[解析] △DB△AE于点B，DC△AF于点C，且DB＝DC，△AD是△BAC的平分线．△△BAC＝40°，△△CAD＝12△BAC＝20°.△△DGF＝△CAD＋△ADG＝20°＋130°＝150°.13. 【答案】65°14. 【答案】12[解析] 如图，连接BE.∵D为Rt△ABC中斜边BC上的一点，过点D作BC的垂线，交AC于点E，∴∠A=∠BDE=90°.在Rt△DBE和Rt△ABE中，∴Rt△DBE≌Rt△ABE(HL).∴DE=AE.∵AE=12 cm，∴DE=12 cm.15. 【答案】22.5°[解析]根据题意可知△ABD≌△ACD'，∴∠BAC=∠CAD'=45°，AD'=AD，∴∠ADD'=∠AD'D==67.5°.∵D'，D，B三点在同一直线上，∴∠ABD=∠ADD'-∠BAC=22.5°.16. 【答案】16[解析] 如图，过点C作CD⊥AB，垂足为D，则△ADC 是含30°角的直角三角形，那么DC ＝12AC ＝4，∴S △ABC ＝12AB·DC ＝12×8×4＝16.三、解答题17. 【答案】证明：△AF△DE ，△△A ＝△D. △BF△CE ，△△FBC ＝△ECB.△△ABF ＋△FBC ＝180°，△DCE ＋△ECB ＝180°，△△ABF ＝△DCE. △AC ＝BD ，△AC －BC ＝BD －BC ， 即AB ＝DC.在△ABF 和△DCE 中，⎩⎨⎧△A ＝△D ，AB ＝DC ，△ABF ＝△DCE ，△△ABF△△DCE(ASA)．18. 【答案】(1)证明：△AB 为直径， ∴∠ACB ＝90°，∵△AEF 是等边三角形， ∴∠EAF ＝△EFA ＝60°， ∴∠ABC ＝30°，∴∠FDB ＝△EFA －△B ＝60°－30°＝30°，(2分) ∴∠ABC ＝△FDB ， ∴FB ＝FD ，∴△BDF 是等腰三角形．(3分) (2)解：设AF ＝a ，则AD ＝7a ，解图如解图，连接OC ，则△AOC 是等边三角形，由(1)得，BF ＝2－a ＝DF ，∴DE ＝DF －EF ＝2－a －a ＝2－2a ，CE ＝AC －AE ＝1－a ， 在Rt △ADC 中，DC ＝（7a ）2－1＝7a 2－1， 在Rt △DCE 中，tan 30°＝CE DC ＝1－a 7a 2－1＝33， 解得a ＝－2(舍去)或a ＝12，(5分) ∴AF ＝12，在△CAF 和△BAC 中， CA AF ＝BAAC ＝2，且△CAF ＝△BAC ＝60°， ∴△CAF ∽△BAC ，∴∠CFA ＝△ACB ＝90°， 即CF△AB.(6分)19. 【答案】(1)证明：∵BF ＝EC ，∴BF ＋FC ＝EC ＋CF ，即BC ＝EF.(3分) 在△ABC 与△DEF 中，⎩⎨⎧BC ＝EF AB ＝DE AC ＝DF， ∴△ABC ≌△DEF(SSS )．(5分) (2)解：AB ∥DE ，AC ∥DF.(7分) 理由如下：∵△ABC ≌△DEF ，∴∠ABC ＝∠DEF ，∠ACB ＝∠DFE ， ∴AB ∥DE ，AC ∥DF.(9分)20. 【答案】证明：△AE ＝BF ，△AE ＋EF ＝BF ＋EF ， 即AF ＝BE.△AC△BD ，△△CAF ＝△DBE.在△ACF 和△BDE 中，⎩⎨⎧AC ＝BD ，△CAF ＝△DBE ，AF ＝BE ，△△ACF△△BDE(SAS)． △CF ＝DE.初中数学精品教学初中数学精品教学 1121. 【答案】(1)解：△AC ＝2，OA ＝OB ＝OC ＝12AB ＝2，△AC ＝OA ＝OC ，△△ACO 为等边三角形，△△AOC ＝△ACO ＝△OAC ＝60°，△△APC ＝12△AOC ＝30°，又△DC 与△O 相切于点C ，△OC △DC ，△△DCO ＝90°，△△ACD ＝△DCO －△ACO ＝90°－60°＝30°；解图(2)证明：如解图，连接PB ，OP ，△AB 为直径，△AOC ＝60°，△△COB ＝120°，当点P 移动到CB ︵的中点时，△COP ＝△POB ＝60°， △△COP 和△BOP 都为等边三角形，△OC ＝CP ＝OB ＝PB ，△四边形OBPC 为菱形；(3)证明：△CP 与AB 都为△O 的直径，△△CAP ＝△ACB ＝90°，在Rt△ABC 与Rt△CP A 中，⎩⎨⎧AB ＝CPAC ＝AC ，△Rt△ABC △Rt△CP A (HL)．。
2021年九年级数学中考复习——几何专题：全等三角形性质与判定(三)
2021年九年级数学中考复习——几何专题：全等三角形性质与判定（三）1．如图，在△ABC中，∠ACB＝90°，AC＝BC，点E是∠ACB内部一点，连结CE，作AD⊥CE，BE⊥CE，垂足分别为点D，E．（1）求证：△BCE≌△CAD；（2）若BE＝5，DA＝12，则ED的长是．2．如图，已知△ABC中，AB＝AC＝12cm，BC＝10cm，点D为AB的中点．如果点P在线段BC上以2cm/s 的速度由点B向点C运动，同时，点Q在线段AC上由点A向点C以4cm/s的速度运动．若P、Q两点分别从B、A两点同时出发，回答下列问题：（1）经过2s后，此时PB＝cm，CQ＝cm；（2）在（1）的条件下，证明：△BPD≌△CQP；（3）当△CPQ的周长为18cm时，求经过多少秒后，△CPQ为等腰三角形？3．已知：在△ABC中，AB＝AC，点D、点E在边BC上，BD＝CE，连接AD、AE．（1）如图1，求证：AD＝AE；（2）如图2，当∠DAE＝∠C＝45°时，过点B作BF∥AC交AD的延长线于点F，在不添加任何辅助线的情况下，请直接写出图2中的四个等腰三角形，使写出的每个等腰三角形的顶角都等于45°．4．如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE＝CD，AD与BE相交于点F．（1）求证：BE＝AD；（2）求∠BFD的度数．5．若△ABC和△AED均为等腰三角形，且∠BAC＝∠EAD＝90°．（1）如图（1），点B是DE的中点，判定四边形BEAC的形状，并说明理由；（2）如图（2），若点G是EC的中点，连接GB并延长至点F，使CF＝CD．求证：①EB＝DC，②∠EBG＝∠BFC．6．问题1：如图①，在四边形ABCD中，∠B＝∠C＝90°，P是BC上一点，P A＝PD，∠APD＝90°．求证：AB+CD＝BC．问题2：如图②，在四边形ABCD中，∠B＝∠C＝45°，P是BC上一点，P A＝PD，∠APD＝90°．求的值．7．如图，在△ABC中，∠ACB＝90°，AC＝BC，点E是∠ACB内部一点，连接CE，作AD⊥CE，BE⊥CE，垂足分别为点D，E．（1）求证：△BCE≌△CAD；（2）请直接写出AD，BE，DE之间的数量关系：．8．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D在边BC上（不与点B、C重合），BE⊥AD，垂足为E，过点C作CF⊥CE，交线段AD于点F．（1）试说明△CAF≌△CBE的理由；（2）数学老师在课堂上提出一个问题，如果EF＝2AF，试说明CD＝BD的理由．班级同学随后进行了热烈讨论，小明同学提出了自己的想法，可以取EF的中点H，联结CH，就能得出结论，你能否能根据小明同学的想法，写出CD＝BD的理由．9．如图，四边形ABCD中，对角线AC、BD交于点O，AB＝AC，点E是BD上一点，且∠ABD＝∠ACD，∠EAD＝∠BAC．（1）求证：AE＝AD；（2）若∠ACB＝65°，求∠BDC的度数．10．如图，在等腰直角三角形ABC中，∠ABC＝90°，AB＝BC，D为斜边AC延长线上一点，过D点作BC的垂线交其延长线于点E，在AB的延长线上取一点F，使得BF＝CE，连接EF．（1）若AB＝2，BF＝3，求AD的长度；（2）G为AC中点，连接GF，GE，GB，求证：GE＝GF．参考答案1．证明：（1）∵BE⊥CE，AD⊥CE，∴∠E＝∠ADC＝90°，∴∠EBC+∠BCE＝90°．∵∠BCE+∠ACD＝90°，∴∠EBC＝∠DCA，在△BCE和△CAD中，，∴△BCE≌△CAD（AAS）；（2）解：∵△BCE≌△CAD，∴BE＝DC＝5，AD＝CE＝12，∴DE＝CE﹣CD＝12﹣5＝7．故答案为：7．2．（1）解：当P，Q两点分别从B，A两点同时出发运动2秒时，有BP＝2×2＝4cm，AQ＝4×2＝8cm，则CP＝BC﹣BP＝10﹣4＝6cm，∴CQ＝AC﹣AQ＝12﹣8＝4cm，故答案为：4，4；（2）证明：∵D是AB的中点，∴BD＝AB＝6cm，∴BP＝CQ，BD＝CP，又∵△ABC中，AB＝AC，∴∠B＝∠C，在△BPD和△CQP中，，∴△BPD≌△CQP（SAS）；（3）解：设当P，Q两点同时出发运动t秒时，有BP＝2t，CP＝10﹣2t，CQ＝12﹣4t，∴PQ＝18﹣（10﹣2t）﹣（12﹣4t）＝6t﹣4，要使△CPQ是等腰三角形，则可分为三种情况讨论：①当CP＝CQ时，则有10﹣2t＝12﹣4t，解得：t＝1；②当PQ＝PC时，则有6t﹣4＝10﹣2t解得：t＝；③当QP＝QC时，则有6t﹣4＝12﹣4t解得：t＝；综上所述，当t＝1s或s或s时，△CPQ是等腰三角形．3．（1）证明：∵AB＝AC，∵∠B＝∠C，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴AD＝AE；（2）∵AD＝AE，∴∠ADE＝∠AED，∵BF∥AC，∴∠FBD＝∠C＝45°，∵∠ABC＝∠C＝∠DAE＝45°，∠BDF＝∠ADE，∴∠F＝∠BDF，∠BEA＝∠BAE，∠CDA＝∠CAD，∴满足条件的等腰三角形有：△ABE，△ACD，△DAE，△DBF．4．（1）证明：∵△ABC为等边三角形，∴∠BAE＝∠C＝60°，AB＝CA，在△ABE和△CAD中，，∴△ABE≌△CAD（SAS），∴BE＝AD；（2）解：∵∠BFD＝∠ABE+∠BAD，又∵△ABE≌△CAD，∴∠ABE＝∠CAD．∴∠BFD＝∠CAD+∠BAD＝∠BAC＝60°．5．解：（1）四边形BEAC是平行四边形，理由如下：∵△AED为等腰三角形，∠EAD＝90°，B是DE的中点，∴∠E＝∠BAE＝45°，∠ABE＝90°，∵△ABC是等腰三角形，∠BAC＝90°，∴∠ABC＝∠BAE＝45°，∠ABE＝∠BAC＝90°，∴BC∥AE，AC∥BE，∴四边形BEAC是平行四边形；（2）①∵△ABC和△AED均为等腰三角形，∠BAC＝∠EAD＝90°，∴AE＝AD，AB＝AC，∠BAE＝∠CAD，∴△AEB≌△ADC（SAS），∴BE＝CD；②延长FG至点H，使GH＝FG，∵G是EC的中点，∴EG＝DC，又∵∠EGH＝∠FGC，∴△EGH≌△CGF（SAS），∴∠BFC＝∠H，CF＝EH，∵CF＝CD，CD＝BE，∴EH＝BE，∴∠H＝∠EBG，∴∠EBG＝∠BFC．6．证明：（1）∵∠B＝∠APD＝90°，∴∠BAP+∠APB＝90°，∠APB+∠DPC＝90°，∴∠BAP＝∠DPC，又P A＝PD，∠B＝∠C＝90°，∴△BAP≌△CPD（AAS），∴BP＝CD，AB＝PC，∴BC＝BP+PC＝AB+CD；（2）如图2，过点A作AE⊥BC于E，过点D作DF⊥BC于F，由（1）可知，EF＝AE+DF，∵∠B＝∠C＝45°，AE⊥BC，DF⊥BC，∴∠B＝∠BAE＝45°，∠C＝∠CDF＝45°，∴BE＝AE，CF＝DF，AB＝AE，CD＝DF，∴BC＝BE+EF+CF＝2（AE+DF），∴＝＝．7．证明：（1）∵BE⊥CE，AD⊥CE，∴∠E＝∠ADC＝90°，∴∠EBC+∠BCE＝90°．∵∠BCE+∠ACD＝90°，∴∠EBC＝∠DCA，在△BCE和△CAD中，，∴△BCE≌△CAD（AAS）；（2）∵△BCE≌△CAD，∴BE＝DC，AD＝CE，∴AD＝CE＝CD+DE＝BE+DE，故答案为：AD＝BE+DE．8．解：（1）∵BE⊥AD，∴∠ACB＝∠BED＝90°，又∵∠ADC＝∠BDE，∴∠CAF＝∠CBE，∵CE⊥CF，∴∠ECF＝∠ACB＝90°，∴∠ACF＝∠BCE，又∵AC＝BC，∴△CAF≌△CBE（ASA）；（2）如图，取EF的中点H，联结CH，∵△CAF≌△CBE，∴CF＝CE，AF＝BE，∴△CEF是等腰直角三角形，∵点H是EF中点，∴CH＝FH＝EH＝EF，CH⊥EF，∵EF＝2AF，∴CH＝AF＝FH＝EH，∴CH＝BE，又∵∠CDH＝∠BDE，∠CHD＝∠BED＝90°，∴△CHD≌△BED（AAS），∴CD＝BD．9．证明：（1）∵∠BAC＝∠EAD∴∠BAC﹣∠EAC＝∠EAD﹣∠EAC即：∠BAE＝∠CAD在△ABE和△ACD中，∴△ABE≌△ACD（ASA），∴AE＝AD；（2）解：∵∠ACB＝65°，AB＝AC，∴∠ABC＝∠ACB＝65°，∴∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣65°﹣65°＝50°，∵∠ABD＝∠ACD，∠AOB＝∠COD，∴∠BDC＝∠BAC＝50°．10．解：（1）∵DE⊥BE，AB⊥BE，∴DE∥AB，∴△ABC∽△DEC，∵∠ABC＝90°，AB＝BC，∴△CDE为等腰直角三角形，∵CE＝BF＝3，∴CD＝3，∵AB＝2，∴AC＝2，∴AD＝AC+CD＝5；（2）证明：∵G是等腰直角△ABC斜边AC中点。
2021年中考数学第三轮压轴题强化训练：三角形 专题复习(含答案)
2021年中考数学第三轮压轴题强化训练：三角形专题复习1、如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D．（1）求证：BE=CF；（2）当四边形ACDE为菱形时，求BD的长．2、如图，在Rt△ABC中，∠C=90°，BD是△ABC的一条角平分线．点O、E、F 分别在BD、BC、AC上，且四边形OECF是正方形．（1）求证：点O在∠BAC的平分线上；（2）若AC=5，BC=12，求OE的长．3、如图，△ABC是等腰直角三角形，∠ACB=90°，分别以AB，AC为直角边向外作等腰直角△ABD和等腰直角△ACE，G为BD的中点，连接CG，BE，CD，BE与CD交于点F．（1）判断四边形ACGD的形状，并说明理由．（2）求证：BE=CD，BE⊥CD．4、如图1，在四边形ABCD中，点E、F分别是AB、CD的中点，过点E作AB的垂线，过点F作CD的垂线，两垂线交于点G，连接AG、BG、CG、DG，且∠AGD=∠BGC．（1）求证：AD=BC；（2）求证：△AGD∽△EGF；（3）如图2，若AD、BC所在直线互相垂直，求的值．5、如图，是一副学生用的三角板，在△ABC 中，∠C=90°，∠A=60°，∠B=30°；在△A1B1C1中，∠C1=90°，∠A1=45°，∠B1=45°，且A1B1=CB．若将边A1C1与边CA重合，其中点A1与点C重合．将三角板A1B1C1绕点C（A1）按逆时针方向旋转，旋转过的角为α，旋转过程中边A1C1与边AB的交点为M，设AC=a．（1）计算A1C1的长；（2）当α=30°时，证明：B1C1∥AB；（3）若a=，当α=45°时，计算两个三角板重叠部分图形的面积；（4）当α=60°时，用含a的代数式表示两个三角板重叠部分图形的面积．（参考数据：sin15°=，cos15°=，tan15°=2﹣，sin75°=，cos75°=，tan75°=2+）6、如图，两个全等的△ABC和△DFE重叠在一起，固定△ABC，将△DEF进行如下变换：（1）如图1，△DEF沿直线CB向右平移（即点F在线段CB上移动），连接AF、AD、BD．请直接写出S△ABC 与S四边形AFBD的关系；（2）如图2，当点F平移到线段BC的中点时，若四边形AFBD为正方形，那么△ABC应满足什么条件？请给出证明；（3）在（2）的条件下，将△DEF沿DF折叠，点E落在FA的延长线上的点G处，连接CG，请你在图3的位置画出图形，并求出sin∠CGF的值．7、如图1，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM、射线AE于点F、D．（1）直接写出∠NDE的度数；（2）如图2、图3，当∠EAC为锐角或钝角时，其他条件不变，（1）中的结论是否发生变化？如果不变，选取其中一种情况加以证明；如果变化，请说明理由；（3）如图4，若∠EAC=15°，∠ACM=60°，直线CM与AB交于G，BD=，其他条件不变，求线段AM的长．8、我们把两条中线互相垂直的三角形称为“称为中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均称为“中垂三角形”，设BC=a，AC=b，AB=c．特例探索（1）如图1，当∠ABE=45°，c=2时，a= ，b= ．如图2，当∠ABE=30°，c=4时，a= ，b= ．归纳证明（2）请你观察（1）中的计算结果，猜想a2，b2，c2三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．拓展应用（3）如图4，在▱ABCD中，点E、F、G分别是AD，BC，CD的中点，BE⊥EG，AD=2，AB=3，求AF的长．9、如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D、E分别是边BC、AC的中点，连接DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现①当α=0°时，= ；②当α=180°时，= ．（2）拓展探究试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情形给出证明．（3）问题解决当△EDC旋转至A，D，E三点共线时，直接写出线段BD的长．10、已知点P是线段AB上与点A不重合的一点，且AP＜PB．AP绕点A逆时针旋转角α（0°＜α≤90°）得到AP1，BP绕点B顺时针也旋转角α得到BP2，连接PP1、PP2．（1）如图1，当α=90°时，求∠P1PP2的度数；（2）如图2，当点P2在AP1的延长线上时，求证：△P2P1P∽△P2PA；（3）如图3，过BP的中点E作l1⊥BP，过BP2的中点F作l2⊥BP2，l1与l2交于点Q，连接PQ，求证：P1P⊥PQ．11、两个三角板ABC，DEF，按如图所示的位置摆放，点B与点D重合，边AB与边DE在同一条直线上（假设图形中所有的点，线都在同一平面内）．其中，∠C=∠DEF=90°，∠ABC=∠F=30°，AC=DE=6cm．现固定三角板DEF，将三角板ABC 沿射线DE方向平移，当点C落在边EF上时停止运动．设三角板平移的距离为x （cm），两个三角板重叠部分的面积为y（cm2）．（1）当点C落在边EF上时，x= cm；（2）求y关于x的函数解析式，并写出自变量x的取值范围；（3）设边BC的中点为点M，边DF的中点为点N．直接写出在三角板平移过程中，点M与点N之间距离的最小值．12、已知∠MAN=135°，正方形ABCD绕点A旋转．（1）当正方形ABCD旋转到∠MAN的外部（顶点A除外）时，AM，AN分别与正方形ABCD的边CB，CD的延长线交于点M，N，连接MN．①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是；②如图2，若BM≠DN，请判断①中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；（2）如图3，当正方形ABCD旋转到∠MAN的内部（顶点A除外）时，AM，AN分别与直线BD交于点M，N，探究：以线段BM，MN，DN的长度为三边长的三角形是何种三角形，并说明理由．13、已知：△ABC是等腰三角形，动点P在斜边AB所在的直线上，以PC为直角边作等腰三角形PCQ，其中∠PCQ=90°，探究并解决下列问题：（1）如图①，若点P在线段AB上，且AC=1+，PA=，则：①线段PB= ，PC= ；②猜想：PA2，PB2，PQ2三者之间的数量关系为；（2）如图②，若点P在AB的延长线上，在（1）中所猜想的结论仍然成立，请你利用图②给出证明过程；（3）若动点P满足=，求的值．（提示：请利用备用图进行探求）参考答案2021年中考数学第三轮压轴题强化训练：三角形专题复习1、如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D．（1）求证：BE=CF；（2）当四边形ACDE为菱形时，求BD的长．（1）证明：∵△AEF是由△ABC绕点A按顺时针方向旋转得到的，∴AE=AB，AF=AC，∠EAF=∠BAC，∴∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，∵AB=AC，∴AE=AF，∴△AEB可由△AFC绕点A按顺时针方向旋转得到，∴BE=CF；（2）解：∵四边形ACDE为菱形，AB=AC=1，∴DE=AE=AC=AB=1，AC∥DE，∴∠AEB=∠ABE，∠ABE=∠BAC=45°，∴∠AEB=∠ABE=45°，∴△ABE为等腰直角三角形，∴BE=AC=，∴BD=BE﹣DE=﹣1．2、如图，在Rt△ABC中，∠C=90°，BD是△ABC的一条角平分线．点O、E、F 分别在BD、BC、AC上，且四边形OECF是正方形．（1）求证：点O在∠BAC的平分线上；（2）若AC=5，BC=12，求OE的长．解答:（1）证明：过点O作OM⊥AB，∵BD是∠ABC的一条角平分线，∴OE=OM，∵四边形OECF是正方形，∴OE=OF，∴OF=OM，∴AO是∠BAC的角平分线，即点O在∠BAC的平分线上；（2）解：∵在Rt△ABC中，AC=5，BC=12，∴AB===13，设OE=CF=x，BE=BM=y，AM=AF=z，∴，解得：，∴OE=2．3、如图，△ABC是等腰直角三角形，∠ACB=90°，分别以AB，AC为直角边向外作等腰直角△ABD和等腰直角△ACE，G为BD的中点，连接CG，BE，CD，BE与CD交于点F．（1）判断四边形ACGD的形状，并说明理由．（2）求证：BE=CD，BE⊥CD．解答：（1）解：∵△ABC是等腰直角三角形，∠ACB=90°，∴AB=BC，∵△ABD和△ACE均为等腰直角三角形，∴BD==BC=2BC，∵G为BD的中点，∴BG=BD=BC，∴△CBG为等腰直角三角形，∴∠CGB=45°，∵∠ADB=45°，AD∥CG，∵∠ABD=45°，∠ABC=45°∴∠CBD=90°，∵∠ACB=90°，∴∠CBD+∠ACB=180°，∴AC∥BD，∴四边形ACGD为平行四边形；（2）证明：∵∠EAB=∠EAC+∠CAB=90°+45°=135°，∠CAD=∠DAB+∠BAC=90°+45°=135°，∴∠EAB=∠CAD，在△DAC与△BAE中，，∴△DAC≌△BAE，∴BE=CD；∵∠EAC=∠BCA=90°，EA=AC=BC，∴四边形ABCE为平行四边形，∴CE=AB=AD，在△BCE与△CAD中，，∴△BCE≌△CAD，∴∠CBE=∠ACD，∵∠ACD+∠BCD=90°，∴∠CBE+∠BCD=90°，∴∠CFB=90°，即BE⊥CD．4、如图1，在四边形ABCD中，点E、F分别是AB、CD的中点，过点E作AB的垂线，过点F作CD的垂线，两垂线交于点G，连接AG、BG、CG、DG，且∠AGD=∠BGC．（1）求证：AD=BC；（2）求证：△AGD∽△EGF；（3）如图2，若AD、BC所在直线互相垂直，求的值．解答（1）证明：∵GE是AB的垂直平分线，∴GA=GB，同理：GD=GC，在△AGD和△BGC中，，∴△AGD≌△BGC（SAS），∴AD=BC；（2）证明：∵∠AGD=∠BGC，∴∠AGB=∠DGC，在△AGB和△DGC中，，∴△AGB∽△DGC，∴，又∵∠AGE=∠DGF，∴∠AGD=∠EGF，∴△AGD∽△EGF；（3）解：延长AD交GB于点M，交BC的延长线于点H，如图所示：则AH⊥BH，∵△AGD≌△BGC，∴∠GAD=∠GBC，在△GAM和△HBM中，∠GAD=∠GBC，∠GMA=∠HMB，∴∠AGB=∠AHB=90°，∴∠AGE=∠AGB=45°，∴，又∵△AGD∽△EGF，∴==．5、如图，是一副学生用的三角板，在△ABC 中，∠C=90°，∠A=60°，∠B=30°；在△A1B1C1中，∠C1=90°，∠A1=45°，∠B1=45°，且A1B1=CB．若将边A1C1与边CA重合，其中点A1与点C重合．将三角板A1B1C1绕点C（A1）按逆时针方向旋转，旋转过的角为α，旋转过程中边A1C1与边AB的交点为M，设AC=a．（1）计算A1C1的长；（2）当α=30°时，证明：B1C1∥AB；（3）若a=，当α=45°时，计算两个三角板重叠部分图形的面积；（4）当α=60°时，用含a的代数式表示两个三角板重叠部分图形的面积．（参考数据：sin15°=，cos15°=，tan15°=2﹣，sin75°=，cos75°=，tan75°=2+）解：（1）在Rt△ABC中，∠B=30°，AC=a，由特殊锐角三角函数可知：，∴BC=．∴B1C=在Rt△A1B1C1，∠B1=∠45°，∴．∴A1C1==．（2）∵∠ACM=30°，∠A=60°，∴∠BMC=90°．∴∠C1=∠BMC．∴B1C1∥AB．（3）如下图：由（1）可知：A1C1===3+∴△A1B1C1的面积==∵∠A1B1C1=45°，∠ABC=30°∴∠MBC1=15°在Rt△BC1M中，C1M=BCtan15°=（3+）（2﹣）=3﹣，∴Rt△BC1M的面积===3．∴两个三角板重叠部分图形的面积=△A1B1C1的面积﹣△BC1M的面积=3+3．（4）由（1）可知：BC=，A1C1=，∴C1F=A1C1•tan30°=a，∴==×a×a=a2，∵∠MCA=60°，∠A=60°，∴∠AMC=60°∴MC=AC=MA=a．∴C1M=C1A1﹣MC=．∵∠MCA=60°，∴∠C1A1B=30°，∴∠C1MD=∠B+∠C1A1B=60°在Rt△DC1M中，由特殊锐角三角函数可知：C1D=C1M•tan60°=a，∴=C1M•C1D=a2，两个三角板重叠部分图形的面积=﹣=C1M=a2﹣a2=a2．6、如图，两个全等的△ABC和△DFE重叠在一起，固定△ABC，将△DEF进行如下变换：（1）如图1，△DEF沿直线CB向右平移（即点F在线段CB上移动），连接AF、AD、BD．请直接写出S△ABC 与S四边形AFBD的关系；（2）如图2，当点F平移到线段BC的中点时，若四边形AFBD为正方形，那么△ABC应满足什么条件？请给出证明；（3）在（2）的条件下，将△DEF沿DF折叠，点E落在FA的延长线上的点G处，连接CG，请你在图3的位置画出图形，并求出sin∠CGF的值．解：（1）S△ABC =S四边形AFBD，理由：由题意可得：AD∥EC，则S△ADF =S△ABD，故S△ACF =S△ADF=S△ABD，则S△ABC =S四边形AFBD；（2）△ABC为等腰直角三角形，即：AB=AC，∠BAC=90°，理由如下：∵F为BC的中点，∴CF=BF，∵CF=AD，∴AD=BF，又∵AD∥BF，∴四边形AFBD为平行四边形，∵AB=AC，F为BC的中点，∴AF⊥BC，∴平行四边形AFBD为矩形，∵∠BAC=90°，F为BC的中点，∴AF=BC=BF，∴四边形AFBD为正方形；（3）如图3所示：由（2）知，△ABC为等腰直角三角形，AF⊥BC，设CF=k，则GF=EF=CB=2k，由勾股定理得：CG=k，sin∠CGF===．7、如图1，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM、射线AE于点F、D．（1）直接写出∠NDE的度数；（2）如图2、图3，当∠EAC为锐角或钝角时，其他条件不变，（1）中的结论是否发生变化？如果不变，选取其中一种情况加以证明；如果变化，请说明理由；（3）如图4，若∠EAC=15°，∠ACM=60°，直线CM与AB交于G，BD=，其他条件不变，求线段AM的长．解：（1）∵∠ACB=90°，∠MCN=90°，∴∠ACM=∠BCN，在△MAC和△NBC中，，∴△MAC≌△NBC，∴∠NBC=∠MAC=90°，又∵∠ACB=90°，∠EAC=90°，∴∠NDE=90°；（2）不变，在△MAC≌△NBC中，，∴△MAC≌△NBC，∴∠N=∠AMC，又∵∠MFD=∠NFC，∠MDF=∠FCN=90°，即∠NDE=90°；（3）作GK⊥BC于K，∵∠EAC=15°，∴∠BAD=30°，∵∠ACM=60°，∴∠GCB=30°，∴∠AGC=∠ABC+∠GCB=75°，∠AMG=75°，∴AM=AG，∵△MAC≌△NBC，∴∠MAC=∠NBC，∴∠BDA=∠BCA=90°，∵BD=，∴AB=+，AC=BC=+1，设BK=a，则GK=a，CK=a，∴a+a=+1，∴a=1，∴KB=KG=1，BG=，AG=，∴AM=．8、我们把两条中线互相垂直的三角形称为“称为中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均称为“中垂三角形”，设BC=a，AC=b，AB=c．特例探索（1）如图1，当∠ABE=45°，c=2时，a= 2，b= 2．如图2，当∠ABE=30°，c=4时，a= 2，b= 2．归纳证明（2）请你观察（1）中的计算结果，猜想a2，b2，c2三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．拓展应用（3）如图4，在▱ABCD中，点E、F、G分别是AD，BC，CD的中点，BE⊥EG，AD=2，AB=3，求AF的长．解：（1）∵AH⊥BE，∠ABE=45°，∴AP=BP=AB=2，∵AF，BE是△ABC的中线，∴EF∥AB，EF=AB=，∴∠PFE=∠PEF=45°，∴PE=PF=1，在Rt△FPB和Rt△PEA中，AE=BF==，∴AC=BC=2，∴a=b=2，如图2，连接EF，同理可得：EF=×4=2，∵EF∥AB，∴△PEF～△ABP，∴，在Rt△ABP中，AB=4，∠ABP=30°，∴AP=2，PB=2，∴PF=1，PE=，在Rt△APE和Rt△BPF中，AE=，BF=，∴a=2，b=2，故答案为：2，2，2，2；（2）猜想：a2+b2=5c2，如图3，连接EF，设∠ABP=α，∴AP=csinα，PB=ccosα，由（1）同理可得，PF=PA=，PE==，AE2=AP2+PE2=c2sin2α+，BF2=PB2+PF2=+c2cos2α，∴=c2sin2α+，=+c2cos2α，∴+=+c2cos2α+c2sin2α+，∴a2+b2=5c2；（3）如图4，连接AC，EF交于H，AC与BE交于点Q，设BE与AF的交点为P，∵点E、G分别是AD，CD的中点，∴EF∥AC，∵BE⊥EG，∴BE⊥AC，∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC=2，∴∠EAH=∠FCH，∵E，F分别是AD，BC的中点，∴AE=AD，BF=BC，∴AE=BF=CF=AD=，∵AE∥BF，∴四边形ABFE是平行四边形，∴EF=AB=3，AP=PF，在△AEH和△CFH中，，∴△AEH≌△CFH，∴EH=FH，∴EH，AH分别是△AFE的中线，由（2）的结论得：AF2+EF2=5AE2，∴AF2=5﹣EF2=16，∴AF=4．9、如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D、E分别是边BC、AC的中点，连接DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现①当α=0°时，= ；②当α=180°时，= ．（2）拓展探究试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情形给出证明．（3）问题解决当△EDC旋转至A，D，E三点共线时，直接写出线段BD的长．解：（1）①当α=0°时，∵Rt△ABC中，∠B=90°，∴AC=，∵点D、E分别是边BC、AC的中点，∴，∴．②如图1，，当α=180°时，可得AB∥DE，∵，∴=．故答案为：．（2）如图2，，当0°≤α＜360°时，的大小没有变化，∵∠ECD=∠ACB，∴∠ECA=∠DCB，又∵，∴△ECA∽△DCB，∴．（3）①如图3，，∵AC=4，CD=4，CD⊥AD，∴AD==，∵AD=BC，AB=DC，∠B=90°，∴四边形ABCD是矩形，∴．②如图4，连接BD，过点D作AC的垂线交AC于点Q，过点B作AC的垂线交AC 于点P，，∵AC=4，CD=4，CD⊥AD，∴AD==，在△ABC和△CDA中，∴BP=DQ，BP∥DQ，PQ⊥DQ，∴四边形BDQP为矩形，∴BD=PQ=AC﹣AP﹣CQ==．综上所述，BD的长为4或10、已知点P是线段AB上与点A不重合的一点，且AP＜PB．AP绕点A逆时针旋转角α（0°＜α≤90°）得到AP1，BP绕点B顺时针也旋转角α得到BP2，连接PP1、PP2．（1）如图1，当α=90°时，求∠P1PP2的度数；（2）如图2，当点P2在AP1的延长线上时，求证：△P2P1P∽△P2PA；（3）如图3，过BP的中点E作l1⊥BP，过BP2的中点F作l2⊥BP2，l1与l2交于点Q，连接PQ，求证：P1P⊥PQ．解答：（1）解：由旋转的性质得：AP=AP1，BP=BP2．∵α=90°，∴△PAP1和△PBP2均为等腰直角三角形，∴∠APP1=∠BPP2=45°，∴∠P1PP2=180°﹣∠APP1﹣∠BPP2=90°；（2）证明：由旋转的性质可知△PAP1和△PBP2均为顶角为α的等腰三角形，∴∠APP1=∠BPP2=90°﹣，∴∠P1PP2=180°﹣（∠APP1+∠BPP2）=180°﹣2（90°）=α，在△PP2P1和△P2PA中，∠P1PP2=∠PAP2=α，又∵∠PP2P1=∠AP2P，∴△P2P1P∽△P2PA．（3）证明：如图，连接QB．∵l1，l2分别为PB，P2B的中垂线，∴EB=BP，FB=BP2．又BP=BP2，∴EB=FB．在Rt△QBE和Rt△QBF中，，∴Rt△QBE≌Rt△QBF，∴∠QBE=∠QBF=∠PBP2=，由中垂线性质得：QP=QB，∴∠QPB=∠QBE=，由（2）知∠APP1=90°﹣，∴∠P1PQ=180°﹣∠APP1﹣∠QPB=180°﹣（90°﹣）=90°，即 P1P⊥PQ．11、两个三角板ABC，DEF，按如图所示的位置摆放，点B与点D重合，边AB与边DE在同一条直线上（假设图形中所有的点，线都在同一平面内）．其中，∠C=∠DEF=90°，∠ABC=∠F=30°，AC=DE=6cm．现固定三角板DEF，将三角板ABC 沿射线DE方向平移，当点C落在边EF上时停止运动．设三角板平移的距离为x （cm），两个三角板重叠部分的面积为y（cm2）．（1）当点C落在边EF上时，x= 15 cm；（2）求y关于x的函数解析式，并写出自变量x的取值范围；（3）设边BC的中点为点M，边DF的中点为点N．直接写出在三角板平移过程中，点M与点N之间距离的最小值．解：（1）如图1所示：作CG⊥AB于G点．，在Rt△ABC中，由AC=6，∠ABC=30，得BC==6．在Rt△BCG中，BG=BC•cos30°=9．四边形CGEH是矩形，CH=GE=BG+BE=9+6=15cm，故答案为：15；（2）①当0≤x＜6时，如图2所示．，∠GDB=60°，∠GBD=30°，DB=x，得DG=x，BG=x，重叠部分的面积为y=DG•BG=×x×x=x2②当6≤x＜12时，如图3所示．，BD=x，DG=x，BG=x，BE=x﹣6，EH=（x﹣6）．重叠部分的面积为y=S△BDG ﹣S△BEH=DG•BG﹣BE•EH，即y=×x×x﹣（x﹣6）（x﹣6）化简，得y=﹣x2+2x﹣6；③当12＜x≤15时，如图4所示．，AC=6，BC=6，BD=x，BE=（x﹣6），EG=（x﹣6），重叠部分的面积为y=S△ABC ﹣S△BEG=AC•BC﹣BE•EG，即y=×6×6﹣（x﹣6）（x﹣6），化简，得y=18﹣（x2﹣12x+36）=﹣x2+2x+12；综上所述：y=；（3）如图5所示作NG⊥DE于G点．（4），点M在NG上时MN最短，NG是△DEF的中位线，NG=EF=．MB=CB=3，∠B=30°，MG=MB=，MN最小=3﹣=．12、已知∠MAN=135°，正方形ABCD绕点A旋转．（1）当正方形ABCD旋转到∠MAN的外部（顶点A除外）时，AM，AN分别与正方形ABCD的边CB，CD的延长线交于点M，N，连接MN．①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是MN=BM+DN ；②如图2，若BM≠DN，请判断①中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；（2）如图3，当正方形ABCD旋转到∠MAN的内部（顶点A除外）时，AM，AN分别与直线BD交于点M，N，探究：以线段BM，MN，DN的长度为三边长的三角形是何种三角形，并说明理由．解：（1）①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是MN=BM+DN．理由如下：在△ADN与△ABM中，，∴△ADN≌△ABM（SAS），∴AN=AM，∠NAD=∠MAB，∵∠MAN=135°，∠BAD=90°，∴∠NAD=∠MAB=（360°﹣135°﹣90°）=67.5°，作AE⊥MN于E，则MN=2NE，∠NAE=∠MAN=67.5°．在△ADN与△AEN中，，∴△ADN≌△AEN（AAS），∴DN=EN，∵BM=DN，MN=2EN，∴MN=BM+DN．故答案为MN=BM+DN；②如图2，若BM≠DN，①中的数量关系仍成立．理由如下：延长NC到点P，使DP=BM，连结AP．∵四边形ABCD是正方形，∴AB=AD，∠ABM=∠ADC=90°．在△ABM与△ADP中，，∴△ABM≌△ADP（SAS），∴AM=AP，∠1=∠2=∠3，∵∠1+∠4=90°，∴∠3+∠4=90°，∵∠MAN=135°，∴∠PAN=360°﹣∠MAN﹣（∠3+∠4）=360°﹣135°﹣90°=135°．在△ANM与△ANP中，，∴△ANM≌△ANP（SAS），∴MN=PN，∵PN=DP+DN=BM+DN，∴MN=BM+DN；（2）如图3，以线段BM，MN，DN的长度为三边长的三角形是直角三角形．理由如下：∵四边形ABCD是正方形，∴∠BDA=∠DBA=45°，∴∠MDA=∠NBA=135°．∵∠1+∠2=45°，∠2+∠3=45°，∴∠1=∠3．在△ANB与△MAD中，，∴△ANB∽△MAD，∴=，∴AB2=BN•MD，∵AB=DB，∴BN•MD=（DB）2=BD2，∴BD2=2BN•MD，∴MD2+2MD•BD+BD2+BD2+2BD•BN+BN2=MD2+BD2+BN2+2MD•BD+2BD•BN+2BN•MD，∴（MD+BD）2+（BD+BN）2=（DM+BD+BN）2，即MB2+DN2=MN2，∴以线段BM，MN，DN的长度为三边长的三角形是直角三角形．13、已知：△ABC是等腰三角形，动点P在斜边AB所在的直线上，以PC为直角边作等腰三角形PCQ，其中∠PCQ=90°，探究并解决下列问题：（1）如图①，若点P在线段AB上，且AC=1+，PA=，则：①线段PB= ，PC= 2 ；②猜想：PA2，PB2，PQ2三者之间的数量关系为PA2+PB2=PQ2；（2）如图②，若点P在AB的延长线上，在（1）中所猜想的结论仍然成立，请你利用图②给出证明过程；（3）若动点P满足=，求的值．（提示：请利用备用图进行探求）解：（1）如图①：①∵△ABC是等腰直直角三角形，AC=1+∴AB===+，∵PA=，∴PB=，作CD⊥AB于D，则AD=CD=，∴PD=AD﹣PA=，在RT△PCD中，PC==2，故答案为，2；②如图1．∵△ACB为等腰直角三角形，CD⊥AB，∴CD=AD=DB．∵AP2=（AD﹣PD）2=（DC﹣PD）2=DC2﹣2DC•PD+PD2，PB2=（DB+PD）2=（DC+DP）2=CD2+2DC •PD+PD2∴AP2+BP2=2CD2+2PD2，∵在Rt△PCD中，由勾股定理可知：PC2=DC2+PD2，∴AP2+BP2=2PC2．∵△CPQ为等腰直角三角形，∴2PC2=PQ2．∴AP2+BP2=PQ2（2）如图②：过点C作CD⊥AB，垂足为D．∵△ACB为等腰直角三角形，CD⊥AB，∴CD=AD=DB．∵AP2=（AD+PD）2=（DC+PD）2=CD2+2DC•PD+PD2，PB2=（DP﹣BD）2=（PD﹣DC）2=DC2﹣2DC•PD+PD2，∴AP2+BP2=2CD2+2PD2，∵在Rt△PCD中，由勾股定理可知：PC2=DC2+PD2，∴AP2+BP2=2PC2．∵△CPQ为等腰直角三角形，∴2PC2=PQ2．∴AP2+BP2=PQ2．（3）如图③：过点C作CD⊥AB，垂足为D．①当点P位于点P处时．1∵，∴．∴．D中，由勾股定理得：==DC，在Rt△CP1在Rt△ACD中，由勾股定理得：AC===DC，∴=．处时．②当点P位于点P2∵=，∴．D中，由勾股定理得：==，在Rt△CP2在Rt△ACD中，由勾股定理得：AC===DC，∴=．综上所述，的比值为或已知∠MAN=135°，正方形ABCD绕点A旋转．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2021中考数学三轮专题突破：全等三角形一、选择题1. 如图所示，P是∠BAC内一点，PE⊥AB于点E，PF⊥AC于点F，PE＝PF，则直接得到△PEA≌△PF A的理由是()A．HL B．ASA C．AAS D．SAS2. 如图，P为OC上一点，PM⊥OA，PN⊥OB，垂足分别为M，N，PM＝PN，∠BOC＝30°，则∠AOB的度数为()A．30°B．45°C．60°D．50°3. 如图，BE⊥AC，CF⊥AB，垂足分别是E，F.若BE＝CF，则图中全等三角形有()A．1对B．2对C．3对D．4对4. 如图，在Rt△ABC中，∠C＝90°，∠BAC的平分线AD交BC于点D，BC＝7，BD＝4，则点D到AB的距离是()A．3 B．4C．5 D．75. 如图，在正方形ABCD中，连接BD，点O是BD的中点．若M、N是边AD 上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有()A. 2对B. 3对C. 4对D. 5对6. 如图，已知点A，B，C，D在同一条直线上，△AEC≌△DFB.如果AD=37 cm，BC=15 cm，那么AB的长为()A.10 cmB.11 cmC.12 cmD.13 cm7. 如图，AB⊥CD，且AB＝CD.E，F是AD上两点，CE⊥AD，BF⊥AD.若CE ＝a，BF＝b，EF＝c，则AD的长为()A．a＋c B．b＋cC．a－b＋c D．a＋b－c8. 如图，点G在AB的延长线上，∠GBC，∠BAC的平分线相交于点F，BE⊥CF 于点H.若∠AFB＝40°，则∠BCF的度数为()A．40°B．50°C．55°D．60°二、填空题9. 如图，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B＝________.10. 如图，AC＝BD，AC与BD相交于点O，要使△ABC≌△BAD，则应添加的一个条件为__________(只需填一个)．11. 如图，在△ABC中，AD⊥BC于点D，要使△ABD≌△ACD，若根据“HL”判定，还需要添加条件：____________．12. 如图，在△ABC中，D，E分别是边AB，AC上的点，过点C作平行于AB 的直线交DE的延长线于点F.若DE＝FE，AB＝5，CF＝3，则BD的长是________．13. 如图，在△ABC中，∠C＝90°，AC＝BC，AD是∠BAC的平分线，DE⊥AB，垂足为E.若△DBE的周长为20，则AB＝________．14. 如图，在Rt△ABC中，∠ACB＝90°，BC＝2 cm，CD⊥AB，在AC上取一点E，使EC＝BC，过点E作EF⊥AC交CD的延长线于点F.若EF＝5 cm，则AE ＝________cm.15. 如图，在Rt△ABC中，∠C=90°，E为AB的中点，D为AC上一点，BF∥AC，交DE的延长线于点F，AC=6，BC=5，则四边形FBCD周长的最小值是.16. 如图，△ABC的两条外角平分线BP，CP相交于点P，PE⊥AC交AC的延长线于点E.若△ABC的周长为11，PE=2，S△BPC =2，则S△ABC=.三、解答题17. 如图所示，在△ADF和△BCE中，∠A＝∠B，点D，E，F，C在同一条直线上，有如下三个关系式：①AD＝BC；②DE＝CF；③BE∥AF.(1)请你用其中两个关系式作为条件，另一个作为结论，写出所有你认为正确的命题(用序号写出命题的书写形式，如：如果⊗⊗，那么⊗)；(2)选择(1)中你写的一个命题，说明它的正确性．18. 如图，△ABC中，AB＝AC，E在BA的延长线上，AD平分∠CAE.(1)求证：AD∥BC；(2)过点C作CG⊥AD于点F，交AE于点G.若AF＝4，求BC的长．19. (2019•苏州)如图，ABC △中，点E在BC 边上，AE AB =，将线段AC 绕点A旋转到AF 的位置，使得CAF BAE ∠=∠，连接EF ，EF 与AC 交于点G ． (1)求证：EF BC =；(2)若65ABC ∠=︒，28ACB ∠=︒，求FGC ∠的度数．20. 如图所示，已知在△ABC中，AB=AC=10 cm ，BC=8 cm ，D 为AB 的中点，点P 在线段BC 上以3 cm/s 的速度由点B 向点C 运动，同时，点Q 在线段CA 上由点C 向点A 以a cm/s 的速度运动，设运动的时间为t s(t>0). (1)求CP 的长(用含t 的式子表示);(2)若以C ，P ，Q 为顶点的三角形和以B ，D ，P 为顶点的三角形全等，且∠B 和∠C 是对应角，求a 的值.21. 如图，已知AP ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于点E ，过点E的直线分别交AP ，BC 于点D ，C .求证：AD ＋BC ＝AB .22. 如图①，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点． (1)观察猜想图①中，线段PM 与PN 的数量关系是________，位置关系是________； (2)探究证明把△ADE 绕点A 逆时针方向旋转到图②的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由； (3)拓展延伸把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．2021中考数学 三轮专题突破：全等三角形-答案一、选择题1. 【答案】A2. 【答案】C[解析] ∵点P 在OC 上，PM ⊥OA ，PN ⊥OB ，PM ＝PN ，∴OC 是∠AOB 的平分线．∵∠BOC ＝30°，∴∠AOB ＝60°.3. 【答案】C[解析] ①∵BE ⊥AC ，CF ⊥AB ，∴∠CFB ＝∠BEC ＝90°.在Rt △BCF 和Rt △CBE 中，⎩⎨⎧CF ＝BE ，BC ＝CB ，∴Rt △BCF ≌Rt △CBE(HL)．②∵BE ⊥AC ，CF ⊥AB ，∴∠AFC ＝∠AEB ＝90°.在△ABE 和△ACF 中，⎩⎨⎧∠AEB ＝∠AFC ，∠A ＝∠A ，BE ＝CF ，∴△ABE ≌△ACF(AAS)． ③设BE 与CF 相交于点O. ∵BE ⊥AC ，CF ⊥AB ， ∴∠OFB ＝∠OEC ＝90°.∵△ABE ≌△ACF ，∴AB ＝AC ，AE ＝AF. ∴BF ＝CE.在△BOF 和△COE 中，⎩⎨⎧∠OFB ＝∠OEC ，∠BOF ＝∠COE ，BF ＝CE ，∴△BOF ≌△COE(AAS)．4. 【答案】A5. 【答案】C【解析】由题意可知，△ABD ≌△CBD ，△MON ≌△M ′ON ′，△DON ≌△BON ′，△DOM ≌△BOM ′共4对．6. 【答案】B [解析] ∵△AEC ≌△DFB ，∴AC=DB.∴AC-BC=DB-BC ，即AB=CD. ∵AD=37 cm ，BC=15 cm ， ∴AB==11(cm).7. 【答案】D[解析] ∵AB ⊥CD ，CE ⊥AD ，BF ⊥AD ，∴∠CED ＝∠AFB ＝90°，∠A ＝∠C.又∵AB ＝CD ，∴△CED ≌△AFB.∴AF ＝CE ＝a ，DE ＝BF ＝b ，DF ＝DE －EF ＝b －c.∴AD ＝AF ＋DF ＝a ＋b －c.故选D.8. 【答案】B[解析] 如图，过点F 分别作FZ ⊥AE 于点Z ，FY ⊥CB 于点Y ，FW ⊥AB 于点W.∵AF 平分∠BAC ，FZ ⊥AE ，FW ⊥AB ， ∴FZ ＝FW.同理FW ＝FY . ∴FZ ＝FY .又∵FZ ⊥AE ，FY ⊥CB ， ∴∠FCZ ＝∠FCY .由∠AFB ＝40°，易得∠ACB ＝80°. ∴∠ZCY ＝100°.∴∠BCF ＝50°.二、填空题 9. 【答案】120° 【解析】由于△ABC ≌△A′B′C′，∴∠C ＝∠C′＝24°，在△ABC 中，∠B ＝180°－24°－36°＝120°.10. 【答案】答案不唯一，如BC ＝AD11. 【答案】AB ＝AC12. 【答案】2[解析] ∵CF ∥AB ，∴∠A ＝∠FCE.在△ADE 和△CFE 中，⎩⎨⎧∠A ＝∠FCE ，∠AED ＝∠CEF ，DE ＝FE ，∴△ADE ≌△CFE(AAS)． ∴AD ＝CF ＝3.∴BD ＝AB －AD ＝5－3＝2.13. 【答案】20[解析] 由角平分线的性质可得CD ＝DE.易证Rt △ACD ≌Rt △AED ，则AC ＝AE ，DE ＋DB ＝CD ＋DB ＝BC ＝AC ＝AE ，故DE ＋DB ＋EB ＝AE ＋EB ＝AB.14. 【答案】3[解析] ∵∠ACB ＝90°，∴∠ECF ＋∠BCD ＝90°.∵CD ⊥AB ，∴∠BCD ＋∠B ＝90°.∴∠ECF ＝∠B.在△ABC 和△FCE 中，⎩⎨⎧∠B ＝∠ECF ，BC ＝CE ，∠ACB ＝∠FEC ，∴△ABC ≌△FCE(ASA)．∴AC ＝FE. ∵AE ＝AC －CE ，BC ＝2 cm ，EF ＝5 cm ， ∴AE ＝5－2＝3(cm)．15. 【答案】16[解析] ∵BF ∥AC ，∴∠EBF=∠EAD. 在△BFE 和△ADE 中，∴△BFE ≌△ADE (ASA).∴BF=AD.∴BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD. ∵当FD ⊥AC 时，FD 最短，此时FD=BC=5， ∴四边形FBCD 周长的最小值为5+11=16.16. 【答案】7[解析] 过点P 作PF ⊥BC 于点F ，PG ⊥AB 于点G ，连接AP .∵△ABC 的两条外角平分线BP ，CP 相交于点P ，∴PF=PG=PE=2.∵S △BPC =2，∴BC ·2=2，解得BC=2.∵△ABC 的周长为11，∴AC+AB=11-2=9.∴S △ABC =S △ACP +S △ABP -S △BPC =AC ·PE+AB ·PG-S △BPC =×9×2-2=7.三、解答题17. 【答案】解：(1)如果①③，那么②；如果②③，那么①. (2)对于“如果①③，那么②”说明如下： 因为BE ∥AF ，所以∠AFD ＝∠BEC.在△ADF 和△BCE 中，⎩⎨⎧∠AFD ＝∠BEC ，∠A ＝∠B ，AD ＝BC ，所以△ADF ≌△BCE.所以DF ＝CE.所以DF －EF ＝CE －EF ，即DE ＝CF. 对于“如果②③，那么①”说明如下： 因为BE ∥AF ， 所以∠AFD ＝∠BEC. 因为DE ＝CF ，所以DE ＋EF ＝CF ＋EF ，即DF ＝CE. 在△ADF 和△BCE 中，⎩⎨⎧∠AFD ＝∠BEC ，∠A ＝∠B ，DF ＝CE ，所以△ADF ≌△BCE ， 所以AD ＝BC.18. 【答案】(1)证明：∵AB ＝AC ，AD 平分∠CAE ，∴∠B ＝∠ACB ，∠CAD ＝∠EAD ＝12∠CAE ， 又∵∠CAE ＝∠B ＋∠ACB ， ∴∠B ＝∠EAD ，(3分) ∴ AD ∥BC.(4分) (2)解：∵CG ⊥AD ， ∴∠CFA ＝∠GFA ＝90°， 在△ACF 和△AGF 中，⎩⎨⎧∠CFA ＝∠GFAAF ＝AF∠CAF ＝∠GAF， ∴△ACF ≌△AGF(ASA )， ∴AC ＝AG ，CF ＝GF ，(7分) 又∵AB ＝AC ， ∴AB ＝AG ，(9分)∴AF 是△BCG 的中位线， ∵AF ＝4，∴BC ＝2AF ＝8.(10分)19. 【答案】(1)∵CAF BAE ∠=∠， ∴BAC EAF ∠=∠，∵AE AB AC AF ==，， ∴BAC EAF △≌△，∴EF BC =．(2)∵65AB AE ABC =∠=︒，，∴18065250BAE ∠=︒-︒⨯=︒，∴50FAG ∠=︒，∵BAC EAF △≌△，∴28F C ∠=∠=︒，∴502878FGC ∠=︒+︒=︒．20. 【答案】解:(1)依题意得BP=3t cm ，BC=8 cm ，∴CP=(8-3t )cm .(2)∵∠B 和∠C 是对应角，∴分两种情况讨论:①若△BDP ≌△CPQ ，则BD=CP ，BP=CQ.∵AB=10 cm ，D 为AB 的中点，∴BD=5 cm .∴5=8-3t ，解得t=1.∴CQ=BP=3 cm .∴a==3.②若△BDP ≌△CQP ，则BD=CQ ，BP=CP .∵BP=3t cm ，CP=(8-3t )cm ， ∴3t=8-3t ，解得t=.∵BD=CQ ，∴5=a ，解得a=.综上所述，a 的值为3或.21. 【答案】证明：如图，在AB 上截取AF ＝AD ，连接EF.∵AE 平分∠PAB ，∴∠DAE ＝∠FAE.在△DAE 和△FAE 中，⎩⎨⎧AD ＝AF ，∠DAE ＝∠FAE ，AE ＝AE ，∴△DAE ≌△FAE(SAS)．∴∠AFE ＝∠ADE.∵AD ∥BC ，∴∠ADE ＋∠C ＝180°.又∵∠AFE ＋∠EFB ＝180°，∴∠EFB ＝∠C.∵BE 平分∠ABC ，∴∠EBF ＝∠EBC.在△BEF 和△BEC 中，⎩⎨⎧∠EFB ＝∠C ，∠EBF ＝∠EBC ，BE ＝BE ，∴△BEF ≌△BEC(AAS)．∴BF ＝BC.∴AD ＋BC ＝AF ＋BF ＝AB.22. 【答案】(1)PM ＝PN ，PM ⊥PN ；【解法提示】∵AB ＝AC ，AD ＝AE ，∴BD ＝CE ，∵M ，P ，N 分别为DE ，DC ，BC 的中点，∴PM //CE 且PM =12CE ，PN ∥BD 且PN =12BD ， ∴PM ＝PN ，∠DPM ＝∠DCE ，∠CNP ＝∠B ，∴∠DPN ＝∠PNC ＋∠PCN ＝∠B ＋∠PCN ，∵∠A ＝90°，∴∠B ＋∠ACB ＝90°，∴∠MPN ＝∠MPD ＋∠DPN ＝∠ACD ＋∠PCN ＋∠B ＝∠ACB ＋∠B ＝90°， ∴PM ⊥PN ；(2)△PMN 为等腰直角三角形．理由如下：由题可知△ABC 和△ADE 均为等腰直角三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，∴∠BAD＋∠DAC＝∠DAC＋∠CAE，∴∠BAD＝∠CAE，∴△BAD≌△CAE(SAS)，∴∠ABD＝∠ACE，BD＝CE，又∵M，P，N分别是DE，CD，BC的中点，∴PM是△CDE的中位线，∴PM∥CE且PM=12 CE，同理PN∥BD且PN=12 BD，∴PM＝PN，∴∠MPD＝∠ECD＝∠ACD＋∠ACE＝∠ACD＋∠ABD，∠DPN＝∠PNC＋∠PCN＝∠DBC＋∠PCN，∴∠MPN＝∠MPD＋∠DPN＝∠ACD＋∠ABD＋∠DBC＋∠PCN＝∠ABC＋∠ACB＝90°，∴△PMN为等腰直角三角形；(3)49 2.【解法提示】∵△PMN为等腰直角三角形，∴S△PMN ＝12PM2，要使△PMN的面积最大，即PM最大，由(2)得，PM＝12CE，即当CE最大时，PM最大．如解图，当点C、E在点A异侧，且在同一条直线上时，CE最大，此时CE＝AE ＋AC＝AD＋AB＝14，解图∴PM＝12CE＝12×14＝7，故△PMN的最大面积为S△PMN ＝12×7×7＝492.。