2016年复旦附中自招数学试卷
【自招】2004-2015年上海自主招生数学试题

6
2011 年华师二附自主招生数学试题及答案
一、 填空题(每题 4 分) 1. 已知关于 x 的多项式 ax7 bx5 x2 x 12 ( a 、 b 为常数),且当 x 2 时,该多项 式的值为 8 ,则当 x 2 时,该多项式的值为__________.
2. 已知关于 x 的方程 x2 a 2 x a 1 0 的两实根 x1 、 x2 满足 x12 x22 4 ,则实
15. 某养鱼户为了估计鱼塘内鱼的条数和重量,先网出 100 条鱼,做上标记后全部放回
鱼塘,过些时候捕捞出 90 条鱼,发现其中有 4 条鱼带有标记,估计该鱼塘内养鱼
约有_________条.
16. 如图,四边形 ABCD 中, ADC 和 ABC 都是直角,
D
DE 垂直于 AB , AD 边与 CD 边长度相等.已知四边
C 形 ABCD 的 面 积 为 16 , 那 么 线 段 DE 的 长 度 是
_________. A
17. 在 ABC 中, D 为 BC 的中点, E 为 AD 的中点,如
果延长 BE 交 AC 于 F ,那么 AF : FC ________.
E
B
第 16 题
18. 如图, ABC 中,已知 AB AC , DEF 是 ABC 的内接正三角形, BDF ,
圆括号内),一律得零分.
1
1.
计算
3
4
3
9 2
32
1 9
2
,得()
A. 11 9
B. 1
C. 5 9
D. 1 9
2. 如果 a b ,那么下列结论正确的是()
上海四校自招-数学复旦附中卷_含答案

a2 b2 (ab)2
(ab)2
(7)2
49
49
4. 【注】原题应为 p 是奇质数 (2x p)(2 y p) p2
则 2x p 1, 2y p p2
∴ x p 1 , y p2 p
2
2
5. 显然 x 0
两边平方得 x2 x 1 1 1 2 (x 1)(1 1)
xx
xx
两边同乘 x ,得 x3 x2 x 2 2 (x2 1)(x 1)
因此,经过 70s 时,甲乙位于同一条边
7. 设点 P 速度为 6 , Q 的速度为 3 , R 的速度为 2 ,边长 AB 6
则 SAPR
3 AP·AR 4
3 6t (6 2t) 4
SBPQ
3 BP·BQ 4
3 3t (6 6t) 4
SCQR
3 CQ·CR 4
3 2t (6 3t) 4
【高中知识点】解析几何——圆的方程、两根差公式、分离变量、均值不等式
9. 【注】原题应为“有且仅有一个实数根”,这样表达的更准确一些 原方程
2x 3
ax
(x 1)(x 2) (x 1)(x 2)
2x 3 ax
x 1
x
2
4x2 12x 9 ax
x
3 2
x 2
a
4x
9 x
12
坐标;
2015 年初升高·自招真题解析·数理化
1
(3) 设点 P 是 x 轴上的任意一点,分别连结 AC 、 BC 。比较 PA PB 与 AC BC 的大小关系,说明理 由。
【试卷总结与分析】
1. 高中知识点分析
涉及到的重要高中知识点几乎很少,但有些考察的并不浅,如第 9, 10, 11 题 并不是简单的通过初中知识就能解决的,需要较好的掌握才足以解决问题(如参变分离思想,对勾函 数的图像,均值不等式等) 因此,建议考生对于高中的这些特有的思想和知识,又与初中知识相关的,加强补习与训练,才能在 考试中占据优势
复旦附中自招真题解析

海
7. 已知锐角 ABC 的三边长恰为三个连续正整数,AB BC CA , 若 BC 边上的高为 AD, 则 BD DC ______________. 【答】4. A 【解析】设 AB 、 BC 、 CA 分别为 n 1 、 n 、 n 1 ,则
昂
立
智
立 方
B
C
上
2
2
B
D C
有 c 2 a 2 b2 2b2 c 2b ab 2 b b 2b 2 而 ab 2 a b c 2 0 b b a 5 ,
2 2 b 7b a 7 ,
若 a 5 ,25 c b c b c b 25 ,c b 1 c 13 ,b 12 代入两式验证成立; 若 a 6 , 36 c b c b c b 18 , c b 2 c 10 , b 8 代入两式验证成立;
2
若它们为不同解,则 19m n 19 矛盾 19m n
原式
m 19m 4m 1 19m2 99m 1 95m 5 . 19m 19m
9. 若关于 x 的方程 x 2 x 2 4 x m 0 有三个根,且这三个根恰好可以作为一个三角形 的三边长,则 m 的取值范围是______________. 【答】 3 m 4 . 【解析】显然 x 2 是原方程的根,设另两个根分别为 a 、 b , a b 4 2 ,
15 sin120 a a 2 3 2 4 则 a 2 2a 1 16 sin 60 2 S 2a 2 ABCD 2
上海中考自招真题26套及其答案

四校八大历年自招真题答案目录2013年上中自招试卷2014年上中自招试卷2015年上中自招试卷2011年华二自招试卷2012年华二自招试卷2014年华二自招试卷2013年华二冬令营数学试卷2015年年华二自招试卷2017年年华二自招试卷2013年复附自招试题2014年复附自招试题一2014年复附自招试题二2015年复附自招试题一2015年复附自招试题二2012年交附自招试题2013年交附自招试题2014年交附自招试题2015年交附自招试题2016年交附自招试题2014年七宝自招试题2016年七宝自招试题2016年南模自招试题2016年建平自招试题2017年建平自招试题建平数学培训资料试卷2015年控江自招试题2013年华二冬令营数学试卷1、“帽子函数”的图像如图所示:(1)求此函数的解析式;(2)若有抛物线23(),4y x a a =-+<求它与“帽子函数”图像的交点个数; (3)请试写出一个抛物线解析式,使它与“帽子函数”图像有且只有2个交点,横坐标分别为5722,.【解析】:⑴1,211,12x k x k y x k k x k ⎧≤<+⎪⎪=⎨⎪-+++≤<+⎪⎩⑵0a <时,无交点0a =时,一个交点304a <<时,两个交点 ⑶考虑到34a =时,抛物线234y x =-+与帽子函数交于11,22⎛⎫- ⎪⎝⎭、11,22⎛⎫ ⎪⎝⎭两点, 所以可以将234y x =-+向右平移3个单位,即满足条件 该抛物线解析式为()2334y x =--+2、在一个8×8的正方形方格纸中,一个角剪去一个2×2的小正方形,问其余部分可否剪成15块“L ”型(如图)纸片,若能剪,给出剪切方法,若不能剪,请说明理由。
【解析】(一道基础的染色问题)如图进行黑白相间染色,那么L 型放入方格纸中,必定可以盖住1个黑格子和3个白格子,或者3个黑格子和1个白格子。
复旦大学自主招生考试数学试题及答案
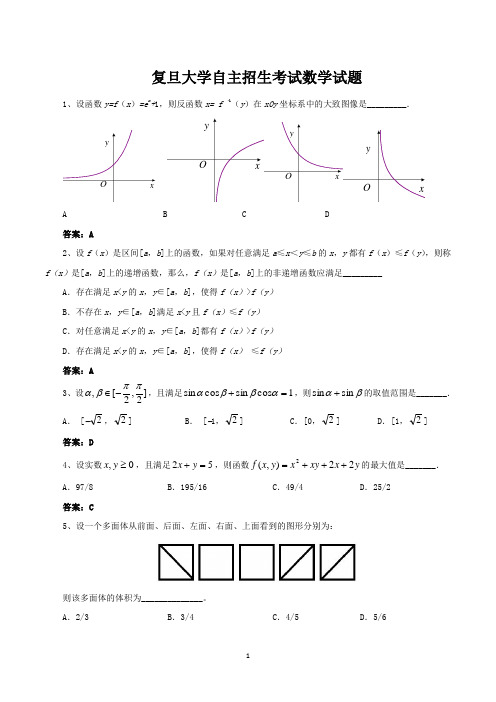
1、设函数y=f(x)=e x+1,则反函数OyxOyxO x答案:A2、设f(x)是区间[a,b]f(x)是[a,b]上的递增函数,那么,f(xA.存在满足x<y的x,y∈[a,b]B.不存在x,y∈[a,b]满足x<y且fC.对任意满足x<y的x,y∈[a,b]D.存在满足x<y的x,y∈[a,b]答案:A3、设]2,2[,ππβα-∈,且满足sinαA. [−2,2] B. [答案:D4、设实数0,≥yx,且满足2=+yxA.97/8 B.答案:C5则该多面体的体积为______________。
A.2/3 B.3/4答案:D6、在一个底面半径为1/2,高为1的圆柱内放入一个直径为1的实心球后,在圆柱内空余的地方放入和实心球、侧面以及两个底面之一都相切的小球,最多可以放入这样的小球个数是___________。
A .32个;B .30个;C .28个;D .26个答案:B7、给定平面向量(1,1),那么,平面向量(231-,231+)是将向量(1,1)经过________. A .顺时针旋转60°所得; B .顺时针旋转120°所得; C .逆时针旋转60°所得;D .逆时针旋转120°所得;答案:C8、在直角坐标系O xy 中已知点A 1(1,0),A 2(1/2,3/2),A 4(−1,0),A 5(−1/2,−3/2)和A6(1/2, −3/2).问在向量−−→−ji A A (i ,j=1,2,3,4,5,6,i≠j)中,不同向量的个数有_____. A .9个; B .15个; C .18个; D .30个答案:C9、对函数f:[0,1]→[0,1],定义f 1(x )=f (x ),……,f n(x ) =f (f n −1(x )),n=1,2,3,…….满足f n (x )=x 的点x ∈[0,1]称为f 的一个n −周期点.现设⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤=121,22,210,2)(x x x x x f 问f 的n −周期点的个数是___________.A .2n 个;B .2n 2个;C .2n个;D .2(2n−1)个.答案:C10、已知复数z 1=1+3i ,z 2=−3+3i ,则复数z 1z 2的幅角__________. A .13π/12 B .11π/12 C .−π/4 D .−7π/12答案:A11、设复数βαβαcos sin ,sin cos i w i z +=+=满足z w =3/2,则sin (β−α)=______. A .±3/2B .3/2,−1/2C .±1/2D .1/2,−3/2答案:D12、已知常数k 1,k 2满足0<k 1<k 2,k 1k 2=1.设C 1和C 2分别是以y =±k 1(x −1)+1和y =±k 2(x −1)+1为渐近线且通过原点的双曲线.则C 1和C 2的离心率之比e 1/e 等于_______.A .222111k k ++ B .212211k k ++ C .1 D .k 1/k 2答案:C13、参数方程0,)cos 1()sin (>⎩⎨⎧-=-=a t a y t t a x 所表示的函数y=f (x )是____________.A .图像关于原点对称;B .图像关于直线x =π对称;C .周期为2a π的周期函数D .周期为2π的周期函数.答案:C14、将同时满足不等式x −k y −2≤0,2x +3y −6≥0,x +6y −10≤0 (k>0)的点(x ,y )组成集合D 称为可行域,将函数(y +1)/x 称为目标函数,所谓规划问题就是求解可行域中的点(x ,y )使目标函数达到在可行域上的最小值.如果这个规划问题有无穷多个解(x ,y ),则k 的取值为_____.A .k≥1;B .k≤2C .k=2D .k=1.答案:C15、某校有一个班级,设变量x 是该班同学的姓名,变量y 是该班同学的学号,变量z 是该班同学的身高,变量w 是该班同学某一门课程的考试成绩.则下列选项中正确的是________.A .y 是x 的函数;B .z 是y 的函数;C .w 是z 的函数;D .w 是x 的函数.答案:B16、对于原命题“单调函数不是周期函数”,下列陈述正确的是________. A .逆命题为“周期函数不是单调函数”; B .否命题为“单调函数是周期函数”; C .逆否命题为“周期函数是单调函数”; D .以上三者都不正确 答案:D17、设集合A={(x ,y )|log a x +log a y >0},B={(x ,y )|y +x <a}.如果A∩B=∅,则a 的取值范围是_______ A .∅ B .a>0,a≠1 C .0<a≤2, a≠1 D .1<a≤2答案:D18、设计和X 是实数集R 的子集,如果点x 0∈R 满足:对任意a>0,都存在x ∈X 使得0<|x −x 0|<a ,则称x 0为集合X 的聚点.用Z 表示整数集,则在下列集合(1){n/(n+1)|n ∈Z , n≥0}, (2) R\{0}, (3){1/n|n ∈Z , n≠0}, (4)整数集Z 中,以0为聚点的集合有_____. A .(2),(3)B .(1),(4)C .(1),(3)D .(1),(2),(4)答案:A19、已知点A (−2,0),B (1,0),C (0,1),如果直线kx y =将三角形△ABC 分割为两个部分,则当k =______时,这两个部分得面积之积最大?A .23-B .43-C .34-D .32-答案:A20、已知x x x x f 2cos 3cos sin )(+=,定义域⎥⎦⎤⎢⎣⎡=ππ127,121)(f D ,则=-)(1x f_____A .π12123arccos 21+⎪⎪⎭⎫ ⎝⎛-x B .π6123arccos 21-⎪⎪⎭⎫ ⎝⎛-x C .π12123arcsin 21+⎪⎪⎭⎫ ⎝⎛--x D .π6123arcsin 21-⎪⎪⎭⎫ ⎝⎛-x 答案:A21、设1l ,2l 是两条异面直线,则直线l 和1l ,2l 都垂直的必要不充分条件是______ A .l 是过点11l P ∈和点22l P ∈的直线,这里21P P 等于直线1l 和2l 间的距离 B .l 上的每一点到1l 和2l 的距离都相等 C .垂直于l 的平面平行于1l 和2lD .存在与1l 和2l 都相交的直线与l 平行 答案:D22、设ABC −A’B’C’是正三棱柱,底面边长和高都为1,P 是侧面ABB’A’的中心,则P 到侧面ACC’A’的对角线的距离是_____A .21B .43C .814D .823答案:C23、在一个球面上画一组三个互不相交的圆,成为球面上的一个三圆组.如果可以在球面上通过移动和缩放将一个三圆组移动到另外一个三圆组,并且在移动过程中三个圆保持互不相交,则称这两个三圆组有相同的位置关系,否则就称有不同的位置关系.那么,球面上具有不同的位置关系的三圆组有______A .2种B .3种C .4种D .5种 答案:A24、设非零向量()()()321321321,,,,,,,,c c c c b b b b a a a a ===为共面向量,),,(31x x x x x = 是未知向量,则满足0,0,0=⋅=⋅=⋅x c x b x a的向量x 的个数为_____A .1个B .无穷多个C .0个D .不能确定 答案:B25、在Oxy 坐标平面上给定点)1,2(),3,2(),2,1(C B A ,矩阵⎪⎪⎭⎫⎝⎛-112k 将向量OC OB OA ,,分别变换成向量,,,如果它们的终点',','C B A 连线构成直角三角形,斜边为''C B ,则k 的取值为______A .2±B .2C .0D .0,−2 答案:B26、设集合A ,B ,C ,D 是全集X 的子集,A∩B≠∅,A∩C≠∅.则下列选项中正确的是______. A .如果B D ⊂或C D ⊂,则D∩A≠∅; B .如果A D ⊂,则C x D∩B≠∅,C x D∩C≠∅; C .如果A D ⊃,则C x D∩B=∅,C x D∩C=∅; D .上述各项都不正确.27、已知数列{}n a 满足21=a 且n a n ⎧⎫⎨⎬⎩⎭是公比为2的等比数列,则∑==nk k a 1______A .221-+n nB .22)1(1+-+n n C .)1(22-+n n n D .n n n 22)1(+-28、复平面上圆周2211=+--iz z 的圆心是_______ A .3+i B .3−iC .1+iD .1−i29.已知C 是以O 为圆心、r 为半径的圆周,两点P 、P *在以O 为起点的射线上,且满足|OP|∙|OP *|=r 2,则称P 、P *关于圆周C 对称.那么,双曲线22x y -=1上的点P (x ,y )关于单位圆周C':x 2+y 2=1的对称点P *所满足的方程是(A )2244x y x y -=+(B )()22222x y x y-=+(C )()22442x y x y-=+(D )()222222x y x y-=+30、经过坐标变换⎩⎨⎧+-=+=θθθθcos sin 'sin cos 'y x y y x x 将二次曲线06532322=-+-y xy x 转化为形如1''2222=±b y a x 的标准方程,求θ的取值并判断二次曲线的类型_______ A .)(6Z k k ∈+=ππθ,为椭圆 B .)(62Z k k ∈+=ππθ,为椭圆C .)(6Z k k ∈-=ππθ,为双曲线D .)(62Z k k ∈-=ππθ,为双曲线31、设k , m , n 是整数,不定方程mx+ny=k 有整数解的必要条件是____________ A .m ,n 都整除kB .m ,n 的最大公因子整除kC .m ,n ,k 两两互素D .m ,n ,k 除1外没有其它共因子。
复旦附中2016学年第一学期高二期中考试试卷

复旦附中2016学年第一学期高二期中考试试卷一、填空题()()1,,9,6a k b k ==-,假设//a b ,那么实数k = . 32521x y x y +=⎧⎨+=-⎩的增广矩阵为 . 23014x x +<,那么实数x 的取值范围是 .4.计算:1111393lim 1111242n n n →∞++++=++++ . ,x y 知足1000x y x y --≤⎧⎪≥⎨⎪≤⎩,那么z x y =+的最大值是 . l 通过点()3,2,且在量坐标轴上的截距相等,那么直线l 的方程是 .1l 与2l 的斜率别离是方程2610x x +-=的两根,那么直线1l 与2l 的夹角为 .()()1,12,3A B -、,直线1y ax =-与线段AB 相交,那么实数a 的取值范围是 .l 过点()3,3P ,点()1,1Q -到它的距离等于4,那么直线l 方程是 .ABC ∆为等边三角形,2AB =,设点,P Q 知足(),1AP AB AQ AC λλ==-,R λ∈,假设32BQ CP ⋅=-,那么λ= .2360x y +-=别离交,x y 轴于,A B 两点,点P 在直线1y x =--上,那么PA PB +,的最小值是 .a ,b ,两组向量12345,,,,x x x x x 和12345,,,,y y y y y 均由2个a 和3个b 排列而成,记1122334455S x y x y x y x y x y =⋅+⋅+⋅+⋅+⋅,min S 表示S 因此可能取值中的最小值,那么以下命题中真命题的序号是 (写出所有真命题的序号)①S 有5个不同的值;②若a ⊥b ,那么min S 与a 无关;③若a //b ,那么min S 与b 无关; ④若4b a >,那么min 0S >;⑤若2b a =,min 8S =2a 则a 与b 夹角为4π二、选择题13.有以下四个命题:①若22lim n n a A →∞=,那么lim n n a A →∞=,②若0,lim n n n a a A →∞>=,那么0A >;③若lim n n a A →∞=,那么22lim n n a A →∞=,④若()lim 0n n n a b →∞-=,那么lim lim n n n n a b →∞→∞=.其中正确结论的个数是( ).A 1个 .B 2个 .C 3个 .D 4个 m ,直线130mx y m -+-=必通过的定点坐标是( ).A ()3,1 .B ()1,3 .C 1,3m m ⎛⎫- ⎪⎝⎭.D 无法确信{},min ,,y x yx y x x y ≥⎧=⎨<⎩,设,a b 为平面内的非零向量,那么( ) .A {}{}min ,min ,a b a b a b +-≤ .B {}{}min ,min ,a b a b a b +-≥ .C {}22min ,a b a b a b +-≥+ .D {}22min ,a b a b a b +-≤+16. 已知()111,b a P 与()222,b a P 是直线2+=kx y (k 是常数)上两个不同的点,那么关于x 和y 的方程组⎩⎨⎧=+=+112211y b x a y b x a 的解得情形是( ) A.不管21,,p p k 如何,老是无解 B 不管21,,p p k 如何,总有唯一解21,,p p k 如何,使之恰有两解 D 存在21,,p p k 如何,使之有无穷多解三、解答题a 与b 所成的角为56π,且2,3a b ==,求32a b +,并求32a b +与a 的夹角.()()1:2350l m x m y +++-=和()2:62150l x m y +--=,问当m 为何值时,别离有:(1)1l 与2l 相交?(2)12l l :(3)1l 与2l 重合.xoy 中,已知点()()()1,1,2,3,3,2A B C ,点(),P x y 在ABC ∆三边围成的区域(含边界)上.(1)假设0PA PB PC ++=,求OP ;(2)设(),OP mAB nAC m n R =+∈,用,x y 表示m n -,并求m n -的最大值.12:2,:2l y x l y x ==-,过点()2,0M -的直线l 别离与直线12,l l 交于,A B ,其中点A 在第三象限,点B 在第二象限,点()1,0N .(1)假设NAB ∆的面积为16,求直线l 的方程;(2)直线AN 交2l 于点P ,直线BN 交1l 于点Q ,假设直线l ,PQ 的斜率都存在,别离设为12,k k ,判定12k k 是不是为定值?假设为定值,求出该定值;假设不为定值,请说明理由?21. 在直角坐标平面xOy 上的一列点()()11221,,2,,,A a A a (,),n n A n a ,简记为{}n A .假设由1n n n b A A j +=⋅组成的数列{}n b 知足1,1,2,n n b b n +>=,其中j 为方向与y 轴正方向相同的单位向量,那么称{}n A 为T 点列. (1) 判定()123111,1,2,,3,,,23A A A ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭1,,n A n n ⎛⎫⎪⎝⎭,是不是为T 点列,并说明理由;(2)假设{}n A 为T 点列,且点2A 在点1A 的右上方. 任取其中持续三点1k k A A +、、2k A +,判定△12k k k A A A ++的形状 (锐角三角形、直角三角形、钝角三角形),并证明;(3)(附加题)若{}n A 是T 点列,正整数1m n p q ≤<<<知足m q n p +=+, 求证:n q m p A A j A A j ⋅>⋅.。
2016年复旦附中自主招生试卷

5. 如图,在梯形 ABCD 中, AB∥CD ,CD AB ,设 E 、F 分别是 AC 、BD 的中点, AC
与 BD 交于点 O ,已知 △OEF 是边长为1 的正三角形, △BOC 的面积为 15 3 , 4
则梯形 ABCD 的面积为__________.
A
B
【答】16 3 【解析】设 BO a ,则 OD OC a 2 ,由 △AOB 、△ODC 均为正三角形,
19m
19m
9. 若关于 x 的方程 x 2 x2 4x m 0 有三个根,且这三个根恰好可以作为一个三角形
的三边长,则 m 的取值范围是___________.
【答】 3 m ≤ 4
【解析】显然 x 2 是原方程的根,设另两个根分别为 a 、b , a b 4 2 ,
则
sin120 2
a
a
2
15 43Fra bibliotek
S
ABCD
sin 60 2a
2
22
a2
2a
1
16
S
3 4 16 16 4
3
F
O E
D
C
6. 已知矩形 ABCD 中, AB 1,BC a ,若在边 BC 上存在点 Q ,满足 AQ QD ,则 a 的 取值范围是___ _______.
x 3,BH x2 32
BB ' 3 x2 32
4
BH
18x x2 9
2x2
9x
18
0
无解
历年上海复旦大学自主招生试题汇总

⽆忧考为⼤家整理的历年上海复旦⼤学⾃主招⽣试题汇总,供⼤家参考。
2012年复旦⼤学⾃主招⽣千分考试题 据复旦招办预计,2012年通过千分考进⼊⾃主招⽣⾯试的学⽣⽐例将与2011年基本持平,成绩和⾯试⽅案将于⼀周内公布。
以下是中国教育在线为您整理的2012年复旦“千分考”部分考题。
选摘考题如下: 1.冷战以后,我国规模的⼀次撤侨是从哪个国家撤离的? 2.中国的13个船员是在哪条河遇难的? 3.在欧债危机中,有哪些国家的政权发⽣了更迭? 4.请从东到西排出“iPhone4S”第⼀批上市的⼏个国家。
5.“《社戏》、《藤野先⽣》、《从百草园到三味书屋》等是否都出⾃《朝花⼣拾》? 6.按照时间顺序排列鲁迅的四⼤名著《药》、《狂⼈⽇记》、《阿Q正传》、《祝福》。
7."五⽉渡泸,深⼊不⽑"出⾃哪⾥?” 8.清朝哪位⽂⼈将⽂体分为阴柔派和阳刚派? 9.以下哪个地⽅对柑橘的⽣长危险因素? 10.中国的四个卫星发射中⼼哪个耗能? 11.上海出租车在3公⾥以内收费14元,超过3公⾥10公⾥以内,是每公⾥2.4元,请计算要付的钱和公⾥数的函数关系。
12.伊丽莎⽩⼥王的权⼒受限是因为哪个法案? 13.根据⽔稻育种、播种的时间,请判断这是什么地区? 14.根据某地茶叶上市的时节来判断当地⽓候。
15.⼀个磁铁矿完全变成氯化铁矿,会有多少四氧化三铁的含量? 16.1M字节等于多少K字节? 17.如果⾦属钠失⽕,要⽤什么来扑灭? 18.中国有4个卫星发射中⼼,哪个发射中⼼的能耗? 19.把⼗元钱换成1元、5⾓、1⾓零钱,有⼏种不同的组合⽅法? 20.⼆进制1101011转化成⼗进制是多少? 21. 1M字节等于多少K字节?2011年复旦⼤学千分考试题选摘: 辨别莎⼠⽐亚作品台词; ⼼绞痛可以⽤何种药物治疗; 列举陀思妥耶夫斯基的代表作; 朝韩炮击事件是在哪⾥发⽣的; 去年联合国⽓候⼤会在哪⾥举⾏; 世界杯半决赛对阵的是哪四⽀球队; 《达·芬奇密码》是什么类型的⼩说; 《六书》中哪些是造字⽅法、哪些是⽤字⽅法; 辨别“⼲涸、征伐、蜡烛、多余”等繁体字正误; 说是⼀辆辆车⼦进站出站,考汽车进出站的顺序; 给出了⾜球世界杯中对阵的⼏组国家的名字,问哪组国家⽂化背景相似; 世博园中⼀位游客的⼿表显⽰6点,当时北京时间是7点,这位游客来⾃哪个时区2010年复旦⼤学⾃主招⽣试题 复旦⼤学⾃主招⽣笔试全是选择题,考查内容囊括语⽂、数学、外语、物理、化学、⽣物、政治、历史、地理和计算机⼗门学科。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年复旦附中自招数学试卷
1. 已知
a b c x
b c a c a b ===
++
+
,则x=
2.
已知函数2
2(5)3
y x a x
=-+-+(23)
b x b
≤≤+图像关于y轴对称,则a b
+=
3. 已知函数2
(2)2(1)
y k x kx k
=--++的图像与x轴只有一个交点,则k=
4. 在同一个直角坐标系中,已知直线y kx
=与函数
28,3
2,33
24,3
x x
y x
x x
-≥
⎧
⎪
=--<<
⎨
⎪+≤-
⎩
图像恰好有三个
公共点,则k的取值范围是
5. 如图,在梯形ABCD中,AB∥CD,CD AB
>,设E、F分别是AC、BD的中点,AC与BD交于点O,已知OEF
V是边长为1的正三角形,BOC
V的面积为
15
3
4
,则梯形ABCD 的面积为
6. 已知矩形ABCD中,1
AB=,BC a
=,若在边BC上存在点Q,满足AQ⊥QD,则a的取值范围是
7. 已知锐角三角形ABC的三边长恰为三个连续正整数,AB BC CA
>>,若BC边上的高为AD,则BD DC
-=
8. 已知实数m、n(其中1
mn≠)分别满足:2
199910
m m
++=,299190
n n
++=,则41
mn m
n
++
=
9. 若关于x的方程2
(2)(4)0
x x x m
--+=有三个根,且这三个根恰好可以作为一个三角形的三边长,则m的取值范围是
10. 如图,矩形ABCD中,3
AB=,4
BC=,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B'处,当CEB'
V为直角三角形时,BE的长为
11. 如图,OA、OD是圆O的半径,延长OA至B,使OA AB
=,C是OA的中点,∠AOD 为锐角α,连接CD、BD,且CD a
=,则BD=
12. 已知直角三角形的三边长都是整数,且其面积与周长在数值上相等,若将全等的三角形都作为同一个,那么这样的直角三角形的个数是
13. 设n(10
n≥)个机场,每一机场起飞一架飞机,飞到离起飞机场最近的机场降落,且任何两机场之间的距离都不相等,则任意一个机场降落的飞机架数的最大值为
14. 关于x的方程22
(21)20
x m x m m
--++=的两个根分别为
1
x、
2
x.
(1)若
12
||5
x x
-=,求m的值;(2)若
1
x、
2
x均为整数,求m的值.
15. 如图,ABC
V中,5
AB BC
==,6
AC=,过点A作AD∥BC,点P、Q分别是射线AD、线段BA上的动点,且AP BQ
=,过点P作PE∥AC交线段AQ于点O,联结PQ,记AP x
=,POQ
V面积为y.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)联结QE,若PQE
V与POQ
V相似,求AP的长.
16. 一幢33层的大楼有一部电梯停在第一层,它一次最多能容纳32人,而且只能在第2层到第33层中的某一层停一次,对于每个人来说,他往下走一层楼感到1分不满意,往上走一层楼感到3分不满意,现在有32个人在第一层,并且他们分别住在第2至第33层的每一层,问:电梯停在哪一层,可以使得这32个人不满意的总分达到最小?最小值是多少?(有些人可以不乘电梯而直接从楼梯上楼)
17. 设x是实数,不大于x的最大整数叫做x的整数部分,记作[]x,如[1.2]1
=,[3]3
=,[ 1.3]2
-=-.
(1)
222
111
(10111)(11121)(201620171)
[][][]
1011111220162017
S=++⋅⋅⋅+
⨯-⨯-⨯-
⨯⨯⨯
,求[90]S;
(2)解关于x的方程:2
1
2312[]
2
x
x x
-
--=.
参考答案
1. 12
或1- 2. 4 3. 2± 4. 223k << 5. 6. 2a ≥ 7. 4 8. 5- 9. 34m <≤ 10.
32或3 11. 2a 12. 2 13. 5
14.(1)1-;(2)2-、32-、12-、0. 15.(1)22412255y x x =-+,502
x ≤<;(2)5 16. 第27层,最小值316
17.(1)9;(2)1或1.。
