第11章磁场作业解答磁场分解
大学物理（下）十一章十二章作业与解答
⼤学物理（下）⼗⼀章⼗⼆章作业与解答第⼗⼀章恒定磁场⼀. 选择题1．在⼀平⾯内，有两条垂直交叉但相互绝缘的导线，流经两条导线的电流⼤⼩相等，⽅向如图，在哪些区域中有可能存在磁感应强度为零的点？(A) 在Ⅰ、Ⅲ象限(B) 在Ⅰ、Ⅳ象限(C) 在Ⅱ、Ⅲ象限(D) 在Ⅱ、Ⅳ象限[ ]2. 载流导线在同⼀平⾯内，形状如图，在圆⼼O处产⽣的磁感应强度⼤⼩为(A)(B)(C)(D) [ ]注意见第11章课件最后的总结的那个图，半圆载流回路在圆⼼处的磁感强度是多少？3. ⼀圆形回路1及⼀正⽅形回路2，圆的直径与正⽅形边长相等，⼆者中通有⼤⼩相同电流，则它们在各⾃中⼼处产⽣的磁感应强度⼤⼩之⽐为(A) 0.90(B) 1.00(C) 1.11(D) 1.22 [ ]注意教材page304,及课件最后总结的那个图4. 在磁感应强度为的均匀磁场中做⼀半径为r的半球⾯S，S边线所在平⾯的法线⽅向单位⽮量与的夹⾓为θ，则通过半球⾯S 的磁通量（取半球⾯向外为正）为(A)(B)(C)(D)[ ]5. 如图，⽆限长载流直导线附近有⼀正⽅形闭合曲⾯S，当S向导线靠近时，穿过S的磁通量和S上各点的磁感应强度的⼤⼩B 将(A) 增⼤，B增强(B) 不变，B不变(C) 增⼤，B不变(D) 不变，B增强[ ]6. 取⼀闭合积分回路L，使若⼲根载流导线穿过它所围成的⾯，若改变这些导线之间的相互间隔，但不越出积分回路，则(A) 回路L内的电流的代数和不变，L上各点的不变(B) 回路L内的电流的代数和不变，L上各点的改变(C) 回路L内的电流的代数和改变，L上各点的不变(D) 回路L内的电流的代数和改变，L上各点的改变[ ]7. 如图，两根导线ab和cd沿半径⽅向被接到⼀个截⾯处处相等的铁环上，恒定电流I 从a端流⼊⽽从d端流出，则磁感应强度沿闭合路径L的积分等于(A)(B)(C)(D)[ ]8. ⼀电荷为q的粒⼦在均匀磁场中运动，下列说法正确的是(A) 只要速度⼤⼩相同，粒⼦所受的洛仑兹⼒就相同(B) 在速度不变的前提下，若电荷q变为 -q，则粒⼦受⼒反向，数值不变(C) 粒⼦进⼊磁场后，其动能和动量都不变(D) 洛仑兹⼒与速度⽅向垂直，所以带电粒⼦运动的轨迹必定是圆[ ]9. 质量为m、电量为q的粒⼦，以速度v垂直射⼊均匀磁场中，则粒⼦运动轨道包围范围的磁通量与磁感应强度的⼤⼩之间的关系曲线为[ b ]注意见P317,(11.30)10. 如图，长直载流导线与⼀圆形电流共⾯，并与其⼀直径相重合(两者间绝缘),设长直电流不动，则圆形电流将(A) 向上运动(B) 绕旋转(C) 向左运动(D) 向右运动(E) 不动[ ]11. 磁场中有⼀载流圆线圈，其既不受⼒也不受⼒矩作⽤，这说明(A) 该磁场⼀定均匀，且线圈的磁矩⽅向⼀定与磁场⽅向平⾏(B) 该磁场⼀定不均匀，且线圈的磁矩⽅向⼀定与磁场⽅向平⾏(C) 该磁场⼀定均匀，且线圈的磁矩⽅向⼀定与磁场⽅向垂直(D) 该磁场⼀定不均匀，且线圈的磁矩⽅向⼀定与磁场⽅向垂直[ ]注意见P325 第⼆段表述，11.36式12. ⽤细导线均匀密绕成长为l、半径为a（l >>a）、总匝数为N的螺线管，管内充满相对磁导率为的均匀磁介质，线圈中载有电流I，则管中任⼀点(A) 磁感应强度⼤⼩为(B) 磁感应强度⼤⼩为(C) 磁场强度⼤⼩为(D) 磁场强度⼤⼩为[ ]⼆. 填空题13.如图，电流元在P点产⽣的磁感应强度的⼤⼩为___________________.14. 真空中有⼀载有电流I的细圆线圈，则通过包围该线圈的闭合曲⾯S的磁通量Φ=________________. 若通过S⾯上某⾯元的磁通为，⽽线圈中电流增加为2I时，通过该⾯元的磁通为，则_______________.0 ； 1︰215. 如图，两平⾏⽆限长载流直导线中电流均为I，两导线间距为a，则两导线连线中点P的磁感应强度⼤⼩，磁感应强度沿图中环路L的线积分_______________________.0 ；16. 恒定磁场中，磁感应强度对任意闭合曲⾯的积分等于零，其数学表⽰式是____________，这表明磁感应线的特征是_________________________. ；闭合曲线17. ⼀长直螺线管是由直径的导线密绕⽽成，通以的电流，其内部的磁感应强度⼤⼩B =_____________________.（忽略绝缘层厚度）18. 带电粒⼦垂直磁感应线射⼊匀强磁场，它做______________运动；带电粒⼦与磁感应线成300⾓射⼊匀强磁场，则它做__________________运动；若空间分布有⽅向⼀致的电场和磁场，带电粒⼦垂直于场⽅向⼊射，则它做__________________运动.圆周；螺旋线；变螺距的螺旋线19. 在霍尔效应实验中，通过导电体的电流和的⽅向垂直（如图）.如果上表⾯的电势较⾼，则导电体中的载流⼦带___________电荷；如果下表⾯的电势较⾼，则导电体中的载流⼦带___________电荷.正；负20. 如图，⼀载流导线弯成半径为R的四分之⼀圆弧，置于磁感应强度为的均匀磁场中，导线所受磁场⼒⼤⼩为______________，⽅向为_____________.； y轴正向注意：积分IRBdθ，θ的积分上下限？21. 如图，半径为R的半圆形线圈通有电流I，线圈处在与线圈平⾯平⾏指向右的均匀磁场中，该载流线圈磁矩⼤⼩为___________，⽅向____________；线圈所受磁⼒矩的⼤⼩为_________________，⽅向_____________.；垂直纸⾯向外；；向上22. 磁场中某点，有⼀半径为R、载有电流I的圆形实验线圈，其所受的最⼤磁⼒矩为M，则该点磁感应强度的⼤⼩为_________________.注意见教材324页三. 计算题23. 如图，两长直导线互相垂直放置，相距为d，其中⼀根导线与z轴重合，另⼀与x轴平⾏且在Oxy平⾯内，设导线中皆通有电流I，求y轴上与两导线等距的P点处的磁感应强度.解：长直载流导线在距其r处的磁感应强度为两长直载流导线在P点产⽣的磁感应强度⽅向⼀沿z轴⽅向，⼀沿x轴负⽅向且⽅向平⾏于Oxz平⾯与Oxy⾯成45o，如图⽰。
《大学物理》11磁场习题解析共141页文档
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！
《大学物理》11磁场习题解 析
31、别人笑我太疯癫，我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣，抱怨者 的牢骚 ，这是 羊群中 的瘟疫 ，我不 能被它 传染。 我要尽 量避免 绝望， 辛勤耕 耘，忍 受苦楚 。我一 试再试 ，争取 每天的 成功， 避免以 失败收 常在别 人停滞 不前时 ，我继 续拼搏 。
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。Байду номын сангаас—培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
33、如果惧怕前面跌宕的山岩，生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ，睁大 眼睛， 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ，心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的，也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ，也不 要以为 过去的 光荣可 以被永 远肯定 。
11稳恒电流和稳恒磁场习题解答讲解
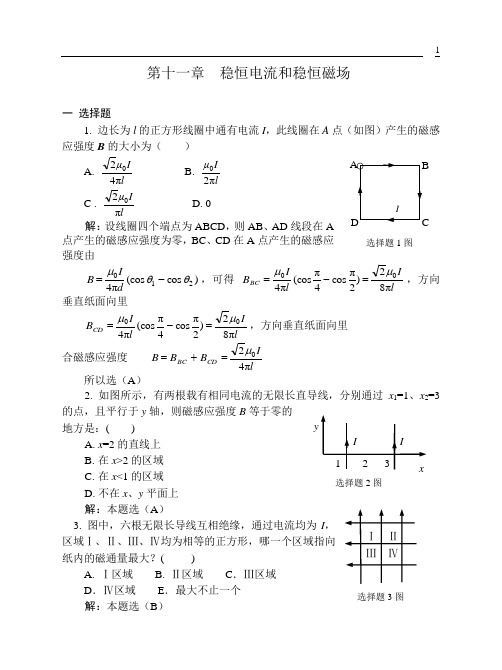
第十一章 稳恒电流和稳恒磁场一 选择题1. 边长为l 的正方形线圈中通有电流I ，此线圈在A 点（如图）产生的磁感应强度B 的大小为（ ）A. l I μπ420B. lIμπ20 C .lIμπ20 D. 0 解：设线圈四个端点为ABCD ，则AB 、AD 线段在A 点产生的磁感应强度为零，BC 、CD 在A 点产生的磁感应强度由)cos (cos π4210θθμ-=dIB ，可得 lIl IB BC π82)2πcos 4π(cosπ400μμ=-=，方向垂直纸面向里lI l I B CD π82)2πcos 4π(cos π400μμ=-=，方向垂直纸面向里合磁感应强度 lIB B B CD BC π420μ=+=所以选（A ）2. 如图所示，有两根载有相同电流的无限长直导线，分别通过x 1=1、x 2=3的点，且平行于y 轴，则磁感应强度B 等于零的地方是：( )A. x =2的直线上B. 在x >2的区域C. 在x <1的区域D. 不在x 、y 平面上 解：本题选（A ）3. 图中，六根无限长导线互相绝缘，通过电流均为I ，区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形，哪一个区域指向纸内的磁通量最大？( )A. Ⅰ区域B. Ⅱ区域 C ．Ⅲ区域D ．Ⅳ区域E ．最大不止一个解：本题选（B ）选择题2图Ⅰ Ⅱ Ⅲ Ⅳ 选择题3图选择题1图4. 如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知：（ ）A. ∮L B ·d l =0，且环路上任意一点B =0B. ∮L B ·d l =0，且环路上任意一点B ≠0C. ∮L B ·d l ≠0，且环路上任意一点B ≠0D. ∮L B ·d l ≠0，且环路上任意一点B =常量解：本题选（B ）5. 无限长直圆柱体，半径为R ，沿轴向均匀流有电流，设圆柱体内（r <R ）的磁感应强度为B i ，圆柱体外（r >R ）的磁感应强度为B e ，则有：（ ）A. B t 、B e 均与r 成正比B. B i 、B e 均与r 成反比C. B i 与r 成反比，B e 与r 成正比D. B i 与r 成正比，B e 与r 成反比解：导体横截面上的电流密度2πR IJ =，以圆柱体轴线为圆心，半径为r的同心圆作为安培环路，当r <R ，20ππ2r J r B i ⋅=⋅μ，20π2R IrB i μ=r <R ，I r B e ⋅=⋅0π2μ， rIB e π20μ=所以选（D ）6. 有三个质量相同的质点a 、b 、c ，带有等量的正电荷，它们从相同的高度自由下落，在下落过程中带电质点b 、c 分别进入如图所示的匀强电场与匀强磁场中，设它们落到同一水平面的动能分别为E a 、E b 、E c ，则（ ）A. E a <E b =E cB. E a =E b =E cC. E b >E a =E cD. E b >E c >E a解：由于洛伦兹力不做功，当它们落到同一水平面上时，对a 、c 只有重力做功， 则E a =E c ，在此过程中，对b 不仅有重力做功，电场力也要做正功，所以E b >E a =E c所以选（C ）7. 图为四个带电粒子在O 点沿相同方向垂直于磁力线射入均匀磁场后的偏转轨迹的照片，磁场方向垂直纸面向外，四个粒子的质量相等，电量大小也相等，则其中动能最大的带负电的粒子的轨迹是：( )A. OaB. ObC. Oc D . Od解：根据B F ⨯=v q ，从图示位置出发，带负选择题7图c dba B O• B× × × × × × Ea bc 选择题6图 选择题4图电粒子要向下偏转，所以只有Oc 、Od 满足条件，又带电粒子偏转半径Bqm R v=，22k 22qB m E R =∴，质量相同、带电量也相等的粒子，动能大的偏转半径大，所以选Oc 轨迹所以选（C ）8. 如图，一矩形样品，放在一均匀磁场中，当样品中的电流I 沿X 轴正向流过时，实验测得样品A 、A '两侧的电势差V A -V A '>0，设此样品的载流子带负电荷，则磁场方向为：（ ）A ． 沿X 轴正方向B ．沿X 轴负方向C ．沿Z 轴正方向D ．沿Z 轴负方向 解：本题选（C ）9. 长直电流I 2与圆形电流I 1共面，并与其一直径相重合如图（但两者间绝缘），设长直电流不动，则圆形电流将：（ ）A. 绕I 2旋转B. 向左运动C. 向右运动D. 向上运动E. 不动 解：圆形电流左半圆和右半圆受到长直电流安培力的方向均向右，所以圆形电流将向右运动所以选（C ）二 填空题1. 成直角的无限长直导线，流有电流I =10A ，在直角决定的平面内，距两段导线的距离都是a =20cm 处的磁感应强度B = 。
大学物理习题答案第十一章
[习题解答]11-7 在磁感应强度大小为B = 0.50 T 的匀强磁场中，有一长度为l = 1.5 m 的导体棒垂直于磁场方向放置，如图11-11所示。
如果让此导体棒以既垂直于自身的长度又垂直于磁场的速度v 向右运动，则在导体棒中将产生动生电动势。
若棒的运动速率v = 4.0 m ⋅s -1 ，试求：(1)导体棒内的非静电性电场K ；(2)导体棒内的静电场E ；(3)导体棒内的动生电动势ε的大小和方向；(4)导体棒两端的电势差。
解(1)根据动生电动势的表达式,由于()的方向沿棒向上，所以上式的积分可取沿棒向上的方向，也就是d l 的方向取沿棒向上的方向。
于是可得.另外，动生电动势可以用非静电性电场表示为.以上两式联立可解得导体棒内的非静电性电场，为,方向沿棒由下向上。
图11-11(2)在不形成电流的情况下，导体棒内的静电场与非静电性电场相平衡，即,所以，E 的方向沿棒由上向下，大小为.(3)上面已经得到,方向沿棒由下向上。
(4)上述导体棒就相当一个外电路不通的电源，所以导体棒两端的电势差就等于棒的动生电动势，即,棒的上端为正，下端为负。
11-8 如图11-12所表示，处于匀强磁场中的导体回路ABCD ，其边AB 可以滑动。
若磁感应强度的大小为B = 0.5 T ，电阻为R = 0.2 Ω，AB 边长为 l = 0.5 m ，AB 边向右平移的速率为v = 4 m ⋅s -1 ，求：(1)作用于AB 边上的外力；(2)外力所消耗的功率；(3)感应电流消耗在电阻R 上的功率。
解(1)当将AB 向右拉动时，AB 中会有电流通过，流向为从B 到A 。
AB 中一旦出现电流，就将受到安培力F 的作用，安培力的方向为由右向左。
所以，要使AB 向右移动，必须对AB施加由左向右图11-12的力的作用，这就是外力F外。
在被拉动时，AB中产生的动生电动势为,电流为.AB所受安培力的大小为,安培力的方向为由右向左。
外力的大小为,外力的方向为由左向右。
川师大学物理第十一章-恒定电流的磁场习题解
第十一章 恒定电流的磁场11–1 如图11-1所示，几种载流导线在平面内分布，电流均为I ，求它们在O 点处的磁感应强度B 。
（1）高为h 的等边三角形载流回路在三角形的中心O 处的磁感应强度大小为 ，方向 。
（2）一根无限长的直导线中间弯成圆心角为120°，半径为R 的圆弧形，圆心O 点的磁感应强度大小为 ，方向 。
…解：（1）如图11-2所示，中心O 点到每一边的距离为13OP h =，BC 边上的电流产生的磁场在O 处的磁感应强度的大小为012(cos cos )4πBC I B dμββ=-^IB21图11–2图11–1…B（a ）AE（b ）0(cos30cos150)4π/3Ih μ︒︒=-=方向垂直于纸面向外。
另外两条边上的电流的磁场在O 处的磁感应强度的大小和方向都与BC B 相同。
因此O 处的磁感应强度是三边电流产生的同向磁场的叠加，即3BC B B ===方向垂直于纸面向外。
（2）图11-1（b ）中点O 的磁感强度是由ab ，bcd ，de 三段载流导线在O 点产生的磁感强度B 1，B 2和B 3的矢量叠加。
由载流直导线的磁感强度一般公式012(cos cos )4πIB dμββ=- 可得载流直线段ab ，de 在圆心O 处产生的磁感强度B 1，B 3的大小分别为01(cos0cos30)4cos60)IB R μ︒=︒-︒π(0(12πI R μ=-031(cos150cos180)4πcos60IB B R μ︒==︒-︒0(12πI R μ=-】方向垂直纸面向里。
半径为R ，圆心角α的载流圆弧在圆心处产生的磁感强度的大小为04πI B Rμα=圆弧bcd 占圆的13，所以它在圆心O 处产生的磁感强度B 2的大小为00022π34π4π6II I B R R Rμμαμ===方向垂直纸面向里。
因此整个导线在O 处产生的总磁感强度大小为000012333(1)(1)0.212π22π26I I I I B B B B R R R Rμμμμ=++=-+-+=方向垂直纸面向里。
普通物理学第五版第11章磁场答案题.
结束
目录
11-5 如图所示的被折成钝角的长导线 中通有20A的电流。求：A点的磁感应强度。 设 d = 2cm, a =1200
Q
A
a
d
O
I
P
结束
目录
已知： I = 20A d = 2cm 求：B A 解： B A = B OP + B OQ
a = 120
Q d
0
A
B OP =0
0
a P O I
I1
I2
结束
目录
已知：I 1 = I 2 = 10A 求：B P
解：
m I1 B 1P = B 2P = πa 2
0
P I 1 P I 2 a = 0.5m B 2P P BP a B 2P a I1 I2
2 B P = B 1P +B 2 P = 2 B 1P 2
-7×10 × 10 2×4 π -6 T 5.66 × 10 = = π× 0.50 2 B 2P q = arc tg 45 = B 1P
结束
目录
已知： B=1 求： Φ 解：
Wb/m2
S = 2m
2
(1) Φyz = B . S = B S = 1×2 = 2Wb
(2) Φxz = B . S = B S cos 900 y n
45 0
(3) Φ y = B . S = B S cos 45 0 2 =1×2 × 2 = 1.41Wb
11-1 在地球北半球的某区域,磁感应强 度的大小为4×10-5 T,方向与铅直线成600角 求: (1)穿过面积为1m2的水平面的磁通量; (2)穿过面积为1m2的竖直平面的磁通量的 最大值和最小值
第十一章稳恒电流的磁场(一)作业解答
一、利用毕奥—萨法尔定律计算磁感应强度毕奥—萨法尔定律：304r rl Id B d⨯=πμ1.有限长载流直导线的磁场)cos (cos 4210ααπμ-=a I B ,无限长载流直导线a IB πμ20=半无限长载流直导线a IB πμ40=,直导线延长线上0=B2. 圆环电流的磁场232220)(2x R IR B +=μ，圆环中心R I B 20μ=，圆弧中心πθμ220∙=R I B电荷转动形成的电流：πωωπ22q q T q I === 【 】基础训练1、载流的圆形线圈(半径a 1 )与正方形线圈(边长a 通有相同电流I ．如图若两个线圈的中心O 1 、O 2处的磁感强度大小相同，则半径a 1与边长a 2之比a 1∶a 2为 (A) 1∶1 (B) π2∶1 (C) π2∶4 (D) π2∶8【 】基础训练3、有一无限长通电流的扁平铜片，宽度为a ，厚度不计，电流I 在铜片上均匀分布，在铜片外与铜片共面，离铜片右边缘为b 处的P 点的磁感强度B的大小为(A))(20b a I+πμ． (B)b b a aI +πln20μ．(C) b b a b I +πln 20μ． (D) )2(0b a I+πμ． 解法：【 】自测提高2、通有电流I 的无限长直导线有如图三种形状，则P ，Q ，O 各点磁感强度的大小B P ，B Q ，B O 间的关系为 (A) B P > B Q > B O . (B) B Q > B P > B O ． B Q > B O > B P ． (D) B O > B Q > B P ． 解法：根据直线电流的磁场公式和圆弧电流产生磁场公式可得【 】自测提高7、边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷．此正方形以角速度ω 绕AC 轴旋转时，在中心O 点产生的磁感强度大小为B 1；此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时，在O 点产生的磁感应强度的大小为B 2，则B 1与B 2间的关系为 (A) B 1 = B 2． (B) B 1 = 2B 2． (C) B 1 = 21B 2． (D) B 1 = B 2 /4． 解法：设正方形边长为a ω 相同，所以每个点电荷随着正方形旋转时形成的等效电流相同， 为当正方形绕AC 轴旋转时，一个点电荷在O 旋转产生电流，在O 点产生的总磁感小为O 点产生的磁感应强度的大小为基础训练12、一长直载流导线，沿空间直角坐标Oy 轴放置，电流沿y 正向．在原点O 处取一电流元l Id ，则该电流元在(a ，0，0)点处的磁感强度的大小为 ，方向为 。
利用“分解磁场”解题的方法
利用“分解磁场”解题的方法1. 磁场的分解原理磁场可以被分解为平行分量和垂直分量。
平行分量指的是磁场沿着特定方向的分量，垂直分量指的是磁场与特定方向垂直的分量。
通过将磁场分解为这两个分量，我们可以更好地理解和处理磁场问题。
2. 问题的分解与解答在解题过程中，我们可以根据具体问题的要求将磁场进行适当的分解，并分别分析和处理每个分量。
以下是一些常见问题的解答示例：2.1. 磁场的叠加问题当有多个磁场同时存在时，我们可以将它们的分量分别求和得到最终的结果。
假设有两个磁场A和B，它们的磁场矢量分别为A和B。
我们可以将每个磁场的矢量分解为平行分量Ax、Bx和垂直分量Ay、By。
然后，将平行分量和垂直分量分别求和得到最终的结果，即A = Ax + Ay，B = Bx + By。
通过这种方式，我们可以简化叠加磁场的问题。
2.2. 磁场的影响问题当一个磁场对物体产生影响时，我们可以将该磁场分解为平行分量和垂直分量，并分别对它们的影响进行分析。
通过这种方式，我们可以更好地理解和解答磁场的影响问题。
2.3. 磁场的计算问题在某些情况下，我们需要计算磁场的大小和方向。
利用“分解磁场”的方法，我们可以将磁场分解为不同方向的分量，并利用相应的计算公式求解每个分量的大小。
然后，将每个分量的大小和方向合并，得到最终的结果。
3. 注意事项在利用“分解磁场”解题的过程中，需要注意以下几点：- 确保正确地分解磁场为平行分量和垂直分量，避免出现计算错误。
- 理解和运用磁场的相关知识和公式，以便正确地处理每个分量。
- 仔细分析和理解问题的要求，将磁场进行适当的分解，以便更好地解答问题。
总结利用“分解磁场”解题的方法是物理学中常用且有效的策略之一。
通过将磁场分解为不同部分，我们可以更好地理解和处理磁场问题，解答各种与磁场相关的问题。
在运用该方法时，需要正确地分解磁场，理解磁场的特性，并仔细分析问题的要求。
这样，我们可以更好地应用“分解磁场”解题的方法，提高解决问题的效率和准确性。
第11章 稳恒磁场
z
D
无限长载流长直导线的磁场 无限长载流长直导线的磁场. 载流长直导线的磁场
θ2
v B
B=
4 π r0
（cosθ 1 − cosθ 2 ）
B=
I
o
µ0 I
2 π r0
θ1 → 0 θ2 → π
x
C
θ1
P y
无限长载流长直导线的磁场
B=
µ0I
2πr
I B
I
X
B
电流与磁感应 电流与磁感应强度成右螺旋关系 半无限长载流长直导线的磁场
=
I
2π R
v B
o
l
R
v v ∫ B ⋅ dl =
l
∫ 2πR
µ0 I
v dl
dl
v v µ0 I ∫l B ⋅ d l = 2 π R ∫l d l v v 设闭合回路 l 为圆形 ∫l B ⋅ dl = µ0 I 回路（ 成右螺旋） 回路（ l 与 I 成右螺旋）
I
o
v B
R
若回路绕向为顺时针时， 若回路绕向为顺时针时，则
z
带电粒子在磁场中沿其他方向运动时 F 垂直于 v 与特定直线所组成的平面 与特定直线所组成的平面. 当带电粒子在磁场中垂直于此特定直线运动 时受力最大. 时受力最大
F = Fmax = F⊥
Fmax ∝ qv
Fmax q , v 无关 qv 大小与
磁感应 的定义： 磁感应强度 B 的定义：当 正电荷垂直于 特定直线运动 时，受力 Fmax 将 Fmax ×v 方向 的方向. 定义为该点的 B 的方向
I I I
I S S N I N
磁通量 磁场的高斯定理
v ∆S B
大学物理第十一章习题解答..
第十一章：恒定电流的磁场习题解答1．题号：40941001分值：10分如下图所示，是一段通有电流I 的圆弧形导线，它的半径为R ，对圆心的张角为θ。
求该圆弧形电流所激发的在圆心O 处的磁感强度。
解答及评分标准：在圆弧形电流中取一电流元l Id （1分），则该电流元l Id 在圆心处的磁感强度为： θπμπμd R I RIdl dB 490sin 40020==（2分） 其中θRd dl =则整段电流在圆心处的磁感强度为：θπμθπμθR I d R I dB B 44000===⎰⎰（2分）2．题号：40941002分值：10分一无限长的载流导线中部被弯成圆弧形，如图所示，圆弧形半径为cm R 3=，导线中的电流为A I 2=。
求圆弧形中心O 点的磁感应强度。
解答及评分标准：两根半无限长直电流在O 点的磁感应强度方向同为垂直图面向外，大小相等，以垂直图面向里为正向，叠加后得RI R I B πμπμ242001-=•-= （3分） 圆弧形导线在O 点产生的磁感应强度方向垂直图面向里，大小为R I R I B 83432002μμ==（3分） 二者叠加后得 T RI R I B B B 500121081.1283-⨯=-=+=πμμ （3分） 方向垂直图面向里。
（1分）3．题号：40941003分值：10分难度系数等级：1一段导线先弯成图（a ）所示形状，然后将同样长的导线再弯成图（b ）所示形状。
在导线通以电流I 后，求两个图形中P 点的磁感应强度之比。
（a ） （b ）解答及评分标准：图中（a ）可分解为5段电流。
处于同一直线的两段电流对P 点的磁感应强度为零，其他三段在P 点的磁感应强度方向相同。
长为l 的两段在P 点的磁感应强度为 lI B πμ4201= （2分） 长为2l 的一段在P 点的磁感应强度为 l I B πμ4202=（2分） 所以lI B B B πμ22012=+= （2分） 图（b ）中可分解为3段电流。
大学物理答案第11章
第十一章 恒定磁场11－1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管，两个螺线管的长度相同，R ＝2r ，螺线管通过的电流相同为I ，螺线管中的磁感强度大小r R B B 、满足（ ）（A ） r R B B 2= （B ） r R B B = （C ） r R B B =2 （D ）r R B B 4=分析与解 在两根通过电流相同的螺线管中，磁感强度大小与螺线管线圈单位长度的匝数成正比．根据题意，用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为（C ）.11－2 一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量 为（ ）（A ）B r 2π2 （B ） B r 2π（C ）αB r cos π22（D ） αB r cos π2题 11-2 图分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面，根据磁场的高斯定理，磁感线是闭合曲线，闭合曲面的磁通量为零，即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量；S B ⋅=m Φ．因而正确答案为（D ）．11－3 下列说法正确的是（ ）（A ） 闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过 （B ） 闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零 （C ） 磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D ） 磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零 分析与解 由磁场中的安培环路定律，磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度不一定为零；闭合回路上各点磁感强度为零时，穿过回路的电流代数和必定为零.因而正确答案为（B ）．11－4 在图（ａ）和（ｂ）中各有一半径相同的圆形回路L1 、L2 ，圆周内有电流I1 、I2 ，其分布相同，且均在真空中，但在（ｂ）图中L2 回路外有电流I3 ，P 1 、P 2 为两圆形回路上的对应点，则（ ）（A ） ⎰⎰⋅=⋅21L L d d l B l B ，21P P B B =（B ） ⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B = （C ） ⎰⎰⋅=⋅21L L d d l B l B ，21P P B B ≠ （D ） ⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B≠题 11-4 图分析与解 由磁场中的安培环路定律，积分回路外的电流不会影响磁感强度沿回路的积分；但同样会改变回路上各点的磁场分布．因而正确答案为（C ）．11－5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中，若导体中流过的恒定电流为I ，磁介质的相对磁导率为μｒ （μｒ＜1），则磁介质内的磁化强度为（ ） （A ）()r I μr π2/1-- （B ） ()r I μr π2/1- （C ） r I μr π2/- （D ） r μI r π2/分析与解 利用安培环路定理可先求出磁介质中的磁场强度，再由M ＝（μｒ－1）H 求得磁介质内的磁化强度，因而正确答案为（B ）．11－6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道，当环中电子流强度为8 mA 时，在整个环中有多少电子在运行？ 已知电子的速率接近光速. 分析 一个电子绕存储环近似以光速运动时，对电流的贡献为c I e I /Δ=，因而由lNec I =，可解出环中的电子数.解 通过分析结果可得环中的电子数10104⨯==ecIlN 11－7 已知铜的摩尔质量M ＝63.75 ｇ·mol －1，密度ρ ＝8.9 g · cm －3，在铜导线里，假设每一个铜原子贡献出一个自由电子，（1）为了技术上的安全，铜线内最大电流密度26.0A mm m j -=⋅ ，求此时铜线内电子的漂移速率v d ；（2） 在室温下电子热运动的平均速率是电子漂移速率v d 的多少倍？分析 一个铜原子的质量A N M m /=,其中N A 为阿伏伽德罗常数，由铜的密度ρ 可以推算出铜的原子数密度m ρn /=根据假设，每个铜原子贡献出一个自由电子，其电荷为e ，电流密度d m ne j v = ．从而可解得电子的漂移速率v d ．将电子气视为理想气体，根据气体动理论，电子热运动的平均速率em kTπ8=v 其中k 为玻耳兹曼常量，m e 为电子质量．从而可解得电子的平均速率与漂移速率的关系．解 （1） 铜导线单位体积的原子数为M ρN n A /=电流密度为j m 时铜线内电子的漂移速率14A s m 1046.4--⋅⨯===eN M j ne j m m d ρv （2） 室温下（T ＝300 Ｋ）电子热运动的平均速率与电子漂移速率之比为81042.2π81⨯≈=edd m kTv v v 室温下电子热运动的平均速率远大于电子在恒定电场中的定向漂移速率．电子实际的运动是无规热运动和沿电场相反方向的漂移运动的叠加．考虑到电子的漂移速率很小，电信号的信息载体显然不会是定向漂移的电子．实验证明电信号是通过电磁波以光速传递的． 11－8 有两个同轴导体圆柱面，它们的长度均为20 m ，内圆柱面的半径为3.0 mm ，外圆柱面的半径为9.0 mm.若两圆柱面之间有10 μA 电流沿径向流过，求通过半径为6.0 mm 的圆柱面上的电流密度．题 11-8 图分析 如图所示是同轴柱面的横截面，电流密度j 对中心轴对称分布．根据恒定电流的连续性，在两个同轴导体之间的任意一个半径为r 的同轴圆柱面上流过的电流I都相等，因此可得rlI j π2=解 由分析可知，在半径r ＝6.0 mm 的圆柱面上的电流密度2m A μ3.13π2-⋅==rlIj 11－9 如图所示，已知地球北极地磁场磁感强度B 的大小为6.0×10－5T ．如设想此地磁场是由地球赤道上一圆电流所激发的，此电流有多大？ 流向如何？解 设赤道电流为I ，则由教材第11－4节例2 知，圆电流轴线上北极点的磁感强度()RIRR IR B 24202/32220μμ=+=因此赤道上的等效圆电流为A 1073.12490⨯==μRBI 由于在地球地磁场的Ｎ 极在地理南极，根据右手螺旋法则可判断赤道圆电流应该是由东向西流，与地球自转方向相反．题 11-9 图11－10 如图所示，有两根导线沿半径方向接触铁环的a 、b 两点，并与很远处的电源相接.求环心O 的磁感强度．题 11-10 图分析 根据叠加原理，点O 的磁感强度可视作由ef 、be 、fa 三段直线以及acb 、a d b 两段圆弧电流共同激发．由于电源距环较远，0=ef B ．而be 、fa 两段直线的延长线通过点O ，由于0Idl r ⨯=，由毕奥－萨伐尔定律知0be fa ==B B ．流过圆弧的电流I 1 、I 2的方向如图所示，两圆弧在点O 激发的磁场分别为21101π4r l I μB =,22202π4r l I μB = 其中l 1 、l 2 分别是圆弧acb 、a d b 的弧长，由于导线电阻R 与弧长l 成正比，而圆弧acb 、a d b又构成并联电路，故有2211l I l I =将21B B 、叠加可得点O 的磁感强度B ． 解 由上述分析可知，点O 的合磁感强度0π4π42220211021=-=-=r l I μr l I μB B B 11－11 如图所示，几种载流导线在平面内分布，电流均为I ，它们在点O 的磁感强度各为多少？题 11-11 图分析 应用磁场叠加原理求解．将不同形状的载流导线分解成长直部分和圆弧部分，它们各自在点O 处所激发的磁感强度较容易求得，则总的磁感强度∑=iB B 0.解 （ａ） 长直电流对点O 而言，有0d =⨯rl I ，因此它在点O 产生的磁场为零，则点O 处总的磁感强度为1/4 圆弧电流所激发，故有RIμB 800=B 0 的方向垂直纸面向外．（ｂ） 将载流导线看作圆电流和长直电流，由叠加原理可得RIμR I μB π22000-=B 0 的方向垂直纸面向里．（c ） 将载流导线看作1/2 圆电流和两段半无限长直电流，由叠加原理可得RIμR I μR I μR I μR I μB 4π24π4π4000000+=++=B 0 的方向垂直纸面向外．11－12 载流导线形状如图所示（图中直线部分导线延伸到无穷远），求 点O 的磁感强度B ．题 11-12 图分析 由教材11－4 节例题2的结果不难导出，圆弧载流导线在圆心激发的磁感强度RαI μB π40=，其中α为圆弧载流导线所张的圆心角，磁感强度的方向依照右手定则确定；半无限长载流导线在圆心点O 激发的磁感强度R IμB π40=，磁感强度的方向依照右手定则确定.点O 的磁感强度O B 可以视为由圆弧载流导线、半无限长载流导线等激发的磁场在空间点O 的叠加. 解 根据磁场的叠加 在图（ａ）中，k i k k i B RI μR I μR I μR I μR I μπ24π4π44000000--=---= 在图（ｂ）中，k i k i i B RI μR I μR I μR I μR I μπ41π14π44π4000000-⎪⎭⎫ ⎝⎛+-=---= 在图（c ）中，k j i B RIμR I μR I μπ4π4830000---= 11－13 如图(a)所示，载流长直导线的电流为I ，试求通过矩形面积的磁通量．题 11-13 图分析 由于矩形平面上各点的磁感强度不同，故磁通量Φ≠BS ．为此，可在矩形平面上取一矩形面元d S ＝l d x ，如图（ｂ）所示，载流长直导线的磁场穿过该面元的磁通量为x l xId π2d d 0μ=⋅=ΦS B矩形平面的总磁通量ΦΦ⎰=d解 由上述分析可得矩形平面的总磁通量⎰==Φ211200lnπ2d π2d dd d Ilx l xIμμ 11－14 已知10 mm 2裸铜线允许通过50 A 电流而不会使导线过热．电流在导线横截面上均匀分布．求导线内、外磁感强度的分布.题 11-14 图分析 可将导线视作长直圆柱体，电流沿轴向均匀流过导体，故其磁场必然呈轴对称分布，即在与导线同轴的圆柱面上的各点，B 大小相等、方向与电流成右手螺旋关系．为此，可利用安培环路定理，求出导线表面的磁感强度．解 围绕轴线取同心圆为环路L ，取其绕向与电流成右手螺旋关系，根据安培环路定理，有∑⎰=⋅=⋅I μB 0πr 2d l B在导线内r ＜R ， 2222ππRIr r R I I ==∑，因而 202πR IrμB =在导线外r ＞R ，I I =∑，因而rIμB 2π0=磁感强度分布曲线如图所示．11－15 有一同轴电缆，其尺寸如图（ａ）所示．两导体中的电流均为I ，但电流的流向相反，导体的磁性可不考虑．试计算以下各处的磁感强度：（1） r ＜R 1 ；（2） R 1 ＜r ＜R 2 ；（3） R 2 ＜r ＜R 3 ；（4） r ＞R 3 ．画出B －r 图线．题 11-15 图分析 同轴电缆导体内的电流均匀分布，其磁场呈轴对称，取半径为r 的同心圆为积分路径，πr 2d ⋅=⋅⎰B l B ，利用安培环路定理∑⎰=⋅I μ0d l B ，可解得各区域的磁感强度．解 由上述分析得r ＜R 122101ππ12πr R μr B =⋅ 21012πR Ir μB =R 1 ＜r ＜R 2I μr B 022π=⋅rI μB 2π02=R 2 ＜r ＜R 3()()⎥⎦⎤⎢⎣⎡---=⋅I R R R r I μr B 22232203ππ2π 2223223032πR R r R r I μB --= r ＞R 3()02π04=-=⋅I I μr B04=B磁感强度B （r ）的分布曲线如图（ｂ）．11－16 如图所示，N 匝线圈均匀密绕在截面为长方形的中空骨架上．求通入电流I 后，环内外磁场的分布．题 11-16 图分析 根据右手螺旋法则，螺线管内磁感强度的方向与螺线管中心轴线构成同心圆，若取半径为r 的圆周为积分环路，由于磁感强度在每一环路上为常量，因而πr 2d ⋅=⋅⎰B l B依照安培环路定理∑⎰=⋅I μ0d l B ，可以解得螺线管内磁感强度的分布．解 依照上述分析，有∑=⋅I μr B 02πr ＜R 102π1=⋅r B01=BR 2 ＞r ＞R 1NI μr B 022π=⋅rNI μB 2π02=r ＞R 202π3=⋅r B 03=B在螺线管内磁感强度B 沿圆周，与电流成右手螺旋．若112R R R <<- 和R 2 ，则环内的磁场可以近似视作均匀分布，设螺线环的平均半径()1221R R R +=，则环内的磁感强度近似为 RNIμB 2π0≈11－17 电流I 均匀地流过半径为R 的圆形长直导线，试计算单位长度导线内的磁场通过图中所示剖面的磁通量．题 11-17 图分析 由题11－14 可得导线内部距轴线为r 处的磁感强度()202πR Irμr B =在剖面上磁感强度分布不均匀，因此，需从磁通量的定义()S B d ⎰=r Φ来求解．沿轴线方向在剖面上取面元ｄS ＝l ｄr ，考虑到面元上各点B 相同，故穿过面元的磁通量ｄΦ＝B ｄS ，通过积分，可得单位长度导线内的磁通量⎰=Sr B Φd解 由分析可得单位长度导线内的磁通量4πd 2π0020Iμr R Ir μΦR==⎰11－18 已知地面上空某处地磁场的磁感强度40.410T B -=⨯，方向向北．若宇宙射线中有一速率715.010m s -=⨯v 的质子，垂直地通过该处．求：（1）洛伦兹力的方向；（2） 洛伦兹力的大小，并与该质子受到的万有引力相比较．题 11-18 图解 （1） 依照B F ⋅=v q L 可知洛伦兹力L F 的方向为B ⊥v 的方向，如图所示． （2） 因B ⊥v ，质子所受的洛伦兹力N 102.316-⨯==B F v q L在地球表面质子所受的万有引力N 1064.126p -⨯==g m G因而，有101095.1/⨯=G F L ，即质子所受的洛伦兹力远大于重力．11－19 霍尔效应可用来测量血流的速度，其原理如图所示．在动脉血管两侧分别安装电极并加以磁场．设血管直径为d ＝2.0 mm ，磁场为B ＝0.080 T ，毫伏表测出血管上下两端的电压为U H ＝0.10 mV ，血流的流速为多大？题 11-19 图分析 血流稳定时，有H qE B q =v由上式可以解得血流的速度． 解 依照分析m/s 63.0===dBU B E HH v 11－20 带电粒子在过饱和液体中运动，会留下一串气泡显示出粒子运动的径迹．设在气泡室有一质子垂直于磁场飞过，留下一个半径为3.5 cm 的圆弧径迹，测得磁感强度为0.20 Ｔ，求此质子的动量和动能．解 根据带电粒子回转半径与粒子运动速率的关系有m /s kg 1012.121⋅⨯===-ReB m p vkeV 35.222==mp E k11－21 从太阳射来的速度为0.80×108m/ｓ 的电子进入地球赤道上空高层范艾伦辐射带中，该处磁场为4.0 ×10－7Ｔ，此电子回转轨道半径为多大？ 若电子沿地球磁场的磁感线旋进到地磁北极附近，地磁北极附近磁场为2.0 ×10－5Ｔ，其轨道半径又为多少？ 解 由带电粒子在磁场中运动的回转半径高层范艾伦辐射带中的回转半径m 101.1311⨯==eB m R v地磁北极附近的回转半径m 2322==eB m R v11－22 如图（ａ）所示，一根长直导线载有电流I 1 ＝30 A ，矩形回路载有电流I 2 ＝20 A ．试计算作用在回路上的合力．已知d ＝1.0 cm ，b ＝8.0 cm ，l ＝0.12 m ．题 11-22图分析 矩形上、下两段导线受安培力F 1 和F 2 的大小相等，方向相反，对不变形的矩形回路来说，两力的矢量和为零．而矩形的左右两段导线，由于载流导线所在处磁感强度不等，所受安培力F 3 和F 4 大小不同，且方向相反，因此线框所受的力为这两个力的合力．解 由分析可知，线框所受总的安培力F 为左、右两边安培力F 3 和F 4 之矢量和，如图（ｂ）所示，它们的大小分别为d lI I μF π22103=()b d l I I μF +=π22104故合力的大小为()N 1028.1π2π2321021043-⨯=+-=-=b d lI I μd l I I μF F F 合力的方向朝左，指向直导线．11－23 一直流变电站将电压为500kV 的直流电，通过两条截面不计的平行输电线输向远方．已知两输电导线间单位长度的电容为3.0×10－11F ·m －1，若导线间的静电力与安培力正好抵消．求：（1） 通过输电线的电流；（2） 输送的功率．分析 当平行输电线中的电流相反时，它们之间存在相互排斥的安培力，其大小可由安培定律确定．若两导线间距离为d ，一导线在另一导线位置激发的磁感强度dIμB π20=,导线单位长度所受安培力的大小BI F B =．将这两条导线看作带等量异号电荷的导体，因两导线间单位长度电容C 和电压U 已知，则单位长度导线所带电荷λ＝CU ，一导线在另一导线位置所激发的电场强度dελE 0π2=，两导线间单位长度所受的静电吸引力λE F E =．依照题意，导线间的静电力和安培力正好抵消，即0=+E B F F从中可解得输电线中的电流．解 （1） 由分析知单位长度导线所受的安培力和静电力分别为d I μBI F B π220==dεU C λE F E 022π2== 由0=+E BF F 可得dεU C d I μ02220π2π2=解得A 105.4300⨯==μεCUI （2） 输出功率W 1025.29⨯==IU N11－24 在氢原子中，设电子以轨道角动量π2/h L =绕质子作圆周运动，其半径为m 1029.5110-⨯=a ．求质子所在处的磁感强度．h 为普朗克常量，其值为s J 1063.634⋅⨯-分析 根据电子绕核运动的角动量π20h a m L ==v 可求得电子绕核运动的速率v ．如认为电子绕核作圆周运动，其等效圆电流v/π20a e T e i ==在圆心处，即质子所在处的磁感强度为02a i μB =解 由分析可得，电子绕核运动的速率π2ma h=v其等效圆电流2020π4/π2ma he v a e i ==该圆电流在圆心处产生的磁感强度T 5.12π82202000===ma heμa i μB 11－25 如图[a]所示，一根长直同轴电缆，内、外导体之间充满磁介质，磁介质的相对磁导率为μr （μr ＜1），导体的磁化可以忽略不计．沿轴向有恒定电流I 通过电缆，内、外导体上电流的方向相反．求：（1） 空间各区域内的磁感强度和磁化强度；*（2） 磁介质表面的磁化电流．题 11-25 图分析 电流分布呈轴对称，依照右手定则，磁感线是以电缆对称轴线为中心的一组同心圆．选取任一同心圆为积分路径，应有⎰⋅=⋅r H d π2l H ，利用安培环路定理⎰∑=⋅fI d l H求出环路内的传导电流，并由H μB =，()H μM r 1-=，可求出磁感强度和磁化强度．再由磁化电流的电流面密度与磁化强度的关系求出磁化电流．解 （1） 取与电缆轴同心的圆为积分路径，根据磁介质中的安培环路定理，有∑=fπ2I r H对r ＜R 1221f ππrR I I =∑ 得2112πR IrH =忽略导体的磁化（即导体相对磁导率μr =1），有01=M ，21012πR IrμB =对R 2 ＞r ＞R 1I I=∑f得rI H 2π2=填充的磁介质相对磁导率为μr ，有()r I μM r 2π12-=，rI μμB r 2π02= 对R 3 ＞r ＞R 2()()2223223ππR r R R I I I f -⋅--=∑ 得()()222322332πR R r r R I H --= 同样忽略导体的磁化，有03=M ，()()2223223032πR R r r R I μB --= 对r ＞R 30=-=∑I I If得04=H ，04=M ，04=B（2） 由r M I s 2π⋅=，磁介质内、外表面磁化电流的大小为()()I μR R M I r si 12π112-=⋅= ()()I μR R M I r se 12π222-=⋅=对抗磁质（1r μ<），在磁介质内表面（r ＝R 1 ），磁化电流与内导体传导电流方向相反；在磁介质外表面（r ＝R 2 ），磁化电流与外导体传导电流方向相反．顺磁质的情况与抗磁质相反．H （r ）和B （r ）分布曲线分别如图（ｂ）和（c ）所示．。
第十一章 恒定电流的磁场(二)作业答案
一、 选择题【 C 】1.（基础训练2）三条无限长直导线等距地并排安放，导线Ⅰ、Ⅱ、Ⅲ分别载有1 A ，2 A ，3 A 同方向的电流．由于磁相互作用的结果，导线Ⅰ，Ⅱ，Ⅲ单位长度上分别受力F 1、F 2和F 3，如图所示．则F 1与F 2的比值是：(A) 7/16． (B) 5/8． (C) 7/8． (D) 5/4．【答】设导线Ⅰ、Ⅱ、Ⅲ的电流强度分别为321,,I I I ，产生的磁感应强度分别为321,,B B B ，相邻导线相距为a ，则()()0203011123110301022231227,2224222II F I l B B I l a a a I I F I l B B I l a a aμμμπππμμμπππ⎛⎫=+=+= ⎪⋅⎝⎭⎛⎫=-=-= ⎪⎝⎭式中121231, 1, I 1A, I 2A, I 3A l m l m =====，得 8/7/21=F F .【 D 】2. (基础训练6)两个同心圆线圈，大圆半径为R ，通有电流I 1；小圆半径为r ，通有电流I 2，方向如图．若r << R (大线圈在小线圈处产生的磁场近似为均匀磁场)，当它们处在同一平面内时小线圈所受磁力矩的大小为 (A) Rr I I 22210πμ． (B)Rr I I 22210μ． (C)rR I I 22210πμ． (D) 0．【答】大圆电流在圆心处的磁感应强度为，方向垂直纸面朝内2RI B 101μ=； 小圆电流的磁矩为方向垂直纸面朝内，,222r I p m π=所以，小圆电流受到的磁力矩的大小为2211sin 00m m M p B p B =⨯=︒=[ B ]3.（自测提高2）如图所示，一电子以速度v垂直地进入磁感强度为B的均匀磁场中，此电子在磁场中运动轨道所围的面积内的磁通量将(A) 正比于B ，反比于v 2． (B) 反比于B ，正比于v 2． (C)正比于B ，反比于v ． (D) 反比于B ，反比于v ．【答】 电子在磁场中做匀速率圆周运动，运动平面的法向平行于磁感应强度方向，因此，磁通量为2R B πΦ=，其中半径R 可由式2v evB m R =求得：mv R eB =，所以222mv m v B eB eB ππ⎛⎫Φ== ⎪⎝⎭.F 1F 2F 31 A2 A3 A ⅠⅡⅢOrR I 1 I 2[ B ]4、（自测提高4）一个动量为p 的电子，沿图示方向入射并能穿过一个宽度为D 、磁感强度为B(方向垂直纸面向外)的均匀磁场区域，则该电子出射方向和入射方向间的夹角为 (A)p eBD 1cos-=α．(B)p eBD 1sin -=α． (C)epBD 1sin -=α． (D) ep BD 1cos -=α．【答】电子在磁场中的轨迹为一段圆弧，如图。
大学普通物理学习题答案-第十一章-恒定电流与恒定磁场
第十一章恒定电流与恒定磁场一、选择题1.如图11-1所示，有两根载有相同电流的无限长直导线，分别通过x1=1m、x2=3m的点，且平行于y轴，则磁感应强度B等于零的地方是（）。
A.x=2m的直线上B.在x>2m的区域C.在x<1m的区域D.不在x、y平面上图11-11.【答案】A。
解析：根据对称性可得，两条载流导线在x=2m的直线上产生的磁感应强度大小相等；用右手螺旋定则可判断两磁感应强度的方向相反，相互抵消，合磁感应强度为零，故选A。
2.图11-2中6根无限长导线互相绝缘，通过电流均为I，区域Ⅰ、Ⅰ、Ⅰ、Ⅰ均为全等的正方形，哪一个区域指向纸内的磁通量最大（）。
A. Ⅰ区域B. Ⅰ区域C. Ⅰ区域D. Ⅰ区域2.【答案】B。
解析：通过Ⅰ区域的磁通量为0，通过Ⅰ区城的磁通量最大且指向纸内，通过Ⅰ区域的磁通量最大但指向纸外，通过IV区域的磁通量为0。
故选B。
3.如图11-3所示，在一圆形电流I所在的平面内，选取一个同心圆形闭合回路L，则由安培环路定理可知（）。
A.d 0LB l ⋅=⎰，且环路上任意一点B =0 B.d 0LB l ⋅=⎰，且环路上任意一点B ≠0 C.d 0LB l ⋅≠⎰，且环路上任意一点B ≠0 D.d 0LB l ⋅≠⎰，且环路上任意一点B =常量3.【答案】B 。
解析：根据安培环路定理，闭合回路内没有电流穿过，所以环路积分等于0.但是由于圆形电流的存在，环路上任意一点的磁感应强度都不等于0。
故选B 。
4.无限长直圆柱体，半径为R ，沿轴向均匀流有电流，设圆柱体内（r <R ）的磁感应强度为B i ，圆柱体外（r>R ）的磁感应强度为B e ，则有：（）。
A.B i 、B e 均与r 成正比B.B i 、B e 均与r 成反比C.B i 与r 成反比，B e 与r 成正比D.B i 与r 成正比，B e 与r 成反比4.【答案】B 。
解析：导体横截面上的电流密度2πR I J =，以圆柱体轴线为圆心，半径为r 的同心圆作为安培环路，当r <R ，20ππ2r J r B i ⋅=⋅μ，20π2R IrB i μ=；当r <R ，I r B e ⋅=⋅0π2μ，rIB e π20μ=；所以选D 。
大学物理学下册答案解析第11章
第11章 稳恒磁场习 题一 选择题11-1 边长为l 的正方形线圈，分别用图11-1中所示的两种方式通以电流I （其中ab 、cd 与正方形共面），在这两种情况下，线圈在其中心产生的磁感应强度的大小分别为：[ ]（A ）10B =，20B =（B ）10B =，02IB lπ=（C）01IB lπ=，20B =（D）01I B l π=，02IB lπ= 答案：C解析：有限长直导线在空间激发的磁感应强度大小为012(cos cos )4IB dμθθπ=-，并结合右手螺旋定则判断磁感应强度方向，按照磁场的叠加原理，可计算01IB lπ=，20B =。
故正确答案为（C ）。
11-2 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置，一个处于竖直位置，两个线圈的圆心重合，如图11-2所示，则在圆心O 处的磁感应强度大小为多少? [ ]习题11-1图习题11-2图（A ）0 （B ）R I 2/0μ （C ）R I 2/20μ （D ）R I /0μ 答案：C解析：圆线圈在圆心处的磁感应强度大小为120/2B B I R μ==，按照右手螺旋定则判断知1B 和2B 的方向相互垂直，依照磁场的矢量叠加原理，计算可得圆心O处的磁感应强度大小为0/2B I R =。
11-3 如图11-3所示，在均匀磁场B 中，有一个半径为R 的半球面S ，S 边线所在平面的单位法线矢量n 与磁感应强度B 的夹角为α，则通过该半球面的磁通量的大小为[ ]（A ）B R 2π （B ）B R 22π （C ）2cos R B πα （D ）2sin R B πα 答案：C解析：通过半球面的磁感应线线必通过底面，因此2cos m B S R B παΦ=⋅=。
故正确答案为（C ）。
11-4 如图11-4所示，在无限长载流直导线附近作一球形闭合曲面S ，当曲面S 向长直导线靠近时，穿过曲面S 的磁通量Φ何变化？[ ]（A ）Φ增大，B 也增大 （B ）Φ不变，B 也不变 （C ）Φ增大，B 不变 （D ）Φ不变，B 增大I习题11-4图习题11-3图答案：D解析：根据磁场的高斯定理0SBdS Φ==⎰，通过闭合曲面S 的磁感应强度始终为0，保持不变。
第十一章恒定电流的磁场作业磁介质磁介质中的安培环路定理小结
作业11.1、11.211.4、11.8、11.9、11.15、11.1787磁介质90顺磁质B B >（铝、氧、锰等）弱磁质B B >>铁磁质（铁、钴、镍等）强磁性物质B B <抗磁质（铜、铋、氢等）弱磁质抗磁质顺磁质SI SI B L宏观上构成沿介质表面的等效环形电流, 称为表面束缚电流或磁化电流。
B AI 0I cbad.l113五、磁场对载流导线和运动电荷的作用（1）磁场对载流导线的作用力—安培力微分形式积分形式B l I F ⨯=d d Bl I F l⨯=⎰d 其中，是载流导线上的电流元，是所在处的磁感应强度。
l Id l I d B（2）均匀磁场对平面载流线圈的作用合力=∑F 磁力矩B p M m ⨯=式中，是载流线圈的磁矩，，其中N 是线圈匝数，I 是线圈中的电流，S 是线圈的面积，且S 的方向与电流环绕方向满足右螺旋法则。
m p S NI p m=114（3）磁力的功⎰=m1m2m d ΦΦΦI A mm1m2)(ΦI ΦΦI ∆=-=磁力的功等于电流强度I 乘以通过回路磁通量的增量∆Φm 。
（4）磁场对运动电荷的作用Bq F⨯=v 洛仑兹力:116六、磁介质（1）磁介质的分类抗磁质1<r μ顺磁质1>r μ铁磁质1>>r μ（2）磁介质的磁化在外磁场中固有磁矩沿外磁场的取向或感应磁矩的产生使磁介质的表面（或内部）出现束缚电流。
大学物理第11章习题答案
第11章 电磁感应11.１ 基本要求 １理解电动势的概念。
２掌握法拉第电磁感应定律和楞次定律，能熟练地应用它们来计算感应电动势的大小，判别感应电动势的方向。
３理解动生电动势的概念及规律，会计算一些简单问题中的动生电动势。
４理解感生电场、感生电动势的概念及规律，会计算一些简单问题中的感生电动势。
５理解自感现象和自感系数的定义及物理意义，会计算简单回路中的自感系数。
６理解互感现象和互感系数的定义及物理意义，能计算简单导体回路间的互感系数。
７理解磁能（磁场能量）和磁能密度的概念，能计算一些简单情况下的磁场能量。
８了解位移电流的概念以及麦克斯韦方程组（积分形式）的物理意义。
11.２ 基本概念１电动势ε：把单位正电荷从负极通过电源内部移到正极时，非静电力所作的功，即Wqε=２动生电动势：仅由导体或导体回路在磁场中的运动而产生的感应电动势。
３感生电场k E ：变化的磁场在其周围所激发的电场。
与静电场不同，感生电场的电 场线是闭合的，所以感生电场也称有旋电场。
４感生电动势：仅由磁场变化而产生的感应电动势。
５自感：有使回路保持原有电流不变的性质，是回路本身的“电磁惯性”的量度。
自感系数L ：//m L I N I =ψ=Φ６自感电动势L ε：当通过回路的电流发生变化时，在自身回路中所产生的感应电动势。
７互感系数M ：211212M I I ψψ== ８互感电动势12ε：当线圈２的电流2I 发生变化时，在线圈１中所产生的感应电动势。
９磁场能量m W ：贮存在磁场中的能量。
自感贮存磁能：212m W LI =磁能密度m w ：单位体积中贮存的磁场能量22111222m B w μH HB μ===１０位移电流：D d d I dt Φ=s d t∂=∂⎰DS ，位移电流并不表示有真实的电荷在空 间移动。
但是，位移电流的量纲和在激发磁场方面的作用与传导电流是一致的。
１１位移电流密度：d t∂=∂D j 11.３ 基本规律１电磁感应的基本定律：描述电磁感应现象的基本规律有两条。
第11 章 恒定电流的磁场
第11章 恒定电流的磁场习 题6.1 一条很长的直输电线，载有100A 的电流，在离它0.5m 远的地方，它产生的磁感强度B 有多大?6.2四条平行的载流无限长直导线，垂直地通过一边长为a 的正方形顶点，每根导线中的电流都是I ，方向如附图所示。
（1）求正方形中心的磁感应强度B ； （2）当a =20cm ，I =20A 时，B ＝?6.3 求图中P 点的磁感应强度B 的大小和方向。
6.4 高压输电线在地面上空25m 处，通过电流为1.8×103A ，求： （1）在地面上由这电流所产生的磁感应强度多大?（2）在上述地区，地磁场为0.6×10-4Ｔ，问输电线产生的磁场与地磁场相比如何?6.5 在闪电中电流可高达2×104A ，问距闪电电流1.0m 处的磁感应强度多大?把闪电电流视作长直电流。
6.6 一个塑料圆盘，半径为R ，表面均匀分布电量q 。
试证明：当它绕通过盘心而垂直于盘面的轴以角速度ω转动时，（1）盘心处的磁感应强度为：B =R qπωµ20；（2）圆盘的磁矩为：241R q P m ω=6.7 10A 的电流均匀地流过一根长直铜导线。
在导线内部作一平面S ，一边为轴线，另一边在导线外壁上，长度为1m ，如题6.7图所示。
试计算通过此平面的磁通量（铜材料本身对磁场分布无影响）。
6.8 氢原子处在正常状态(基态)时，它的电子可看作是在半径为a ＝0.53×10-8cm 的轨道（叫做玻尔轨道）上做匀速圆周运动，速率为v =2.2×108cm/s ，已知电子电荷的大小为e =1.6×10-19C ，求电子的这种运动在轨道中心产生的磁感强度B 的值。
6.9 边长为a 的正方形的两个角上固定有两个电量皆为q （q ＞0）的点电荷，以该正方形不带电荷的一边为轴，使正方形以角速度ω快速旋转，试求与作为轴的正方形边的中点O 相距x 处的平均磁感应强度，并说明轴线上O 处附近磁场分布的特点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
11-1 求图中各种情况下O 点处的磁感应强度B 。
解：图a 的电流可以看成是由1、2两个电流合成的。
故合场强为 直线电流，和矩形电流产生的磁感应强度的矢量和。
直线电流1在O 点产生的磁感应强度)2/(20a Iπμ，方向垂直纸面向外。
矩形电流2由两条长度为a 、两条长度为b 的直线电流组成在O 点产生的磁感应强度为：)]2/sin()2/[sin()2/(42)]2/sin()2/[sin()2/(4200ααπμϕϕπμ--+--b Ia I2202200022)2/sin(2)2/sin(2ba a bI ba b a Ib I a I +++=+=πμπμαπμϕπμ)(2220b aa b b a I++=πμ方向垂直纸面向内。
O 点的磁感应强度为：220022002)(2b a abI a I b aa b b a I a I B +-=++-=πμπμπμπμ 这里利用了载流直导线外的磁感应强度公式：]sin )[sin 4120ββπμ-=rIB电流b 由两条直线电流，和一个圆弧组成：)0sin 90(sin 42360135200-︒+=RIR I B πμμ RIR I R I 00035.02163μπμμ=+=电流c 中两条直线电流的延长线都过圆心，由毕-萨定律知道在圆心处产生的磁感应强度为0，圆弧产生的磁感应强度为RlR I R l R I B πμπμ2222220110-=由于两端的电压相同有2211I SlI S l V ρρ==带入上式得到B=0 11-2．如图所示，一扇形薄片，半径为R ，张角为θ，其上均匀分布正电荷，电荷密度为σ，薄片绕过角顶O 点且垂直于薄片的轴转动，角速度为ω，求O 点处的磁感应强度。
解答1：将扇形薄片分割成半径为r 的圆弧形面积元，电荷量为：dr r dq θσ=转动时相当于园电流，对应的电流强度为： rdr dr r T dq dI σωπθωπθσ2/2===产生的磁场为 dr rdIdB σωμπθμ0042==圆心处的磁场为R dr B Rσωμπθσωμπθ00044==⎰ 解答2：以o 为圆心，采用极坐标系将扇形薄片分割成小的面积元 dr rd ds dq θσσ==利用运动电荷产生磁场的公式 dr d rdrr rd r dqv dB θσωπμωθσπμπμ44402020===对上式积分得：πσωθμθσωπμθσωπμθ44400000R dr d dr d B R===⎰⎰⎰⎰ 11-3 在半径cm 0.1=R 的无限长半圆柱形金属薄片中，自下而上地通有电流A I 0.5=，求圆柱轴线上任一点P 处的磁感应强度。
（这里把自上而下改为自下而上，求解时对应右图。
如不改时方向相反。
）解：从电流的顶上看是个半圆形，在其上取一段圆弧（对应于一无限长载流直导线）， 电流强度为：πθθπId Rd R I dI ==产生的磁场方向如图，由此可见合磁场方向沿水平向右为：θπθμθππθμπμsin 2)2/cos(2220200RId R Id R dI dB x =-==磁感应强度为：R I R I RId B B x 200200202sin 2πμπμθπθμππ=-===⎰=6.37×10-5T方向在x 轴正向。
11-4 图中所示为实验室中用来产生均匀磁场的亥姆霍兹圈。
它由两个完全相同的匝数为N 的共轴密绕短线圈组成（N 匝线圈可近似视为在同一平面内）。
两线圈中心12O O ,间的距离等于线圈半径R ，载有同向平行电流J 。
以12O O ,连线中点为坐标原点，求轴线上在1O 和2O 之间、坐标为x 的任一点P 处的磁感应强度B 的大小，并算出02010B B B 、、进行比较。
解：由园电流在轴线上一点的磁感应强度公式：2/32220)(2x R IR B +=μ用到上式 线圈1产生的磁感应强度2/322201))2/((2R x R NIR B ++=μ线圈2产生的磁感应强度2/322202))2/((2R x R NIR B -+=μRNIRNIR R NIR B B x 02/302/32220010715.0)4/5())2/((2μμμ==+===RNI R NI R R NIR RNIB B 02/302/3222000201678.0))2(2121()(22μμμμ=+=++== 两个圆环之间的磁场变化缓慢。
11-5 有一半径为R 的半圆形电流，求在过圆心O 垂直于圆面的轴线上离圆心距离为x 处P 点的磁感应强度。
解：如右图利用毕-萨定律分析可知z 方向的B 分量为0：204r IRd dB πθμ=x 轴分量为：απθμαππθμsin 4)2/cos(42020rIRd r IRd dB x =-=320202/2/204sin 4)2/cos(4r IR r IR rIRd B x μαμαππθμππ==-=⎰- y 轴分量为：θπθμθαπθμθαππθμcos 4cos cos 4cos )2/sin(4202020rxr IRd r IRd r IRd dB y ==-= 302/2/302/2/202cos 4cos 4r IRxd r IRx r x rIRd B y πμθθπμθπθμππππ===⎰⎰-- j rIRx i r IR B3032024πμμ+= 这里 22x R r +=是圆环到轴线的距离。
11-6 半径为R 的均匀带电球面的电势为U ，圆球绕其直径以角速度ω转动，求球心处的磁感应强度。
由球面的电势表示式Rq U 04πε=得到球面电荷量RU q 04πε= 电荷面密度 R U R q 024επσ==取求坐标系，将圆球分割成圆环，圆环带电量为ϕπσrRd dq 2=等效的电流为ϕσωωπϕπσrRd rRd T dq dI ===/22 利用园电流轴线上的磁感应强度公式2/32220)(2x R IR B +=μ这里R 是圆环的半径，在本例中为r ,可以得到2/32220)(2)(x r r rRd dB +=ϕσωμx 是圆环的圆心到轴线上一点的距离，在本例中为y.。
则有;sin ϕR r = ϕc o s R y = ϕϕσωμϕσωμd Rx r r rRd dB 302/32220sin 2)(2)(=+=⎰⎰⎰--===πππϕϕσωμϕϕσωμϕϕσωμ020030030cos )cos 1(2sin 2sin 2d R d R d RB U R R Rωεμσωμσωμϕϕσωμπ00000303232)311(22)cos 31(cos 2==-=--=11-7 地球上某处的磁感应强度水平分量为T 5107.1-⨯，试计算该处沿水平方向的磁场强度。
解：由m A HB /5.13104107.1750=⨯⨯==--πμ 11-8 螺线环中心周长cm l 10=，环上线圈匝数200=N 匝，线圈中通有电流mA I 100=。
（1）求管内的磁感应强度B ，及磁场强度H ；（2）若管内充满相对磁导率4200=r μ的铁磁质时，管内的磁感应强度和磁场强度为多大?（3）铁磁质内由传导电流I 产生的磁场B ，与由磁化电流产生的磁场'B 各为多大? 解：（1）由安培环路定律 ∑⎰=∙ii I l d H选择螺线环中心为环路路径：NI Hl l d H ==∙⎰得到磁场强度m A l NI H /2001.01.0200=⨯==磁感应强度 T lNIB 4700105.2200104--⨯=⨯⨯==πμ（2）管内充满相对磁导率4200=r μ的铁磁质时磁场强度不变，磁感应强度为T lNIB r 06.1105.2420040=⨯⨯==-μμ（3）传导电流I 产生的磁场0B 为：T lNIB 400105.2-⨯==μ磁化电流产生的磁场'B 为：T B B B 06.1'0≈-=11-9 在半径为R 的长圆柱导体内与轴线平行地挖去一个半径为r的圆柱形空腔．两圆柱形轴线之间的距离为)(r d d >。
电流I 在截面内均匀分布，方向平行于轴线。
求： （1）实心圆柱轴线上磁感应强度的大小；（2）空心部分中任一点的磁感应强度。
解：这个电流可以看成是：在空腔内补上同样电流密度的电流，在于同一位置再加上一条方向相反的电流，这时磁场是这两个电流各自产生的磁场的矢量和。
柱体的电流密度为)(22r R Ij -=π在实心圆柱轴线上大圆柱产生的磁感应强度为0，小园柱产生的磁感应强度由安培环路定律求解为：圆柱内的电流密度为：)(22r R Ij -=π202r j d B l d B πμπ=⨯=∙⎰可求得：)(22222020r R d Ir djr B -==πμμ空心部分的磁感应强度由大圆柱与小园柱各自产生的磁感应强度的矢量和 大圆柱产生的磁感应强度可以由安培环路定律求解为2101112r j r B l d B πμπ=⨯=∙⎰10121r j B μ=1r 是由大圆柱的圆心指向场点的位置适量的模，同样可得小园柱的磁感应强度20221r j B μ=下图表示的是小的那个圆柱的截面 合场强为：)cos (sin 21)cos (sin 21201021j i r j j i r j B B B ββμααμ+++=+=j jd j r x d i r y r j j r x i r y r j 022*******1)(21)(21μμμ=-+-++= j r R Id)(2220-=πμ方向在y 轴向上。
11-11 根据安培环路定理0B dl I μ=∑⎰， 求得磁感应强度为：020()2()2Irr R R B I r R rμπμπ⎧≤⎪⎪=⎨⎪>⎪⎩ 方向垂直纸面向里，取矩形法线方向为垂直纸面向里2000020ln 22242RRRIr I I IB dS dr dr R r μμμμφππππ==+=+⎰⎰⎰ 11-12 把圆盘割成许多圆环，其中对单个小圆环，设它的半径为r ，宽为dr ，带电为dq ，则，32 dq rdrdqdI rdr dm r drdtσπσωπσω=∴=== 则整个圆盘的磁矩为5345R RRk r m dm r dr k r dr πωπσωπω====⎰⎰⎰ 垂直纸面向外， 所以55k r M B πω=平行于纸面且垂直于B 向上11-13 根据霍尔效应51928311200 1.52.5310()1.6107.410110HIB IB V R b qn bV ---==⨯==-⨯-⨯⨯⨯⨯电场强度53122.5310 1.2710(.)2.010V E N C a ----⨯===⨯⨯ 11-1436.6510()A A AA U U V -''=-=-⨯所以这块导体是n 型，又1,A A HA AIB IB IB U R n b qn b bqU ''==∴=， 带入数据，得2032.8210()n m =⨯11-15：由安培力公式可知，当两条导线电流方向相同时，两导线相互吸引，如下图，导线2对导线1单位长度的引力的大小为：2001212f 22I I I r aμμππ==，导线3对导线1单位长度的引力2013f 2I a μπ=，引力13f 和12f 正好在等边三角形的两条边上，它们之间的夹角为060，而且在数值上大小相等，所以合力的大小为204011312f f cos30f cos30cos30 3.4610/I N cm aμπ-=+==⨯ 方向如图11-16.在线圈的上下两段弧da 和bc 上，因长直电流1I 产生的磁场与和电流2I 方向平行，所以圆弧da 和bc 受力为零。