锐角三角函数、解三角形
三角函数及解三角形测试题(含答案)

三角函数及解三角形测试题(含答案)三角函数及解三角形1.在锐角三角形ABC中,角A的对边为a,角B的对边为b,角C的对边为c。
根据正弦定理,$\frac{a}{\sinA}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$,其中R为三角形外接圆的半径。
根据余弦定理,$c^2=a^2+b^2-2ab\cos C$。
根据正切的定义,$\tan A=\frac{a}{b}$。
根据余切的定义,$\cotA=\frac{b}{a}$。
根据正割的定义,$\sec A=\frac{c}{a}$。
根据余割的定义,$\csc A=\frac{c}{b}$。
2.选择题:1.设$\alpha$是锐角,$\tan(\frac{\pi}{4}+\alpha)=3+\sqrt{22}$,则$\cos\alpha=\frac{2\sqrt{22}}{36}$。
2.一艘船向XXX,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时5海里。
4.已知函数$f(x)=3\sin\omega x+\cos\omega x$,$y=f(x)$的图象与直线$y=2$的两个相邻交点的距离等于$\pi$,则$f(x)$的单调递增区间是$(\frac{k\pi}{2}-\frac{\pi}{12},\frac{k\pi}{2}+\frac{5\pi}{12})$,其中$k\in Z$。
5.圆的半径为4,$a,b,c$为该圆的内接三角形的三边,若$abc=162$,则三角形的面积为$22$。
6.已知$\cos\alpha=-\frac{4}{\pi}$,且$\alpha\in(\frac{\pi}{4},\frac{\pi}{2})$,则$\tan(\alpha+\frac{\pi}{4})=-\frac{7}{7}$。
锐角三角函数及解直角三角形
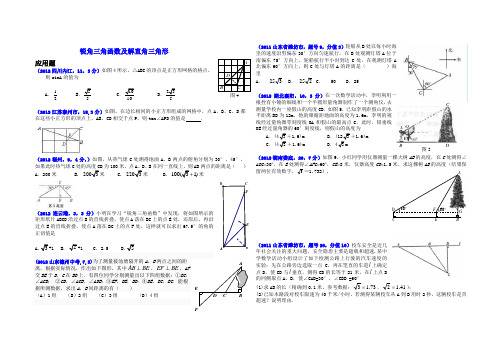
锐角三角函数及解直角三角形应用题(2012四川内江,11,3分)如图4所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为A .12B .55C .1010D .255(2012江苏泰州市,18,3分)如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P ,则tan ∠APD 的值是 .(2012福州,9,4分,)如图,从热气球C 处测得地面A 、B 两点的俯角分别为30°、45°,如果此时热气球C 处的高度CD 为100米,点A 、D 、B 在同一直线上,则AB 两点的距离是( ) A .200米 B. 2003米 C. 2203米 D. 100(31)+米(2012连云港,3,3分)小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD 沿过点B 的直线折叠,使点A 落在BC 上的点E 处,还原后,再沿过点E 的直线折叠,使点A 落在BC 上的点F 处,这样就可以求出67.5°的角的正切值是A.3+1B. 2+1C. 2.5D.5(2012山东德州中考,7,3)为了测量被池塘隔开的A ,B 两点之间的距离,根据实际情况,作出如下图形,其中AB BE ⊥,EF BE ⊥,AF 交BE 于D ,C 在BD 上.有四位同学分别测量出以下四组数据:①BC ,∠ACB ; ②CD ,∠ACB ,∠ADB ;③EF ,DE ,BD ;④DE ,DC ,BC .能根据所测数据,求出A ,B 间距离的有( ) (A )1组 (B )2组 (C )3组 (D )4组(2011山东省潍坊市,题号9,分值3)轮船从B 处以每小时海里的速度沿男偏东30°方向匀速航行,在B 处观测灯塔A 位于南偏东75°方向上,轮船航行半小时到达C 处,在观测灯塔A 北偏东60°方向上,则C 处与灯塔A 的距离是( )海里A . 325B . 225C . 50D .25(2012湖北襄阳,10,3分)在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD .如图5,已知李明距假山的水平距离BD 为12m ,他的眼睛距地面的高度为1.6m ,李明的视线经过量角器零刻度线OA 和假山的最高点C ,此时,铅垂线OE 经过量角器的60°刻度线,则假山的高度为A .3 1.6)mB .3 1.6)mC .2 1.6)mD .3(2012湖南娄底,20,7分)如图9,小红同学用仪器测量一棵大树AB 的高度,在C 处测得∠ADG =30︒,在E 处测得∠AFG =60︒,CE =8米,仪器高度CD =1.5米,求这棵树AB 的高度(结果保留两位有效数字,3≈1.732).(2011山东省潍坊市,题号20,分值10)校车安全是近几年社会关注的重大问题,安全隐患主要是超载和超速.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C ,再在笔直的车道l 上确定点D ,使CD 与l 垂直,测得CD 的长等于21米,在l 上点D 的同侧取点A 、B ,使∠CAD=30°,∠CBD =60°(1)求AB 的长(精确到0.1米,参考数据:73.13=,41.12=);(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A 到B 用时2秒,这辆校车是否超速?说明理由.CB A图4D EC DABFABC D E 图5 CDA B O E A G B F C D 30︒ 60︒(2012四川攀枝花,19,6分)如图6,我渔政310船在南海海面上沿正东方向匀速航行,在A 地观测到我渔船C 在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B 处,此时观测到我渔船C 在北偏东30°方向上.问渔政310船再航行多久,离我渔船C 的距离最近?(假设我渔船C 捕鱼时移动距离忽略不计,结果不取近似值.)(2012山东省聊城,22,8分)周末,小亮一家在东昌湖游玩,妈妈在湖心岛P 处观看小亮与爸爸在湖中划船(如图),小船从P 处出发,沿北偏东60°方向划行200米到A 处,接着向正南方向划行一段时间到B 处.在B 处小亮观测妈妈所在的P 处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?(2012浙江丽水,19,6分)学校校园内有一小山坡,经测量,坡角∠ABC=30°,斜坡AB 长为12米.为方便学生行走,决定开挖小山坡,使斜坡BD 的坡比是1:3(即为CD 与BC 的长度之比),A ,D 两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.(2012四川省资阳市,20,8分)小强在教学楼的点P 处观察对面的办公大楼.为了测量点P 到对面办公大楼上部AD 的距离,小强测得办公大楼顶部点A 的仰角为45°,测得办公大楼底部点B 的俯角为60°,已知办公大楼高46米,CD =10米.求点P 到AD 的距离(用含根号的式子表示).(2012广东汕头,20,7分)如图,小山岗的斜坡AC 的坡度是tan α=,在与山脚C 距离200米的D 处,测得山顶A 的仰角为26.6°,求小山岗的高AB (结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).(2012山西,23,9分)如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A .B 的距离,飞机在距海平面垂直高度为100米的点C 处测得端点A 的俯角为60°,然后沿着平行于AB 的方向水平飞行了500米,在点D 测得端点B 的俯角为45°,求岛屿两端A .B 的距离(结果精确到0.1米,参考数据:)(2012深圳市 11 ,3分)、小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图3,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( ) A.(6米 B. 12米 C(+4米 D. 10(2012广安中考试题第23题,8分)(8分)如图10,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A 地侦察发现,在南偏东60o 方向的B 地,有一艘某国军舰正以每小时13海里的速度向正西方向的C 地行驶,企图抓捕正在C 地捕鱼的中国渔民。
锐角三角函数与解直角三角形

选择适当的三角函数
根据已知条件选择适当的三角 函数(正弦、余弦、正切), 以便建立方程。
建立方程
利用三角函数定义和勾股定理 ,建立关于未知边的方程。
解方程
解方程求出未知边或角。
解直角三角形的实际应用
测量问题
在测量中,经常需要解直 角三角形来计算高度、距 离等。
在直角三角形中,如果一个角是 60度,那么它所对的直角边等于
斜边的√3倍。
特殊角的三角函数值
sin30度=1/2, cos30度=√3/2, tan30度=1/√3
sin60度=√3/2, cos60度=1/2, tan60度=√3
sin45度=√2/2, cos45度=√2/2, tan45度=1
建筑学
在建筑设计、施工等过程 中,需要利用解直角三角 形来计算角度、长度等参 数。
物理学
在力学、电磁学等领域中, 解直角三角形也是常用的 工具。
03
特殊角的解法
30度、45度、60度角的解法
30度角
在直角三角形中,如果一个角是 30度,那么它所对的直角边等于
斜边的一半。
45度角
在等腰直角三角形中,如果一个角 是45度,那么它所对的直角边等于 斜边的长度。
了解三角函数在实际问题中的应用, 如测量、工程等。
掌握利用三角函数图象解方程的方法。
综合练习题
综合运用三角函数的性质和图 象解决复杂问题。
结合其他数学知识,如代数、 几何等,综合运用三角函数。
了解三角函数与其他数学知识 的联系,如微积分、线性代数 等。
THANKS
感谢观看
求出对角的正切值。
三角函数对解直角三角形的影响
专题七、锐角三角函数及解直角三角形

7 2
,
B a C
c b A
7.若 α为锐角,且cos α= -2<m<1 值范围__________.
1- m ,则m的取 3
8.若∠A为锐角,且tan2A+2tanA-3=0,
则∠A=
45°
.
广安怎么考
2009.在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设 计的测量方案及数据如下: (1) 在大树前的平地上选择一点 A, 测得由点 A 看大树顶端 C 的仰角为 30°; (2)在点 A 和大树之间选择一点 B(A、B、D 在同一直线上),测得由点 B 看大树顶端 C 的仰角恰好为 45°; (3)量出 A、B 间的距离为 4 米.请你根据以上数据求出大树 CD 的高度. (精确到 0.1,参考数据: 2 ≈1.41
4.在△ ABC中,∠C=90°,c=26,
24 则a=_____. A 5k =10 C 26 = 13k
5 cosA = 13
B
5. 在△ ABC中,∠C=90°,c=2,
1 tanA = 2
4 5 则S△ABC=________.
B k C
c=2 2k A
6. 在△ ABC中,∠C=90°,a+b= S△ABC=
b c
C
tanA=
a b
tanα>0;
一 .知识网络构建
3.特殊角的三角函数值:
30° sinA2
60°
3 2
1 2
一 知 识 网 络 构 建 .
2 2
tanA
若Α为锐角,则:
3 3
1
3
sinA的值随∠A度数的增大而增大; cosA的值随∠A度数的增大而减小; tanA的值随∠A度数的增大而增大.
锐角三角函数与解直角三角形

解:(1)∵BD⊥AC, ∴∠ADB=90° 在Rt△ADB中,AB=6,∠A=30°
BD 1 2 AB 3
AD AB2 BD2 62 32 3 3
3 3 3 2 3
2CD AC AD 5
在Rt△BCD中,
BD CD
tan∠C=
3 2 3
1 2
2 2 2 2
3..(1)锐角三角函数是在直角三角形中定义的.
3 2 (333)锐角三角函数的大小仅与角的大小有关,与该角所处的直角三角形的大小无关 .
2)sinA,cosA,tanA表示的是一个整体,是指两条线段的比,没有单位.
1 2
3 3
1
3
sin cos
3.三角函数之间的关系:
2 2 (1)同角三角函数之间的关系:sin cos 1; tan
AD AB
1 3 且AD 1
∵BD2=AB2﹣AD2
BD
3 2
2
2
2 2
在Rt△ADC中,∵∠C=45° ∴CD=AD=1
BC BD DC 2 2 1
11.如图,在△ABC中,BD⊥AC,AB=6,AC= 5 3 ,∠A=30°. ①求BD和AD的长; ②求tan∠C的值.
第23课时
锐角三角函一:锐角三角函数
1锐角函数的定义: 如图,在△ABC中,∠C=90°∠A, ∠B ,∠C的对边分别是a,b,c,
则sinA=
a c
cosA=
b c
tanA =
a b
。
c
b
45
0
2.特殊角的三角函数值:
特殊角
温馨提示:
锐角三角函数与解直角三角形

ቤተ መጻሕፍቲ ባይዱ
【例1】在△ABC中,∠C=90°. ABC中 C=90° cosA=1/2, (1)若cosA=1/2,则tanB=______; (2)若cosA=4/5,则tanB=______. ) , . 则锐角α的取值范围 【例2】(1)已知:cosα=2/3, 则锐角 的取值范围 已知: 是( ) 45°<α<60° A.0°<α<30° <α<30° B.45°<α<60° 30°<α<45° 60°<α<90° C.30°<α<45° D.60°<α<90° )(2006年潜江市) 45°<θ<90° 2006年潜江市 (2)(2006年潜江市)当45°<θ<90°时,下列各式中 正确的是( ) 正确的是( B. A.tanθ>cosθ>sinθ B.sinθ>cosθ>tanθ D. C.tanθ>sinθ>cosθ D.cotθ>sinθ>cosθ
(2006年聊城市)如图所示,某居民小区有一朝向为正南方向的 2006年聊城市)如图所示, 年聊城市 居民楼,该居民楼的一楼是高6米的小区超市, 居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住 在该楼的前面15米处要盖一栋高20米的新楼. 20米的新楼 房,在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳 光与水平线的夹角为32 32° 光与水平线的夹角为32°时. 问超市以上的居民住房采光是否有影响,为什么? (1)问超市以上的居民住房采光是否有影响,为什么? 若要使超市采光不受影响,两楼应相距多少米? (2)若要使超市采光不受影响,两楼应相距多少米? 53 结果保留整数,参考数据:sin32° (结果保留整数,参考数据:sin32°≈ 100 106 5 cos32°≈ , tan 30° ≈ ° .) 125 8
初三数学第5讲锐角三角函数与解直角三角形

锐角三角函数与解直角三角形一、知识点训练:知识点1、锐角三角函数的定义四个三角函数的求法。
在Rt △ABC 中,∠C=90°,锐角∠A 所对的边为a ,锐角∠B 所对的边为b ,直角∠C 所对的边为斜边c 。
则: 正弦:余弦:正切: 余切:注:①初中阶段研究的正弦、余弦、正切、余切都是指直角三角形中,锐角三角函数,其本质是指两条线段长度之比,它是一个值,没有单位。
②三角函数的大小只与角的大小有关,与三角形的大小无关。
③若一个三角函数值确定,则它所对应的角的大小也确定,反之亦然。
④∠ABC 的正切不能写成:,而应写成中考题型:1. 在Rt △ABC 中,∠C=90°,,则2. 3. 4.Bc aC b A5.6.7.知识点2、特殊角30°,45°,60°的三角函数值。
度数30°45°60°三角函数11中考题型:8.9.10.12. 13.知识点3、各锐角三角函数之间的关系(1)互余关系: (2)平方关系:(3)倒数关系:(4)大小关系: ① ②若,则,中考题型:14. 15. 16.BcaC b A18.知识点4、解直角三角形(1)由直角三角形中的已知条件求其他未知元素的过程叫做解直角三角形。
(2)需要用到的直角三角形中的依据:①②∠A+∠B=90°③④(3)解直角三角形中,已知其中2个元素(至少有一个是边),就可以求出其余未知的元素。
中考题型:19.20.21.22.23.二、中考专题24. 25. 26. 27. 28. 29. 30. 31.32. 如图,在四边形ABCD 中,AB=2,CD=1,∠A=60°,∠B=∠D=90°,求四边形ABCD 的面积。
DCt2参考答案:1. 2. 。
家庭作业:23.一、知识点训练:知识点1、解直角三角形的应用问题中考题型:1.2.如图,水坝的横截面是梯形,坝顶宽4m,坝高6m,迎水坡AB的坡度,背水坡CD的坡度,则斜坡AB的坡角,斜坡AB的长=米,坝底宽为米,3.A DB E F C。
锐角三角函数及解直角三角形

4a
4
3).计算tan 60°+2sin 45°-2cos 30°的结果是(c A.2 B. 3 C. 2 D.1 解:原式=
)
3
2 +2× 2
3 - 2× 2
=2
(4)在△ABC中, ∠ B、 2∠ C均为锐角,且
1 3 sin B cos C 2 2 0 ,求∠A的度数。
(2)(2010· 黄冈)在△ABC中,∠C=90°,sinA= ,则tanB=_ 5 3 4 A. B. C.5(3) D.5(4) 4 3 BC 4 4 (2)∵sinA= ,∴ = ,于是可设BC=4a, AB 5 5
4
AB=5a.在Rt△ABC中,由勾股定理,可得AC= 3a. AC 3a 3 ∴tanB= = = .故选B.
分:作PD⊥BC于点D,设 PD=x,则BD=x,AD=x+12,根据AD= 3 3 PD,得x+12= x,求出x的值,再 比较PD与18的大小关系.
D
⑴正弦
1.锐角三角函数的定义 ⑵余弦 ⑶正切 2.30°、45°、60°特殊角的三角函数值
⑴定义
①三边间关系
锐 角 三 角 函 数
⑵解直角三角形的依据
(1)(2010· 哈尔滨)在Rt△ABC中,∠C=90°,∠B=35°, AB=7,则BC的长为( ) 7 A.7sin35° B. C.7cos35° D.7tan35°
BC 解答:在Rt△ABC中,∠C=90°,cosB= AB
cos 350
,
∴BC=AB· cosB=7 cos35°,故选C.
如图,直径为5的⊙A经过点C(0,3)和 点O(0,0),B是y轴右侧⊙A优弧上一点, 则∠OBC的余弦值为_______。
