解直角三角形及其应用导学案
28.1-2 解直角三角形及其应用导学案(3个课时)

28.2-1 锐角三角函数【学习目标】⑴: 使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形⑵: 通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.⑶: 渗透数形结合的数学思想,培养学生良好的学习习惯.【学习重点】直角三角形的解法.【学习难点】三角函数在解直角三角形中的灵活运用【导学过程】一、情境引入,目标导学, (时间分配:3分钟) [课堂前置·进门测]1.在三角形中共有几个元素? 2.直角三角形ABC 中,∠C=90°,a 、b 、c 、∠A 、∠B 这五个元素间有哪些等量关系呢? (1)边角之间关系a b A b a A c b A c a A ====cot ;tan ;cos ;sin b aB a b B c a B c b B ====cot ;tan ;cos ;sin如果用α∠表示直角三角形的一个锐角,那上述式子就可以写成. 的对边的邻边;的邻边的对边;斜边的邻边;斜边的对边αααααααααα∠∠=∠∠=∠=∠=cot tan cos sin(2)三边之间关系 (3)锐角之间关系∠A+∠B=90°.a 2 +b 2 =c 2 (勾股定理) 以上三点正是解直角三角形的依据.二、提出问题,合作探究(时间分配:10—12分钟)[合作学习、互动探究]要想使人安全地攀上斜靠在墙面上的梯子的顶端.梯子与地面所成的角一般要满足,(如图).现有一个长6m的梯子,问: (1)使用这个梯子最高可以安全攀上多高的墙(精确到0. 1 m)(2)当梯子底端距离墙面2.4 m时,梯子与地面所成的角等于多少(精确到1o) 这时人是否能够安全使用这个梯子三、初用新知,小试牛刀(时间分配:10—15分钟):例1在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b=2,例2在Rt△ABC中,∠B =35o,b=20,解这个三角形.35四、当堂检测,达标反馈(时间分配:10—12分钟)1.【课堂练习·当堂测】完成课本91页练习2.[拓展提升·能力测]1.根据直角三角形的__________元素(至少有一个边),求出________•其它所有元素的过程,即解直角三角形.2、在Rt △ABC 中,a=104.0,b=20.49,解这个三角形.3、 在△ABC 中,∠C 为直角,AC=6,BAC 的平分线AD=43,解此直角三角形。
解直角三角形导学案

《解直角三角形》学案一、学习目标1、了解解直角三角形的定义,能通过已知条件解直角三角形。
2、通过本节课的学习,培养自己知识的运用能力和计算能力。
二、重点难点学习重点:对解直角三角形的理解。
学习难点:对解直角三角形的应用。
三、前置学习1、计算:︒︒+︒+︒-︒46tan 44tan 45tan 60cos 230sin 22、在ABC ∆中,若0)cos 23(|1sin |2=-+-B A ,则∠C=_______度 3、如图,在ABC Rt ∆中,∠C 为直角,其余5个元素之间有以下关系:(1)三边之间关系:222c b a =+ (勾股定理)(2)锐角之间的关系:∠A+∠B=90°(直角三角形的两个锐角互余) (3)边角之间的关系:c a A =sin 、c b A =cos 、baA =tan 。
利用以上关系,如果知道其中的2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素。
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形。
例1、在ABC Rt ∆中,∠C=90°,∠A=30°,5=a ,解这个直角三角形。
例2、在ABC Rt ∆中,∠C=90°,3=a ,3=b ,求:(1)c 的大小;(2)∠A 、∠B 的大小。
四、展示交流在ABC Rt ∆中,CD 是斜边上的高,若AC=8,cosB=0.6,求ABC ∆的面积。
五、达标拓展在ABC Rt ∆中,∠C=90°,根据下列条件解直角三角形:(1)32=b ,4=c ; (2)8=c ,∠A=60°;(3)7=b ,∠A=45°; (4)24=a ,38=b 。
六、学习评价在ABC Rt ∆中,∠C=90°,∠A=60°,13+=+b a ,解这个直角三角形。
七、合作探究如图是小朋友玩的“滚铁环”游戏的示意图,⊙O 向前滚动时,铁棒DE 保持与OE 垂直。
解直角三角形的应用导学案

桃溪中学师生共用导学案内容:解直角三角形(1) 执笔:【学习目标】⑴: 使学生理解直角三角形中五个元素的关系,会使用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形⑵: 通过综合使用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的水平.⑶: 渗透数形结合的数学思想,培养学生良好的学习习惯. 【学习重点】直角三角形的解法. 【学习难点】三角函数在解直角三角形中的灵活使用 【导学过程】 一、自学提纲: 知识回顾:在Rt △ABC 中,∠C =900,a ,b ,c ,分别为∠A,∠B,∠C 所对的边,则边之间的关系为 ,角之间的关系为 , 角与边之间的关系为 , 自主预习:1.在三角形中共有几个元素? 2、解直角三角的概念:有直角三角形中 求出 元素的过程,叫做解直角三角形。
3、解直角三角形的两种情况。
(1)已知 ,求第三边及两锐角。
(2)已知 和一个 ,求其它两边及另一锐角。
导学探究:1、在Rr △ABC 中,共有六个量,三条边a ,b ,c ,三个角∠A ,∠B ,∠C ,其中∠C 是已知的,其它的五个量都是未知的。
(1) 已知∠A ,∠B ,能求出其它的三个量a ,b ,c 吗? (2) 已知两条边的长,能求出其它的三个量吗? (3) 已知一角和一边,能求出其它的三个量吗? 你有什么发现?2、直角三角形ABC 中,∠C=90°,a 、b 、c 、∠A 、∠B 这五个元素间有哪些等量关系呢? (1)边角之间关系如果用α∠表示直角三角形的一个锐角,那上述式子就能够写成.(2)三边之间关系 (3)锐角之间关系∠A+∠B=90°. a 2 +b 2 =c 2 (勾股定理) 以上三点正是解直角三角形的依据.二、合作交流:要想使人安全地攀上斜靠在墙面上的梯子的顶端.梯子与地面所成的角一般要满足, (如图).现有一个长6m 的梯子,问:(1)使用这个梯子最高能够安全攀上多高的墙(精确到0. 1 m)(2)当梯子底端距离墙面2.4 m 时,梯子与地面所成的角等于多少(精确到1o ) 这时人是否能够安全使用这个梯子b aA c b A c a A = = = ;tan ; cos ; sin abB c a B c b B = = = ;tan ; cos ; sin ; 的邻边的对边; 斜边 的邻边 ; 斜边 的对边α α α α α α α∠ ∠ = ∠ = ∠ =tan cos sin三、教师点拨:例1在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,且,解这个三角形.例2在Rt △ABC 中, ∠B =35o ,b=20,解这个三角形.四、学生展示: 完成课本87页练习 补充题1、 在△ABC 中,∠C 为直角,AC=6,BAC 的平分线AD=43,解此直角三角形。
解直角三角形及应用导学案

新人教九年级数学(下)导学案主备人:叶小凤审核人:唐海霞杨栓祥解直角三角形及其应用(1)学案班级姓名得分【学习目标】理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形【学习重点】灵活运用知识点,准确解直角三角形【学习难点】三角函数在解直角三角形中的灵活运用一、自学课本,完成下列知识点1.Rt△ABC中,∠C=90°,∠A=30°,BC=8,则可求出AB= ,AC= 。
∠B= 。
2 结合上面题目的解决,归纳:(1)在三角形中共有几个元素(边、角):(2)Rt△ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?①三边之间关系:②两锐角之间关系:③边角之间关系:3.解直角三角形概念:二、合作探究例1:在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b=,例2:在Rt△ABC中,∠C=90°,∠B =45o,b=20,解这个直角三角形.三、课堂检测1.根据直角三角形的__________元素(至少有一个边),求出________•其它所有元素的过程,即解直角三角形.352、Rt △ABC 中,若sinA=54,AB=10,那么BC=_____,tanB=______.3、在△ABC 中,∠C=90°,AC=6,BC=8,那么sinA=________.4、在△ABC 中,∠C=90°,sinA=则cosA 的值是5、在Rt △ABC 中,∠C=90°,a=3,b=3,解这个三角形.6、 在△ABC 中,∠C 为直角,AC=6,BAC ∠的平分线AD=43,解此直角三角形。
四、达标检测2.在Rt △ABC 中,∠C =90°.(1)已知:a =35,235=c ,求∠A 、∠B ,b ;(2)已知:32sin =A ,6=c ,求a 、b ;(3)已知:,9,23tan ==b B 求a 、c ;(4)已知:∠A =60°,△ABC 的面积,312=S 求a 、b 、c 及∠B .新人教九年级数学(下)导学案 主备人:叶小凤 审核人:唐海霞 杨栓祥解直角三角形及其应用(2)学案班级 姓名 得分学习目标:能将解斜三角形的问题转化为解直角三角形. 学习重难点:灵活构造直角三角形解决问题 导学过程:一、自主学习1.直角三角形的边角关系是 2.已知:如图,△ABC 中,∠A =30°,∠B =60°,AC =10cm .求AB 及BC 的长.3.已知:如图,Rt △ABC 中,∠D =90°,∠B =45°,∠ACD =60°.BC =10cm .求AD 的长.4.已知:如图,△ABC 中,∠A =30°,∠B =135°,AC =10cm .求AB 及BC 的长.5.已知:如图,△ABC 中,∠A =60°,∠B =45°,AB =8cm .求△ABC 的面积A CB二、课堂练习1.已知:如图,Rt △ABC 中,∠A =30°,∠C =90°,∠BDC =60°,BC =6cm . 求AD 的长.2.已知:如图,△ABC 中,∠A =45°,∠B =120°,AB =10cm .求AC 及BC 的长.三、达标检测1.△ABC 中,∠A =120°,∠B =30°,AC =2cm .求AB 及BC 的长.2.已知:如图,△ABC 中,∠C =60°,∠B =45°,AB =6cm .求BCCA BB AC新人教九年级数学(下)导学案 主备人:叶小凤 审核人:唐海霞 杨栓祥解直角三角形及其应用(3)学案 仰角、俯角班级 姓名 得分学习目标:1.认识仰角、俯角,并能结合实际标准角度。
解直角三角形及其应用导学案
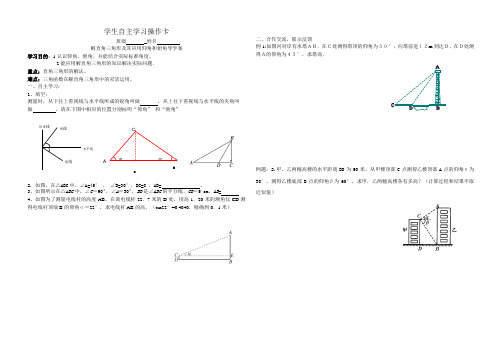
学生自主学习操作卡班级 _姓名解直角三角形及其应用仰角和俯角导学案学习目的:1.认识仰角、俯角,并能结合实际标准角度。
2.能应用解直角三角形的知识解决实际问题.重点:直角三角形的解法。
难点:三角函数在解直角三角形中的灵活运用。
一、自主学习: 1、填空:测量时,从下往上看视线与水平线所成的锐角叫做 ,从上往下看视线与水平线的夹角叫做 。
请在下图中相应的位置分别标明“仰角” 和“俯角”2. 如图,在△ABC 中,∠A=45° , ∠B=30°,BC=8 ,AB= 。
3、如图所示在△ABC 中,∠C =90°,∠A =30°,BD 是∠ABC 的平分线,CD =5 cm ,AB = 4、如图为了测量电线杆的高度AB ,在离电线杆22.7米的D 处,用高1.20米的测角仪CD测得电线杆顶端B 的仰角α=22°,求电线杆AB 的高.(tan22°=0.4040,精确到0.1米)二、合作交流,展示反馈例1:如图河对岸有水塔AB.在C处测得塔顶的仰角为30°,向塔前进12m 到达D,在D处测得A的仰角为45°,求塔高.例题:2.甲、乙两幢高楼的水平距离BD 为90米,从甲楼顶部C 点测得乙楼顶部A 点的仰角α为30°,测得乙楼底部B 点的仰角β为60°,求甲,乙两幢高楼各有多高?(计算过程和结果不取近似值)A三、分层训练:1. 如图,某飞机于空中A 处探测到目标C ,此时飞行高度AC =1200米,从飞机上看地面控制点B 的俯角α=30°,求飞机A 到控制点B 的距离.(精确到1米)2. 两座建筑AB 与CD ,其地面距离AC 为50米,从AB 的顶点B 测得CD 的顶部D 的仰角β=30°,测得其底部C 的俯角α=60°,求两座建筑物AB 与CD 的高.(精确到0.1米) 3、如图,小明想测量塔CD 的高度。
导学案282解直角三角形及其应用

一、素质教育目标1.知识教学点使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.2.能力训练点通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.3.德育渗透点渗透数形结合的数学思想,培养学生良好的学习习惯. 二、教学重点、难点和疑点1.重点:直角三角形的解法.2.难点:三角函数在解直角三角形中的灵活运用.3.疑点:学生可能不理解在已知的两个元素中,为什么至少有一个是边.三、教学步骤(一)新课引入1.在三角形中共有几个元素?2.直角三角形ABC 中,∠C=90°,a 、b 、c 、∠A 、∠B 这五个元素间有哪些等量关系呢? (1)边角之间关系a b A b a A c b A c a A ====cot ;tan ;cos ;sinb aB a b B c a B c b B ====cot ;tan ;cos ;sin(2)三边之间关系a 2 +b 2 =c 2(勾股定理)(3)锐角之间关系∠A+∠B=90°.以上三点正是解直角三角形的依据,通过复习,使学生便于应用. (二)新课问题1: 如图所示,在一次强烈的地震中一棵百年大树被折断倒在地上,你知道这棵大树在折断之前有多高吗?方案1:直接测量被折断的两部分树干AC 和AB 的长度,再把它们加起来. 方案2;测量地面距离BC 和被折断的树干AC 或AB 的长度,再用勾股定理解答.方案3;先用测角仪测量∠B 的度数,再测量地面距离BC 的长度,用锐角三角函数知识解答问题2:星期天,小华去图书超市购书,因他所买书类在二楼,故他乘电梯上楼,已知电梯AB段的长度8 m,倾斜角为300,则二楼的高度(相对于底楼)是__________m2.由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。
3.例题评析例 1在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b= 2 a=6,解这个直角三角形.∠=350,例2在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b= 20 B解这个直角三角形(精确到0.1).解直角三角形的方法很多,灵活多样,学生完全可以自己解决,但例题具有示范作用.因此,此题在处理时,首先,应让学生独立完成,培养其分析问题、解决问题能力,同时渗透数形结合的思想.其次,教师组织学生比较各种方法中哪些较好,选一种板演。
2.5《解直角三角形的应用(3)》导学案

2.5解直角三角形的应用(3)
学习目标:
1.会用解直角三角形的有关知识解某些简单的实际问题。
2.了解一些常用的测量名词方位角、坡度、坡角的意义,能根据及测量术语绘出示意图。
学习重点、难点:理解坡度、坡角的概念,利用解直角三角形解决实际问题。
课前预习案
1、如图,建筑学中把斜坡起止点A,B的_______________与它们的______________的比叫做坡度(或坡比)
2、表示:通常用字母i表示,即i=____________,
表示坡度时,一般吧比的前项取作1.
3、如上图,斜坡AB与水平线AC的夹角记作α,那
么i=_______ =_______,这就是说,坡度等于锐角α的
___________________。
课中探究案
方法指导:解决此类问题往往会遇到梯形,一般会过上底的两个顶点作出梯形的两条高,将梯形问题转化为直角三角形和矩形的问题
探究2:如图,要测量铁塔的高AB,在地面上选取一点C,在A、C两点间选取一点D,测得CD=14米,在C、D两点处分别用测角仪测得铁塔顶端B的仰角为α=30°和β=45°.测角仪支架的高为1.2米,求铁塔的高(精确到0.1米).
巩固练习。
人教九年级下册数学- 解直角三角形的简单应用导学案

28.2.2 应用举例镇海中学陈志海第1课时解直角三角形的简单应用【学习目标】1.使学生根据直角三角形的知识解决实际问题.2. 逐步培养学生分析问题、解决问题的能力.3.渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识【学习重点】将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.【学习难点】实际问题转化成数学模型【导学过程】一、课前热身:1.解直角三角形的类型:已知____________;已知___________________.2.如图解直角三角形的公式:(1)三边关系:__________________.(2)角关系:∠A+∠B=_____,(3)边角关系:sinA=___,sinB=____,cosA=_______.cosB=____,tanA=_____ ,tanB=_____.3.已知,如图,在△ABC中,∠B = 45°,∠C = 60°,AB = 6.求BC的长. (结果保留根号).cbaAC B二、合作交流:要想使人安全地攀上斜靠在墙面上的梯子的顶端.梯子与地面所成的角一般要满足, (如图).现有一个长6m的梯子,问:(1)使用这个梯子最高可以安全攀上多高的墙(精确到0. 1 m)(2)当梯子底端距离墙面2.4 m时,梯子与地面所成的角等于多少(精确到1o) 这时人是否能够安全使用这个梯子?(可用计算器)【素材积累】1、黄鹂方才唱罢,摘村庄的上空,摘树林子里,摘人家的土场上,一群花喜鹊便穿戴着黑白相间的朴裙裾而闪亮登场,然后,便一天喜气的叽叽喳喳,叽叽喳喳叫起来。
2、摘湖的周围有些像薄荷的小草,浓郁时,竟发出泥的气息!仔细看几朵小花衬着绿绿的小草显得格外美丽。
夏天,大大的荷叶保护着那一朵朵娇粉的荷花。
摘整个湖泊中格外显眼。
如果你用手希望对您有帮助,谢谢来捧一捧这里的水,那可真是凉爽它会让你瞬间感到非常凉爽、清新。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形及其应用
导学案
-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
九年级(上)数学导学案
课题:23.2 解直角三角形及其应用(2)编号9S046
教学思路(纠错栏)
教学思路(纠错栏)学习目标:
1.知道仰角、俯角等有关概念;
2.能把实际问题转化为数学问题来解决.
学习重点:利用三角函数解决实际问题;
学习难点:把实际问题转化为数学问题.
☆预习导航☆
一、链接:什么叫解直角三角形在解直角三角形时用到的边、角数量关系有哪些
二、导读:
1.阅读课本126页,重点思考如何把实际问题转化为数学问题来解答,边角之间的关系有:
sinA = ______ , cosA = ________ , tanA =
_______ .
2.仰角、俯角的定义:
从低处观测高处的目标时,
视线与水平线所成的锐角叫做仰
角;
从高处观测低处的目标时,
视线与水平线所成的锐角叫做俯
角.
☆合作探究☆
1. 上海东方明珠塔于1994 年10 月1
日建成,在各国广播电视塔的排名榜
中,当时其高度列亚洲第一、世界第
三.与外滩的“万国建筑博览群”隔江相
望.在塔顶俯瞰上海风景,美不胜
收.运用本章所学过的知识,能测出东
方明珠塔的高度来吗?
为了测量东方明珠塔的高度,小亮和同学们在距离东方明珠塔200 米处的地面上,用高1.20 米的测角仪测得东方明珠塔顶的仰角为60°48 ′.
A
B
E
C
D
根据测量的结果,小亮画了一张示意图,其中AB表示东方明珠塔,DC为测角仪的支架,DC=1.20米,CB=200米,∠ADE=60°48 ′
根据在前一学段学过的长方形对边相等的有关知识,你能求出AB 的长吗?
2. 如图,厂房屋顶人字架的跨度为10 米,上弦AB=BD,∠A = 260 .求中柱BC 和上弦AB 的长(精确到0 . 01 米).
☆归纳反思☆
☆达标检测☆
1 .如图,在电线杆上离地面6 米处
用拉线固定电线杆,拉线和地面之间的
夹角为60° , 求拉线AC 的长和拉线下
端点A 与线杆底部D 的距离(精确到
0 . 1 米).
2.如图,一架梯子斜靠在墙上,梯子顶
端到地面的距离BC = 3.2 米,底端到墙
根的距离AC = 2.4 米.
(1)求梯子的长度和梯子与地面所成角的大小(精确到1 ' ) ;
(2) 如果把梯子的底端到墙角的距离减少0 . 4 米,那么梯子与地面所成的角是多少?
6
米
A B
C
D
A
C
B。
