线面平行与面面平行
线面、面面平行和垂直的八大定理

线面、面面平行和垂直的八大定理一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平a a P'b 二.•「a// ■-面平行。
符合表示:a//b2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:a広oa//«=■ a//ba -:-b二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
n 〃b "m // aa"b = Mm □ n = N符号表示:2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
a //P ]符号表示:: =| = l//d (更加实用的性质:一个平厂L: d面内的任一直线平行另一平面)三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面符号表示:$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直符号表示:oA 二、:po -:2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
a _ ■ ,a---:2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面:=b, a x 上,a_b= a -:Welcome !!! 欢迎您的下载, 资料仅供参考!。
线线平行、线面平行、面面平行的判定方法(本人原创)

创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*在空间“线线平行、线面平行、面面平行”的判定方法一、两条直线平行的判定方法(1)在同一平面内没有公共点的两条直线平行(定义)(2)先证在同一平面内,再用平面几何中的平行线的判定理或者相关图形的性质进行证明。
如①在同一平面内,两条直线被第三条直线所截,如果同位角或内错角相等,或同旁内角互补,则两直线平行。
②三角形、梯形中位线定理。
③平行四边形、矩形、菱形、正方形性质(对边平行)。
④在同一个平面内,同垂直于一条直线的两条直线平行(注意:此结论在空间不适合)。
(3)(线面平行的性质)如果一条直线和一个平面平行,则经过这条直线的一个平面与这个平面相交,那么这条直线和交线平行。
(4)如果两直线都平行于第三条直线,那么这两条直线互相平行(平行的传递性)。
(5)(面面平行的性质)如果两个平行平面分别和第三个平面相交,则它们的交线平行。
(6)(线面垂直的性质之一)如果两条直线垂直于同一个平面,那么这两条直线平行。
(7)用向量证明。
二、一条直线和一个平面平行的判定(1)如果一直线和一平面没有公共点,那么这条直线就和这个平面平行(定义)(2)平面外的一条直线,如果和这个平面内的一条直线平行,那么这条直线就和这个平面平行(线面平行的判定定理)。
(3)如果两个平面相互平行,那么在一个平面内的任何一条直线都平行于另一个平面.(线面平行的性质)。
(4)向量法。
三、两个平面平行的判定(1)如果两个平面没有公共点,那么这两个平面互相平行(定义)(2)如果一个平面内的两条相交直线分别和另一个平面平行,那么这两个平面平行。
(3)如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
(4)如果两个平面分别平行于第三个平面,那么这两个平面平行。
(5)如果两个平面垂直于同一条直线,那么这两个平面平行。
在空间“线线垂直、线面垂直、面面垂直”的判定方法一、两条直线垂直的判定(1)在同一个明面内证明两条直线垂直可按照平面几何的有关定理和方法判定。
2.2线面平行、面面平行的判定
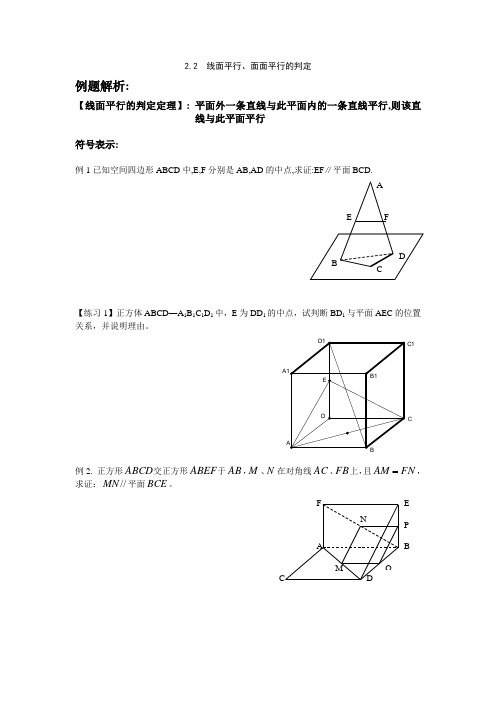
2.2 线面平行、面面平行的判定例题解析:【线面平行的判定定理】: 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行符号表示:例1已知空间四边形ABCD 中,E,F 分别是AB,AD 的中点,求证:EF ∥平面BCD.【练习1】正方体ABCD —A 1B 1C 1D 1中,E 为DD 1的中点,试判断BD 1与平面AEC 的位置关系,并说明理由。
例2. 正方形ABCD 交正方形ABEF 于AB ,M 、N 在对角线AC 、FB 上,且FN AM ,求证://MN 平面BCE 。
C1A C【练习求证:例3.已知P 是平行四边形ABCD 所在平面外一点,E 、F 分别为AB 、PD 的中点,求证:AF ∥平面PEC【练习3】:在正方体ABCD -A 1B 1C 1D 1中,E 、F BC 、C 1D 1的中点 求证:EF ∥平面BB 1D 1DPDBA C1A CA例4.(如图)已知正方体ABCD-A 1B 1C 1D 1,求证平面AB 1D 1∥平面C 1BD练习4 正方体ABCD-A 1B 1C 1D 1,中,M,N,E,F 分别为棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点,求证: 平面AMN ∥平面EFDB例5:在正方体ABCD-A 1B 1C 1D 1中,E 、F 、G 、P 、Q 、R 分别是所在棱AB 、BC 、BB '、A 'D '、D 'C '、DD '的中点,求证:平面PQR ∥平面EFG 。
CB 1A 1C 1D 1ABDC'CB 1A 1C 1D 1ABD练习5:已知四棱锥P-ABCD 中,地面ABCD 为平行四边形,点M,N,Q 分别为PA,BD,PD 上的中点,求证:平面MNQ ∥平面PBC【巩固练习】一、选择题1、a ∥β,则a 平行于β内的( ) A 、一条确定的直线 B 、任意一条直线 C 、所有直线 D 、无数多条平行线2、如果直线a ∥平面a ,那么直线a 与平面a 内的( ) A 、一条直线不相交 B 、两条直线不相交 C 、无数条直线不相交 D 、任意一条直线都不相交3 两条平行线中的一条平行于一个平面,那么另一条与此平面的位置关系是( ) A.平行 B.相交或平行C.平行或在平面内.D.相交或平行或在平面内 4. 已知直线l ∥平面α,直线a α⊂,则l 与 a 必定 ( ) A.平行. B.异面. C.相交. D.无公共点.5、直线a ∥面α,面α内有n 条互相平行的直线,那么这n 条直线和直线a ( ) A 、全平行B 、全异面C 、全平行或全异面D 、不全平行也不全异面6、直线a ∥平面a ,平面a 内有n 条直线相交于一点,那么这n 条 直线中与直线a 平行的( ) A 、至少有一条B 、至多有一条C 、有且只有一条D 、不可能有二、填空题7、若直线a ∥平面 α,直线b ∥平面β,且 a ⊂β,b ⊂α,且 α∩β=c ,则 a 、b 的位置关系是8、若直线a ∥平面 α,直线b ∥ 平面β,a ⊂β,b ⊂α,则a 、b 的位置关系是B9. 空间四边形ABCD 中,AC=2cm ,BD=4cm ,AC 与BD 成45°角,M ,N ,P ,Q 分别是四边中点,则四边形MNPQ 的面积是 . 三.解答题10.在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE :EB=CF :FB=1:3,则对角线AC 和平面DEF 的位置关系如何?11.正方体ABCD —A 1B 1C 1D 1的棱长为a ,E ,F 是线段AD 1,DB 上的点,且AE =BF . 求证:EF ∥平面CD 1.12.已知,如图P 是平行四边形ABCD 外一点同M ,N 分别是PC ,AB 的中点。
线面平行 面面平行 的判定

2.2.3 直线与平面平行的性质 2.2.4 平面与平面平行的性质1.文字语言:一条直线与一个平面平行,则__过这条直线的任一平面与此平面的交线__与该直线平行.2.图形语言:3.符号语言:⎭⎪⎬⎪⎫a ∥α__a ⊂β____α∩β=b __⇒a ∥b 4.作用:线面平行⇒线线平行.要点二 面面平行的性质定理1.文字语言:如果两个平行平面同时和第三个平面__相交__,那么它们的交线__平行__.2.图形语言:3.符号语言:⎭⎪⎬⎪⎫α∥β__α∩γ=a ____β∩γ=b __⇒a ∥b 4.作用:面面平行⇒线线平行.要点三 平行关系性质的应用1.若平面α与平面β平行,则α上的任何直线与平面β的位置关系是__平行__. 2.若两个面互相平行,则分别在这两个平行平面内的直线的关系是__平行或异面__. 3.A 是异面直线a ,b 外一点,过A 最多可作__0或1__个平面同时与a ,b 平行. 4.过平面外一点能作__无数__条直线和这个平面平行.思考: 如果两个平面平行,那么分别位于两个平面内的直线也互相平行,这句话正确吗?为什么?提示 不正确,因为这两个平面平行,那么位于两个平面内的直线没有公共点,它们平行或异面.考点一线面平行、面面平行的性质定理定理可简记为“线面平行,则线线平行”“面面平行,则线线平行”.定理揭示了直线与平面平行中蕴涵着直线与直线平行,即通过直线与平面平行、平面与平面平行可得到直线与直线平行,这给出了一种作平行线的方法.【例题1】在下列命题中,正确的有__④__(填序号).①若α∩β=a,b⊂α,则a∥b;②若a∥平面α,b⊂α,则a∥b;③若平面α∥平面β,a⊂α,b⊂β,则a∥b;④平面α∥平面β,点P∈α,a∥β且P∈a,则a⊂α.思维导引:此类题一般是以符号语言为载体的判断题,熟悉相关定理是前提,全面分析是关键,一般通过合理利用模型及排除法解题.解析①若α∩β=a,b⊂α,则a,b可能平行也可能相交,①不正确;②若a∥α,b⊂α,则a与b异面或a∥b,②不正确;③若α∥β,a⊂α,b⊂β,则a∥b或a与b异面,③不正确;④若α∥β,点P∈α,知P∉β,所以过点P且平行于β的直线a必在α内,故④正确.【变式1】(1)若直线a,b均平行于平面α,那么a与b的位置关系是__平行、相交或异面__.(2)若直线a∥b,且a∥平面β,则b与β的位置关系是__b∥β或b⊂β__.(3)若直线a,b是异面直线,且a∥β,则b与β的关系是__b∥β或b⊂β或b与β相交__.解析(1)a∥α,b∥α,则知a,b与α无公共点,而a,b平行、相交、异面都有可能.(2)a∥b,a∥β知b∥β或b在β内.(3)b与β的三种位置关系都有可能.考点二线面平行的性质及应用利用线面平行的性质定理判断两直线平行的步骤:(1)先找过已知直线且与已知平面相交的平面;(2)再找两个平面的交线;(3)由定理得出结论.【例题2】如图,已知两条异面直线AB与CD,平面MNPQ与AB,CD都平行,且点M,N,P,Q依次在线段AC,BC,BD,AD上,求证:四边形MNPQ是平行四边形.思维导引:AB∥平面MNPQ,CD∥平面MNPQ→MN∥PQ,NP∥MQ→四边形MNPQ是平行四边形证明因为AB∥平面MNPQ,且过AB的平面ABC交平面MNPQ于MN,所以AB∥MN.又过AB的平面ABD交平面MNPQ于PQ,所以AB∥PQ,所以MN∥PQ.同理可证NP ∥MQ.所以四边形MNPQ为平行四边形.【变式2】如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于点F.求证:EF∥B1C.证明由正方形的性质可知A1B1∥AB∥DC,且A1B1=AB=DC,所以四边形A1B1CD 为平行四边形,从而B1C∥A1D,又A1D⊂平面A1DFE,B1C⊄平面A1DFE,于是B1C∥平面A1DFE.又B1C⊂平面B1CD1,平面A1DFE∩平面B1CD1=EF,所以EF∥B1C.考点三面面平行的性质及应用应用平面与平面平行的性质定理的基本思路:【例题3】在长方体ABCD-A1B1C1D1中,E为棱DD1上的点.当平面AB1C∥平面A1EC1时,点E的位置是__与D重合__.思维导引:平面AB1C∥平面A1EC1,且都与对角面BB1D1D相交,则交线平行.在平行四边形BB1D1D中再来论证平行线的位置.解析如图,连接B1D1,BD,设B1D1∩A1C1=M,BD∩AC=O.连接ME,B1O,因为平面AB1C∥平面A1EC1,平面AB1C∩平面BDD1B1=B1O,平面A1EC1∩平面BDD1B1=ME,所以B1O∥ME.又由长方体的性质可知四边形B1MDO为平行四边形,则B1O∥MD.故E与D重合.【变式3】已知三棱柱ABC-A′B′C′中,D是BC的中点,D′是B′C′的中点,设平面A′D′B∩平面ABC=a,平面ADC′∩平面A′B′C′=b,判断直线a,b的位置关系,并证明.解析直线a,b的位置关系是平行.如图所示,连接DD′.因为平面ABC∥平面A′B′C′,平面A′D′B∩平面ABC=a,平面A ′D ′B ∩平面A ′B ′C ′=A ′D ′, 所以A ′D ′∥a . 同理可证AD ∥b .又D 是BC 的中点,D ′是B ′C ′的中点,所以DD ′BB ′,又BB ′AA ′,所以DD ′AA ′,所以四边形AA ′D ′D 为平行四边形,所以A ′D ′∥AD ,所以a ∥b .考点四 空间平行关系的相互转换线线平行、线面平行、面面平行这三种关系是紧密相连的,可以进行转换.相互间的转换关系如下.【例题4】 如图,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,P ,Q 分别是AD 1,BD 的中点.(1)求证:PQ ∥平面DCC 1D 1; (2)求PQ 的长;思维导引:通过作辅助线构造平面,从而证得线面平行;或通过线线平行证得线面平行. 解析 (1)证明:方法一 如图,连接AC ,CD 1.AC 与BD 交于点Q .因为P ,Q 分别是AD 1,AC 的中点,所以PQ ∥CD 1. 又PQ ⊄平面DCC 1D 1, CD 1⊂平面DCC 1D 1, 所以PQ ∥平面DCC 1D 1.方法二 取AD 的中点G ,连接PG ,GQ , 则有PG ∥DD 1,GQ ∥DC ,且PG ∩GQ =G , 则平面PGQ ∥平面DCC 1D 1.又因为PQ ⊂平面PGQ ,则PQ ∥平面DCC 1D 1. (2)由(1)易知PQ =12D 1C =22a .【变式4】 如图,在正方体ABCD -A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E ,F ,且B 1E =C 1F .求证:EF ∥平面ABCD .证明 过E 作EG ∥AB 交BB 1于点G ,连接GF ,则B 1E B 1A =B 1GB 1B.因为B 1E =C 1F ,B 1A =C 1B ,所以C 1F C 1B =B 1GB 1B .所以FG ∥B 1C 1∥BC ,又因为EG ∩FG =G ,AB ∩BC =B , 所以平面EFG ∥平面ABCD ,又因为EF ⊂平面EFG ,EF ⊄平面ABCD , 所以EF ∥平面ABCD .。
线面平行与面面平行的判定

两边中点的 边所在的平面
A
.
E B C
F D
变式 1、空间四边形 BCD 的重心,求证
ABCD 中 P , Q 分别是 ABC 和 PQ // 平面 ACD .
A
E P
B
O
C Q D F
变式 2、 E , F , G , H 分别是空间四边形 的中点,求证
ABCD 各边
AC // 平面 EFGH , BD // 平面 EFGH .
分别为BAC、
与 BCD 面积的比值.
A
F
M B P H E D
G
C
变式 3、如图所示,已知正方
体 ABCD A 1 B 1 C 1 D 1 ,
面对角线 AB 1 , BC 1 上分别有点 E , F , 且 B 1 E C 1 F . 求证:(1 ) EF // 面 A BCD ; ( 2 ) 面 ACD
1
// 面 A 1 BC 1 .
D1 C1 B1
E F
A1
D
C
A B
变式4、如图,设AB、CD为夹在两个平行平 面 、 之间的线段,且直线AB、CD为 异面直线,M、P 分别为AB、CD 的中点, 求证: 直线MP // 平面 .
A
C
P
M
N
D
B
E
练习4、教材58页:1,2,3题
必做题、 选做题、
β。
问2、三角板的一条边所在的直线与桌面平行, 这个三角板所在的平面与桌面平行吗?三角板 的两条边所在的直线分别与桌面平行,情况又 如何?
问3、(1)平面β 内有一条直线与平面α平行, α与β 平行吗?
(2)平面β 内有两条直线与平面α平行, α与
2.2.1线面平行、面面平行的判定

√ β∥γ
α∥γ
α∥β
× a∥c
⑤
α∥c
α∥a ⑥
×a∥γ
α∥γ
a∥α
例题分析
例2、如图:A、B、C为不在同一直线上的
三点,AA1 ∥ BB1∥ CC1 =求证:平面ABC//平面A1B1C1
C1 A1 B1 C A B
例3、已知正方体ABCD-A1B1C1D1,求证:平 面AB1D1∥平面C1BD。
2.2.1直线与平面平行的判定 2.2.2平面与平面平行的判定
(1)
直线和平面有哪些位置关系? a
a a
α
直线在平面α 内a α 有无数个交点
α
A
α
直线与平面α 平行 a∥α无交点
直线与平面α相交 a ∩ α= A 有且只有一个交点
定义:一条直线和一个平面没有公共点, 叫做直线与平面平行.
(2)怎样判定直线和平面平行?
小结
线面平行的判定定理 线线平行
线面平行
如果不在一个平面内的一条直线和平面内的 一条直线平行,那么这条直线和这个平面平行.
平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行, 则这两个平面平行。
定理的推论
如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线,那么这两个平面平行
(2)直线 a∥平面α,平面α内有无数条直线 交于 一点,那 么这无数条直线中与直线 a 平行的( B ) (A)至少有一条 (C)有且只有一条 (B)至多有一条 (D)不可能有
例题分析
例1、求证:空间四边形相邻两边中点的连线平行于经过 另外两边所在的平面。 已知:空间四边形ABCD,E、F分别是AB、AD的中点。
线面平行、面面平行的判定

6:下面说法正确的有( ) ①平面外直线与平面内的一条直线平行,则直线与平面平 行;②直线与平面内的两条直线平行,则直线与平面平行;③ 直线与平面内的任意一条直线平行,则直线与平面平行;④直 线与平面内的无数条直线平行,则直线与平面平行.
A.1 个
B.2 个
C.3 个
D.4 个
错因剖析:没有考虑直线在平面内的情况.
∴EF∥平面MNQ.
图8
又∵EF∩FG=F,
∴平面EFG∥平面MNQ.
1.直线 l 与平面α内无数条直线平行,则 l 与α的位置关系
是( D )
A.平行
B.相交
C.平行或相交
D.以上答案都不对
2.下列说法中错误的个数是( C ) ①过平面外一点有一条直线和该平面平行 ②过平面外一点只有一条直线和该平面平行
③过平面外有且只有一条直线和该平面平行
A.0
B.1
C.2
D.3
3.给出下列四个命题: ①若一条直线与一个平面内的一条直线平行, 则这条直线 与这个平面平行; ②若一条直线与一个平面内的两条直线平行, 则这条直线 与这个平面平行; ③若平面外的一条直线和这个平面内的一条直线平行, 那 么这条直线和这个平面平行;
图4
同理可证,BD∥平面 EFG.
证面面平行
例 3:如图 5,已知正方体 ABCD-A1B1C1D1. 求证:平面 AD1B1∥平面 C1DB.
图5
证明:∵D1B1∥DB,D1B1⊄平面C1DB,DB⊂平面C1DB, ∴D1B1∥平面C1DB,同理 AB1∥平面C1DB, 又 D1B1∩AB1=B1,AB1、D1B1 同在平面AD1B1 内, ∴平面AD1B1∥平面C1DB.
1.如图 3,P 是平行四边形 ABCD 所在平面外一点,Q 是 PA 的中点.求证:PC∥平面 BDQ.
线面平行、面面平行的性质

(
(2)若直线a、b都和平面平行, 则a与b平行.
)
)
(3)若直线a和平面, 都平行, 则与平行.
(4)若平面外的两条平行直线中的一条平行 于这个平面,则另一条也平行于这个平面.
( )
例1:如图所示的一块木料中,棱BC平行于面A'C'. (1)要经过面内的一点P和棱BC将木料锯开,应 怎样画线?
l //
l m
试证:平面外的两条平行直线中的一条平行 于这个平面,则另一条也平行于这个平面.
已知:a , b , a // b, a // , 求证:b // ,
且 证明:过a作平面,
a // a
c
c
a c
b
a // c
b // c a // b c
解: (2) 由(1),得 EF//BC, D' F C' EF//BC P A' E BC 面AC EF//面AC B' D EF 面AC C A B
直线和平面平行这条直线和这个平面内的直线 位置关系?
a b α α a b
平行
异面
证明或判定直线与平面平行的方法:
1、定义法(直线与平面无公共点)
a 2、直线与平面平行的判定定理 b a // a // b
3、两平面平行的性质定理2: //
a }
a //
证明或判定两平面与平行的方法:
1、定义法(两平面没有公共点)
a b 2、平面与平面平行的判定定理 a b P // a // b //
已知: // , A , C , B ,D . AB // CD, 求证: AB=CD C AB // DC 证明: A 过AB,CD可作平面 D B AD AC BD AC//BD BC AB // CD //
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线面平行与面面平行专题复习
【知识梳理】
线线平行
线面平行面面平行
1、,,//l a b a l
α
βαβ=⊂⊂已知:平面平面,求证:
归纳
m β⎬⎪=⎭
,//b b A b αβ⊂⎫
⎪=⇒⎬⎪⎭
//a b βγγ⎫
⎪
=⇒⎬⎪=⎭
//a βα⎫
⇒⎬⊂⎭
D
B
1B 1
A 1
C B A
D E
C 2、在正方体中,O 为面ABC
D 的中心,
求证:1
11//.AO B CD 平面
归纳: 3、已知:点是平行四边形ABCD 所在平面外一点,
Q 是PA 的中点,
求证:PC//平面BQD.
归纳:
4、如图,两个正方形ABCD 和ABEF 所在的平面相交于AB,M,N 分别是对角线AC,BF 上的点,AM=FN ,求证:MN//平面BCE.
小结1:证明线面平行的方法常常转化为面外线与面内线平行,而证明两线平行的方法常有: , , ,
B 1
D B
A
C 1C
B 题型二、面面平行的判定与性质
1、1111111//.ABCD A B C D AB D C BC -在正方体中,求证:平面平面
归纳:
11111111111,,:(1)//;(2)//.
ABC A B C D AC BC AB D D AC B DA BC D -2、如图已知正三棱柱中,点为的中点求证平面为的中点,求证:平面平面
归纳:
3//,,,,,,////AB CD A C B D E F AB CD EF αβααββαβ
∈∈∈∈、已知平面平面,是异面直线,分别为,的中点,求证:
归纳:
练习: 1.
如图,E D ,分别是正三棱柱111ABC A B C -的棱1AA 、11B C 的中点,
求证:1//A E 平面1BDC ;
2.在直三棱柱111C B A ABC -中, E 、F 分别为
11A C 、11B C 的中点,D 为棱1CC 上任一点.
求证:直线EF ∥平面ABD ;
3、如图,在正方体1111ABCD A B C D -中,E ,F 分别是棱
BC ,11C D 的中点,求证:EF //平面11BB D D .
4. 如图,在四棱锥P ABCD -中,ABCD 是平行四边形,M ,N 分别是AB ,PC 的中点.
求证:MN //平面PAD .
C 1 A
B
C
D
E F
A 1
B 1
第2题
1A
1B 1D
1C
F
E A
B
C D A
P
D
M
N
B
C。
