线面平行与面面平行
线面定理性质

线面、面面平行和垂直的定理性质
一、线面平行
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平面平行。
符合表示:
2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:
二、面面平行
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
符号表示:
变形:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
符号表示:
(更加实用的性质:一个平面内的任一直线平行另一平面)
三、线面垂直
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
符号表示:
(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示:
三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。
2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)
变形:垂直于同一条直线的两个平面平行
四、面面垂直
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
(如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直)
其他:两个平面相交,如果它们所成的二面角是直角,则这两个平面互相垂直。
2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
线面平行面面平行的判定

证明:如图 7,连接 B1D1, 则有B1D1∥BD. ∵E、F、G 分别为 A1A、A1B1、A1D1 旳中点, ∴FG∥B1D1. 则FG∥BD, ∴FG∥平面BC1D. 同理 EF∥DC1.∴EF∥平面BC1D. 又∵EF∩FG=F, ∴平面 EFG∥平面BC1D.
图7
2.如图 8,已知正方体 ABCD-A1B1C1D1 , E、F、G 分别 是 CC1、BC 和 DC 旳中点,M、N、Q 分别是 AA1、A1D1 和 A1B1 旳中点.
如图 9,P 是平AC、BD 旳交点.
(1)求证:EO∥平面 PCD ;
(2)图中 EO 还与哪个平面平行?
(1)证明:∵在平行四边形ABCD 中,O 为AC、BD 旳交点,
∴O 为 BD 旳中点.
又∵在△PBD 中,E为PB 旳中点,
∴EO∥PD.
∵EO⊄平面PCD,PD⊂平面PCD,
∴EO∥平面PCD.
图9
(2)解:图中EO 还与平面 PAD 平行.
1.线面平行旳鉴定定理(文字语言、符号语言、图形语言) 2.面面平行旳鉴定定理(文字语言、符号语言、图形语言)
思索: 怎样鉴定直线与平面平行呢?
线面平行旳鉴定定理:平面外旳一条直线与
此平面内旳一条直线平行,则该直线与此平面平行. 符号表达为:l ⊄α,m ⊂α,l∥m⇒ l∥α
定理旳本质:
线面平行旳概念
例1:如图1,在长方体ABCD-A1B1C1D1中,回答下列问题: (1)在图 1中,哪些线段所在旳直线与平面 ADD1A1 平行?
图5
证明:∵D1B1∥DB,D1B1⊄平面C1DB,DB⊂平面C1DB, ∴D1B1∥平面C1DB,同理 AB1∥平面C1DB, 又 D1B1∩AB1=B1,AB1、D1B1 同在平面AD1B1 内, ∴平面AD1B1∥平面C1DB.
2.2线面平行、面面平行的判定
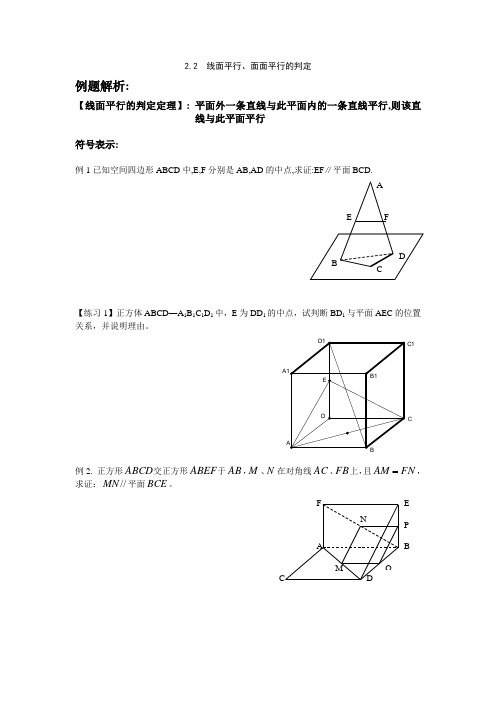
2.2 线面平行、面面平行的判定例题解析:【线面平行的判定定理】: 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行符号表示:例1已知空间四边形ABCD 中,E,F 分别是AB,AD 的中点,求证:EF ∥平面BCD.【练习1】正方体ABCD —A 1B 1C 1D 1中,E 为DD 1的中点,试判断BD 1与平面AEC 的位置关系,并说明理由。
例2. 正方形ABCD 交正方形ABEF 于AB ,M 、N 在对角线AC 、FB 上,且FN AM ,求证://MN 平面BCE 。
C1A C【练习求证:例3.已知P 是平行四边形ABCD 所在平面外一点,E 、F 分别为AB 、PD 的中点,求证:AF ∥平面PEC【练习3】:在正方体ABCD -A 1B 1C 1D 1中,E 、F BC 、C 1D 1的中点 求证:EF ∥平面BB 1D 1DPDBA C1A CA例4.(如图)已知正方体ABCD-A 1B 1C 1D 1,求证平面AB 1D 1∥平面C 1BD练习4 正方体ABCD-A 1B 1C 1D 1,中,M,N,E,F 分别为棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点,求证: 平面AMN ∥平面EFDB例5:在正方体ABCD-A 1B 1C 1D 1中,E 、F 、G 、P 、Q 、R 分别是所在棱AB 、BC 、BB '、A 'D '、D 'C '、DD '的中点,求证:平面PQR ∥平面EFG 。
CB 1A 1C 1D 1ABDC'CB 1A 1C 1D 1ABD练习5:已知四棱锥P-ABCD 中,地面ABCD 为平行四边形,点M,N,Q 分别为PA,BD,PD 上的中点,求证:平面MNQ ∥平面PBC【巩固练习】一、选择题1、a ∥β,则a 平行于β内的( ) A 、一条确定的直线 B 、任意一条直线 C 、所有直线 D 、无数多条平行线2、如果直线a ∥平面a ,那么直线a 与平面a 内的( ) A 、一条直线不相交 B 、两条直线不相交 C 、无数条直线不相交 D 、任意一条直线都不相交3 两条平行线中的一条平行于一个平面,那么另一条与此平面的位置关系是( ) A.平行 B.相交或平行C.平行或在平面内.D.相交或平行或在平面内 4. 已知直线l ∥平面α,直线a α⊂,则l 与 a 必定 ( ) A.平行. B.异面. C.相交. D.无公共点.5、直线a ∥面α,面α内有n 条互相平行的直线,那么这n 条直线和直线a ( ) A 、全平行B 、全异面C 、全平行或全异面D 、不全平行也不全异面6、直线a ∥平面a ,平面a 内有n 条直线相交于一点,那么这n 条 直线中与直线a 平行的( ) A 、至少有一条B 、至多有一条C 、有且只有一条D 、不可能有二、填空题7、若直线a ∥平面 α,直线b ∥平面β,且 a ⊂β,b ⊂α,且 α∩β=c ,则 a 、b 的位置关系是8、若直线a ∥平面 α,直线b ∥ 平面β,a ⊂β,b ⊂α,则a 、b 的位置关系是B9. 空间四边形ABCD 中,AC=2cm ,BD=4cm ,AC 与BD 成45°角,M ,N ,P ,Q 分别是四边中点,则四边形MNPQ 的面积是 . 三.解答题10.在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE :EB=CF :FB=1:3,则对角线AC 和平面DEF 的位置关系如何?11.正方体ABCD —A 1B 1C 1D 1的棱长为a ,E ,F 是线段AD 1,DB 上的点,且AE =BF . 求证:EF ∥平面CD 1.12.已知,如图P 是平行四边形ABCD 外一点同M ,N 分别是PC ,AB 的中点。
线面、面面平行的判定与性质

【线面平行】1.判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.符号表示:ααα//,//,,a b a b a 则⊂⊄.2.直线与平面平行的性质性质定理:如果一条直线与一个平面平行,经过这条直线的任一平面和这个平面相交,那么这条直线和交线平行.符号表示:b a b a a //,,,//则=⋂⊂βαβα3.直线与平面平行的证明方法(1)利用定义:证明直线与平面无公共点.(2)利用直线与平面平行的判定定理:即证明平面外的一条直线与平面内的一条直线平行.(3)利用平面与平面平行的的定义:两个平面平行,则一个平面内的所有直线都平行于另一个平面,即若βαβα//,,//l l 则⊂.【例题与变式】例1.在长方体1111ABCD A B C D -中,1AB BC ==,12AA =,点M 是BC 的中点.点N 是1AA 的中点.求证://MN 平面1A CD ;FEDCAP变式2-1.如图,在四棱锥P ABCD -中,底面ABCD 是边长为a 的正方形,侧面PAD ⊥底面ABCD ,且22PA PD AD ==,若E 、F 分别为线段PC 、BD 的中点.求证:直线EF //平面PAD ;变式2-2.已知,,,E F G H 为空间四边形ABCD 的边,,,AB BC CD DA 上的点,且//EH FG .求证://EH BD .变式2-3.如图,在正方体ABCD D C B A 1111-中,(1)求证:1BC ∥平面11D AB ;(2)若E、F 分别为C D 1、BD 的中点,则EF∥平面11A ADD .H G FE D BAC【面面平行】2.平面与平面平行的判定:定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.符号表示:.//,//,//,,,βαααββ则b a P b a b a =⋂⊂⊂3.平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.【例题与变式】例2.已知m、n 是两条直线,βα、是两个平面,有以下命题:①m,n 相交且都在平面βα、外,βαβαβα//,//,//,//,//则n n m m ;②若βαβα//,//,//则m m ;③若βαβα//,//,//,//则n m n m .其中正确的命题个数是()A.0B.1C.2D.3变式2-1.已知βα、是两个不重合的平面,在下列条件中,可确定βα//的是()A.βα、都平行于直线lB.α内有三个不共线的点到β的距离相等C.l,m 是α内两条直线,且ββ//,//m l D.l,m 是两条异面直线,且ααββ//,////,//m l m l ,例3.如图,在三棱锥S −ABC 中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A 作AF⊥SB,垂足为F,点E,G 分别是棱SA,SC 的中点.求证:(1)平面EFG∥平面ABC;变式3-1.如图所示,在三棱柱1111D C B A ABCD -中,点D,E 分别是BC 与11C B 的中点.求证:平面EB A 1//平面1ADC .1.如图,已知在正方体''''D C B A ABCD -中,对角线'AB 、'BC 上分别有两点E、F,且FC E B ''=求证:(1)EF∥平面ABCD;(2)平面'ACD ∥平面''BC A .。
9.3线面平行与面面平行

因为 AB /
/ A1 B1所以 NF / / AB 所以AN∥BF
因为AN和MN是平面AMN内两相交直线, BF和EF是平面EFBD内两相交直线,所以平 面AMN∥平面EFBD. 点评:本题证面面平行的方法是分别在两 个平面中找两组平行直线,需注意的是平面内 的两条直线必须是相交直线.证面面平行还有其 他方法,如证两平面同垂直于一条直线,两平 面同平行于第三平面等.
连结BN并延长交CD于F,由重心性质
可知,E、F重合为一点,且该点为
CD的中点E,由
得MN ∥ A B,
EM MA
EN NB
1 2
,
因此,MN∥平面ABC
且MN∥平面ABD.
题型1
线面平行的判定与证明
1. 如图,两个全等的正方形ABCD和ABEF 所在平面相交于AB,M∈AC,N∈FB且
A M = FN,求证:MN∥平面BCE.
设a、b为异面直线,α、β为平 面, 已知aα,bβ, 且a∥β,b∥α,求证:α∥β.
证明:经过直线a作平面γ,
使β∩γ=c.因为a∥β,
所以a∥c. 又aα,c α,
所以c∥α.因为a、b为异面直线,
所以b、c为平面β内两相交直线.
又b∥α, 所以α∥β.
参 考 题
线面平行背景下的求值问题 1. 在正四棱锥S-ABCD中,P为SC上 SP 1 一点,且 P C 2 ,M、N分别是SB、SD上 的点.若BD∥平面PMN, SA∥平面PMN, 求MNBD的值. 解:连结AC交BD于O 点,连结SO交MN于E点, 连结PE并延长交AC于F点. 因为SA∥平面PMN,所以SA∥PF. 题型
因为BD∥平面PMN, 所以BD∥MN. 因为 所以
线面、面面平行和垂直的八大定理-平面八大定理

线面、面面平行和垂直的八大定理之蔡仲巾千创作
一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条
直线与这个平面平行。
符合暗示:
2、性质定理:如果一条直线与平面平行,经过这条直线的平面和
这个平面相交,那么这条直线和交线平行。
符号暗示:
二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个
平面内的两条相交直线,那么这两个平面平行。
符号暗示:
2、性质定理:如果两个平面平行同时与第三个平面相交,那它们
的交线平行。
符号暗示:(更加实用的性质:一个平面内的任一直线平行另一平面)
三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂
直,那么这条直线垂直这个平面。
符号暗示: α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a
$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号暗示: 2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)
四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,,。
面面平行,线面平行,线线平行之间的关系

面面平行,线面平行,线线平行之间的关系平面几何作为数学中的一个重要分支,其中涉及到一些基本的概念,其中就包括线面平行、面面平行和线线平行等三个概念,这些概念在日常生活中很常见,比如我们常常会听到地平线与天平线在水平面上平行等。
一、面面平行面面平行,是指两个平面之间没有交点,且在三维空间中,它们的法线向量方向相同。
当两个不同平面是面面平行时,两个平面看起来就像是彼此不同的两个平行的平面,并且它们之间的距离是不变的。
图1是一个很好的例子,其中PABCD与QWXYZ两个平面是面面平行的。
在图中可以看出,这两个平面没有交点,且它们的法线向量方向相同。
图1中的平面PABCD和QWXYZ,并不是你常见的平分面,为了更好地解释这个概念,我们可以举个例子。
比如常见的斜视图投影中,地面和墙面之间就是面面平行的。
二、线面平行线面平行,是指一条直线与一个平面之间没有交点,且这个直线在与平面相交的任何一条直线上的投影,都和这个平面上的任何一点垂直。
如果一个平面和一条直线是线面平行的,那么这条直线在这个平面上的投影将是一条平行线。
图2是一个简单的线面平行的示意图。
在该示意图中可以看出直线l与平面ABC是线面平行的,这也就意味着平面ABC通过平行于它的直线l的投影,得到的投影线也将会保持平行。
三、线线平行线线平行,是指两条直线互相没有交点,且在三维空间中,它们都位于不同平面上。
如果两条直线是线线平行的,则它们不管在什么距离内,始终都不可能相交。
图3是一个线线平行的示意图。
在图中,如果一条直线和一个平面平行,那么与这条直线在同一平面中的另一条直线必须与该平面平行,这样这两条直线才能既平行于同一平面,又互相平行。
通过以上的解释,可以发现,这三个理念之间存在一些必要的联系。
例如,如果有两个平面,它们之间是面面平行的,那么这两个平面上的任何一条线与第三个平面都是线面平行的。
因为这两个面彼此平行,所以在它们之间的任何一条线都与这两个面平行,因此在第三个平面上所投影出的线也将是平行的。
线面平行与面面平行

2、若直线l//平面 EMBED Equation.3 ,则下列命题中,正确的是( )
A.l平行于 EMBED Equation.3 内的所有直线
B.l平行于过l的平面与 EMBED Equation.3 的交线
3、一条直线若同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是( )
A.异面 B.相交 C.平行 D.不能确定
4、设 EMBED Equation.3 为两两不重合的平面,l、m、n为两两不重合的直线,给出下列四个命题:①若α⊥ EMBED Equation.3
9、已知直线a//平面 EMBED Equation.3 ,a与平面 EMBED Equation.3 相距4cm,平面 EMBED Equation.3 内直线b与c相距6cm,a//b并且相距5cm,则直线a与c相距_________。
10、在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA上的一点,且EFGH为菱形,若AC//平面EFGH,BD//平面EFGH,AC=m,BD=n,则AE:BE =____________
8、在长方体ABCD-A1B1C1D1中,经过其对角线BD1的平面分别与棱AA1、CC1相交于E、F两点,则四边形EBFD1形状为_________.
9、已知a、b为不垂直的异面直线, EMBED Equation.3 是一个平面,则a、b在 EMBED Equation.3 上的射影有可能是:(1)两条平行直线;(2)两条互相垂直的直线;(3)同一条直线;(4)一条直线及其外一点。在上面的结论中,正确结论的编号是_________(写出所有正确结论的编号)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
B
线面平行与面面平行专题复习
1、,,//l a b a l
α
βαβ=⊂⊂已知:平面平面,求证:
归纳 23一
点, Q 是
1文档来源为:从网络收集整理.word 版本可编辑.
B
N
M D
A
F E
C
C 1
A 1
D 1D C
B
A
归纳:
4、如图,两个正方形ABCD 和ABEF 所在的平面相交于AB,M,N 分别是对角线AC,BF 上的点,AM=FN ,求证:MN//平面BCE.
小结1:证明线面平行的方法常常转化为面外线与面内线平行,而证明两线平行的方法常有:
, , , 题型二、面面平行的判定与性质
1、1111111//.ABCD A B C D AB D C BC -在正方体中,求证:平面平面 归纳:
归纳: 归纳: 练习: 1.
如图,E D ,分别是正三棱柱111ABC A B C -的棱1AA 、11B C 的中点, 求证:1//A E 平面1BDC ;
2.在直三棱柱111C B A ABC -中, E 、F 分别为
11A C 、11B C 的中点,D 为棱1CC 上任一点.
求证:直线EF ∥平面ABD ;
3、如图,在正方体1111ABCD A B C D -中,E ,F 分别是棱
BC ,11C D 的中点,求证:EF //平面11BB D .
4. 如图,在四棱锥P ABCD -中,ABCD 是平行四边形,M ,N 分别是AB ,PC 的中点. 求证:MN //平面PAD .
C 1 A
B
C
D
E F
A 1
B 1
第2题。
