第三章 贝叶斯估计
合集下载
贝叶斯估计
我们可能在观测数据之前就有一些主观观 点或真正的先验知识。
但是，通常我们并没有真正的先验知识或 者我们在贝叶斯估计时想更客观些，这时 可以选择无信息的先验(noninformative prior)。
或者可以从数据估计先验。这被称为经验
贝叶斯(empirical Bayes)。
H
26
反对贝叶斯学派的观点
后验分布( x1, x2 , …, xn )的计算公式就
是用密度函数表示的贝叶斯公式。它是用
总体和样本对先验分布( )作调整的结果，
贝叶斯统计的一切推断都基于后验分布进 行。
H
14
6.4.3 贝叶斯估计
基于后验分布( x1, x2 , …, xn )对 所作的
贝叶斯估计有多种，常用有如下三种：
➢ 使用后验分布的密度函数最大值作为 的 点估计，称为最大后验估计；
概率描述的是主观信念的程度，而不是频率 。这样除了对从随机变化产生的数据进行概 率描述外，我们还可以对其他事物进行概率 描述。
可以对各个参数进行概率描述，即使它们是 固定的常数。
为参数生成一个概率分布来对它们进行推导 ，点估计和区间估计可以H 从这些分布得到 6
批评1：置信区间
置信区间：
解释：区间[u1,u2]覆盖u的概率
观点：概率就是频率
参数就是参数
联合分布密度：p(x1,x2,..xn ; )
H
3
频率学派的观点
统计学更多关注频率推断
到目前为止我们讲述的都是频率（经典的）统计学
概率指的是相对频率，是真实世界的客观属性。
参数是固定的未知常数。由于参数不会波动，因 此不能对其进行概率描述。
统计过程应该具有定义良好的频率稳定性。如： 一个95％的置信区间应覆盖参数真实值至少95％ 的频率。
但是，通常我们并没有真正的先验知识或 者我们在贝叶斯估计时想更客观些，这时 可以选择无信息的先验(noninformative prior)。
或者可以从数据估计先验。这被称为经验
贝叶斯(empirical Bayes)。
H
26
反对贝叶斯学派的观点
后验分布( x1, x2 , …, xn )的计算公式就
是用密度函数表示的贝叶斯公式。它是用
总体和样本对先验分布( )作调整的结果，
贝叶斯统计的一切推断都基于后验分布进 行。
H
14
6.4.3 贝叶斯估计
基于后验分布( x1, x2 , …, xn )对 所作的
贝叶斯估计有多种，常用有如下三种：
➢ 使用后验分布的密度函数最大值作为 的 点估计，称为最大后验估计；
概率描述的是主观信念的程度，而不是频率 。这样除了对从随机变化产生的数据进行概 率描述外，我们还可以对其他事物进行概率 描述。
可以对各个参数进行概率描述，即使它们是 固定的常数。
为参数生成一个概率分布来对它们进行推导 ，点估计和区间估计可以H 从这些分布得到 6
批评1：置信区间
置信区间：
解释：区间[u1,u2]覆盖u的概率
观点：概率就是频率
参数就是参数
联合分布密度：p(x1,x2,..xn ; )
H
3
频率学派的观点
统计学更多关注频率推断
到目前为止我们讲述的都是频率（经典的）统计学
概率指的是相对频率，是真实世界的客观属性。
参数是固定的未知常数。由于参数不会波动，因 此不能对其进行概率描述。
统计过程应该具有定义良好的频率稳定性。如： 一个95％的置信区间应覆盖参数真实值至少95％ 的频率。
贝叶斯估计法
贝叶斯估计法贝叶斯估计法是统计学中常用的一种方法，它是基于贝叶斯定理的推论而来的，可以用于估计一个未知参数的值。
其核心思想是先假设一个先验分布，然后根据已知的样本数据和假设的先验分布，通过贝叶斯定理计算后验分布，最终得到对未知参数的估计。
在使用贝叶斯估计法时，我们需要首先定义以下概念：先验分布：指在未观测到数据前，对参数的概率分布的估计。
常见的先验分布有均匀分布、正态分布等。
似然函数：指在已知参数下，给定样本的条件下所有样本出现的概率密度函数，是样本数据给出参数信息的度量。
后验分布：指在已知数据后，对参数的概率分布的估计。
它是在先验分布和似然函数的基础上，通过贝叶斯公式计算得到的。
在实际数据分析中，我们需要对先验分布做出适当的假设，通过先验分布的假设来反映我们对参数的先验认知。
然后根据已知数据和似然函数，计算出参数的后验分布，并用其来估计未知参数。
贝叶斯估计法与点估计法的区别贝叶斯估计法与点估计法是统计学中常用的两种估计方法，它们之间的区别在于：点估计法：通常是求得一个能代表总体参数未知数的值作为估计，例如样本的平均数、中位数等。
点估计法估计参数时，只考虑来自样本的信息。
贝叶斯估计法：将样本和先验信息结合在一起，通过后验分布对未知参数进行估计。
在贝叶斯估计法中，我们对参数的先验知识和数据信息进行综合考虑，最终得到一个更加准确的估计值。
因此，相比于点估计法，贝叶斯估计法更加具有弹性，它不仅可以考虑已知数据的影响，还可以利用专家知识或先验信息来修正估计值，从而提高估计的准确性。
为了说明贝叶斯估计法的实际应用，我们以估计某测试设备的故障率为例进行说明。
假设我们已经收集了100个设备的测试数据，其中有5个出现故障。
我们希望用贝叶斯估计法来估计设备的故障率。
首先，我们需要对故障率做出一个先验分布的估计。
由于我们缺乏关于该设备故障率的信息，因此我们选择假设故障率服从0到1之间的均匀分布，即先验分布为P(θ)=1。
《贝叶斯估计》PPT课件
前面的分析总结如下：人们根据先验信息对参数θ
已有一个认识，这个认识就是先验分布π (θ )。通
过试验，获得样本。从而对θ 的先验分布进行调整，
调整的方法就是使用上面的贝叶斯公式，调整的结
果就是后验分布 ( x1,。, xn后) 验分布是三种信息 的综合。获得后验分布使人们对θ 的认识又前进一
1)
,
x
0,1, n
( x)
(n 2)
x (1 )nx ,0 1
(x 1)(n x 1)
即
X ~ Be(x 1, n x 1)
9
贝叶斯统计学首先要想方设法先去寻求θ的先验分布。 先验分布的确定大致可分以下几步： 第一步，选一个适应面较广的分布族作先验分布族， 使它在数学处理上方便一些，这里我们选用β分布族
步，可看出，获得样本的的效果是把我们对θ的认识
由π(θ)调整到 应建立在后验分布
( 。x1,所,以xn)对θ的统计推断就 ( 的x1,基础, xn上) 。
7
例1 设事件A(产品为废品)的概率为 ，即P(A) 。 为了估计 而作n次独立观察，其中事件A出现次数
为X，则有X服从二项分布 b(n, )
第三章 贝叶斯估计
§3.1贝叶斯推断方法 一 、统计推断中可用的三种信息
美籍波兰统计学家耐(E.L.Lehmann1894~1981) 高度概括了在统计推断中可用的三种信息：
1．总体信息，即总体分布或所属分布族给我们 的信息。譬如“总体是指数分布”或“总体是正 态分布”在统计推断中都发挥重要作用，只要有 总体信息，就要想方设法在统计推断中使用。
假设Ⅱ 当给定θ后，从总体p(x|θ)中随机抽取一个样 本X1，…，Xn，该样本中含有θ的有关信息。这种信 息就是样本信息。
第三章 信号检测与估计
第三章 信号的统计检测理论
1
3.3 Bayes Criterion(贝叶斯准则)
基本要求： ① 充分理解平均代价(Average Risk)的概念 ② 贝叶斯准则的判决表达式 ③ 判决性能分析
贝叶斯准则的基本原理：在划分观察空间时，使平均风险最小.
2
1 平均代价的概念和贝叶斯准则
通信系统中，二元信号的平均解调错误概率：
PH1 c01 c11 px H1 0 PH0 c10 c00 px H0 0
因此，平均代价C的大小与判决区域R0有关。
把使被积函数取负值的观察值x值划分给R0区域，而把其余的观察值x值划分给R1，
即可保证平均代价最小。
12
1 平均代价的概念和贝叶斯准则
合并
C P H 0 c10 c00 p x H 0 dx c10 p x H 0 dx
P H1 c11 c01 p x H1 dx c11 p x H1 dx
R0 R0
R0
R0
11
合并
C c10 PH 0 c11 PH1 R PH1 c01 c11 p x H1 PH 0 c10 c00 p x H 0 dx 0
9
1 平均代价的概念和贝叶斯准则
3. 平均代价取到最小值的条件 C PH 0 c00 R px H 0 dx c10 R px H 0 dx 0 1 PH1 c01 R px H1 dx c11 R px H1 dx 0 1
注：一般假设
c10 c00 c01 c11
5
1 平均代价的概念和贝叶斯准则
1
3.3 Bayes Criterion(贝叶斯准则)
基本要求： ① 充分理解平均代价(Average Risk)的概念 ② 贝叶斯准则的判决表达式 ③ 判决性能分析
贝叶斯准则的基本原理：在划分观察空间时，使平均风险最小.
2
1 平均代价的概念和贝叶斯准则
通信系统中，二元信号的平均解调错误概率：
PH1 c01 c11 px H1 0 PH0 c10 c00 px H0 0
因此，平均代价C的大小与判决区域R0有关。
把使被积函数取负值的观察值x值划分给R0区域，而把其余的观察值x值划分给R1，
即可保证平均代价最小。
12
1 平均代价的概念和贝叶斯准则
合并
C P H 0 c10 c00 p x H 0 dx c10 p x H 0 dx
P H1 c11 c01 p x H1 dx c11 p x H1 dx
R0 R0
R0
R0
11
合并
C c10 PH 0 c11 PH1 R PH1 c01 c11 p x H1 PH 0 c10 c00 p x H 0 dx 0
9
1 平均代价的概念和贝叶斯准则
3. 平均代价取到最小值的条件 C PH 0 c00 R px H 0 dx c10 R px H 0 dx 0 1 PH1 c01 R px H1 dx c11 R px H1 dx 0 1
注：一般假设
c10 c00 c01 c11
5
1 平均代价的概念和贝叶斯准则
风险理论损失分布的贝叶斯方法-0926
§ 三种信息
一、总体信息：即总体分布或总体所属分布提供 的信息。 例如：“总体是正态分布” 说明：总体信息是很重要的信息，为了获取此种信 息往往耗资巨大。 二、样本信息：抽取样本所得观测值提供的信息。 人们希望通过对样本的加工和处理对总体的某些特 征做出较为精确的统计推断。 例：有了样本观察值，我们可根据它大概知道总体 的一些特征数（均值、方差等）在一个什么范围内
在最决策。为此又做了一批试验，试验结果（记为B）
如下：
B：试制10个产品，有9个是高质量产品
(1 ) 0.7, ( 2 ) 0.3
P ( B 1 ) 10 0.99 0.1 0.387,
P( B 2 ) 10 0.79 0.3 0.121, P( B) P( B 1 ) (1 ) P( B 2 ) ( 2 ) 0.307
或 (2 A) 1 (1 A)
经理根据试验A的信息调整自己的看法，把对1和2的 可信程度由0.4和0.6调整到0.7和0.3.后者是综合了经 理的主观概率和试验结果而获得的，要比主观概率更 贴近当今的实际，这就是贝叶斯公式的应用
经过试验A后，经理对增加投资改进质量的兴趣增大。 但因投资额大，还想再做一次小规模试验，观此结果
3.2.1 离散型参数的先验概率
n x n x P ( X x | ) (1 ) , x
x 0,1, , n
的先验分布为
1,0 1 ( ) 0, 其它
3.3 后验概率
(1 )
x
n x
英国学者T.贝叶斯1763年在《论有 关机遇问题的求解》中提出一种归 纳推理的理论，后被一些统计学者 发展为一种系统的统计推断方法， 称为贝叶斯方法。采用这种方法作 统计推断所得的全部结果，构成贝 叶斯统计的内容。认为贝叶斯方法 是唯一合理的统计推断方法的统计 学者，组成数理统计学中的贝叶斯 学派，其形成可追溯到20世纪 30 年代。到50～60年代，已发展为一 个有影响的学派。时至今日，其影 响日益扩大
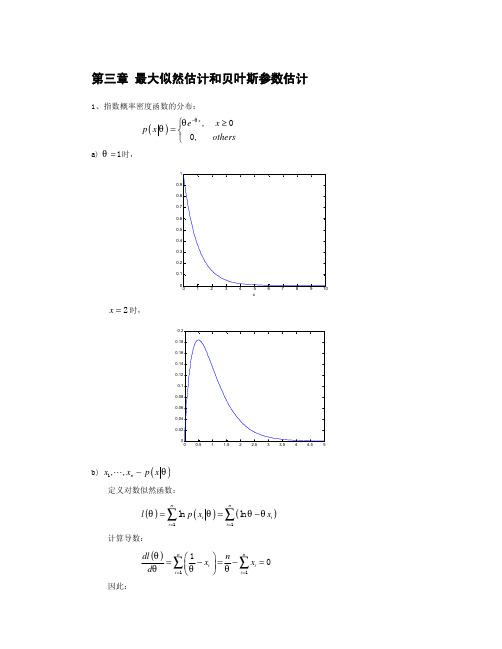
第三章 最大似然估计和贝叶斯参数估计习题答案
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
b) x1 , , xn p x θ
(
)
n n
定义对数似然函数：
l (θ ) = ∑ ln p ( xi θ ) = ∑ ( ln θ − θ xi )
i =1 i =1
计算导数：
dl (θ ) n 1 n n = ∑ − xi = − ∑ xi = 0 dθ θ i =1 i =1 θ
显然，当 θ ≥ max ( D ) 时， l (θ ) 为 θ 的单调下降函数，而 θ < max ( D ) 时，l (θ ) = 0 ， 因此 l (θ ) 的最大值产生在 θ max ( D ) 的最小值处，即 θ = max ( D ) 。 b)
14
{
}
12
10
8
6
4
2
0
0
0.5 0.6
1
c) 由(41)式：
1 −1 1 Σ− + Σ− n = nΣ 0
等式两边求逆：
−1 Σ n = ( nΣ −1 + Σ0 ) = ( Σ0−1 + nΣ−1 ) −1 −1
等式右边利用(a)的恒等式，有：
1 1 Σ n = Σ 0 Σ0 + Σ Σ n n
1 1 1 1 1 ˆ n + Σ Σ + Σ0 Σ 0 Σ − = Σ0 Σ 0 + Σ Σ nΣ −1μ 0 μ0 n n n n 1 1 1 ˆn + Σ = Σ0 Σ 0 + Σ μ Σ0 + Σ μ 0 n n n
第三章贝叶斯估计理论 LMMSE综述
可采用 “谱因式分解”求得 维纳滤波为IIR时不变的
定长FIR维纳滤波
数据：
FIR平滑器
为便于解释，考虑N=1的情况：
IIR平滑器
基于数据 估计
维纳-霍夫方程为：
1步预测的结果：对于AR（3）
贝叶斯估计理论——内容安排
主要内容 引言
线性贝叶斯估计量（LMMSE）
估计量总结
估计方法
在经典方法 中，数据信息总结在概率密度函数p(x;θ)中， 其中PDF是θ的函数。 在贝叶斯方法 中，由于先验PDFp(θ)描述了有关θ的知识 而增加了数据的信息。数据信息总结在联合PDF p(x,θ)中。
应用正交原理
假定
可逆
矢量LMMSE估计
待估参数 线性估计量 目标：对每个元素，使 最小 的标量
可将矩阵A的第i行和矢量a第i个元素，看成 LMMSE估计量的形式 已知每个待估参数的标量LMMSE形式 • 得出相应的解 • 组合为矢量形式
矢量LMMSE的解
矢量LMMSE估计
若 相似地，可得 矩阵
定理4.2
若 则
一般线性模型的MVUE 定理11.1
贝叶斯线性模型下MMSE估计
序贯LMMSE估计
与序贯LS方法相同 固定参数个数（在此为随机的），增加数据样本数目
数据模型
目标： 给定基于 的估计 到达时，更新估计到
，当新的数据样本
求序贯LMMSE
在此，我们利用矢量空间得到“白噪声中的直流电平”的解，再推广 到一般情况
CRLB
CRLB
BLUE
BLUE
MLE
MLE
LSE
LSE
ME
ME
MMSE
贝叶斯先验概率贝叶斯估计
贝叶斯先验概率贝叶斯估计你有没有想过，我们每天做的决定背后，其实有很多不确定性？我们做的选择是根据过去的经验，也我们选择的结果并不完全能预测。
举个例子，假设你早上出门前看了天气预报，说今天有50%的可能下雨。
那么问题来了，你是带伞呢，还是不带呢？如果你经历了好几次天气预报错得离谱，是不是就会开始怀疑这些概率的准确性了？这时候，你可能会觉得，自己的经验比这些预测更靠谱。
嘿，这其实就跟贝叶斯估计有点关系！贝叶斯估计的核心思想就是：把我们的“信念”或者说“先入为主”的看法，结合新的信息，做出更合理的判断。
拿天气预报来说，假如你这几年过得比较顺风顺水，基本上从来没遇到过下雨的预报被错过过，天公作美，你心里可能会觉得今天下雨的可能性更小些。
这时候，你的“先验知识”就开始发挥作用了。
你并不是完全相信50%的下雨几率，而是结合自己以往的经验，觉得这50%的概率其实没那么准确，可能实际下雨的几率还得往低的方向调整。
对，先验概率，这名字听起来有点高深，但其实说白了，就是你在面对不确定的事物时，最初的判断和看法。
举个例子，假设你今天第一次见到一个人，想知道他是不是喜欢看足球。
你完全不了解他，只知道他长得高大，看起来像个运动员。
你的“先验”就是——他可能喜欢足球。
这个先验的看法，源自你对运动员的刻板印象。
可是，如果你后来得知，这个人其实从不碰球，反而热衷于下围棋，那你的想法肯定得做调整。
你会慢慢抛开原本的看法，开始根据实际信息重新评估他的兴趣。
贝叶斯估计的巧妙之处就在于，它鼓励你做这种“更新”。
每当有新的信息进来时，你就该重新调整自己原本的“信念”。
在上面的例子中，一开始你完全凭直觉判断这个人爱足球，结果一查，他竟然喜欢围棋，那你就得调整看法了，把新的信息加进来，改成一个更加准确的估计。
更有意思的是，贝叶斯估计的魅力不仅在于它能够帮助我们调整决策，还在于它不要求我们一开始就知道真相。
嘿，谁能一开始就知道自己做的决定百分之百正确呢？生活就是这样，充满了不确定。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
最后在给出X=x的条件下，θ的后验密度为
( x)
p ( x, ) ( a b n) a x 1 (1 )b n x 1 , 0 x 1 p( x) (a x)(b n x)
显然这个后验分布仍然是β分布，它的两个参数分别 是a+x和b+n-x。我们选后验期望作为θ的贝叶斯估计， 则θ的贝叶斯估计为
16
如果用（0，1）上的均匀分布作为θ的先验分布， 则θ的贝叶斯估计为
ˆB
x 1 n2
三、 常用的一些共轭先验分布
对于一些常用的指数分布族，如果仅对其中的参数 θ感 兴趣，下表列出了它们的共轭先验分布及后验期望。 总体分布 共 轭 先 验 分 后验分布期 布 望 正态分布
N ( , )612014-9-29是样本的边际分布，或称样本 X 1 , , X n 的无条件 分布，它的积分区域就是参数 θ的取值范围，随具 体情况而定。 前面的分析总结如下：人们根据先验信息对参数θ 已有一个认识，这个认识就是先验分布π(θ)。通 过试验，获得样本。从而对θ的先验分布进行调整， 调整的方法就是使用上面的贝叶斯公式，调整的结 ( x1 ,。后验分布是三种信息 , xn ) 果就是后验分布 的综合。获得后验分布使人们对θ的认识又前进一 步，可看出，获得样本的的效果是把我们对θ的认识 ( 。所以对 x1 , , xn ) θ的统计推断就 由π(θ)调整到 ( 的基础上。 x1 ,, xn ) 应建立在后验分布
2014-9-29
第三章 贝叶斯估计
§3.1贝叶斯推断方法 一 、统计推断中可用的三种信息
美籍波兰统计学家耐(E.L.Lehmann1894~1981) 高度概括了在统计推断中可用的三种信息： 1 ．总体信息，即总体分布或所属分布族给我们 的信息。譬如“总体是指数分布”或“总体是正 态分布”在统计推断中都发挥重要作用，只要有 总体信息，就要想方设法在统计推断中使用。 2．样本信息，即样本提供给我们的信息，这是 任一种统计推断中都需要的信息。
ˆB ( x)d
0 1
ax abn
于是X的边际分布为
p( x) p ( x, )d
0 1
与其极大似然估计是不同的。
注：X ~ (a, b), E ( X )
a ab
( a b) (a x) (b n x) n x , x 0,1, , n. ( a ) (b) (a b n) 15
0 1
正态分布
N ( , )
2
2 x 2 2 2
a x a bn
二项分布
b( n, p )
β分布 (a, b) Γ分布 Γ(a,b)
Poisson分 布 ( )
17
a x b 1
18
后验分布为
( x 1, n x 1)
3
2014-9-29
样本X与参数的联合分布为
p x , Cnx x (1 ) n x , x 0,1, , n,0 1
此式在定义域上与二项分布有区别。再计算 X的 边际密度为
贝叶斯统计学首先要想方设法先去寻求 θ的先验分布。 先验分布的确定大致可分以下几步： 第一步，选一个适应面较广的分布族作先验分布族， 使它在数学处理上方便一些，这里我们选用β分布族
14
2
如果从先验信息获得
0.2, S 0.01
则可解得 a=3，b=12 这意味着 θ 的先验分布是参数 a=3，b=12的β分布。 假如我们能从先验信息中较为准确地把握θ的两个分 位数，如确定 θ确定的 10％分位数 θ0.1和 50％的中位 数θ0.5，那可以通过如下两个方程来确定a与b。
从贝叶斯观点来看，未知参数θ是一个随机变量。描 述这个随机变量的分布可从先验信息中归纳出来，这 个分布称为先验分布，其密度函数用π(θ)表示。 1 先验分布 定义3.1 将总体中的未知参数θ∈Θ看成一取值于Θ 的随机变量，它有一概率分布，记为π(θ), 称为参 数θ的先验分布。 2 后验分布 在贝叶斯统计学中，把以上的三种信息归纳起来的 最好形式是在总体分布基础上获得的样本X1，…， Xn和参数的联合密度函数 5
2
计算如下： p( x, ) p( X x ) ( ) Cnx x (1 ) n x , x 0,1,, n.0 1
( x 1)(n x 1) ( n 2) p( x, ) ( n 2) ( x) x (1 ) n x ,0 x 1 p ( x) ( x 1)( n x 1) p( x) Cnx x (1 ) n x d Cnx
13
贝叶斯本人认为，当你对参数θ的认识除了在有限区 间（ c，d）之外，其它毫无所知时，就可用区间（c， d）上的均匀分布作为θ的先验分布，即对θ做“贝叶 斯假设”。 确定了先验分布后, 就可计算出后验分布, 过程如下： p ( x, ) p( X x ) ( )
( a b) n a x 1 (1 )b n x1 x=0，1，…，n，0<θ<1 ( a)(b) x
( a b) a 1 (1 )b 1 ,0 1, a 0, b 0 (a ) (b)
p ( x) p( x, )d Cnx
0
1
( x 1)(n x 1) , x 0,1, n (n 2)
( )
( x)
EX1 设θ是一批产品的不合格率，已知它不是0.1就是 0.2，且其先验分布为π(0.1)=0.7,π(0.2)=0.3。假如 从这批产品中随机取8个进行检查，发现有2个不合格， 求θ的后验分布。 解： P ( X 2 ) C82 2 (1 ) 6
7
例1 设事件A(产品为废品)的概率为 ，即 P( A) 。 为了估计 而作n次独立观察，其中事件A出现次数 为X，则有X服从二项分布 b( n, ) 即
P( X x ) Cnx x (1 ) n x , x 0,1,, n.
如果此时我们对事件A的发生没有任何了解，对 的大小也没有任何信息。在这种情况下，贝叶斯建议 用区间（0，1）上的均匀分布作为 的先验分布。因 为它在（0，1）上每一点都是机会均等的。这个建议 被后人称为贝叶斯假设, 1,0 1 ( ) 8 0, others
12
作为θ的先验分布族是恰当的，从以下几方面考虑： 1. 参数 θ是废品率，它仅在（ 0，1）上取值。因此， 必须用区间（0，1）上的一个分布去拟合先验信息。 β分布正是这样一个分布。 2. β分布含有两个参数 a与b，不同的a与 b就对应不同 的先验分布，因此这种分布的适应面较大。 11
2
2014-9-29
( n 2) x (1 ) n x ,0 1 ( x 1)( n x 1)
即
X ~ Be( x 1, n x 1)
9 10
注：
( s ) x s 1e x dx, s 0, (n 1) n !
0
B( p, q ) x p 1 (1 x) q 1 dx, p 0, q 0
p ( x1 , , xn , ) p( x1 , , xn ) ( )
在这个联合密度函数中。当样本 X 1 ,, X n 给定之后， 未知的仅是参数 θ了，我们关心的是样本给定后， θ的 条件密度函数，依据密度的计算公式，容易获得这个 条件密度函数 p ( x1 , , xn , ) ( x1 , , xn )
p ( x1 , , xn ) p ( x1 , , xn ) ( )
p( x ,, x
1
n
) ( )d
这就是贝叶斯公式的密度函数形式， ( x1 , , xn ) 称为θ的后验密度函数，或后验分布。而
p ( x1 , , xn ) p ( x1 , , xn ) ( )d
1
二、贝叶斯公式的密度函数形式
贝叶斯统计学的基础是著名的贝叶斯公式，它是英国 学者贝叶斯（ T.R.Bayes1702~1761）在他死后二年发 表的一篇论文《论归纳推理的一种方法》中提出的。 经过二百年的研究与应用，贝叶斯的统计思想得到很 大的发展，形成一个统计学派—贝叶斯学派。为了纪 念他，英国历史最悠久的统计杂志《 Biometrika》在 1958年又全文刊登贝叶斯的这篇论文。 初等概率论中的贝叶斯公式是用事件的概率形式给出 的。可在贝叶斯统计学中应用更多的是贝叶斯公式的 密度函数形式。下面结合贝叶斯统计学的基本观点来 引出其密度函数形式。贝叶斯统计学的基本观点可以 用下面三个观点归纳出来。 3
3．先验信息，即在抽样之前有关统计推断的一些 信息。譬如，在估计某产品的不合格率时，假如工 厂保存了过去抽检这种产品质量的资料，这些资料 （包括历史数据）有时对估计该产品的不合格率是 有好处的。这些资料所提供的信息就是一种先验信 息。又如某工程师根据自己多年积累的经验对正在 设计的某种彩电的平均寿命所提供的估计也是一种 先验信息。由于这种信息是在“试验之前”就已有 的，故称为先验信息。 以前所讨论的点估计只使用前两种信息，没有使用 先验信息。假如能把收集到的先验信息也利用起来， 那对我们进行统计推断是有好处的。只用前两种信 息的统计学称为经典统计学，三种信息都用的统计 学称为贝叶斯统计学。本节将简要介绍贝叶斯统计 2 学中的点估计方法。
假设Ⅰ 随机变量X有一个密度函数p(x;θ)，其中θ是一 个参数，不同的 θ对应不同的密度函数，故从贝叶斯 观点看， p(x;θ) 在给定 θ 后是个条件密度函数，因此 记为 p(x|θ)更恰当一些。这个条件密度能提供给我们 的有关θ的信息就是总体信息。 假设Ⅱ 当给定 θ后，从总体p(x|θ)中随机抽取一个样 本 X1，…，Xn，该样本中含有 θ的有关信息。这种信 息就是样本信息。 假设Ⅲ 我们对参数θ已经积累了很多资料，经过分析、 整理和加工，可以获得一些有关θ的有用信息，这种信 息就是先验信息。参数θ不是永远固定在一个值上，而 4 是一个事先不能确定的量。