节点法ppt课件
合集下载
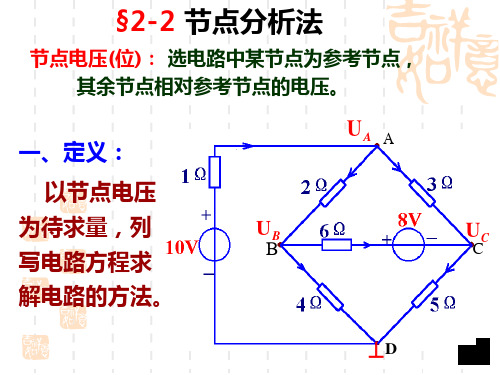
节点分析法
补： uB uD 8
UB 8
1
11
10
UA
4
UB
(1
4
5 )U Dຫໍສະໝຸດ 111四、无伴的理想电压源处理
方法3：含有两条无伴电压源支路的，将一条 电压源支路的一端接地；设另一条理想电压源 支路的电流，将此电流暂当作电流源电流列写 方程，并利用理想电压源与相应节点电位关系 补充方程。
12
例9 ：求图示电路中电流i。
电阻不计自电导与互电导）
解： 选择参考节
A
UA
点， 列写方程：
I1
I2
I3
(1 10
1 4
1 2 )uA
1.6
70 2
1.6 70
uA
(
1
2 1 1)
10 4 2
若电路只有一个独立节点，其节点
43.06V
I1 =-4.306A I2 = 10.76A
电压方程为： u
I3 = -13.47A
Rs Us
(1)
图(1)伏安关系:
u = Us - iRs
图(2)伏安关系:
Is
u = (Is - i) Rs'
= Is Rs ' - i Rs '
Rs'
(2)
等效变换关系： Us = Is Rs′ Rs= Rs′
4
三、节点分析法： 依据：KCL
支路VCR UA
UB
UC
步骤：
1、选择参考节点，
标出其余节点电压
I sk Gk ( 弥尔曼定理)
9
四、无伴的理想电压源处理
方法1： 含有一条无伴电压源支路的，可选合 适的参考节点使理想电压源成为一个已知节点 电压，列写其余节点电压方程。
节点电压法经典例题ppt课件
(3) 列出所有未知节点电压的节点方程，其中自电 导恒为正，互电导恒为负。
(4) 联立求解节点电压，继而求出其余量。
数据结构(C#语言版)
解决图的编程问题
节点电压法的习题
例1.用节点法求各支路电流。（类型1：支路含有电压源与电阻串联）
I1 20kVA 10k VB 40k I3
+120V +
知识的回顾
支路电流法（以支路电流为变量求解方程） n个节点，b条支路的电路图.
（1）假设各支路电流的参考方向和网孔的 巡回方向。
（2）对（n-1）个节点列KCL方程。 对（b-n+1）个网孔列写以支路电流为
变量表示 的 KVL方程，并加入元件VCR约束 条件。 （3）求解b个支路方程，从而求解各支路电流。
Va
S
R5 i5 + US -
R1 Vb R3
i1
i3
R2 i2
i1=i2+i3 i3=i4-i5 Vc i4 R4
----（2） i1=(Va-Vb)/R1=(Va-Vb)G1
-----（3）
=VbG2
i3=(Vb-Vc)/R3=(Vb-Vc)G3 i4=(Vc-0)/R4 =VcG4
i5=(Va-Vc-US)/R5 =(Va-Vc-U
缺点：这种方法比较解方程比较繁琐。
数据结构(C#语言版)
解决图的编程问题
知识回顾 （引入以网孔电流为独立变量，列写KVL方程） 网孔分析法：
(1) 选定一组网孔，标明网孔电流及其参考方向；（孔b方-n程+1）个网 (2) 以网孔电流的方向为网孔的巡行方向，列写实质是KVL方
程；（自电阻，互电阻，电压源）
数据结构(C#语言版)
(4) 联立求解节点电压，继而求出其余量。
数据结构(C#语言版)
解决图的编程问题
节点电压法的习题
例1.用节点法求各支路电流。（类型1：支路含有电压源与电阻串联）
I1 20kVA 10k VB 40k I3
+120V +
知识的回顾
支路电流法（以支路电流为变量求解方程） n个节点，b条支路的电路图.
（1）假设各支路电流的参考方向和网孔的 巡回方向。
（2）对（n-1）个节点列KCL方程。 对（b-n+1）个网孔列写以支路电流为
变量表示 的 KVL方程，并加入元件VCR约束 条件。 （3）求解b个支路方程，从而求解各支路电流。
Va
S
R5 i5 + US -
R1 Vb R3
i1
i3
R2 i2
i1=i2+i3 i3=i4-i5 Vc i4 R4
----（2） i1=(Va-Vb)/R1=(Va-Vb)G1
-----（3）
=VbG2
i3=(Vb-Vc)/R3=(Vb-Vc)G3 i4=(Vc-0)/R4 =VcG4
i5=(Va-Vc-US)/R5 =(Va-Vc-U
缺点：这种方法比较解方程比较繁琐。
数据结构(C#语言版)
解决图的编程问题
知识回顾 （引入以网孔电流为独立变量，列写KVL方程） 网孔分析法：
(1) 选定一组网孔，标明网孔电流及其参考方向；（孔b方-n程+1）个网 (2) 以网孔电流的方向为网孔的巡行方向，列写实质是KVL方
程；（自电阻，互电阻，电压源）
数据结构(C#语言版)
2-4节点法
§2.4 节点法
2、4
节点法
i5
G5
节点电压（节点电位）:节点到 参考点之间的电压。 取该电路中节点4为参考点， 则其它三个节点电压分别为：
1 i1 G1 2 G3 i3 3 is i4 i2 G2 G4 4
u1、u2 、u3。
对于具有n个节点的电路，一定有(n-1)个 节点电压是一组完备的独立电压变量， 节点电压具有独立性和完备性。
本节重点:
节点法：节点方程的列写规则；
特殊情况的处理。
作业：
2-8
2-9
u=u2=6V i=3 A
练习 2-5 2-13
小结：
（1）实际电压源支路等效转换成实际电流源。 （2） 理想电压源有两种处理方法： 其一: 将理想电压源负极所在节点设为参考点， 则理想电压源正极所在节点电压已知; 2-12例1 其二: 在理想电压源支路上设电流，补列一个 KVL方程。 （3）受控源列方程时类似独立源，列完方程后控制 量用节点电压表示。 （4） 电导与理想电流源串联支路的等效。
1S
5 5
解：节点1：
(0.1 1 0.1)u1 u2 1 u4 0.1 1
节点2： u1 1 (1 1 0.5)u2 u3 0.5 0.125 节点3： u2 0.5 (0.5 0.5 0.25)u3 u4 0.25 0.125 节点4：
u1 0.1 u3 0.25 (0.1 0.25 0.25)u4 0
解出u1,u2,u3,u4, 既可求出各个支路的电压和电流。
例1 求节点电压u1、u2， u3 。
解：
节点1：
节点2： (0.5+1+0.5)u1- u2 -0.5 u3= 1.5-3.5 - u1 +(1+0.5) u2 -0.5 u3 =1+1.5
2、4
节点法
i5
G5
节点电压（节点电位）:节点到 参考点之间的电压。 取该电路中节点4为参考点， 则其它三个节点电压分别为：
1 i1 G1 2 G3 i3 3 is i4 i2 G2 G4 4
u1、u2 、u3。
对于具有n个节点的电路，一定有(n-1)个 节点电压是一组完备的独立电压变量， 节点电压具有独立性和完备性。
本节重点:
节点法：节点方程的列写规则；
特殊情况的处理。
作业：
2-8
2-9
u=u2=6V i=3 A
练习 2-5 2-13
小结：
（1）实际电压源支路等效转换成实际电流源。 （2） 理想电压源有两种处理方法： 其一: 将理想电压源负极所在节点设为参考点， 则理想电压源正极所在节点电压已知; 2-12例1 其二: 在理想电压源支路上设电流，补列一个 KVL方程。 （3）受控源列方程时类似独立源，列完方程后控制 量用节点电压表示。 （4） 电导与理想电流源串联支路的等效。
1S
5 5
解：节点1：
(0.1 1 0.1)u1 u2 1 u4 0.1 1
节点2： u1 1 (1 1 0.5)u2 u3 0.5 0.125 节点3： u2 0.5 (0.5 0.5 0.25)u3 u4 0.25 0.125 节点4：
u1 0.1 u3 0.25 (0.1 0.25 0.25)u4 0
解出u1,u2,u3,u4, 既可求出各个支路的电压和电流。
例1 求节点电压u1、u2， u3 。
解：
节点1：
节点2： (0.5+1+0.5)u1- u2 -0.5 u3= 1.5-3.5 - u1 +(1+0.5) u2 -0.5 u3 =1+1.5
节点法
诺顿定律
• 一个含独立电源、线性电阻和受控源的一 端口，对外电路来说，可以用一个电流源 和电导的并联组合来等效置换，电流源的 电流等于该一端口的短路电流，而电导等 于把该一端口的全部独立电源置零后的输 入电导。
诺顿定律
i Ns
(a) 1 1
u
1`
i Req uoc
(b)
i isc
Geq
1
u
1`
=
G11 G1 G4 G6 G22 G2 G4 G5 G33 G3 G5 G6
G12 G21 G4 G23 G32 G5 G13 G31 G6
可以推广得到具有(n-1)个独立节点的电路的节点电压方程
G11un1 G12un 2 G13un3 G1( n 1)un ( n 1) is11 G21un1 G22un 2 G23un3 G2( n 1)un ( n 1) is 22 G31un1 G32un 2 G33un3 G3( n 1)un ( n 1) is 33 G( n 1)1un1 G( n 1) 2un 2 G( n 1)3un3 G( n 1)( n 1)un ( n 1) is ( n 1)( n 1)
u4 un1 un2
u5 un2 un3
u3 un3
u6 un1 un3
对节点1、2、3，应用KCL可以得到
is6
i1 i4 i6 0 i2 i4 i5 0 i3 i5 i6 0
is1
i6 i1
1 i4 R1
R4 i2
R6 2
i5 R5
• （1）画出电路图。 • （2）指定参考节点，其余节点与参考节点之间的电压就 是节点电压，一般都是取各独立节点为"+"极端，参考接 点为"-"极端。 • （3）对各独立节点列写KCL约束方程，方程个数与独立 节点个数相等。 • （4）联立求解KCL约束方程组，即可得各独立节点电位。 • （5）设定各支路电流的大小和参考方向，根据所求得的 独立节点电位，即可求得各支路电压和支路电流。至此， 求解工作即告完毕。 节点法的应用极为广泛。这是因为：（1）它既适用 与平面网络，也适用与非平面网络；（2）在实际电路中， 其独立节点数往往要比网孔数少。
教学课件第四章船体结构节点的画法
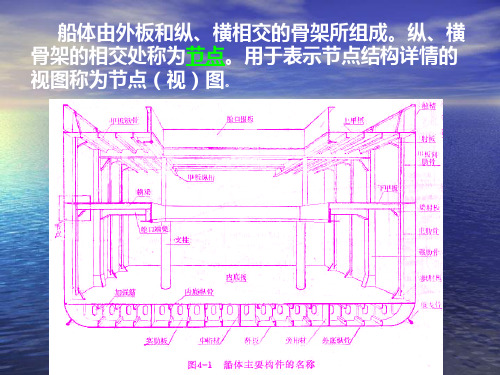
3.作图步骤
结构视图的作图可以根据构件的投影规律，采用构件叠加的方法, 几个视图相互对应同时绘制。本例的作图步骤如下:
1)合理布置视图,画出主、俯视图的基本准线,见图4-5(a); 2)画出底板1的投影,见图4-5(b); 3)画出T型钢2和3的投影,见图4-5(c); 4)画出垫板4的投影,见图4-5(d); 5)画出管子5的投影,见图4-5(e); 6)画出肘板6的投影,见图4-5(f);
由于节点是船体中的局部结构，因此，节点视图中的板在长、宽方向，型材在 长度方向一般采用断裂画法，同时，船体结构图样通常采用较小的比例绘制，所 以本节仅介绍小比例节点视图的绘制和识读方法。
第四章 船体结构节点的画法 一、节点视图的画法
下面以支柱节点为例(图4-3),说明绘制节点视图的方法和步骤。
1.构件分析
下图是甲板下顶边舱结构的节点视图,它由主、左两个视图组成,下面 以此为例,说明读图的方法和步骤。其步骤如下:
1) 分析节点的构件组成,搞清构件的形状和大小。
2）根据构件在视图中的投影关系，搞清构件之间的相对位 置关系和连接方式，综合形成节点的整体概念。
图4-7 节点的构件分析
1) 选择主视图的视向,确定主视图。主视图一般要求能明显反映出节 点的主要结构特征,如构件的形状、构件的相对位置和连接方式等。对 于图4-3所示的支柱节点选择“A”向作为主视图的投影方向。
2) 确定其它视图的视向。主视图中没有表达清楚的结构需要选择其 它视图来表达,以使节点视图能完整地反映出节点的结构情况。视图的 数量视节点的复杂程度而定，原则是清晰表达节点结构，且视图最少。 本例中,主视图未把垫板的形状表达清楚,因此再选择“C”向作为投影 方向,画出俯视图就可把支柱节点的结构表达清楚。
节点法
1 R3
1 R4
)u1
(
1 R3
1 R4
)u2
方 程 的
形
us1 us4
成
—
R1 R4
节
点
法
②节点
( 1 R3
1 R4
)u1
( 1 R3
1 R4
1 R5
1 R6
)u2
us4 R4
us6 R6
2.1
1 (
R1
1 R2
1 R3
1 R4
)u1
1 (
R3
1 R4
)u2
us1 R1
us4 R4
( 1 R3
%在显示屏显示提示信息 法
U=Y\I
%解线性方程组得节点电压
Y的逆与I左乘
运行结果：
2.1
U=
3.7093
电 路
方
5.8135
程 的
形
16.5941
成
—
节 点 法
2.1
例2-1-2 写出图示电路的节点方程
电 路 方 程 的 形 成
节 点 法
—
2.1
以③节点为参考节点
①节点
电
路
(
1 R1
1 R2
路 方
程
的
i
j
行
i
形
j成
—
列
Yn i
yii
yij
i
i节点自导 （取正）
节
i、j节点
点 法
间的互导
（取负）
j
y ji
y jj
j i、j节点间 j节点自导
的互导
直接列写节点电流源向量In 的规则：2.1
9-节点电位法
1.3.3 节点电位法
一．节点电位法的基本思路
如果已知电路中各节点的电位，那么一条支路两节点之
间的电压等于电位之差，支路的电流运用欧姆定律就可以求 得，所以，求电路中各节点的电位是关键。 节点电位为未知量，写出节点方程，从而解出节点电位， 然后求出支路电流，这种分析方法叫节点电位法，简称节点 法。 运用节点电位法求解电路支路电流，可以将电路方程减 少到n-1个。
上式可以归纳得出列写节点电位方程的一般形式为：
该点的电位×自电导+相邻点的电位×互电导=流入该点电流的代数和
即
G jjVj GjkVk I sjj
Gjj：所选节点的自电导（总取正）；
Vj：所选节点的电位； Gjk：相邻节点的互电导（总取负）
Vk：相邻节点的电位；
Isjj：所选节点流入的电流代数和。 （电流从节点流出取负，流入节点取正）
解得：V1=14V
电流源两端的电压
V2=10V
由V1 1 20 U IS 得U IS V1 20 34 V
电流源发出的功率为： PIS U IS 1A 34W
例 3
用节点电位法求图中各支路的电流 A
IR1 R1 4Ω
B
R2 IR2
解：设电路中C点为零电位点，
则： 对节点A有： V A 3V
其二，如果电路含有理想电压源支路，应选择电阻不影响各个节点的电位
（因为理想电流源的内阻为无穷大）。（见例2）
（5）与理想电压源并联的电阻两端电压恒定，对其它 支路的电流和各节点的电位不产生任何影响。 （6）对含有受控源的电路，在列节点方程时应将它与 独立源同样对待，需要时再将控制量用节点电位表示。
二．节点电位法的基本原理 节点电位：电路中某节点与参考节点之间的电压。 参考节点：在电路中可以任意选取。 图中有0、1、2三个节点，设以 节点0为参考点。 标出各支路电流方向，根据KCL 定律写出节点1、2的KCL方程为： 节点1 节点2
一．节点电位法的基本思路
如果已知电路中各节点的电位，那么一条支路两节点之
间的电压等于电位之差，支路的电流运用欧姆定律就可以求 得，所以，求电路中各节点的电位是关键。 节点电位为未知量，写出节点方程，从而解出节点电位， 然后求出支路电流，这种分析方法叫节点电位法，简称节点 法。 运用节点电位法求解电路支路电流，可以将电路方程减 少到n-1个。
上式可以归纳得出列写节点电位方程的一般形式为：
该点的电位×自电导+相邻点的电位×互电导=流入该点电流的代数和
即
G jjVj GjkVk I sjj
Gjj：所选节点的自电导（总取正）；
Vj：所选节点的电位； Gjk：相邻节点的互电导（总取负）
Vk：相邻节点的电位；
Isjj：所选节点流入的电流代数和。 （电流从节点流出取负，流入节点取正）
解得：V1=14V
电流源两端的电压
V2=10V
由V1 1 20 U IS 得U IS V1 20 34 V
电流源发出的功率为： PIS U IS 1A 34W
例 3
用节点电位法求图中各支路的电流 A
IR1 R1 4Ω
B
R2 IR2
解：设电路中C点为零电位点，
则： 对节点A有： V A 3V
其二，如果电路含有理想电压源支路，应选择电阻不影响各个节点的电位
（因为理想电流源的内阻为无穷大）。（见例2）
（5）与理想电压源并联的电阻两端电压恒定，对其它 支路的电流和各节点的电位不产生任何影响。 （6）对含有受控源的电路，在列节点方程时应将它与 独立源同样对待，需要时再将控制量用节点电位表示。
二．节点电位法的基本原理 节点电位：电路中某节点与参考节点之间的电压。 参考节点：在电路中可以任意选取。 图中有0、1、2三个节点，设以 节点0为参考点。 标出各支路电流方向，根据KCL 定律写出节点1、2的KCL方程为： 节点1 节点2
电路03 回路电流法、节点电压法
1.节点法
选某一节点为参考节点，其它节点与此节点的参考电 压称节点电压。
节点法或节点电压法是以节点电压为独立变量列电路
方程求解电路的一种方法。 节点电压法的独立方程数为 (n-1)个。与支路电流法 相比，方程数可减少。
举例说明： i1 R1
iS3
un1
1 i3 i4 R4 0
R3
iS1
i2 iS2 R2
令 Gk=1/Rk，k=1, 2, 3, 4, 5 上式简记为 G11un1+G12un2 = iSn1 G11un1+G12un2 = iSn1
标准形式的节点电压方程。
其中 G11=G1+G2+G3+G4—节点1的自电导，等于接在节点1上 所有支路的电导之和。 G22=G3+G4+G5 — 节点2的自电导，等于接在节点2上所 有支路的电导之和。 G12= G21 =-(G3+G4)—节点1与节点2之间的互电导，等 于接在节点 1 与节点 2 之间的所有 支路的电导之和，并冠以负号。 * 自电导总为正，互电导总为负。 * 电流源支路电导为零。 iSn1=iS1-iS2+iS3—流入节点1的电流源电流的代数和。
(1) 选定参考节点，标明其 un2 余n-1个独立节点的电压 2 i5 (2) 列KCL方程： iR出= iS入 R5 i1+i2+i3+i4=iS1-iS2+iS3
-i3-i4+i5=-iS3
代入支路特性：
un1 un2 un1 un2 un1 un2 iS1 iS2 iS3 R1 R2 R3 R4
例1. 用回路法求各支路电流。 I1 I2 I3 R2 R1 Ib Ia + + US2 US1 _ _
选某一节点为参考节点，其它节点与此节点的参考电 压称节点电压。
节点法或节点电压法是以节点电压为独立变量列电路
方程求解电路的一种方法。 节点电压法的独立方程数为 (n-1)个。与支路电流法 相比，方程数可减少。
举例说明： i1 R1
iS3
un1
1 i3 i4 R4 0
R3
iS1
i2 iS2 R2
令 Gk=1/Rk，k=1, 2, 3, 4, 5 上式简记为 G11un1+G12un2 = iSn1 G11un1+G12un2 = iSn1
标准形式的节点电压方程。
其中 G11=G1+G2+G3+G4—节点1的自电导，等于接在节点1上 所有支路的电导之和。 G22=G3+G4+G5 — 节点2的自电导，等于接在节点2上所 有支路的电导之和。 G12= G21 =-(G3+G4)—节点1与节点2之间的互电导，等 于接在节点 1 与节点 2 之间的所有 支路的电导之和，并冠以负号。 * 自电导总为正，互电导总为负。 * 电流源支路电导为零。 iSn1=iS1-iS2+iS3—流入节点1的电流源电流的代数和。
(1) 选定参考节点，标明其 un2 余n-1个独立节点的电压 2 i5 (2) 列KCL方程： iR出= iS入 R5 i1+i2+i3+i4=iS1-iS2+iS3
-i3-i4+i5=-iS3
代入支路特性：
un1 un2 un1 un2 un1 un2 iS1 iS2 iS3 R1 R2 R3 R4
例1. 用回路法求各支路电流。 I1 I2 I3 R2 R1 Ib Ia + + US2 US1 _ _
电路-节点分析法
U1 U2 4
联立求解得
U1 10V U2 6V I4 2A
111
1
15 10
( 5
20
4 )U 1
4U2
5
4
I4
1
11 1
10 4
4U1
( 4
20
10)U 2
I4
4
10
11
11
15 4
( 5
20 )U1
( 20
10 )U 2
5
10
（将节点①、②、4V电压源 支路、10V电压源支路构成 的闭合面作为一个广义节点）
0.5A
I4 I1 I2 I3 2A
I5
U3 20
0.3A
I6
U3 10
4
0.2A
解法二 ：
以节点③为参考节点
（用电流为I4的电流源替换 无伴电压源）
混合变量方程
111
1
15 10
( 5
20
4 )U1
4U2
5
4
I4
1 4 U1
1 ( 4
1 20
1 10)U 2
I4
10 4
4 10
补充方程
(1) 选定参考节点(节点③)和各支路电流的参考方向，对 独立节点列KCL方程
i1 i2 i3 i4 0
i3 i4 i5 i6 0
(2)用节点电压u1、u2表示支路电流
i1
us1 u1 R1
i3
u1 u2 R3
i2
u1 R2
i4
us4
(u1 R4
u2 )
i5
u2 R5
i6
解法三 ：
(1 5
1 20 )U1
《电路》课件 节点电压法
第3章 电阻电路的一般分析
目录
3.1 支路电流法 3.2 网孔电流法和回路电流法 3.3 节点电压法
电路
南京理工大学自动化学院
3.3 节点电压法
节点电压
任意选择电路中某一节点作为参考节点，其余节点与 此参考节点间的电压分别称为对应的节点电压，节点 电压的参考极性均以参考节点为负极性端，以所对应 节点为正极性端
2
0
G3 G4 G5 Un3 0
电路
南京理工大学自动化学院
3.3 节点电压法
Gkk——第k个节点的自G电5 导
. . . GISkkjk——U——nk1流节I1s入点节和点Gj节k1的点所公2U有共n电2支流G路3源上电的流互3的电Un代导3 数（和一律为负）
G2
G4
4.
节点电流源
列向量
G1 G5
G1
G5
G1 G1 G2 G3
G3
G5 Un1 Is
G3
U
n
2
0
G3 G4 G5 Un3 0
电路
南京理工大学自动化学院
3.3 节点电压法
问：如果G5支路有两个电导串在一起，那么 下面方程中的参数该怎么修改？
G3
Un1
G2 Un2 IS4
Un3
IS1
c: 求解
电路
南京理工大学自动化学院
3.3 节点电压法
含多条不具有公共端点的理想电压源支路 G5
. Un1 1
+ Us_
G1
.2Un2
G2
. I
+
_ 3 Un3
Us3
G4
4.
a: 适当选取其中一个电压源的端点作参考点:令 Un4＝0， 则Un1＝ Us1
目录
3.1 支路电流法 3.2 网孔电流法和回路电流法 3.3 节点电压法
电路
南京理工大学自动化学院
3.3 节点电压法
节点电压
任意选择电路中某一节点作为参考节点，其余节点与 此参考节点间的电压分别称为对应的节点电压，节点 电压的参考极性均以参考节点为负极性端，以所对应 节点为正极性端
2
0
G3 G4 G5 Un3 0
电路
南京理工大学自动化学院
3.3 节点电压法
Gkk——第k个节点的自G电5 导
. . . GISkkjk——U——nk1流节I1s入点节和点Gj节k1的点所公2U有共n电2支流G路3源上电的流互3的电Un代导3 数（和一律为负）
G2
G4
4.
节点电流源
列向量
G1 G5
G1
G5
G1 G1 G2 G3
G3
G5 Un1 Is
G3
U
n
2
0
G3 G4 G5 Un3 0
电路
南京理工大学自动化学院
3.3 节点电压法
问：如果G5支路有两个电导串在一起，那么 下面方程中的参数该怎么修改？
G3
Un1
G2 Un2 IS4
Un3
IS1
c: 求解
电路
南京理工大学自动化学院
3.3 节点电压法
含多条不具有公共端点的理想电压源支路 G5
. Un1 1
+ Us_
G1
.2Un2
G2
. I
+
_ 3 Un3
Us3
G4
4.
a: 适当选取其中一个电压源的端点作参考点:令 Un4＝0， 则Un1＝ Us1
节点电压法课件
i6
is2
整理后得到的节点电压方程： (
1 R3
1 R4
)un2
1 R3
un3
is2
1 R3
un2
(
1 R3
1 R5
)un 3
i6
us5 R5
un1 un3
us6
X
此时方程数比节点电压数多一个。电路中有几个这样 的理想电压源支路，就要增加几个方程。
列写方程时，如果电路中未事先指定参考节点， 则应尽可能将连接理想电压源支路的其中一个节点作 为参考节点。
u n3 )
i5
G
5u n2
i 6 G 6 u n 3
X
2.节点电压法
节点电压方程
(G 1G 2G )u 2u n1n1(G 2G 2G un 42G 5)un2G 04un3 0is1is3
0 G 4un2 (G 4G 6)un3is3
具有四个节点的电路的节点电压方程的一般形式：
GG2111uunn11
(b)电压源接在两个非参考节点之间， 则设电压源所在支路电流i为未知量，同时增列 一个电压源支路电压与相关节点电压的方程。
X
例题2 列写图示电路的节点电压方程。
us6
us6
i6
is2 1
2
R3
3
is2 1
2
R3
3
R1
R4
R5
R1
R4
R5
us5 4
us5 4
解：选节点4为参考节点，假定电压源u s所6 在支路电流
X
3.几种特殊情况
(3)若电路中含有电流源与电阻串联的支路，
则在列节点方程时不考虑此电阻。
对于节点②
精品PPT课件----节点法34页PPT
39、没有不老的誓言，没有不变的承 诺，踏 上旅途 ，义无 反顾。 40、对时间的价值没有没有深切认识 的人， 决不会 坚ห้องสมุดไป่ตู้勤 勉。
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
精品PPT课件----节点法
36、“不可能”这个字(法语是一个字 )，只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气，不要看破要突 破，不 要嫉妒 要欣赏 ，不要 托延要 积极， 不要心 动要行 动。 38、勤奋，机会，乐观是成功的三要 素。(注 意：传 统观念 认为勤 奋和机 会是成 功的要 素，但 是经过 统计学 和成功 人士的 分析得 出，乐 观是成 功的第 三要素 。
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
精品PPT课件----节点法
36、“不可能”这个字(法语是一个字 )，只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气，不要看破要突 破，不 要嫉妒 要欣赏 ，不要 托延要 积极， 不要心 动要行 动。 38、勤奋，机会，乐观是成功的三要 素。(注 意：传 统观念 认为勤 奋和机 会是成 功的要 素，但 是经过 统计学 和成功 人士的 分析得 出，乐 观是成 功的第 三要素 。
节点法画电路(共7张PPT)
节点法画电路图的步骤：从干路到支路
1：在实物图中找节点a、b
2：画干路，并点出节点a、b
3：画支路，1）从a到b画第一条支路；
2）从a到b画第二条支路。
例题：画出下面并联电路的电路图 并联电路中，电流形成分支或电流汇合的地方。
2: 画干路，并点出节点a、b 2：画干路，并点出节点a、b 1：在电路图中标出节点a、b 并联电路中，电流形成分支或电流汇合的地方。 例题：画出下面并联电路的电路图 1：在实物图中找节点a、b 例题：按图甲所示的并联电路 例题：按图甲所示的并联电路 2) 将两支路另一端点连接，找到节点b. 与并联的区别，也是并联电路中干路与支路的分界点。 2) 将两支路另一端点连接，找到节点b. 与并联的区别，也是并联电路中干路与支路的分界点。
3：画支路，1）从a到b画第一条支路； 2）从a到b画第二条支路。 4: 连接干路：1）从电源正极连到一个节点上，2）从负极
4: 连接干路：1）从电源正极连到一个节点上，2）从负极 2）从a到b画第二条支路。
例题：画出下面并联电路的电路图 2: 连接支路：先按电路图连接第一条支路，再连第二条支路
1：在实物图中找节点a、b 节点法画电路图的步骤： 例题：判断下列电路是串联还是并联？ 3：画支路，1）从a到b画第一条支路； 节点法连接实物的步骤： 例题：画出下面并联电路的电路图 3: 找节点：1）将两支路一个端点连接，找到节点a; 2: 画干路，并点出节点a、b 1：在实物图中找节点a、b 连接图乙实物。 2：画干路，并点出节点a、b
s1 D
a
a
b
b
s2
L
1：在实物图中找节点a、连b 到另一节点上。
例题：判断下列电路是串联还是并联？
例题：按图甲所示的并联电路 并联电路中，电流形成分支或电流汇合的地方。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 R5
1 R6
)u2
us4 R4
us6 R6
2.1
1 (
R1
1 R2
1 R3
1 R4
)u1
1 (
R3
1 R4
)u2
us1 R1
us4 R4
( 1 R3
1 R4
)u1
(
1 R3
1 R4
1 R5
1 R6
)u2
us4 R4
us6 R6
电 路 方
程
将节点方程整理为矩阵形式
(1 10
1 30
1 40
)U2
1 30
U3
0
1 1 11 20 U1 30 U2 ( 20 30)U3 1
电 路 方
程
节点方程的矩阵形式
的 形
成
—
1 2
1 10 1
1 20
10
1 20
1 10
111 10 30 40
1 30
的 形
成
—
1 R1
1 R2
1 R3
1 R4
( 1 1 )
R3 R4
节
1
( 1 1 ) R3 R4
11
1
u1 u2
us1 R1
us4点 法
R4
us4 us6
R3 R4 R5 R6
R4 R6
电路分析方法
2.1
• 经典的电路分析方法
– 支路分析法
– 节点分析法
电 路
– 回路分析法
方 程
• 现代电路分析方法
的 形
成
—
– 割集分析法
节
– 状态变量分析法
点
– 稀疏表格法
法
– 拓扑矩阵法
– 改进的节点分析法
– 双图法
第 2章 电路方程的形成 2.1
采用计算机分析稳态电路时 ，多使用
节点分析法和改进的节点分析法
。
因为：
电 路
方
程
的
形
大多数电路的节点数少于回路
成
—
节 点 法
采用节点法，只要选定参考节点，则所有节点
电压就唯一得确定了，节点方程也容易用计算
机来形成。
2.1
电网络方程必须满足两类基本约束条件：
• 电路联接形式所确定的拓扑约束关系：
电
基尔霍夫电压定律（KVL）
路 方
程
基尔霍夫电流定律（KCL）
1 20
1
20 1
30 1
30
U U U
1 2 3
2
2 0
1
节 点 法
MATLAB 求解程序：
2.1
Y = [ 0.65 -0.1 -0.05;
-0.1 0.158 -0.033;
电 路
-0.05 -0.033 0.083];
数和。
电 路
方
程
的
列
In
形 成
—
i
-Is+Us /R
节 点
法
j
Is -Us /R
（二）若电路中含有受控源，则增加控制方程，2.1重 整理为矩阵形式进行计算。通常Yn为非对称阵。
方法二：矩阵形式 的节点分析法；
方法三：改进节点 法
(1
1 2
1 3
)
U
1
1 3
U2
1 1
2I
1/ 3 3电 路
2.1
整理得到的节点方程矩阵 形式：
YnU n In
电 路 方
程
的
其中：Un为节点电压向量
形 成
—
Yn为节点导纳矩阵
节 点 法
In为节点电流源向量
方程以节点电压为求解变量
（一）直接列写
2.1
只有不含受控源、耦合电感元件、无伴电压源
的电路适合直接列写节点方程的矩阵形式（观
察法）
电 路
方
程
的
形
Yn是一个对称阵，其主对角上的每一个元素 成
2.1
本节给出了利用节点法求解电路方程的 基本思路。
选择好参考节点
对各独立节点据KCL列出节点方程
电 路 方
增加必要的补充方程
程 的
整理为标准矩阵形式
形 成
—
利用MATLAB编程求解。
节 点
法
矩阵形式节点分析法
先求出各矩阵，包括节点电压、支路电流等，省去了很多中间过程， 便于MATLAB编程求解
1
1 3
1
U 2
1
U
3
7 12 12 2
2 2 3
无伴电压源
2.1
（四）若电路中含有耦合电感元件，不能直接写 出节点方程
方法一. 转化为受控源模型，按前述方法处理； 电
路
方法二. 采用矩阵形式的节点分析法
方 程
的
形
成
—
节 点 法
小结：
2.1
例2-1-2 写出图示电路的节点方程
电 路 方 程 的 形 成
节 点 法
—
2.1
以③节点为参考节点
①节点
电
路
(
1 R1
1 R2
1 R3
1 R4
)u1
(
1 R3
1 R4
)u2
方 程 的
形
us1 us4
成
—
R1 R4
节
点
法
②节点
( 1 R3
1 R4
)u1
( 1 R3
1 R4
—
是相应节点的自导纳，非主对角上的每一个
节 点
法
元素是相关节点的互导纳。
直接列写节点导纳矩阵Yn 的规则：2.1
1. 定义：直接汇集到某一节点的导纳称为自导，相邻 两节点之间的导纳称为互导
2. 自导纳总是取正值，而互导纳则总是取负值
电
3. 设网络有n个独立节点，Yn为n阶方阵：
路 方
程
的
i
j
行
的 形
成
—
节
• 电路元件自身特性所确定的电流电压关系：点 法
VCR
2.1 节点分析法
2.1
例2-1-1 采用节点分析法求解图示电路的节点电 压
电
路 方 程 的 形 成
—
节 点 法
以④节点为参考节点
2.1
①节点
11 1 1 1 2
( 2 10 20)U1 10 U2 20 U3 2
电 路
方
②节点
程
的
形
1 111 1
成
—
10
U1
( 10
30
40
)U2
30
U3
0
节 点
法
③节点
1 1 11 20 U1 30 U2 ( 20 30)U3 1
11 1 1 1 2 ( 2 10 20)U1 10 U2 20 U3 2
2.1
1 10
U1
1 3
U1
(1 3
1 4
)U
2
1/ 3 3
方 程 的 形
补充方程
I U2 4
—
成
节 点
1 121
1 3
11 32 11
U1 U 2
1
1
1 9
法
3 3 4
9
受控源
（三）若电路中含有无伴电压源（无伴受控电压2源.1 ）
%输入节点导纳矩阵
方 程
I = [1;0;1];
的
%输入节点电流源向量形 成
—
fprintf('节点电压U1, U2 , U3 : \n')
节
点
%在显示屏显示提示信息 法
U=Y\I
%解线性方程组得节点电压
Y的逆与I左乘
运行结果：
2.1
U=
3.7093电 路方ຫໍສະໝຸດ 5.8135程 的
形
16.5941
成
—
节 点 法
则适当选择参考点；若含有多个无伴电压源
（无伴受控电压源），采用广义节点法。然后整理
为矩阵形式进行计算。
电
路
方法二：改进的节点分析法
方 程
U1 12V
的 形
U1
(1
1 3 )U2
1 3
U3
7
—
成 节
11
111
2 U1
3U2
( 2
2
3)U 3
0
点 法
1113 3
i
形
j成
—
列
Yn i
yii