北京三十一中2013届九年级上学期期中考试数学试题
北京市东城区普通校2013届九年级上学期期中联考数学试题

东城区普通校2012-2013学年第一学期联考试卷初三数学命题校:国子监中学 2012年11月本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共120分,考试用时120 分钟。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷一、选择题:(本大题共8小题,每小题4分,共32分)1.在下列四个图案中,既是轴对称图形,又是中心对称图形的是A. B. C. D.2. 袋子中有两个同样大小的4个小球,其中3个红球,1个白球,从袋中任意地同时摸出一个小球,则摸到白球概率是( )A、21B、43C、31D、413.将抛物线22y x=的图象先向右平移2个单位,再向上平移3个单位后,得到的抛物线的解析式是A.22(2)3y x=--B.22(2)3y x=-+C.22(2)3y x=+-D.22(2)3y x=++4.已知两圆的半径分别为7和1,当它们外切时,圆心距为()A.6 B.7 C.8 D.95.下列说法正确的是( )①平分弦的直径,必平分弦所对的两条弧.②圆的切线垂直于圆的半径.③三角形的外心到三角形的三个顶点的距离相等。
④三点可以确定一个圆.A.4个 B.3个 C.2个 D.1个6.如图,△MBC中,∠B=90°,∠C=60°,MB=,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为A. 2 B.3 C.2 D.3(第6题7.边长为a 的正六边形的边心距等于( )A .a 23 B .2a C .aD .223a8.如图所示, 二次函数 y = ax 2 + bx + c (a ≠ 0) 的图像经过点(-1, 2), 且与x 轴交点的横坐标分别为x 1, x 2, 其中 -2 < x 1 < -1, 0 < x 2 < 1, 下列结论⑴ 4a - 2b + c < 0; ⑵ 2a - b < 0;⑶ a - 3b > 0; ⑷ b 2 + 8a < 4ac ; 其中正确的有( )A . 1个B . 2个C . 3个D . 4个第Ⅱ卷二、填空题:(本大题共4小题,每小题4分,共16分)9. 二次函数y=3 (x-1)(x+3)的对称轴方程是______________. 10.如图3,在Rt △ABC 中,∠C=90°,CA=CB=2。
2013-2014学年北京市东城区普通校九年级(上)期中数学试卷

第1页(共27页)
A.π
B.2π
C.3π
D.6π
8.(4 分)如图,直角梯形 ABCD 中,AD∥BC,AB⊥BC,AD=3,BC=5,将腰 DC 绕点
D 逆时针方向旋转 90°至 DE,连接 AE,则△ADE 的面积是( )
A.1
B.2
C.3
D.4
二、填空题(本大题共 4 小题,每小题 4 分,共 16 分)
3),连接 EF,当 t 为
s 时,△BEF 是直角三角形.
三、解答题(本大题共 5 小题,每小题 5 分,共 25 分) 13.(5 分)解方程:x2+4x﹣12=0.
第2页(共27页)
14.(5 分)如图,在 Rt△OAB 中,∠OAB=90°,且点 B 的坐标为(4,2).画出△OAB 绕点 O 逆时针旋转 90°后的△OA1B1,并求点 A 旋转到点 A1 所经过的路线长(结果保留 π)
小伟是这样思考的:如图 2,利用旋转和全等的知识构造△AP′C,连接 PP′,得到两
个特殊的三角形,从而将问题解决.
请你回答:图 1 中∠APB 的度数等于
.
参考小伟同学思考问题的方法,解决下列问题:
(1)如图 3,在正方形 ABCD 内有一点 P,且 PA= ,PB=1,PD= ,则∠APB
的度数等于
7.(4 分)如图,C,D 是以 AB 为直径的半圆周的三等分点,CD=6,则阴影部分的面积是 ()
A.π
B.2π
C.3π
D.6π
【分析】连接 OC、OD,根据 C,D 是以 AB 为直径的半圆周的三等分点,可得∠COD
=60°,△OCD 是等边三角形,将阴影部分的面积转化为扇形 OCD 的面积求解即可.
北京-mjt-初三上数学期中试题及答案
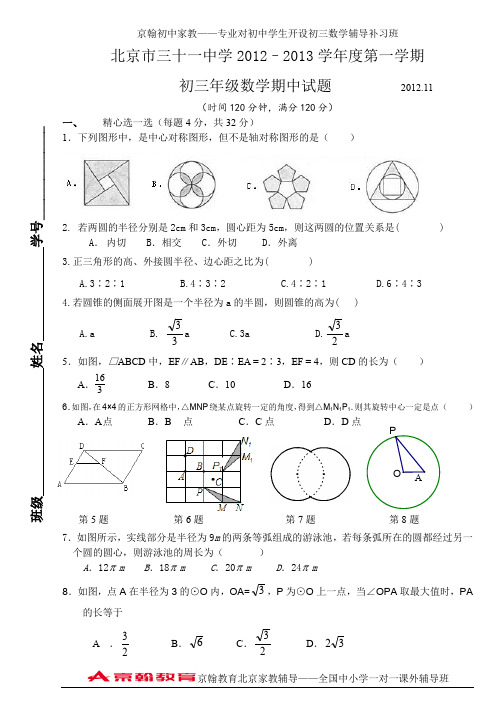
北京市三十一中学2012–2013学年度第一学期 初三年级数学期中试题 2012.11(时间120分钟,满分120分)一、 精心选一选(每题4分,共32分)1.下列图形中,是中心对称图形,但不是轴对称图形的是( )2. 若两圆的半径分别是2cm 和3cm ,圆心距为5cm ,则这两圆的位置关系是( )A . 内切B .相交C .外切D .外离 3.正三角形的高、外接圆半径、边心距之比为( )A.3∶2∶1B.4∶3∶2C.4∶2∶1D.6∶4∶3 4.若圆锥的侧面展开图是一个半径为a 的半圆,则圆锥的高为( )A.aB.33a C.3a D.23a5.如图,□ABCD 中,EF ∥AB ,DE ∶EA = 2∶3,EF = 4,则CD 的长为( )A .163B .8C .10D .167.如图所示,实线部分是半径为9的两条等弧组成的游泳池,若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长为( )A .12πmB .18πmC .20πmD .24πm 第7题二、填空题(共4道小题,每小题4分,共16分)9.如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC 与△A 1B 1C 1是位似图形,且顶点都在格点上,则位似中心的坐标是___________. 10. 如图,PA ,PB 是⊙O 是切线,A ,B 为切点, AC 是⊙O 的直径,若∠BAC=25°,则∠P= _度.11.如图,正方形ABCD 的边长为2,AE=EB ,MN=1,线段MN 的两端在CB 、CD 上滑动,当CM=时,ΔAED 与N ,M ,C 为顶点的三角形相似. 12. 如图,n +1个边长为2的等边三角形有一条边在同一直线上,设△211B D C 的面积为1S ,△322B D C 的面积为2S ,…,△1n n n B D C +的面积为n S ,则2S = ;n S =____ (用含n 的式子表示).三、解答题(本题共28分) 13.(本题5分)计算:2cos60tan 45sin 45sin30︒-︒+︒︒14.(本题4分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC 的顶点均在格点上,O 、M 也在格点上.(1)画出△ABC 关于直线OM 对称的△A 1B 1C 1; (2)画出△ABC 绕点O 按顺时针方向旋转90°后所得的△A 2B 2C 2;(3)△A 1B 1C 1与△A 2B 2C 2组成的图形是轴对称图形吗?如果是轴对称图形,请画出对称轴.第9题15.(本题5分)如图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,连接DE ,F 为线段DE 上一点,且∠AFE =∠B. (1) 求证:△ADF ∽△DEC ;(2) 若AB =4,AD =33,AE =3,求ED ,AF 的长.16.(本题5分)如图,在△ABC 中,AB =AC ,以AB 为直径的⊙O 分别交BC 、AC 于点D 、E ,连结EB 交OD 于点F . (1)求证:OD ⊥BE ; (2)若DE =25,AB =25,求AE 的长.17. (本题5分)如图,Rt△ABC 的斜边AB=4,O 是AB 的中点,以O 为圆心的半圆分别与两直角边相切于点D 、E , (1)求证∠A=∠B.(2)求图中阴影部分的面积.18.(本题4分)已知:如图,∠MAN =45°,B 为AM 上的一个定点, 若点P 在射线AN 上,以P 为圆心,P A 为半径的圆与射线AN 的另一个交点为C ,请确定⊙P 的位置,使BC 恰与⊙P 相切.(1)画出图形(不要求尺规作图,不要求写画法); (2)连结BP 并填空:① ∠ABC = °;② 比较大小:∠ABP ∠CBP . (用“>”、“<”或“=”连接)四、解答题(本题共23分) 19.(本题6分)如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB 的高度,他发现当斜坡正对着太阳时,旗杆AB 的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC =20米,斜坡坡面上的影长CD =8米,太阳光线AD 与水平地面成30°角,斜坡CD 与水平地面BC 成30°的角,求旗杆AB 的高度(结果保留根号).20.(本题6分)已知:如图,等腰△ABC 中,AB= BC ,AE ⊥BC 于E , EF ⊥AB 于F ,4cos 5AEF ∠=, (1)当BE=4时,求EF长. (2)若CE=2求EF 的长. 21.(本题6分)已知:如图,在△ABC 中,点D 在AC 上,点E 在CB 的延长线上,且AD=BE ,求证:BCACFD EF =.22. (本题5分)阅读下列材料:问题:如图1,在正方形ABCD 内有一点P ,P A =5,PB =2,PC =1,求∠BPC 的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC 绕点B 逆时针旋转90°,得到了△BP ′A (如图2),然后连结PP ′.请你参考小明同学的思路,解决下列问题:(1) 图2中∠BPC的度数为;(2) 如图3,若在正六边形ABCDEF内有一点P,且P A=132,PB=4,PC=2,则∠BPC 的度数为,正六边形ABCDEF的边长为.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E 与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=92a 时,P、Q两点间的距离 (用含a的代数式表示).24.如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.25.已知:AOB △中,2AB OB ==,COD △中,3CD OC ==,ABO DCO =∠∠. 连接AD 、BC ,点M 、N 、P 分别为OA 、OD 、BC 的中点.图1 图2(1) 如图1,若A 、O 、C 三点在同一直线上,且60ABO =∠,则PMN △的形状是__________,此时ADBC=________; (2) 如图2,若A 、O 、C 三点在同一直线上,且2ABO α=∠,证明PMN BAO △∽△,并计算ADBC的值(用含α的式子表示); (3) 在图2中,固定AOB △,将COD △绕点O 旋转,直接写出PM 的最大值.北京市三十一中学2012–2013学年度第一学期初三年级数学期中答案一、选择题1——4 ACAD 5——8 CBDB 9、(9,0) 10 、50 11、()552,55 12、13,332+n n 13.解:2c o s 60t a n 45s i n 45s i n 30︒-︒+︒︒.212112=-+- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -4分1.2=- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 5分 14.(1)——————1` (2)——————2` (3)——————4`15.(1)——————2` (3)求出ED=6 ——————3`,求出AF=32————5` 16.(1)连结AD 证出OD ⊥BE-----2分 (2)证出△CED ∽△EBA--------3分 求出CE=1-------4分 求出AE=1.5--------5分 17、(1)连结OD 、OE------------1分证出∠A=∠B------------2分 (2)求出扇形半径------------3分S 阴=2-2π------------6分18.解:(1)图形见右. - - - - - - - - - - - - - - - - - - 2分(2)① ∠ABC = 45 °;- - - - - - -3分② ∠ABP < ∠CBP . - - - - - - 4分 19、画出求法示意图------------1分求出CE=34------------2分图(1)图(2)求出BF=20+38(或DF=20+34)-----------4分求出AB=83320+-----------6分20.解:(1)求出BE=2.4 - - - - - - - - - - - - - - - - - - - - - - - - 2分∵ AE ⊥BC , EF ⊥AB ,∴ ∠1+∠2=90°,∠B+∠2=90°. ∴ ∠1=∠B . ∵ 4cos 5AEF ∠=, ∴ Rt △ABE 中,4cos 5BE B AB ==. 设BE =4k ,则AB=BC=5k ,2EC BC BE k =-==. ∴ BE =8. - - - - - - - - - - - - - - - - - - - - - - - - - - - - -4分∴ Rt △BEF 中,324sin 855EF BE B =⋅=⨯=.- - - - - - - - - - - - - - - - - - - - - - - -6分21.辅助线 ;………………………………………………………………………… 1分 转化一组比;………………………………………………………………………… 2分 转化二组比 ;………………………………………………………………………… 3分 等量代换 ;………………………………………………………………………… 4分 答案 ;………………………………………………………………………… 5分22.解:(1)135°;………………………………………………………………………… 2分(2)120°;………………………………………………………………………… 3分. ……………………………………………………………………… 5分23:(1)证明:∵△ABC 是等腰直角三角形, ∴∠B=∠C=45°,AB=AC , ∵AP=AQ , ∴BP=CQ ,∵E 是BC 的中点, ∴BE=CE ,在△BPE 和△CQE 中,21FC BA∵,∴△BPE ≌△CQE (SAS );……………………………………………… 2分 (2)解:∵△ABC 和△DEF 是两个全等的等腰直角三角形, ∴∠B=∠C=∠DEF=45°, ∵∠BEQ=∠EQC+∠C ,即∠BEP+∠DEF=∠EQC+∠C , ∴∠BEP+45°=∠EQC+45°, ∴∠BEP=∠EQC ,∴△BPE ∽△CEQ ,……………………………………………… 4分 ∴,∵BP=a ,CQ=a ,BE=CE , ∴BE=CE=a ,∴BC=3a ,∴AB=AC=BC •sin45°=3a ,∴AQ=CQ ﹣AC=a ,PA=AB ﹣BP=2a , 连接PQ ,在Rt △APQ 中,PQ==a .……………………………………………… 7分25. 解:(1)等边三角形,1;(每空1分) --------------------2分(2)证明:连接BM 、CN . 由题意,得BM OA ⊥,CN OD ⊥,α-︒=∠=∠90COD AOB .∵ A 、O 、C 三点在同一直线上, ∴ B 、O 、D 三点在同一直线上.∴ 90BMC CNB ==∠∠. ∵ P 为BC 中点, ∴ 在Rt △BMC 中,BC PM 21=.京翰初中家教——专业对初中学生开设初三数学辅导补习班京翰教育北京家教辅导——全国中小学一对一课外辅导班 在Rt △BNC 中,BC PN 21=. ∴ PN PM =.---------------------------3分 ∴ B 、C 、N 、M 四点都在以P 为圆心,12BC 为半径的圆上. ∴ 2MPN MBN =∠∠.又∵ α=∠=∠ABO MBN 21, ∴ MPN ABO =∠∠.∴ PMN BAO △∽△. ----------------------------------4分∴ BAAO PM MN =. 由题意,12MN AD =,又BC PM 21=. ∴ PMMN BC AD =.------------------------------------5分 ∴ AD AO BC BA=. 在Rt BMA △中,αsin =ABAM . ∵ AM AO 2=,∴ 2sin AO BAα=. ∴ αsin 2=BCAD .------------------------------6分 (3)52.--------------------------------7分。
2013-2014学年人教版九年级上期中考试数学试题(含答案)

海淀区九年级第一学期期中测评数学试卷(分数:120分时间:120分钟) 2013.11班级姓名学号 成绩试题答案一律填涂或书写在答题卡上,在试卷上做答无效. 一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.一元二次方程2230x x --=的二次项系数、一次项系数、常数项分别是A. 1,2,3--B. 1,-2,3C. 1,2,3D. 1,2,3- 2.在角、等边三角形、平行四边形、圆中,既是中心对称图形又是轴对称图形的是 A .角B .等边三角形 C .平行四边形 D .圆 3.函数2y x =-中,自变量x 的取值范围是A .2≠xB .2≤xC .2>xD .2≥x4.如图,点A 、B 、C 在O ⊙上,若110AOB ∠=o ,则ACB ∠的大小是 A .35o B .ο45 C .55o D .110o5.用配方法解方程09102=++x x ,配方正确的是 A .16)5(2=+x B .34)5(2=+x C .16)5(2=-x D .25)5(2=+x6.如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是 A .ο60B .ο72 C .90oD .120o7.若230a b ++-=,则a b +的值为A .-1B .1C .5D .6OCBA8.如图,⊙O 的半径为5,点P 到圆心O 的距离为10,如果过点P 作弦,那么长度为整数值的弦的条数为 A .3 B .4C .5D .6二、填空题(本题共16分,每小题4分)9.如图,将ABC △绕点C 顺时针旋转至''A B C △的位置,若 15ACB ∠=o ,120B ∠=o ,则'A ∠的大小为________.10.已知一元二次方程有一个根是0,那么这个方程可以是(填上你认为正确的一个方程即可).11.如图,AB 是⊙O 的直径,点C 、D 为⊙O 上的两点,若 ο40=∠ABD ,则BCD ∠的大小为.12.下面是一个按某种规律排列的数阵:1第1行 2 3 2第2行 5 6 7 22 3第3行 1011 2313 1415 4第4行 L L L L根据数阵排列的规律,则第5行从左向右数第5个数为,第n (3≥n ,且n 是整数)行从左向右数第5个数是(用含n 的代数式表示). 三、解答题(本题共30分,每小题5分) 13.计算:36324⨯+÷.14.用公式法解一元二次方程:241x x +=.15.如图,ABC △与AED △均是等边三角形,连接BE 、CD .请在图中找出一条与CD 长度相等的线段,并证明你的结论.结论:CD =. 证明:ODCBAPO ED CBA16.当15-=x 时,求代数式522-+x x 的值.17.如图,两个圆都以点O 为圆心,大圆的弦AB 交小圆于C 、D 两点.求证:AC =BD . 证明:18.列方程(组)解应用题:如图,有一块长20米,宽12米的矩形草坪,计划沿水平和竖直方向各修一条宽度相同的小路,剩余的草坪面积是原来的34,求小路的宽度.解:四、解答题(每小题5分,共20分)19.已知关于x 的一元二次方程210x mx m -++=的一个根为2. (1) 求m 的值及另一根;(2)若该方程的两个根分别是等腰三角形的两条边的长,求此等腰三角形的周长.20.如图,DE 为半圆的直径,O 为圆心,DE =10,延长DE 到A ,使得EA =1,直线AC 与半圆交于B 、C 两点,且ο30=∠DAC .(1)求弦BC 的长; (2)求AOC △的面积.21.已知关于x 的方程0)1(222=++-k x k x 有两个不相等的实数根. (1)求k 的取值范围;(2)求证:1-=x 不可能是此方程的实数根.DCBA O ECADBO22.阅读下面的材料:小明在研究中心对称问题时发现:如图1,当点1A 为旋转中心时,点P 绕着点1A 旋转180°得到1P 点,点1P 再绕着点1A 旋转180°得到2P 点,这时点P 与点2P 重合.如图2,当点1A 、2A 为旋转中心时,点P 绕着点1A 旋转180°得到1P 点,点1P 绕着点2A 旋转180°得到2P 点,点2P 绕着点1A 旋转180°得到3P 点,点3P 绕着点2A 旋转180°得到4P 点,小明发现P 、4P 两点关于点2P 中心对称.(1)请在图2中画出点3P 、4P , 小明在证明P 、4P 两点关于点2P 中心对称时,除了说明P 、2P 、4P 三点共线之外,还需证明;(2)如图3,在平面直角坐标系xOy 中,当)3,0(1A 、)0,2(2 A 、)0,2(3A 为旋转中心时,点)4,0(P 绕着点1A 旋转180°得到1P 点;点1P 绕着点2A 旋转180°得到2P 点;点2P 绕着点3A 旋转180°得到3P 点;点3P 绕着点1A 旋转180°得到点4P L 点. 继续如此操作若干次得到点56P P L 、、,则点2P 的坐标为,点2017P 的坐为.图3图2图1五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.已知关于x 的一元二次方程02)12(2=++-x m mx . (1)求证:此方程总有两个实数根;(2)若此方程的两个实数根都是整数,求m 的整数值; (3)若此方程的两个实数根分别为1x 、2x ,求代数式5)(2))(12()(2122213231+++++-+x x x x m x x m 的值.24.已知在ABC △中,ο90=∠ACB ,26==CB CA ,AB CD ⊥于D ,点E 在直线CD 上,CD DE 21=,点F 在线段AB 上,M 是DB 的中点,直线AE 与直线CF 交于N 点. (1)如图1,若点E 在线段CD 上,请分别写出线段AE 和CM 之间的位置关系和数量关系:___________,___________;(2)在(1)的条件下,当点F 在线段AD 上,且2AF FD =时,求证:ο45=∠CNE ; (3)当点E 在线段CD 的延长线上时,在线段AB 上是否存在点F ,使得ο45=∠CNE .若存在,请直接写出AF 的长度;若不存在,请说明理由.DCBANM FED CBA 图1备用图25.在平面直角坐标系xOy 中,点A 、B 分别在x 轴、y 轴的正半轴上,且10=AB ,点M 为线段AB 的中点.(1)如图1,线段OM 的长度为________________;(2)如图2,以AB 为斜边作等腰直角三角形ACB ,当点C 在第一象限时,求直线OC 所对应的函数的解析式; (3)如图3,设点D 、E 分别在x 轴、y 轴的负半轴上,且10=DE ,以DE 为边在第三象限内作正方形DGFE ,请求出线段MG 长度的最大值,并直接写出此时直线MG 所对应的函数的解析式.GFEDxy O ABM图1图2CxyOABM BAOyx图3海淀区九年级第一学期期中练习2013.11数学试卷答案及评分参考阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写的较为详细,阅卷时,只要考生将主要过程正确写出即可.2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.3.评分参考中所注分数,表示考生正确做到此步应得的累加分数. 一、选择题(本题共32分,每小题4分) 题号 12345 6 7 8 答案A D D CABBC二、填空题(本题共16分,每小题4分)9.45°;10.20x x -=(二次项系数不为0,且常数项为0均正确);11.50°;12.21,622+-n n (每空2分).三、解答题(本题共30分,每小题5分) 13.(本小题满分5分)解:36324⨯+÷818=+………………………………………………………………………2分2322+=…………………………………………………………………4分 25=.……………………………………………………………………………5分14.(本小题满分5分)解:原方程可化为2+410x x -=,……………………………………………………1分141a ,b ,c ===-,2441(1)=20>0,∆=-⨯⨯-…………………………………………………………2分方程有两个不相等的实数根,244202522b b ac x a -±--±===-±,……………………………………4分即122525x ,x =-+=--.……………………………………………………5分15.(本小题满分5分)结论:CD BE =.……………………………………………………………………1分 证明:Θ△ABC 与△AED 是等边三角形,∴AE AD =,AB AC =,60CAB DAE ∠=∠=o.…2分 ∴CAB DAB DAE DAB ∠-∠=∠-∠,即CAD BAE ∠=∠.………………………………3分 在△CAD 和△BAE 中,EDCBAAC AB,CAD BAE,AD AE,=⎧⎪∠=∠⎨⎪=⎩∴△CAD ≌△BAE .…………………………………………………………4分 ∴CD =BE .…………………………………………………………………5分16.(本小题满分5分)解:Θ15-=x ,∴15x +=.∴5)1(2=+x .………………………………………………………………1分∴2215x x ++=.………………………………………………………………2分∴224x x +=.…………………………………………………………………3分 ∴225451x x +-=-=-.……………………………………………………5分17.(本小题满分5分)证明:过点O 作AB OM ⊥于M ,…………………………1分由垂径定理可得DM CM BM AM ==,.……………3分∴DM BM CM AM -=-.…………………………4分 即BD AC =.…………………………………………5分18.(本小题满分5分)解:设小路的宽度是x 米.………………………………………………………1分由题意可列方程,3(20)(12)20124x x --=⨯⨯.……………………………2分化简得, 232600x x -+=.解得, 12302x ,x ==.………………………………………………………3分由题意可知3020x =>不合题意舍去,2x =符合题意.…………………4分 答:小路的宽度是2米.……………………………………………………5分四、解答题(本题共20分,每小题5分) 19.(本小题满分5分)解:(1)∵关于x 的一元二次方程210x mx m -++=的一个根为2,∴22210m m -++=.……………………………………………………1分 ∴5m =.……………………………………………………………………2分∴一元二次方程为2560x x -+=.解得1223x ,x ==.…………………………………………………………3分∴5m =,方程另一根为3.(2)当长度为2的线段为等腰三角形底边时,则腰长为3,此时三角形的周长为2+3+3=8;………………………………………………………………4分当长度为3的线段为等腰三角形底边时,则腰长为2,此时三角形的周长为2+2+3=7. ………………………………………………………………5分MODCBA20.(本小题满分5分)解:(1)过点O 作OM ⊥BC 于M .由垂径定理可得:BM=CM .…1分∵30DAC ∠=o , ∴12OM OA =.∵直径DE =10, EA =1,∴=5OD OC OE ==.∴516OA OE EA =+=+=. ∴3OM =.…………………2分在R t △COM 中,222225316CM OC OM =-=-=. ∴4CM =. ∴4BM =.∴+8BC BM CM ==.……………………………………………………3分 (2)在R t △AOM 中,222226327AM OA OM =-=-=.∴33AM =.……………………………………………………………………4分 ∴+334AC AM CM ==+. ∵OM ⊥AC , ∴119(334)336222AOC S AC OM =⋅=⨯+⨯=+V .……………………………5分21.(本小题满分5分)解:(1)∵关于x 的方程0)1(222=++-k x k x 有两个不相等的实数根,∴224(1)4=8+4>0k k k ∆=+-.………………………………………………2分 ∴1>2k -.…………………………………………………………………3分 (2)∵当1-=x 时,左边=222(1)x k x k -++22(1)2(1)(1)k k =--+⨯-+223k k =++…………………………………………4分 2(+1)20k =+>.而右边=0,∴左边≠右边.∴1-=x 不可能是此方程的实数根.……………………………………5分22.(本小题满分5分)(1)正确画出34P P 、点(图略).………………………………………………1分224=P P P P .……………………………………………………………………2分(2)(-4,-2).…………………………………………………………………3分(0,2).……………………………………………………………………5分MECA DB O五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.(本小题满分7分)解:(1)由题意可知0m ≠.2(21)42m m ∆=+-⨯⨯22=441(21)0m m m -+=-≥.……………………………………………2分∴此方程总有两个实数根.(2)方程的两个实数根为2(21)(21)2m m x m+±-=,∴1212x ,x m==.…………………………………………………………4分 ∵方程的两个实数根都是整数,且m 为整数,∴1m =±.…………………………………………………………………5分(3)∵原方程的两个实数根分别为1x 、2x ,∴211(21)20mx m x -++= 222(21)20mx m x -++=.……………………………………………………6分∴5)(2))(12()(2122213231+++++-+x x x x m x x m=1323211222[(21)2]+[(21)2]+5mx m x x mx m x x -++-++=12211222[(21)2]+[(21)2]+5x mx m x x mx m x -++-++=12005x x ⨯+⨯+=5.…………………………………………………………………………7分24.(本小题满分8分)(1)AE ⊥CM ,AE =CM .……………………………………………………2分(2)如图,过点A 作AG ⊥AB ,且AG =BM,,连接CG 、FG ,延长AE 交CM 于H .∵ο90=∠ACB ,26==CB CA ,∴∠CAB =∠CBA =45°,AB=2212CA CB +=. ∴∠GAC =∠MBC =45°. ∵AB CD ⊥,∴CD=AD=BD =162AB =. ∵M 是DB 的中点, ∴3BM DM ==. ∴3AG =. ∵2AF FD =,∴4 2.AF DF ==,∴+2+3=5.FM FD DM == ∵AG ⊥AF , ∴2222+3+4=5.FG AG AF ==FHNGM EDCBA∴.FG FM =……………………………………………………………………3分 在△CAG 和△CBM 中, CA CB CAG CBM AG BM =⎧⎪∠=∠⎨⎪=⎩,,, ∴△CAG ≌△CBM .∴CG =CM ,ACG BCM ∠=∠.∴++90MCG ACM ACG ACM BCM ∠=∠∠=∠∠=o .………………………4分 在△FCG 和△FCM 中, CG CM FG FM CF CF =⎧⎪=⎨⎪=⎩,,, ∴△FCG ≌△FCM .∴FCG FCM ∠=∠.………………………………………………………5分 ∴45FCH ∠=o .由(1)知AE ⊥CM , ∴90CHN ∠=o∴ο45=∠CNE .………………………………………………………………6分 (3)存在.AF =8.…………………………………………………………………………8分25.(本小题满分7分)(1)5;…………………………………………………………………………………1分 (2)如图1, 过点C 分别作CP ⊥x 轴于P ,CQ ⊥y 轴于Q .∴∠CQB =∠CPA =90°,∵∠QOP =90°,∴∠QCP =90°. ∵∠BCA =90°,∴∠BCQ =∠ACP . ∵BC=AC ,∴△BCQ ≌△ACP .∴CQ=CP .………………………………3分 ∵点C 在第一象限,∴不妨设C 点的坐标为(a ,a )(其中0a ≠).设直线OC 所对应的函数解析式为kx y =,∴a ka =,解得k =1,∴直线OC 所对应的函数解析式为x y =.…………………………………4分 (3)取DE 的中点N ,连结ON 、NG 、OM .∵∠AOB=90°,∴OM =152AB =.同理ON =5.Fy OBDGNEAMx图2Q C xy O A BP 图1∵正方形DGFE ,N 为DE 中点,DE=10, ∴NG =2222=+10555DN DG =+=.在点M 与G 之间总有MG ≤MO +ON +NG (如图2),由于∠DNG 的大小为定值,只要12DON DNG ∠=∠,且M 、N 关于点O 中心对称时,M 、O 、N 、G 四点共线,此时等号成立(如图3).………………………5分∴线段MG 取最大值10+55.………………6分此时直线MG 的解析式x y 251+-=.……………………………………7分NM BAOyxDEG图3。
北京31中初三期中数学试题答案

北京三十一中第一学期初 三 期 中 数 学 练 习 答 案(考试时间120分钟,满分100分)一、选择题(本题共23分,1-7每小题3分,第8题2分)二、填空题(本题共17分,9-13每小题3分,第14题2分)9. 410. 0 11. 6 12. m<1 13. 答案不唯一 14.324,2- 三、解答题(本题共46分,15-16每小题5分,17-22每小题6分) 15.解:26tan 30cos45︒︒-︒ 26=⨯………………………………………3分 322=- 12=………………………………………5分16.解:b=32 …………3分 c=3102…………5分 17.证明:△ABD ∽△ACB 即得。
证明角等…………3分;相似…………6分18.解:(1)如图,作BH OA⊥,垂足为H ,…………1分 在Rt OHB △中,5BO =,3sin 5BOA ∠=,3BH ∴=. 4OH ∴=.∴点B 的坐标为(43),.…………3分 (2)10OA =,4OH =,6AH ∴=.在Rt AHB △中,3BH =,AB ∴=cos AH BAO AB ∴∠==(得52不扣分)…………6分 19.解:解直角三角形…………3分19m. …………6分x20.解:(1)2000元;…………1分(2)列函数式…………3分 讨论最值…………5分 5元。
…………6分 21.解:(1)它与x 轴交点的坐标为(1,0),(3,0),与y 轴交点的坐标为(0,3),顶点坐标为(2,1)-; ………………………………………3分(2)列表:……………………………4分图象如图3所示. ……………………………5分 (3)t 的取值范围是18t -≤<.……………………6分22.(1)证明:∵ AB =AC , ∴ ∠B =∠C .∵ ∠ADE +∠BDE =∠ADB =∠C +∠CAD , ∠ADE =∠C , ∴ ∠BDE =∠CAD .∴ △BDE ∽△CAD . …………3分 (2)解:由(1)得DB ACBE CD=. ∵ AB =AC = 5,BC = 8,CD =2, ∴ 6DB BC CD =-=. ∴ 622.45DB CD BE AC ⨯⨯===. …………6分五、解答题(本题共14分,第23题3分,第24题5分,第25题6分) 23.解:(1)90α︒+ …………1分(2)图中两对相似三角形:①△ABB '∽△AC C ' ,…………2分②△ACE ∽△FBE ; …………3分、24.解:(1)∵关于x的方程为221(1)04x a -++=为一元二次方程,且有实根。
2013年秋期九年级上册期中数学试卷(附答案)

2013年秋期九年级上册期中数学试卷(附答案)浙江省宁波市锦合、新世纪2013-2014学年第一学期期中考试九年级数学试卷一、选择题:(每小题4分,共48分)1.已知点P(1,-3)在反比例函数的图象上,则的值是()A.3B..-3C.D.2.对于反比例函数,下列说法正确的是()A.图象经过点(1,﹣3)B.y随x增大而减小C.x>0时,y随x的增大而增大D.x<0时,y随x增大而减小3.若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是()A.抛物线开口向上B.抛物线的对称轴是x=1C.当x=1时,y的最大值为﹣4D.抛物线与x轴的交点为(﹣1,0),(3,0)4.将抛物线y=(x﹣1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为()A.y=(x﹣2)2B.y=(x﹣2)2+6C.y=x2+6D.y=x25.如图,在⊙O中,已知∠OAB=22.5°,则∠C的度数为()A.135°B.122.5°C.115.5°D.112.5°6.如图,DC是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是()A.B.AF=BFC.OF=CFD.∠DBC=90°7.如图,函数与的图象相交于点A(1,2)和点B,当时,自变量x 的取值范围是()A.x>1B.-1<x<0C.-1<x<0或x>1D.x<-1或0<x<18.二次函数y=ax2+bx+c图象上部分点的坐标满足下表:x…﹣3﹣2﹣101…y…﹣3﹣2﹣3﹣6﹣11…则该函数图象的顶点坐标为()A.(﹣3,﹣3)B.(﹣2,﹣2)C.(﹣1,﹣3)D.(0,﹣6)9.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()A.B.8C.D.10.如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是()A.①②B.②③C.①②④D.②③④11.二次函数的图像与x轴交于B,C两点,点D平分BC,若在x轴上侧的A点为抛物线上的动点,且∠BAC为锐角,则AD的取值范围是()A.3<AD≤9B.3≤AD≤9C.4<AD≤10D.3≤AD≤812.如图,等腰的直角边BC在轴上,斜边AC上的中线BD交轴于点E,双曲线的图像经过点A,若的面积为,则的值为()A.8B.C.16D.二、填空题:(每小题4分,共24分)13.如图,已知A点是反比例函数的图象上一点,AB⊥y轴于B,且△ABO 的面积为3,则k的值为14.抛物线的最小值是15.如图,已知⊙O半径为5,弦AB长为8,点P为弦AB上一动点,连结OP,则线段OP的最小长度是16.如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线y=x-1经过点C交x轴于点E,双曲线经过点D,则k的值为________.17.某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一颗树,平均每棵树就会少结5个橘子.设果园增种x 棵橘子树,果园橘子总个数为y个,则果园里增种棵橘子树,橘子总个数最多.18.如图,AB是半圆O的直径,,则的度数为三、解答题:(共78分)19.(本题6分)已知反比例函数的常数)的图象经过点A(2,3).(1)求这个函数的解析式;(2)判断点B(﹣1,6),C(3,2)是否在这个函数的图象上,并说明理由;(3)当﹣3<x<﹣1时,求y的取值范围.20.(本题6分)已知抛物线经过点A(3,0),B(﹣1,0).(1)求抛物线的解析式;(2)求抛物线的顶点坐标.21.(本题8分)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.(1)求证:∠B=∠D;(2)若AB=4,BC﹣AC=2,求CE的长.22.(本题10分)某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x 的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:销售单价(元)x销售量y(件)销售玩具获得利润w(元)(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?23.(本题10分)已知反比例函数的图象与一次函数的图象交于A、B 两点,连结AO。
北京三中九年级数学上学期期中试题有答案
北京三中2015-2016九年级数学上学期期中试题(有答案)北京市北京三中2015-2016学年度九年级数学上学期期中试题考生须知1.本试卷共8页,共五道大题,29道小题,满分120分。
考试时间120分钟。
2.试题答案一律书写在答题纸上,在试卷上作答无效。
3.在答题纸上,除作图使用铅笔外,其他试题用黑色字迹签字笔作答。
4.不得使用涂改液(带),没有在指定位置答题或在答题框外答题一律不给分.选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.如图,在△ABC中,若DE∥BC,AD∶BD=1∶2,若△ADE的面积等于2,则△ABC的面积等于().A.6B.8C.12D.182.在平面直角坐标系中,已知点和点,则等于(). A.B.C.D.3.抛物线的顶点坐标是().A.(-2,5)B.(2,5)C.(-2,-5)D.(2,-5)4.在Rt△ABC中,∠C=90°,若BC=1,AC=2,则sinA的值为().A.B.C.D.25.下列三角函数值错误的是().A.sinB.C.D.6.如图,身高为1.6米的某同学想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0米,BC=8.0米,则旗杆的高度是().A.6.4米B.7.0米C.8.0米D.9.0米7.将抛物线绕顶点旋转180°,则旋转后的抛物线的解析式为().A.B.C.D.8.如图,将△ABC的三边分别扩大一倍得到△A1B1C1(顶点均在格点上),若它们是以P点为位似中心的位似图形,则P点的坐标是().A.(-3,-3)B.(-3,-4)C.(-4,-3)D.(-4,4)9.同一直角坐标系中,函数和(是常数,且)的图象可能是()10.如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s 的速度沿BC,CD运动,到点C,D时停止运动.设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为()ABCD二、填空题(本题共18分,每小题3分)11.如图,在△ABC中,DE∥AB分别交AC,BC于点D,E,若AD=3,CD=4,则△CDE与△CAB的周长的比为.12.点A(,)、B(,)在二次函数的图象上,若>>1,则与的大小关系是.(用“>”、“<”、“=”填空)13.在正方形网格中,的位置如图所示,则tanB的值为__________.14.关于x的二次函数的图象与y轴的交点在x轴的上方,请写出一个满足条件的二次函数的表达式:.15.如图,在Rt△ABC中,∠ACB=,AC=12,BC=5,CD⊥AB于点D,那么的值是.16.在平面直角坐标系中,直线和抛物线在第一象限交于点A,过A作轴于点.如果取1,2,3,…,n时对应的△的面积为…,,那么_____;…+=___________.三、解答题(本题共30分,每小题5分)17.计算:.18.若二次函数的图象经过A(1,0)、B(2,-1)两点,求此二次函数的解析式.19.如图,△ABC中,点D在AB上,∠ACD=∠ABC,若AD=2,AB=6,求AC的长.20.已知二次函数(1)用配方法将化成的形式;(2)在平面直角坐标系中,画出这个二次函数的图象;(3)当时,求y的取值范围.21.如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)。
2013年北京市中考数学试卷-答案
1 / 13北京市2013年高级中等学校招生考试年高级中等学校招生考试数学答案解析一、选择题 1.【答案】B【解析】解:将3960用科学记数法表示为33.9610´【提示】科学记数法的表示形式为10n a ´的形式,其中,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值1>时,n 是正数;当原数的绝对值1<时,n 是负数.是负数.【考点】科学记数法—表示较大的数.表示较大的数. 2.【答案】D【解析】解:∵34143æöæö-´-=ç÷ç÷èøèø,∴34-的倒数是43-.【提示】根据倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.,我们就称这两个数互为倒数. 【考点】倒数.【考点】倒数.3.【答案】C【考点】概率公式.【考点】概率公式.【解析】解:根据题意可得:大于2的有3,4,5三个球,共5个球,任意摸出1个,摸到大于2的概率是35. 【提示】根据随机事件概率大小的求法,找准两点:①符合条件的情况数目,②全部情况的总数,二者的比值就是其发生的概率的大小.比值就是其发生的概率的大小.4.【答案】C 【解析】解:∵12Ð=Ð,340Ð=°,∴()1111803180407022()Ð=´°-Ð=´°-°=°,∵a b ∥,∴4170Ð=Ð=°.【提示】根据平角的定义求出1Ð,再根据两直线平行,内错角相等解答.,再根据两直线平行,内错角相等解答. 【考点】平行线的性质.【考点】平行线的性质.5.【答案】B【解析】解:∵AB BC ^,CD BC ^,∴BAE CDE △∽△,∴AB BECD CE=∵20BE =m ,10CE =m ,20CD =m ,∴202010AB =解得:40AB =【提示】由两角对应相等可得BAE CDE △∽△,利用对应边成比例可得两岸间的大致距离AB . 【考点】相似三角形的应用.【考点】相似三角形的应用. 6.【答案】A【解析】解:A .不是轴对称图形,是中心对称图形.故此选项正确;.不是轴对称图形,是中心对称图形.故此选项正确; B .是轴对称图形,也是中心对称图形.故此选项错误;.是轴对称图形,也是中心对称图形.故此选项错误; C .是轴对称图形,不是中心对称图形.故此选项错误;.是轴对称图形,不是中心对称图形.故此选项错误; D .是轴对称图形,不是中心对称图形.故此选项错误..是轴对称图形,不是中心对称图形.故此选项错误. 【提示】根据轴对称图形与中心对称图形的概念求解.【提示】根据轴对称图形与中心对称图形的概念求解. 【考点】中心对称图形,轴对称图形.【考点】中心对称图形,轴对称图形. 7.【答案】B【解析】解:根据题意得:【解析】解:根据题意得:(509014040)50=+++¸32050=¸6.4=(小时). 故这50名学生这一周在校的平均体育锻炼时间是6.4小时.小时.【提示】根据加权平均数的计算公式列出算式5106157208()550´+´+´+´¸,再进行计算即可.,再进行计算即可. 【考点】加权平均数.【考点】加权平均数. 8.【答案】A【解析】解:作OC AP ^,如图,则1122AC AP x ==, 在Rt AOC △中,1OA =,2222111442OC OA AC x x =-=-=-, 所以211402()24y OC AP x x x ==-££g g ,所以y 与x 的函数关系的图像为A 选项.选项.【提示】作OC AP ^,根据垂径定理得1122AC AP x ==,再根据勾股定理可计算出2142OC x =-,然后根据三角形面积公式得到21402()4y x x x =-££g ,再根据解析式对四个图形进行判断.,再根据解析式对四个图形进行判断.【考点】动点问题的函数图像.【考点】动点问题的函数图像. 二、填空题9.【答案】2(2)a b -【解析】解:244ab ab a -+ 2(44)a b b =-+(提取公因式)(提取公因式) 2(2)a b =-(完全平方公式)(完全平方公式)【提示】先提取公因式a ,再根据完全平方公式进行二次分解.完全平方公式:2222()a ab b a b -+=- 【考点】提公因式法与公式法的综合运用.【考点】提公因式法与公式法的综合运用. 10.【答案】21x +【解析】解:抛物线21y x =+开口向上,且与y 轴的交点为(0,1). 【提示】根据二次函数的性质,开口向上,要求a 值大于0即可.即可. 【考点】二次函数的性质.【考点】二次函数的性质.11.【答案】20【考点】矩形的性质,三角形中位线定理.【考点】矩形的性质,三角形中位线定理.【提示】根据题意可知OM 是ADC △的中位线,所以OM 的长可求;根据勾股定理可求出AC 的长,利用直角三角形斜边上的中线等于斜边的一半可求出BO 的长,进而求出四边形ABOM 的周长.的周长. 【解析】解:∵O 是矩形ABCD 的对角线AC 的中点,M 是AD 的中点,的中点,∴112.522OM CD AB ===,∵5AB =,12AD =,∴2251213AC =+=,∵O 是矩形ABCD 的对角线AC 的中点,的中点, ∴16.52BO AC ==,∴四边形ABOM 的周长为56 6.5 2.520AB AM BO OM +++=+++=12.【答案】32-13- 0,1-【解析】解:当12a =时,1B 的纵坐标为12,1B 的纵坐标和2A 的纵坐标相同,的纵坐标相同, 则2A 的横坐标为232a =-,2A 的横坐标和2B 的横坐标相同,的横坐标相同,则2B 的纵坐标为223b =-,2B 的纵坐标和3A 的纵坐标相同,的纵坐标相同,则3A 的横坐标为313a =-,3A 的横坐标和3B 的横坐标相同,的横坐标相同,则3B 的纵坐标为33b =-,3B 的纵坐标和4A 的纵坐标相同,的纵坐标相同, 则4A 的横坐标为42a =,4A 的横坐标和4B 的横坐标相同,的横坐标相同,则4B 的纵坐标为412b =, 即当12a =时,232a =-,313a =-,42a =,532a =-,112b =,223b =-,33b =-,412b =,523b =-,∵20136713=,∴2013313a a ==-;点1A 不能在y 轴上(此时找不到1B ),即0x ¹,点1A 不能在x 轴上(此时2A ,在y 轴上,找不到2B ), 即10y x =--¹,解得:1x ¹-; 综上可得1a 不可取01-、【提示】求出2a ,3a ,4a ,5a 的值,可发现规律,继而得出2013a 的值,根据题意可得1A 不能在x 轴上,也不能在y 轴上,从而可得出1a 不可能取的值.不可能取的值. 【考点】反比例函数综合题.【考点】反比例函数综合题. 三、解答题 13.【答案】见解析【答案】见解析【解析】证明:∵DE AB ∥,∴CAB ADE Ð=Ð,∵在ABC △和DAE △中,CAB ADEAB DA B DAEÐ=Ðìï=íïÐ=Ðî, ∴()ABC DAE ASA △≌△,∴BC AE =.【提示】根据两直线平行,内错角相等求出CAB ADE Ð=Ð,然后利用“角边角”证明ABC △和DAE △全等,再根据全等三角形对应边相等证明即可.等,再根据全等三角形对应边相等证明即可. 【考点】全等三角形的判定与性质.【考点】全等三角形的判定与性质.14.【答案】5【解析】解:原式2122452=+-´+=【提示】分别进行零指数幂、绝对值、特殊角的三角函数值、负整数指数幂等运算,然后按照实数的运算法则计算即可.法则计算即可.【考点】实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值.【考点】实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值.15.【答案】115x -<<【解析】解:32123x x x x >-ìïí+>î①②,解不等式①得,1x >-,解不等式②得,15x <,所以,不等式组的解集是115x -<<. 【提示】先求出两个不等式的解集,再求其公共解.【提示】先求出两个不等式的解集,再求其公共解. 【考点】解一元一次不等式组.【考点】解一元一次不等式组. 16.【答案】12【解析】解:∵2410x x --=,即241x x -=,∴原式222222412931()29343912x x x y y x x x x =-+-+-=-+=-++= .【提示】原式利用完全平方公式及平方差公式化简,去括号合并得到最简结果,把已知等式变形后代入计算即可求出值.算即可求出值.【考点】整式的混合运算—化简求值.化简求值. 17.【答案】2.5平方米平方米【解析】解:设每人每小时的绿化面积x 平方米,由题意,得平方米,由题意,得 18018036(62)x x-=+,解得: 2.5x =经检验, 2.5x =是原方程的解,且符合题意.是原方程的解,且符合题意. 答:每人每小时的绿化面积2.5平方米.平方米.【提示】设每人每小时的绿化面积x 平方米,根据增加2人后完成的时间比原来的时间少3小时为等量关系建立方程求出其解即可.系建立方程求出其解即可. 【考点】分式方程的应用.【考点】分式方程的应用.18.【答案】(1)52k <(2)2【解析】解:(1)根据题意得:44(24)2080k k =--=->△,解得:52k <;(2)由k 为正整数,得到1k =或2,利用求根公式表示出方程的解为152x k =-±-, ∵方程的解为整数,∴52k -为完全平方数,则k 的值为2.【提示】(1)根据方程有两个不相等的实数根,得到根的判别式的值大于0列出关于k 的不等式,求出不等式的解集即可得到k 的范围;的范围;(2)找出k 范围中的整数解确定出k 的值,经检验即可得到满足题意k 的值.的值. 【考点】根的判别式,一元二次方程的解,解一元二次方程—公式法.公式法. 四、解答题19.【答案】(1)见解析)见解析 (2)13【解析】证明:(1)在ABCD Y 中,AD BC ∥,且AD BC =.∵F 是AD 的中点,∴12DF AD =.又∵12CE BC =,∴DF CE =,且DF CE ∥, ∴四边形CEDF 是平行四边形;是平行四边形;(2)解:如图,过点D 作DH BE ^于点H .在ABCD Y 中,∵60B Ð=°,∴60DCE Ð=°.∵4AB =,∴4CD AB ==,∴122CH CD ==,23DH =.在CEDF Y 中,132CE DF AD ===,则1EH = ∴在Rt DHE △中,根据勾股定理知2(23)113DE =+=.【提示】(1)由“平行四边形的对边平行且相等”的性质推知AD BC ∥,且AD BC =;然后根据中点的定义、结合已知条件推知四边形CEDF 的对边平行且相等(DF CE =,且DF CE ∥),即四边形CEDF 是平行四边形;行四边形;(2)如图,过点D 作DH BE ^于点H ,构造含30度角的直角DCH △和直角DHE △.通过解直角DCH △和在直角DHE △中运用勾股定理来求线段ED 的长度.的长度.【考点】平行四边形的判定与性质,含30度角的直角三角形,勾股定理.度角的直角三角形,勾股定理. 20.【答案】(1)见解析)见解析 (2)【解析】(1)证明:P A ,PC 与O e 分别相切于点A ,C ,∴APO EPD Ð=Ð且PA AO ^,∴90P AO Ð=°, ∵AOP EOD Ð=Ð,90PAO E Ð=Ð=°∴APO EDO Ð=Ð,∴EPD EDO Ð=Ð; (2)解:连接OC ,∴6P A PC ==,∵3tan 4PDA Ð=,∴在Rt P AD △中,8AD =,10PD =,∴4CD =,∵3tan 4PDA Ð=,∴在Rt OCD △中,3OC OA ==,5OD =, ∵EPD ODE Ð=Ð,∴DEP OED △∽△,∴2DP PE ED DO DE OE===,∴2DE OE =在Rt OED △中,222OE DE OD +=,即2255OE =,∴5OE =.【提示】(1)根据切线长定理和切线的性质即可证明:EPD EDO Ð=Ð;(2)连接OC ,利用3tan 4PDA Ð=,可求出4CD =,再证明OED DEP △∽△,根据相似三角形的性质和勾股定理即可求出OE 的长.的长.【考点】切线的性质,相似三角形的判定与性质.【考点】切线的性质,相似三角形的判定与性质. 21.【答案】(1)0.03 (2)见解析)见解析 (3)33.710´【解析】解:(1)∵月季园面积为0.04平方千米,月季园所占比例为20%,则牡丹园的面积为:0.0415%0.0320%´=(平方千米); (2)植物花园的总面积为:0.0420%0.2¸=(平方千米), 则第九届园博会会园区陆地面积为:0.218 3.6´=(平方千米), 第七、八界园博会的水面面积之和为:10.5 1.5+=(平方千米), 则第九届园博会水面面积为1.5平方千米,如图:平方千米,如图:(3)由图标可得,停车位数量与单日最多接待游客量成正比例关系,比值约为500,则第十届园博会大约需要设置的停车位数量约为:35007.4 3.710´»´.【提示】(1)根据月季园和牡丹园所占的比例求出牡丹园的面积即可;)根据月季园和牡丹园所占的比例求出牡丹园的面积即可;(2)先算出植物花园的总面积,然后可求出第九届园博会会园区陆地面积,根据图像求出第七、八界园博会的水面面积之和,补全条形统计图即可;会的水面面积之和,补全条形统计图即可;(3)根据图表所给的信息,求出停车位数量与单日最多接待游客量成正比例关系,算出比值,求出大约需要设置的停车位数量.要设置的停车位数量.【考点】条形统计图,用样本估计总体,统计表,扇形统计图.【考点】条形统计图,用样本估计总体,统计表,扇形统计图. 22.【答案】(1)a (2)2(3)23【解析】解:(1)四个等腰直角三角形的斜边长为a ,则斜边上的高为12a ,每个等腰直角三角形的面积为:2111224a a a =g ,则拼成的新正方形面积为:22144a a ´=,即与原正方形ABCD 面积相等,∴这个新正方形的边长为a ;(2)∵四个等腰直角三角形的面积和为2a ,正方形ABCD 的面积为2a ,∴2144122ARE DWH GCT SBF AREMNPQ S S S S S S =+++==´´=△△△△△正方形; (3)如答图1所示,分别延长RD ,QF ,PE ,交F A ,EC ,DB 的延长线于点S ,T ,W .由题意易得:RSF △,QET △,PDW △均为底角是30°的等腰三角形,其底边长均等于ABC △的边长. 不妨设等边三角形边长为a ,则SF AC A ==. 如答图2所示,过点R 作RM SF ^于点M ,则1122MF SF a ==,在Rt RMF △中,133tan30236RM MF a a =°=´=g ,∴21332612RSFSa a a ==g △ 过点A 作AN SD ^于点N ,设AD AS x ==,则1sin302AN AD x =°=g ,22cos303SD ND AD x ==°=,∴2111332224ADS S SD AN x x x ===g g g △ ∵三个等腰三角形RSF △,QET △,PDW △的面积和223333124RSF S a a ==´=△,∴3RPQ ADS CFT BEW ADSS S S S S =++=△△△△△,∴233334x =´,得249x =,解得23x =或23x =-(不合题意,舍去)舍去)∴23x =,即AD 的长为23.【考点】四边形综合题.【考点】四边形综合题.【提示】(1)四个等腰直角三角形的斜边长为a ,其拼成的正方形面积为2a ,边长为a ;(2)如题图2所示,正方形MNPQ 的面积等于四个虚线小等腰直角三角形的面积之和,据此求出正方形MNPQ 的面积;的面积;(3)参照小明的解题思路,对问题做同样的等积变换.)参照小明的解题思路,对问题做同样的等积变换.如答图1所示,三个等腰三角形RSF △,QET △,PDW △的面积和等于等边三角形ABC △的面积,的面积,故阴影三角形PQR △的面积等于三个虚线等腰三角形的面积之和.据此列方程求出AD 的长度.的长度. 五、解答题23.【答案】(1)(0,2)A -(1,0)B(2)22y x =-+; (3)2242y x x =--【解析】解:(1)当0x =时,2y =-,∴(0,2)A -,抛物线的对称轴为直线212m x m-=-=,∴(1,0)B ;(2)易得A 点关于对称轴直线1x =的对称点(2,2)A ¢-,则直线l 经过A ¢、B ,设直线l 的解析式为(0,)y kx b k =+¹,则220k b k b +=-ìí+=î,解得22k b =-ìí=î,所以,直线l 的解析式为22y x =-+; (3)∵抛物线的对称轴为直线1x =,∴抛物线在23x <<这一段与在10x -<<这一段关于对称轴对称,结合图像可以观察到抛物线在21x -<<-这一段位于直线l 的上方,在10x -<<这一段位于直线l 的下方,的下方, ∴抛物线与直线l 的交点的横坐标为1-,当1x =-时,2(1)24y =-´-+=,所以,抛物线过点(1,4)-,当1x =-时,224m m +-=,解得2m =,∴抛物线的解析式为2242y x x =--【提示】(1)令0x =求出y 的值,即可得到点A 的坐标,求出对称轴解析式,即可得到点B 的坐标;的坐标; (2)求出点A 关于对称轴的对称点(2,2)-,然后设直线l 的解析式为()0y kx b k =+¹,利用待定系数法求一次函数解析式解答即可;一次函数解析式解答即可;(3)根据二次函数的对称性判断在23x <<这一段与在10x -<<这一段关于对称轴对称,然后判断出抛物线与直线l 的交点的横坐标为1-,代入直线l 求出交点坐标,然后代入抛物线求出m 的值即可得到抛物线解析式.解析式.【考点】二次函数的性质,一次函数图像与几何变换,二次函数图像上点的坐标特征.24.【答案】(1)1302ABD a Ð=°-(2)见解析)见解析(3)30a =°【解析】(1)解:∵AB AC =,A a Ð=,∴ABC ACB Ð=Ð,180ABC ACB A Ð+Ð=°-Ð, ∴1118(92)002ABC ACB A a Ð=Ð=°-Ð=°-, ∵ABD ABC DBC Ð=Ð-Ð,60DBC Ð=°,即1302ABD a Ð=°-;(2)ABE △是等边三角形,证明:连接AD ,CD ,ED ,∵线段BC 绕B 逆时针旋转60°得到线段BD ,则BC BD =,60DBC Ð=°,∵60ABE Ð=°,∴160302ABD DBE EBC a Ð=°-Ð=Ð=°-, 且BCD △为等边三角形,在ABD △与ACD △中AB AC AD AD BD CD=ìï=íï=î∴()ABD ACD SSS △≌△,∴1122BAD CAD BAC a Ð=Ð=Ð=,∵150BCE Ð=°, ∴111803015022BEC BAD a a æöç÷èÐ=°-°--°==Ðø,在ABD △和EBC △中BEC BAD EBC ABD BC BDÐ=ÐìïÐ=Ðíï=î ∴()ABD EBC AAS △≌△,∴AB BE =,∴ABE △是等边三角形;是等边三角形;(3)解:∵60BCD Ð=°,150BCE Ð=°,∴1506090DCE Ð=°-°=°,∵45DEC Ð=°,∴DEC △为等腰直角三角形,∴DC CE BC ==,∵150BCE Ð=°,∴1(180150)152EBC Ð=°-°=°, ∵130152EBC a Ð=°-=°,∴30a =°.【提示】(1)求出ABC Ð的度数,即可求出答案;的度数,即可求出答案;(2)连接AD ,CD ,ED ,根据旋转性质得出BC BD =,60DBC Ð=°,求出1302ABD EBC a Ð=Ð=°-,且BCD △为等边三角形,证ABD ACD △≌△, 推出1122BAD CAD BAC a Ð=Ð=Ð=,求出12BEC BAD a Ð==Ð,证ABD EBC △≌△,推出AB BE =即可;可;(3)求出90DCE Ð=°,DEC △为等腰直角三角形,推出DC CE BC ==,求出15EBC Ð=°, 得出方程130152a °-=°,求出即可.,求出即可. 【考点】全等三角形的判定与性质,等边三角形的性质,等腰直角三角形,旋转的性质.25.【答案】(1)①,D E②03m ££(2)1r ³【解析】解:(1)①如图1所示,过点E 作O 的切线设切点为R ,∵O e 的半径为1,∴1RO =,∵2EO =,∴∠30OER =°,根据切线长定理得出O e 的左侧还有一个切点,使得组成的角等于30°,∴E 点是O e 的关联点,的关联点,∵11,22D æöç÷èø,(0,2)E -,()23,0F ,∴OF EO >,DO EO <,∴D 点一定是O e 的关联点,而在O e 上不可能找到两点与点F 的连线的夹角等于60°,故在点D .E 、F 中,O e 的关联点是,D E ;②如图2,由题意可知,若P 要刚好是C e 的关联点,需要点P 到C e 的两条切线P A 和PB 之间所夹的角为60°,由图2可知60APB Ð=°,则30CPB Ð=°,连接BC ,则22sin BC PC BC r CPB===Ð,∴若P 点为C e 的关联点,则需点P 到圆心的距离d 满足02d r ££;由上述证明可知,考虑临界点位置的P 点,如图3,点1P 到原点的距离1212OP =´=,过点O 作直线l 的垂线OH ,垂足为H ,23tan 32FO OGF OG Ð===,∴60OGF Ð=°,∴sin 603OH OG =°=; 13sin 2OH OPH OP Ð==,∴160OPH Ð=°,可得点1P 与点G 重合,过点2P 作2P M x ^轴于点M ,可得230P OM Ð=°,∴2cos303OM OP =°=,从而若点P 为O e 的关联点,则P 点必在线段12P P 上,∴03m ££;(2)若线段EF 上的所有点都是某个圆的关联点,欲使这个圆的半径最小,则这个圆的圆心应在线段EF 的中点;的中点;考虑临界情况,如图4,即恰好E 、F 点为K e 的关联时,则1222KF KN EF ===,此时,1r =,故若线段EF 上的所有点都是某个圆的关联点,这个圆的半径r 的取值范围为1r ³.【提示】(1)①根据关联点的定义得出E 点是O e 的关联点,进而得出F 、D ,与O e 的关系;的关系;②若P 要刚好是⊙C 的关联点,需要点P 到C e 的两条切线P A 和PB 之间所夹的角为60°,进而得出PC 的长,进而得出点P 到圆心的距离d 满足02d r ££,再考虑临界点位置的P 点,进而得出m 的取值范围;的取值范围;(2)若线段EF 上的所有点都是某个圆的关联点,欲使这个圆的半径最小,则这个圆的圆心应在线段EF 的中点;再考虑临界情况,即恰好E 、F 点为K 的关联时,则1222KF KN EF ===,即可得出圆的半径r 的取值范围.的取值范围.【考点】圆的综合题.【考点】圆的综合题.。
2013年九年级上册期中数学试卷(含答案)
2013年九年级上册期中数学试卷(含答案)吉林长春二中13—14学年九年级上学期期中试卷—数学(120分钟;满分120分)一,选择题(每小题2分,共16分)1.下列图形既是轴对称图形,又是中心对称图形的是()2下列各式是二次根式的是()3化简的结果是()A.10B.2C.4D.204.一元二次方程3x2-x=0的解是()A.x=0B.x1=0,x2=3C.x1=0,x2=D.x=5.用配方法解方程x2-2x-5=0时,原方程应变形为()A.(x+1)2=6B.(x-1)2=6C.(x+2)2=9D.(x-2)2=96.如图,在ΔABC中,∠CAB=70º,在同一平面内,将ΔABC绕点A旋转到ΔAB'C'的位置,使得CC'∥AB,则∠BAB'等于()A.30ºB.35ºC.40ºD.50º6题图7题图8题图7.如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC 的度数是()A.35°B.55°C.65°D.70°8.将5个边长都为2㎝的正方形按如图所示的样子摆放,点A.B.C.D.分别是四个正方形的中心,则图中四块阴影部分的面积的和为().A.2B.4C.6D.8填空题(每小题3分,共24分)9.当x_____时,二次根式有意义10.计算:+=_____.11.请你写出一个有一根为2的一元二次方程:______12.如果关于Χ的方程Χ-4Χ+Κ=0(Κ为常数)有两个相等的实数根,那么Κ=__13..三角形两边长是3和4,第三边的长是方程-12+35=0的根,则该三角形的周长为.14.如图,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD、CB的延长线相交于点P,则∠P=.15.当x_____时,2=1-2x16.如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CAB=15°,则CD的长为.三,(每小题6分,共36分)17.计算.18.解方程:x(x-2)+x-2=0(1+)(1-)(+1)(-1)19.若+2=0求a2011b2013的值20.如图,在4×4正方形网格中,请你在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形.21.已知关于x的一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,求a的取值范围.四(每小题8分,共16分)22先化简再求值.,其中=+123某厂2011年投入600万元用于研制新产品的开发,计划以后每年以相同的增长率投资,2013年投入1176万元用于研制新产品的开发。
北京市第三十一中学2019-2020学年九年级上学期期中数学试题(学生版)
18.已知:二次函数 y = ax2 + bx + c(a 0) 中的 x 和 y 满足下表:
x
0
1
2
3
4
5
y
3
0
−1
0
m
8
]
(1)请直接写出 m 的值为_________. (2)求出这个二次函数的解析式.
(3)当 0 x 3 时,则 y 的取值范围为______________________________.
19.已知二次函数 y= x2-4x+3.
(1)把这个二次函数化成 y = a(x − h)2 + k 的形式并写出抛物线的顶点坐标;
(2)画出这个二次函数的图象,并利用图象直接写出当 y>0 时,x 的取值范围. 当 x 取何值时,y 随 x 的 增大而减小;
(3)若抛物线与 x 轴的交点记为 A,B,该图象上存在一点 C,且△ABC 的面积为 3,求点 C 的坐标.
1
3
y
﹣1
3
5
3
下列结论:(1)ac<0; (2)抛物线顶点坐标为(1,5); (3)3 是方程 ax2+(b﹣1)x+c=0 的一个根; (4)当﹣1<x<3 时,ax2+(b﹣1)x+c>0.其中正确的序号为___________________.
三、解答题(本题共 68 分,17-25 题其中 18 题 6 分,19 题 7 分,其余各题每小题各 5 分;26 题 6 分,27、28 题每题 7 分 ) 17.如图,AB 是⊙O 的直径,PA,PC 分别与⊙O 相切于点 A,点 C,若∠P=60°,PA= 3 ,求 AB 的长.
11.为拉动内需促进消费,某品牌的电视机经过两次降价,从原来每台 6000 元降到现在的每台 4860 元,求 平均每次的降价率是多少?设每次降价率为 x,由题意列方程为_____________________________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 精心选一选(每题4分,共32分)1.下列图形中,是中心对称图形,但不是轴对称图形的是( )2. 若两圆的半径分别是2cm 和3cm ,圆心距为5cm ,则这两圆的位置关系是( )A . 内切B .相交C .外切D .外离 3.正三角形的高、外接圆半径、边心距之比为( )A.3∶2∶1B.4∶3∶2C.4∶2∶1D.6∶4∶3 4.若圆锥的侧面展开图是一个半径为a 的半圆,则圆锥的高为( )A.aB.33a C.3a D.23a5.如图,□ABCD 中,EF∥AB,DE∶EA = 2∶3,EF = 4,则CD 的长为( ) A .163B .8C .10D .167.如图所示,实线部分是半径为9的两条等弧组成的游泳池,若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长为( )A .12mB .18mC .20mD .24m 第7题二、填空题(共4道小题,每小题4分,共16分) 9.如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC 与△A 1B 1C 1是位似图形,且顶点都在格点上,则位似中心的坐标是___________.10. 如图,PA ,PB 是⊙O 是切线,A ,B 为切点, AC 是⊙O 的直径,若∠BAC=25°,则∠P= _度.11.如图,正方形ABCD 的边长为2,AE=EB ,MN=1,线段MN 的两端在CB 、CD 上滑动,当CM=时,ΔAED 与N ,M ,C 为顶点的三角形相似. 12. 如图,n +1个边长为2的等边三角形有一条边在同一直线上,设△211B D C 的面积为1S ,△322B D C 的面积为2S ,…,△1n n n B D C +的面积为n S ,则2S = ;n S =____ (用含n 的式子表示).三、解答题(本题共28分) 13.(本题5分)计算:2cos60tan 45sin 45sin30︒-︒+︒︒14.(本题4分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC 的顶点均在格点上,O 、M 也在格点上.(1)画出△ABC 关于直线OM 对称的△A 1B 1C 1; (2)画出△ABC 绕点O 按顺时针方向旋转90°后所得的△A 2B 2C 2;(3)△A 1B 1C 1与△A 2B 2C 2组成的图形是轴对称图形吗?如果是轴对称图形,请画出对称轴.15.(本题5分)如图,在平行四边形ABCD 中,过点A 作AE ⊥BC,垂足为E ,连接DE ,F 为线段DE 上一点,且∠AFE=∠B.(1) 求证:△ADF∽△DEC;(2) 若AB =4,AD =33,AE =3,求ED ,AF 的长.16.(本题5分)如图,在△ABC 中,AB =AC ,以AB 为直径的⊙O 分别交BC 、AC 于点D 、E ,连结EB 交OD 于点F . (1)求证:OD ⊥BE ;(2)若DE =25,AB =25,求AE 的长.17. (本题5分)如图,Rt△ABC 的斜边AB=4,O 是AB 的中点,以O 为圆心的半圆分别与两直角边相切于点D 、E , (1)求证∠A=∠B.(2)求图中阴影部分的面积.18.(本题4分)已知:如图,∠MAN =45°,B 为AM 上的一个定点, 若点P 在射线AN 上,以P 为圆心,PA 为半径的圆与射线AN 的另一个交点为C ,请确定⊙P 的位置,使BC 恰与⊙P 相切.(1)画出图形(不要求尺规作图,不要求写画法); (2)连结BP 并填空:① ∠ABC = °;② 比较大小:∠ABP ∠CBP . (用“>”、“<”或“=”连接)四、解答题(本题共23分)19.(本题6分)如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB 的高度,他发现当斜坡正对着太阳时,旗杆AB 的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC =20米,斜坡坡面上的影长CD =8米,太阳光线AD 与水平地面成30°角,斜坡CD 与水平地面BC 成30°的角,求旗杆AB 的高度(结果保留根号).20.(本题6分)已知:如图,等腰△ABC 中,AB= BC ,AE ⊥BC 于E , EF ⊥AB 于F ,4cos 5AEF ∠=, (1)当BE=4时,求EF长.(2)若CE=2求EF 的长.21.(本题6分)已知:如图,在△ABC 中,点D 在AC 上,点E 在CB的延长线上,且AD=BE ,求证:BCACFD EF =.22. (本题5分)阅读下列材料:问题:如图1,在正方形ABCD 内有一点P ,PA =5,PB =2,PC =1,求∠BPC 的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.请你参考小明同学的思路,解决下列问题:(1) 图2中∠BPC的度数为;(2) 如图3,若在正六边形ABCDEF内有一点P,且PA=132,PB=4,PC=2,则∠BPC的度数为,正六边形ABCDEF的边长为.五、解答题(本题共21分,每题7分)23.如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB 相交于点P,线段EF与射线CA相交于点Q.(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=92a时,P、Q两点间的距离 (用含a的代数式表示).25.已知:AOB △中,2AB OB ==,COD △中,3CD OC ==,ABO DCO =∠∠. 连接AD 、BC ,点M 、N 、P 分别为OA 、OD 、BC 的中点.图1 图2(1) 如图1,若A 、O 、C 三点在同一直线上,且60ABO =∠,则PMN △的形状是__________,此时ADBC=________; (2) 如图2,若A 、O 、C 三点在同一直线上,且2ABO α=∠,证明PMN BAO △∽△,并计算ADBC的值(用含α的式子表示); (3) 在图2中,固定AOB △,将COD △绕点O 旋转,直接写出PM 的最大值.北京市三十一中学2012–2013学年度第一学期 初三年级数学期中答案14.(1)——————1` (2)——————2` (3)——————4`15.(1)——————2` (3)求出ED=6 ——————3`,求出AF=32————6` 16.(1)连结AD 证出OD ⊥BE-----2分 (2)证出△CED ∽△EBA--------3分 求出CE=1-------4分 求出AE=1.5--------5分 17、(1)连结OD 、OE------------1分证出∠A=∠B------------2分 (2)求出扇形半径------------3分S 阴=2-2------------6分18.解:(1)图形见右. - - - - - - - - - - - - - - - - - - 2分(2)① ∠ABC = 45 °;- - - - - - -3分② ∠ABP < ∠CBP . - - - - - - 4分 19、画出求法示意图------------1分求出CE=34------------2分求出BF=20+38(或DF=20+34)-----------4分求出AB=83320 -----------6分21.辅助线 ;………………………………………………………………………… 1分 转化一组比;………………………………………………………………………… 2分 转化二组比 ;………………………………………………………………………… 3分 等量代换 ;………………………………………………………………………… 4分 答案 ;………………………………………………………………………… 5分23:(1)证明:∵△ABC 是等腰直角三角形, ∴∠B=∠C=45°,AB=AC , ∵AP=AQ , ∴BP=CQ ,∵E 是BC 的中点, ∴BE=CE ,在△BPE 和△CQE 中, ∵,∴△BPE ≌△CQE (SAS );……………………………………………… 2分 (2)解:∵△ABC 和△DEF 是两个全等的等腰直角三角形, ∴∠B=∠C=∠DEF=45°, ∵∠BEQ=∠EQC+∠C ,即∠BEP+∠DEF=∠EQC+∠C , ∴∠BEP+45°=∠EQC+45°, ∴∠BEP=∠EQC ,∴△BPE ∽△CEQ ,……………………………………………… 4分 ∴,∵BP=a ,CQ=a ,BE=CE , ∴BE=CE=a ,∴BC=3a ,∴AB=AC=BC •sin45°=3a ,∴AQ=CQ ﹣AC=a ,PA=AB ﹣BP=2a , 连接PQ ,在Rt △APQ 中,PQ==a .……………………………………………… 7分25. 解:(1)等边三角形,1;(每空1分) ------------------------2分(2)证明:连接BM 、CN .由题意,得BM OA ⊥,CN OD ⊥,α-︒=∠=∠90COD AOB . ∵ A 、O 、C 三点在同一直线上, ∴ B 、O 、D 三点在同一直线上.∴ 90BMC CNB ==∠∠. ∵ P 为BC 中点,∴ 在Rt △BMC 中,BC PM 21=.在Rt △BNC 中,BC PN 21=. ∴ PN PM =.---------------------------3分 ∴ B 、C 、N 、M 四点都在以P 为圆心,12BC 为半径的圆上. ∴ 2MPN MBN =∠∠.又∵ α=∠=∠ABO MBN 21, ∴ MPN ABO =∠∠.∴ PMN BAO △∽△. ----------------------------------4分∴ BAAO PM MN =. 由题意,12MN AD =,又BC PM 21=.。
