万向传动轴径向全跳动计算
传动轴的设计及校核

第一章轻型货车原始数据及设计要求发动机的输出扭矩:最大扭矩285.0N·m/2000r/min;轴距:3300mm;变速器传动比: 五挡1 ,一挡7.31,轮距:前轮1440毫米,后轮1395毫米,载重量2500千克设计要求:第二章万向传动轴的结构特点及基本要求万向传动轴一般是由万向节、传动轴和中间支承组成。
主要用于在工作过程中相对位置不节组成。
伸缩套能自动调节变速器与驱动桥之间距离的变化。
万向节是保证变速器输出轴与驱动桥输入轴两轴线夹角的变化,并实现两轴的等角速传动。
一般万向节由十字轴、十字轴承和凸缘叉等组成。
传动轴是一个高转速、少支承的旋转体,因断改变的两根轴间传递转矩和旋转运动。
重型载货汽车根据驱动形式的不同选择不同型式的传动轴。
一般来讲4×2驱动形式的汽车仅有一根主传动轴。
6×4驱动形式的汽车有中间传动轴、主传动轴和中、后桥传动轴。
6×6驱动形式的汽车不仅有中间传动轴、主传动轴和中、后桥传动轴,而且还有前桥驱动传动轴。
在长轴距车辆的中间传动轴一般设有传动轴中间支承.它是由支承架、轴承和橡胶支承组成。
传动轴是由轴管、伸缩套和万向此它的动平衡是至关重要的。
一般传动轴在出厂前都要进行动平衡试验,并在平衡机上进行了调整。
因此,一组传动轴是配套出厂的,在使用中就应特别注意。
图 2-1 万向传动装置的工作原理及功用图 2-2 变速器与驱动桥之间的万向传动装置基本要求:1.保证所连接的两根轴相对位置在预计范围内变动时,能可靠地传递动力。
2.保证所连接两轴尽可能等速运转。
3.由于万向节夹角而产生的附加载荷、振动和噪声应在允许范围内。
4.传动效率高,使用寿命长,结构简单,制造方便,维修容易等第三章轻型货车万向传动轴结构分析及选型由于货车轴距不算太长,且载重量2.5吨属轻型货车,所以不选中间支承,只选用一根主传动轴,货车发动机一般为前置后驱,由于悬架不断变形,变速器或分动器输出轴轴线之间的相对位置经常变化,根据货车的总体布置要求,将离合器与变速器、变速器与分动器之间拉开一段距离,考虑到它们之间很难保证轴与轴同心及车架的变形,所以采用十字轴万向传动轴,为了避免运动干涉,在传动轴中设有由滑动叉和花键轴组成的伸缩节,以实现传动轴长度的变化。
万向联轴节设计计算
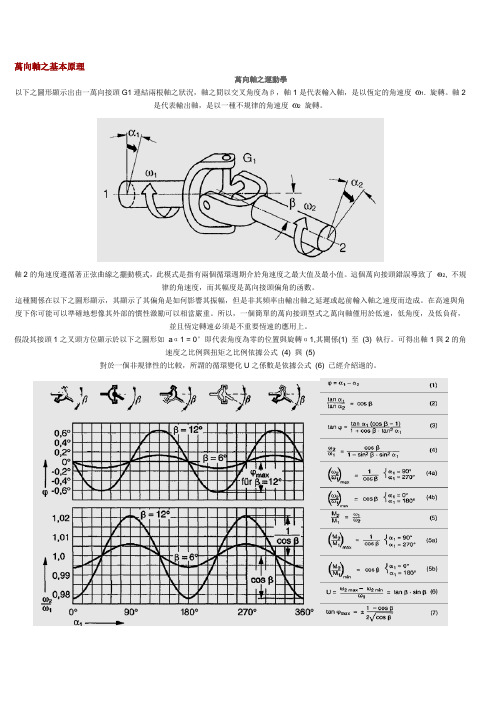
萬向軸之基本原理萬向軸之運動學以下之圖形顯示出由一萬向接頭G1連結兩根軸之狀況,軸之間以交叉角度為β,軸1是代表輸入軸,是以恆定的角速度1. 旋轉。
軸2是代表輸出軸,是以一種不規律的角速度2旋轉。
軸2的角速度遵循著正弦曲線之擺動模式,此模式是指有兩個循環週期介於角速度之最大值及最小值。
這個萬向接頭錯誤導致了2, 不規律的角速度,而其幅度是萬向接頭偏角的函數。
這種關係在以下之圖形顯示,其顯示了其偏角是如何影響其振幅,但是非其頻率由輸出軸之延遲或起前輸入軸之速度而造成。
在高速與角度下你可能可以準確地想像其外部的慣性激勵可以相當嚴重。
所以,一個簡單的萬向接頭型式之萬向軸僅用於低速,低角度,及低負荷,並且恆定轉速必須是不重要恆速的應用上。
假設其接頭1之叉頭方位顯示於以下之圖形如aα1 = 0°即代表角度為零的位置與旋轉α1,其關係(1) 至(3) 執行。
可得出軸1與2的角速度之比例與扭矩之比例依據公式(4) 與(5)對於一個非規律性的比較,所謂的循環變化U之係數是依據公式(6) 已經介紹過的。
雙萬向接頭上一段落解釋一個卡登式萬向接頭之運動學以及其如何產生非規律之角速,當它在一偏角工作時。
然而,假如兩個萬向軸我佈置如以下之方式,如圖中的Z或W模式,所以接頭之角度β1等於β2,其外部軸將會是規律的速度。
第二個接頭G2產生非規律性之速度相同且相反於G1,造成相消之效果。
再者,內部1與外部3將會以同週期旋轉,但是中央部分2將會以非恆速旋轉。
軸部分1與3的同步旋轉,在下列情形時可得到保證。
a. 萬向接軸的所有部分需在同一平面上b. 中央部分的內叉頭需位於同一平面上c. 其工作角度β1與β2需相同a)b)c)滿足以上之三個條件可保證其第二個接頭以正弦波模式並與第一個接頭有90度的偏差,所以這代表著完美的相消。
這個理想的調整被稱為一種〝相位〞而且是其主要之目標。
若無法滿足三條件其中之一項將會導致傳動軸無法同步地運行。
轴向移动计算公式

轴向移动计算公式轴向移动在机械工程、物理学等领域中可是个相当重要的概念呢!咱们先来说说啥是轴向移动。
简单来讲,轴向移动就是沿着轴的方向发生的位置变化。
那轴向移动计算公式是咋来的呢?这就得从一些基础的物理原理说起啦。
想象一下,你有一根长长的杆子,就像那种晾衣服的杆子,然后你推动它沿着杆子的长度方向移动,这就是轴向移动。
在实际应用中,比如汽车发动机里的活塞运动,就是一种典型的轴向移动。
活塞在气缸内上下往复运动,这个运动的距离和速度就得通过轴向移动计算公式来算。
举个例子吧,我曾经在一家汽车修理厂工作过,当时有一辆车发动机出了问题,动力不足。
师傅带着我们几个徒弟一起排查,最后发现是活塞的轴向移动出现了异常。
这可把我们急坏了,因为要修好它,就得准确算出活塞的轴向移动数据。
我们拿着工具,仔细测量活塞的行程、缸径等数据,然后运用轴向移动计算公式来分析。
那时候,满手都是油污,心里还特别紧张,就怕算错了,修不好这发动机。
说到这计算公式,它通常会涉及到一些关键的参数,比如移动的距离、时间、速度等等。
比如说,速度等于移动的距离除以时间。
如果已知移动的距离是 10 米,时间是 5 秒,那速度就是 10÷5 = 2 米每秒。
再复杂一点,要是考虑到加速度的话,那就得用到更高级的公式啦。
加速度等于速度的变化量除以时间。
假设一开始速度是 1 米每秒,经过 3 秒变成了 7 米每秒,那加速度就是(7 - 1)÷ 3 = 2 米每二次方秒。
在机械设计中,准确计算轴向移动至关重要。
要是算错了,零件可能就装不上,或者装上了也没法正常工作。
我还记得有一次,厂里接到一个新的订单,要设计一个特殊的传动轴,这传动轴的轴向移动要求特别精确。
我们几个设计师可真是绞尽脑汁,反复计算、验证,生怕出一点差错。
对于学习物理或者工程的同学们来说,掌握轴向移动计算公式那是必须的。
可别觉得这些公式枯燥,它们可是能解决很多实际问题的好帮手。
总之,轴向移动计算公式虽然看起来有点复杂,但只要用心去理解,多做一些实际的例子,就能掌握好它,让它为我们的工作和学习服务。
传动轴的设计及校核

第一章轻型货车原始数据及设计要求发动机的输出扭矩:最大扭矩·m/2000r/min;轴距:3300mm;变速器传动比: 五挡1 ,一挡,轮距:前轮1440毫米,后轮1395毫米,载重量2500千克设计要求:第二章万向传动轴的结构特点及基本要求万向传动轴一般是由万向节、传动轴和中间支承组成。
主要用于在工作过程中相对位置不节组成。
伸缩套能自动调节变速器与驱动桥之间距离的变化。
万向节是保证变速器输出轴与驱动桥输入轴两轴线夹角的变化,并实现两轴的等角速传动。
一般万向节由十字轴、十字轴承和凸缘叉等组成。
传动轴是一个高转速、少支承的旋转体,因断改变的两根轴间传递转矩和旋转运动。
重型载货汽车根据驱动形式的不同选择不同型式的传动轴。
一般来讲4×2驱动形式的汽车仅有一根主传动轴。
6×4驱动形式的汽车有中间传动轴、主传动轴和中、后桥传动轴。
6×6驱动形式的汽车不仅有中间传动轴、主传动轴和中、后桥传动轴,而且还有前桥驱动传动轴。
在长轴距车辆的中间传动轴一般设有传动轴中间支承.它是由支承架、轴承和橡胶支承组成。
传动轴是由轴管、伸缩套和万向此它的动平衡是至关重要的。
一般传动轴在出厂前都要进行动平衡试验,并在平衡机上进行了调整。
因此,一组传动轴是配套出厂的,在使用中就应特别注意。
图 2-1 万向传动装置的工作原理及功用图 2-2 变速器与驱动桥之间的万向传动装置基本要求:1.保证所连接的两根轴相对位置在预计范围内变动时,能可靠地传递动力。
2.保证所连接两轴尽可能等速运转。
3.由于万向节夹角而产生的附加载荷、振动和噪声应在允许范围内。
4.传动效率高,使用寿命长,结构简单,制造方便,维修容易等第三章轻型货车万向传动轴结构分析及选型由于货车轴距不算太长,且载重量吨属轻型货车,所以不选中间支承,只选用一根主传动轴,货车发动机一般为前置后驱,由于悬架不断变形,变速器或分动器输出轴轴线之间的相对位置经常变化,根据货车的总体布置要求,将离合器与变速器、变速器与分动器之间拉开一段距离,考虑到它们之间很难保证轴与轴同心及车架的变形,所以采用十字轴万向传动轴,为了避免运动干涉,在传动轴中设有由滑动叉和花键轴组成的伸缩节,以实现传动轴长度的变化。
万向联轴节设计计算

萬向軸之基本原理萬向軸之運動學以下之圖形顯示出由一萬向接頭G1連結兩根軸之狀況,軸之間以交叉角度為β,軸1是代表輸入軸,是以恆定的角速度1. 旋轉。
軸2是代表輸出軸,是以一種不規律的角速度2旋轉。
軸2的角速度遵循著正弦曲線之擺動模式,此模式是指有兩個循環週期介於角速度之最大值及最小值。
這個萬向接頭錯誤導致了2, 不規律的角速度,而其幅度是萬向接頭偏角的函數。
這種關係在以下之圖形顯示,其顯示了其偏角是如何影響其振幅,但是非其頻率由輸出軸之延遲或起前輸入軸之速度而造成。
在高速與角度下你可能可以準確地想像其外部的慣性激勵可以相當嚴重。
所以,一個簡單的萬向接頭型式之萬向軸僅用於低速,低角度,及低負荷,並且恆定轉速必須是不重要恆速的應用上。
假設其接頭1之叉頭方位顯示於以下之圖形如aα1 = 0°即代表角度為零的位置與旋轉α1,其關係(1) 至(3) 執行。
可得出軸1與2的角速度之比例與扭矩之比例依據公式(4) 與(5)對於一個非規律性的比較,所謂的循環變化U之係數是依據公式(6) 已經介紹過的。
雙萬向接頭上一段落解釋一個卡登式萬向接頭之運動學以及其如何產生非規律之角速,當它在一偏角工作時。
然而,假如兩個萬向軸我佈置如以下之方式,如圖中的Z或W模式,所以接頭之角度β1等於β2,其外部軸將會是規律的速度。
第二個接頭G2產生非規律性之速度相同且相反於G1,造成相消之效果。
再者,內部1與外部3將會以同週期旋轉,但是中央部分2將會以非恆速旋轉。
軸部分1與3的同步旋轉,在下列情形時可得到保證。
a. 萬向接軸的所有部分需在同一平面上b. 中央部分的內叉頭需位於同一平面上c. 其工作角度β1與β2需相同a)b)c)滿足以上之三個條件可保證其第二個接頭以正弦波模式並與第一個接頭有90度的偏差,所以這代表著完美的相消。
這個理想的調整被稱為一種〝相位〞而且是其主要之目標。
若無法滿足三條件其中之一項將會導致傳動軸無法同步地運行。
万向联轴节的运动学及受力分析计算

万向联轴节的运动学及受力分析计算万向联轴节的运动学及受力分析计算是一种比较复杂的主题,在机械设计工程中受到广泛的应用。
广泛应用于机械系统中的联轴节是用来连接多个机械元件,它使得它们能够以万向运动及多种方向受力,以在机械系统中承受运动及载荷。
因此,通过对万向联轴节的运动学及受力分析计算可以有效地分析设计机械系统中的运动及载荷,确保其安全可靠性。
首先,在研究万向联轴节的运动学及受力分析计算时,需要确定联轴节的受力方向及大小,并结合机械系统的运动来分析其受力情况。
根据设计分析,可以设定联轴节的受力方向,也可以分析出它们在不同方向上受力的大小,以及对以联轴节构成的机械系统的运动及载荷的影响。
其次,在研究万向联轴节的运动学及受力分析计算时,可以建立数学模型,并用数值分析的方法来研究联轴节的运动及受力特性。
首先,选取合适的数学模型描述联轴节和机械系统的运动特性,其中可以使用齿轮模型、滑轮模型等来描述联轴节的运动特性。
然后,根据该模型,可以计算联轴节受力的大小以及受力方向,为此,可以使用有限元分析法来计算联轴节的受力情况。
此外,在研究万向联轴节的运动学及受力分析计算时,还可以使用实验方法对联轴节的运动及受力情况进行实验测量,以分析联轴节的运动及受力行为。
在实验测量中,可以使用诸如磁控滑移测量器、回转角百分表、压力表等传感器来直接测量联轴节的运动及受力特性,找出运动及受力的数字化分布,以获得更准确的结果。
最后,在研究万向联轴节的运动学及受力分析计算时,也可以使用计算机辅助设计(CAD)来进行运动及受力分析,以实现更加精确及快速的计算,而不需要过多的计算量。
通过CAD分析,可以进行三维结构建模,并利用有限元分析法来研究联轴节的运动及受力分布,根据计算结果可以对联轴节的结构及受力特性做出相应的调整,以提高机械系统的整体性能。
综上所述,万向联轴节的运动学及受力分析计算是一种比较复杂的主题,为了确保机械系统的安全可靠性,需要深入分析联轴节的运动及受力特性。
万向联轴器计算范文

万向联轴器计算范文万向联轴器是一种广泛应用于机械传动系统中的装置,其作用是传递动力和扭矩,并且能够允许轴的非对齐。
它常用于传输轴与轴之间具有一定角度偏差或轴之间需要具有其中一种相对移动的情况。
万向联轴器可以分为机械式、弹性式和液体式三种类型。
本文将围绕着如何计算万向联轴器进行详细阐述。
首先,我们来讨论机械式万向联轴器的计算。
机械式万向联轴器可以根据其结构形式分为十字轴和万向节两种。
我们以十字轴为例进行计算。
十字轴万向联轴器的计算需要考虑以下几个参数:传动扭矩、角度偏差、轴的径向间隙和结构材料的承载能力。
1.传动扭矩的计算:传动扭矩是指通过万向联轴器传递到接收端的扭矩。
传动扭矩的计算公式为:传动扭矩=引起扭矩的力x传动杆长x传动杆倾角。
2.角度偏差的计算:角度偏差是指传动轴与被传动轴之间的夹角。
角度偏差的计算公式为:角度偏差=转动角速度x传动杆长。
3.轴的径向间隙的计算:轴的径向间隙是指联轴器连接处轴与轴的无间隙连接。
径向间隙的计算公式为:轴的径向间隙=(交联距离-轴的直径)/24.结构材料的承载能力的计算:结构材料的承载能力是指联轴器承受力矩的能力。
结构材料的承载能力的计算公式为:结构材料的承载能力=传动扭矩/密度x断面二阶矩。
以上是机械式万向联轴器的计算方法,接下来我们讨论弹性式万向联轴器的计算。
弹性式万向联轴器的计算需要考虑以下几个参数:传动扭矩、相对角速度、弯曲刚度和材料的强度。
1.传动扭矩的计算:传动扭矩的计算方法与机械式万向联轴器的计算方法相同。
2.相对角速度的计算:相对角速度是指联轴器两端轴的角速度之差。
相对角速度的计算公式为:相对角速度=(被传动轴角速度-传动轴角速度)/传动轴角速度。
3.弯曲刚度的计算:弯曲刚度是指联轴器在受到扭转力矩时的弯曲变形程度。
弯曲刚度的计算公式为:弯曲刚度=(材料的弹性模量x断面二阶矩)/联轴器长度。
4.材料的强度的计算:材料的强度是指联轴器材料能够承受的最大力矩。
万向传动的运动和受力分析

第三节 万向传动的运动和受力分析一、单十字轴万向节传动当十字轴万向节的主动轴与从动轴存在一定夹角α 时,主动轴的角速度ω1与从动轴的角速度ω2之间存在如下关系12212cos sin 1cos ϕααωω-= (4-1)式中,φ1为主动轴转角,定义为万向节主动叉所在平面与万向节主、从动轴所在平面的夹角。
由于cos α是周期为 2π 的周期函数,所以ω2/ω1,也为同周期的周期函数。
当φ1为0、π时,ω2达最大值ω2max 。
且为ω1/cos α; 当φ1为 π/2、3π/2时, ω2有最小值ω2min 。
且为ω1 cos α。
因此,当主动轴以等角速度转动时,从动轴时快时慢,此即为普通十字轴万向节传动的不等速性。
十字轴万向节传动的不等速性可用转速不均匀系数 k 来表示 ααωωωtan sin 1min 2max 2=-=k (4-2) 如不计万向节的摩擦损失,主动轴转矩T 1和从动轴转矩T 2与各自相应的角速度有关系式T 1ω1= T 2ω2,这样有 11222cos cos sin 1T T αϕα-= (4-3) 显然,当ω2/ω1最小时,从动轴上的转矩为最大T 2max =T 1/cos α;当ω2/ω1最大时, 从动轴上的转矩为最小T 2min =T 1cos α。
当T l 与α一定时,T 2在其最大值与最小值之间每一转变化两次;具有夹角 α 的十字轴万向节,仅在主动轴驱动转矩和从动轴反转矩的作用下是不能平衡的。
这是因为这两个转矩作用在不同的平面内,在不计万向节惯性力矩时,它们的矢量互成一角度而不能自行封闭,此时在万向节上必然还作用有另外的力偶矩。
从万向节叉与十字轴之间的约束关系分析可知,主动叉对十字轴的作用力偶矩,除主动轴驱动转矩T l ,之外,还有作用在主动叉平面的弯曲力偶矩T l′。
同理,从动叉对十字轴也作用有从动轴反转矩T2和作用在从动叉平面的弯曲力偶矩T2′。
在这四个力矩作用下,使十字轴万向节得以平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
万向传动轴径向全跳动计算
万向传动轴是一种常见的机械传动装置,用于将动力从一个位置传递到另一个位置。
它通常由两个万向节和一根轴组成,可以在不同的角度和位置上传递扭矩。
在传动轴的运行过程中,径向全跳动是一个重要的参数。
径向全跳动是指万向传动轴在转动过程中,两个万向节之间的径向距离的变化。
这种跳动会对传动轴的运行稳定性和传动效率产生影响,因此需要进行准确的计算和分析。
要计算万向传动轴的径向全跳动,我们首先需要了解万向节的结构和工作原理。
万向节通常由两个十字形的轴头和一个十字形的中心轴组成。
当传动轴转动时,轴头和中心轴之间会产生一定的相对角度,从而引起径向距离的变化。
为了准确计算万向传动轴的径向全跳动,我们需要确定一些关键参数。
首先是万向节的角度范围,即两个轴头之间可以扭转的最大角度。
其次是轴头的尺寸和形状,这会影响径向全跳动的大小和特性。
还需要考虑传动轴的转速和扭矩,以及传动轴的工作环境和使用条件。
根据这些参数,我们可以进行径向全跳动的计算。
一种常用的计算方法是基于几何关系和角度的变化。
首先,我们可以利用几何关系确定轴头之间的初始径向距离。
然后,根据转动角度和轴头的尺寸,
计算出转动过程中径向距离的变化量。
最后,将初始径向距离和变化量相加,得到最终的径向全跳动。
除了几何计算,还可以使用数值模拟和计算机辅助设计软件进行径向全跳动的分析。
这些方法可以更准确地模拟和预测传动轴的运行情况,以及不同参数对径向全跳动的影响。
通过这些分析,我们可以优化传动轴的设计和参数选择,使其在工作过程中具有更好的性能和稳定性。
在实际应用中,径向全跳动的控制是非常重要的。
过大的跳动会导致传动轴的不稳定性和振动,甚至可能导致传动系统的故障。
因此,在设计和制造传动轴时,需要合理选择材料、加工工艺和装配精度,以控制径向全跳动的大小和变化范围。
万向传动轴径向全跳动的计算是传动系统设计和分析的重要内容。
通过准确计算和分析,可以优化传动轴的设计和参数选择,提高传动效率和稳定性。
在实际应用中,需要合理控制径向全跳动的大小,以确保传动系统的正常运行和长寿命。
